胥文泉，施龙飞，肖顺平
(国防科技大学电子信息系统复杂电磁环境效应国家重点实验室， 湖南长沙 410073)
摘 要：雷达主瓣压制干扰具有接收功率大、时-频-空域难以分离的特点，是雷达探测的重要威胁。已有文献提出基于极化-空间谱特征从主瓣干扰中检测目标的方法，但在主瓣多紧邻干扰、变极化干扰等情况下误判率难以忍受。针对这一问题提出了基于雷达发射极化均匀相位分集，利用到达信号极化散度特征和极化分布特征进行联合判别的方法，能够有效降低主瓣多紧邻干扰、变极化干扰背景下的误判率。理论分析和仿真结果均表明了该检测方法的良好性能。
关键词：主瓣干扰； 极化-空间联合谱； 均匀相位分集； 目标检测
主瓣干扰从雷达主瓣进入雷达接收机，接收增益大，易形成主瓣压制干扰，严重影响雷达的探测性能。针对主瓣干扰，传统的时域、频域和空域抗干扰措施均难以取得理想效果。时域自适应抗干扰利用干扰与目标之间可预测的区别实现干扰抑制，但对多个窄带信号或时变干扰，算法性能下降很大[1]。频率捷变与分集能对主瓣有源干扰进行频率躲避，但需要雷达捷变带宽大于干扰带宽[2]。自适应波束形成能在一定程度上从空域实现干扰抑制，但若干扰位于主瓣3 dB波束内，其性能将严重下降[3]。
极化域作为时域、频域、空域的重要补充，利用干扰信号与目标回波信号在极化域的差异，往往能获得独特的抗干扰效果[4]。因此极化滤波已成为对抗主瓣干扰的有效手段之一，现已提出的极化滤波器有APC迭代滤波算法[5]、快速自适应极化滤波器[6]、零相移极化滤波器[7]等。但是上述极化滤波器对于干扰的极化度要求较高，对主瓣内同时存在两个及以上干扰的情况性能较差。
国防科学技术大学的施龙飞等针对主瓣多点源干扰另辟蹊径，放弃基于干扰能量抑制的传统滤波思路，利用有源干扰与目标在极化散射特性响应方面的差异，基于雷达发射极化分集体制，利用极化-空间谱图像上谱峰极化散度特征的差异鉴别目标和干扰。但该方法在主瓣多紧邻干扰、变极化干扰等情况下易出现“虚警”。本文在此基础上，进一步提取目标回波极化的分布特征进行联合判别检测，仿真分析了改进方法的检测性能，验证了本文方法的有效性和稳定性。
极化-空间谱估计是基于极化敏感阵列对信号的极化状态、空间到达方向进行联合估计，目前研究主要围绕极化MUSIC算法展开[8]，下面简要介绍极化MUSIC方法信号模型。
设一包含M个双正交偶极子对的均匀线阵，现有K(K<M)个窄带信源到达该阵列，则阵列的接收信号响应表示为
(1)
式中，ak为第k个信号的极化-空间联合导向矢量，a=as⊗ap,as为空间导向矢量，ap为极化导向矢量，⊗为kronecker积，sk(t)为第k个信号源的时域复包络，N(t)为高斯白噪声矩阵。由式(1)可得阵列协方差矩阵：
Rx=E[X(t)XH(t)]
(2)
对Rx作特征分解，在信源数准确估计基础上，利用最小的2M-K-1个特征值对应的特征向量构成噪声子空间UN，利用噪声子空间和信号子空间的正交性构成如下极化空间谱，可实现对信号波达方向和极化参数的估计，如下式所示：
(3)
干扰信号、目标回波均会在上述联合谱Pmusic上呈现峰值，基于联合谱特征的目标检测方法是利用干扰谱峰与目标谱峰的差异从干扰、噪声背景中判别目标，实现目标检测，其利用的主要特征差异是目标回波极化随发射极化变化而有源干扰信号极化状态与其无关，实现方法是：雷达发射极化分集(设分集数为N)，对N组信号极化-空间联合谱Pmusic的幅度谱进行叠加得到合成谱P(如式(4)所示)，利用合成谱图像中目标在相同方位角、俯仰角上极化状态变化而呈现出的“直线特征”进行检测，如图1所示。
(4)
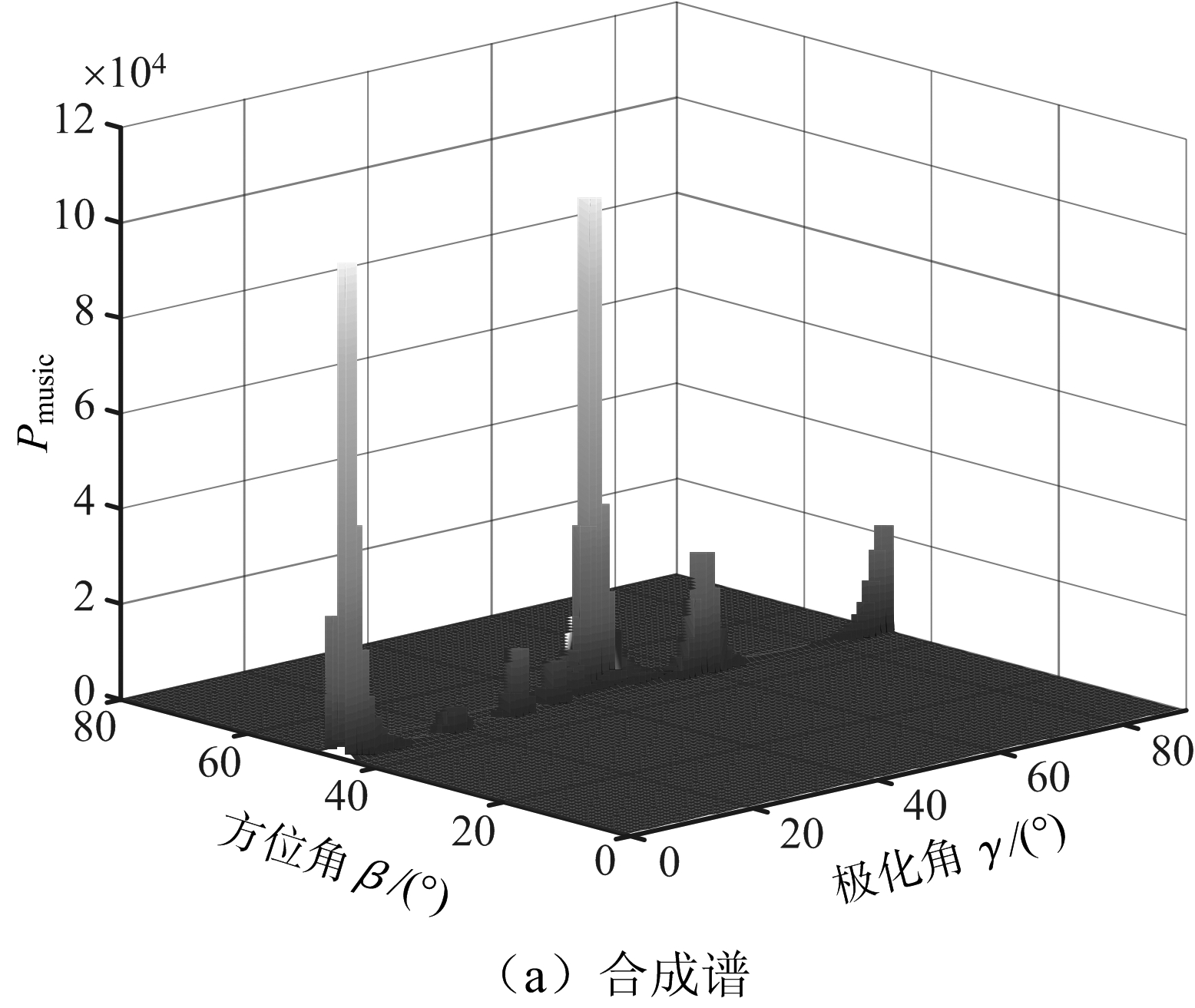
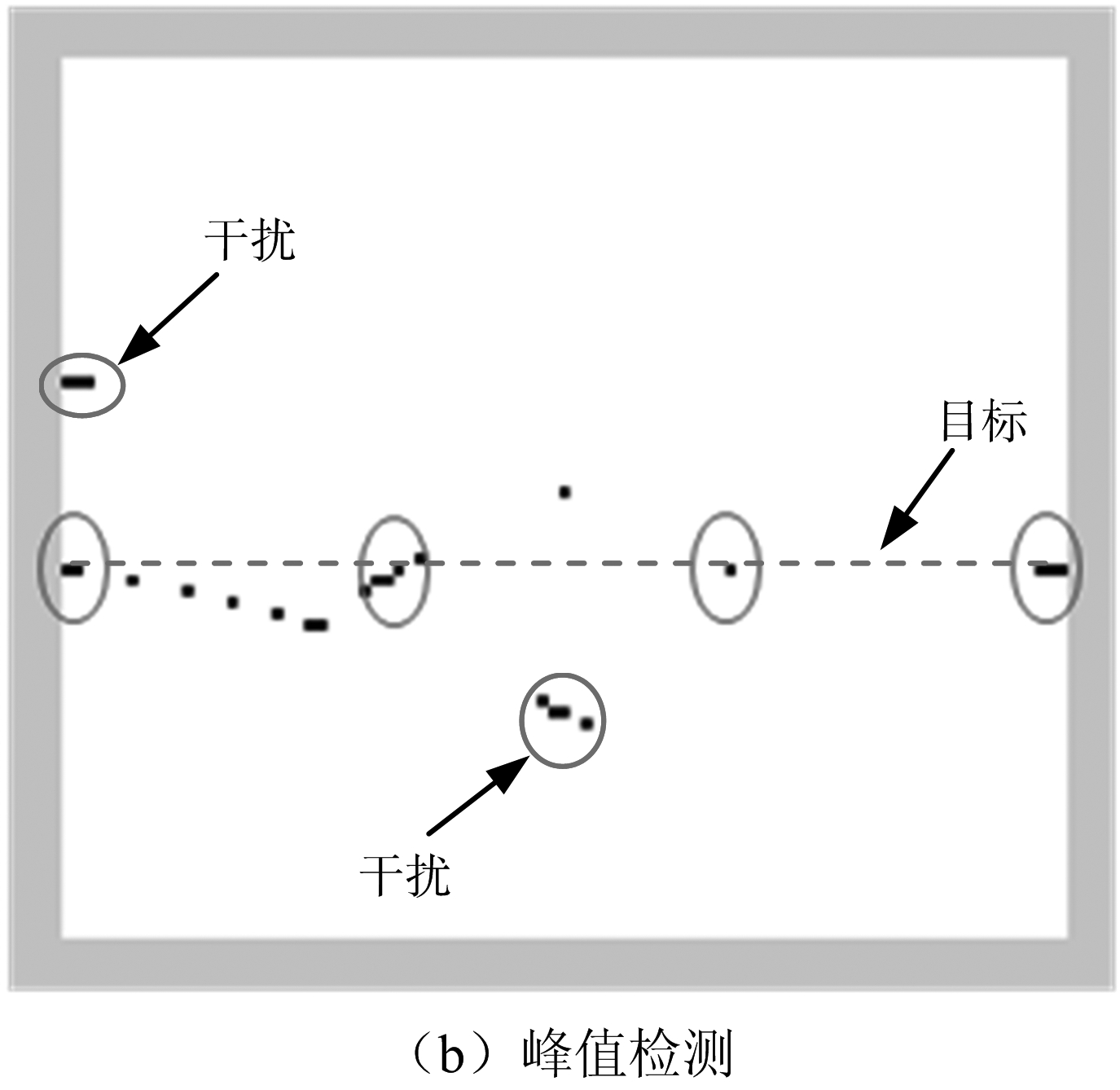
图1 发射极化分集体制下合成谱及其峰值检测效果
(1个目标、2个干扰；发射极化分集数为4)
1.2节阐述了基于极化-空间谱特征的目标检测方法的基本原理，更进一步地，该方法是在方位-俯仰的角度空间划分网格，对落入同一网格的谱峰统计“极化状态标准差”(描述极化散度特征)，高于门限的判定为目标，否则判为干扰。
然而，仅凭“极化状态标准差”检测统计量易导致误判，如主瓣存在多个干扰(主瓣多点源干扰)且处于相同方位-俯仰网格时，或主瓣存在变极化干扰情况，都会对检测性能带来很大影响。因此，本文拟对其进行改进，在利用极化散度特征的基础上，进一步利用“极化分布特征”提升检测性能。
本文提出一种综合利用极化散度特征、极化分布特征的双重特征检测方法。设H0假设为存在目标，H1假设为不存在目标，本文方法的主要步骤(如图2所示)如下：
步骤1：雷达发射N组不同极化状态信号，对N组接收信号分别生成极化-空间MUSIC谱，并叠加得到合成谱；
步骤2：对合成谱进行谱峰检测、点迹合并，统计各谱峰所对应的到达方向(方位角、俯仰角)和极化角；
步骤3：找出同一到达方向(方位角、俯仰角)上存在多谱峰的“疑似目标”，并计算极化状态标准差，大于某一门限值则进行确认检测(步骤4)，否则判为H0；
步骤4：利用相邻两组回波极化角之差的标准差(称为“极化状态距离标准差”)作为判决量，小于某一门限值判定为目标，即H1，否则判为H0。
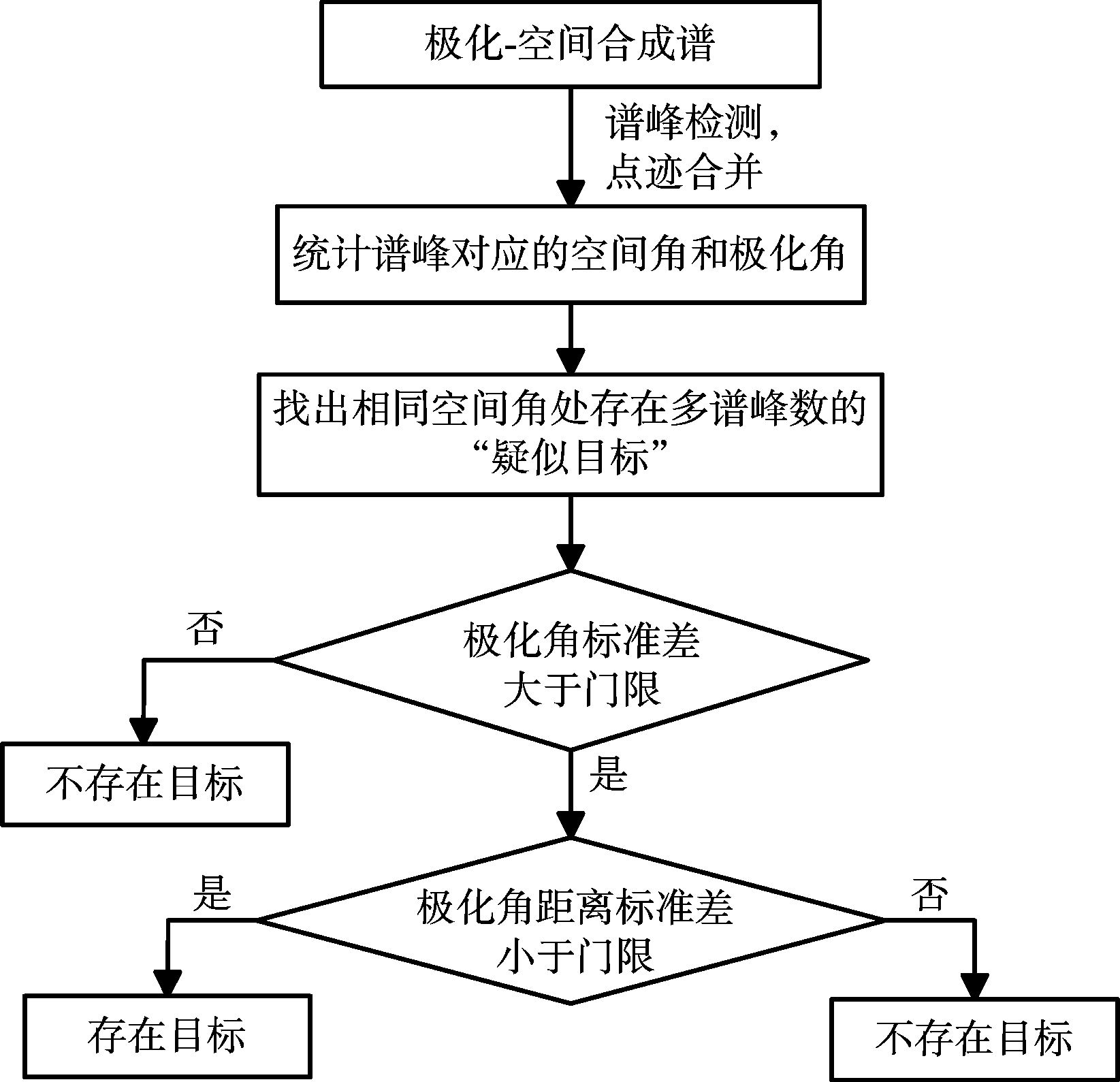
图2 改进目标检测方法基本流程
下面分别给出上述步骤3、步骤4的两个检测判决量——极化状态标准差和极化状态距离标准差。
设雷达发射极化为tanγt(n)ejηt(n)(n=1,…,N，N为发射极化分集数目)，对应的信号回波极化为tanγr(n)ejηr(n)。考虑η角的极化散度，其极化状态标准差定义为
(5)
式中，N为一次极化分集中的分集数目，
为一次分集中N组回波信号极化η角的均值。
极化状态距离标准差表征极化分布特性，下式为针对回波极化η角的极化状态距离标准差，表征了发射极化激励下目标回波相邻极化状态距离的起伏情况：
(6)
式中，Δηr(n)=ηr(n+1)-ηr(n)，n=1,…,N-1，N为发射极化分集数目，
为一次分集中Δηr的均值。
考虑到发射极化相位分集方式既保证了雷达威力，又易于工程实现，本文采用发射极化相位分集方式。
根据前述分析，2.1节中新引入的极化状态距离标准差特征量主要是为了降低主瓣多点源干扰或主瓣变极化干扰等情况下的“虚警”。为使目标回波极化状态距离起伏较缓，以更好地区分于干扰，雷达发射极化应采用均匀相位分集方式(具体论述见本节分析)。本节以此为出发点，研究目标极化散射矩阵特性对极化状态距离标准差特征量检测的影响，进而设计检测门限。
雷达目标回波极化状态与雷达发射极化、目标极化散射矩阵之间的关系如下：
(7)
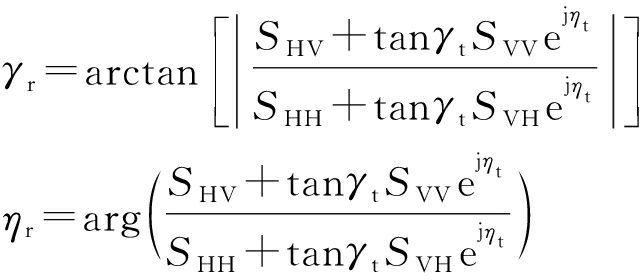
(8)
式中，下标t,r分别表示发射和接收，下标H,V分别表示水平极化和垂直极化，|·|表示取幅值运算，arg()表示取相位运算。考虑到雷达天线的互易性，本文的分析中均假设SHV=SVH。
首先，考虑目标极化散射矩阵交叉极化分量可忽略不计的情况。为分析方便，假设SHV=SVH=0，且令
当雷达发射极化采用均匀相位分集方式时，即
(n=1,…,N，N为极化分集数)时，由式(8)，其对应的目标回波极化η角为ηr(n)=ηt(n)+φ1，目标回波极化η角的极化状态距离标准差的数学期望为
E[STD(Δηr)]=E[STD(Δηt)]=0
(9)
由式(9)可以看出，在目标交叉极化分量可以忽略的情况下，当雷达发射极化采用均匀相位分集方式时，目标回波极化状态距离标准差趋近0。那么结合检测步骤4可知，利用极化状态距离标准差能够较好地鉴别目标与干扰。
其次，考虑目标极化散射矩阵交叉极化分量不可忽略时目标极化状态距离标准差的变化情况，并在此基础上设计该检测量的判决门限。
为分析简便，假设归一化后的目标散射矩阵写为
雷达发射极化为均匀相位分集时目标回波极化相位角及回波极化状态距离标准差分别为
(10)
STD(Δηr)=
(11)
定义目标散射矩阵交叉极化分量与共极化分量的幅度比例系数为
为得到检测判决门限，图3示出了分集数N=4时，回波极化状态距离标准差最大值max[STD(Δηr)](通过遍历φ1，φ2仿真计算得到)随ρ1和R的变化图，图中“▲”标记处为max[STD(Δηr)]中的最大值。由图3可以看出，不同ρ1，R(或ρ2)情况下max[STD(Δηr)]均不同，总体来看，max[STD(Δηr)] 随共极化分量的差异增大而增大，随交叉极化分量的相对值增大而增大。
需说明的是，考虑到大多数雷达目标共极化分量强度相当，交叉极化分量相对较弱，图3中两坐标范围设为0.2≤ρ1≤5和
(即交叉极化分量不超过-20 dB)。本文即以这一范围为前提，将图3中的纵坐标最大值作为极化状态距离标准差检测统计量的判定门限。
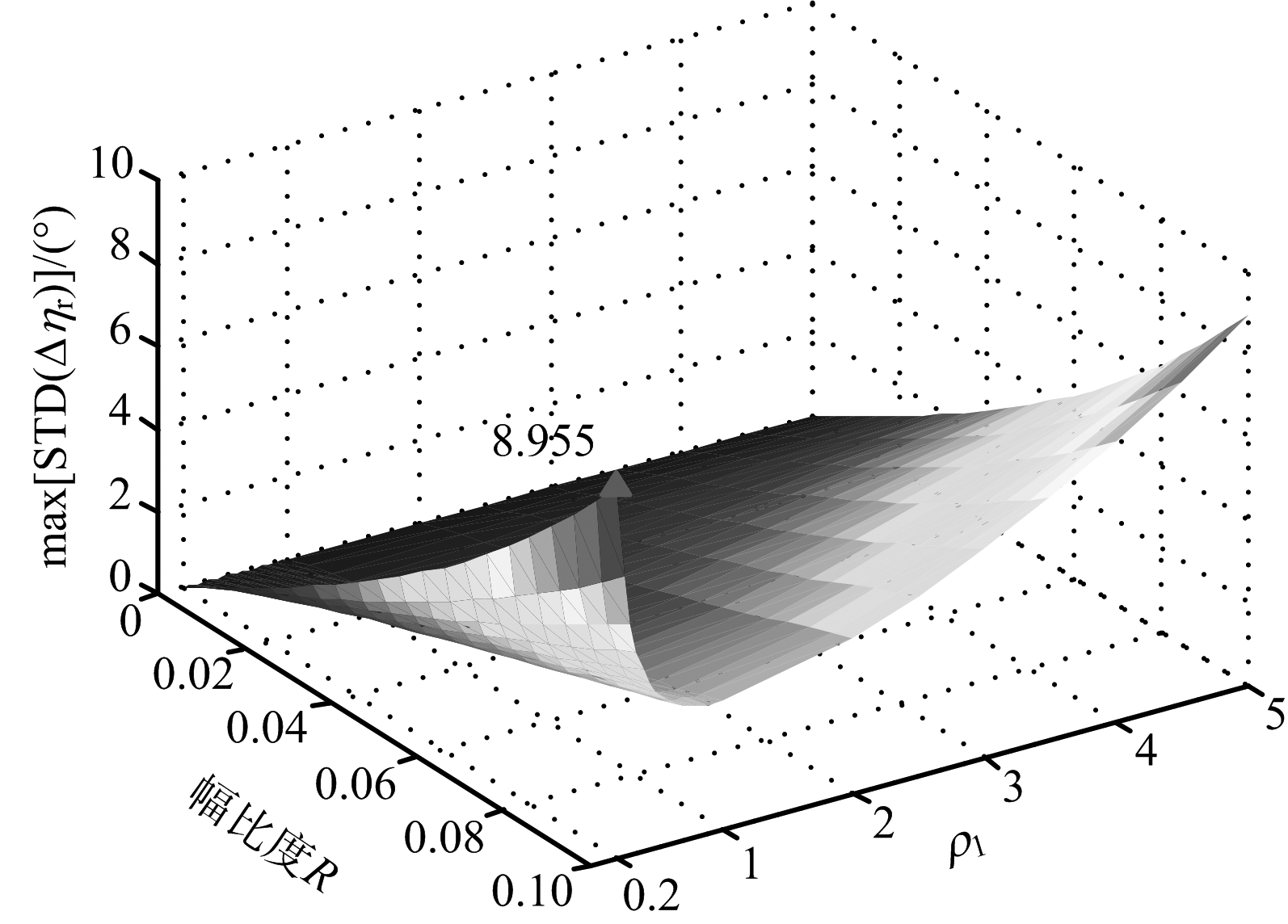
图3 max[STD(Δηr)]随ρ1，R的变化
(x轴为共极化分量幅度比ρ1，y轴为交叉极化分量与共极化分量幅度之比R，z轴为STD(Δηr)的最大值；相位分集数为4)
为验证本文目标检测方法的有效性，进行了Matlab仿真实验。极化敏感阵列流型为10元均匀线阵，阵元间距d=λ/2。由于阵列为线阵，对空间角只有一维分辨能力，仿真中固定各信源的俯仰角为0°，只考虑方位角。雷达主瓣宽度为5°，信噪比为20 dB。雷达采用分时发射极化体制，极化分集方式同第2节，极化相位描述子分别为(45°,0°)，(45°,30°)，(45°,60°)，(45°,90°)。取雷达发射极化相邻极化距离之差的二分之一为极化状态标准差的门限，即
取2.2节分析中STD(Δηr)最大值为极化状态距离标准差的门限，即T[STD(Δηr)]=8.955°。目标极化散射矩阵为
均服从[0,2π)的均匀分布。蒙特卡洛仿真次数为1 000次。
首先，检验2.2节中判决门限设置的合理性。
仿真1：雷达主瓣内设置一个目标信号、3个紧邻干扰(干扰1、干扰2、干扰3)和一个变极化干扰(干扰4)，各信源具体参数如表1所示。图4给出了不同ρ1，ρ2情况下，各方位角检测单元的极化状态距离标准差在多次蒙特卡洛仿真中的统计结果，并与门限进行对比。由图4可以看出，在不同ρ1，ρ2情况下目标回波STD(Δηr)均在门限值以下，紧邻干扰所在的方位角检测单元中STD(Δηr)均大于门限值，而变极化干扰绝大多数情况下其STD(Δηr)更大。综合以上分析，该门限的设置能较好地区分鉴别目标和干扰。
表1 各信源空间方位和极化状态参数
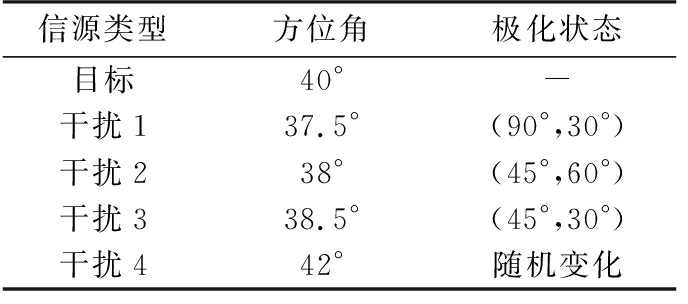
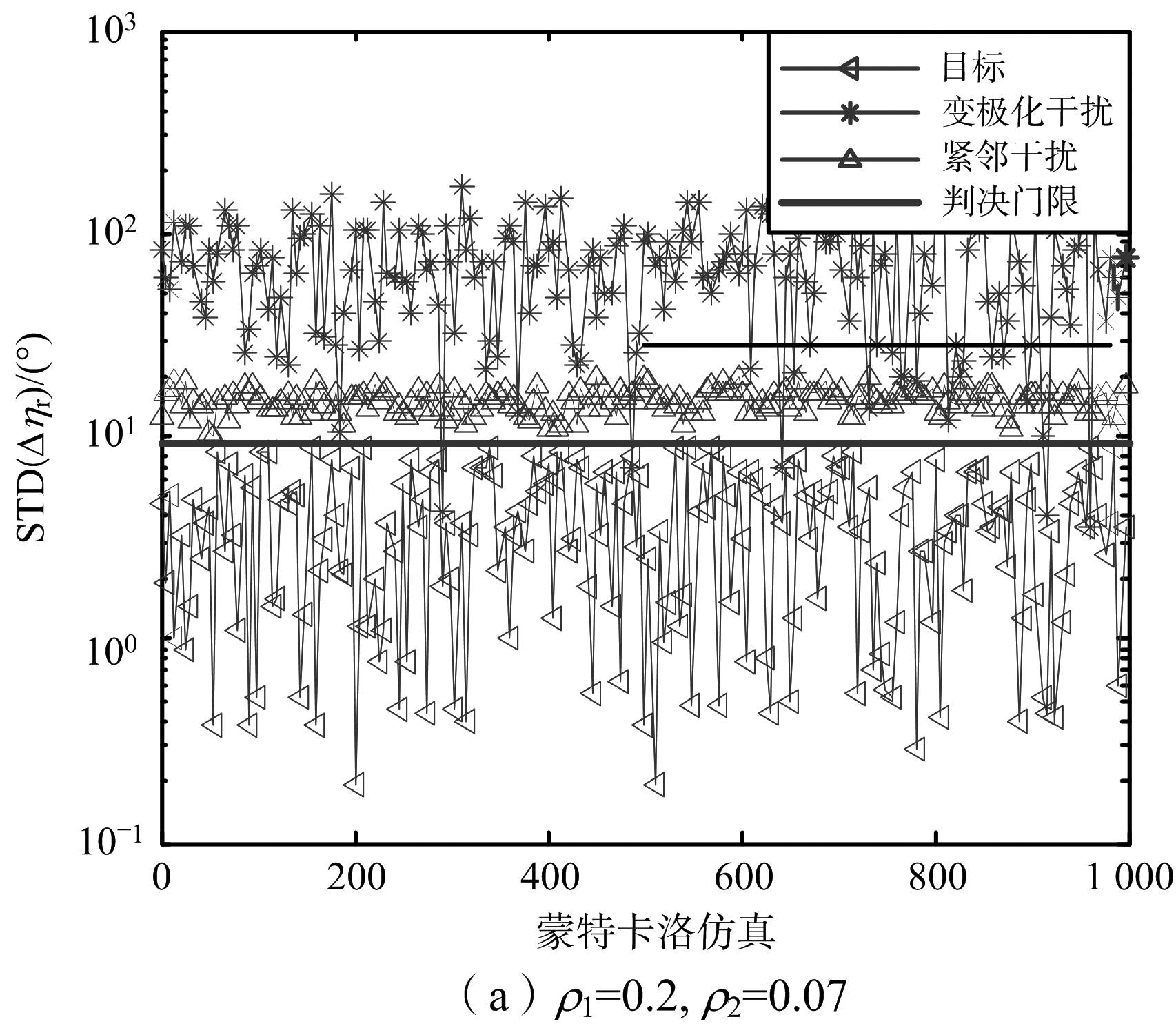
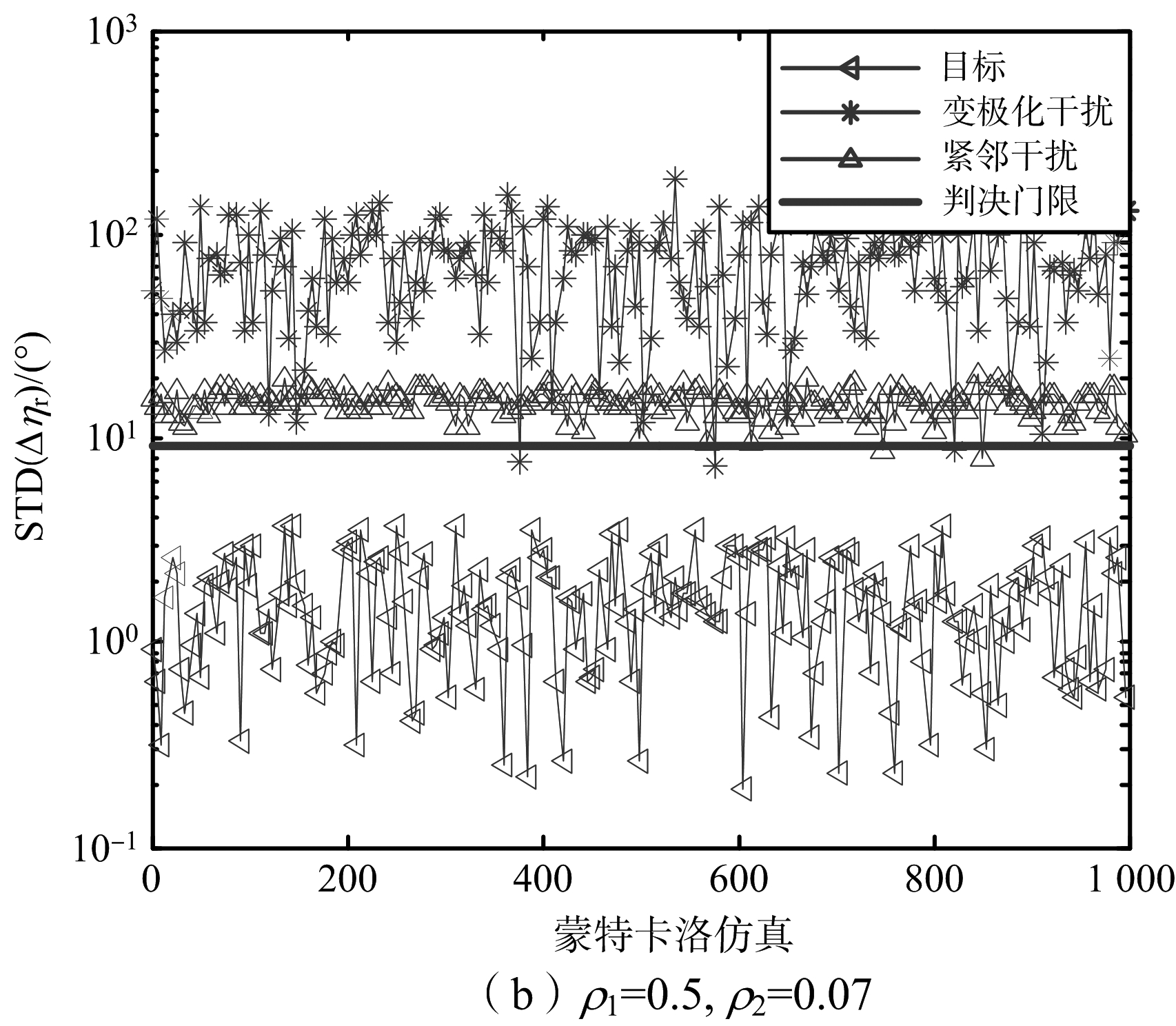
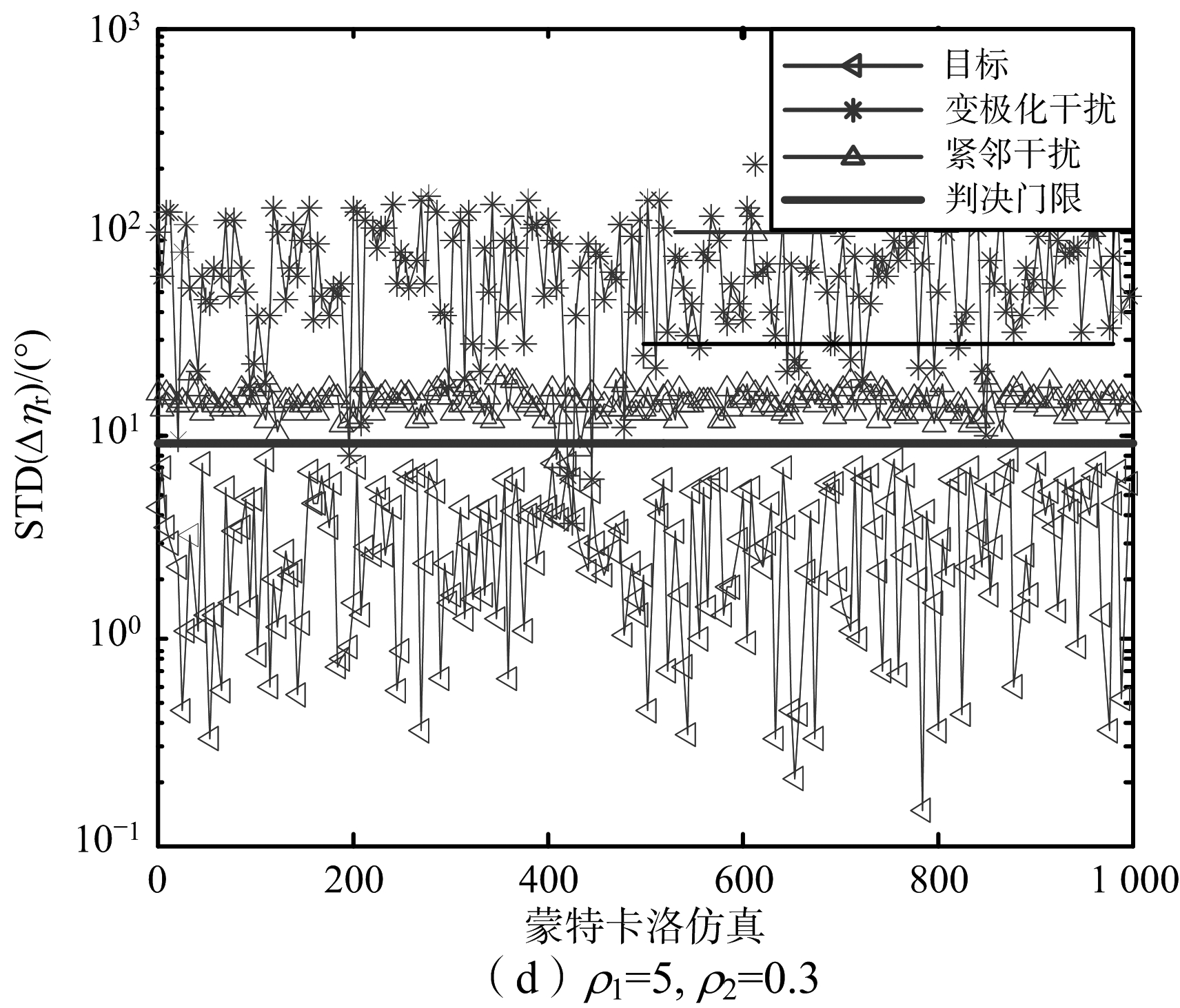
图4 目标/干扰极化状态距离标准差对比
其次，验证本文提出的改进检测方法在主瓣紧邻干扰、变极化干扰情形中对目标的检测性能。蒙特卡洛仿真统计该方法的检测成功概率和误判率，并与原有目标检测方法进行比较。其中，检测成功概率为在目标真实角度检测出目标次数与蒙特卡洛仿真次数之比；误判率为在非目标方向单元中检测出目标次数与蒙特卡洛仿真次数之比。
仿真2：主瓣内设置3个干扰和一个目标，干扰均为噪声压制干扰，且功率相等。干扰的方位角分别为37.5°，38°，38.5°，极化状态分别为(45°,30°)，(45°,60°)，(0°,30°)。目标方位角为40°，散射矩阵中ρ1=1.5，ρ2=0.1。图5分别给出了原有目标检测方法及本文中改进检测方法的检测成功率和误判率随干信比的变化曲线。
由图5(a)可以看出，改进检测方法对目标的检测成功率略低于原有检测方法，但总体检测成功率仍保持较高。由图5(b)可以看出，当主瓣内存在3个紧邻干扰时，原有检测方法的误判率随干信比增大而增大，干信比为30 dB时，误判率达到50%，而改进检测方法的误判率几乎为零。这是因为方位角较近的多个干扰谱峰之间互相影响，且随着干信比增大这种影响不断增大，多个干扰的谱峰可能落入同一空间角网格，形成“疑似目标”。当这些干扰的极化差异较大时，“疑似目标”的极化散度特征明显，在原有检测方法中易被判定为目标，造成误判。而改进检测方法通过极化分布特征的鉴别可滤除这些“疑似目标”，降低检测误判率。
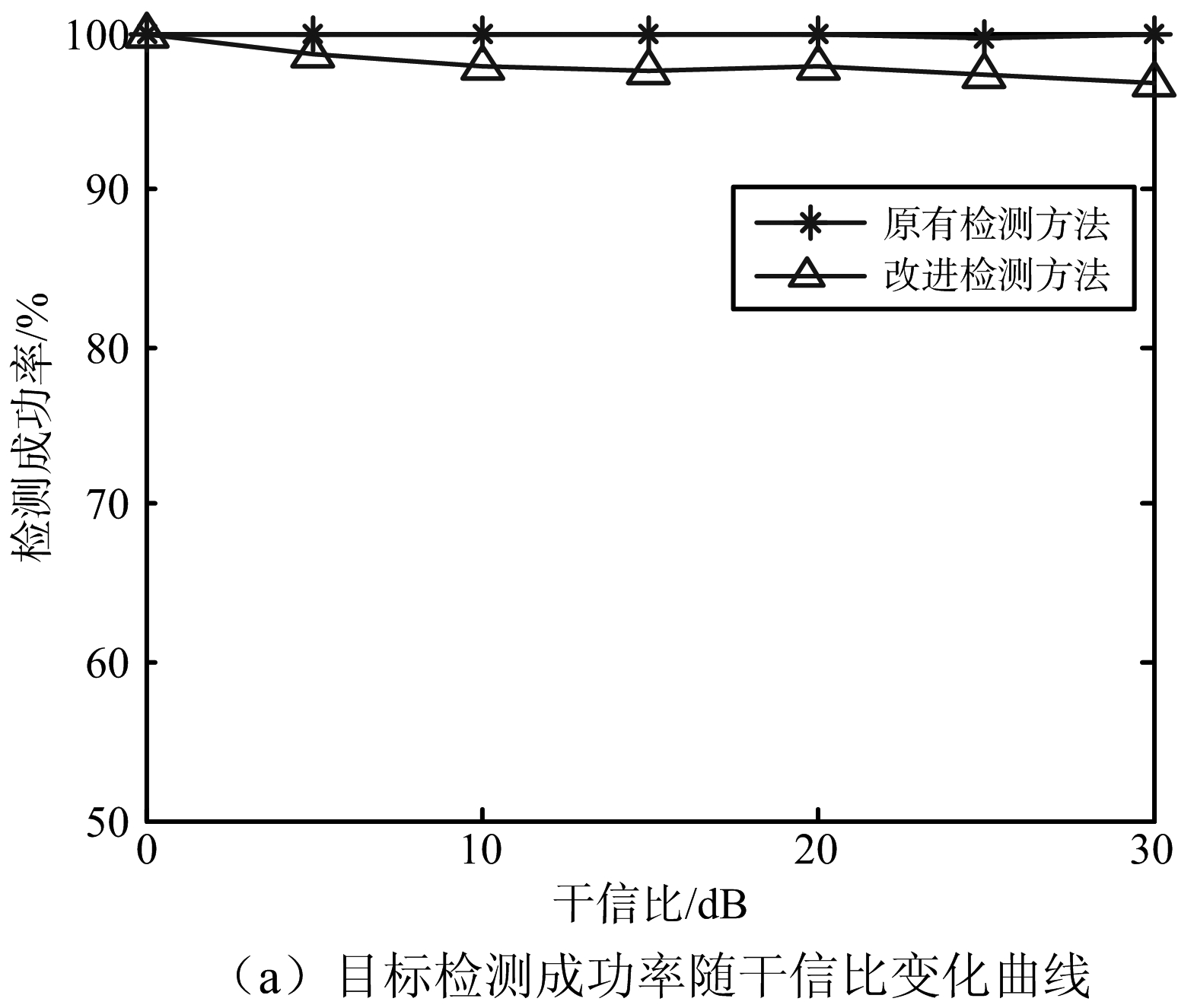
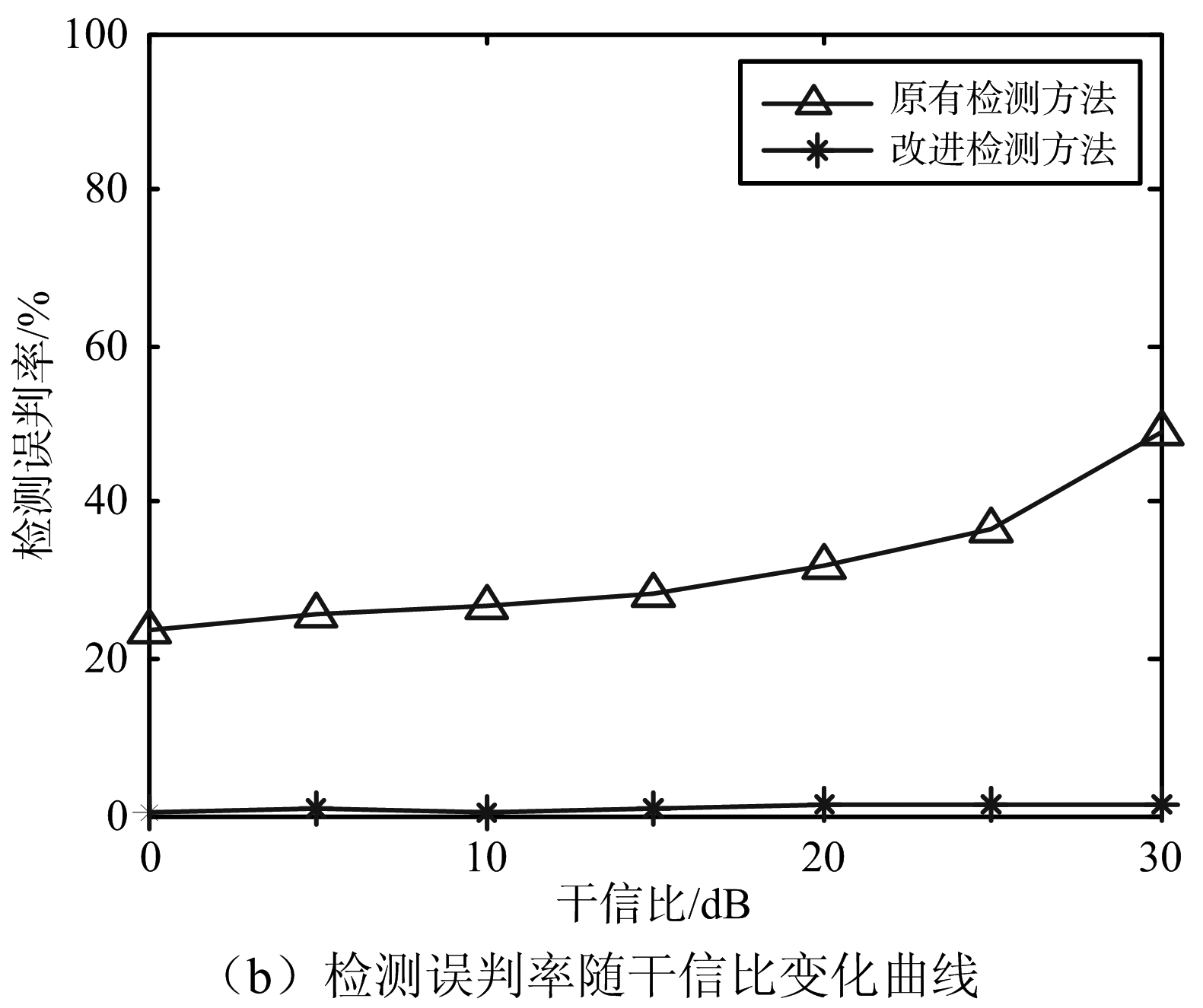
图5 多紧邻干扰情形检测性能对比分析
仿真3：主瓣内设置一个变极化干扰和一个目标，其中变极化干扰的方位角为38°，极化状态为随机变化，目标参数设置同仿真2。图6分别给出了原有目标检测方法及本文中改进检测方法的检测成功率和检测误判率随干信比的变化曲线。
在变极化干扰情形中，由图6(a)可以看出，两种检测方法对目标均能保持较高的检测成功率。由图6(b)可以看出，改进检测方法的误判率较低，接近0，而原有检测方法误判率保持在95%左右，与其目标检测成功概率相当。这是因为变极化干扰的极化状态随机变化，其回波极化散度特征保持稳定，因此原有检测方法几乎无法区分变极化干扰和目标。而干扰极化状态随机变化时，在一次极化分集中呈现等间距分布特征的概率较低，因此在改进检测方法中，利用回波极化分布特征对具备极化散度特征的“假目标”进行确认判别可滤除绝大多数“假目标”，大大降低检测误判概率。
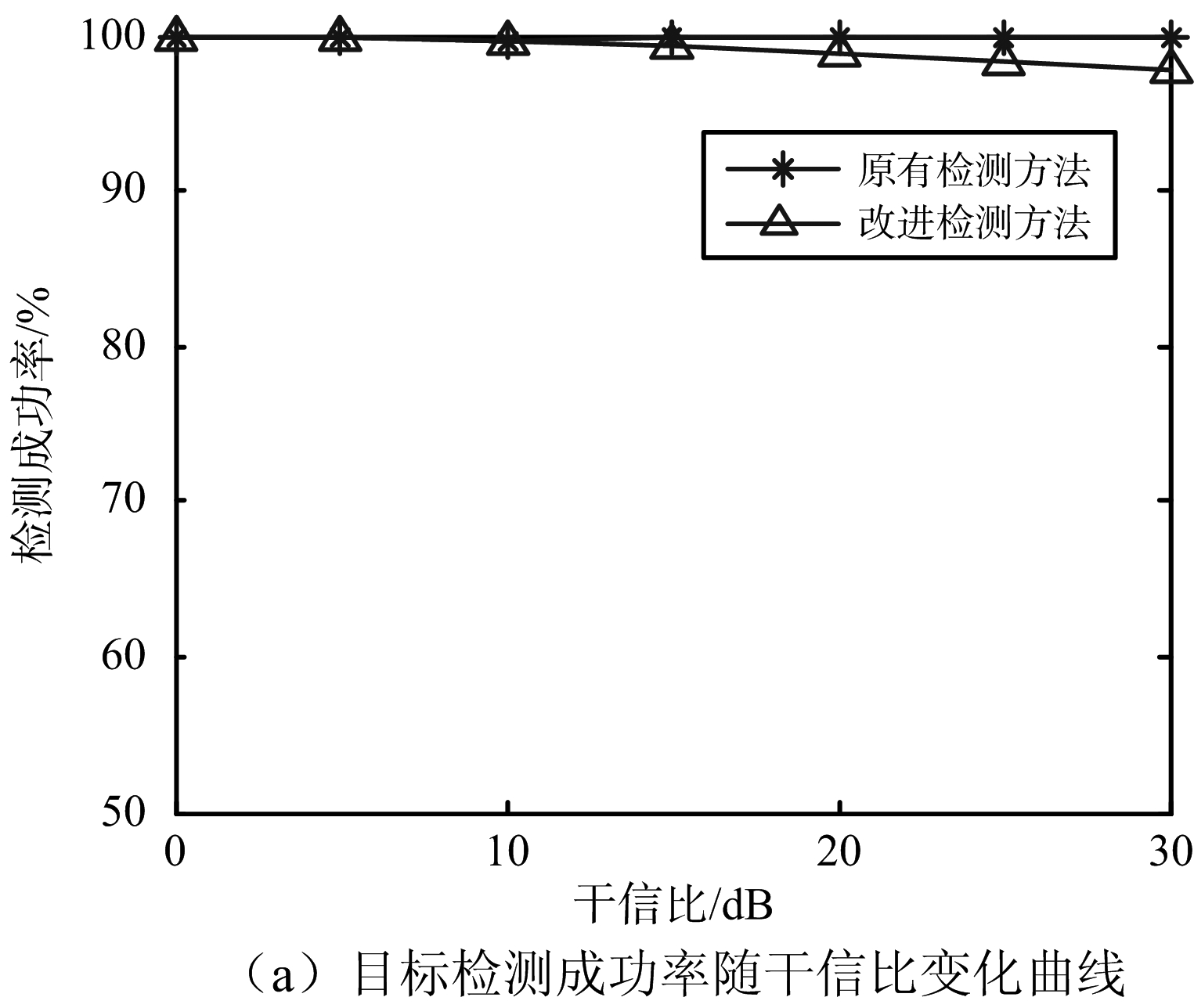
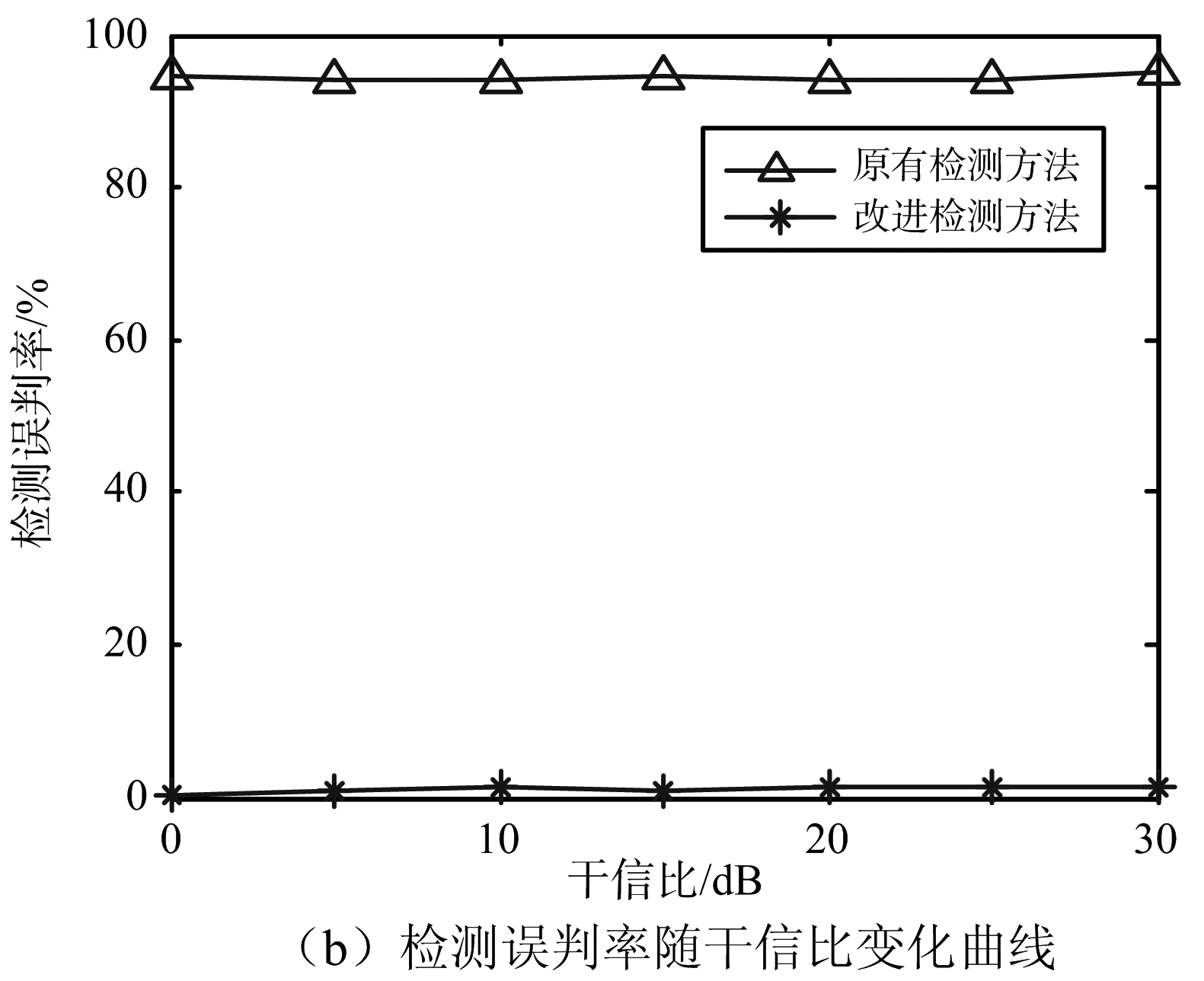
图6 变极化干扰情形检测性能对比分析
本文针对雷达主瓣内存在多点源干扰、变极化干扰等复杂背景，提出了一种改进的基于极化-联合谱估计的目标检测方法。该方法通过利用在极化分集体制下，目标在极化-空间联合谱中谱峰的散度特征和分布特征联合鉴别目标和干扰，能够有效地降低干扰误判为目标的概率。仿真分析证明该方法在主瓣多紧邻干扰及变极化干扰中具有良好的检测性能。
参考文献：
[1] 宗志伟. 弹道中段目标极化雷达识别方法[D]. 长沙: 国防科学技术大学, 2016:52-53.
[2] 冯涛, 王永明, 贺齐辉. 对频率捷变雷达的干扰及效果分析[J]. 电子信息对抗技术, 2015, 30(5):55-58.
[3] 黄颖. 远距支援干扰机阵位设计方法研究[J]. 舰船电子对抗, 2015, 38(2):4-6.
[4] 庄钊文, 肖顺平, 王雪松. 雷达极化信息处理及其应用[M]. 北京:国防工业出版社, 1999:715-716.
[5] 施龙飞, 王雪松, 徐振海, 等. APC迭代滤波算法与性能分析[J]. 电子与信息学报, 2006, 28(9):1560-1564.
[6] 任博, 罗笑冰, 邓方刚, 等. 应用极化聚类中心设计快速自适应极化滤波器[J]. 国防科技大学学报, 2015, 37(4):87-92.
[7] MAO Xingpeng, LIU Yongtan. Null Phase-Shift Polarization Filtering for High-Frequency Radar[J]. IEEE Trans on Aerospace and Electronic System, 2007, 43(4):1397-1408.
[8] 徐振海, 王雪松, 肖顺平, 等. 极化域-空域联合谱估计[J]. 国防科技大学学报, 2004, 26(3):63-67.
XU Wenquan, SHI Longfei, XIAO Shunping
(State Key Laboratory of Complex Electromagnetic Environment Effects on Electronics and Information System,National University of Defense Technology,Changsha410073,China)
Abstract:The barrage interference located in radar mainlobe has the characteristics of large receiving power and the difficulty to separate from the target in time, frequency and special. It is an important threat to radar detection. A method has been proposed to detect targets from mainlobe interference based on polarization-space spectral characteristics. However, when there are multiple adjacent interferences or variable polarization interference, the false alarm rate is unbearable. To solve this problem, a method of joint discrimination based on uniform phase diversity is proposed by using polarization divergence characteristics and polarization distribution characteristic of arrival signal. The theoretical analysis and simulation results show that this method can effectively reduce the misjudgment in the presence of multiple adjacent interference or variable polarization.
Key words:mainlobe interference; polarization-space joint spectrum; uniform phase diversity; target detection
中图分类号：TN973.3
文献标志码：A
文章编号：1672-2337(2018)03-0275-06
DOI:10.3969/j.issn.1672-2337.2018.03.007
收稿日期：2017 08 14；
修回日期：2017 09 05
基金项目：国家自然科学基金重大项目(No.61490690, 61490692)
作者简介：
胥文泉 女，1993年出生于湖南岳阳，硕士研究生，主要研究方向为雷达极化信息处理与抗干扰技术。E-mail: xuwqynl@163.com
施龙飞男，1978年出生于安徽，博士，副研究员，主要研究方向为雷达信号处理、雷达对抗技术。
肖顺平男，1964年出生于江西南昌，博士，教授，主要研究方向为极化信息处理、雷达目标识别。