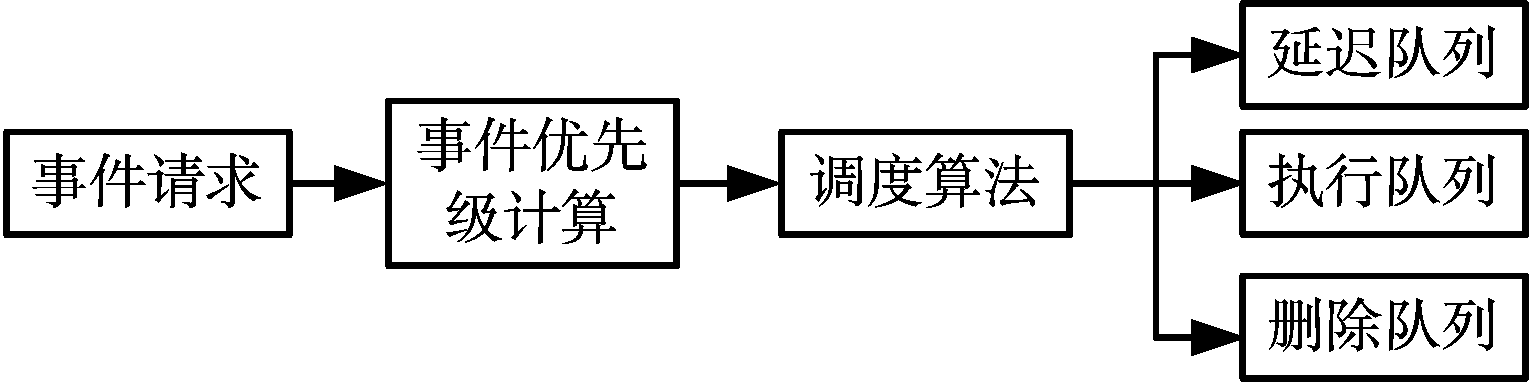
图1 调度流程示意图
段 毅1,2,谭贤四1,曲智国1,王 红1,李向楠2
(1.空军预警学院, 湖北武汉 430019;2.中国人民解放军95174部队, 湖北武汉 430010)
摘 要:针对相控阵雷达事件调度问题中求解目标综合优先级时未考虑事件驻留时间的问题,提出一种基于“价值密度”的相控阵雷达事件调度算法。通过引入作业车间调度领域“价值密度”概念,根据目标属性、运动状态、雷达硬件条件、事件截止期等参数,共同计算雷达完成该事件时单位时间内所能具有的价值,即该事件的价值密度;并基于价值密度进行调度。仿真实验表明,基于价值密度的调度算法与传统基于综合优先级排序调度算法相比,能有效提高调度成功率和实现价值率。
关键词:相控阵雷达; 事件调度; 综合优先级; 驻留时间; 价值密度
相控阵雷达具有波束捷变、天线波束快速扫描、空间功率合成与多波束形成等能力[1],能够完成多目标跟踪、多区域搜索等复杂任务,因此在现代战争中得到广泛运用。但同时大型相控阵雷达跟踪目标数量多、监视区域大,不同任务间存在相互冲突的可能,因此必须选择灵活有效的调度策略发挥相控阵雷达性能,完成作战任务[2]。
目前相控阵雷达调度策略主要有固定模板、多模板、部分模板和自适应调度策略。模板类策略虽然具有设计简单、易于实现、占用资源少等优点,但其调度效率低下,难以适应现代战争需要[3];自适应调度策略由于具有雷达资源利用率高、环境适应力强、可开发性大等优点,在相控阵雷达任务调度中得到广泛应用[4-5]。
在相控阵雷达使用自适应调度策略中,基于综合优先级排序的调度策略具有算法思路简单、易于工程实现、调度成功率相对较高等优点[6-8]。该算法的主要思想是将参与调度的事件按综合优先级由高至低次序依次调度,当产生冲突时对综合优先级较低的事件进行平移或者删除。可见对事件综合优先级判定是该算法的首要任务。
传统的事件综合优先级计算方法仅考虑任务属性,即固定优先级,例如“宙斯盾”设计总师Baugh[9]根据任务特点给出12个优先级,但该类方法自适应能力较差。Liu,Jeffay等[10-11]提出基于事件截止期确定其综合优先级的方法,即抢占式EDF算法与非抢占式EDF算法,但这两种方法未结合目标属性与运动状态;卢建斌等[12]指出事件综合优先级应由目标属性与状态,即工作优先级与事件截止期共同确定,并将其归纳为HPF,MHPF,MEDF,HPEDF四种算法;在此基础上,文献[13-17]分别利用公式法[13]、层次分析法[14]、模糊数学[15]、贝叶斯网络[16]、神经网络[17]等多种方法确定事件优先级。
但这些算法在计算过程中未考虑事件驻留时间,调度过程中部分事件综合优先级较高,但所需雷达资源过多,调度该类事件“性价比”不高。针对这个问题,本文引入作业车间调度领域中“价值密度(Value Density, DV)”概念[18],提出一种基于VD的调度算法:首先通过目标工作优先级与截止期计算事件综合优先级;再根据目标远近、大小、位置以及雷达性能等参数计算事件驻留时间;然后计算雷达探测该批目标时单位时间内所能实现的价值,即该事件的价值密度;最后基于价值密度进行调度。实验结果表明,基于价值密度调度算法能有效提高调度成功率与实现价值率。
雷达中央处理器把下一调度间隔[19](Scheduling Interval, SI)内的所有事件请求提取出来,送入优先级分配网络,经优先级分配网络计算综合优先级后送入调度模块,经调度后生成执行队列、延迟队列、删除队列,其中执行队列送入发射机执行,延迟队列送入下个调度间隔调度,删除队列不予执行。其具体过程如图1所示。

图1 调度流程示意图
相控阵雷达自适应调度算法步骤如下:
Step 1 初始化,调取事件请求序列。
Step 2 对事件请求序列进行排序。
Step 3 提取事件i,判断该事件在时间窗[20]内是否可执行:若判断为真,进入Step 4,反之进入Step 5。
Step 4 选择最接近期望执行时刻的可执行时刻执行该事件。
Step 5 判断该事件是否满足下个调度间隔:若判断为真,将该事件输入至延迟序列,反之输入至删除序列,进入Step 6。
Step 6 令i=i+1,判断是否遍历全部事件,若判断为真,结束调度,反之重返Step 3。
算法框图如图2所示。
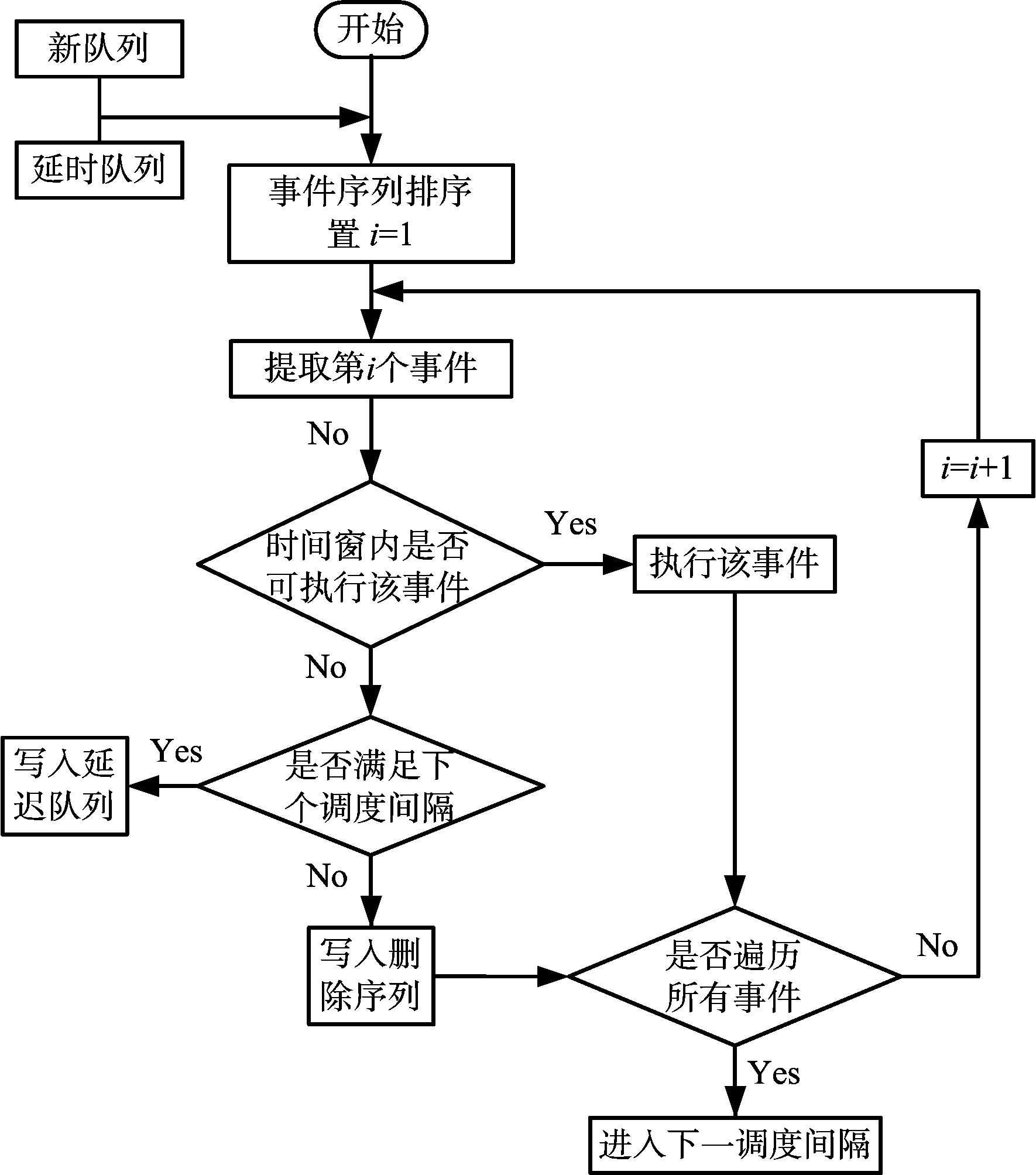
图2 基于事件排序的调度算法
为验证算法效果,前人已提出多项衡量指标,如调度成功率(Scheduling Success Rate, SSR)、时间利用率(Time Utilization Rate, TUR)、时间偏移率(Time Shifting Rate, TSR)、截止期错失率(Deadline Lose Rate, DLR)、实现价值率(Hit Value Rate, HVR)等[6-7,21],本文选用SSR与HVR作为评价指标,其计算方法如下:
(1)
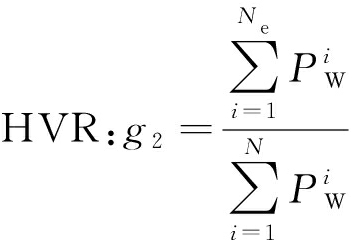
(2)
式中,N为参与调度事件数目,Ne为调度成功事件数目,PW为事件综合优先级。
由文献[12]可知,事件综合优先级由事件工作方式优先级与事件截止期共同决定。本文在此基础上引入“价值密度”概念,考虑事件驻留时长。因此事件的价值密度应由事件的工作方式优先级、截止期、驻留时长共同决定。
事件的工作方式优先级由目标属性决定,且目标属性又包含多种不同因素,本文主要考虑以下几点:目标威胁度、目标速度、目标距离和目标航向。现分别将这些因素映射至同一量纲上,再通过线性加权得出事件综合优先级。
1) 目标威胁度
现代战争中雷达所面对的目标有弹道导弹、临空目标、反辐射导弹、常规飞机、直升机等,依次给出这些目标威胁度优先级参数![]() 其具体值由事先设定得出。
其具体值由事先设定得出。
2) 目标距离
假设目标距离优先级参数随目标距离增大而减小,当距离大于某一门限时其优先级下降为0,则可得目标距离优先级表达式为
(3)
式中,R为目标距离,Rmax为距离门限。
3) 目标速度
设定目标速度优先级参数随着目标速度增大而增大,当速度超过某一门限时,优先级稳定为一常值,则可得目标速度确定的优先级参数表达式为
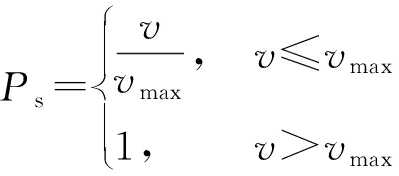
(4)
4) 目标航向
假设飞行器航向与雷达法线方向夹角为α,其中以向站飞行为0°,以背站飞行为180°,则设置目标航向优先级参数为
(5)
根据PT,PR,Ps,PA得事件i工作优先级![]() 为
为![]() 其中λ1,λ2,λ3,λ4为权重系数。
其中λ1,λ2,λ3,λ4为权重系数。
事件综合优先级由事件工作优先级与截止期共同决定,分别可由线性加权、非线性加权、优先级列表[19]等多种方法计算得出。为简化计算,本文选用线性加权法,即
PW=η·Pj+(1-η)·TD
(6)
式中,η为权重参数,TD为事件截止期。
如图3所示,一次完整事件可分为发射阶段、等待阶段、接收阶段,对于非抢占式EDF算法来说,事件一旦开始无法停止(对于采用交错脉冲技术雷达来说,事件等待阶段可以抢占,本文不作考虑)。
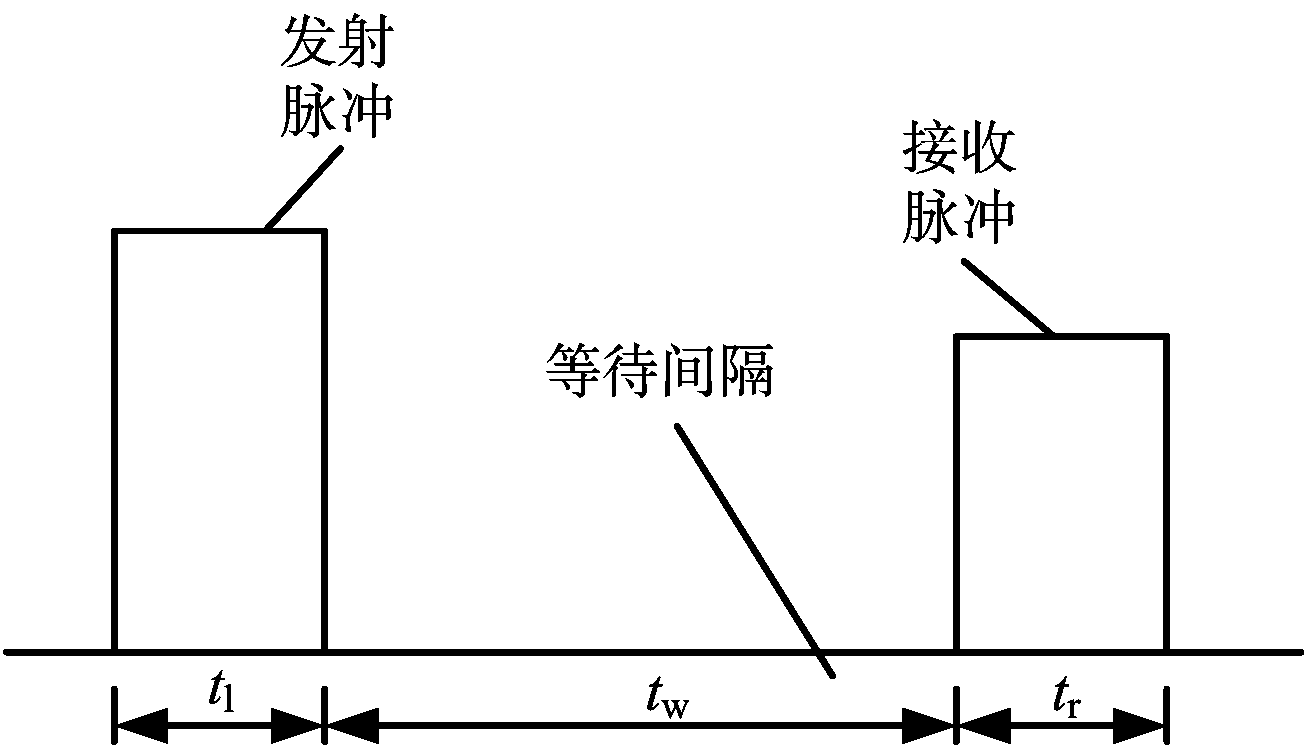
图3 事件驻留时长示意图
由上图可得事件驻留时间tτ计算式为
tτ=tl+tw+tr
(7)
式中,tl为发射脉冲时长,tw为等待间隔,tr为接收脉冲时长。
当目标RCS过小或战场电磁环境较为复杂时,单个脉冲难以实现对目标有效检测。采用多脉冲积累,提高目标回波信号信噪比,进而提升雷达探测性能是解决此类问题最有效的方法手段。其具体过程如图4所示。
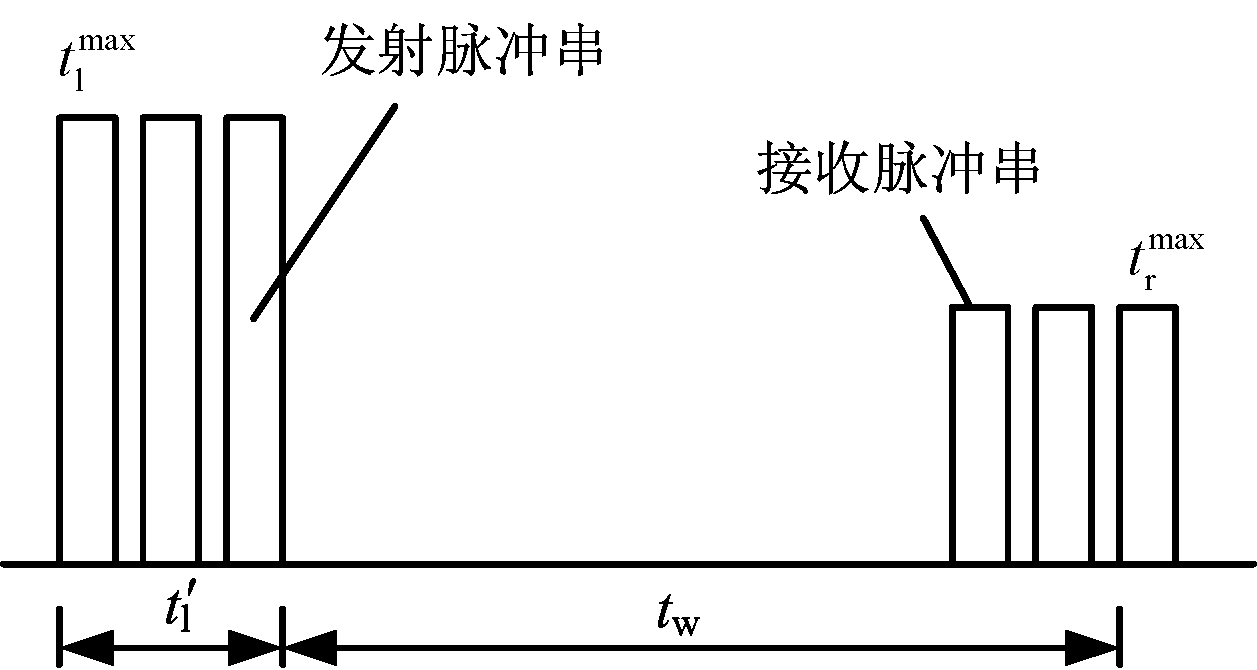
图4 多脉冲雷达事件驻留时长示意图
图4中,![]() 为雷达发射脉冲最大时宽,由发射机硬件条件与雷达能量资源约束决定,相应接收信号最大脉宽为
为雷达发射脉冲最大时宽,由发射机硬件条件与雷达能量资源约束决定,相应接收信号最大脉宽为![]() 则发射脉冲串时长
则发射脉冲串时长![]() 可表示为
可表示为
(8)
式中,DCshort为雷达短期占空比限制,n为脉冲串中脉冲个数,在相参积累时有
(9)
可得多脉冲雷达事件驻留时间tτ为
(10)
1) 发射时长
当雷达正对目标时雷达距离方程为
(11)
式中,R为雷达探测距离,Pt为发射信号峰值功率,Gt为发射天线增益,Ar为接收天线等效面积,σ为目标RCS,tl为发射脉冲宽度,Ls为雷达系统和电磁波传输总损耗,k为玻耳兹曼常数,Te为噪声温度,(S/N)为给定的Pf,Pd条件下检测信噪比。
对于给定雷达来说,式(11)中除目标截面积σ与发射脉冲宽度tl外均为一定值,则式(11)可简写为
R4=Ωσtl
(12)
不妨将Ω称为“雷达参数”。
对于相控阵雷达来说,当目标偏离阵面法线方向时天线等效面积会相应减小,其过程如图5所示。
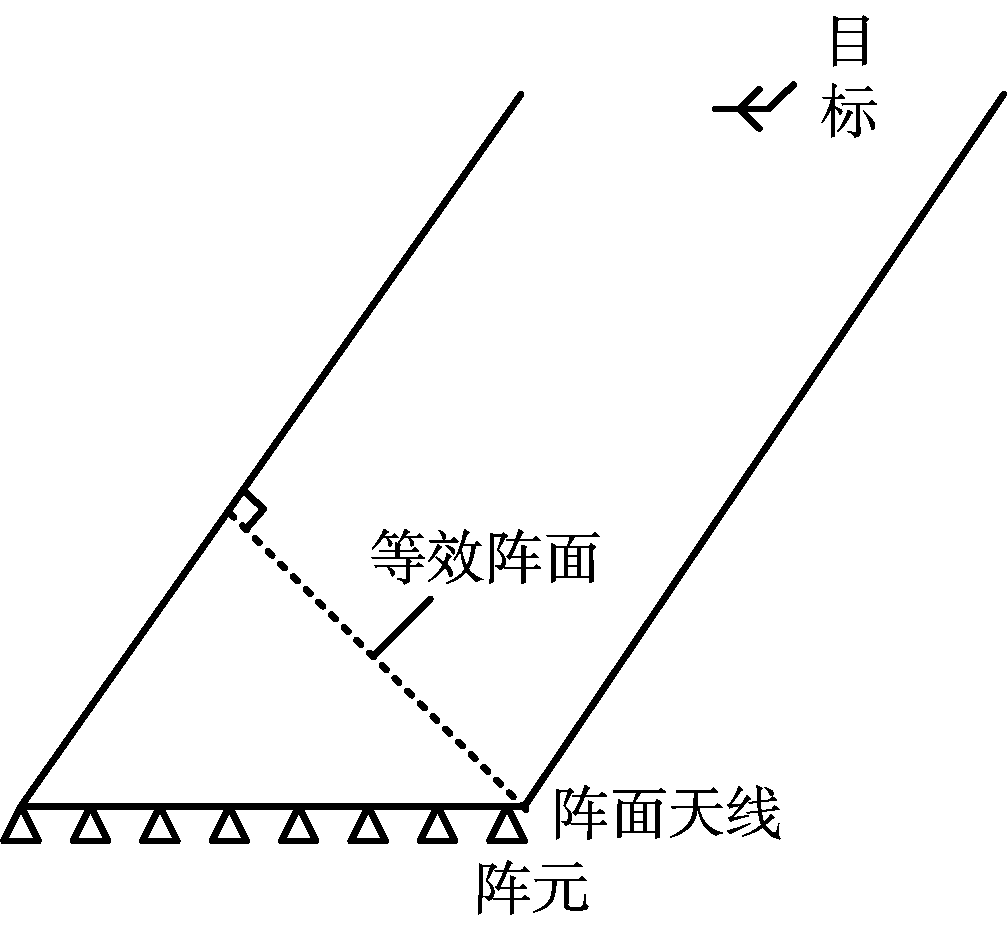
图5 方位角偏离示意图
设雷达观测目标时目标方位角与俯仰角分别为(α,β),则此时雷达发射天线增益与接收天线等效面积为
(13)
代入式(13)可得雷达探测距离为R,RCS为σ,位置为(α,β)的目标时发射阶段时长为
(14)
2) 等待时长
事件中等待时长为电磁脉冲在雷达与目标之间往返所花费的时间,有![]() 式中,R为雷达与目标间距离,c为光速。
式中,R为雷达与目标间距离,c为光速。
3) 接收时长
雷达所接收的回波时长与发射时长成正相关,考虑目标速度时有
(15)
与式(15)类似,在多脉冲情况下有
(16)
式中,v′为目标径向速度,有v′=v·cosα。
由事件综合优先级与驻留时长可得事件价值密度VD为
(17)
现代战争中雷达面临隐身飞机、低慢小目标、反辐射武器等多种威胁。本文针对这些威胁,分别选取B-2隐身飞机、AH-64武装直升机、AGM-88反辐射导弹以及F-15战斗机四种目标,4种目标参数如表1所示。
表1 典型目标参数
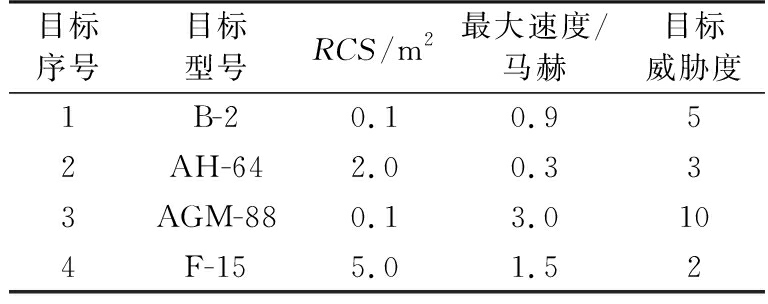
假设某型雷达峰值功率为Pt=1.5 MW,工作频率f0=5.6 GHz,天线增益G=45 dB,噪声温度Te=290 K,噪声系数F=3 dB,雷达损耗L=4 dB,检测门限(S/N)=20 dB。
由式(9)计算得出,雷达参数Ω=908.893,即该雷达对于单位目标(RCS=1 m2),在单位时长内(1 μs)内最大探测距离(法线方向)为908.893 km,为简化计算,下文中取900 km。
1) 战场环境生成
根据4种目标的战术性能与攻击半径,设置4种目标的活动范围与数量,如表2所示。
表2 战场参数
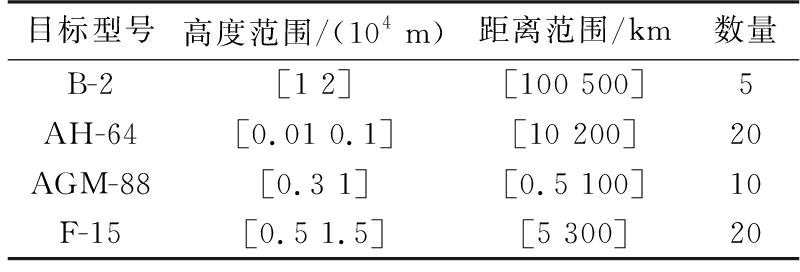
根据表2参数生成战场环境,其中F-15战机速度在[0.5,1.5]马赫内均匀分布,其余3型目标均以最大速度巡航飞行。
建立以雷达为原点,雷达阵面为X轴的战场坐标,如图6所示,且所有目标均位于雷达探测范围内(法线夹角60°范围)。
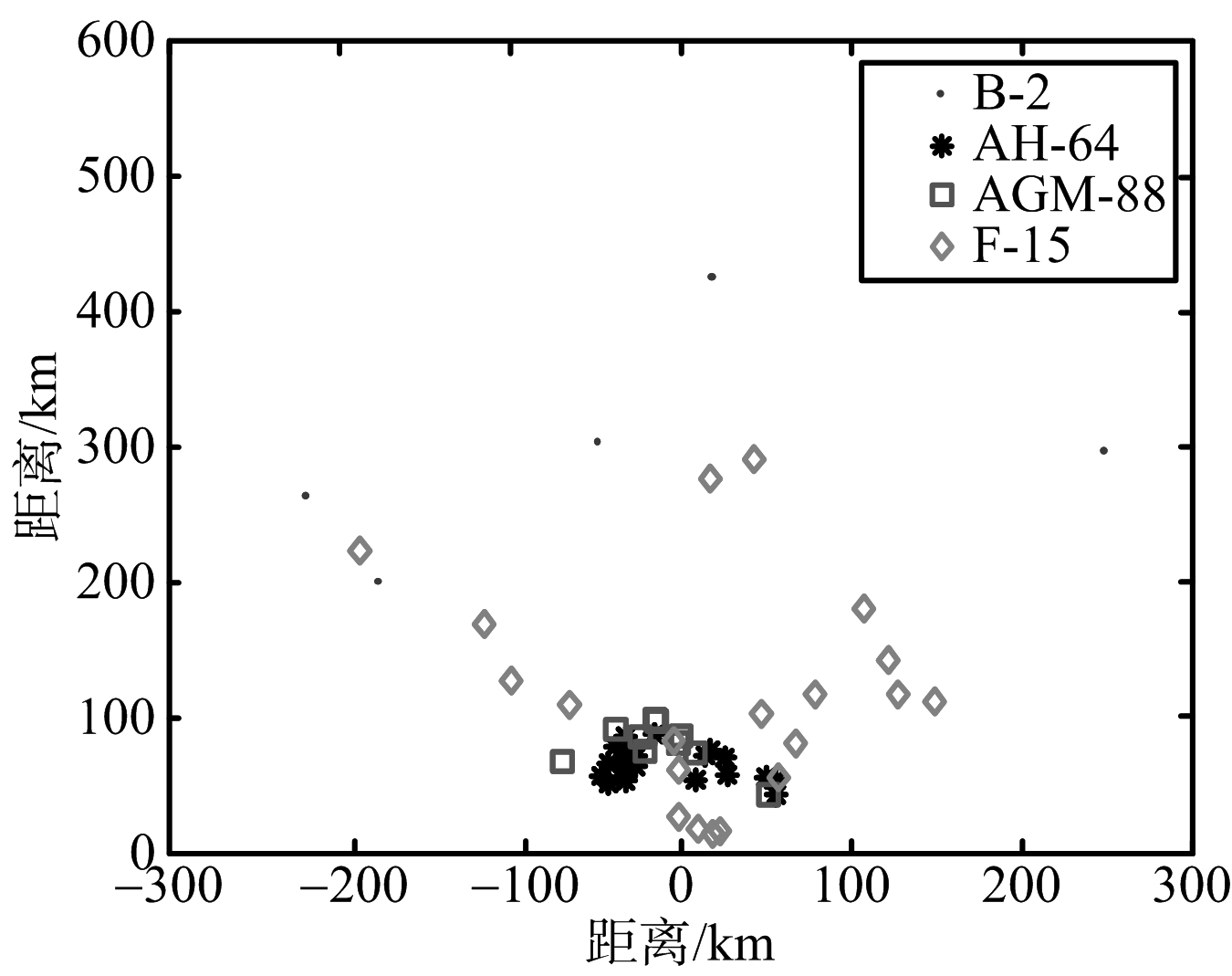
图6 战场态势
依据战场态势计算各事件驻留时长与综合优先级,分别如图7所示(此处仅计算单脉冲雷达,多脉冲情况下计算结果类似,限于篇幅此处不作讨论),其中权重向量设置为:λ=[0.4,0.2,0.2,0.2],选用MHPF准则,即η=1,速度门限与距离门限分别设置为:Rmax=200 km,Vmax=1 马赫。
由图7(a)可以看出,B-2隐身飞机由于隐身性能好、作战距离远,需要雷达长时间观测才能发现,占用大量雷达资源;AH-64武装直升机RCS大、作战距离近、观测时长较短;AGM-88“哈姆”反辐射导弹作战距离较近,但由于弹体较小,因此观测时间长于AH-64;F-15战斗机作战空域较大,因此观测时长起伏较大。
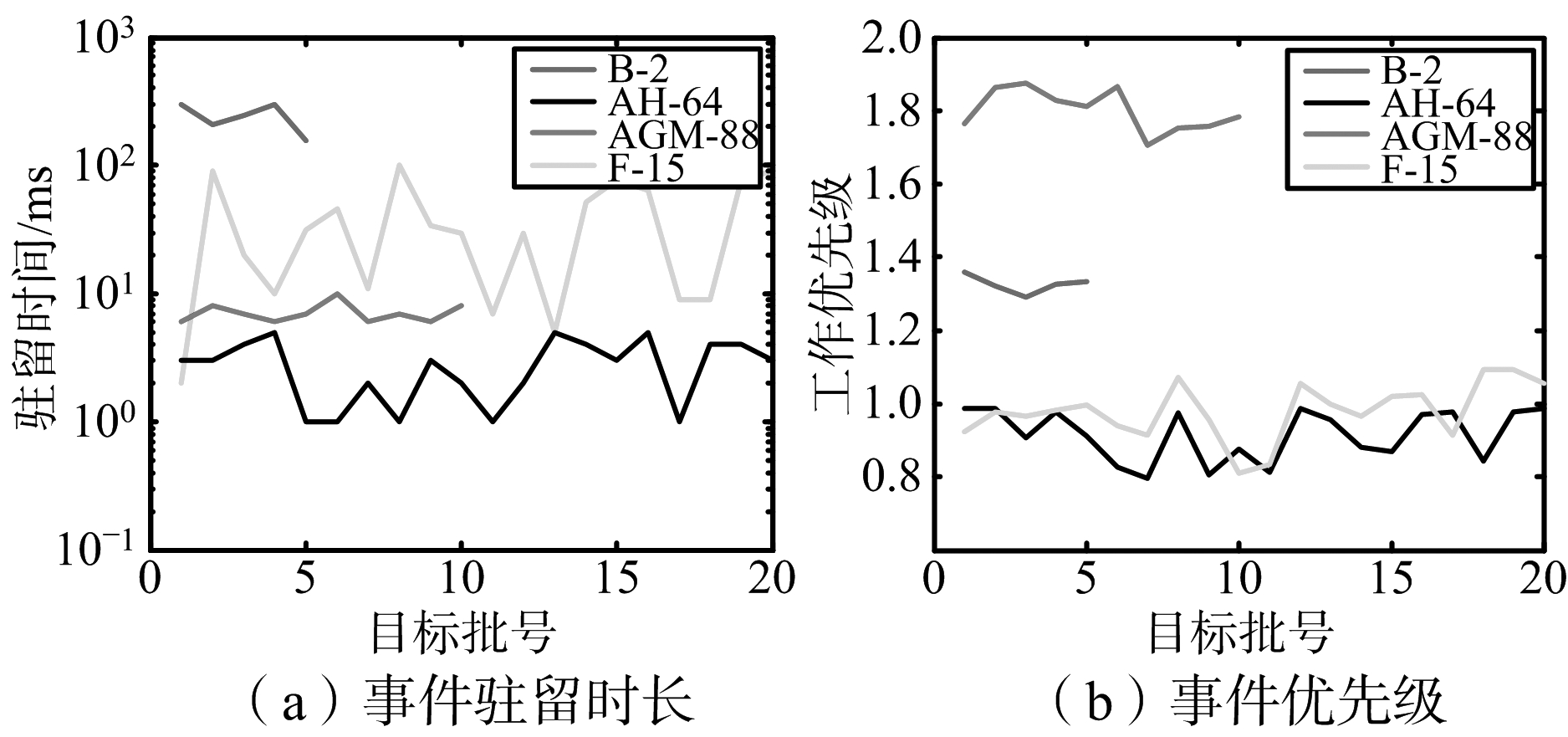
图7 事件属性
由图7(b)可以看出,4种目标中AGM-88对雷达威胁最大,因此工作优先级远高于其他目标;B-2威胁次之;AH-64与F-15类似,工作优先级最低。
由上文所求参数生成事件请求,如图8所示,其中调度间隔SI=500 ms,事件到达时间在调度间隔内呈均匀分布,4种目标时间窗分别为[20,40,10,30](单位:ms)。
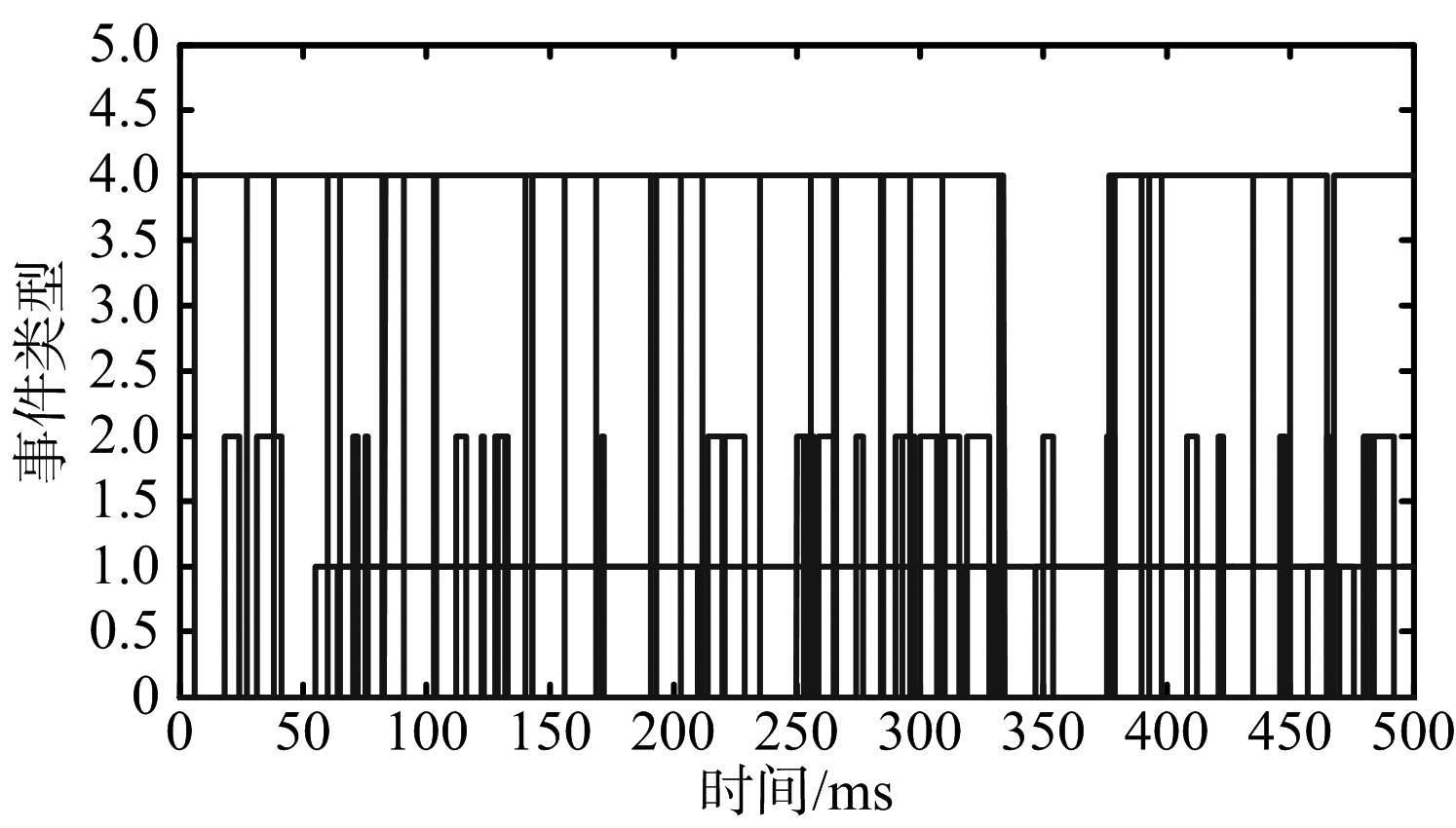
图8 事件请求
在上文事件请求基础上,分别利用基于综合优先级排序的调度算法(简称Pw法)与基于价值密度排序的调度算法(简称VD法)进行调度,调度结果性能与调度结果分别如表3和图9所示。
表3 算法调度性能比较
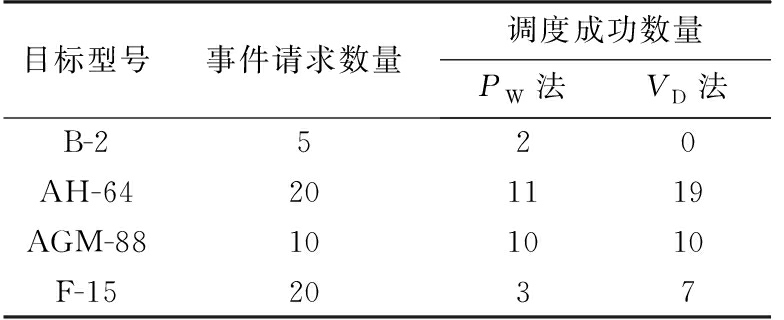
由图9和表3可以看出,两种算法对于优先级最高目标AGM-88反辐射导弹都能有效跟踪;同时PW法成功探测两批B-2隐身飞机,但探测该批目标花费大量雷达资源,探测“性价比”较低,因此VD法中雷达将更多资源分配至其他目标探测上,尤其是对AH-64武装直升机的探测,虽然此类目标综合优先级较低,但探测过程中消耗雷达资源较少,探测“性价比”高,因此VD法该类目标调度成功率较高。
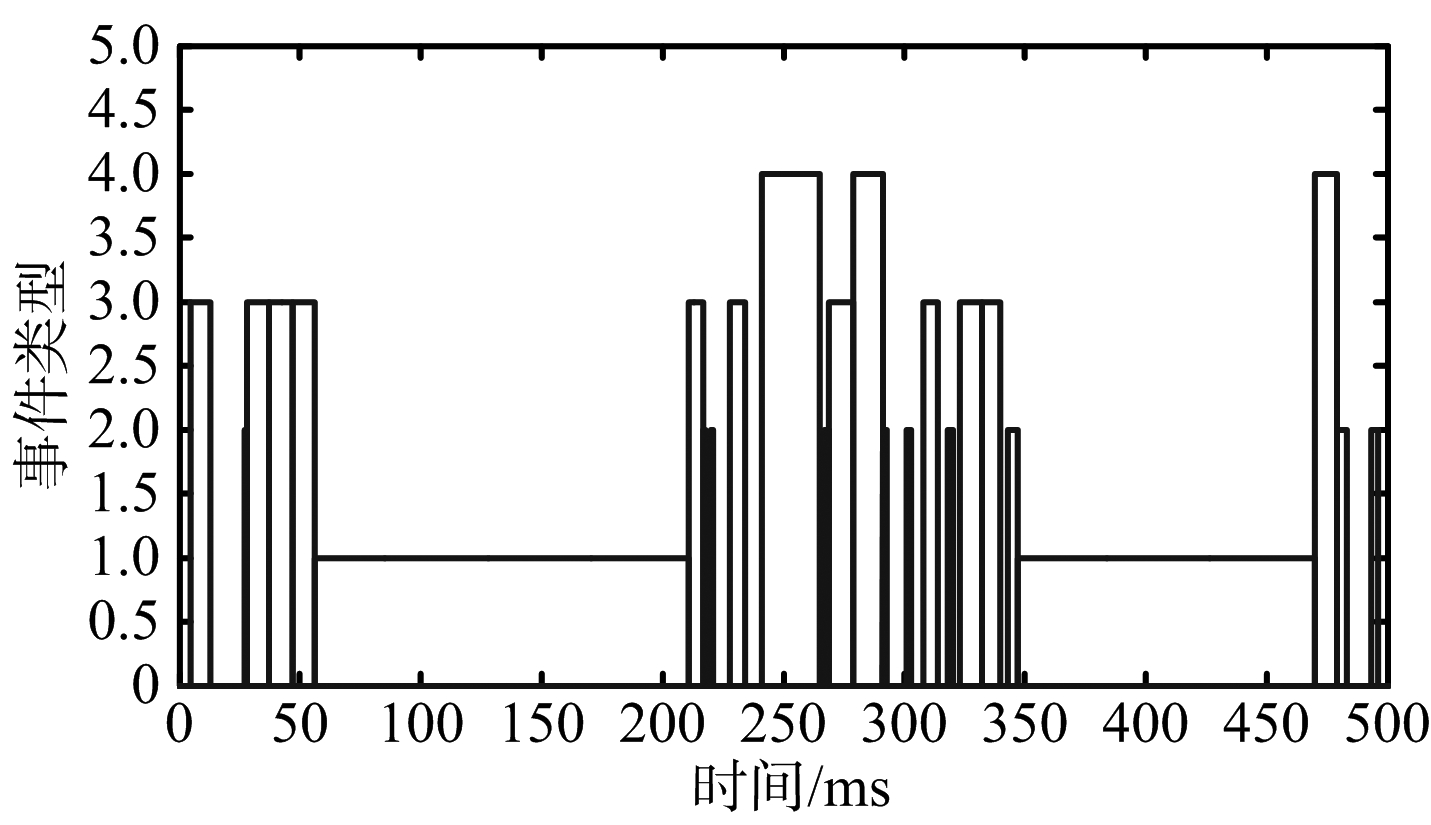
(a) 基于综合优先级排序
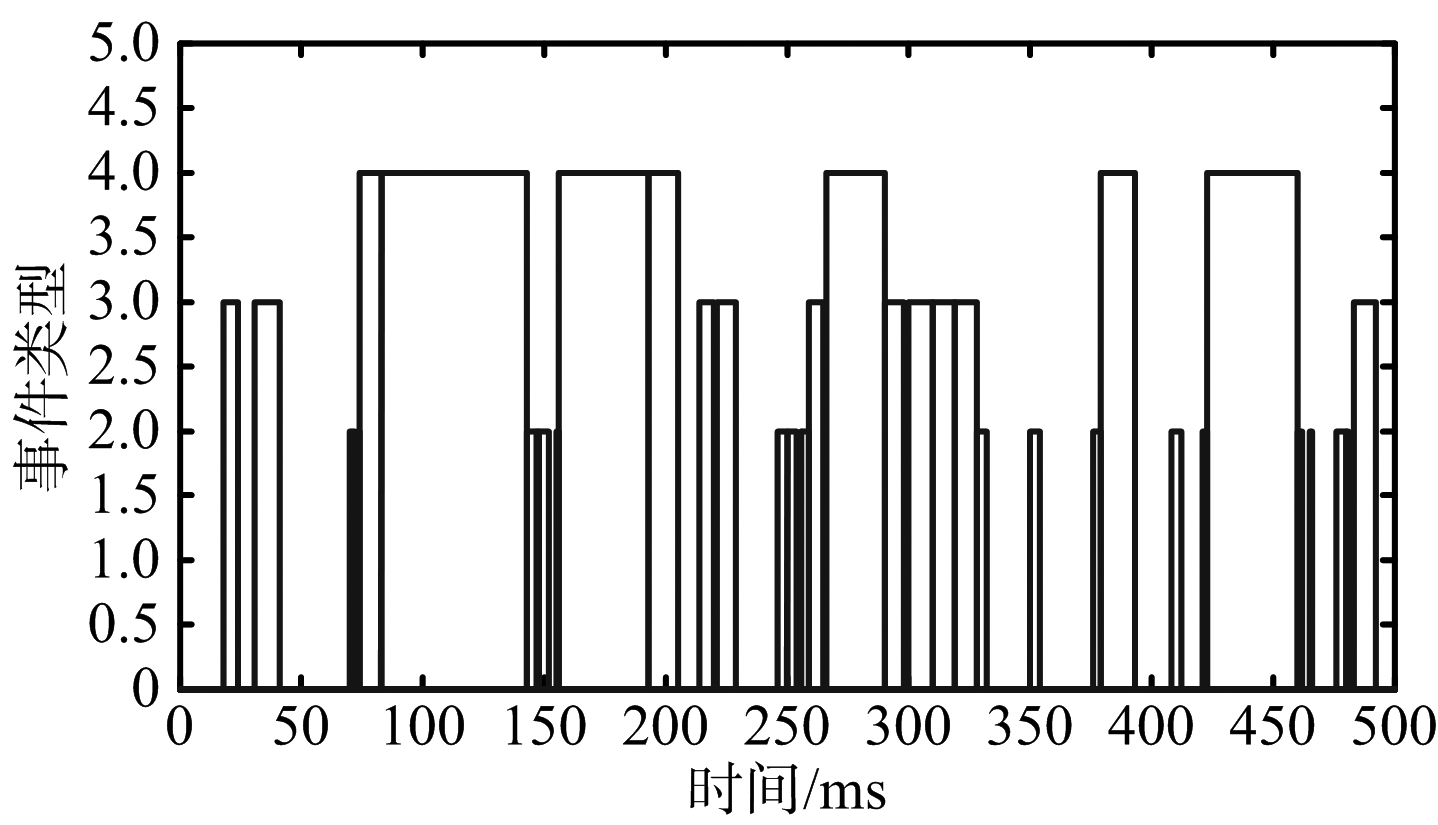
(b) 基于价值密度
图9 两种算法调度结果比较
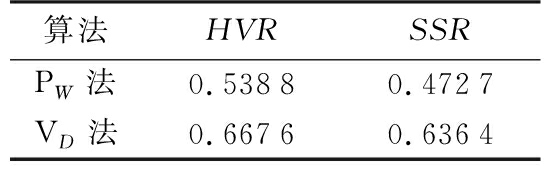
两种算法的HVR与SSR分别如表4所示,可见VD法的HVR与SSR均高于PW法,综合考虑该选用VD法。
表4 调度结果
为进一步对VD算法与PW算法的性能进行比较,本文通过改变参与调度的目标数量,比较两种算法的HVR与SSR,分别如图10所示。其中目标参数与上文中F-15战斗机参数设置相同;为提高实验结果准确性,该处进行1 000次蒙特卡洛仿真。
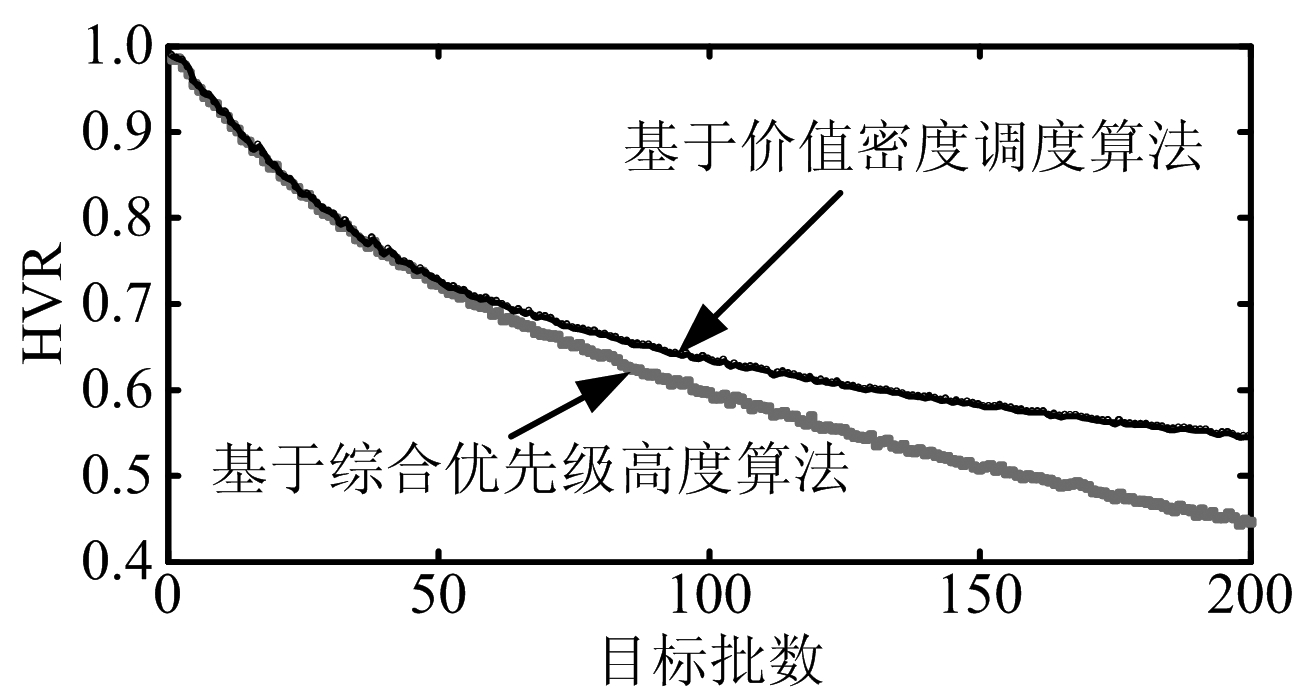
(a) 实现价值率比较
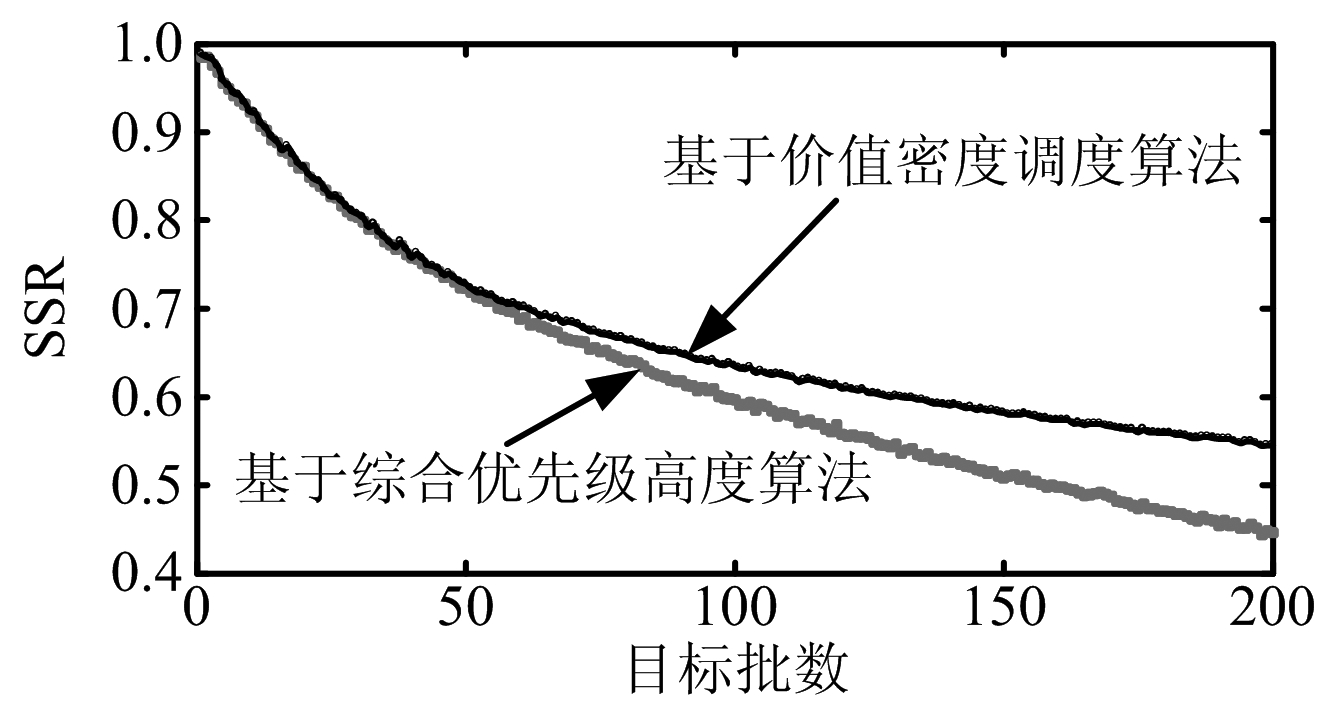
(b) 调度成功率比较
图10 算法性能
由图10可以看出,随着目标数量的增多,两种算法的HVR与SSR均呈下降趋势;当目标数量较少(小于40批)时,雷达资源尚未饱和,两种算法调度结果较为类似;但在密集目标条件下,VD算法的HVR与SSR明显优于PW算法。
本文针对相控阵雷达事件调度中传统算法未考虑事件驻留时长的问题,引入作业车间调度领域的“价值密度”概念;首先计算事件的综合优先级与事件驻留时间,再在此基础上计算事件“价值密度”,最后基于“价值密度”进行调度。仿真实验表明,基于“价值密度”的调度算法能更加有效地利用雷达资源,提高调度成功率与实现价值率,验证算法有效性。
但本文在计算价值密度过程中仅考虑了驻留时长,即雷达时间资源,此外雷达资源约束还有能量资源约束、计算机资源约束、硬件条件资源约束等[22],如何在计算“价值密度”时考虑多种资源约束将是下一步研究重点。
参考文献:
[1] 张光义,赵玉洁. 相控阵雷达技术[M]. 北京: 电子工业出版社, 2006:15-22.
[2] MOO P W, DING Z. Adaptive Radar Resource Management[M]. [S.l.]: Academic Press, 2015.
[3] 郭坤鹏. 相控阵雷达自适应调度算法研究[D]. 杭州: 杭州电子科技大学, 2015.
[4] HEBERT D C. Radar Resource Management in a Dense Target Environment[D]. Monterey, CA: Naval Postgraduate School, 2014.
[5] CHARLISH A. Autonomous Agents for Multi-Function Radar Resource Management[D]. London: University College London, 2011.
[6] CHEN J, TIAN Z, WANG L, et al. Adaptive Simultaneous Multi-Beam Dwell Scheduling Algorithm for Multifunction Phased Array Radars[J]. Journal of Information and Computational Science, 2011, 8(14):3051-3061.
[7] ZHANG Yu, YUAN Yunneng, WANG Jun, et al. Improved Adaptive Scheduling Algorithm for Real-Time Dwells in Multifunction Phased Array Radars[C]∥ 12th International Conference on Signal Processing, Hangzhou: IEEE, 2014:2018-2021.
[8] MIR H S, WILKINSON J D. Task Scheduling Algorithm for an Air and Missile Defense Radar[C]∥ IEEE Radar Conference, Rome: IEEE, 2008: 1-6.
[9] BAUGH R A. Computer Control of Modern Radars[M]. New York: RCA, 1973.
[10] LIU C L, LAYLAND J W. Scheduling Algorithms for Multiprogramming in a Hard-Real-Time Environment[J]. Journal of the ACM, 1973, 20(1):46-61.
[11] JEFFAY K, STANT D F, MARTEL C U. On Non-Preemptive Scheduling of Periodic and Sporadic Tasks[C]∥ 12th IEEE Real-Time Systems Symposium, San Antonio, Texas: IEEE, 1991:129-139.
[12] 卢建斌, 胡卫东, 郁文贤. 多功能相控阵雷达实时任务调度研究[J]. 电子学报, 2006, 34(4):732-736.
[13] KUO T W, CHAO Y S, KUO C F, et al. Real-Time Dwell Scheduling of Component-Oriented Phased Array Radars[J]. IEEE Radar Conference, Long Beach, CA: IEEE, 2002:92-97.
[14] CUI Yujuan, CHA Hao. Evaluation of Detection Efficiency on Radar Network[C]∥ International Conference on Economics, Social Science, Arts, Education and Management Engineering, [S.l.]: Atlantis Press, 2015:427-431.
[15] MIRANDA S L, BAKER C J, WOODBRIDGE K, et al. Fuzzy Logic Approach for Prioritisation of Radar Tasks and Sectors of Surveillance in Multifunction Radar[J]. IET Radar, Sonar and Navigation, 2007, 1(2):131-141.
[16] YAN Junkun, PU Wenqiang, LIU Hongwei, et al. Cooperative Target Assignment and Dwell Allocation for Multiple Target Tracking in Phased Array Radar Network[J]. Signal Processing, 2017, 141:74-83.
[17] 郑玉军, 田康生, 张金林, 等. 基于模糊神经网络的相控阵雷达任务调度设计[J]. 兵工学报, 2016, 37(11):2010-2013.
[18] 崔峻华, 陈进, 邓玉峰, 等. 基于价值密度的Job-shop车间生产计划控制[J]. 计算机系统应用, 2015, 24(6):1-7.
[19] 胡卫东, 郁文贤, 卢建斌, 等. 相控阵雷达资源管理[M]. 北京: 国防工业出版社, 2010:135-140.
[20] JANG D S, CHOI H L, CHOI J E. A Time-Window-Based Task Scheduling Approach for Multi-Function Phased Array Radars[C]∥ 11th Interna-tional Conference on Control, Automation and Systems, Gyeonggi-do: IEEE, 2011: 1250-1255.
[21] MIR H S, GUITOUNI A. Variable Dwell Task Scheduling for Multifunction Radar[J]. IEEE Trans on Automation Science and Engineering, 2014, 11(2):463-467.
[22] WANG Shuaijie, HE Jun, WANG Bin, et al. Research on Adaptive Scheduling Algorithm Based on Improved Genetic Algorithm for Multifunctional Phased Array Radar[C]∥ International Conference on Future Computer and Communication Engine-ering, [S.l.]: Atlantis Press, 2014:24-28.
DUAN Yi1,2, TAN Xiansi1, QU Zhiguo1, WANG Hong1, LI Xiangnan2
(1.Air Force Early Warning Academy,Wuhan430019,China;2.Unit95174of PLA,Wuhan430010,China)
Abstract:In the task scheduling of phased array radar, the common algorithms don’t take the dwell time of tasks into consideration when solving the comprehensive priority of target. For this problem, a task scheduling algorithm for phased array radar based on the “value density” concept which is used for job scheduling problem is proposed. First, the comprehensive priority of task is calculated by the job priority and deadline. Secondly, the task residence time is calculated based on the distance, size, location of target and the radar performance. Then the value in unit time of this task, namely the value density of the task, is calculated. Finally, scheduling is carried out based on the value density. Simulation shows that the proposed scheduling algorithm based on the value density can effectively improve the scheduling success rate and the hit value rate.
Key words:phased array radar; task scheduling; comprehensive priority; dwell time; value density
中图分类号:TN958.92
文献标志码:A
文章编号:1672-2337(2018)03-0291-07
DOI:10.3969/j.issn.1672-2337.2018.03.010
收稿日期:2017 06 23;
修回日期:2017 09 19
基金项目:国家自然科学基金(No.61401504); 中国博士后科学基金(No.2014M562562)
作者简介:

段 毅 男,1989年生,硕士研究生,工程师,主要从事相控阵雷达资源管理研究工作。E-mail:1074146275@qq.com

谭贤四 男,1967年生,教授、博士生导师,主要从事预警监视装备体系建设与运用研究工作。

曲智国 男,1982年生,博士,讲师,主要从事图像处理、预警监视研究工作。

王 红 女,1962年生,教授、博士生导师,主要从事预警监视装备体系建设与运用研究工作。

李向楠 男,1981年生,工程师,主要从事装备管理与保障研究工作。