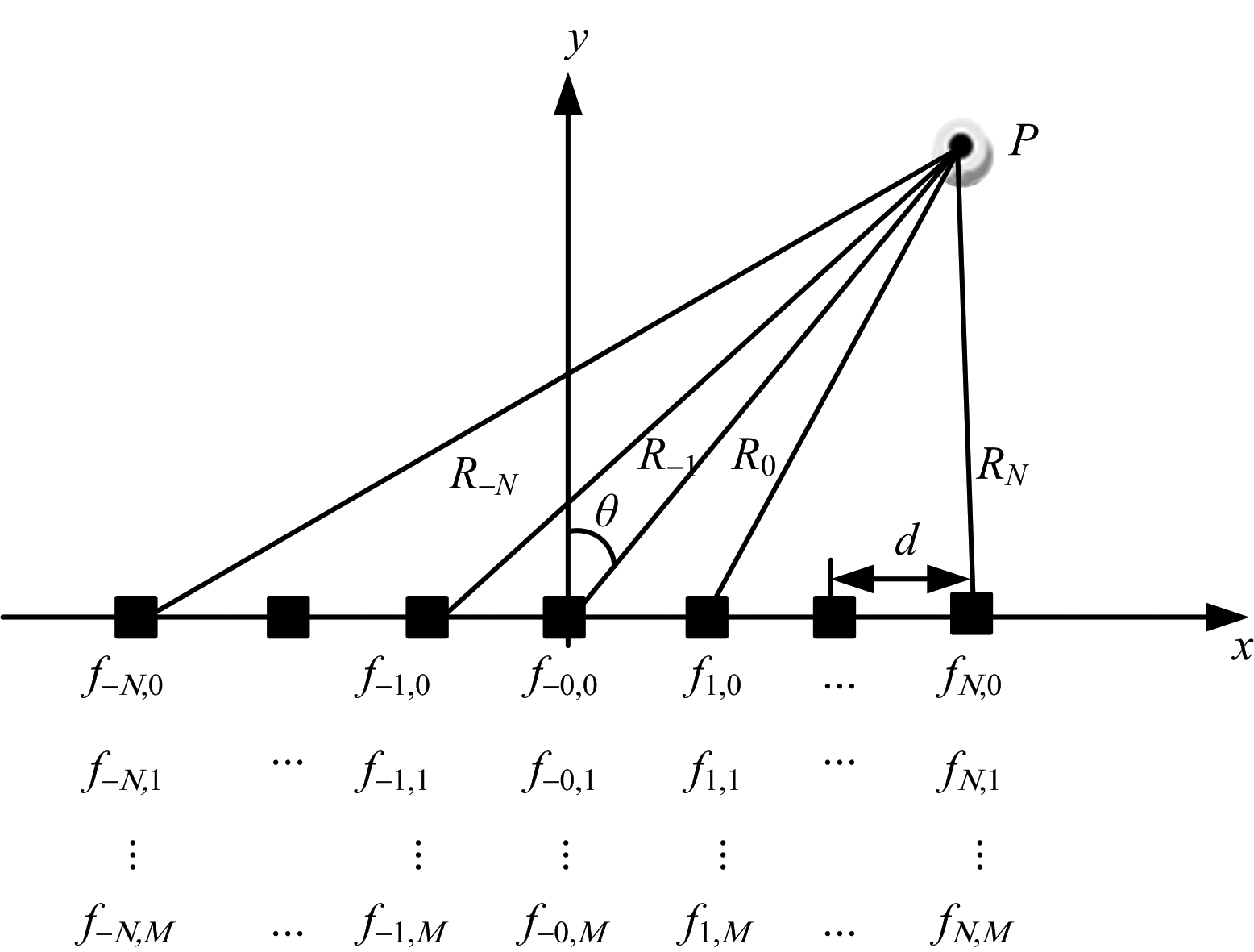
图1 FDA阵列结构
庄宇乾,宋耀良,穆 童
(南京理工大学电子工程与光电技术学院, 江苏南京 210094)
摘 要:波束综合技术可将雷达发射功率在感兴趣的空域汇聚,相关研究已从角度维上的聚焦发展到距离-角度二维空间上的聚焦,这种技术在高分辨率成像、远距离能量传输和医学靶向治疗等方面有广阔应用前景。针对现有基于频率分集阵列的“点”型发射方向图综合方法在分辨率和阵元间发射功率均衡性方面存在的不足,在理论分析“点”型发射方向图综合求解算法的同时,提出了基于凸优化的约束加权矩阵综合新算法。仿真结果表明,该算法在有效性、分辨率和旁瓣抑制性能方面比现有算法有较大提高。
关键词:发射方向图综合; 频率分集阵列; 凸优化; “点”型发射方向图
频率分集阵列(Frequency Diversity Array,FDA)由Antonik等于2006年提出[1-2]。FDA和传统阵列的不同之处在于每个阵元发射信号都有着相比于载频很小的频移而不是相移。文献[3-4]利用实验证实了阵列波束指向与距离和阵元间线性频率偏移量有关,利用这种频率偏移就可以使发射方向图成为一个关于距离-角度-时间的函数[5],且由于不需要移相器因而功耗更小[6]。
早先基于线性频率偏移的FDA[7-10]综合得出的距离-角度相关发射方向图是“S”型,且存在周期性,故能量集中度并不理想。为了设计出聚焦度更高的“点”型发射方向图,文献[11]提出一种利用对数形式的频率偏移的FDA方案,能使方向图在目标位置达到最大值,但这种方法的“点”型发射方向图在角度维和距离维分辨率并不理想,尤其是在距离维上分辨率低。文献[12]在其基础上设计了一种多载频和非线性频率偏移相结合的方向图综合优化方法,仿真结果表明该方法能将能量聚焦至目标处,呈现出“点”型方向图,不存在周期性旁瓣值,不足之处是每个阵元的发射功率差距较大,且就分辨率而言仍有优化的空间。
本文基于文献[12]对阵列结构和信号设计进行研究,采用指数形式频率偏移量,理论分析综合算法并推导加权矩阵表达式,实现“点”型方向图综合。为提升分辨率并抑制旁瓣提出一种改进型的多重频率变量综合方法,利用凸优化算法对加权矩阵进行设计,在确保方向图于不感兴趣区域的功率达到最小的条件下,使得每个阵元发射功率相近。
如图1所示,假设天线结构每个阵元之间的间隔为d。P为在远场的观察点,Rn为第n个阵元到P点的距离。设中心阵元为参考点,θ为方位角。信号设计采用与传统FDA不同的频率偏移量函数,同时每个阵元含有多个信号分量。

图1 FDA阵列结构
设fn,m为第n个阵元中第m个频率分量,可表示成如下形式:
fn,m=f0+Δfn+Δfm
-N≤n≤N,0≤m≤M
(1)
式中,f0为载频,一共有2N+1个阵元,每个阵元发射M+1个分量,各频率间隔满足指数形式,Δfn和Δfm分别定义为
Δfn=Δf×e|n|, -N≤n≤N
Δfm=Δf×em, 0≤m≤M
(2)
式中,Δf满足Δf≪f0,采用指数形式非线性函数的目的是为了消除方向图的周期性,尽可能降低旁瓣。
第n个阵元中的第m个被传输的信号分量可以表示为
xn,m(t)=wn,mej2πfn,mt
-N≤n≤N,0≤m≤M
(3)
式中,wn,m为第n个阵元中第m个信号分量的权重,传播到观察点(R,θ)处的信号可表示为
xn,m(t)=![]()
-N≤n≤N,0≤m≤M
(4)
假设目标在远场,则每个阵元的方位角都近似相同,即
Rn≈R-ndsinθ
(5)
那么在(R,θ)处的所有信号叠加的结果为
x(t;R,θ)=![]()
(6)
将式(1)和式(2)代入式(6)中可得
x(t;R,θ)≈![]()
(7)
由于f0≫Δf(e|n|+em),则式(7)可以进一步近似为
x(t;R,θ)≈![]()
(8)
由式(8)可得出在远场(R,θ)处的发射信号辐射功率,即FDA阵列发射方向图可以表示为
B(t;R,θ)=
![]()
(9)
此方向图是时间-距离-角度相关,为分析距离-角度相关方向图,现将t值固定,为方便分析令t=0。从式(9)中可以明显看出当t=0时,R=0,θ=0则方向图值取得最大,为了使得在目标点(Rt,θt) 处达到最大可以定义权重wn,m为
(10)
将式(10)代入式(9)后方向图可表示为
B(t;R,θ)=![]()
(11)
上述研究对文献[12]中“点”型发射方向图综合算法进行理论分析,利用公式推导得出第n个阵元中第m个子信号的加权量wn,m的表达式,通过计算实现“点”型方向图的综合,可以获得与文献[12]相同的聚焦效果。
由于1.2节中描述的综合算法的加权矩阵是权1矩阵,因此聚焦分辨率并没有提升。下面对加权矩阵进行设计,利用凸优化理论优化加权量wn,m,并控制其值的大小,令其小于一个固定值,即
|wn,m|≤τ
(12)
定义一个[(M+1)(2N+1)]×1维的向量:
a(R,θ)=[a-N(R,θ),…,
an(R,θ),…,aN(R,θ)]T
(13)
式中,an(R,θ)是一个1×(M+1)维的向量:
an(R,θ)=![]()
(14)
综合上文所述,首先对空域进行分隔,令Ξt表示波束需要聚焦的空域,Ξs为旁瓣区域。为方便分析,对这两个空域进行离散化处理,离散点分别为(Rt,θt)和(Rs,θs),个数分别为T和S,(R′,θ′) 是目标点P。随后对于辐射至旁瓣区域Ξs的功率约束,使其最小,结合式(12)~式(14)可以得到基于凸优化理论的优化模型:
s.t.![]() ≤ξs, (Rs,θs)∈Ξs
≤ξs, (Rs,θs)∈Ξs
(15)
WHa(Rt,θt)=(M+1)(2N+1),t=1,…,T
|wn,m|≤τ, -N≤n≤N,0≤m≤M
式中,W表示[(M+1)(2N+1)]×1的加权矩阵:
W=[w-N,0,w-N,1,…,wn,0,wn,1,…,wn,M,…,wN,0,wN,1,…,wN,M]T
(16)
最后利用Matlab仿真软件中的凸优化工具CVX可实现对提出模型的求解。
利用Matlab软件对提出的方法进行验证。假设FDA的发射阵元数为17,每个阵元之间的间距为最大波长的一半。每个阵元发射信号均包含8个基信号,载波频率f0为8 GHz,频率偏移量Δf=3 kHz。为分析距离-角度相关方向图,取t=0,R=[0∶10∶1 000]km,θ=[0°∶1°∶90°]。假设目标点在(520 km,25°)处,则不感兴趣区域即旁瓣区域设置为:Rs=[0∶10∶490]∪[540∶10∶1 000]km和θs=[0°∶1°∶22°]∪[28°∶1°∶90°],总共离散化9 191个点,旁瓣区域离散化点数为9 166,加权矩阵值控制量取τ=3。
图2(a)是文献[12]中得出的综合结果,图2(b)是本文使用指数形式频偏量并用理论推导加权矩阵的发射方向图综合结果,图2(c)和图2(d)分别是改进型利用凸优化理论所得发射方向图的归一化和转换成dB值后的三维视图,图2(e)为文献[12]得出的三维视图。可以看出聚焦精度获得了明显提升,且旁瓣更低。
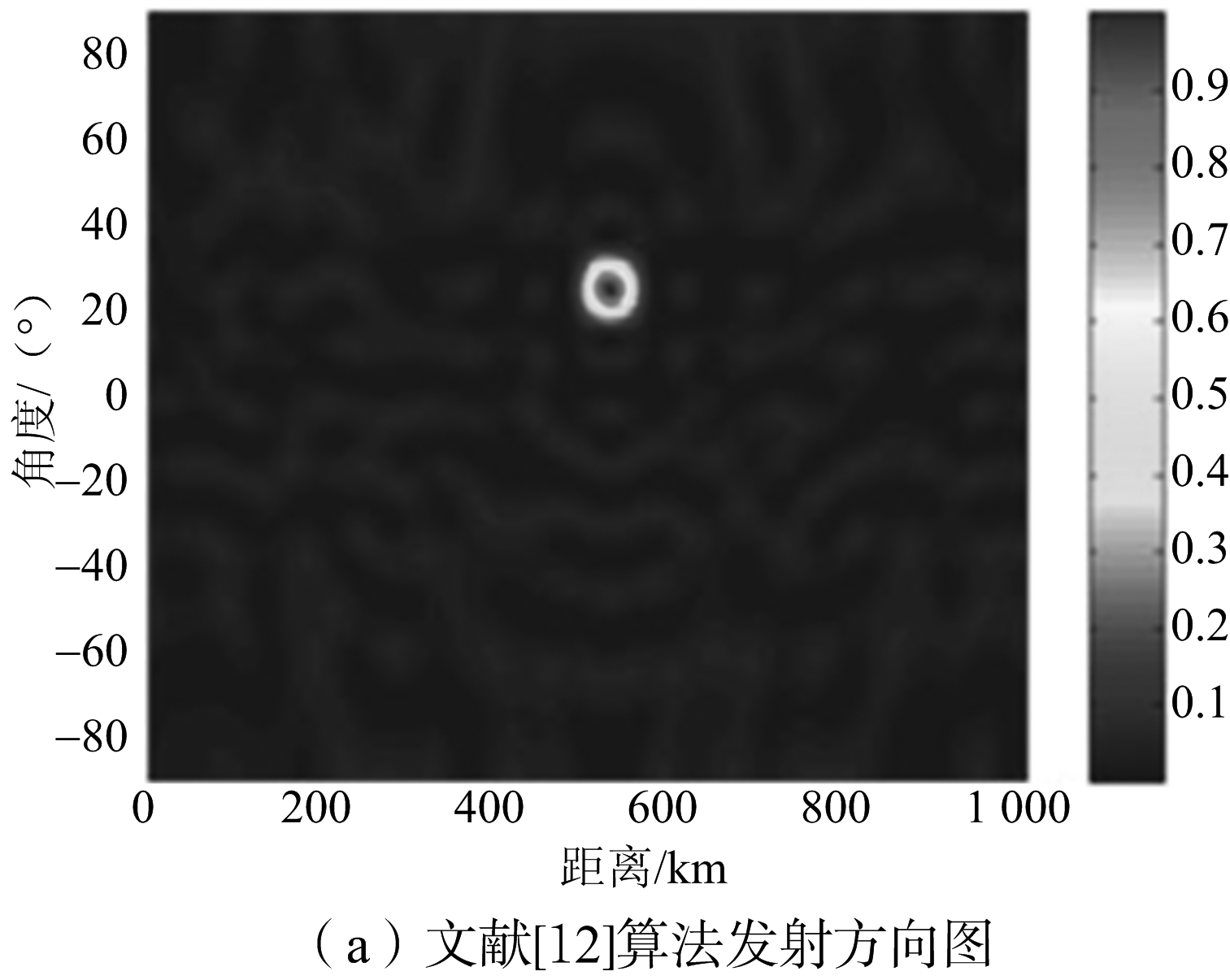
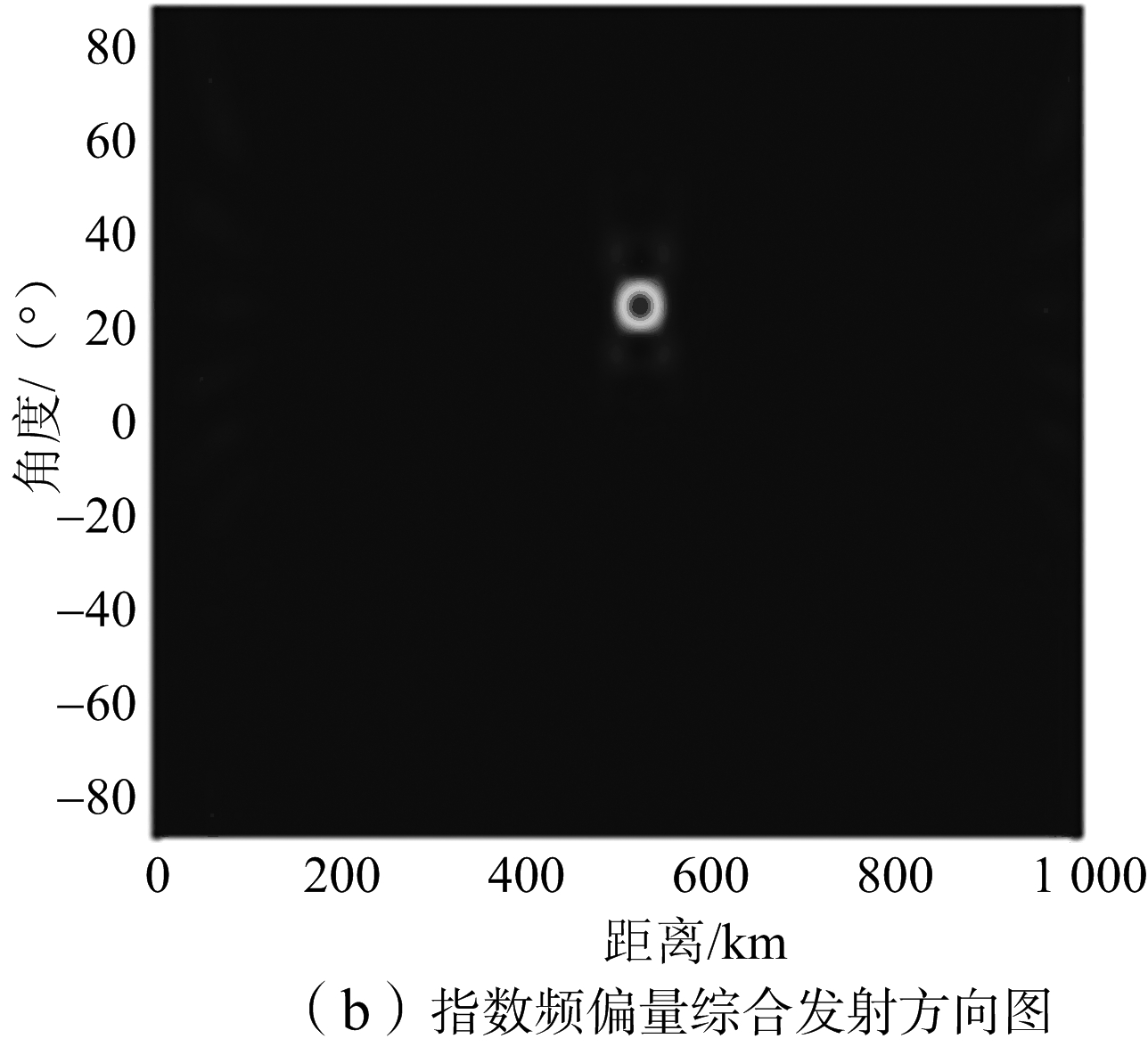

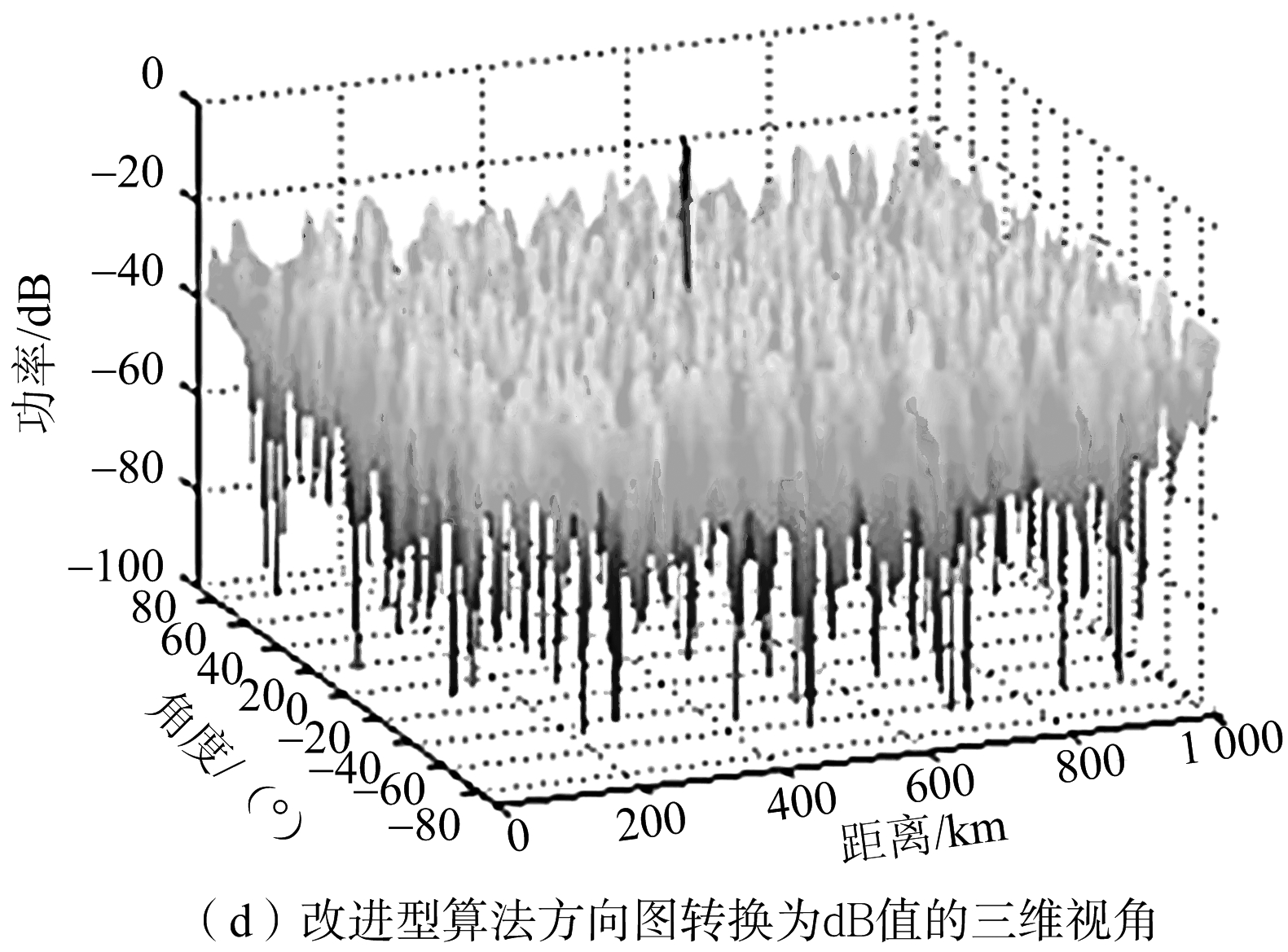
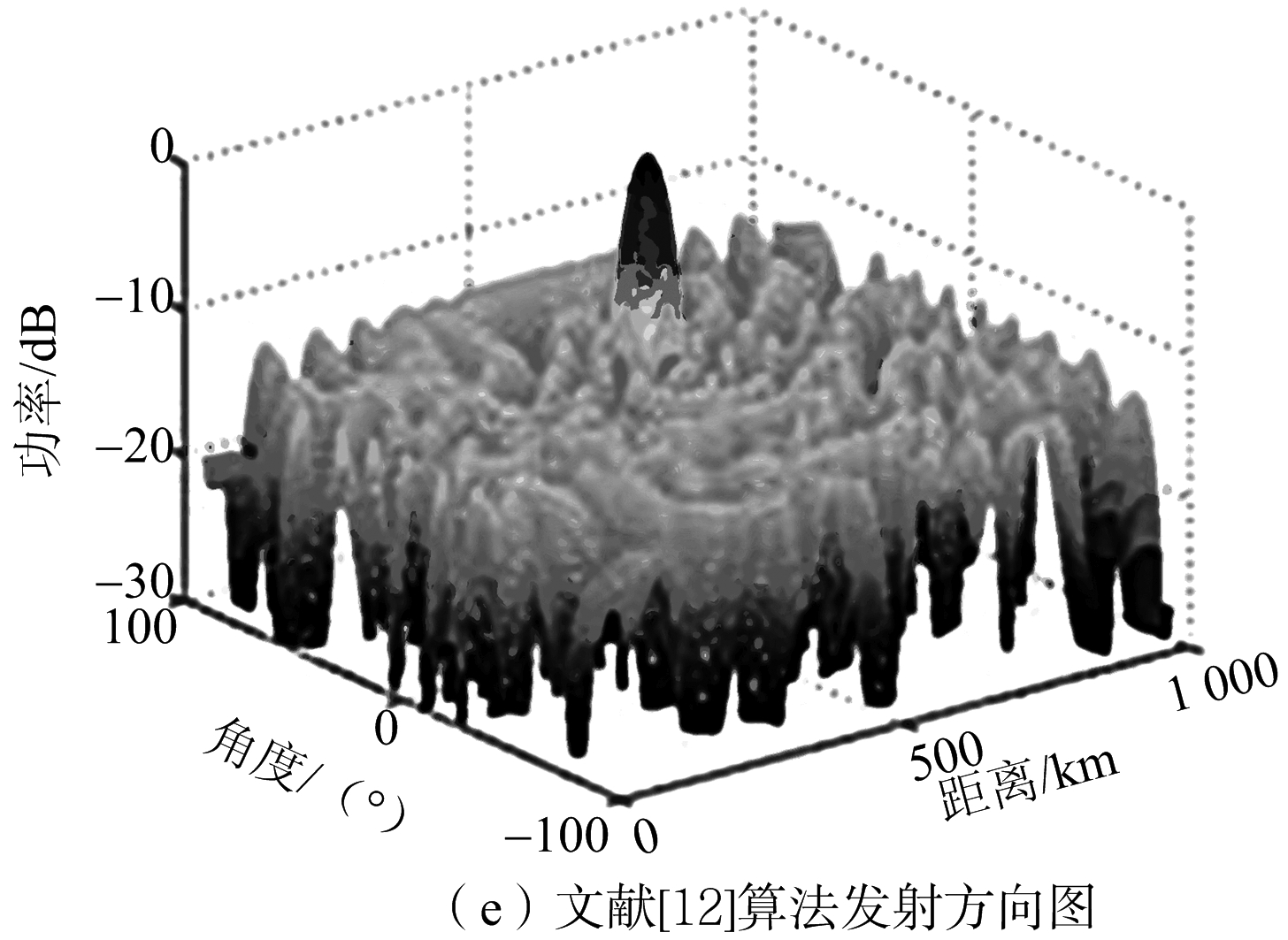
图2 文献[12]与本文改进型算法发射方向图对比分析
为清晰看出本文方法的精度优势,作出在目标点(520 km,25°)处的二维成像图,图3(a)和图3(b)分别为25°和520 km处的成像图。同时作出在24°和510 km处的成像结果图3(c)和图3(d)进行比较,角度维和距离维聚焦精度分别在1°和10 km以内。
表1展示的是本文提出的算法所得的加权矩阵,每个基信号的幅度值都控制在一定范围内。图4(a)是本文计算得出的归一化后单个阵元发射功率分布图,从图4(a)可以看出本文所得的加权矩阵可以使阵列天线的每个阵元发射功率相近,有益于发射功率的利用,相较于文献[12]中单个阵元功率分布(图4(b))结果更优。
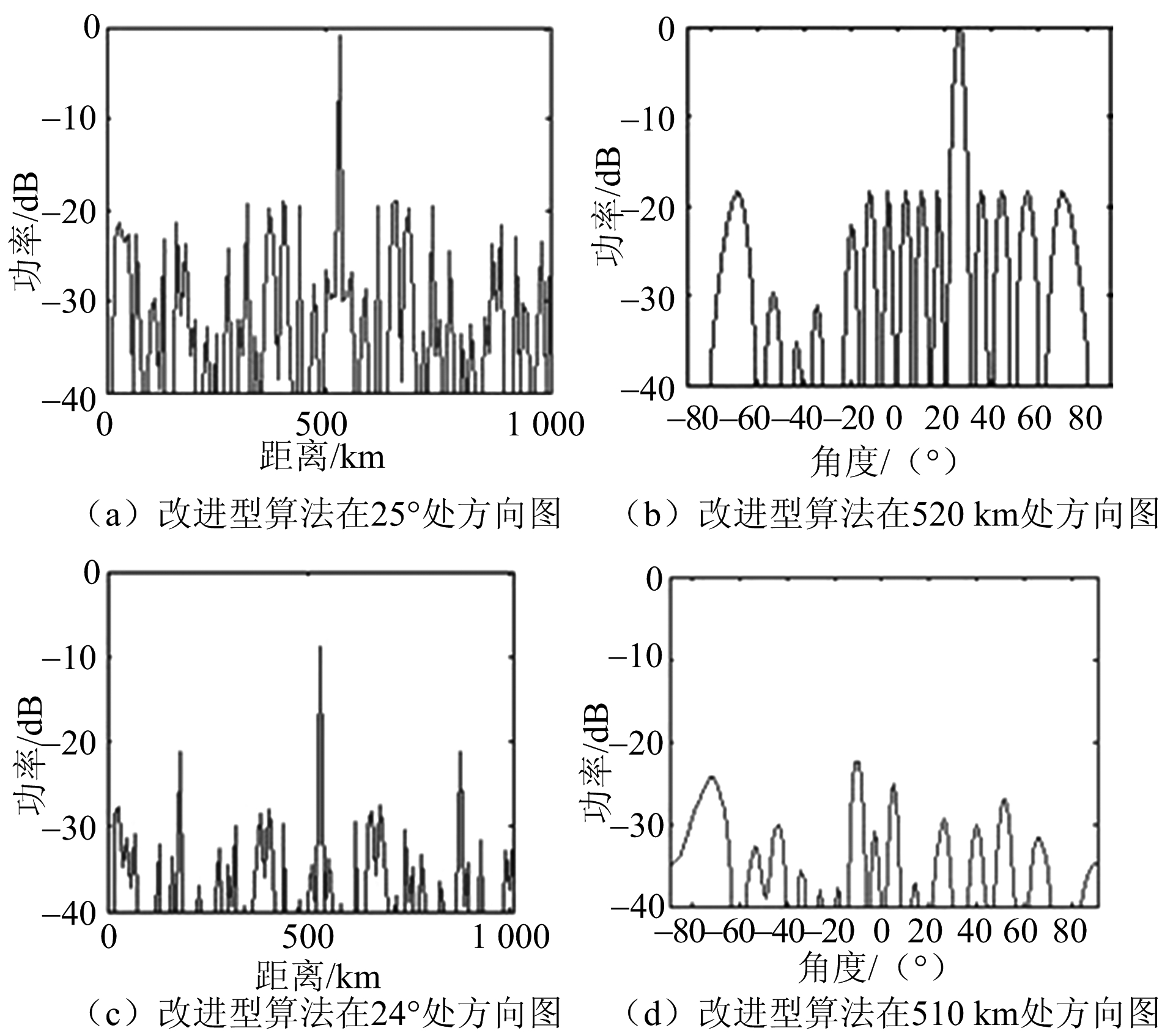
图3 改进型算法在目标点处精度分析
表1 改进型优化算法加权矩阵W
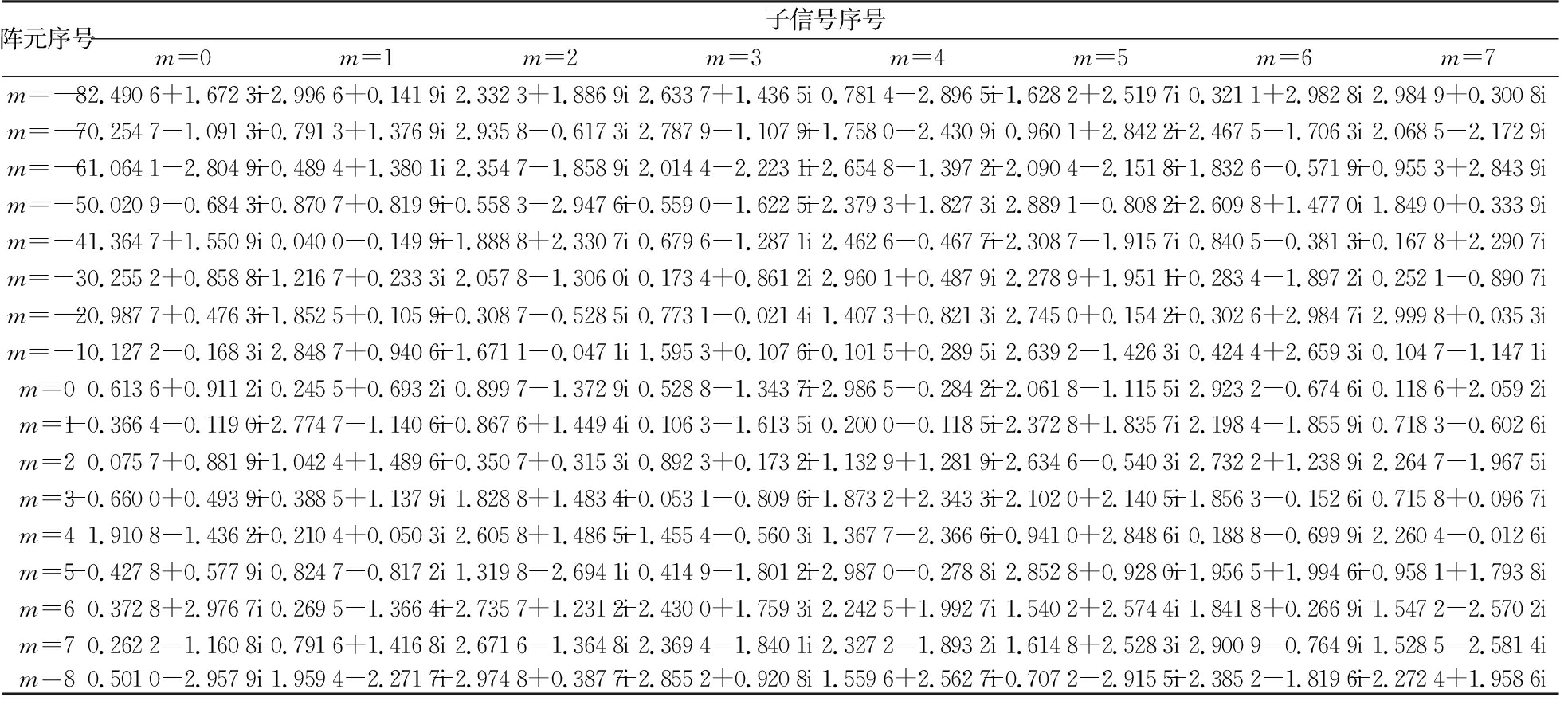
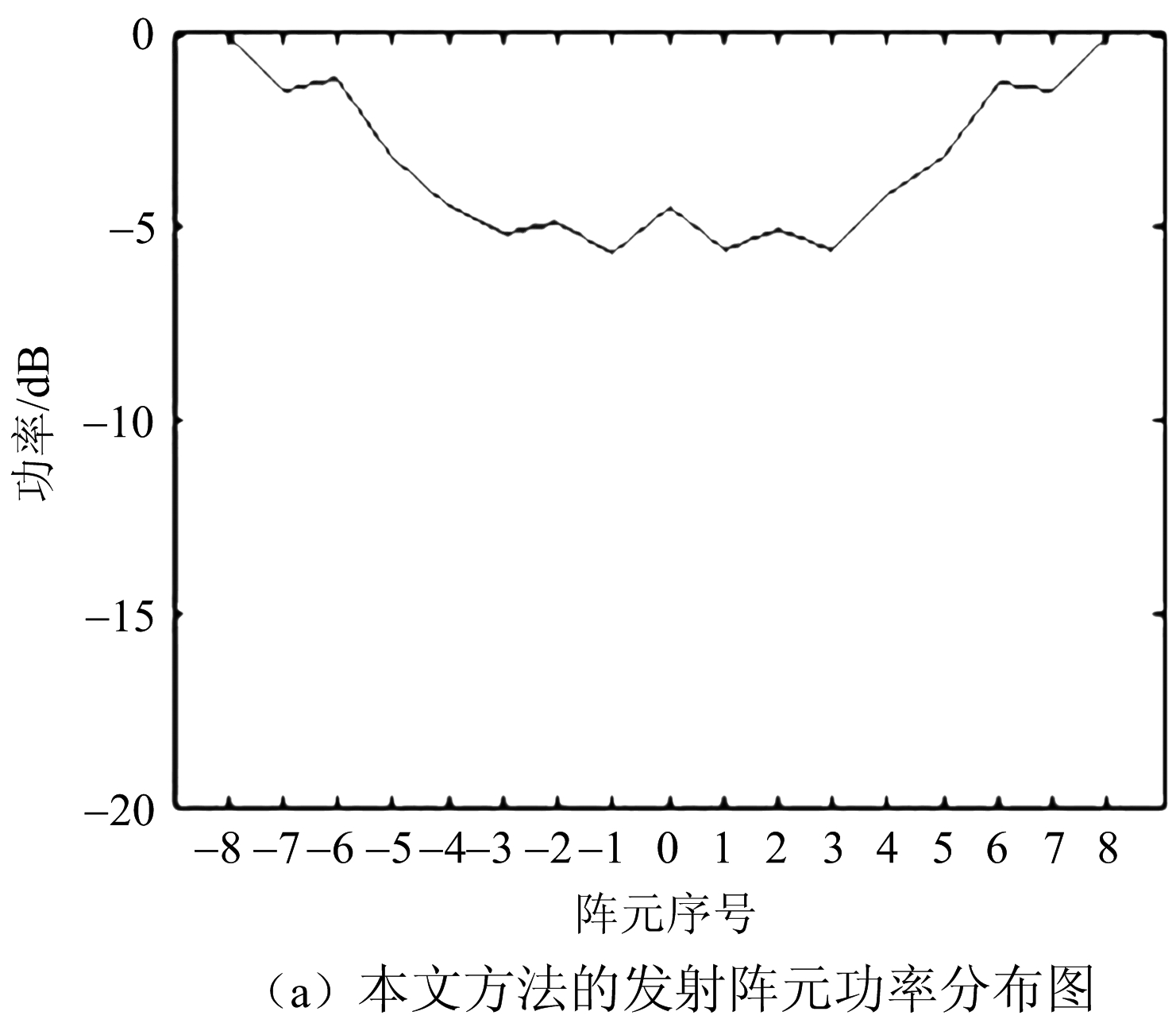
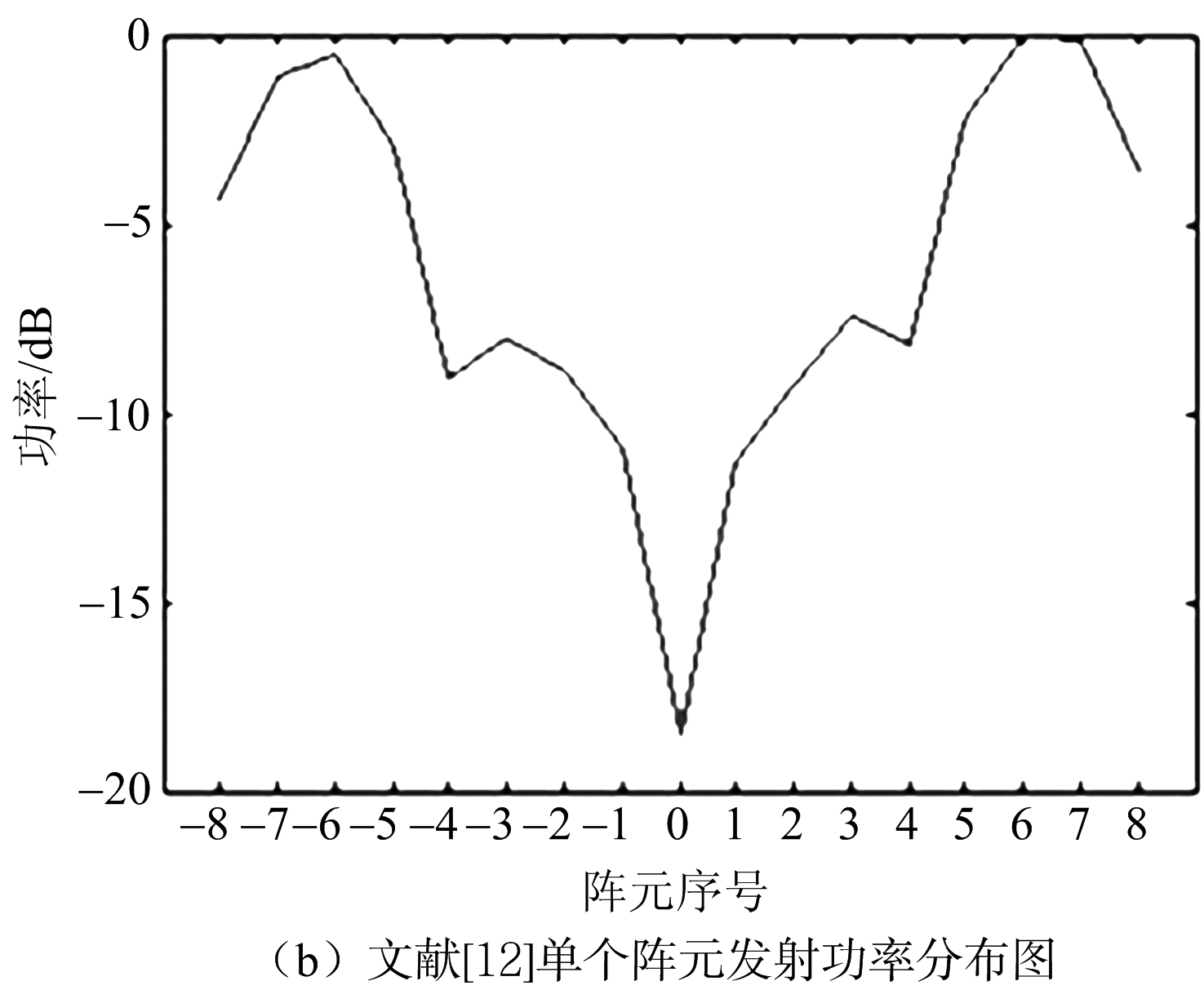
图4 文献[12]与本文方法中阵元发射功率对比分析
基于多载频对数频偏综合算法在分辨率和阵元间发射功率均衡性方面存在的不足,本文理论分析了以指数形式频率偏移量为基础、加权矩阵为权1矩阵的综合算法,利用公式推导出加权矩阵的表达式并实现聚焦。同时提出改进型利用凸优化理论优化加权矩阵的综合算法,使得每个阵元的发射功率更加均匀,提升了聚焦精度,进一步降低了辐射至不感兴趣区域的功率,算法有效性得到提升。
参考文献:
[1] ANTONIK P, WICKS M C, GRIFFITHS H D, et al. Frequency Diverse Array Radars[C]∥ IEEE Conference on Radar, Verona, NY: IEEE, 2006:215-217.
[2] WICKS M C, ANTONIK P. Frequency Diverse Array with Independent Modulation of Frequency, Amplitude, and Phase: US7319427[P]. 2008-01-15.
[3] HUANG J, TONG K, BAKER C J. Frequency Diverse Array with Beam Scanning Feature [C]∥ IEEE Antennas and Propagation Society International Symposium, San Diego, CA: IEEE, 2008:1-4.
[4] HUANG J, TONG K, WOODBRIDGE K, et al. Frequency Diverse Array: Simulation and Design[C]∥ IEEE Radar Conference, Pasadena, CA: IEEE, 2009:1-4.
[5] AYTUN A. Frequency Diverse Array Radar[D]. Monterey, CA: Naval Postgraduate School, 2010:1-109.
[6] HUANG Y Y, JEON H, YOON Y, et al. An Ultra-Compact Linearly-Controlled Variable Phase Shifter Designed with a Novel RC Poly-Phase Filter[J]. IEEE Trans on Microwave Theory and Techniques, 2012, 60(2):301-310.
[7] ANTONIK P, WICKS M C, GRIFFITHS H D, et al. Range Dependent Beamforming Using Element Level Waveform Diversity[C]∥ International Waveform Diversity and Design Conference, Orlando, FL:IEEE, 2006:71-76.
[8] SECMEN M, DEMIR S, HIZAL A, et al. Frequency Diverse Array Antenna with Periodic Time Modulated Pattern in Range and Angle[C]∥ IEEE Radar Conference, Boston, MA: IEEE, 2007:427-430.
[9] ZHUANG Long, LIU Xingzhao, YU Wenxian. Precisely Beam Steering for Frequency Diverse Arrays Based on Frequency Offset Selection[C]∥ International Radar Conference, Bordeaux: IEEE, 2009:1-4.
[10] CHEN Yongguang, LI Yuntao, WU Yanhong, et al. Research on the Linear Frequency Diverse Array Performance [C]∥ IEEE 10th International Conference on Signal Processing Proceedings, Beijing: IEEE, 2010:2324-2327.
[11] KHAN W, QURESHI I M, SAEED S. Frequency Diverse Array Radar with Logarithmically Increasing Frequency Offset[J]. IEEE Antenna Wireless Propagation Letters, 2015, 14:499-502.
[12] SHAO Huaizong, DAI Jun, XIONG Jie, et al. Dot-Shaped Range-Angle Beampattern Sythesis for Frequency Diverse Array[J]. IEEE Antennas and Wireless Propagation Letters, 2016, 15:1703-1706.
ZHUANG Yuqian, SONG Yaoliang, MU Tong
(School of Electronic and Optical Engineering,Nanjing University of Science and Technology,Nanjing210094,China)
Abstract:The beam pattern synthesis technique can converge the radar transmit energy in the interested spatial domain. The related research about focusing has been developed from the angle dimension to the distance-angle two-dimensional space. This technology has wide application prospects in high-resolution imaging, long-range energy transmission, medical targeted therapy and other aspects. According to the defects of the existing dot-shape transmit beam pattern synthesis method based on frequency diversity array (FDA) about its resolution and transmit power balance between the array element, we analyze the theory of the algorithm of the dot-shape transmit beam pattern synthesis method and propose a new synthesis algorithm to constrain the weighting matrix based on convex optimization. The simulation results show that the performance of the proposed algorithm can greatly improve the effectiveness, resolution and sidelobe suppression than the existing algorithms.
Key words:transmit beam pattern synthesis; frequency diversity array (FDA); convex optimization; dot-shape transmit beam pattern
中图分类号:TN958.5
文献标志码:A
文章编号:1672-2337(2018)03-0298-05
DOI:10.3969/j.issn.1672-2337.2018.03.011
收稿日期:2017 08 08;
修回日期:2017 10 10
基金项目:国家自然科学基金(No.61271331, 61571229)
作者简介:

庄宇乾 男,1993年生,江苏人,硕士研究生,主要研究方向为雷达发射波形设计与信号处理。E-mail:993580172@qq.com

宋耀良 男,1960年生,教授、博士生导师,主要研究方向为超宽雷达与超宽带通信和现代信号处理技术。
穆 童男,1993年生,博士研究生,主要研究方向为超宽带雷达与信号处理。