杨云高1，倪 威1，闫 浩2，曹运合2
(1.中船重工集团公司第七一六研究所， 江苏连云港 222006；2.西安电子科技大学， 陕西西安 710071)
摘 要：传统单模型算法很难满足对机动目标的跟踪精度需求，自适应模型、多模型成为该领域的研究热点。转弯模型因其形式简单、计算复杂度低等特点在多模型跟踪中被广泛研究和使用。但是，网格调整算法估计转弯角速度的方法中由于机动目标角速度未知而无法确定最小的网格间隔，导致存在难以精确估计真实角速度且估计速度慢等问题，基于后验概率的机动目标跟踪方法能够有效地解决该问题。通过对多模型后验概率的计算获得各模型对应的权值，提高了真实角速度的估计精度和既定目标跟踪算法的估计性能。最后通过仿真试验说明了改进算法的有效性。
关键词：机动目标跟踪； 网格间隔； 转弯角速度； 后验概率
随着现代航空的迅速发展，各种飞行器的机动性和运动速度越来越高，但可靠而精确的跟踪目标始终是目标跟踪系统设计的主要目的与难点。目标跟踪实际上就是对目标状态的跟踪滤波问题，而实现目标跟踪首先要使所建立的目标运动模型与实际的目标运动模型匹配，建立目标的运动模型和自适应滤波是机动目标的两个关键部分。
在当前目标机动能力日益增强的情况下，传统单模型算法很难满足跟踪精度需求，自适应模型[1-3]、交互多模型[4-5]成为该领域的研究热点。转弯模型因其形式简单、计算复杂度低等特点在多模型跟踪中被广泛研究和使用。 Lerro等[6]对转弯模型进行了改进，通过在线计算转弯率ω，把常转弯率模型改变为自适应模型。Munir， Best等[7-8]围绕如何计算(或准确估计)运动目标的当前转弯率ω，提出了多种不同的改进方案。Li等[9]把具有不同转弯率的模型作为多模型应用于交互多模型算法中，并把它用作构建模型集合的基准模型。
本文针对网格调整法[10]估计转弯角速度方法，提出了改进的多模型方法；并进行了仿真，说明改进算法的有效性。
假设一个机动目标以常线速度和常角速度ω在x-y坐标平面内作转弯运动，则目标位置为
(1)
式中：xc和yc为转弯的中心；r为转弯的半径；φ为转弯开始的初始角；ω为正代表左转弯，ω为负代表右转弯。经过微分可得坐标方向的速度和加速度为
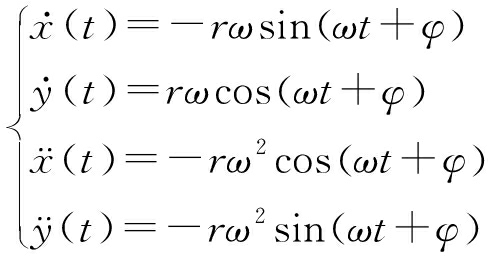
(2)
由上可知，运动公式可表示为
(3)
定义状态向量为
则二维转弯模型连续时间状态方程可表示为
(4)
式中，A由式(3)得到：
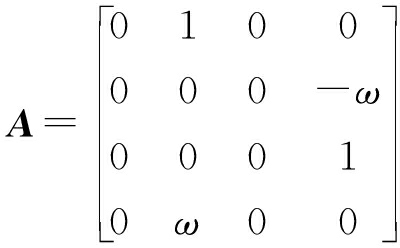
(5)
以周期T采样，得到离散时间目标运动状态方程为
X(k+1)=F2dX(k)
(6)
式中，
为状态向量,F2d为状态转移矩阵，且
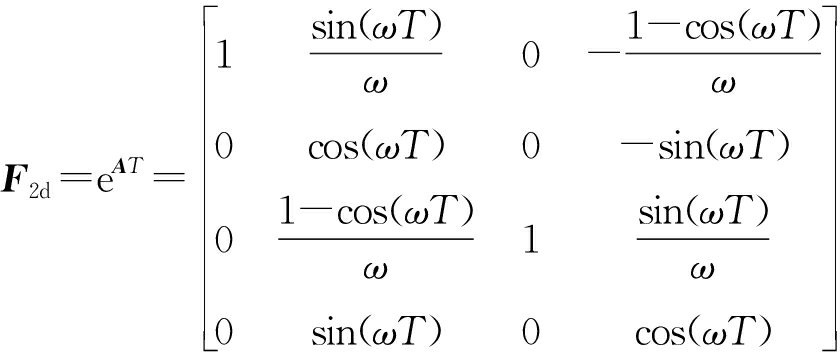(7)
并可拓展状态向量得到三维坐标下的状态转移矩阵F3d：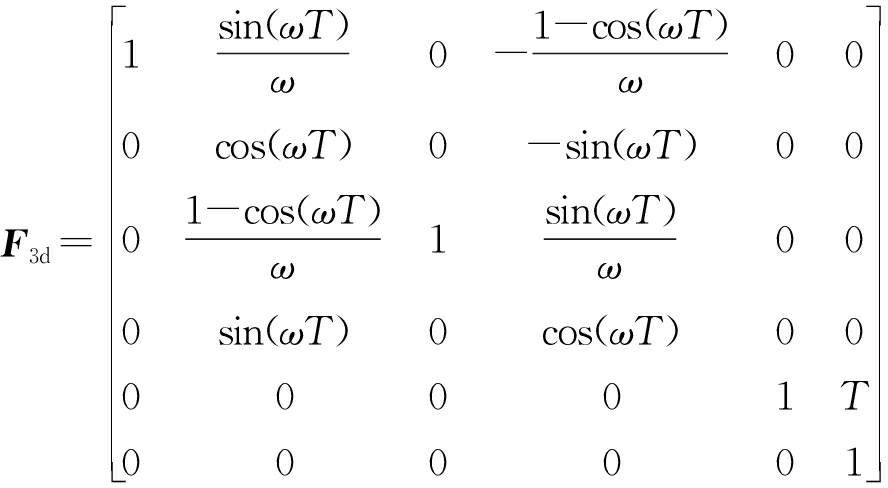
(8)
多模型算法常根据滤波后的新息求得每个模型概率，模型概率可以描述某角速度对应的真实运动模型，当其概率为1时，可认为该角速度对应的模型为机动目标真实运动模型；当该角速度相比其他角速度与真实角速度的差值最大，其对应模型概率为最小。根据网格调整法，可设计角速度变化公式。
若在k时刻的模型集为
其特征参数分别对应多模型的角速度且在模型集中从小到大排列，
称为中心模型；对应模型集的后验概率为
根据图论的思想，中心模型参数为上一时刻所有模型参数与对应概率乘积之和:
假设k时刻模型间距调整参数假设为:
其中δ是设定的最小的网格间隔，可分3种情况来调整左右模型：
1)模型概率重心无跳变：此时，
根据模型概率判定模型集不变或向中心模型靠拢；
(9)
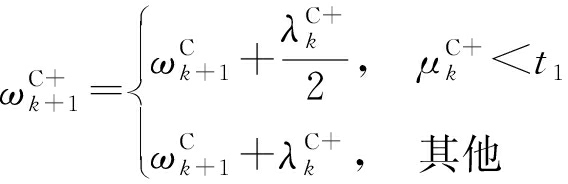
(10)
式中，t1表示不可能模型的门限值，一般取t1<0.1。
2)模型概率重心向左跳变：此时，
根据模型概率判定模型集不变或向左侧模型靠拢；
(11)
(12)
式中，t2表示有效模型的门限值，一般取t2>0.7。
3)模型概率重心向右跳变：此时，
根据模型概率判定模型集不变或向右侧模型靠拢；
(13)
(14)
由以上公式可以看出，整个过程中δ是影响调整模型间距的重要因子，δ过小则调整过慢，无法描述大角度变化，δ过大则调整过度，角速度振荡变化无法维持在精确值。而在跟踪过程中，无法得知下一刻角速度变化，并且误差对角速度的影响极大，δ很难自适应，可考虑更改模型后验概率求解方式。
文献中交互多模型原则上可认为模型集中各模型关系是并列的，在采用自适应网格调整后，已知调整后模型集中有一确定模型(中心模型)是最佳模型，可以考虑分配给最佳模型较大的权重，可获得更好的估计性能。
假定模型集中有r个模型，各模型滤波完成后，对于模型j，由目标运动子模型j的新息Vj(k)及其协方差矩阵Sj(k)计算新息的平方
(15)
对r个目标运动子模型的第k时刻新息的平方
按从小到大的方式排序：
(16)
对较小的新息的平方分配较大的系数，根据系数求得模型后验概率：
(17)
k时刻各模型的权值可根据下面公式获得：
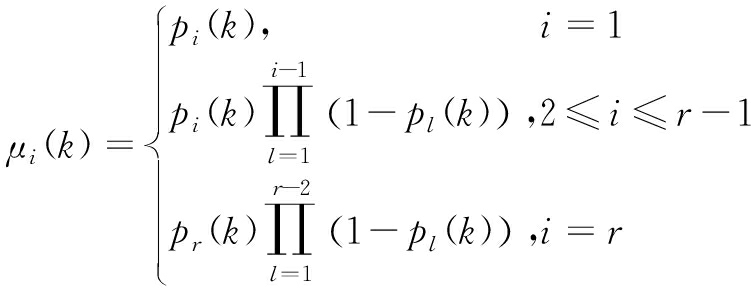
(18)
仿真1：假设目标的起始位置为[60， 40]km,起始速度为[-212， 212]m/s，转弯速度300 m/s，对目标进行300 s的观测，采样间隔T为1 s。在1～60 s，156～180 s，246～300 s目标在x-y平面沿北偏西45°方向作匀速直线运动；在61～155 s目标作左转1.87°圆周运动；在181～245 s目标作右转-2.8°圆周运动。距离误差的标准差为50 m，方位角误差的标准差为0.2°。初始模型集选取M0={-60°,0.01°,60°}，网格间隔δ=0.1°。(IMM-AG为交互多模型-自适应网格算法、AW-IMM-AG为自适应权值-交互多模型-自适应网格算法。)
由图1和图2可以看出，由于仿真1条件下目标真实角速度较小，而传统IMM-AG设计小的网格间隔，此时AW-IMM-AG算法虽然比IMM-AG算法角速度估计效果略好，但滤波误差相差不大。
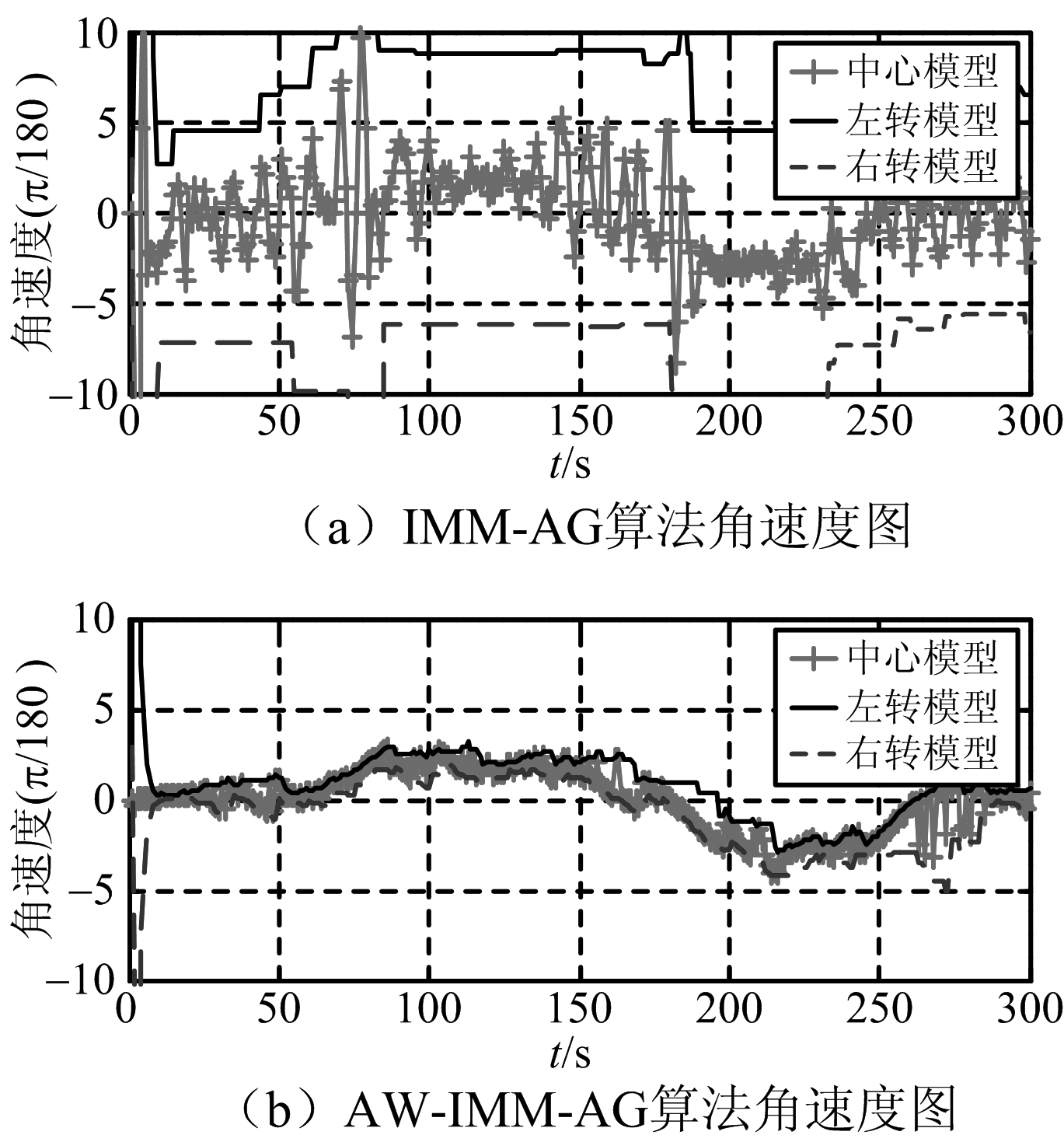
图1 仿真1条件自适应网格法求解角速度图
图2 仿真1条件距离RMSE图
仿真2：其余条件与仿真1相同，在61～155 s目标作左转61.87°圆周运动；在181～245 s目标作右转-42.8°圆周运动。由图3和图4可以看出，由于仿真2条件下目标真实角速度变大，而网格间隔仍是一个很小的值，AW-IMM-AG算法仍能估计角速度，而IMM-AG算法角度调整过慢，已难以精确估计角速度，滤波性能急剧降低。
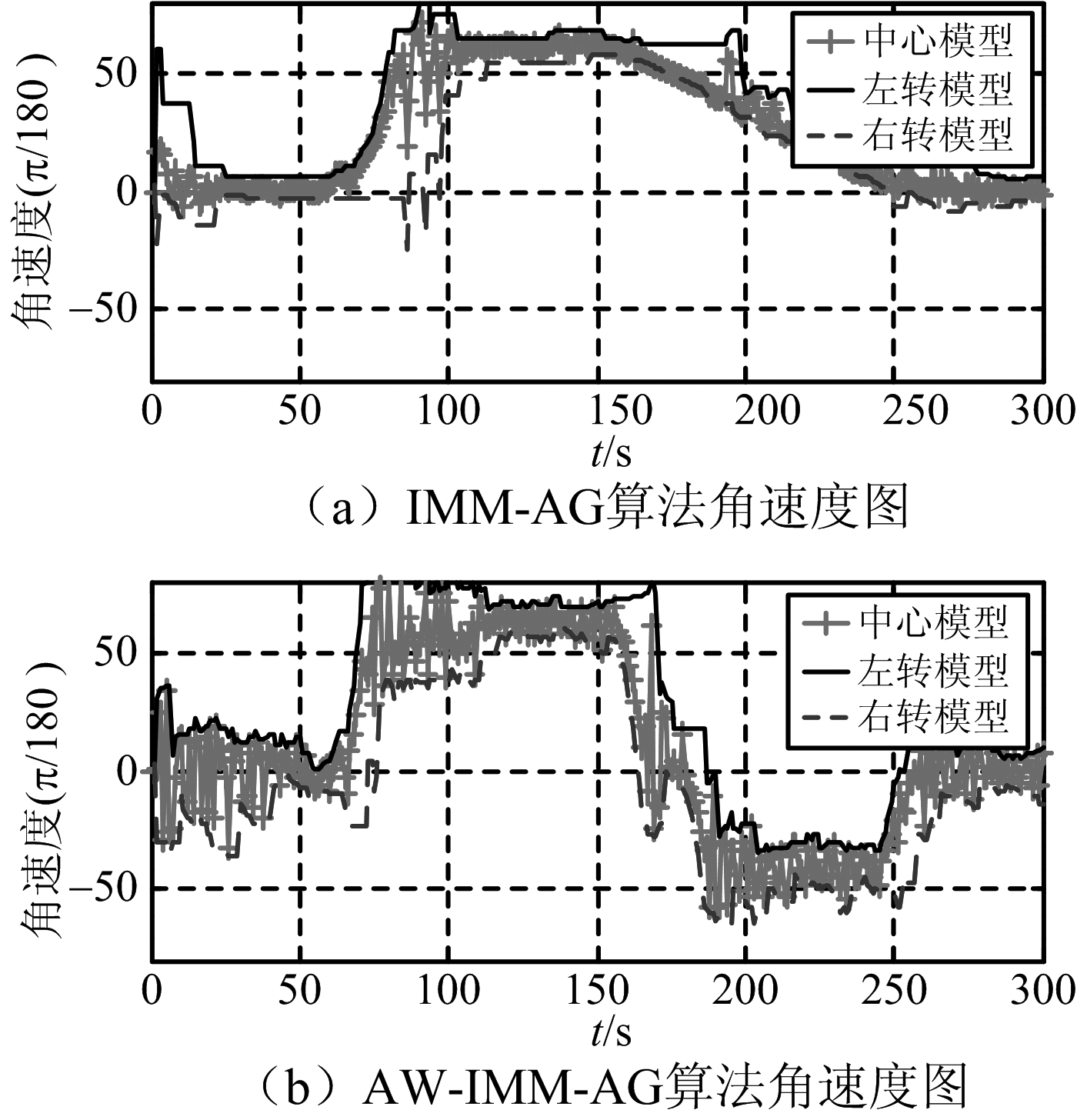
图3 仿真2条件自适应网格法求解角速度图
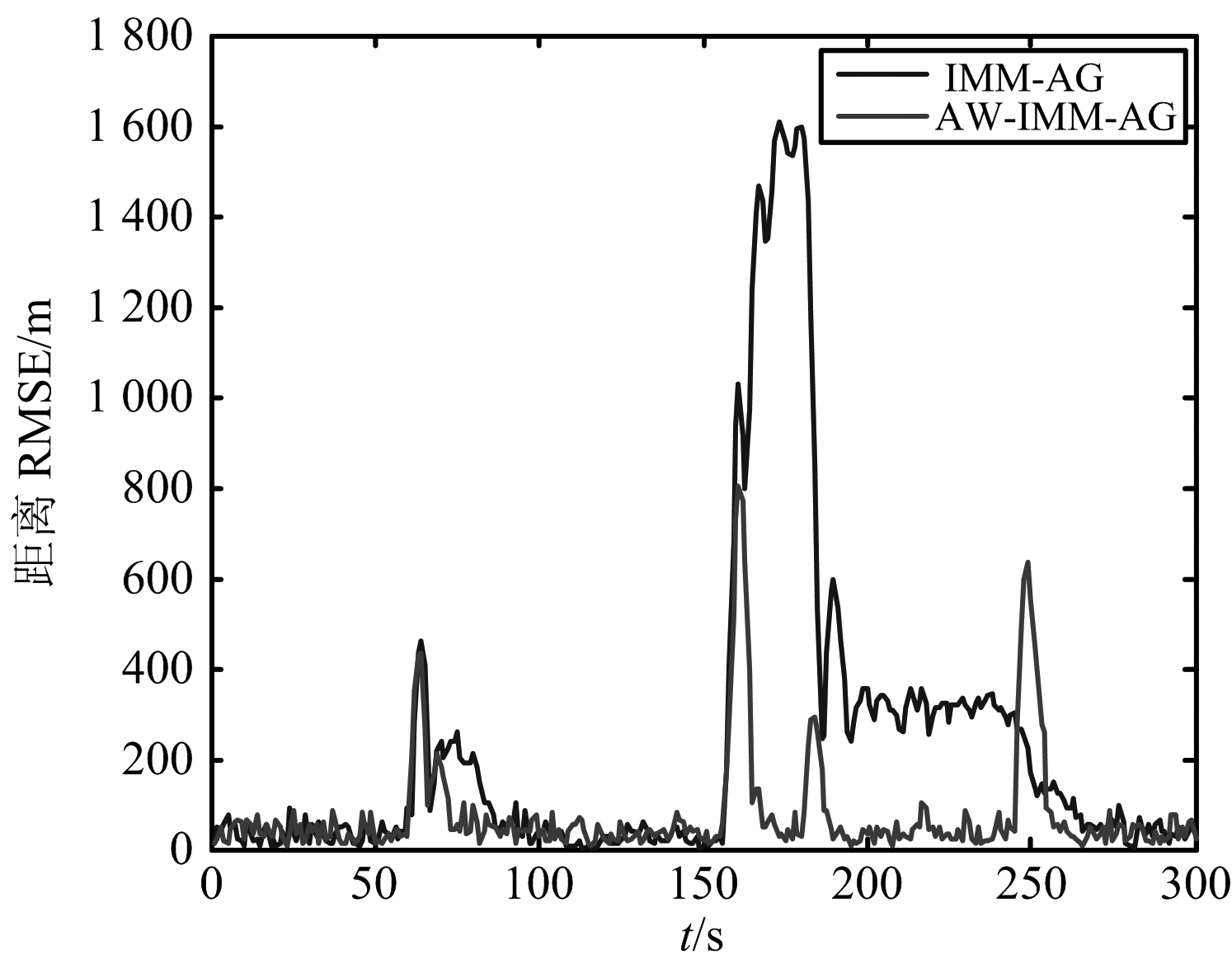
图4 仿真2条件距离RMSE图
仿真3：其余条件与仿真2相同，本文所提AW-IMM-AG算法网格间隔δ不调整，而传统IMM-AG算法调整网格间隔δ=6°。由图5和图6可以看出，由于仿真3条件下IMM-AG算法经过增大网格间隔可以估计较大角速度值的转弯运动，滤波误差相差不大。由于并无先验知识知道目标以多大的角速度转弯甚至目标是不是转弯运动，AW-IMM-AG算法不需要调整网格间隔δ，以一个较小的网格间隔就可以估计较大范围的角速度值，同时保证误差在合理可接受的范围内。
图5 仿真3条件自适应网格法求解角速度图
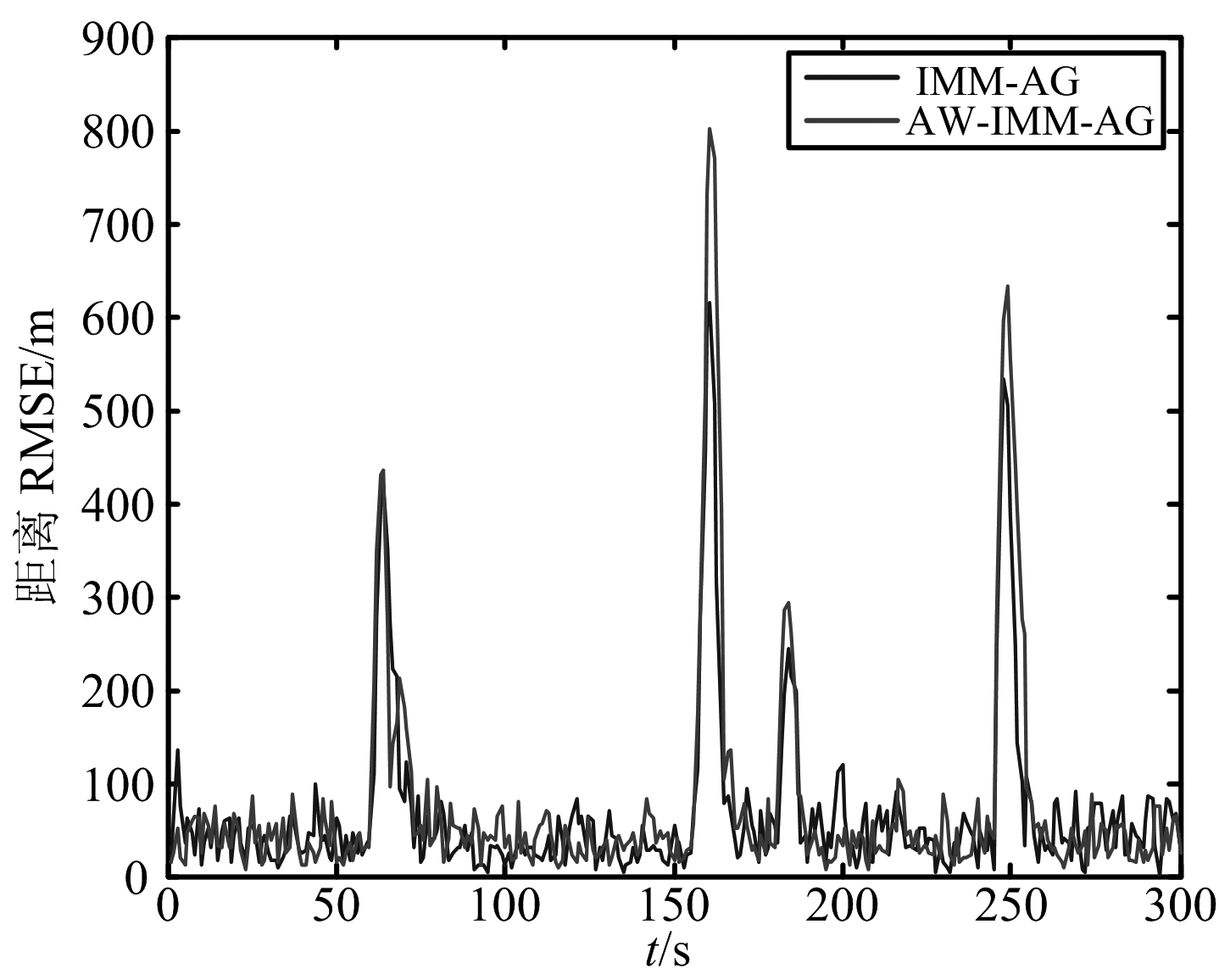
图6 仿真3条件距离RMSE图
仿真4：跟踪一段高超声速飞行器的三维机动轨迹，距离误差的标准差为50 m，方位角误差的标准差为0.2°，俯仰角误差的标准差为0.2°。初始模型集选取M0={-60°,0.01°,60°}，网格间隔δ=0.1°。
由图7和图8可以看出，在真实运动不是转弯运动情况下，AW-IMM-AG算法比IMM-AG算法滤波效果好，本方法可应用于高速机动目标跟踪。
图7 仿真4条件滤波轨迹
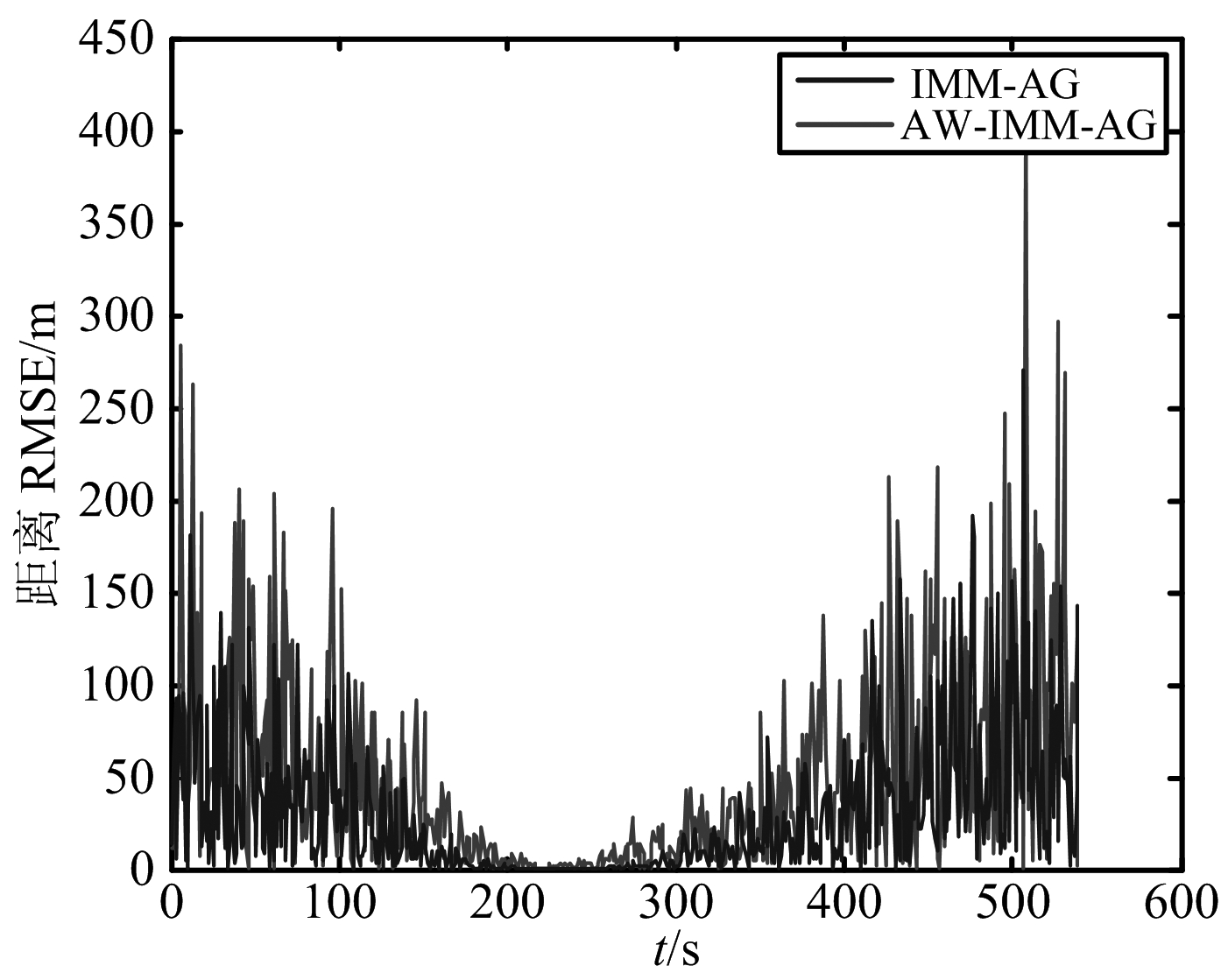
图8 仿真4条件距离RMSE图
本文对自适应转弯模型进行了改进，针对IMM-AG算法依赖于网格间隔的选取提出了相应改进AW-IMM-AG算法。通过仿真试验验证了AW-IMM-AG算法的有效性和必要性，同时由于AW-IMM-AG算法并不是直接针对网格间隔的改进，而是通过对多模型概率的改进，AW-IMM-AG算法或可用于模型集的改进，尤其模型集中总有一模型符合真实运动情况。
参考文献：
[1] 聂晓华, 张夫鸣, 徐一鸣. HSHV机动目标跟踪的自适应模型算法[J].系统工程与电子技术,2016,38(3):507-510.
[2] 杨永建, 樊晓光, 王晟达,等. 基于自适应CS模型的IMM算法[J]. 系统工程与电子技术,2016,38(5):977-983.
[3] 金亮亮, 刘亚云. 一种改进自适应机动目标跟踪算法[J].雷达科学与技术,2014,12(1):98-100.
[4] 崔彦凯,梁晓庚,王志刚,等.高速高机动目标自适应IMM跟踪算法[J].计算机工程与应用,2014,50(8):198-201.
[5] 张新宇, 吴盘龙, 张廉政. 基于 IMM 的改进去偏转换测量目标跟踪算法[J]. 电光与控制, 2014, 21(12):41-44.
[6] LERRO D, BAR-SHALOM Y. Interacting Multiple Model Tracking with Target Amplitude Feature[J]. IEEE Trans on Aerospace and Electronic Systems, 1993, 29(2):494-509.
[7] MUNIR A, MIRZA J A, KHAN A Q. Parameter Adjustment in the Turn Rate Models in the Interacting Multiple Model Algorithm to Track a Maneuvering Target[C]∥ IEEE International Multi Topic Conference, Lahore: IEEE, 2001:262-266.
[8] BEST R A, NORTON J P. A New Model and Efficient Tracker for a Target with Curvilinear Motion[J]. IEEE Trans on Aerospace and Electronic Systems, 1997, 33(3):1030-1037.
[9] LI X R, JILKOV V P. Survey of Maneuvering Target Tracking: Part V Multiple-Model Methods[J]. IEEE Trans on Aerospace and Electronic Systems, 2005, 41(4):1255-1321.
[10] 秦雷, 李君龙, 周荻. 基于AGIMM的临近空间机动目标跟踪滤波算法[J]. 系统工程与电子技术, 2015, 37(5):1010-1014.
YANG Yungao1, NI Wei1, YAN Hao2, CAO Yunhe2
(1.The716th Research Institute of CSIC,Lianyungang222006,China;2.Xidian University,Xi’an710071,China)
Abstract:Traditional single-model methods are hard to meet the tracking accuracy of the maneuvering target, so the adaptive models and multiple models have become the focus in this field. The turn model has been studied widely because of its simple form and low computational complexity. However, due to the unknown turn angular velocity of the maneuvering target, the smallest grid distance cannot be determined in the grid adjusting algorithm, resulting in inaccurate estimation of the true angular velocity and slow estimation velocity. A modified maneuvering target tracking method based on the posterior probability can solve the problem well. Through calculating of the multiple models’ posterior probability, the weights of the corresponding models in the multiple- model algorithm are obtained. The simulation results demonstrate the effectiveness of the modified method.
Key words:maneuvering target tracking; grid distance; turn angular velocity; posterior probability
中图分类号：TN911； TN953+.5
文献标志码：A
文章编号：1672-2337(2018)03-0322-05
DOI:10.3969/j.issn.1672-2337.2018.03.015
收稿日期：2017 09 06；
修回日期：2017 10 23
基金项目：国家自然科学基金(No.61771367)
作者简介：
杨云高 男，1988年生于山东临沂，硕士研究生，工程师，主要研究方向为信号处理与数据处理、自动控制方向。E-mail：yangyungao716@126.com
倪 威男，1984年生于四川内江，博士研究生，高级工程师，主要研究方向为信号处理与数据处理。