
邢煦然1,赵宏钟2,贾 鑫2
(1.装备学院研究生院, 北京 101416; 2.装备学院光电装备系, 北京 101416)
摘 要:极点是谐振区雷达目标的最主要特性。矩阵束法是目前提取雷达目标极点中应用最广泛的算法。在使用矩阵束法提取极点时,现有阶数估计方法普遍存在阶数偏大和虚假极点难以区分的问题。针对这一问题,首先描述了矩阵束法估计得到的极点的分布特性;然后通过对极点集投影估计了真实极点的个数;最后用DBSCAN算法对极点分类,剔除了虚假极点,保留了真实的极点。通过FEKO仿真细杆和球体目标的电磁散射数据验证了算法,有效剔除了虚假极点并提取出了真实极点。
关键词:密度聚类; 极点; 矩阵束法; 谐振区
当雷达信号波长与雷达目标的特征尺寸相当时,雷达工作在谐振区,雷达回波中会存在谐振现象。极点是雷达目标在谐振区的最主要特性[1]。由于极点与目标相对姿态、雷达极化方式无关,只与目标本身的大小、形状、材料等有关,因此可以作为雷达目标识别的一种途径。与光学区相比,可以克服姿态敏感性,具有更大的应用前景。根据奇点展开理论[2],谐振区雷达目标的后时响应可以用极点的衰减复指数和表示。矩阵束法是当前综合性能较好、运用最广的极点提取算法[3-4]。在使用矩阵法提取极点时,普遍存在虚假极点的问题。大量的虚假极点使真实极点难以被区分,更影响了极点作为一种雷达目标识别方式的精度。
针对上述问题,本文首先从试验的角度分析不同定阶参数下矩阵束估计极点的分布规律,根据矩阵束提取极点的分布特性,通过DBSCAN(Density-Based Spatial Clustering of Applications with Noise)对不同阶数下提取的极点集进行聚类,实现了真实极点与虚假极点的区分,最终提取出真实有效的极点。为理论分析与对比方便,本文分别采用了细杆和球体作为谐振区目标,通过理论计算两类目标极点的解析解与电磁计算实验提取的极点对比,验证了算法的正确性。
使用矩阵束法估计信号极点,首先由时域信号y构造Hankel矩阵Y:

(1)
然后对Y进行奇异值分解Y=USVT,U,V分别为Y的左奇异矩阵和右奇异矩阵。分别去掉V第一行和最后一行得到V1,V2。取U的前M列为U′,构造矩阵Y1,Y2:
(2)
(3)
矩阵![]() 的特征值z变换到拉普拉斯域即为极点。其中上标“+”表示伪逆。M为矩阵束法的阶数,也是极点的个数。
的特征值z变换到拉普拉斯域即为极点。其中上标“+”表示伪逆。M为矩阵束法的阶数,也是极点的个数。
矩阵束法提取极点的流程概括为:1)用后时响应构造信号Hankel矩阵Y;2)对矩阵Y进行奇异值分解;3)构造特征矩阵![]() 提取矩阵束的特征值。
提取矩阵束的特征值。
目前用于矩阵束法的阶数估计方法主要有比较奇异值[5]、最小二乘法[6]和最小描述长度(MDL)法[7]。
比较奇异值大小的方式实用性差,因为对于实测或电磁仿真计算获得的信号,其奇异值大小变化通常比较均匀,难以直接以奇异值大小确定阶数。
最小二乘法遍历所有可能阶数,用矩阵束提取极点,然后用留数和极点分别重构信号。得到的重构信号ym与原始信号y比较,计算误差:
(4)
选取平方误差最小时的m值为估计结果。最小二乘法存在两个问题,一是方程病态导致留数误差,此时即使极点准确,重构误差也会很大;二是由于以最佳重构为准则,无法剔除采集信号本身带来的虚假极点。
最小描述长度(MDL)法是1978年Rissane提出的[8]。该方法定义阶数m的函数:
MDL(m)=-2L(θ)+mlnN
(5)
MDL值最小时的m为模型阶数的估计值,文献[7]给出了对于极点阶数问题的L(θm)推导过程。MDL法可以准确估计出理想信号的阶数,但对于仿真和实测信号,其结果会大于真实极点的个数。
矩阵束法虚假极点的成因可以概括为两点:一方面,现有的极点个数估计算法的结果为真实极点与虚假极点个数之和;另一方面,即使在正确的阶数下,某些观测角下也可能因为个别极点对应的奇异值过小而丢失,提取出奇异值更大的虚假极点。矩阵束法的定阶问题概括为:1)定阶比真实值小,遗漏部分真实极点;2)定阶与真实值相符,可能有虚假极点代替真实极点;3)定阶比真实值大时,引入虚假极点。
真实极点和虚假极点具有不同的分布特性,可以通过这些特性确定极点的真实性。真实极点具有以下特性:1)根据奇点展开理论,极点是衰减的,实部小于零;2)获得极点在激励信号的带宽范围之内;3)实信号的极点是共轭对称的。由以上性质,可以剔除一部分虚假极点,但是也存在同时满足以上条件的虚假极点。对比不同阶数的极点结果发现,真实极点的分布具有稳定性,而虚假极点位置变化大。也就是说,不同阶数下,真实极点聚集,虚假极点分散,真实极点附近区域的密度远高于其他区域。
DBSCAN 是一种经典的密度聚类算法。DBSCAN定义了以下概念[9]:1)邻域:给定对象集D,∀p∈D,以对象p为中心,半径为eps的邻域;2)密度:对象p邻域内对象的个数;3)核心点:对象p邻域的密度大于密度阈值Minpts,则定义p为核心点;4)噪声点:对象p不属于任何簇,则p为噪声;5)直接密度可达:对象q和p,q∈p的邻域,且p为核心点,则q从p直接密度可达;6)密度可达:∀[p1,p2,…,pm]∈D,若满足pi+1是从pi直接密度可达的,则pm是从密度可达的p1;7)密度互连:对象o,p,q,对象p和q是从o关于eps和Minpts密度可达,那么p和q关于eps和Minpts密度互连。
DBSCAN的核心思想概括为[10]:从任意选定的数据点出发,不断向密度可达的区域扩张,从而得到一个包含核心点和边界点的最大化区域,区域中任意两点密度互连。聚类过程从对象集D中任意对象p开始,若p的半径eps邻域密度达到密度阈值Minpts,则建立一个p为核心点的簇,否则寻找下一个对象。找到核心点p后,在p邻域内的直接密度可达对象中继续寻找核心对象。重复此过程寻找这些核心点的直接密度可达对象,并合并密度可达的簇。当没有新对象添加到任何簇时,聚类过程结束。
在不同阶数时用矩阵束法计算信号的极点,算得的所有极点构成极点集,用于聚类分析。极点集的阶数选取要大于目标的真实极点个数,小于最小描述长度(MDL)估计的个数。为了减少运算量,不需要对符合上述要求的全部阶数进行计算,选取部分即可,本文选取了要求范围内的11个阶数构成极点集。获得极点集后,根据真实极点特性对极点集进行清理,剔除实部大于零、频率超出激励信号范围和不对称的极点,保留剩余极点的第二象限作为清理后的极点集进行分析。对极点集进行清理可以减少DBSCAN的运算量。
清理极点集后,可以利用极点集的分布确定真实极点的个数。对极点集向频率轴投影,获得极点的频率-个数曲线,得到的峰值在矩阵束次数附近的尖峰个数就是真实极点的个数。选取向频率轴投影的原因有两个:1)频率轴方向范围已知且有限,而极点的实部理论上是无限的;2)信号内有干扰时,极点的频率比衰减量更加稳定。
DBSCAN对半径eps和密度阈值Minpts敏感,这两个参数的选取直接影响到聚类的结果。构造极点集时的矩阵束次数为M,密度阈值Minpts取M-1,因为真实极点在不同阶数的矩阵束估计时,都会出现在真实值附近,因此真实极点附近的密度应当与仿真的矩阵束次数相近。
获得极点的真实个数以后,在选定的密度阈值下,用不同的半径对极点集聚类,选取簇个数等于真实极点个数时的半径为半径的取值。获得DBSCAN的参数取值后,对极点集聚类分析。极点集内符合DBSCAN要求的点会被分到各个簇中,不符合要求的点被记为噪声点。由极点的分布特性,每一个簇会对应一个真实极点,对簇内的点取均值,视为极点的估计值。
DBSCAN改进的矩阵束法提取极点的流程为:1)在选定的M个阶数下,对后时响应信号做矩阵束,获得结果构成极点集;2)对极点集做投影,获得真实极点的个数;3)选定密度阈值为M-1,分析极点集在不同半径下聚类分析的簇个数,在簇个数等于真实极点个数区段选取半径;4)在选定的密度阈值和半径下,对极点集聚类分析,获得真实极点附近的簇;5)对每一个簇的点取均值,获得极点的最终值。
1) 仿真目标
本文用FEKO仿真了长1 m、半径0.005 m的理想导体细杆在60°入射角下的后时响应,以及半径0.5 m的理想导体球的后时响应信号,频段分别为0~1.5 GHz和0~1 GHz。细杆是典型的高Q值目标,球体是典型的低Q值目标,以证明方法适用的普遍性。细杆网格与后时响应如图1所示,球体网格与后时响应如图2所示。
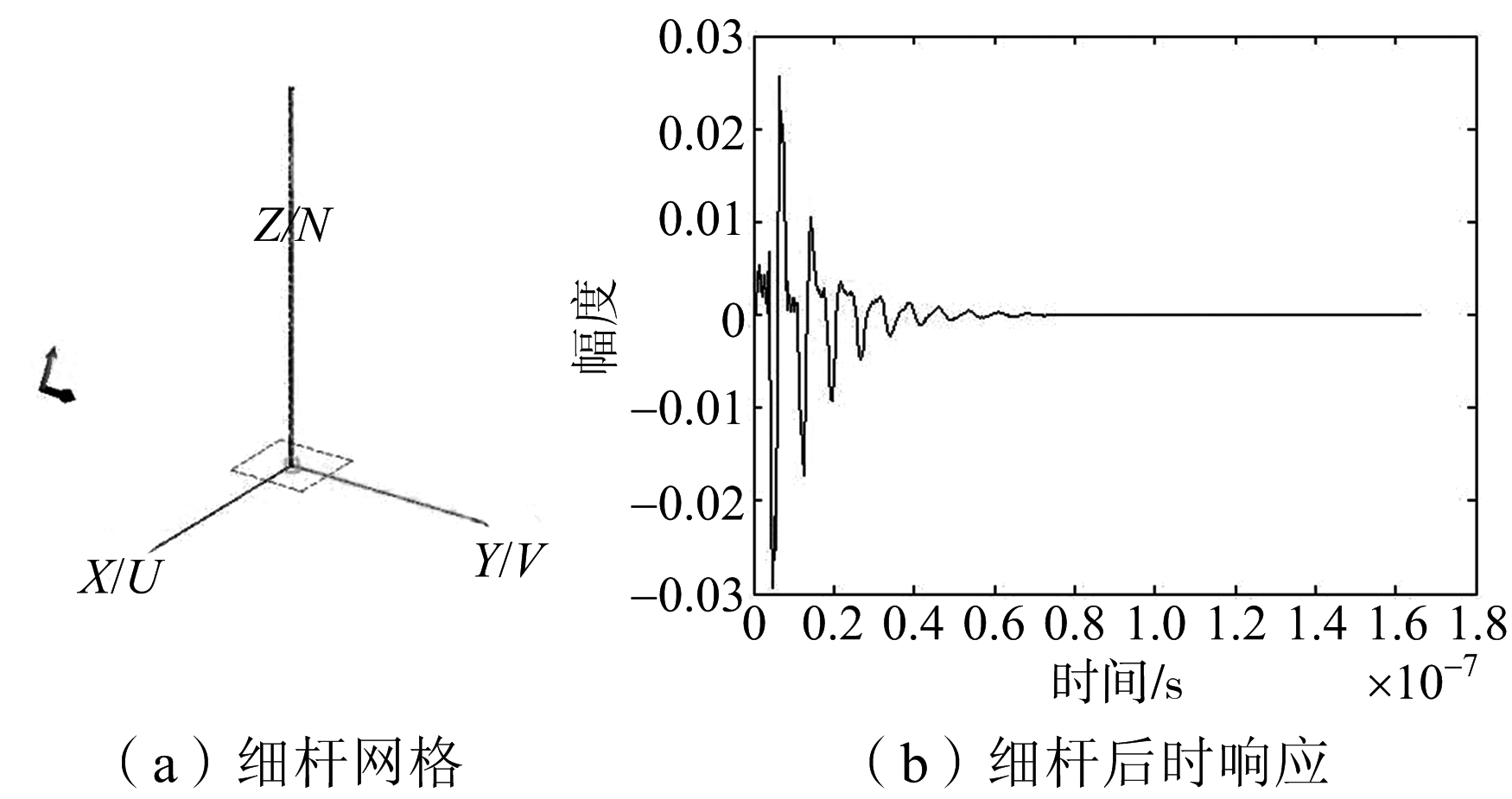
图1 细杆网格与后时响应
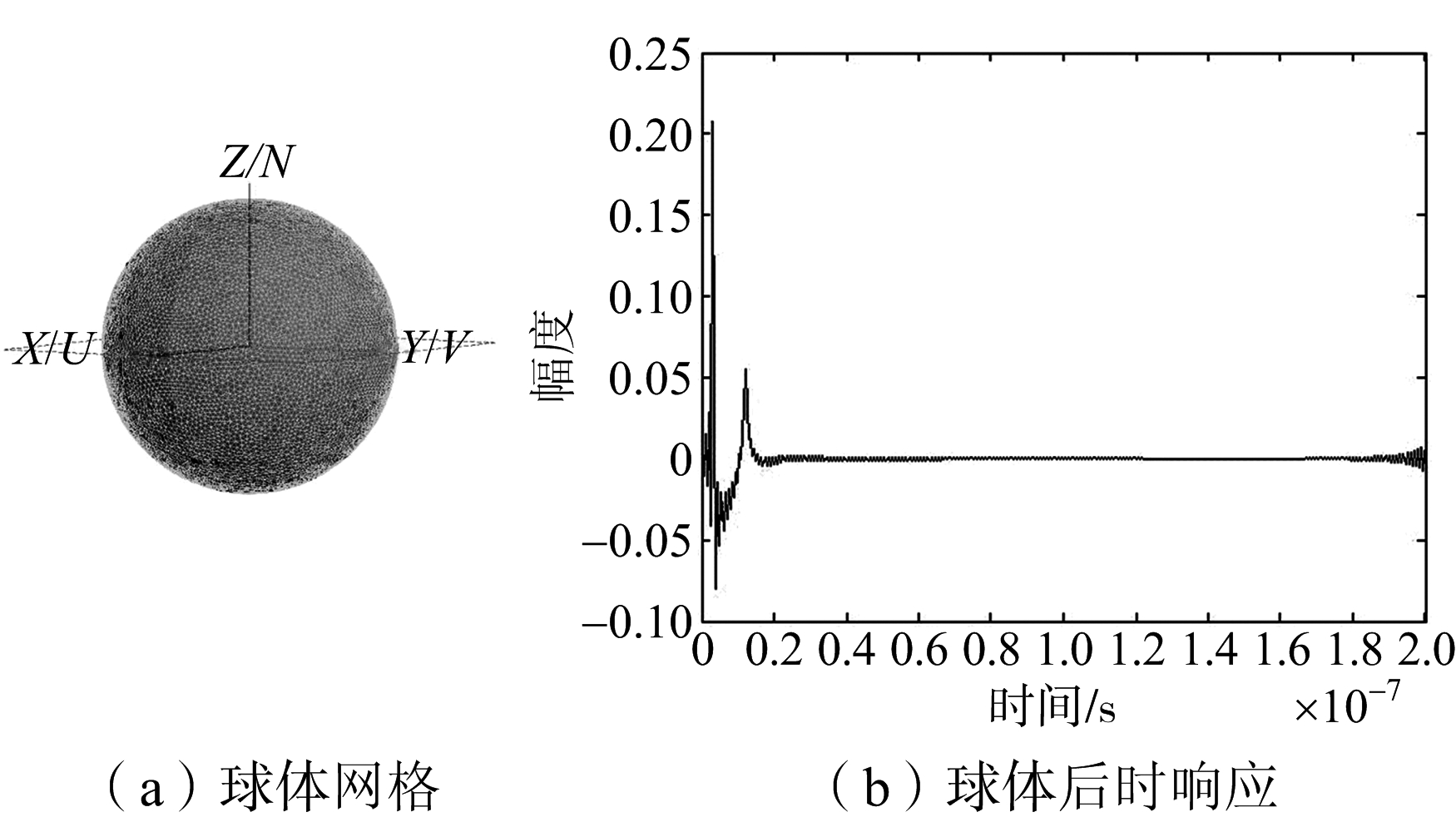
图2 球体网格与后时响应
选取细杆60°入射角是因为此角度的后时响应信号中,第4和第8个极点奇异值很小,在等于极点个数的阶数下使用矩阵束不能估计到这两个点,而会获得两个虚假极点。由理论值可知仿真频段内有10对极点,当阶数取20时,矩阵束估计的结果如图3所示,可见丢失了部分真实极点,高频部分的极点估计值也产生了误差。因此要正确估计全部的真实极点,阶数选取必定大于真实极点个数,这样也必定会带来虚假极点。
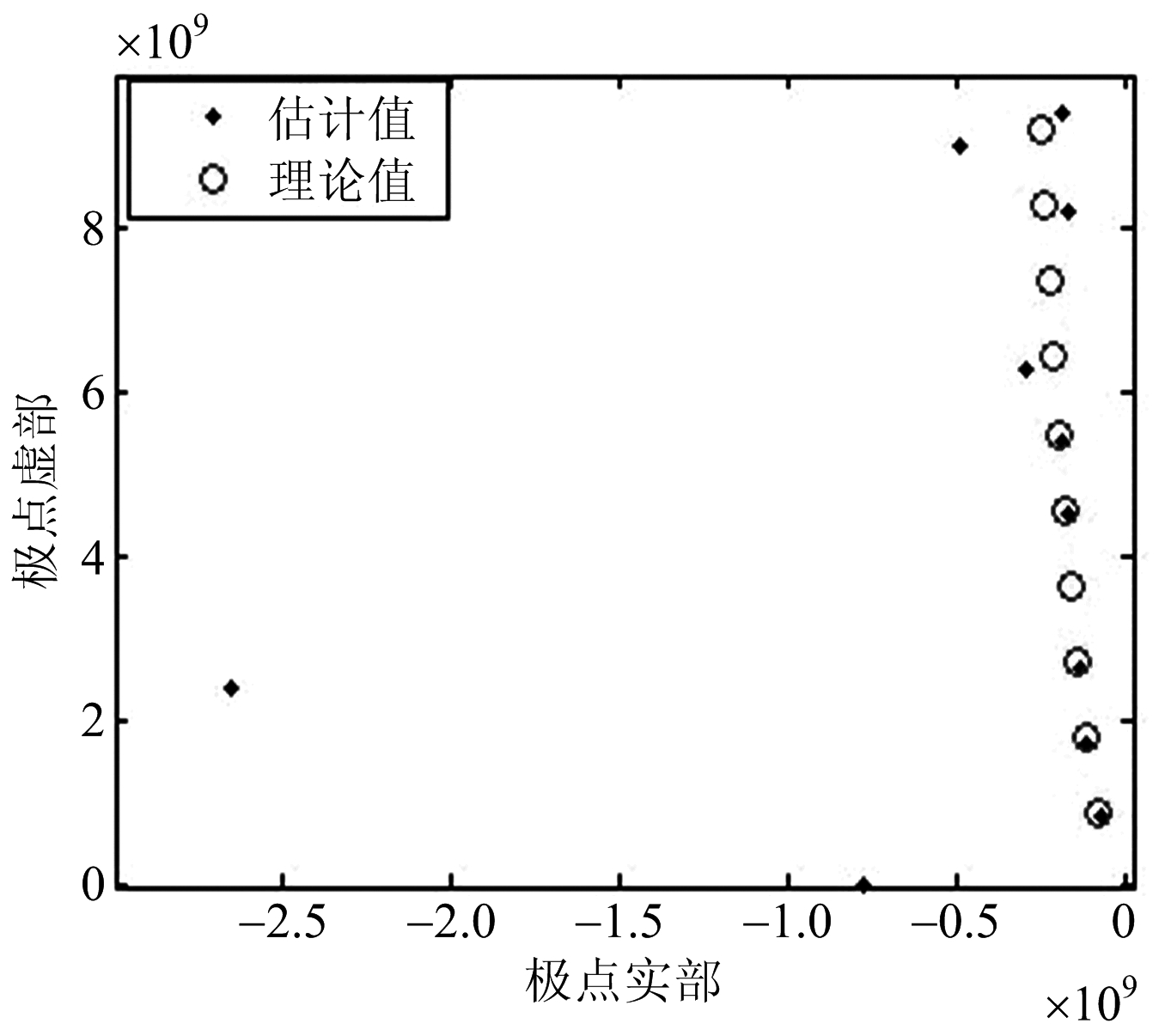
图3 阶数20时的细杆60°估计结果
2) 极点集的构造因为极点共轭对称成对出现,在选取阶数时只选取偶数阶。由上述信号,选取阶数40到60之间的偶数,用矩阵束法提取极点构造极点集,共做11次矩阵束,图4为细杆的极点集。3) 投影估计极点个数以细杆目标为例,仿真验证投影估计极点个数。对极点集向频率轴投影,从图5可以看出,细杆目标极点集中分布的频段有10个。每个集中分布的频段内极点个数达到11,与构成极点集时矩阵束的次数刚好吻合。可以得出结论:在仿真频段内共有10对真实极点。
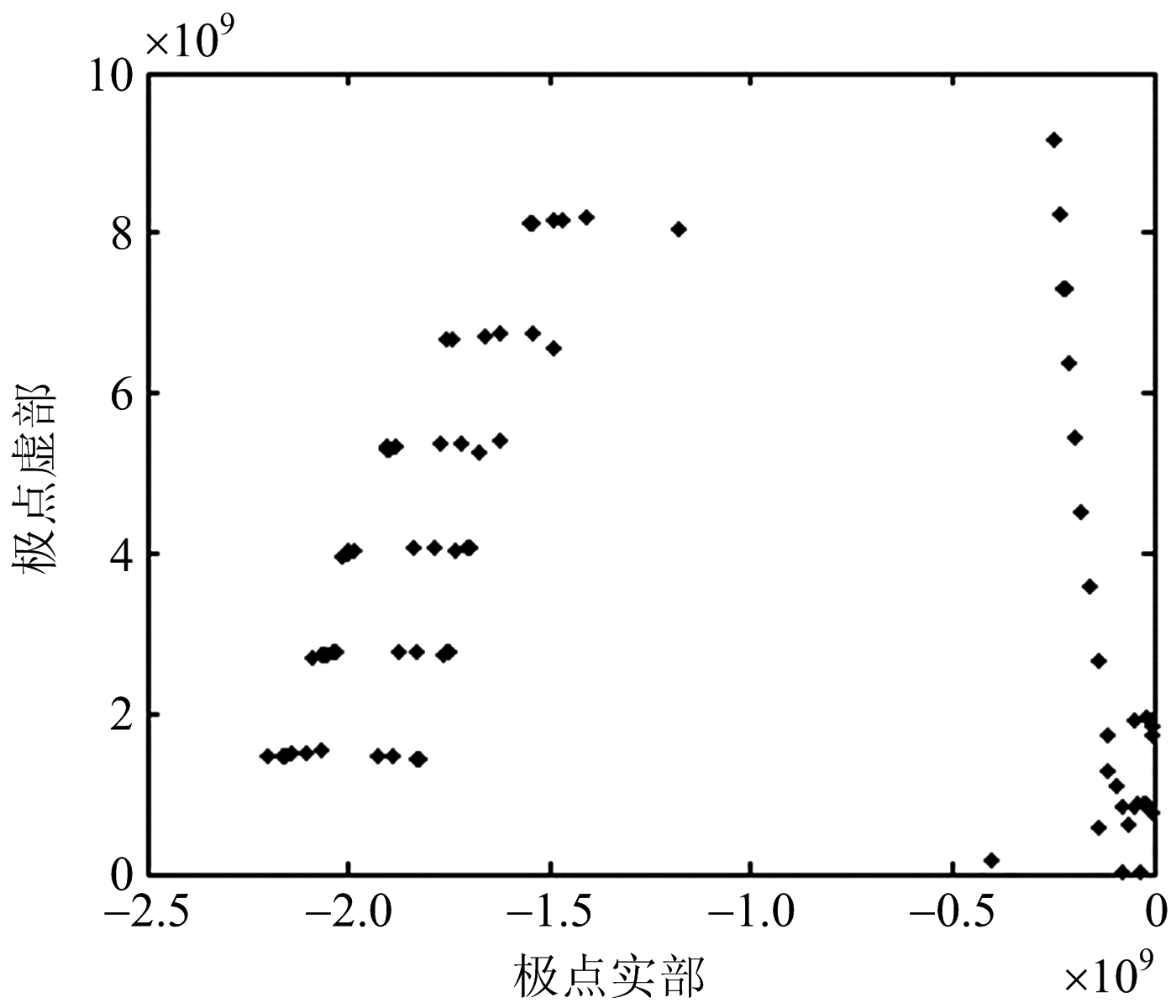
图4 细杆极点集
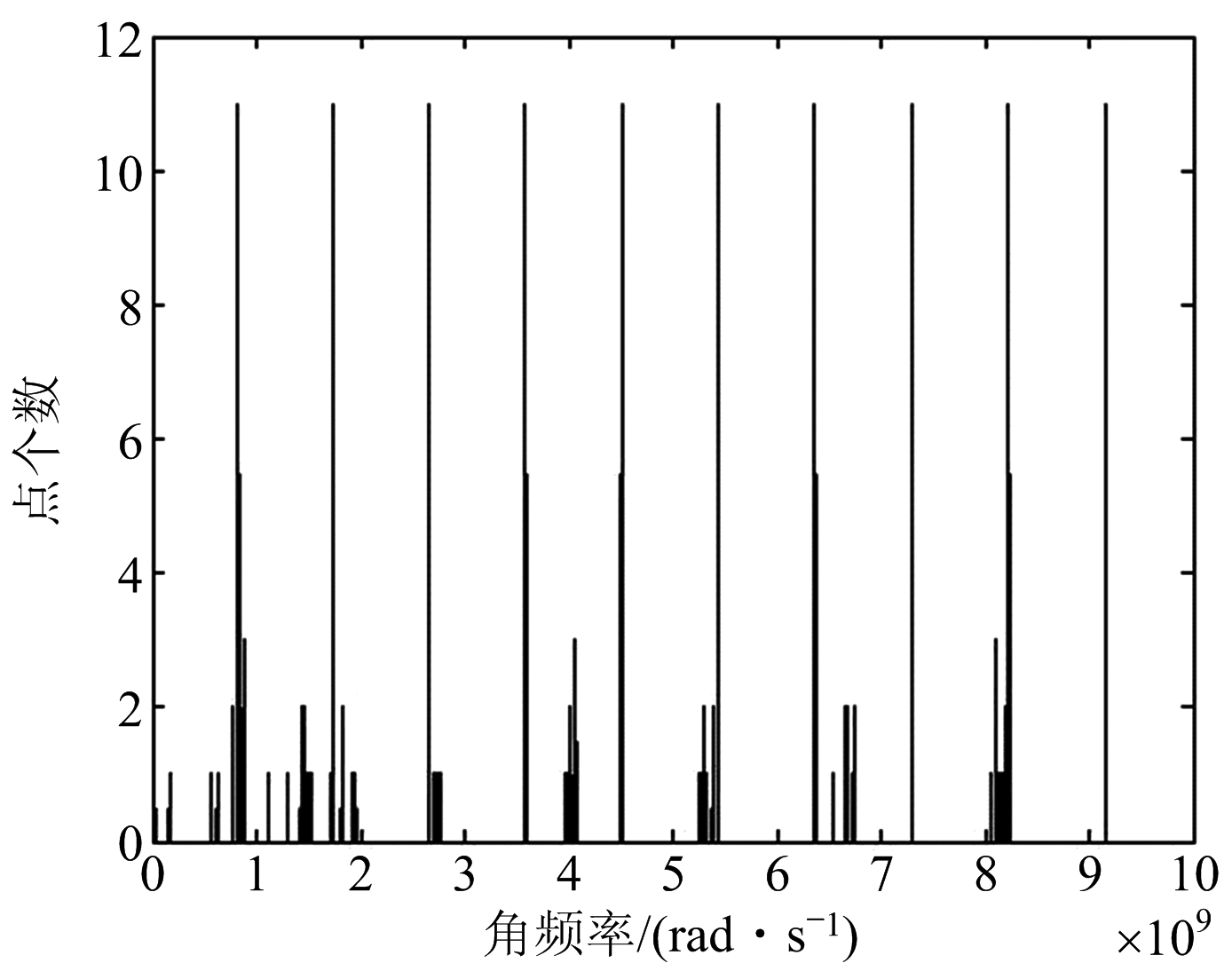
图5 细杆极点集投影结果
对极点集投影估计真实极点个数的优势在于,充分地利用了真实极点聚集的特性,获得真实极点的个数,克服了在信号不理想的情况下,最小二乘法和MDL法获得阶数大于真实极点个数的问题。4) DBSCAN的参数选取和流程以细杆目标为例,绘制密度阈值为10、不同半径下聚类获得的簇个数曲线。由投影可知,频段内有10对真实极点,因此半径的选取范围在簇个数为10的区间内。为了聚类结果只包含真实极点,选取半径时应当选择满足条件范围内的最小值。如图6所示,选取半径106.6。DBSCAN的参数设置为密度阈值10,半径106.6。
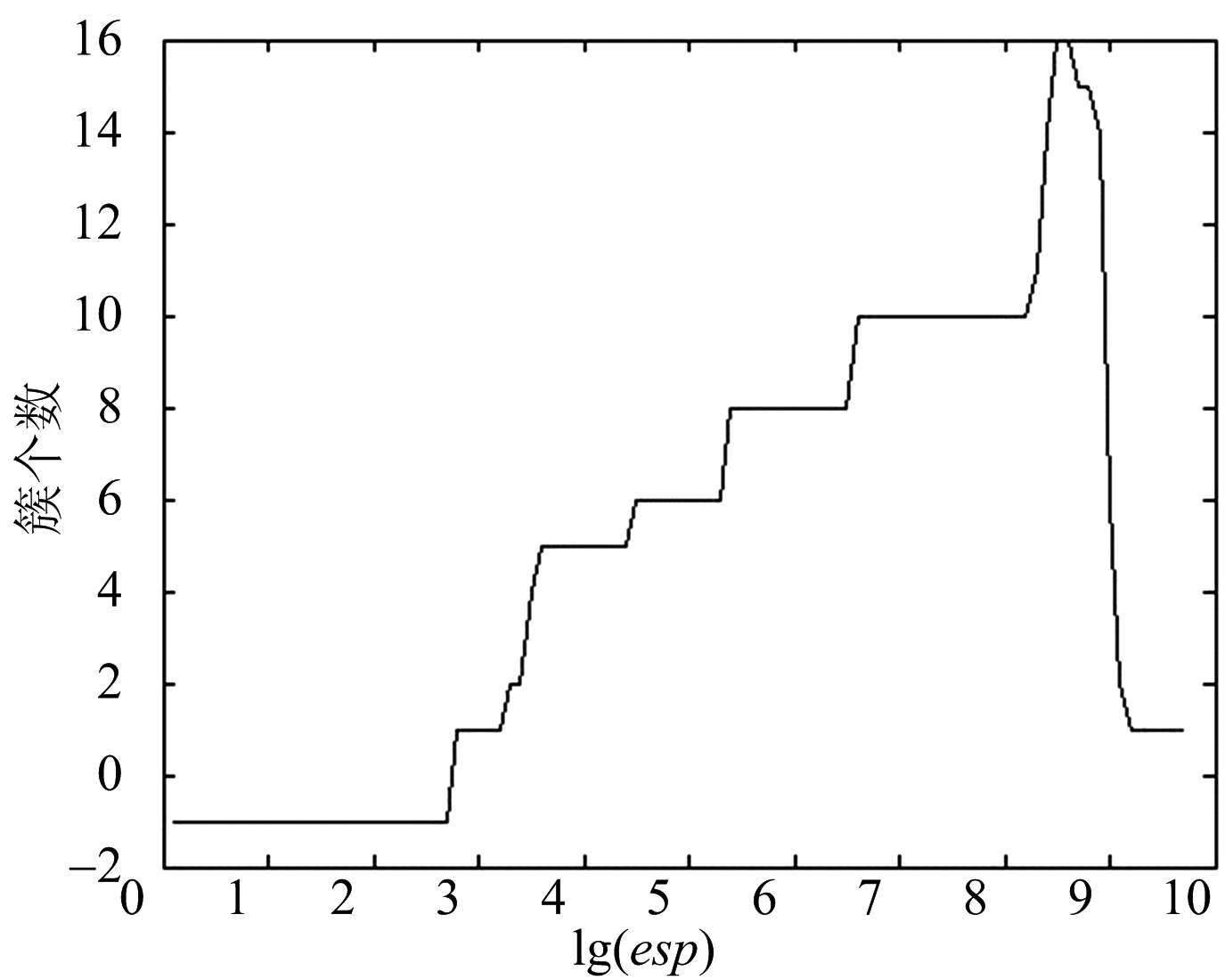
图6 半径-簇总数曲线图
以选取后的参数对极点集聚类,得到的聚类结果如图7所示。
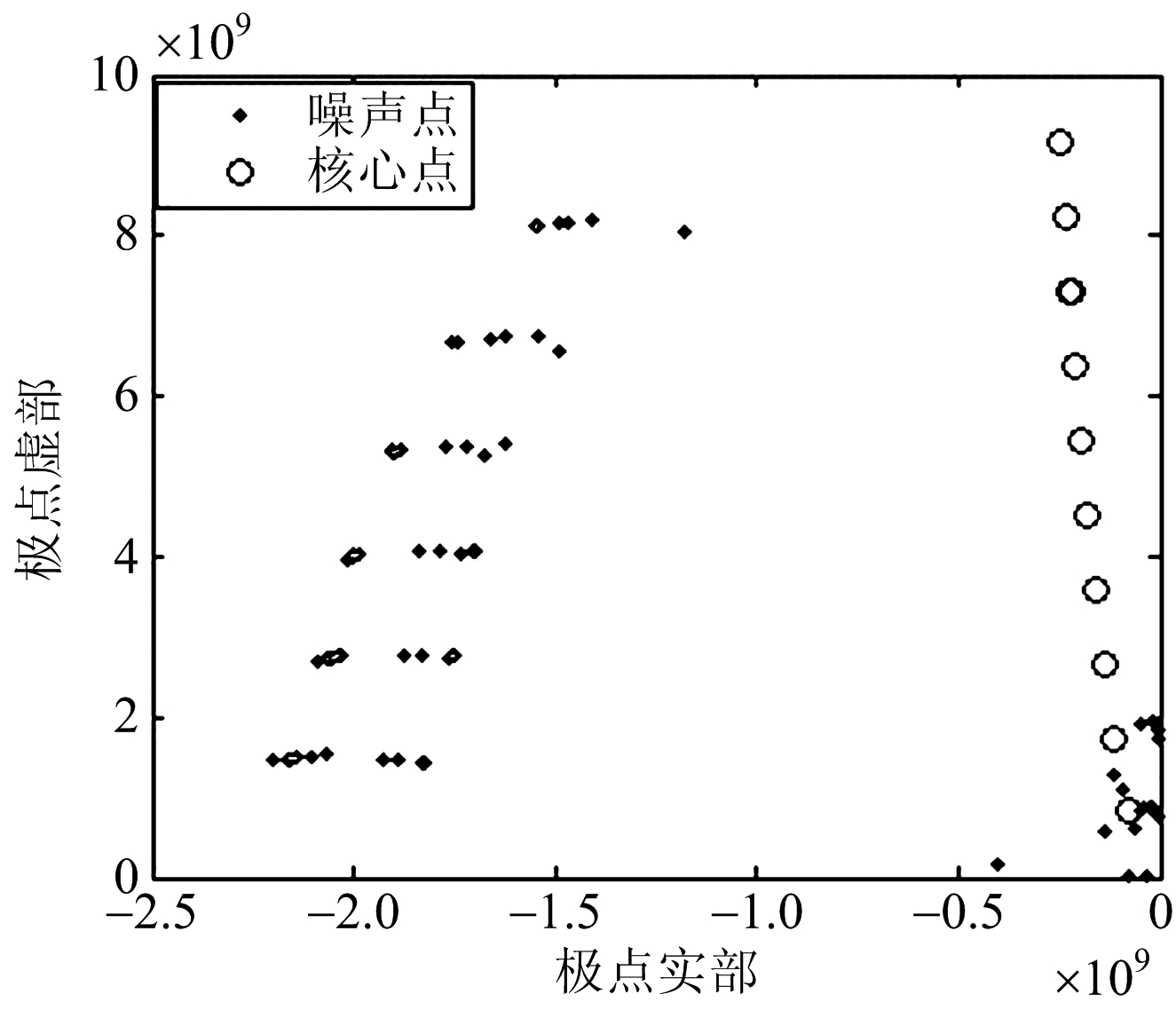
图7 细杆极点集聚类结果
对聚类得到的每一类的点(图7中的核心点)取均值,获得极点的最终值,与理论值对比,如图8所示。

图8 细杆DBSCAN-MPM提取极点结果
从图中可以看出,通过聚类分析,提取出了仿真频段内细杆的全部极点,并且成功剔除了所有的虚假极点。5) 球体仿真验证以相同的方法,对阶数40~60的球体矩阵束极点集聚类,并计算极点,与理论值相比较,如图9所示。
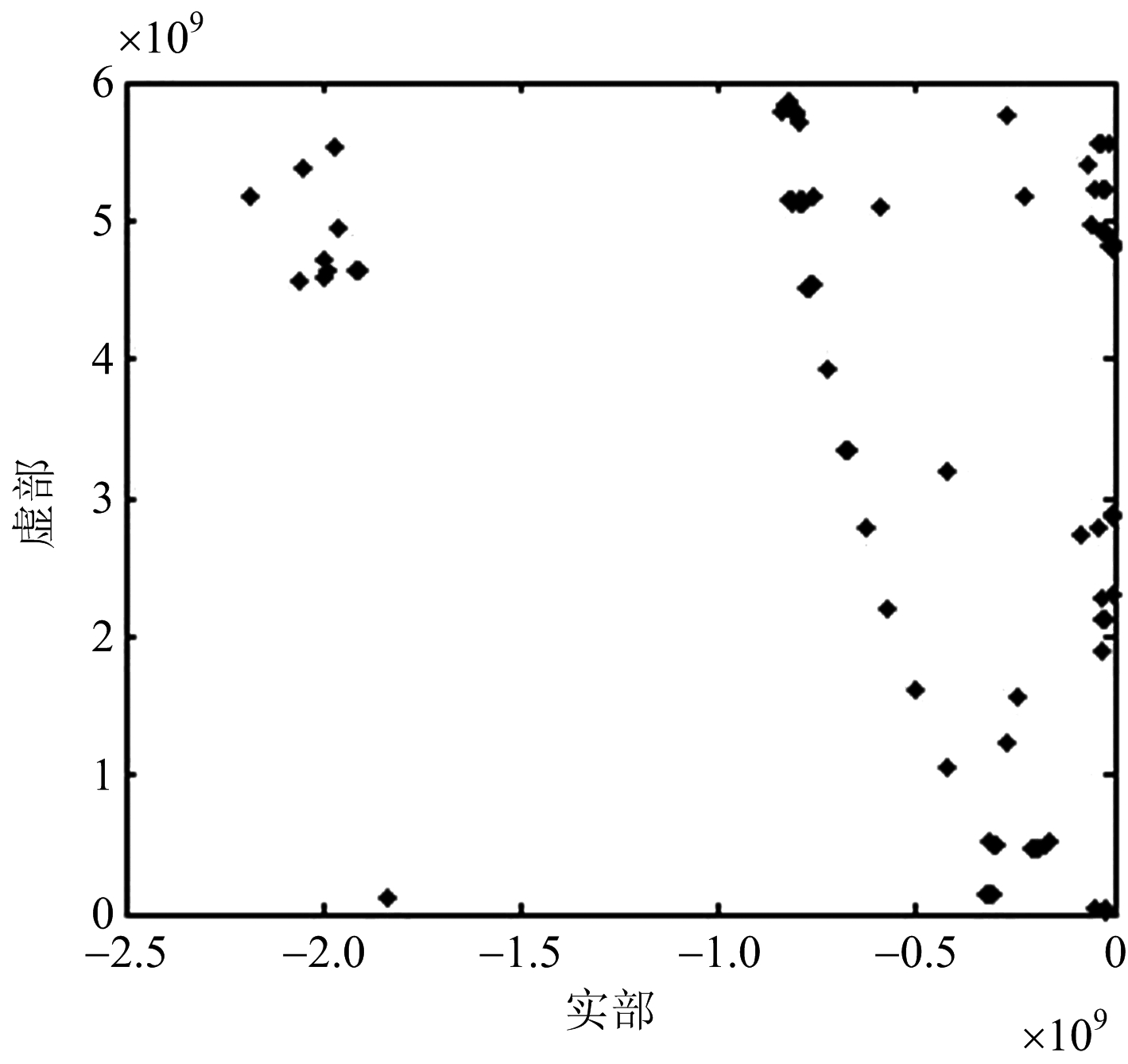
(a) 球体极点集

(b) 球体聚类结果
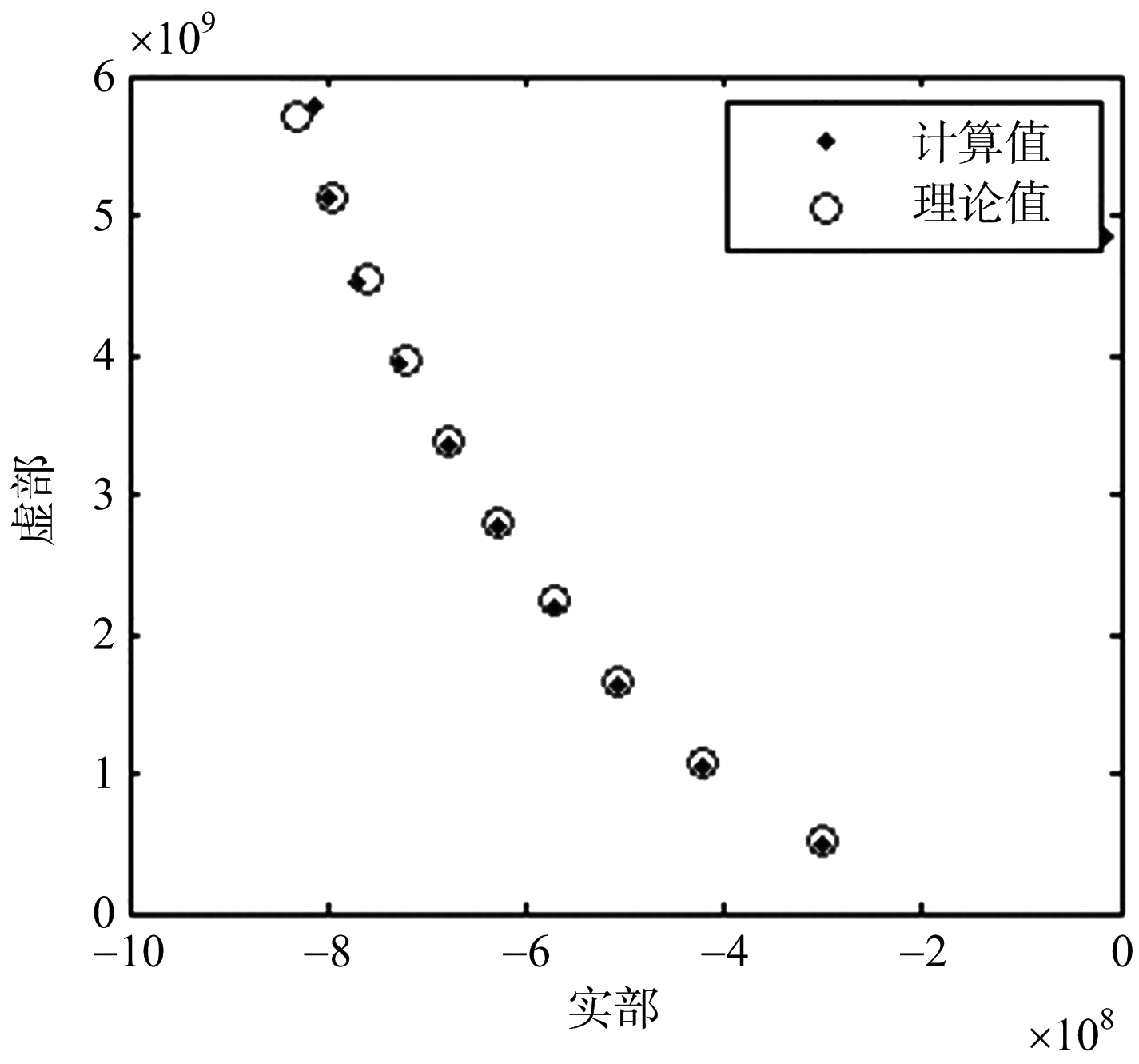
(c) 球体极点提取结果
图9 DBSCAN-MPM球体极点估计结果
从图中可以看出,提取出了球体在仿真频段内的全部真实极点,剔除了大部分虚假极点。6) 聚类结果与其他方法对比以细杆目标为例,对比最小二乘矩阵束法、MDL-MPM和本文提出的DBSCAN-MPM的提取结果,如图10所示。
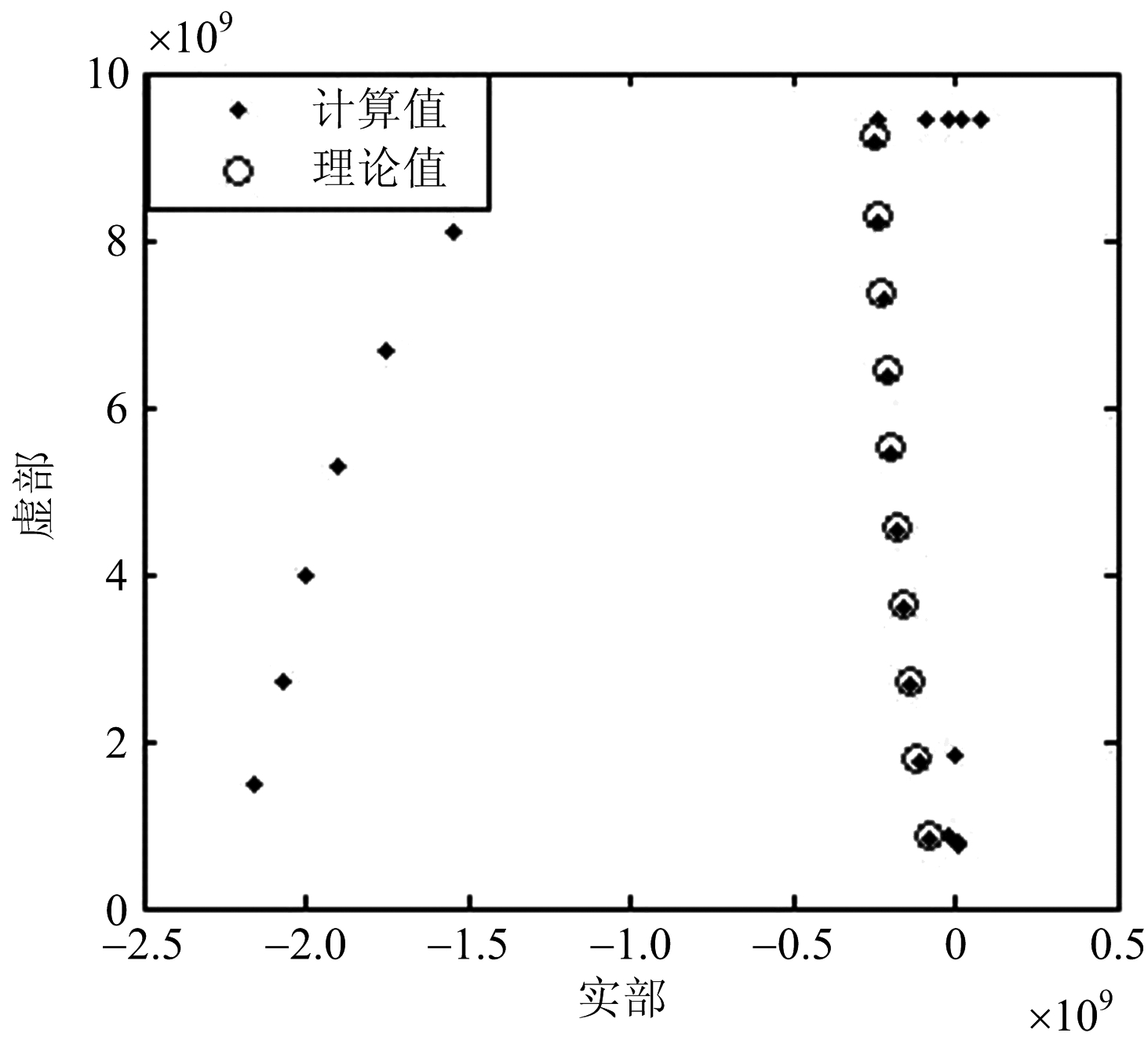
(a) 最小二乘矩阵束结果
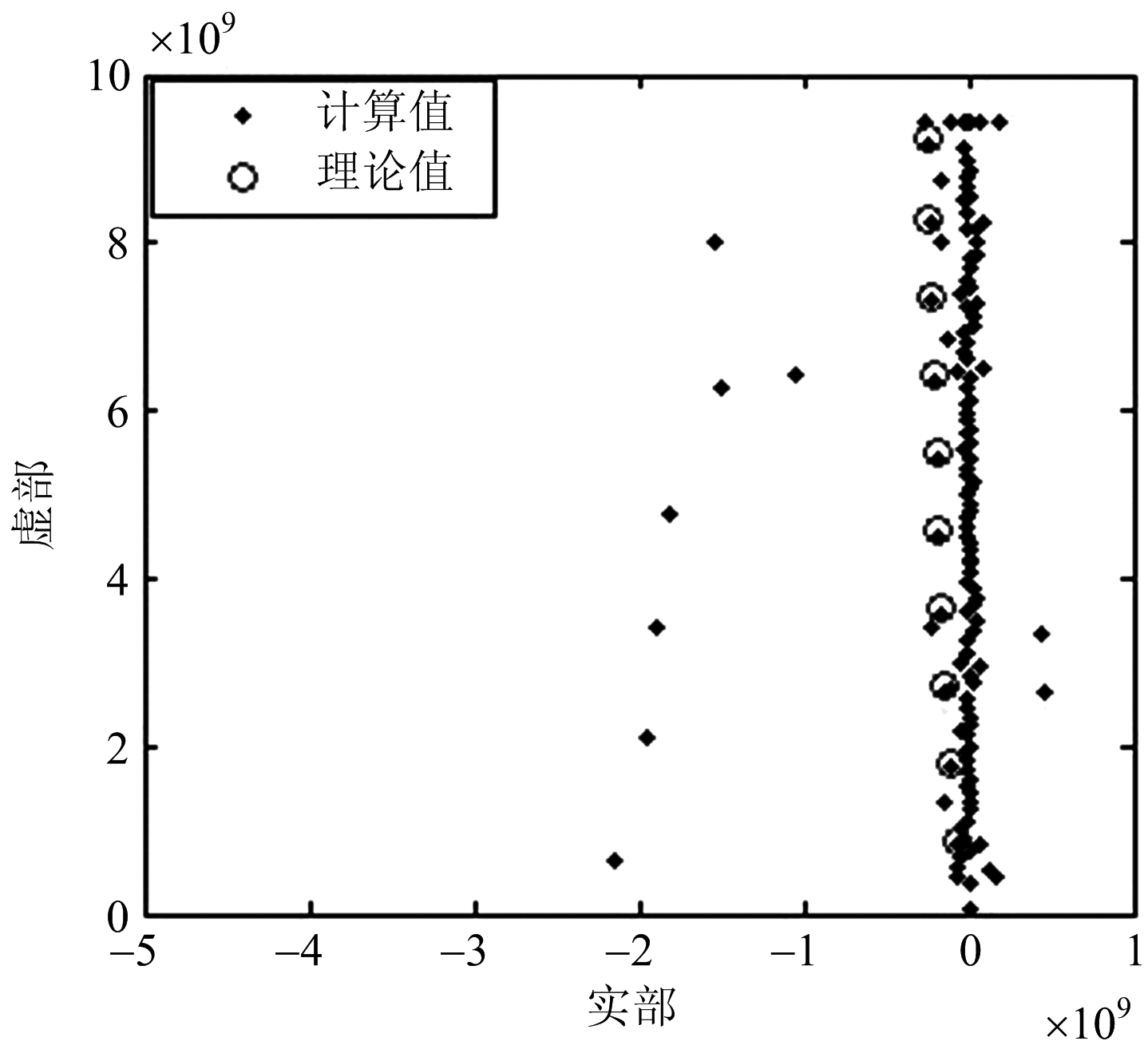
(b) 最小描述长度矩阵束结果
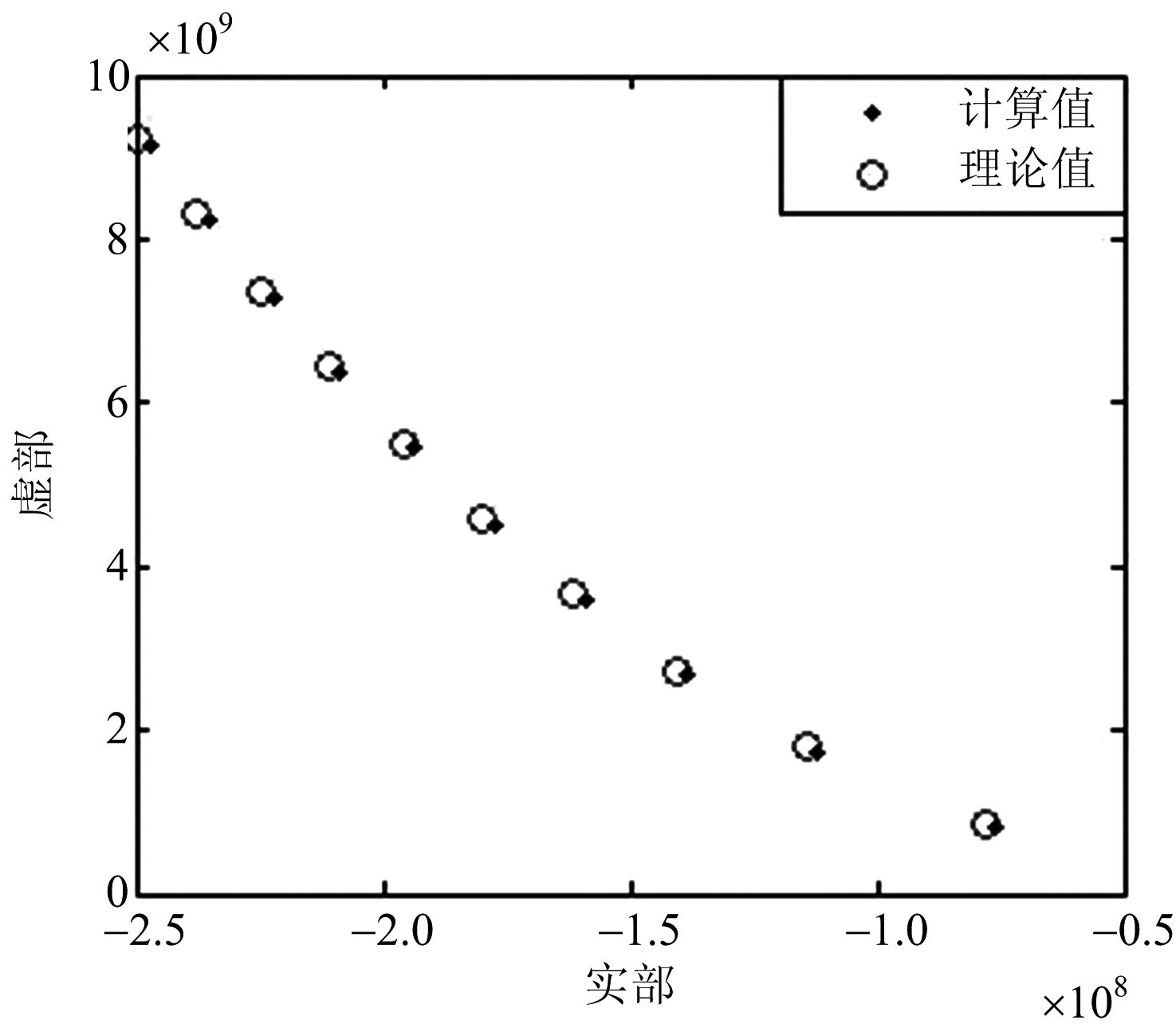
(c) DBSCAN-MPM结果
图10 各方法结果对比图
对本文处理的后时响应信号,最小二乘矩阵束估计阶数为52,最小描述长度估计阶数为250,而投影方法估计阶数为20,与理论值相等。从图中可以看出,最小二乘和最小描述长度得到的极点估计结果存在大量的虚假极点,而本文方法将虚假极点剔除,并完整保留了仿真频段内的真实极点。
矩阵束法属于整体估计算法,受极点定阶的影响,会发生极点遗漏或虚假极点。本文以不同阶数矩阵束构成的极点集为基础,提出了投影定阶确定真实极点个数的方法和DBSCAN聚类分析获得真实极点的方法。通过仿真细杆和球体目标验证了算法,获得了真实极点的个数,有效剔除了虚假极点并准确提取出真实极点。
参考文献:
[1] 杨松岩. 高频波段雷达目标特征提取与识别方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2015.
[2] BAUM C E. On the Singularity Expansion Method for the Solution of Electromagnetic Interaction Problems[Z]. Air Force Weapons Laboratory Interaction Notes, Note 88, 1971.
[3] MAN Liang, WEI Xiao, DONG Chunzhu, et al. Poles Extracting and Analyzing of Complex Stealth Target Based on Matrix Pencil Method[C]∥ IEEE International Conference on Computer and Information Technology, Xi’an: IEEE, 2014:894-898.
[4] 胡大海. 基于波形综合技术的雷达目标识别[D]. 南京:南京理工大学, 2013.
[5] 徐利,邹传云,陈民,等. 基于矩阵束算法的极点提取分析[J]. 通信技术, 2012, 45(6):58-60.
[6] 伍光新. 谐振区雷达目标特征提取与目标识别研究[D]. 哈尔滨:哈尔滨工业大学, 2008.
[7] 陆洪. 基于多频和极点特征的高频超视距雷达目标识别[D]. 青岛:中国海洋大学, 2005.
[8] RISSANEN J. Modeling by Shortest Data Description[M]. Automatica, 1978, 14(5):465-471.
[9] 冯玲,刘克剑,唐福喜,等. 一种基于网格查询的改进DBSCAN算法[J]. 西华大学学报(自然科学版), 2016, 35(5):25-29.
[10] 冯振华. 基于DBSCAN聚类算法的研究与应用[D]. 无锡:江南大学, 2016.
XING Xuran1, ZHAO Hongzhong2, JIA Xin2
(1.Department of Graduate Management,Equipment Academy,Beijing101416,China;2.Department of Optical and Electronic Equipment,Equipment Academy,Beijing101416,China)
Abstract:Poles are the main feature of the radar target in the resonance region. The matrix pencil method (MPM) is the most widely used algorithm in poles extraction. When MPM is used to extract poles of radar target,the estimated order is usually bigger than the number of poles,which leads to false poles mixture with real poles. In this paper, the distribution character of poles extracted by MPM is discussed. Then, a method of estimating the poles number by the projection of pole set is put forward. At last, DBSCAN is used to classify the poles, the false poles are eliminated and the real poles are reserved. Data of two targets created by FEKO are used to prove the effectiveness of the proposed algorithm. The algorithm can remove the false poles effectively.
Key words:density-based spatial clustering of applications with noise (DBSCAN); poles; matrix pencil method (MPM); resonance region
中图分类号:TN957
文献标志码:A
文章编号:1672-2337(2018)03-0327-06
DOI:10.3969/j.issn.1672-2337.2018.03.016
收稿日期:2017 08 15;
修回日期:2017 10 23
作者简介:

邢煦然 男,1993年生,吉林人,硕士研究生,主要研究方向为雷达信号处理。E-mail:xxr01839@mail.ustc.edu.cn

赵宏钟 男,1971年生,河北人,教授,主要研究方向为雷达总体设计、雷达信号处理与目标识别、雷达电子对抗。

贾 鑫 男,1958年生,江苏人,教授、博士生导师,主要研究方向为SAR对抗、现代信号处理理论与应用。