为对期望输出信号的线性估计，即亢龙欢，郑振宇
(海军大连舰艇学院， 辽宁大连 116018)
摘 要：图模型具有广泛的应用，它为许多问题提供了一种新的表达方式和研究思路。因子图作为一类重要的图模型，尤其适用于多变量的复杂统计模型。因子图的引入可以使复杂的多变量问题得到简化。因子图理论在系统建模以及信号检测和估计算法中有着重要的应用。国内外不少学者将因子图理论应用于复杂的通信信号处理，但目前很少见到将因子图理论应用在雷达信号处理中。为了将因子图理论作为一种有效的工具应用于雷达信号处理，提出了用因子图理论实现雷达信号处理中的自适应波束形成技术(ADBF)的方法，这为用图模型研究雷达信号处理提供了一个很好的思路。
关键词：因子图； 消息传递算法； 自适应波束形成； 相控阵雷达
因子图是一类应用非常广泛的图模型[1]，它在信道估计、解码等通信理论以及检测和估计理论中有大量的应用[2-3]。常见的因子图有两种形式，最早的是1981年Tanner提出的用来简化解码问题的Tanner图[4]，后来在2001年Forney提出了另外一种称为Forney图的因子图[5]，本文中主要讨论Forney图，对Tanner图不作详细的解释。大量的研究文献用因子图的方法实现了傅里叶变换、最大期望算法、卡尔曼滤波等许多信号处理中常见的算法[6]。目前还未见到因子图理论在雷达信号处理技术中的应用，本文通过因子图上的高斯消息传递实现相控阵雷达中常用的自适应波束形成技术[7]。
因子图和消息传递算法是不可分离的，通过在因子图上执行消息传递算法来实现相关变量的估计。常见的消息传递算法主要包括和积算法和最大积算法[8]，在因子图上执行消息传递算法可以得到消息更新规则进而估计出任意变量的值。
自适应波束形成(ADBF)技术是相控阵雷达[9]中非常重要的一种技术，它可以根据环境信息的变化，自适应地调整空域滤波器的权系数，使得空域滤波器在干扰方向形成很深的零陷，在目标信号方向形成主瓣，进而最大限度接收目标信号，抑制干扰信号。自适应波束形成技术常用3种准则来实现，即最小均方误差(MMSE)准则、最大信噪比(MSNR)准则、线性约束最小方差(LCMV)准则[10]。对最小均方误差(MMSE)准则进行进一步推广可以得到基于迭代最小二乘(RLS)算法的自适应波束形成技术。本文用因子图方法实现基于迭代最小二乘(RLS)的自适应波束形成。
图1是阵列信号的自适应处理结构示意图，图中输入信号为X(t)=[x1(t),x2(t),…,xN(t)]T，期望输出(参考)信号为为对期望输出信号的线性估计，即
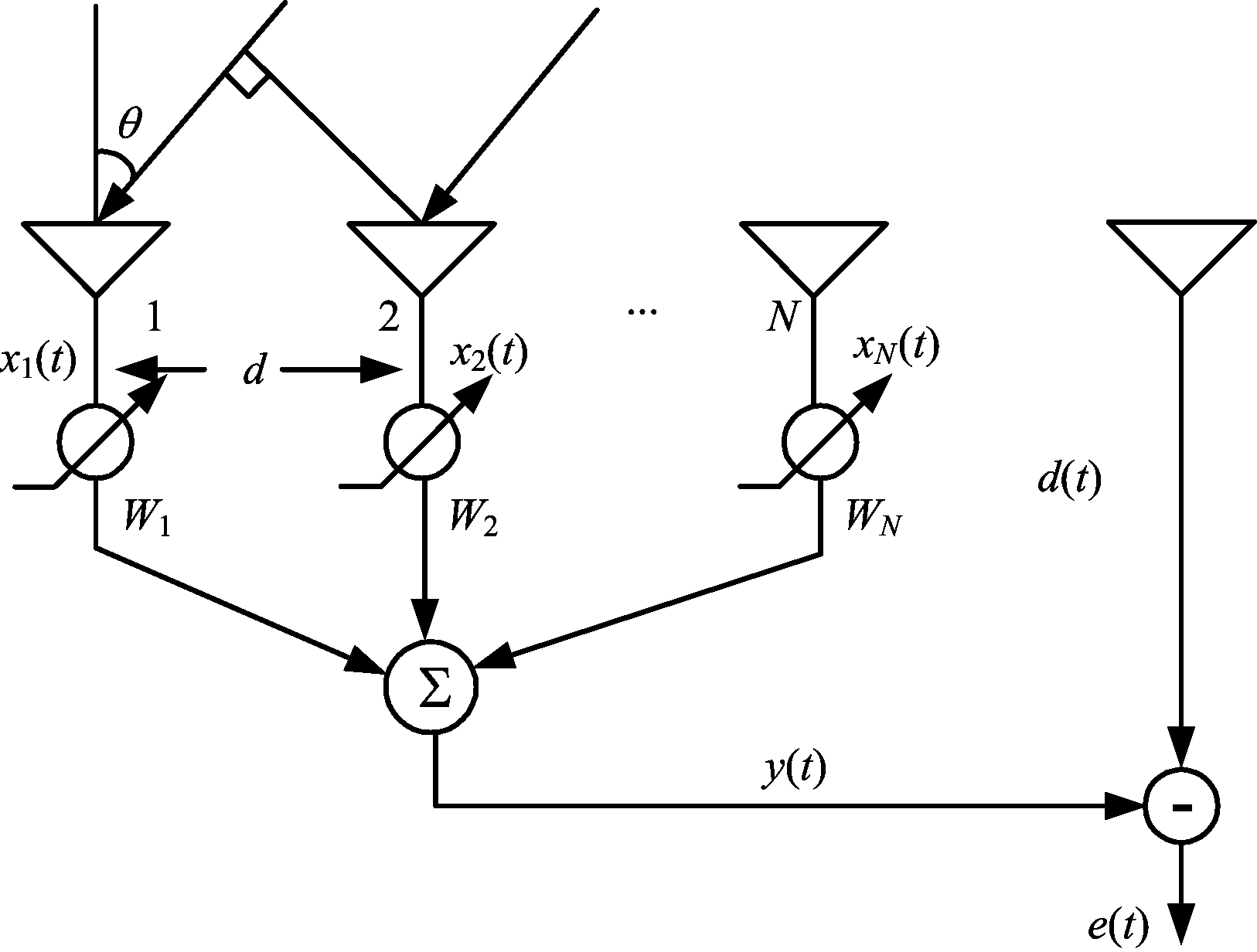
图1 自适应处理结构图
(1)
(2)
式中，e(t)为估计信号与期望输出信号的估计误差。对时域连续信号进行离散化，离散化之后该模型可表示为
(3)
(4)
式中，k表示离散时间。为了后边使用方便将式(3)重写为
(5)
以最小均方误差为准则，求解权系数等价于如下无约束最优化问题：
(6)
式中：
(7)
式(3)～式(6)描述的是离散时间自适应波束形成模型，对该问题的求解可以用迭代最小二乘(RLS)算法[11]，最后可得到k时刻权系数的最小二乘解。在本节中，建立起该问题的模型，但并不求解它。在下一节中，将用基于因子图上消息传递的观点求解这个迭代最小二乘(RLS)问题。
在本小节，非常简要地介绍Forney因子图与和积算法的一般性原理。Forney因子图上包括边和节点，一条边代表一个变量，一个节点代表一个局部函数，一条边与一个局部函数节点相连代表该局部函数中含有这条边表示的变量，所有局部函数的积即为全局函数[8]。图2是基于RLS算法的自适应波束形成的因子图表达。
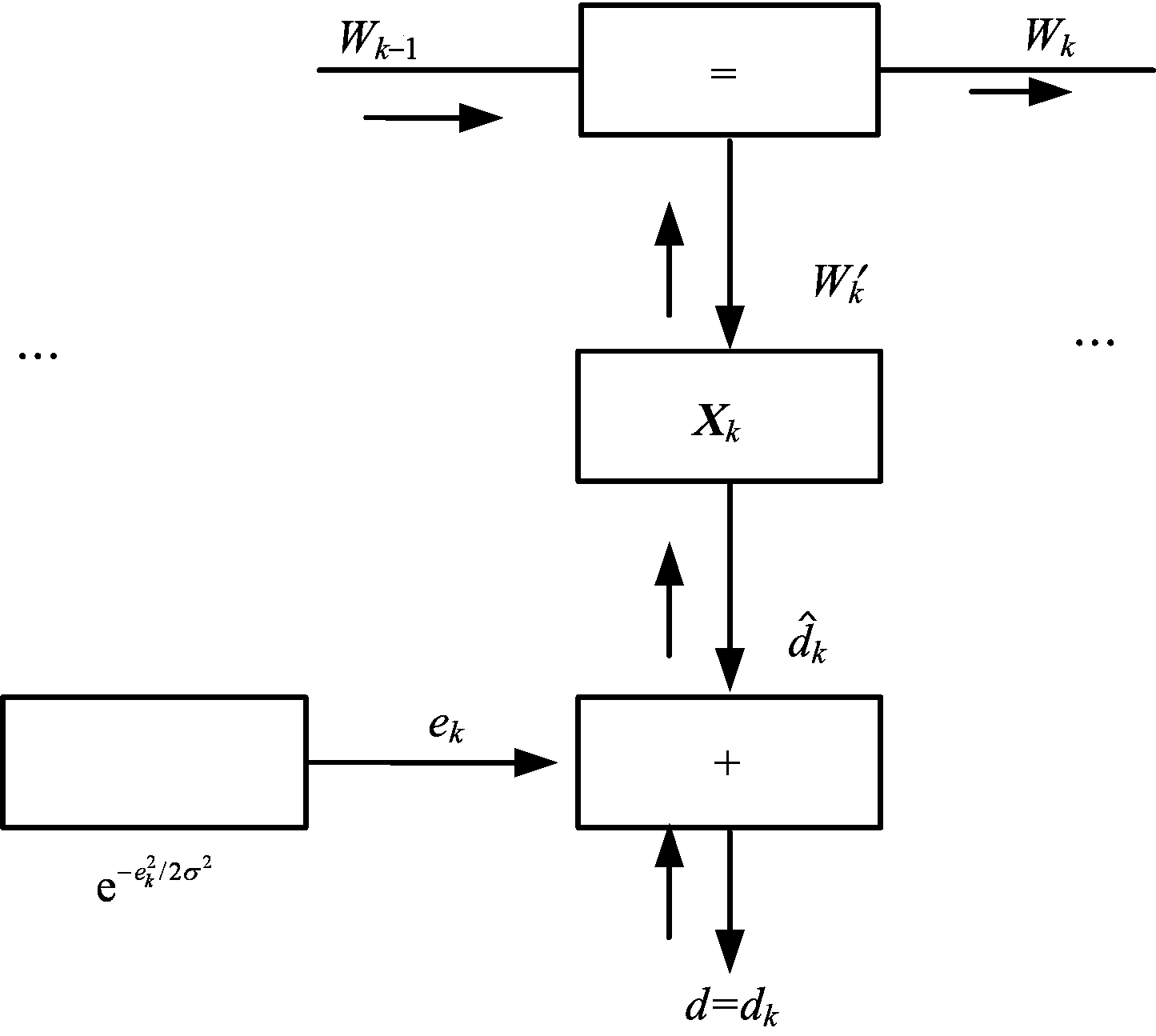
图2 基于RLS算法的自适应波束形成因子图
和积算法用来计算因子图上的消息传递，因子图上的消息传递包括函数节点传向变量节点的消息，以及由变量节点传向函数节点的消息，两类消息的计算公式如下[12]：
1)μx→f(x)表示从变量节点x到函数节点f的消息：
(8)
2)μf→x(x)表示从函数节点f到变量节点x的消息：
(9)
式中，X=n(f)表示与局部函数f相关的全体变量，n(x)表示与变量x相关的所有局部函数的集合。
假设期望信号的估计误差ek服从均值为0、方差为σ2的高斯分布，因子图上的消息均为高斯消息。基于RLS算法的自适应波束形成模型用因子图表达出来如图2所示，最小化式(6)等价于最大化：
(10)
由最大积算法可表达最大积消息
如下：
(11)
根据最大似然估计理论，权系数Wk的估计值[6]为
(12)
式中，
是高斯消息
的均值，因此到此为止求解权系数问题转化为求解高斯消息的均值。
图2所示因子图上的消息都是高斯消息，消息
是因子
本身，其均值
为0，方差
为σ2。d=dk为已知量，可以将其视为输入消息
其均值为
方差
根据和积算法和最大积算法可以计算出图2的消息更新规则。式(13)～式(17)将给出图2的消息更新规则[6]。图3是图2中的基本和节点，式(13)和式(14)给出了基本和节点的消息更新规则：
(13)
(14)
图4是复合框图节点。式(15)～式(17)给出了复合框图节点的消息更新规则，其中式(15)给出了高斯消息的均值表达式，
即为k时刻自适应波束形成的权系数的估计值。
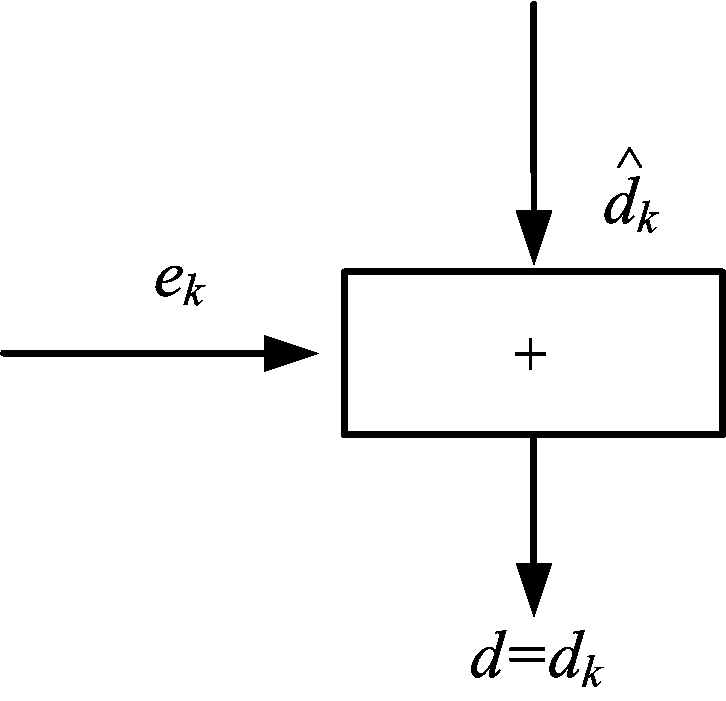
图3 基本和节点消息更新规则
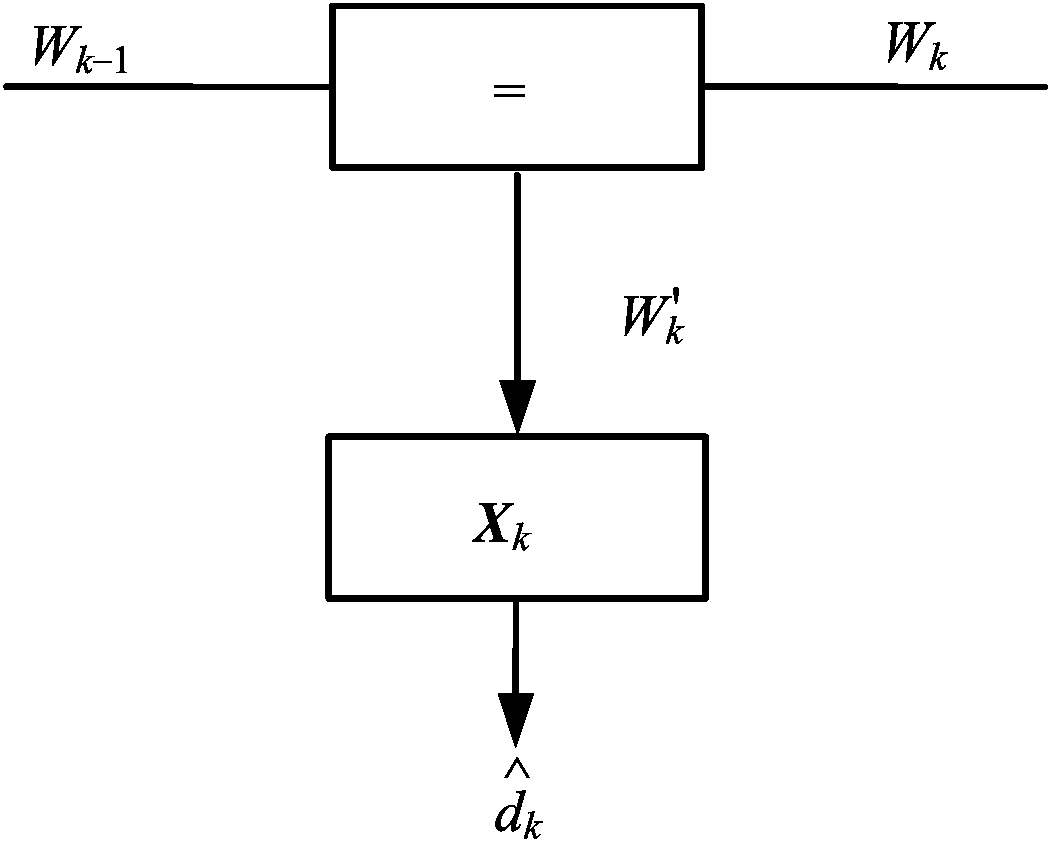
图4 复合框节点消息更新规则
(15)
(16)
(17)
在本小节中用因子图上高斯消息传递的观点求出了基于RLS算法的自适应波束形成权系数。下面将通过数字仿真实验验证该方法的有效性。
在本小节，设置合理的仿真参数，对上述基于因子图的自适应波束形成方法进行仿真实验。设接收阵列为20个阵元的均匀线阵，阵元间距与波长的比值为0.5，波束扫描范围为-60°～60°，目标信号方向为0°，干扰方向为20°和40°，快拍数为121，干噪比为60 dB，噪声是均值为0、方差为1的高斯白噪声。0时刻的初始均值为
初始协方差矩阵为
是单位矩阵。图5是仿真结果。
由图5的仿真结果可以看出，在0°方向形成了主波束，在20°和40°处分别形成了两个“零点”抑制这两个方向的干扰。仿真结果表明，从图模型的观点出发，采用因子图上消息传递的方法可以实现自适应波束形成。
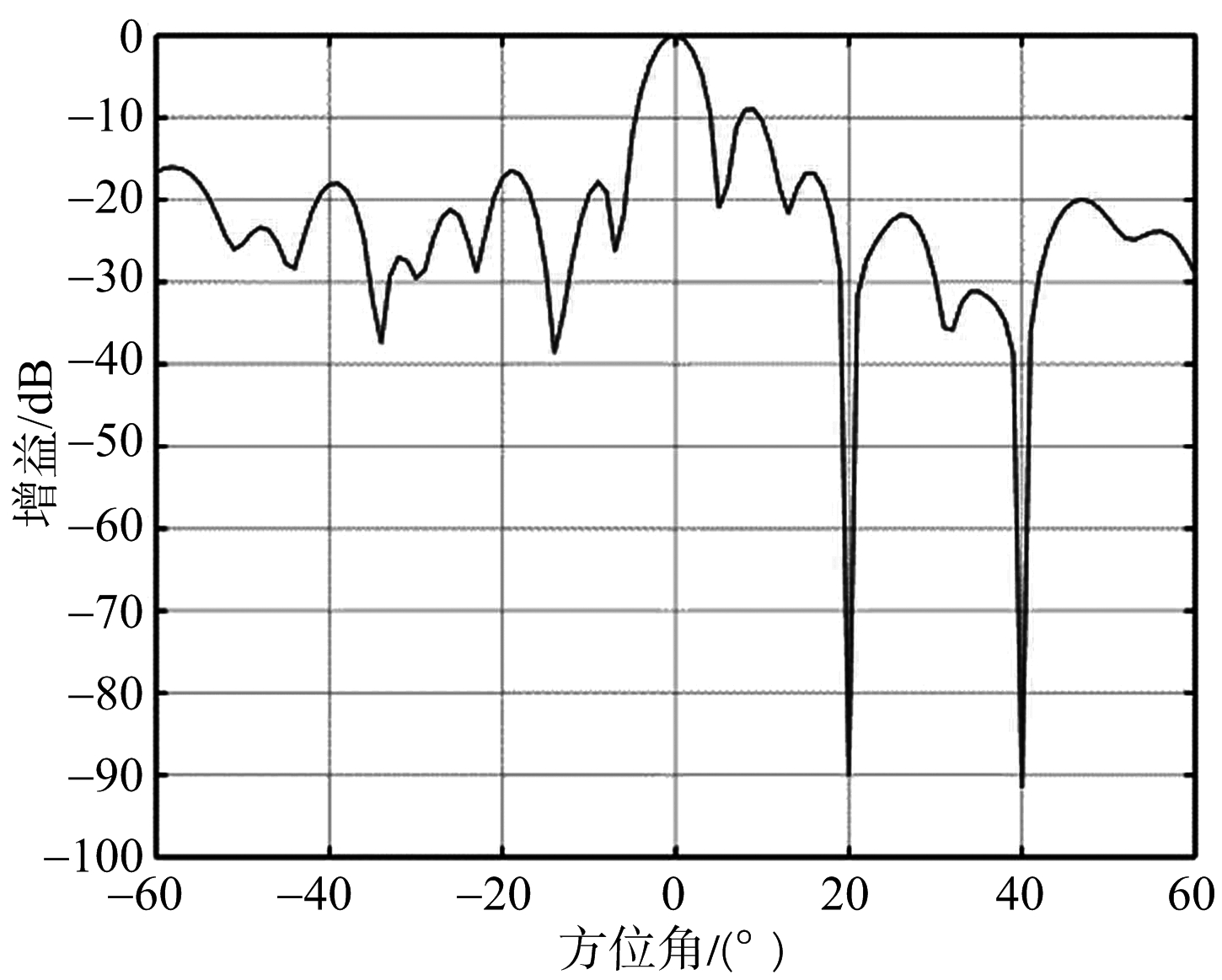
图5 基于因子图的自适应波束形成
因子图理论和消息传递算法在求解复杂问题时具有很大的优势，因此在通信和检测估计领域获得了广泛的应用，但目前在雷达信号处理领域的应用非常少。本文将因子图理论和消息传递算法应用到了相控阵雷达的自适应波束形成技术中，理论分析和仿真实验证明了该方法的有效性。本文所提方法是自适应波束形成技术从图模型的观点来实现的一种新方法，雷达信号处理中有很多复杂问题如参数估计、目标检测都可能通过图模型进一步简化实现，这些问题需要将来进一步研究。
参考文献：
[1] JORDAN M I. Graphical Models [J]. Statistical Science, 2004, 19(1):140-155.
[2] LYU Tiejun, WANG Chanfei, GAO Hui. Factor Graph Aided Multiple-Symbol Differential Detection in the Broadcasting Phase of a Network Coding Based UWB Relay System[J]. IEEE Trans on Vehicular Technology, 2017, 66(6):5364-5371.
[3] LEHMANN F. A Factor Graph Approach to Iterative Channel Estimation, Detection, and Decoding for Two-Path Successive Relay Networks [J]. IEEE Trans on Wireless Communications, 2016, 15(8):5414-5429.
[4] TANNER R M. A Recursive Approach to Low Complexity Codes[J]. IEEE Trans on Information Theory, 1981, 27(5):533-547.
[5] FORNEY G D JR. Codes on Graphs: Normal Realiza-tions[J]. IEEE Trans on Information Theory, 2001, 47(2):520-548.
[6] LOELIGER H A, DAUWELS J, HU J, et al. The Factor Graph Approach to Model-Based Signal Processing[J]. Proceedings of the IEEE, 2007, 95(6):1295-1322.
[7] 吴凯,苏涛,逄锦昊. 时域宽带自适应波束形成器设计[J]. 雷达科学与技术, 2015, 13(3):296-301.
WU Kai, SU Tao, PANG Jinhao. Design of Adaptive Broadband Beamformer in Time Domain[J]. Radar Science and Technology, 2015, 13(3):296-301. (in Chinese)
[8] LOELIGER H A. An Introduction to Factor Graphs[J]. IEEE Signal Processing Magazine, 2004, 21(1):28-41.
[9] 娄宝芳,刘志国. 一种高性价比的相控阵雷达新技术[J]. 雷达科学与技术, 2015, 13(3):245-248.
LOU Baofang, LIU Zhiguo. A New Low-Cost Technology on Phased Array Radar[J]. Radar Science and Technology, 2015, 13(3):245-248. (in Chinese)
[10] HASSANI A, PLATA-CHAVES J, BAHARI M H, et al. Multi-Task Wireless Sensor Network for Joint Distributed Node-Specific Signal Enhancement, LCMV Beamforming and DOA Estimation[J]. IEEE Journal of Selected Topics in Signal Processing, 2017, 11(3):518-533.
[11] CAO X, LIU K J R. Decentralized Sparse Multitask RLS over Networks[J]. IEEE Trans on Signal Processing, 2017, 65(23):6217-6232.
[12] KSCHISCHANG F R, FREY B J, LOELIGER H A. Factor Graphs and the Sum-Product Algorithm[J]. IEEE Trans on Information Theory, 2001, 47(2):498-519.
KANG Longhuan, ZHENG Zhenyu
(Dalian Naval Academy,Dalian116018,China)
Abstract:The graph model is widely applied, which provides a new way of expression and research for many problems. As a kind of important graph model, factor graph is especially suitable for the complex statistical model of multivariate. With factor graph, the complex problem is simplified. Factor graph theory plays an important role in system modeling, signal detection and estimation algorithms. It has been used to complex communication signal processing, but few scholars have paid attention to the applications of factor graph theory in radar signal processing. In order to make the factor graph theory to be a useful tool in radar signal processing, we proposed a method that can accomplishes the adaptive digital beamforming (ADBF) in radar signal processing by factor graph theory. Our work provides a good idea for the study of application of graph model in radar signal processing.
Key words:factor graph; message passing algorithm; adaptive beamforming; phased array radar
中图分类号：TN958.92
文献标志码：A
文章编号：1672-2337(2018)03-0343-04
DOI:10.3969/j.issn.1672-2337.2018.03.019
收稿日期：2017 09 18；
修回日期：2017 10 23
作者简介：
亢龙欢 男，1993年生，陕西宝鸡人，海军大连舰艇学院舰艇航通指挥专业任职培训学员，主要研究方向为通信信号处理和雷达信号处理。E-mail:914318172@qq.com
郑振宇男，1979年生，黑龙江安达人，博士，海军大连舰艇学院工程师，主要研究方向为光纤捷联航姿系统、雷达信号处理。