邓 昊 1 ， 汪 玲 1 ， 杨 娜 1 ， 肖 卓 2
(1.南京航空航天大学雷达成像与微波光子技术教育部重点实验室， 江苏南京 211100；2.中国人民解放军96764部队， 河南洛阳 471000)
摘 要 ： 传统距离多普勒(Range Doppler, RD)成像方法分辨率取决于发射信号的带宽和信号在方位向积累的多普勒带宽。超分辨成像可以在给定带宽条件下，获得比RD方法更优的分辨率。给出一种基于幅度和相位估计(Amplitude and Phase Estimation, APES)的逆合成孔径雷达(Inverse Synthetic Aperture Radar, ISAR)超分辨成像方法，该方法根据回波数据构造自适应滤波器对目标散射点进行重建，仿真和实测ISAR数据成像结果验证了基于APES的ISAR超分辨成像算法的有效性。相比其他超分辨成像方法，该方法重建的散射点幅度更为精确，副瓣更低，图像对比度和图像信噪比增加，整体成像效果较佳。
关键词 ： 逆合成孔径雷达； 成像； 超分辨； 幅度和相位估计； 旁瓣抑制
逆合成孔径雷达可全天候、全天时对远距离运动目标进行高分辨率成像，是一种有效的目标识别途径。RD算法是ISAR成像的常用算法，该方法首先对脉冲压缩后的雷达回波数据进行运动补偿，接着在方位向进行快速傅里叶变换(Fast Fourier Transform, FFT)实现成像。RD算法假设相干积累时间内目标相对雷达转动引起的多普勒频率恒定，因此在实际中限制了成像积累时间和方位向分辨率。在这种情况下，采用超分辨方法 [1-13] ，在不增加成像角度的情况下，可以获得高于理论分辨率的图像分辨率。
超分辨方法可以分为参数化法和非参数化法。参数化法要求获得散射点的个数、位置和幅度，对数据模型误差非常敏感，该类方法包括旋转不变子空间算法(Estimation of Signal Parameters via Rotational Invariance Techniques, ESPRIT) [1] 、多重信号分类法(Multiple Signal Classification, MUSIC) [2-4] 、基于带宽外推的线性预测法 [5] 、基于自适应模型的方法 [6] 等。非参数化法假设场景为连续的函数，不需要获取散射点的个数，包括最小方差法(Minimum Variance Method, MVM) [7-9] 、空间变迹法(Spatially Variant Apodization, SVA) [10-12] 、自适应旁瓣抑制法(Adaptive Sidelobe Reduction, ASR) [13] 等。实际中，精确数据模型的获取相当困难，所以非参数化法的适用性更强，但MVM法频谱估计不够精确，降低了算法的准确性；SVA法对信噪比和频谱的平坦程度有较高要求；ASR法的性能较好，但是运算量较大。
本文将非参数化的APES法用于ISAR方位向和距离向成像，给出具体的成像算法，并通过仿真和实测数据处理分析该成像方法的性能。仿真结果和实测ISAR数据成像结果验证了该算法可以获得超分辨，优于RD成像结果，并可降低旁瓣，提高对比度和信噪比，成像效果与MVM法相当。
成像雷达多采用线性调频信号作为发射波形。在“停-走-停”假设下，经过解调和距离压缩后，目标上某一散射点回波信号可写为
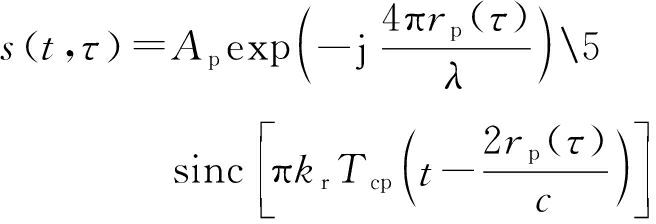
(1)
式中， t 为距离向快时间， τ 为方位向慢时间， k r 为发射波形的调频率， A p 为包含散射点散射率和天线方向图调制的回波幅度因子， r p ( τ )表示 τ 时刻散射点和雷达之间的距离， T cp 表示压缩后的脉冲宽度， λ 为雷达波长。
ISAR成像中，目标与雷达间的相对运动通常被分解为目标上某一参考点相对于雷达的平动和目标上散射点绕该参考点的转动。因此，散射点和雷达之间的距离 [14] 可表示为
r p ( τ )= r 0 ( τ )+( Ω ( τ )× r ( τ ))· R ( τ )
(2)
式中， r 0 ( τ )为 τ 时刻雷达和参考中心点的距离， R 为雷达视线方向的单位矢量， r 为由参考中心点指向散射点的矢量， Ω 为目标相对于参考中心点的转动矢量。平动分量 r 0 ( τ )对ISAR成像没有贡献，相反会影响成像，需要对其补偿，即所谓的ISAR运动补偿。
将式(2)代入式(1)中，并假设运动补偿已完成，可得
s ( t , τ )=
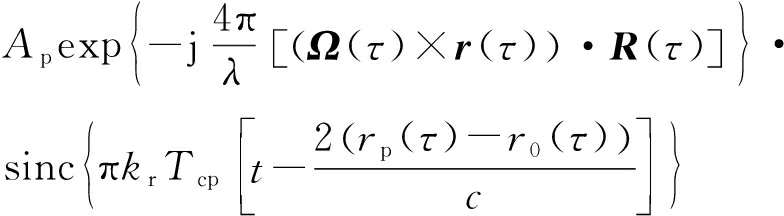
(3)
在小转角假设下，散射点所在距离单元内的方位向回波信号 s c ( τ ) [15] 可以近似表示为
(4)
式中， Ω 0 为有效转动角速率，将 Ω 分解为与 R 正交的分量即可得到有效转动矢量 Ω 0 ， y 为散射点在ISAR图像投影平面(Image Projection Plane, IPP)内的方位向坐标。
由式(4)可见，在小转角假设下，散射点回波方位向为单频信号，频率为 f d, y =2 Ω 0 y / λ ，与散射点在IPP内的方位坐标一一对应。因此，对每个距离单元的回波信号作傅里叶变换，即频谱分析，即可在方位向对目标进行成像。这就是传统ISAR成像广泛使用的距离-多普勒成像方法的原理。
由上节可知，ISAR方位向成像的本质就是频谱分析。APES是一种自适应有限冲击响应(Finite Impulse Response, FIR)方法 [16] ，它依据最小二乘估计的准则对输入的数据进行处理，构造出相应的有限冲击响应滤波器来完成谱估计，可提供更准确、副瓣更低的超分辨性能。在本节给出基于APES频谱估计的ISAR成像方法来提升ISAR成像质量。
假设目标由 N d 个散射点构成，且考虑噪声，由上节给出的ISAR成像模型可知，距离压缩后，每一距离单元内第 n 个脉冲信号可表示为
(5)
式中， S c ( n )= s c ( nT r )为 s c ( τ )的离散形式(注意这里已扩展为多个散射点的情形)， T r 为脉冲重复周期， ω i 为散射点对应的数字多普勒角频率：
(6)
式中， y i 为第 i 个散射点在图像投影平面方位向的坐标。式(5)中， A p, i 是与第 i 个散射点散射率相关的回波幅度， e ( n )为噪声和干扰。
APES成像方法可归纳为如下步骤：
1) 对方位向信号 S c ( n )使用滑窗操作，形成长度为 M 的前向重叠子矢量 
m =0,1,…, N - M
(7)
式中， z m 表示 S c ( n )的第 m 个采样值，(·) T 表示转置。
2) 对方位向信号 S c ( n )由后向前使用滑窗操作，构造后向共轭重叠子矢量 
m =0,1,…, N - M
(8)
式中，(·) * 表示共轭。
3) 由前向重叠子矢量 
构造前向采样协方差矩阵 
由后向共轭重叠子矢量 
构造后向采样协方差矩阵 
(9)
(10)
式中，(·) H 表示共轭转置。为了提高估计精度，由式(9)和式(10)可以进一步获得前后向采样协方差矩阵 [17] ：
(11)
则噪声和干扰的协方差矩阵 [18] 为
(12)
式中，
(13)
(14)
式中, L = N - M +1。
4) 构造长度为 M 的FIR滤波器。
根据近似最大似然法，FIR滤波器的脉冲响应函数 [14] 选为
(15)
式中， 
5) 获得方位向回波频谱的最小二乘估计 [18] ：
(16)
式中， 
为估计出的一个距离单元内的方位向信号的幅度。
实际应用中， 
可由不同 m 值的 构成的矩阵的每一行作 N 点FFT得到， 
可由不同 m 值的 构成的矩阵的每一行作 N 点FFT得到。根据不同方位向频率由式(15)构造相对应的滤波器即可求得对应频率点的幅度估计值。
在实际运用中， M 的值太大会使得 
奇异，所以通常情况下 M ≤ N /2。
对距离向也可以应用上述步骤进行超分辨成像，处理过程与方位向类似。首先将脉压后的一维距离像进行逆傅里叶变换，返回数据域。然后构造自适应滤波器来完成距离向幅度相位估计，具体过程这里不再赘述。APES法对雷达回波的处理流程如图1所示。
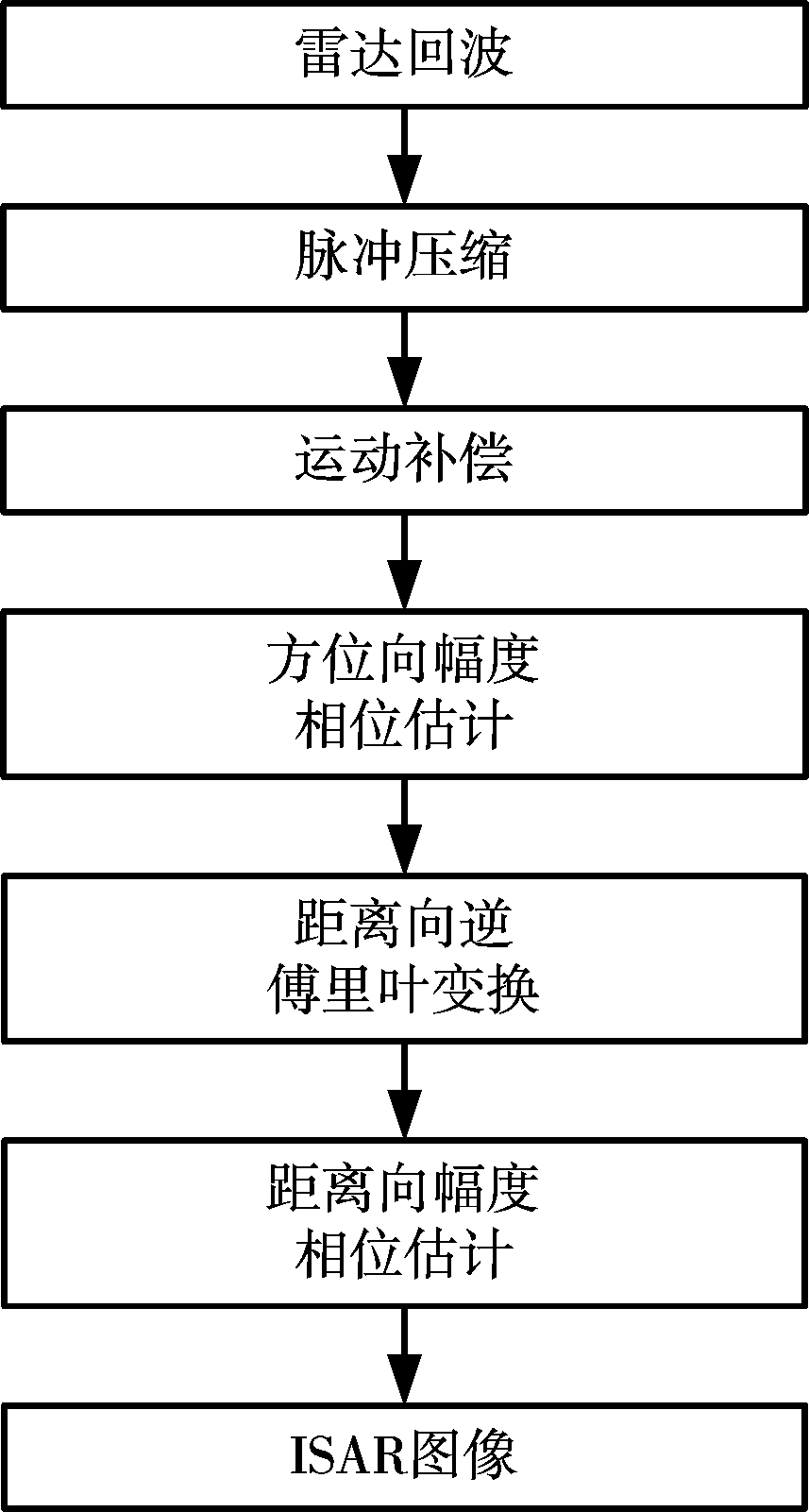
图1 数据处理流程图
基于MVM的方法在选定频率下，滤波器响应必须具有单位增益，且信号通过滤波器后的输出功率最小 [19] 。在式(15)中，用前后向采样协方差矩阵 
替代噪声和干扰的协方差矩阵 可以得到MVM法所用的脉冲响应函数。而在APES法中，按照式(15)构造滤波器，使得滤波器输出与每个频率对应的谐波分量之间的差值的均方最小。
由式(15)可见，当滤波器的阶数 M =1时， a ( ω )=1，式(15)化简为 h ( ω )=1，式(16)变为 
即对方位向信号进行傅里叶变换。在MVM方法中，当滤波器的阶数 M =1时，式(16)同样可以表示为 
因此，RD成像方法是MVM方法和APES方法的一种特殊情况。MVM方法和APES方法均依赖于输入数据，属于自适应滤波方法。构造滤波器使用的协方差矩阵的不同导致MVM和APES二者性能的差异。
本节采用RD法、MVM法和APES法对点目标仿真数据、卫星目标仿真数据，以及飞机和舰船的实测ISAR数据进行处理，验证APES成像算法有效性和优越性。为了更好地评价成像方法的性能，采用两种定量评估图像的指标。
1) 图像对比度为图像强度的标准差和均值之间的定量关系，定义如下 [20] ：
(17)
式中， A {·}为空间平均算子， I 为图像的幅度。对比度可以反映图像的聚焦程度，对比度越大表示图像聚焦效果越好。
2) 图像信噪比的计算方法如下 [21] ：
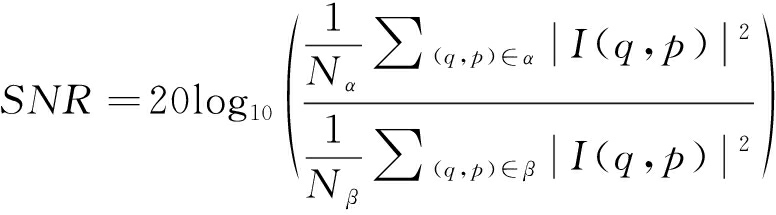
(18)
式中， α 表示目标区域， β 表示背景区域， N α 表示目标区域的像素个数， N β 表示背景区域的像素个数。
为了验证算法的正确性，采用RD法、MVM法和APES法分别对点目标的仿真数据进行处理，并对点目标的成像质量进行比较。
为了便于对成像结果进行分析，ISAR点仿真采用经典的转台模型。ISAR点仿真的参数为脉冲宽度10 μs，信号带宽200 MHz，采样频率480 MHz，工作波长0.03 m，径向距离5 000 m，脉冲重复频率200 Hz，点目标的转动角速度为0.02 rad/s。采用RD法、MVM法和APES法对点仿真进行成像的结果如图2所示。
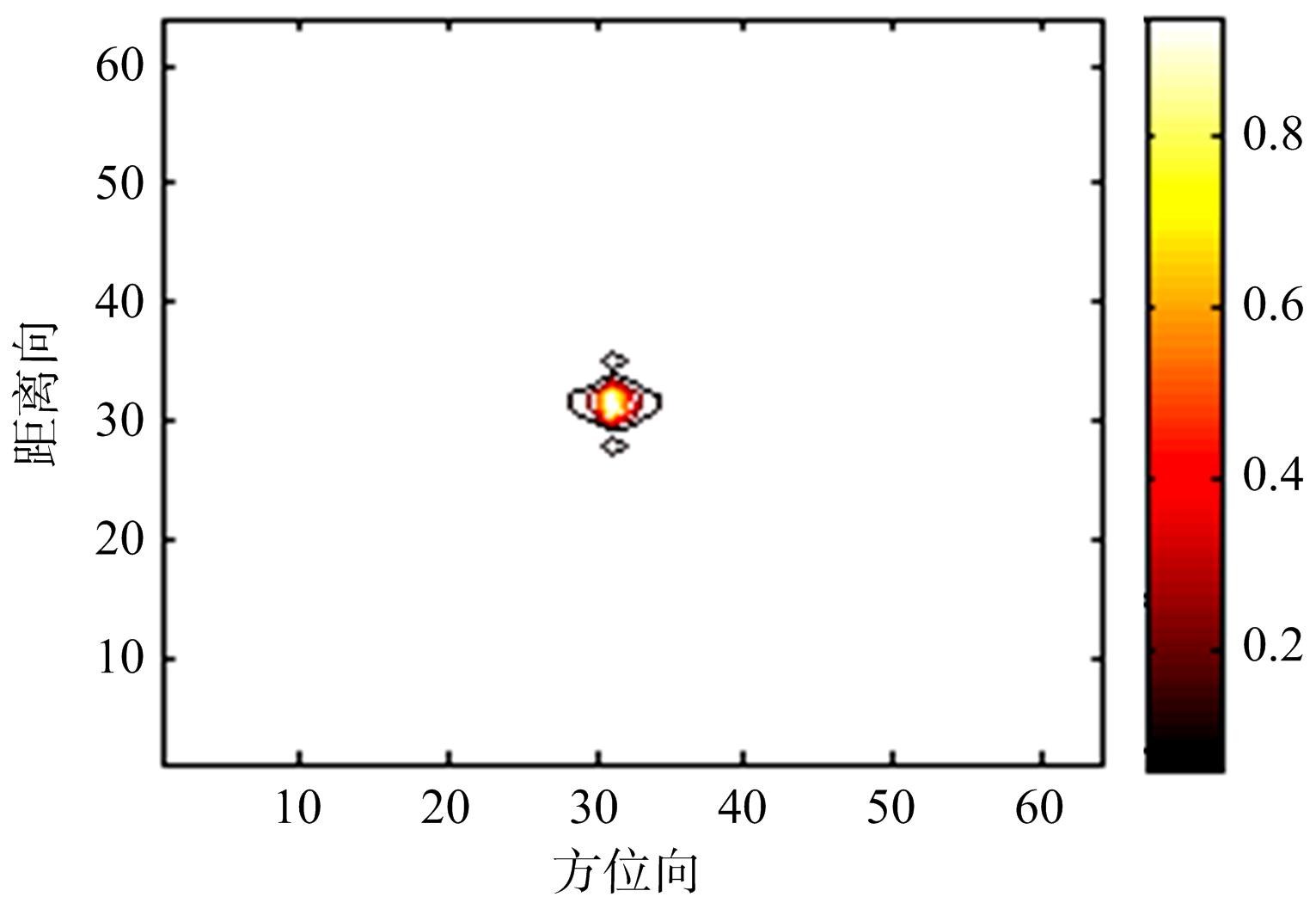
(a) RD法点目标成像结果
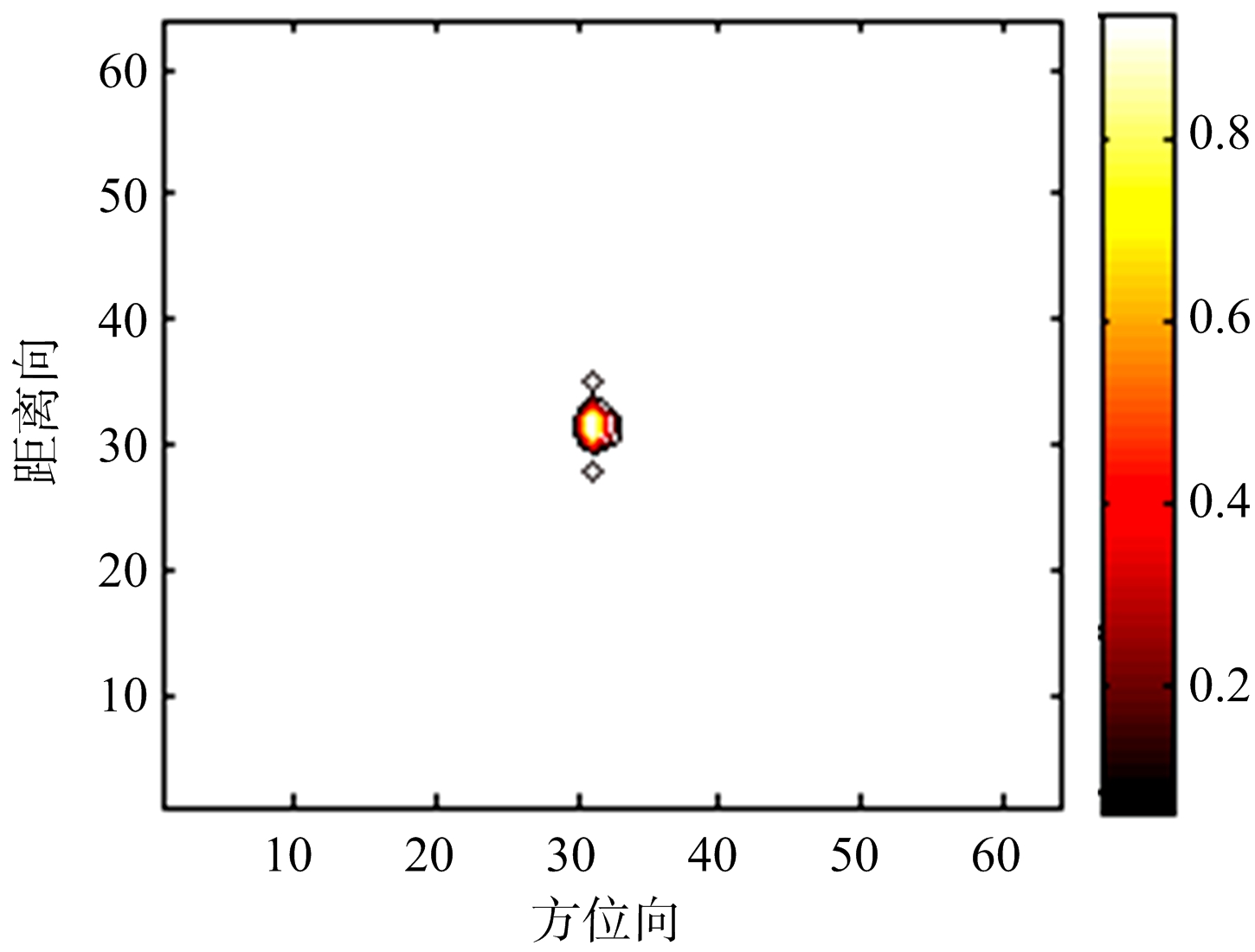
(b) MVM法点目标成像结果
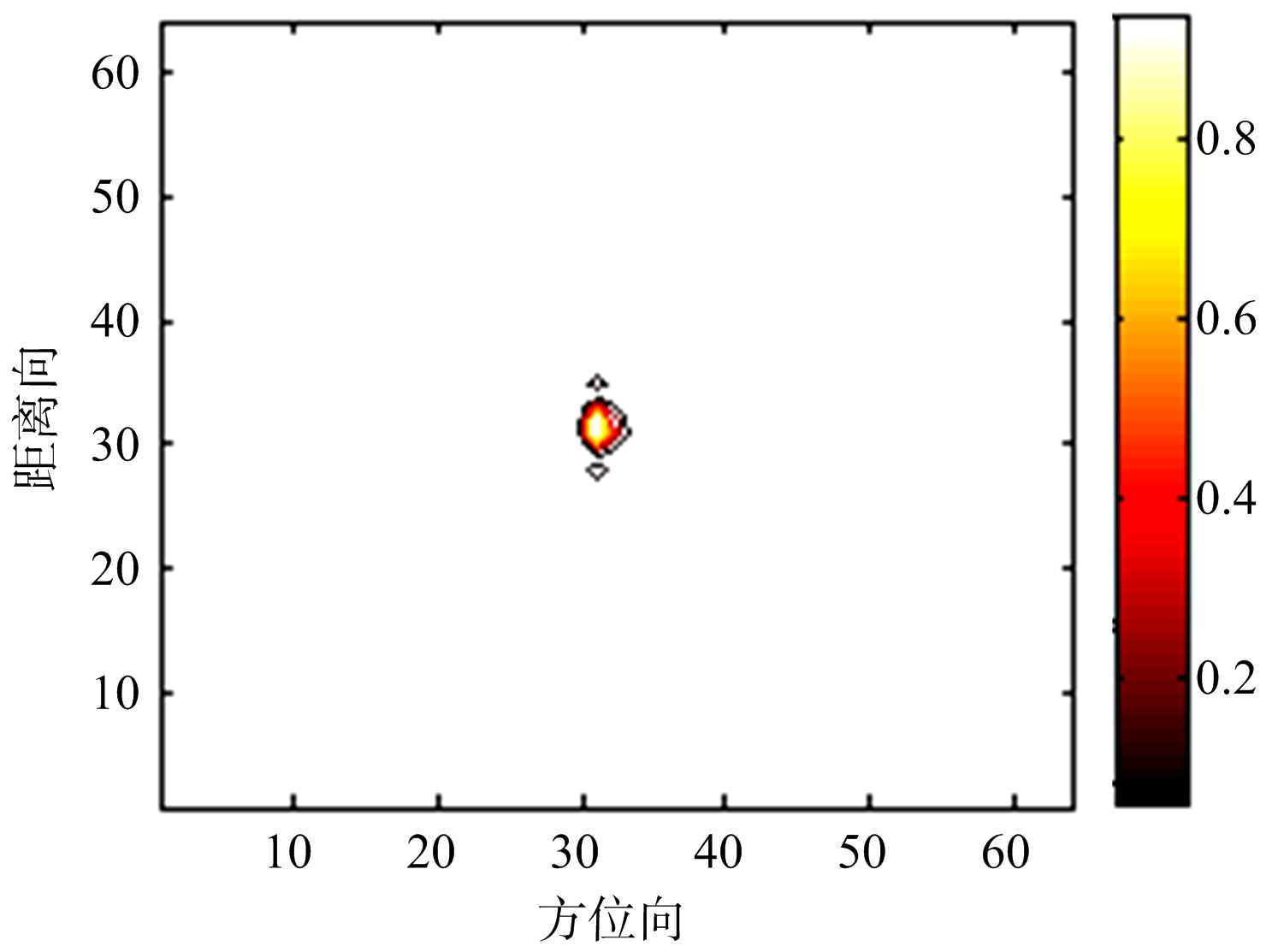
(c) APES法点目标成像结果
图2 点目标仿真结果
表1给出了点目标距离向和方位向的积分旁瓣比(Integrated Side Lobe Ratio, ISLR)和峰值旁瓣比(Peak Side Lobe Ratio, PSLR)。
表1 点目标成像质量比较
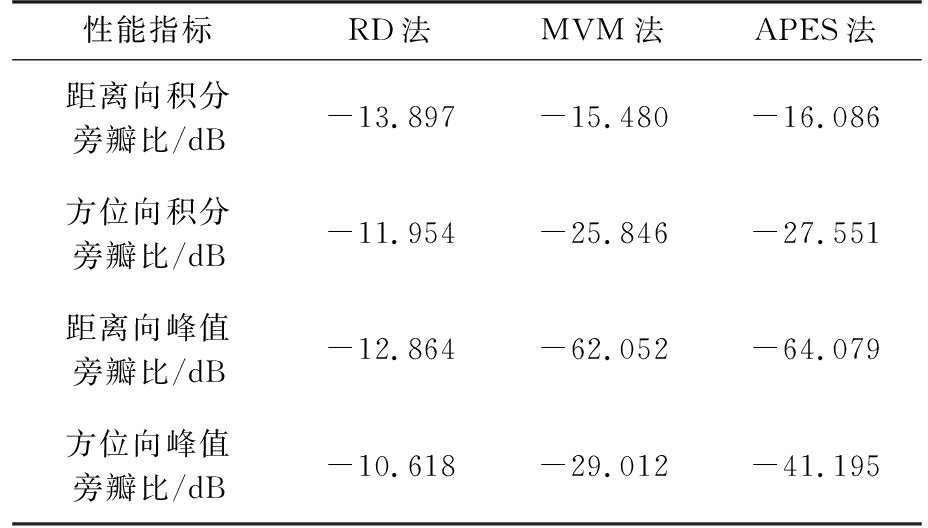
表2给出了点目标的对比度和信噪比。
表2 点目标的定量分析结果
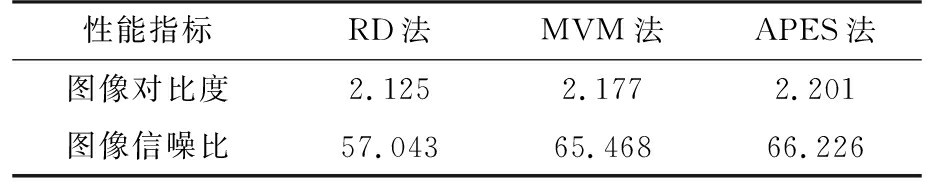
经过计算得到的距离向和方位向的理论分辨率分别为0.75 m和0.3 m，而APES法的距离向和方位向的分辨率分别为0.492 m和0.178 m，因此APES法的分辨率超越了理论分辨率，算法的正确性得到验证。表1说明了相比于RD法和MVM法，APES法能更好地抑制旁瓣。由图像性能指标可以看出，APES法成像的图像质量最好。
仿真所用“长曲棍球”卫星模型共923个散射点，反射系数为单位值，采用卫星工具包(Satellite ToolKit, STK)软件导出卫星轨道，卫星模型如图3所示。
图3 “长曲棍球”卫星散射点模型
卫星仿真时发射信号带宽为1 GHz，雷达信号波长为0.03 m，距离向采样率为1.21 GHz，脉冲重复频率为400 Hz。采用RD法、MVM法和APES法对卫星进行成像的结果如图4所示。
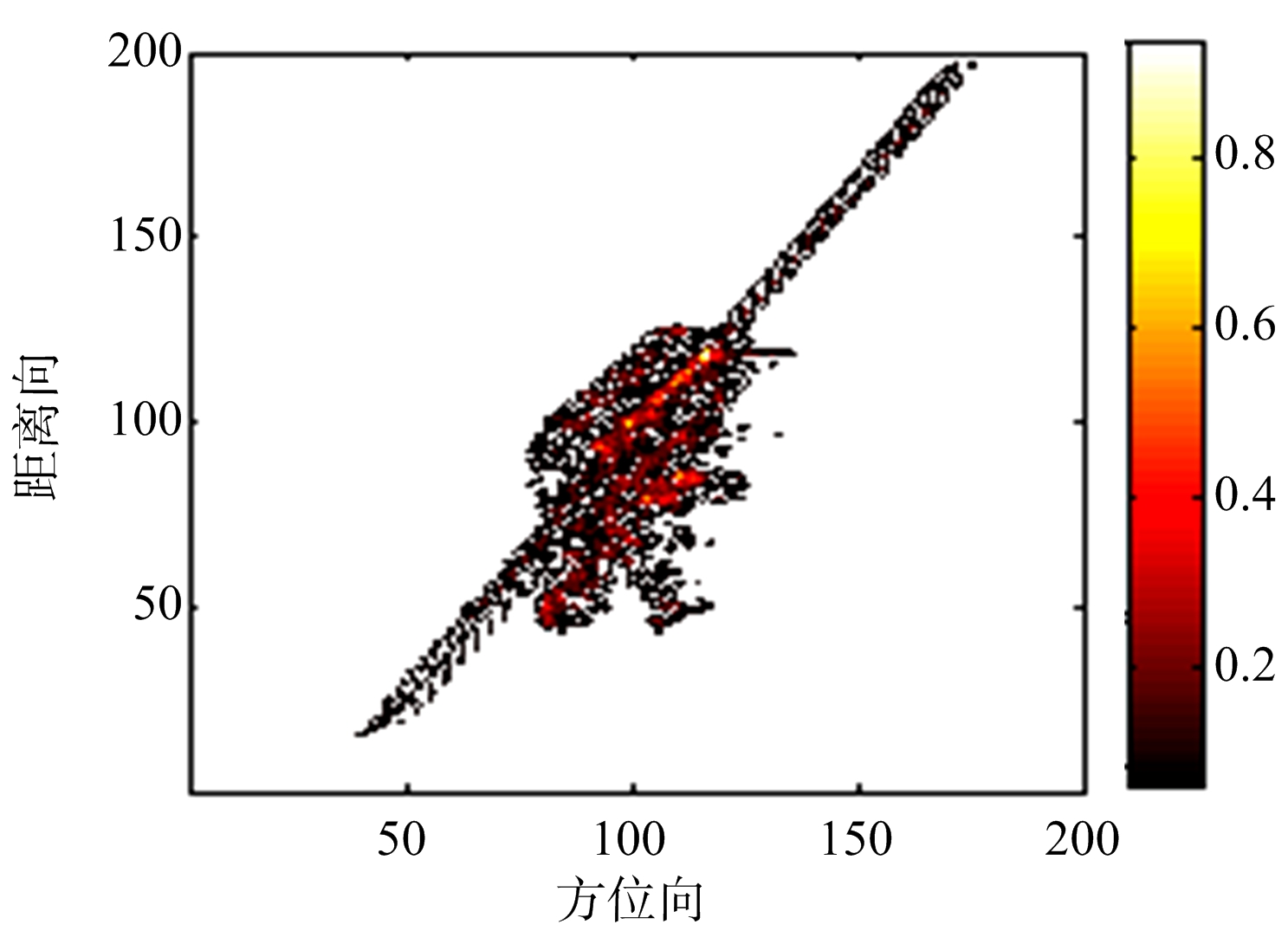
(a) RD法卫星成像结果
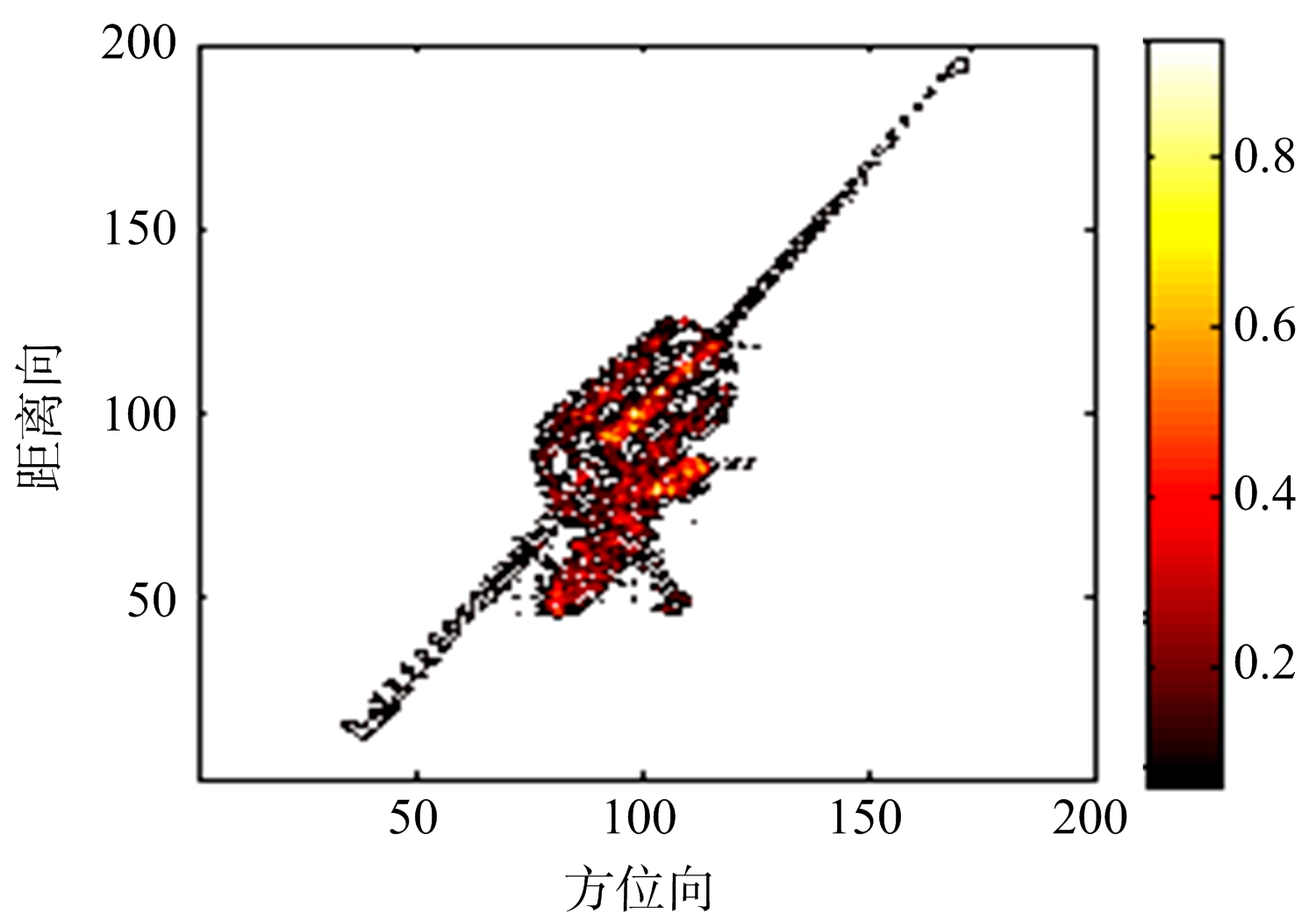
(b) MVM法卫星成像结果
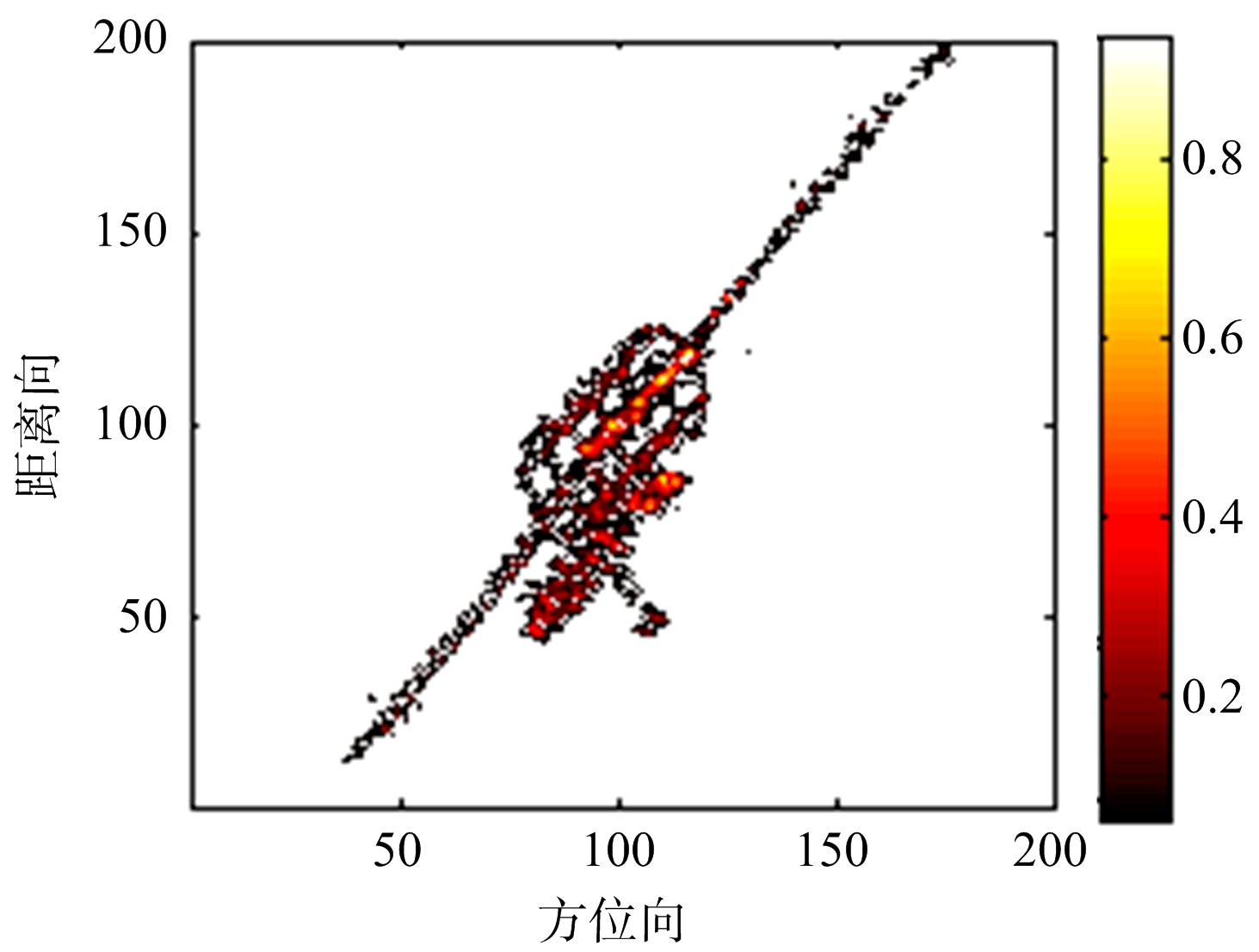
(c) APES法卫星成像结果
图4 卫星仿真结果
表3给出了卫星数据的对比度和信噪比结果。
表3 卫星数据的定量分析结果
经过计算，卫星距离向和方位向的理论分辨率分别为0.15 m和0.159 m，而APES法的距离向和方位向的分辨率分别为0.134 m和0.115 m。说明本文的算法可以实现超分辨成像。从卫星的成像图中可以看出，与RD法相比，MVM法和APES法得到的卫星的主体与天线罩成像效果较好，天线的聚焦效果也更好，且APES法得到的图像旁瓣比MVM法得到的更低。由图像对比度和信噪比可以看出，APES法成像的图像质量与MVM法相当。
为了验证APES方法的有效性和优越性，本节分别对飞机和舰船的ISAR实测数据进行处理，并对成像结果进行分析。
使用工作在C波段的地面雷达进行飞机数据采集，发射波的带宽为400 MHz，成像积累时间为1.28 s。使用工作在X波段的岸基雷达进行舰船数据采集，发射波的带宽为170 MHz，成像积累时间为0.4 s。采用全局最小熵法进行距离对准，相位梯度自聚焦法进行相位补偿。
采用RD法、MVM法和APES法对飞机和舰船数据的成像结果分别如图5和图6所示。
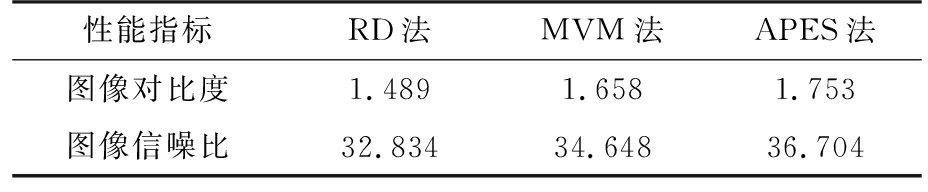
从图中可以看出，相比传统的RD法，MVM法和APES法聚焦更好，旁瓣明显降低，APES法与MVM法的成像效果相当。
经过计算得到，飞机和舰船理论的距离向分辨率分别为0.375 m和0.882 m，APES法得到的距离向分辨率分别为0.342 m和0.735 m，超过了距离向的理论分辨率。
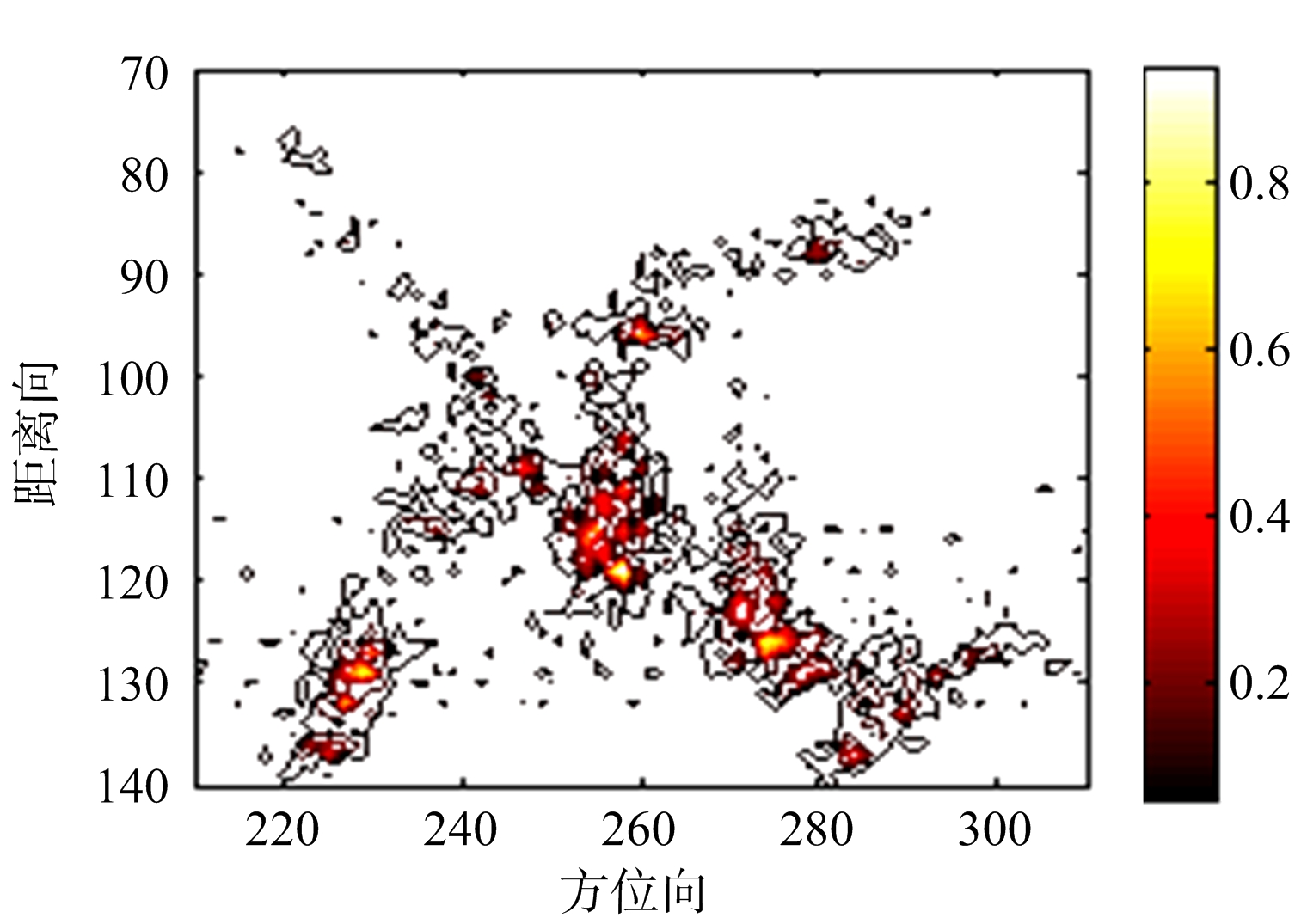
(a) RD法飞机成像结果
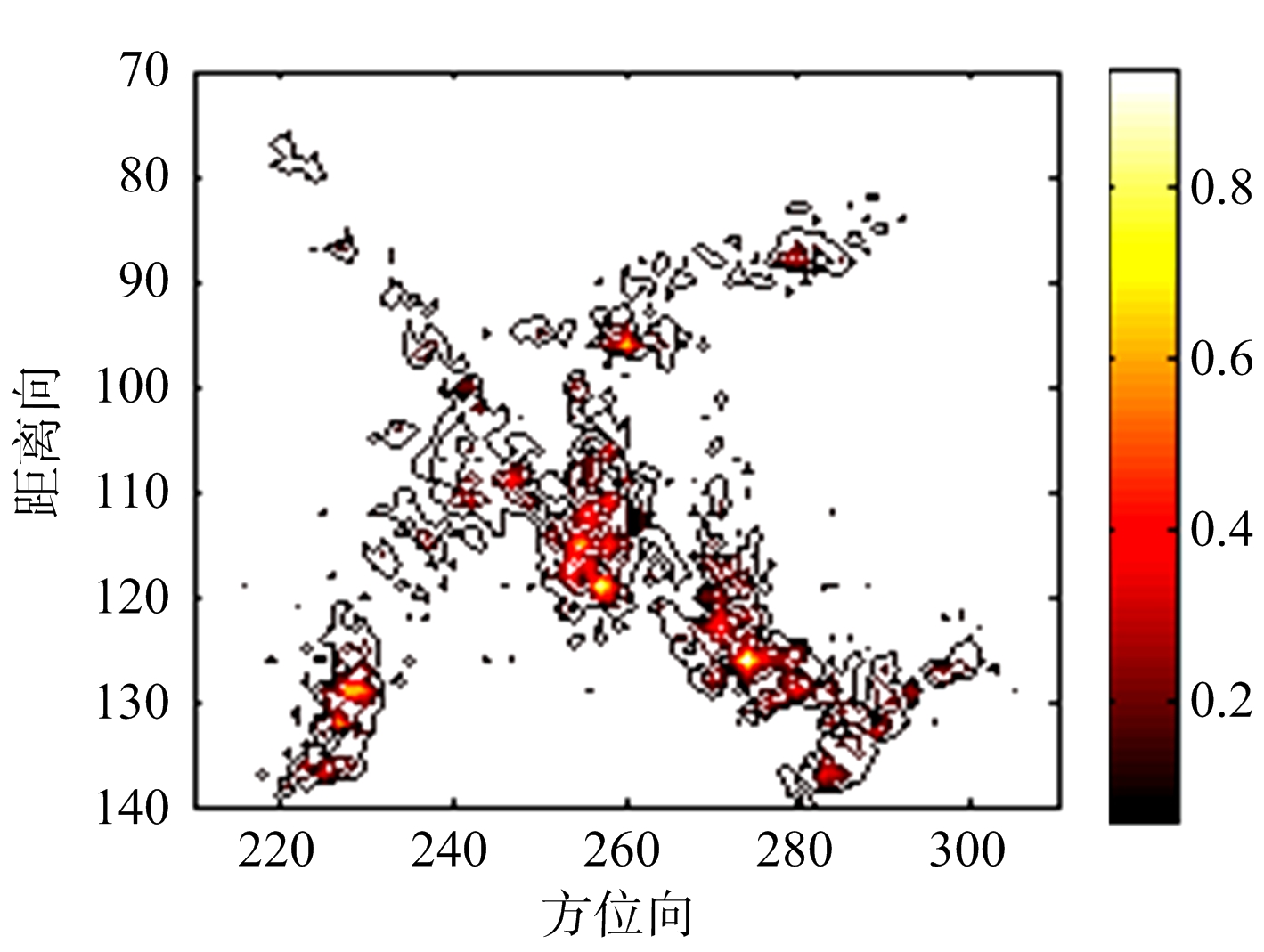
(b) MVM法飞机成像结果
(c) APES法飞机成像结果
图5 对飞机实测数据采用RD，MVM和APES算法的成像结果
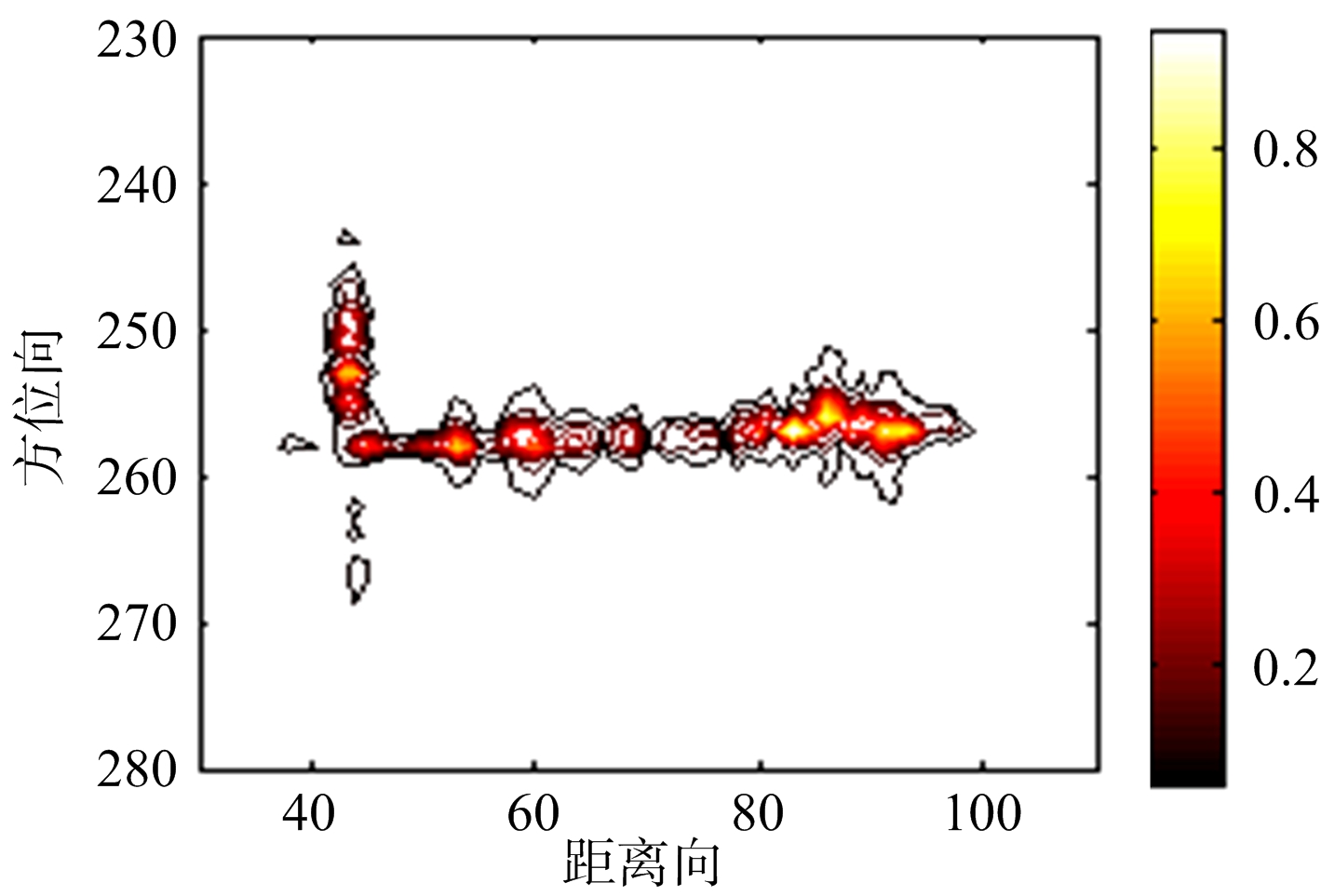
(a) RD法舰船成像结果
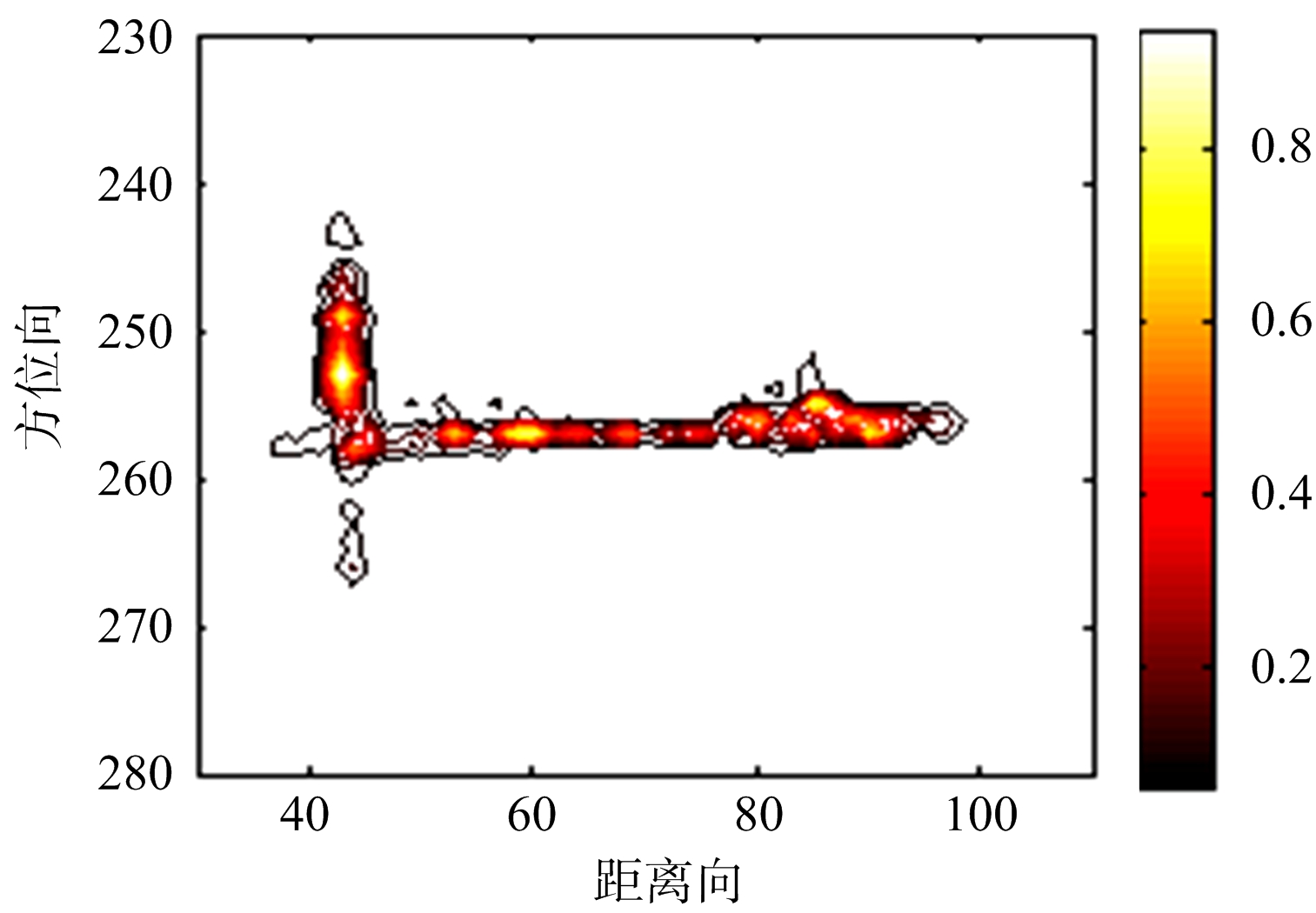
(b) MVM法舰船成像结果
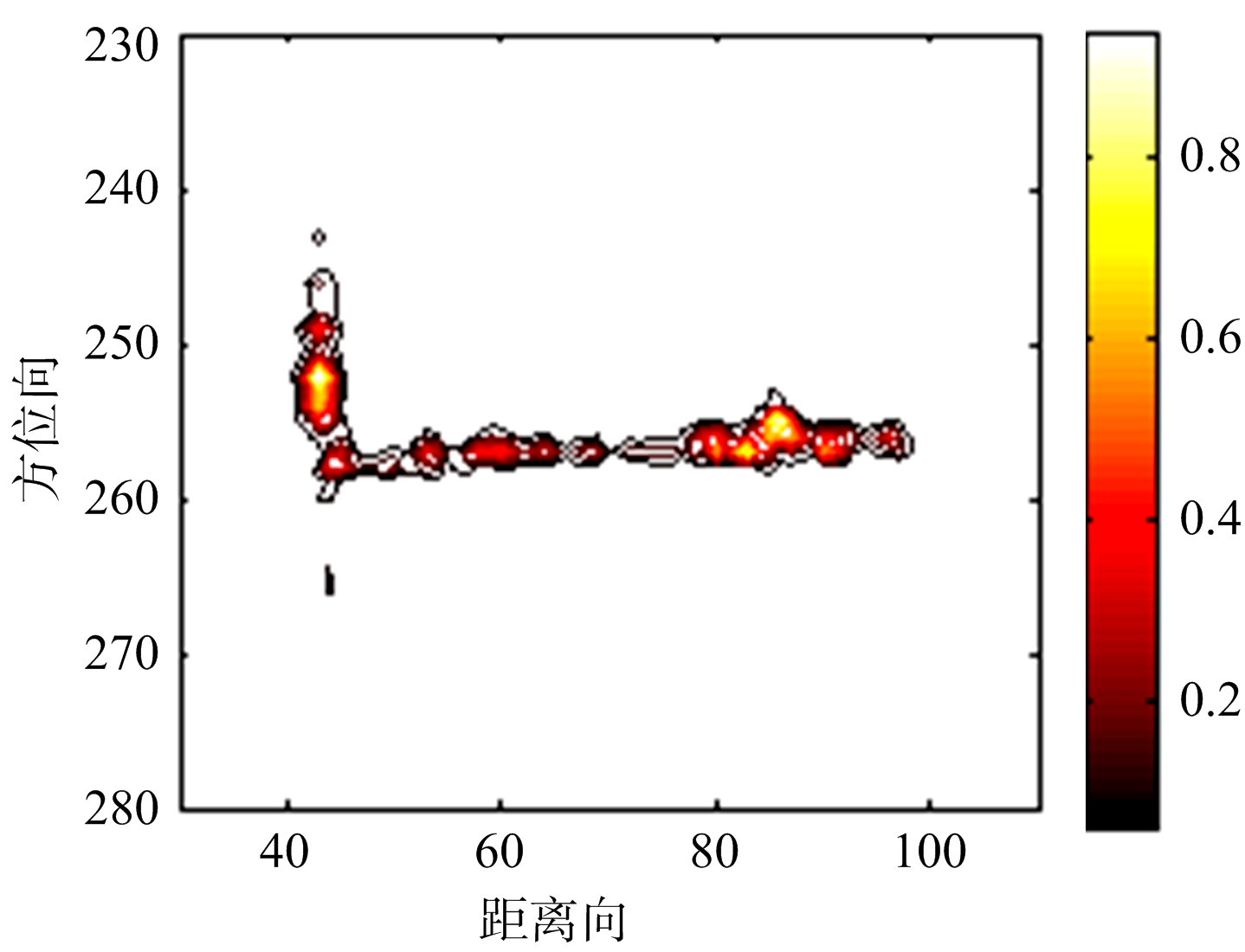
(c) APES法舰船成像结果
图6 对舰船实测数据采用RD，MVM和APES算法的成像结果
由于实测数据缺少方位向的转角信息，无法定量比较各种方法所得图像的方位向分辨率，因此图7和图8分别给出了飞机和舰船实测数据的强散射点方位向的3 dB主瓣宽度图，从而定性比较分辨率。从图中可以看出，相比于RD法，APES法的分辨率提高。
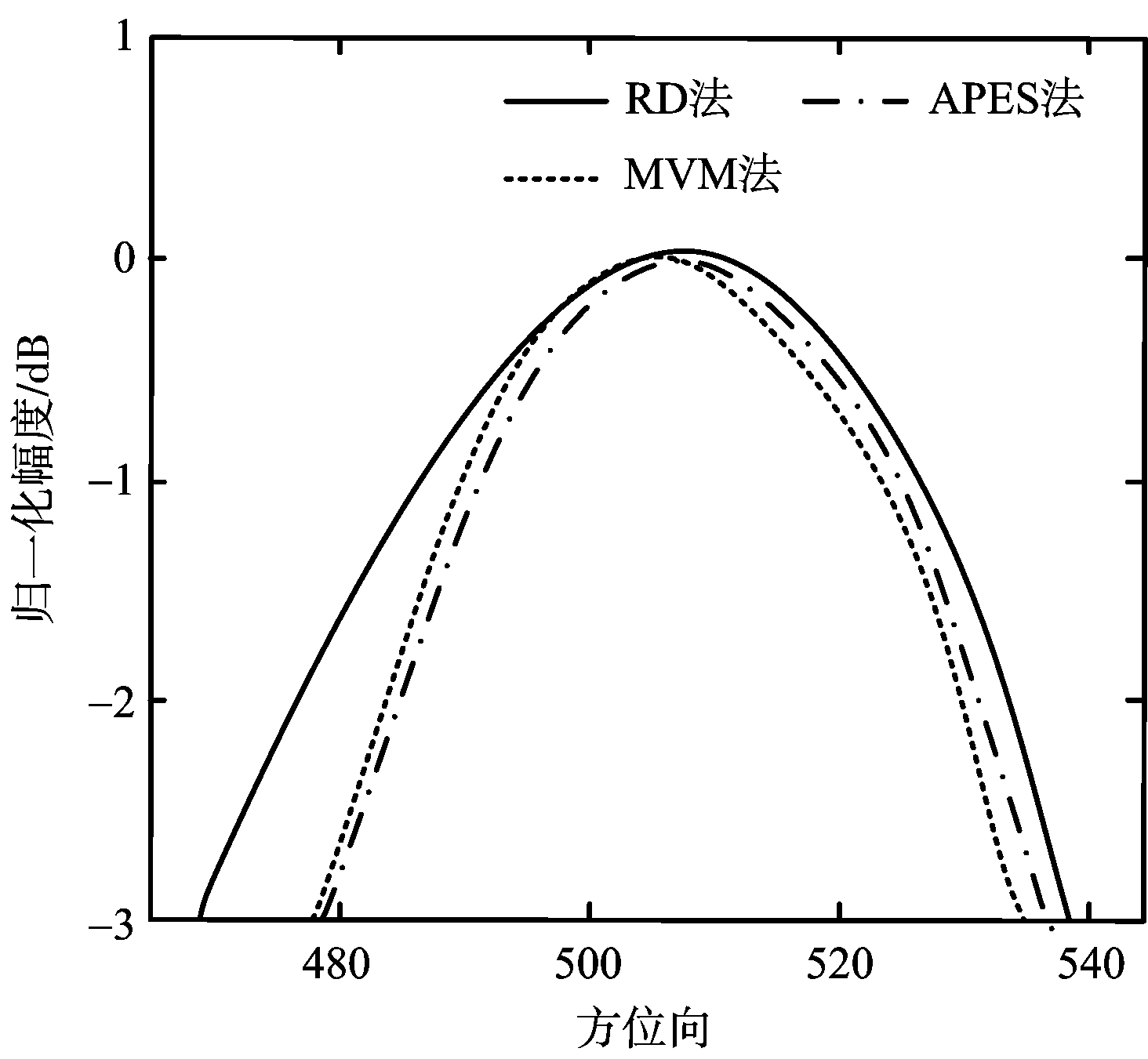
图7 飞机方位向3 dB主瓣宽度
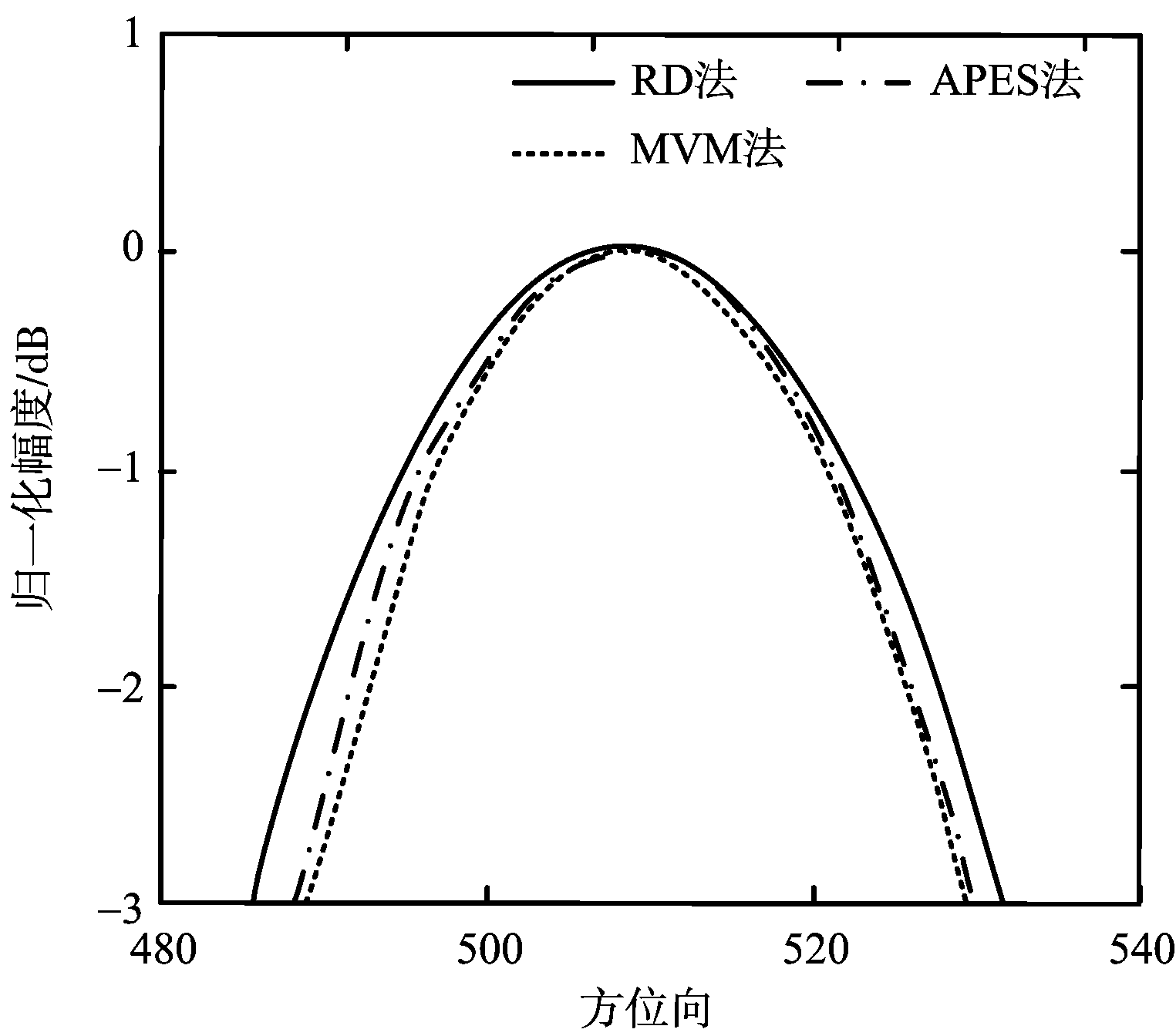
图8 舰船方位向3 dB主瓣宽度
表4和表5给出了飞机和舰船成像结果的对比度和信噪比分析。
表4 飞机实测数据的定量分析结果
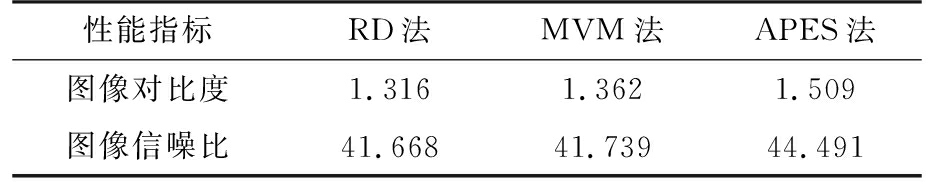
表5 舰船实测数据的定量分析结果
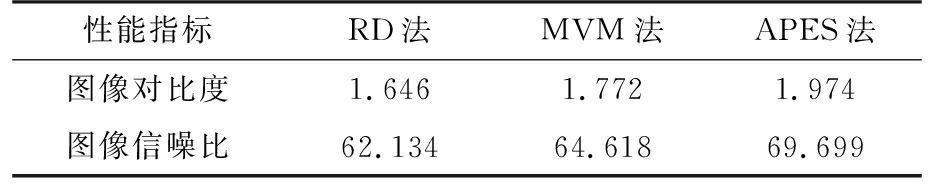
从表中可以看出， APES法重建图像的对比度和信噪比最大，说明APES法成像质量在三者中较优。
本文给出了一种基于APES的ISAR超分辨成像算法。该算法对雷达回波数据脉压、运动补偿后进行处理，采用空间平滑法得到前后向采样协方差矩阵，再通过构造脉冲响应函数重建目标散射点。仿真结果、飞机和舰船的实测数据成像结果表明，APES法可以抑制旁瓣，改善成像效果，实现ISAR超分辨成像，成像效果与常用的MVM方法相当。
参考文献 ：
[1] WANG Xin, ZHANG Min, ZHAO Jia. Super-Resolution ISAR Imaging via 2D Unitary ESPRIT[J]. Electronics Letters, 2015, 51(6):519-521.
[2] CHENG Chen, ZHANG Xiaoling. A New Super-Resolution 3D-SAR Imaging Method Based on MUSIC Algorithm[C]∥ IEEE Radar Conference, Kansas City, MO: IEEE, 2011:525-529.
[3] KOUSHIK A R, SHRUTHI B S, RAJESH R, et al. A Root-Music Algorithm for High Resolution ISAR Imaging[C]∥ IEEE International Conference on Recent Trends in Electronics, Information & Communication Technology, Bangalore, India: IEEE, 2016:522-526.
[4] YU Hanchen, ZHANG Yan, QIAN Weiping. A Novel MUSIC ISAR Method Using the First Principal Component[C]∥ 2nd Advanced Information Technology, Electronic and Automation Control Conference, Chongqing: IEEE, 2017:916-919.
[5] CHEN Lan, CHEN Jie. High Resolution Radar Imaging Using Bandwidth Extrapolation[C]∥ 3rd International Congress on Image and Signal Processing, Yantai: IEEE, 2010:3591-3595.
[6] FARINA A, PRODI F, VINELLI F. Application of Superresolution Techniques to Radar Imaging[J]. Journal of Systems Engineering and Electronics, 1994, 5(1):1-14.
[7] DUAN C, ZHU K, LENG Z. Iterative Realization of the 2-D Capon Method Applied in SAR Image Processing[C]∥ IET International Radar Conference, Hangzhou: IET, 2015:1-5.
[8] 王勇,姜义成. CAPON方法在ISAR成像中的应用[J]. 哈尔滨工业大学学报, 2007, 39(11):1751-1755.
[9] FONTANA A, BERENS P. Super-Resolution ISAR Imaging of Maritime Targets Using PAMIR Data[C]∥ 10th European Conference on Synthetic Aperture Radar, Berlin: VDE, 2014:1-4.
[10] FEI Zhiting. ISAR Imaging Based on SVA and Time Frequency Analysis[C]∥ 8th International Conference on Internet Computing for Science and Engineering, Harbin: IEEE, 2015:130-134.
[11] CATALDO D, MARTORELLA M. Super-Resolution for Bistatic Distortion Mitigation[C]∥ IEEE Radar Conference, Philadelphia, PA: IEEE, 2016:1-6.
[12] XU Xiaojian, NARAYANAN R M. Enhanced Resolution in SAR/ISAR Imaging Using Iterative Sidelobe Apodization[J]. IEEE Trans on Image Processing, 2005, 14(4):537-547.
[13] ZHANG Ping, LI Zhen, ZHOU Jianmin, et al. A New SAR Superresolution Imaging Algorithm Based on Adaptive Sidelobe Reduction[C]∥ International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada: IEEE, 2011:2789-2792.
[14] WANG Genyuan, XIA Xianggen. An Adaptive Filtering Approach to Chirp Estimation and ISAR Imaging of Maneuvering Targets[C]∥ International Radar Conference, Alexandria, VA: IEEE,2000:481-486.
[15] 李源. 逆合成孔径雷达理论与对抗[M]. 北京: 国防工业出版社, 2013.
[16] 陈洪猛,李明,卢云龙,等. 基于APES的超分辨广域成像算法[J]. 系统工程与电子技术, 2015,37(1):6-11.
CHEN Hongmeng, LI Ming, LU Yunlong,et al. Novel supper-Resolution Wide Area Imaging Algorithm Based on APES[J]. System Engineering and Electronics, 2015, 37(1):6-11.(in Chinese)
[17] LI H, LI J, STOICA P. Performance Analysis of Forward-Backward Matched-Filterbank Spectral Estimators[J]. IEEE Trans on Signal Processing, 1998, 46(7):1954-1966.
[18] LI J, STOICA P. An Adaptive Filtering Approach to Spectral Estimation and SAR Imaging[J]. IEEE Trans on Signal Processing, 1996, 44(6):1469-1484.
[19] LOPEZ-DEKKER P, MALLORQUI J J. Capon- and APES-Based SAR Processing: Performance and Practical Considerations[J]. IEEE Trans on Geoscience and Remote Sensing, 2010, 48(5):2388-2402.
[20] HUANG Darong, FENG Cunqian, TONG Ningning, et al. 2D Spatial-Variant Phase Errors Compensation for ISAR Imagery Based on Contrast Maximisation[J]. Electronics Letters, 2016, 52(17):1480-1482.
[21] BACCI A, GIUSTI E, CATALDO D, et al. ISAR Resolution Enhancement via Compressive Sensing: A Comparison with State of the Art SR Techniques[C]∥ 4th International Workshop on Compressed Sensing Theory and its Applications to Radar, Sonar and Remote Sensing, Aachen, Germany: IEEE, 2016:227-231.
DENG Hao 1 , WANG Ling 1 , YANG Na 1 , XIAO Zhuo 2
(1. Key Laboratory of Radar Imaging and Microwave Photonics , Ministry of Education , Nanjing University of Aeronautics and Astronautics , Nanjing 211100, China ;2. Unit 96764 of PLA , Luoyang 471000, China )
Abstract : The resolution of traditional range Doppler (RD) algorithm depends on the bandwidth of the transmitted signal and the Doppler bandwidth in the cross range. Super resolution imaging can obtain a better resolution than the RD algorithm for the same bandwidth. In this paper, we present a super resolution imaging algorithm for inverse synthetic aperture radar (ISAR) using the amplitude and phase estimation (APES) technique. An adaptive filter is constructed to reconstruct the scatterers. The imaging results of the simulated data and real ISAR data verify the effectiveness of this new APES-based ISAR imaging algorithm. Compared with other super resolution algorithms, the proposed algorithm is able to reconstruct the amplitudes of the scatterers with higher accuracy and lower sidelobe. The image contrast and signal and noise ratio (SNR) of the image are also increased, resulting in good image quality.
Key words : inverse synthetic aperture radar (ISAR); imaging; super-resolution; amplitude and phase estimation (APES); sidelobe suppression
基金项目： 研究生创新基地(实验室)开放基金(No.kfjj20160402)； 中央高校基本科研业务费专项资金资助课题
修回日期： 2017-11-21
DOI: 10.3969/j.issn.1672-2337.2018.04.001
收稿日期： 2017-09-25；
文献标志码： A
文章编号： 1672-2337(2018)04-0351-08
作者简介 ：
中图分类号 ： TN951；TN958
邓 昊 女，1992年生，江苏南通人，南京航空航天大学电子信息工程学院硕士研究生，主要研究方向为合成孔径雷达成像。
E-mail：kthy_dh@163.com
汪 玲 女，1977年生，河南洛阳人，南京航空航天大学电子信息工程学院教授、博士生导师，主要研究方向为雷达成像，包括合成孔径雷达成像、逆合成孔径雷达成像、无源雷达成像。
杨 娜 女，1992年生，云南昆明人，南京航空航天大学电子信息工程学院硕士研究生，主要研究方向为雷达信号处理。
肖 卓 男，1982年生，河南洛阳人，现任职于中国人民解放军96764部队，主要研究方向为网络通信。