韩 俊 , 陆晓飞 , 吕明久 , 冯明月
(空军预警学院,湖北武汉 430019)
摘 要 : 针对步进频率波形数据率低、运动补偿难度大的问题,提出了一种新的相位编码调频步进信号(PC-CFS)。新信号在相位编码步进信号的基础上,通过对每个子码进行Chirp调制,在保持子脉冲时宽不变的情况下,增大了载频步进量,减小了子脉冲个数,提高了信号的数据率。在推导新信号模糊函数的基础上,着重分析了其距离、多普勒分辨性能,并在性能比较中得出该信号具有较好的距离、多普勒联合分辨能力,大大降低了运动补偿难度,且信号的低截获、抗干扰性能也得到进一步提升的结论。
关键词 : 相位编码调频步进信号(PC-CFS); 距离分辨性能; 多普勒分辨性能; 模糊函数; 成像处理
步进频率波形(Stepped-Frequency Waveform, SFW)由于具有瞬时带宽小、硬件要求低以及合成带宽大等优势,已成功应用于现代雷达系统中,典型的SFW主要包括频率步进信号(Frequency-Stepped Signal,FS) [1] 、调频步进信号(Chirp Frequency-Stepped Signal,CFS) [2] 以及相位编码步进信号(Phase Coded Frequency-Stepped Signal,PCFS) [3-4] 等。SFW的主要特征是通过发射多个子脉冲信号合成大的信号带宽。当子脉冲个数较多时,在成像时间内目标运动状态将会更为复杂,此时对于目标运动状态的近似条件将不再成立,因而运动补偿的难度将大大增加。另外,过长的成像时间也将占用大量的雷达资源。要想在保证合成带宽不变的前提下提高信号的数据率,就必须增大信号的载频步进量,减少发射的子脉冲个数。因此,如何在总合成带宽一定的条件下提高信号的数据率是步进频率波形设计的一个重要研究内容。
实际上,对于SFW,载频步进量最大可以设置为子脉冲信号的带宽,也即SFW波形设计的“紧约束”条件。对于FS信号,增大载频步进量则意味着减小子脉冲时宽,当载频步进量变大时将会造成子脉冲时宽变窄,进而降低了信号的作用距离。为解决上述矛盾,PCFS,CFS信号通过对子脉冲分别进行相位编码和Chirp调制来增大载频步进量的大小,在保证子脉冲时宽和总合成带宽不变的条件下,减少了发射子脉冲的个数,提高了信号的数据率。对于PCFS信号,载频步进量最大可以设置为子码时宽的倒数 [5] ,但由于受编码序列长度的限制,载频步进量并不能设置得很大,信号数据率提高的潜力有限。与PCFS信号类似,要想提高CFS信号的数据率就必须增大子脉冲调制的带宽,这对于调制线性度提出了较高的要求 [6] 。此外,由于子脉冲为线性调频信号形式,信号的抗干扰和低截获性能有限 [7] 。
针对上述问题,本文从结合相位编码信号与调频步进信号优点的前提出发,提出了一种新的步进频率信号形式:相位编码调频步进信号(Phase Coded Chirp Frequency-Stepped Signal,PC-CFS)。该信号在相位编码步进信号的基础上,通过对每个子码进行频率调制,在保持子码时宽不变的情况下增大了子码带宽,此时信号的载频步进量最大可取为子码带宽,增大了载频步进量的大小,减少了所需发射的子脉冲个数,进一步提高了信号数据率。文中首先给出了PC-CFS信号的表达式,并推导了信号的模糊函数。然后基于模糊函数分析了PC-CFS信号的距离、多普勒特性,给出了相应的成像处理方法,分析了PC-CFS信号的速度补偿难度。通过与常用的步进频率信号进行比较,得出该信号不仅具有较好的距离、多普勒联合分辨性能,且大大降低了运动补偿难度。该信号对于步进频率波形的实用化提供了更好的选择。
相位编码调频步进信号可以表示为
(1)
式中: N 为子脉冲个数; T r 为子脉冲重复时间;Δ f 为频率步进量; f 0 为信号载频; μ ( t )为子脉冲调制函数,当子脉冲为相位编码线性调频信号时, μ ( t )可表示为
μ ( t )= ![]()
exp[jπ K ( t - iT 1 ) 2 ]
(2)
式中: T 1 为子码时宽; P 为编码个数; C i 为编码序列,对于二相编码信号, C i 可以表示为 C i ={exp[j φ i ]=+1,-1}, i =1,2,…, P ; K 为子脉冲调频率。其发射信号示意图如图1所示。
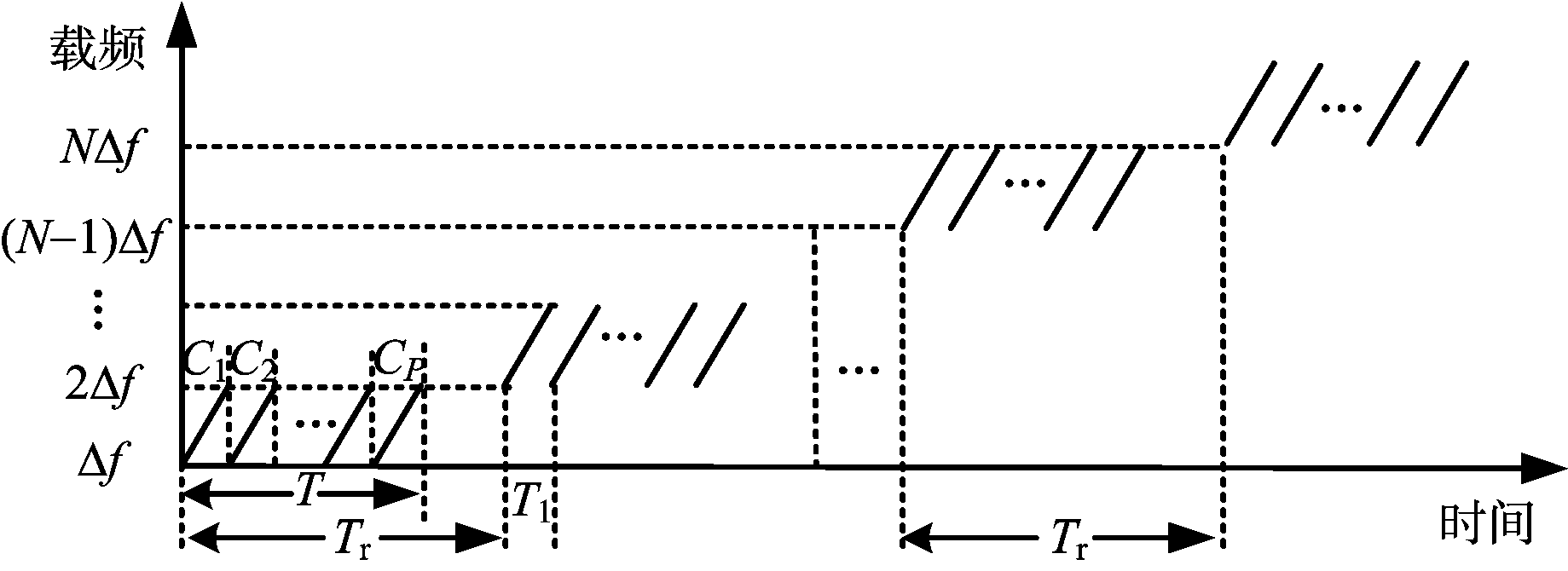
图1 PC-CFS信号示意图
对于PCFS信号,若 T 表示子脉冲时宽,则有 T = PT 1 。其载频步进量Δ f 最大可取Δ f =1/ T 1 = P / T ,合成的总带宽为 NP / T 。当对子码进行调制时,此时载频步进量Δ f 最大可取Δ f = B PCCSF = K / T 1 = KP / T ,合成的总带宽为 NKP / T 。因此,在相同的合成带宽条件下,PC-CFS信号可以显著地减少发射子脉冲的个数。
信号的模糊函数是表征信号分辨性能的重要工具,其表达式为
(3)
将式(1)代入式(3)可得到PCCFS信号的模糊函数为
![]() ( τ , ζ )=
( τ , ζ )= ![]()
![]() exp[j2π n Δ ft ]exp[-j2π m Δ f ( t + τ )] \ 5
exp[j2π n Δ ft ]exp[-j2π m Δ f ( t + τ )] \ 5
exp[-j2π( m - n )Δ ft ]exp(j2π ζt )d t
(4)
令 t - nT r = t ′ 得到
![]() ( τ , ζ )=
( τ , ζ )= ![]()
exp[j2π ζnT r ]exp[-j2π( m - n ) nT r ]· ![]() PCLFM [ τ -( m - n ) T r , ζ -( m - n )Δ f ]
PCLFM [ τ -( m - n ) T r , ζ -( m - n )Δ f ]
(5)
式中, ![]() PCLFM [ τ , ζ ]为相位编码线性调频信号的模糊函数。具体形式 [8] 为
PCLFM [ τ , ζ ]为相位编码线性调频信号的模糊函数。具体形式 [8] 为
![]() PCLFM ( τ , ζ )=
PCLFM ( τ , ζ )= ![]()
(6)
式中, ![]() LFM ( τ , ζ )为线性调频子码的模糊函数,可以表示为
LFM ( τ , ζ )为线性调频子码的模糊函数,可以表示为
| χ LFM ( τ , ζ )|=
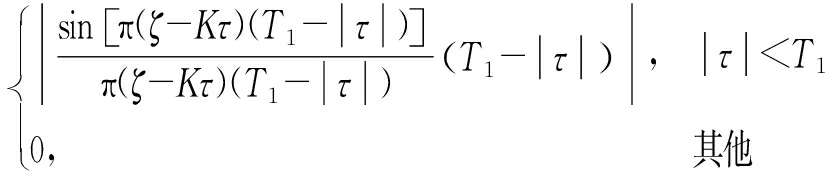
(7)
令 p = m - n ,此时 p 的取值范围为-( N -1)≤ p ≤( N -1)。当 p ≥0时,式(5)可写为
![]() ( τ , ζ )=
( τ , ζ )= ![]()
exp{-j2π m [Δ f ( τ + pT r )- T r ζ ]}· ![]() PCLFM [ τ - pT r , ζ - p Δ f ]=
PCLFM [ τ - pT r , ζ - p Δ f ]=
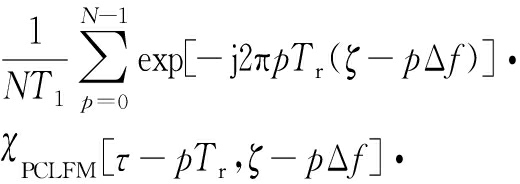
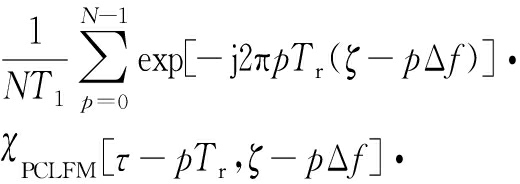
exp{-jπ( N -1- p )[Δ f ( τ + pT r )- T r ζ ]}·
(8)
同理,当 p <0时:
![]() ( τ , ζ )=
( τ , ζ )= ![]()
exp{-j2π m [Δ f ( τ + pT r )- T r ζ ]}· ![]() PCLFM [ τ - pT r , ζ - p Δ f ]=
PCLFM [ τ - pT r , ζ - p Δ f ]=
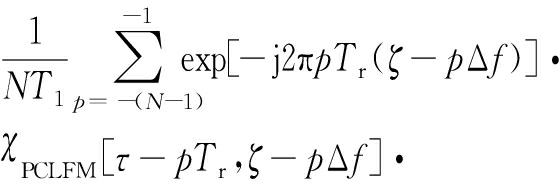
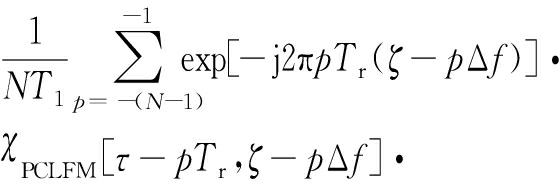
exp{-jπ( N -1+ p )[Δ f ( τ + pT r )- T r ζ ]}·
(9)
结合式(8)、式(9)可得
![]() ( τ , ζ )=
( τ , ζ )= ![]()

exp{-jπ( N -1-| p |)[Δ f ( τ + pT r )- T r ζ ]}
(10)
则
| χ ( τ , ζ )|= ![]()
(11)
考虑其中心模糊带,即令 p =0,代入式(11)中得到
| χ ( τ , ζ )|=
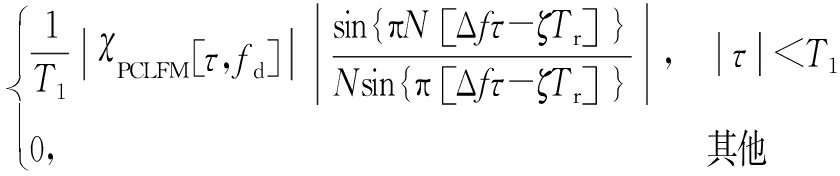
(12)
从上式可以看出,PC-CFS信号的模糊函数主要由脉内线性调频加相位编码模糊函数与步进频率信号模糊函数两部分构成。
为更直观地研究PC-CFS信号的性能,给出PC-CFS信号的三维模糊函数图,如图2所示。假设PC-CFS信号合成总带宽为480 MHz;子脉冲时宽 T =13 μs, T r =10 T ,子码采用13 bit barker码编码形式,子脉冲时宽带宽积 D PCCFS =30,子脉冲个数为 N PCCFS =16。为便于性能比较,给出了PCFS信号、CFS信号的三维模糊函数图,分别如图3、图4所示。其中对于CFS信号,假设信号子脉冲时宽带宽积 D CFS =130,子脉冲个数 N CFS =48,合成的总带宽为480 MHz。对于PCFS信号,同样采用13 bit barker码编码形式,子脉冲个数 N PCFS =120,此时合成的总带宽为120 MHz。
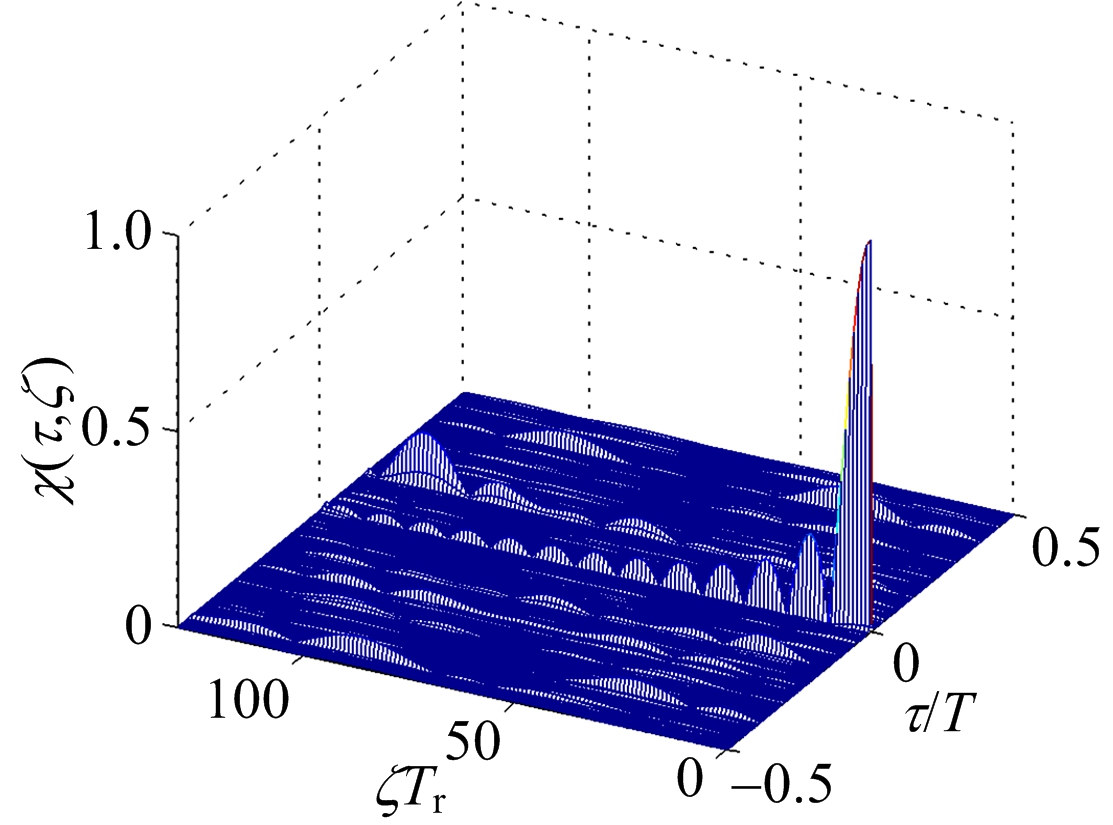
图2 PC-CFS信号模糊函数
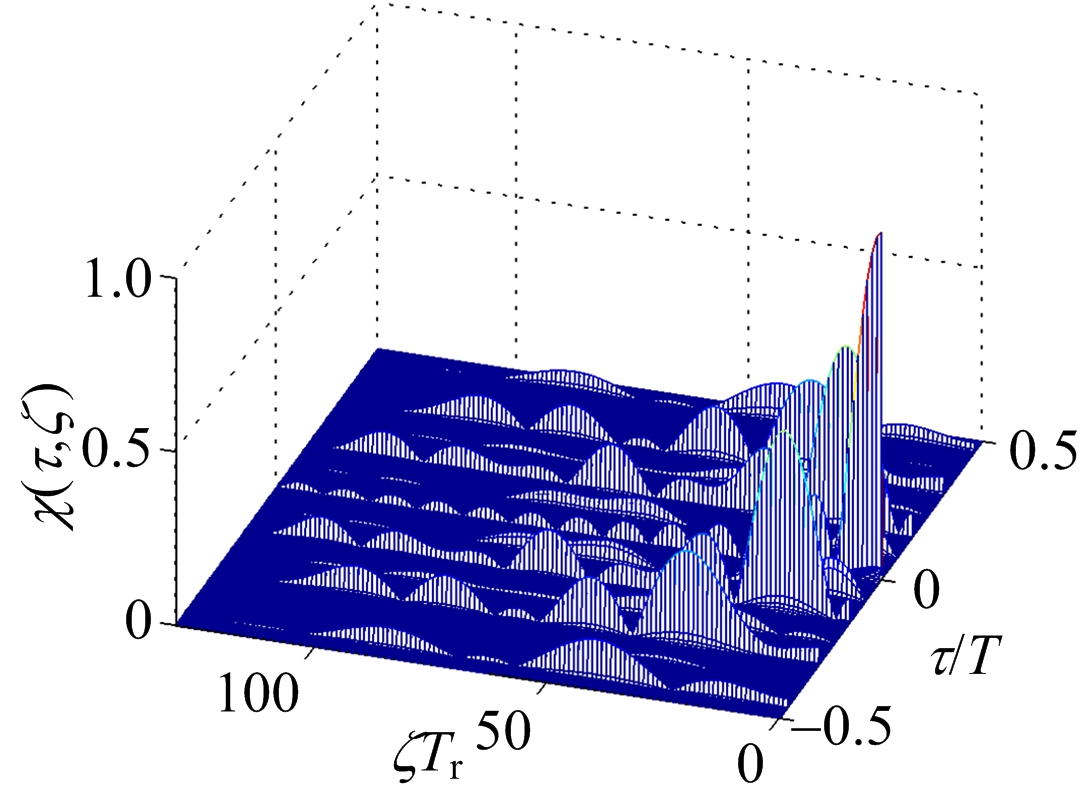
图3 PCFS信号模糊函数
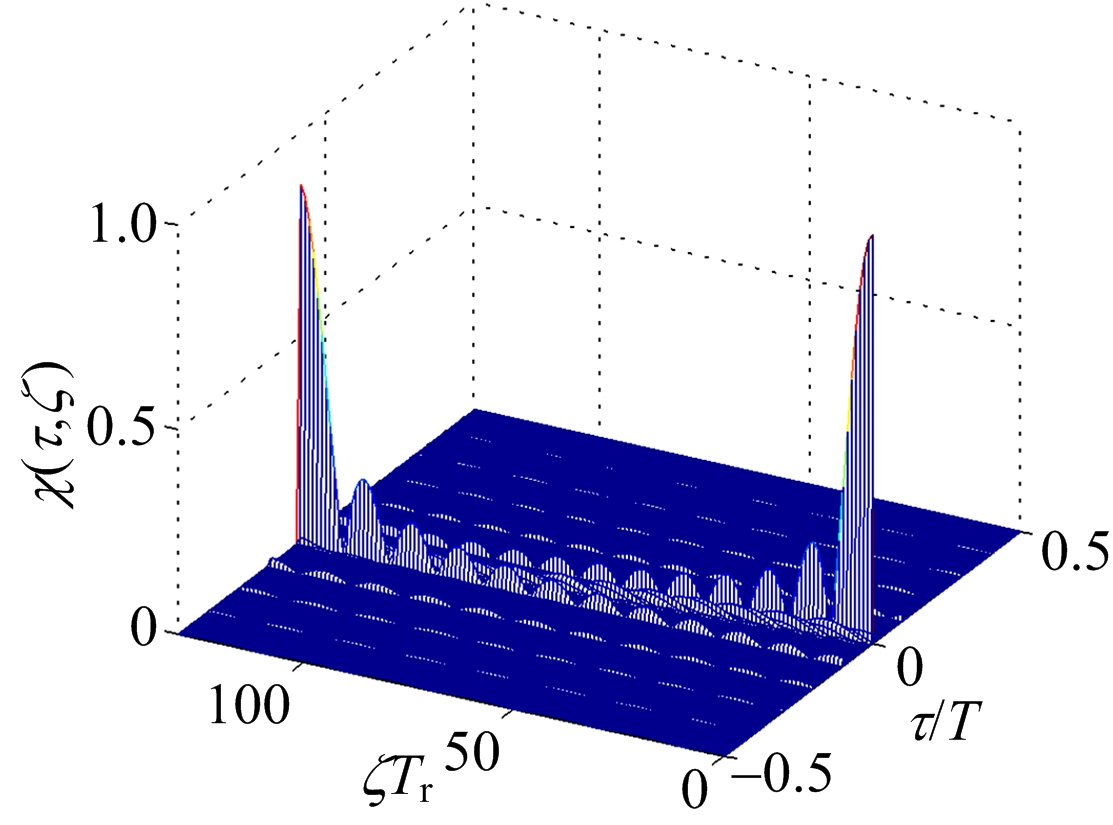
图4 CFS信号模糊函数
图中纵坐标为模糊函数的归一化值,对比图中3种信号的模糊函数可以得到:
1) CFS信号的模糊函数呈现“斜刀刃”形,说明CFS信号具有较强的距离多普勒耦合。PCFS信号的模糊函数呈现近似“图钉”形,这是由于子脉冲采用相位编码调制时,相位调制的随机性使得信号距离多普勒耦合比CFS信号小得多,信号的多普勒敏感性高。PC-CFS信号的模糊函数呈现“图钉”形,具有较好的距离多普勒联合分辨能力,且具有较好的抗干扰和低截获性能。
2) 对比3种信号的栅瓣,CFS信号的栅瓣最少且幅度最小,而PCFS信号由于相位随机调制的原因,出现较多的周期栅瓣,且起伏较大。对于PC-CFS信号,由于子脉冲复合调制,使得周期性栅瓣减少且栅瓣得到抑制。
从上述比较中可以看出,PC-CFS信号的模糊函数同时拥有CFS信号低旁瓣以及PCFS信号低距离多普勒耦合的特点,具有较强的距离、多普勒联合分辨能力,且由于子脉冲的复杂调制使得信号的抗干扰和低截获性能得到增强。
下面分别给出PC-CFS信号的距离中心模糊带模糊函数以及多普勒中心模糊带模糊函数。
令 ζ =0,得到相位编码调频步进信号的距离中心模糊带模糊函数为
| χ ( τ ,0)|=
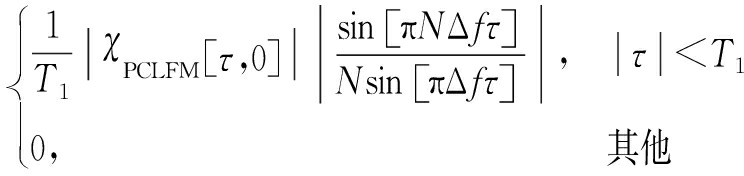
(13)
式中,
| χ PCLFM [ τ ,0]|=
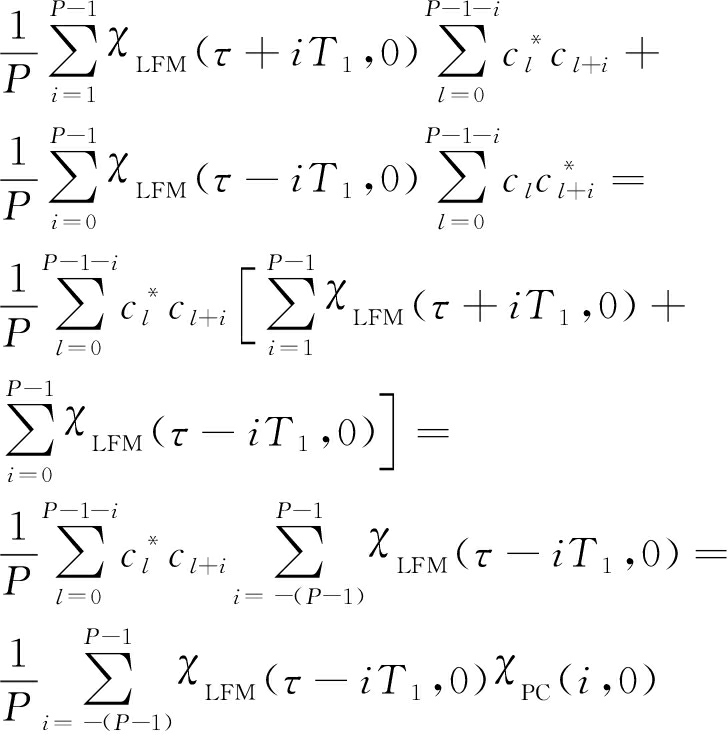
(14)
式中, ![]()
结合式(13)、式(14)得到
| χ ( τ ,0)|=
(15)
基于上述仿真参数,图5~图7为3种信号的距离中心模糊带模糊函数图。
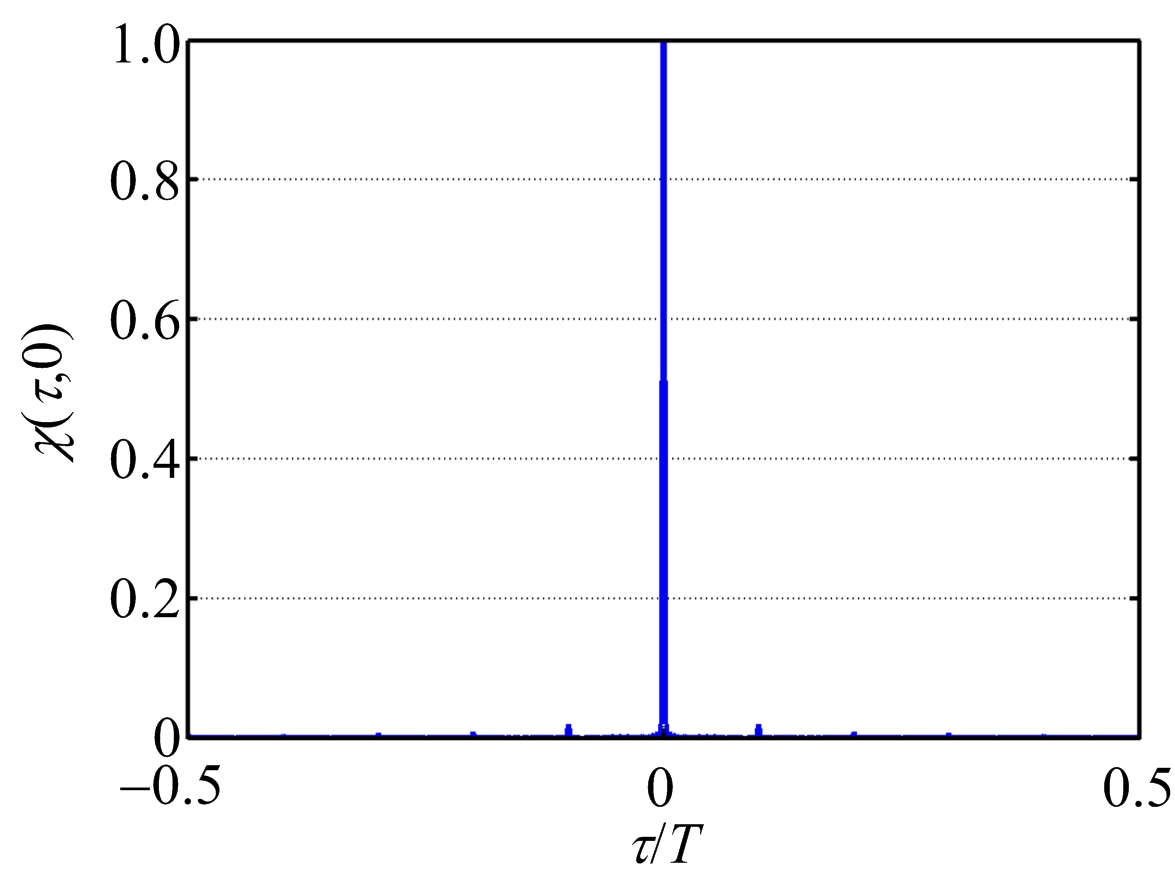
图5 PC-CFS信号距离模糊函数
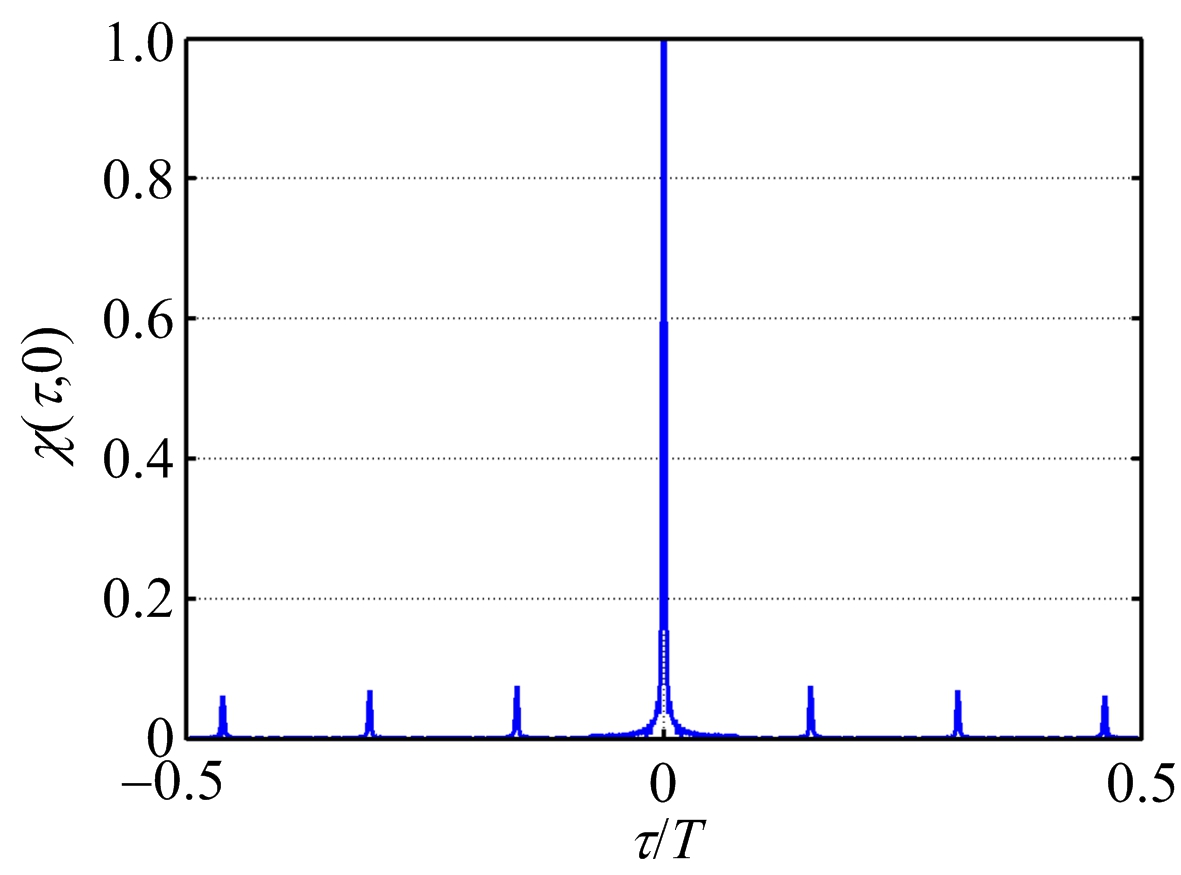
图6 PCFS信号距离模糊函数
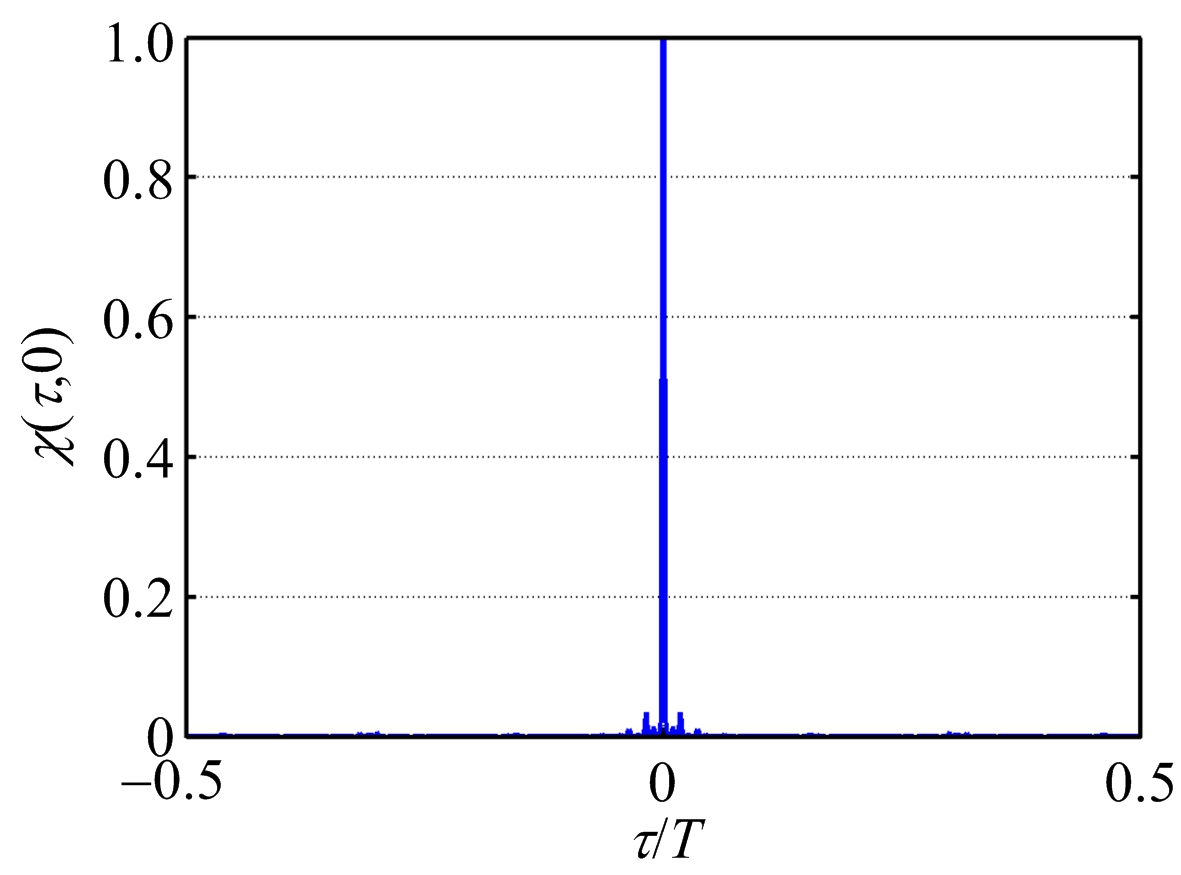
图7 CFS信号距离模糊函数
由上述仿真结果可以看出:3种信号都具有高的距离分辨率。对于PCFS信号,由于子脉冲采用的是相位编码形式,因此距离模糊函数出现了周期性的距离旁瓣,将会影响对弱小目标的分辨 [9] 。而对于PC-CFS信号,由于对子码信号进行了Chirp调制,因此大大压制了周期性的距离旁瓣,因此具有更好的弱目标分辨能力。
此处给出PC-CFS信号的高分辨距离像合成方法。与CFS信号获得高分辨距离像的方法类似,要获得最终的一维距离像PC-CFS信号必须经过“两步”脉压处理。首先须进行子脉冲脉压处理,再进行脉冲间IFFT处理。子脉冲μ(t)经过对应的匹配滤波器即可完成压缩处理,得到粗分辨的一维距离像。而后,通过对子脉冲脉压信号的采样值进行IFFT处理即可得到最终的高分辨距离像结果。具体的PC-CFS信号成像处理过程如图8所示。
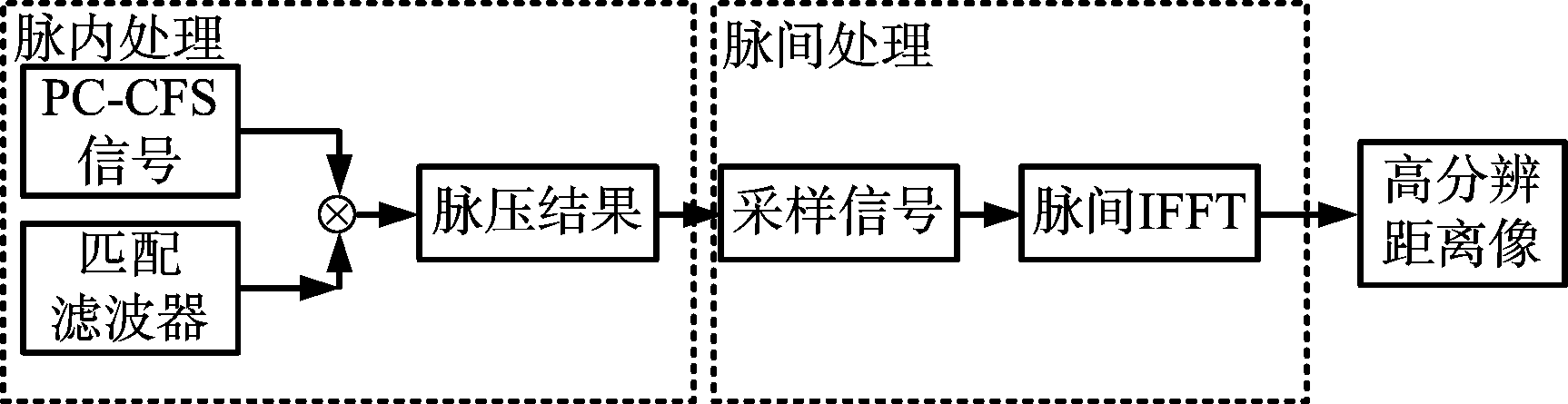
图8 PC-CFS信号处理过程
图9为PC-CFS信号距离像合成结果,设置的3个散射点相对位置为[0.75 1.5 3.5]m,信号参数设置保持不变,此时载频步进量Δ f PCCFS =30 MHz,图9为PC-CFS信号两步脉压的结果。
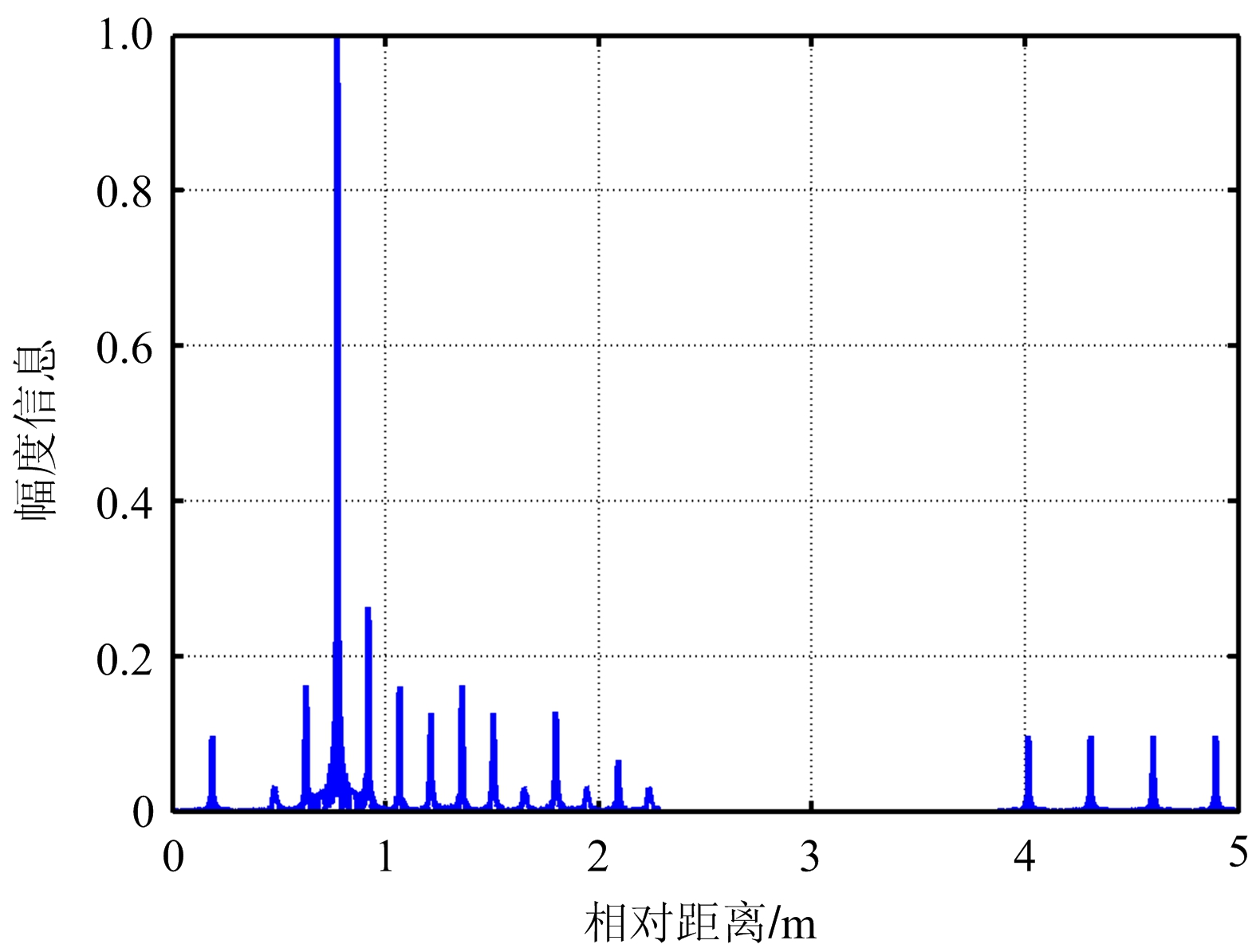
(a) 子脉冲成像结果
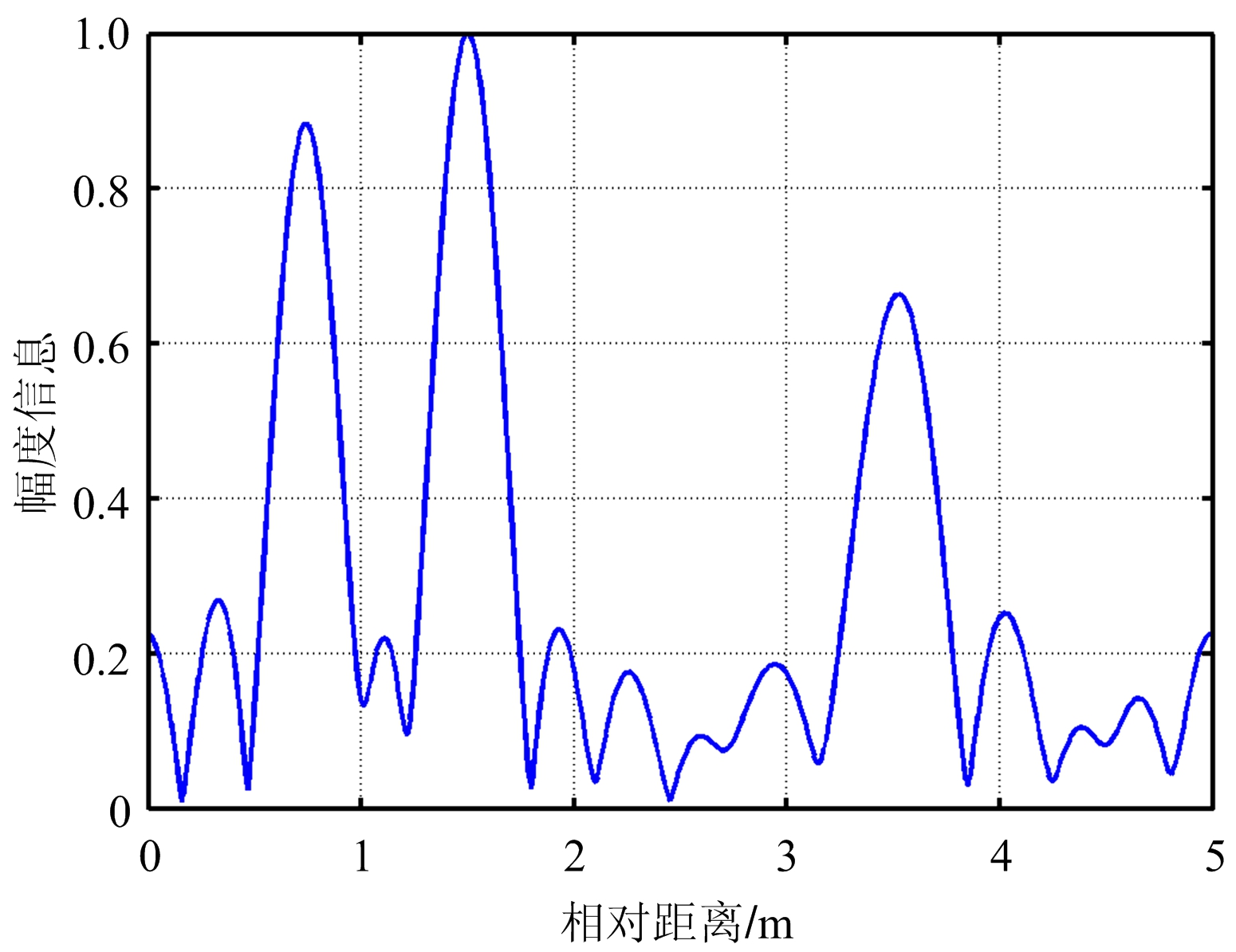
(b) 精分辨距离像
图9 PC-CFS信号距离像合成结果示意图
对于PC-CFS信号子脉冲,其距离分辨率为 c /(2Δ f PCCFS )=5 m,因此其脉压后的结果并不能分辨出3个散射点的准确位置,其脉压结果如图9(a)所示。当进行脉间距离像合成后,此时的距离分辨率为 c /(2 N PCCFS Δ f PCCFS )≈0.32 m,因此可以成功分辨出3个散射点的位置,其具体成像结果如图9(b)所示。
令 τ =0时,可以得到相位编码步进信号多普勒中心模糊带模糊函数为
| χ (0, ζ )|=
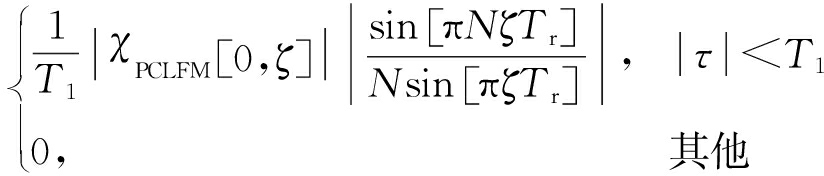
(16)
式中,
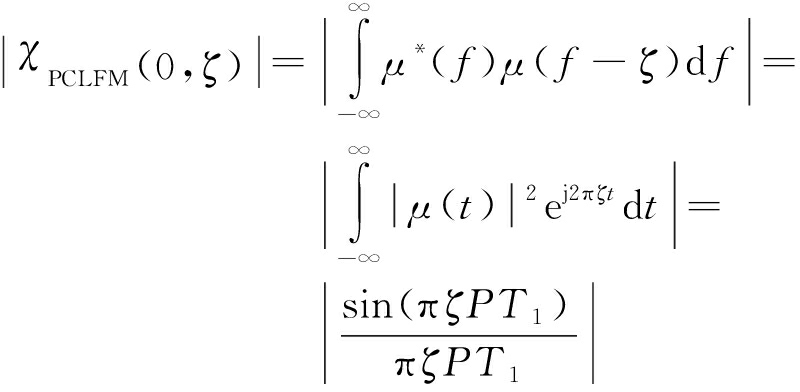
(17)
将式(17)代入式(16)得到
| χ (0, ζ )|=
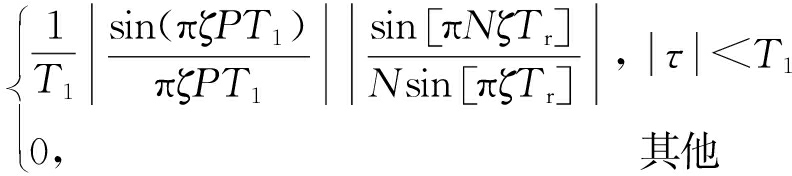
(18)
从上式可知:PC-CFS信号的多普勒中心模糊带模糊函数形式与PCFS信号、CFS信号相同,因此具有相同的速度分辨率,如图10所示。
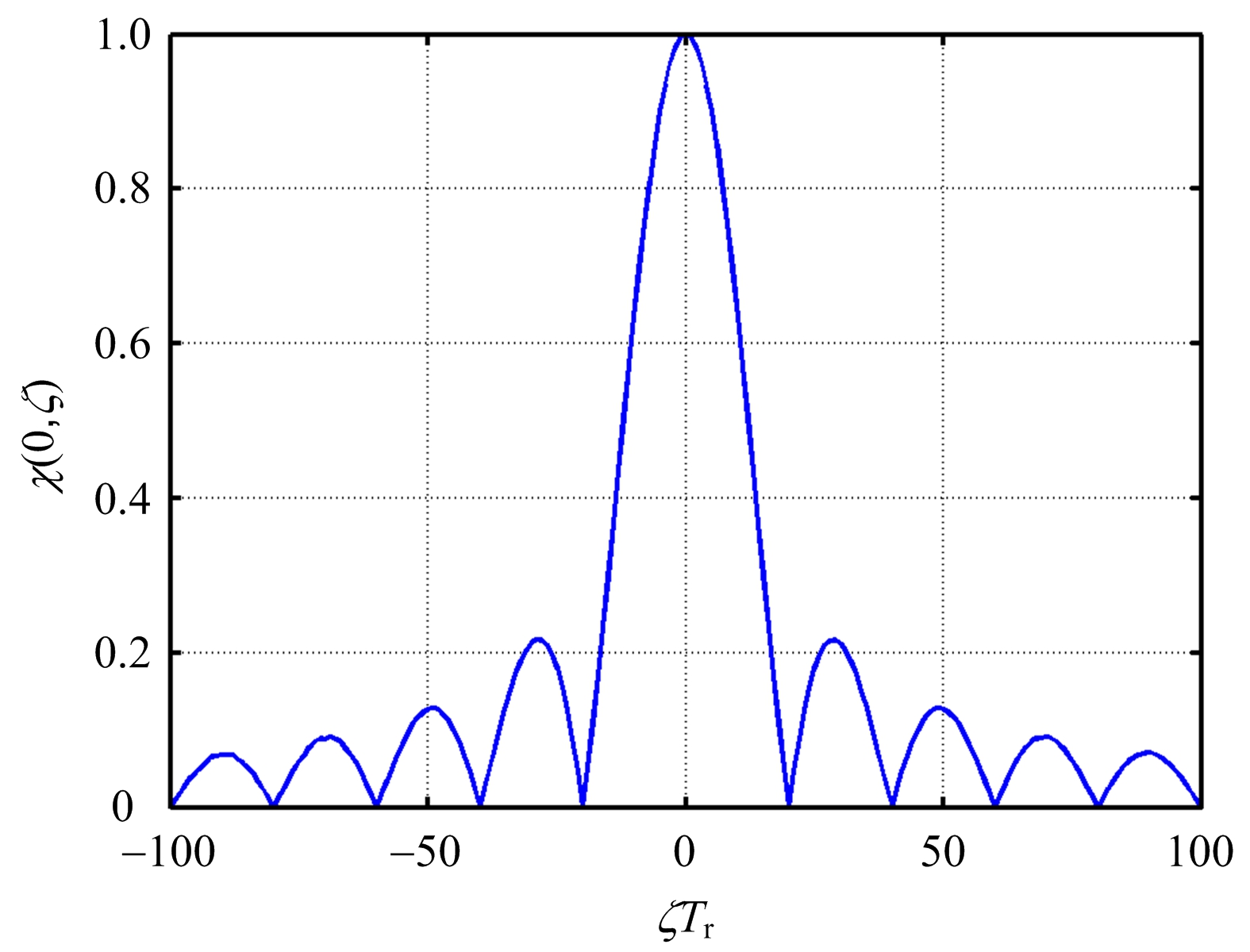
图10 PC-CFS信号多普勒模糊函数
步进频率波形通过牺牲时间资源换取瞬时带宽的降低,因此成像时间通常较长,在成像时间内受目标运动的影响较大。然而,在相同的合成带宽、相同的PRF条件下,与PCFS信号、CFS信号相比,PC-CFS信号所需的步进数最少,因此受目标运动的影响将会减小。目标运动对PC-CFS信号的影响主要分为对子脉冲脉压的影响以及对脉间相参处理的影响。
对于PC-CFS信号,由于子脉冲采用相位编码加线性调频调制,因此子脉冲的脉压实际可分为对子码线性调频信号的脉压以及对相位编码信号的脉压。在压缩处理中,目标运动的影响将会造成脉压结果主瓣的展宽以及旁瓣的升高。对子码线性调频信号来说,假设可容忍的最大时移为半个脉压后的距离单元,即1/2 B PCCFS ,则速度补偿需满足的条件为
2 VT 1 / c ≤1/2 B PCCFS
(19)
对于子脉冲相位编码信号来说,同样要求脉压后的最大时移不超过半个脉压的距离单元,则速度需满足的条件为
2 VPT 1 / c ≤1/2 B PCCFS
(20)
结合式(19)、式(20)可知,对PC-CFS信号子脉冲的速度补偿需满足式(20)的要求。以上节信号参数为例,只要 V <200 km即可忽视速度与子脉冲脉压的影响。因此在实际中上述条件很容易满足。
目标运动对脉间IFFT的影响程度主要受子脉冲个数 N 、子脉冲重复时间 T r 决定。由于脉间合成过程同步进频率信号相同,因此速度需满足一次、二次相位误差的补偿条件分别为
V ≤ c /(4 Nf 0 T r )
(21)
V ≤ c /(4 N 2 Δ f PCCFS T r )
(22)
从上述分析可以看出,目标运动对PC-CFS信号子脉冲的影响较小,可以忽略,主要影响体现在脉间相参合成中,且这种影响与传统步进频率波形相同。但是在相同的合成带宽条件下,PC-CFS信号的步进数明显少于其他步进频率信号,因此对速度的补偿要求最小。在上述参数条件下,PC-CFS信号一次相位项的补偿精度约为3.5 m/s,二次相位项的补偿精度约为75 m/s。而在相同的合成带宽条件下,PCFS信号与CFS信号的补偿精度分别为0.01 m/s,2.5 m/s以及0.1 m/s,25 m/s。可以看出PC-CFS信号的速度补偿精度要求较低,大大降低了运动补偿的难度。
假设PCFS信号子脉冲个数 N PCFS =480,使3种信号具有同样的合成带宽,其他条件保持不变。图11为PC-CFS信号在不同速度条件下距离像合成结果,图12为3种信号在 V =10 m/s时合成距离像受速度影响的示意图。
从图11可以看出,当速度为3 m/s时,距离像走动较小,未超过主瓣3 dB宽度。当速度为100 m/s时,距离像主瓣展宽。这与上述运动补偿要求相一致。对于图12所示的在 V =10 m/s时成像结果,PC-CFS信号的合成距离像受到的影响最小,而PCFS信号的合成距离像发生了散焦,已经无法分辨。因此相比于其他两种信号,PC-CFS信号具有较低的速度补偿精度。
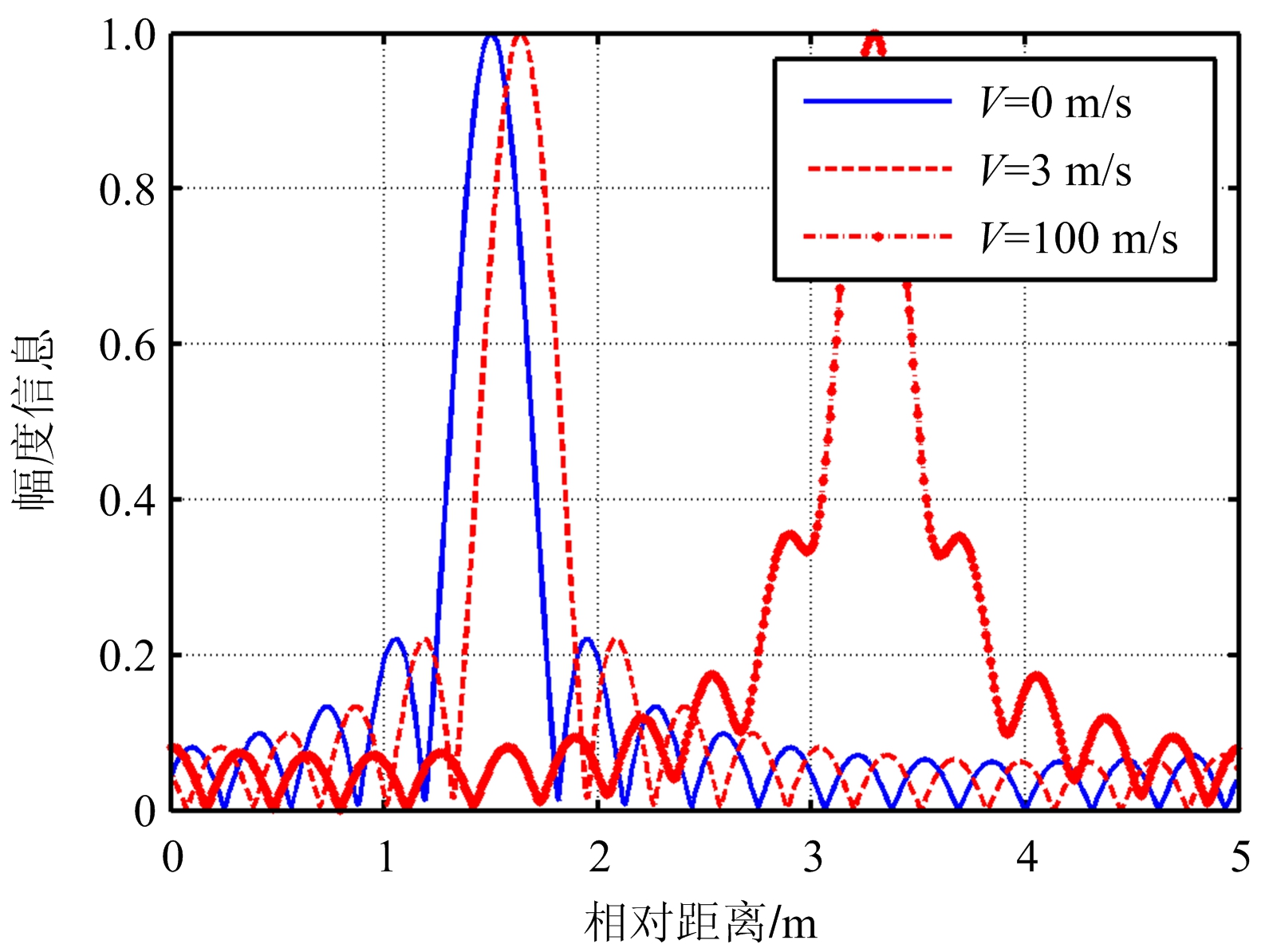
图11 不同速度条件下距离像合成效果
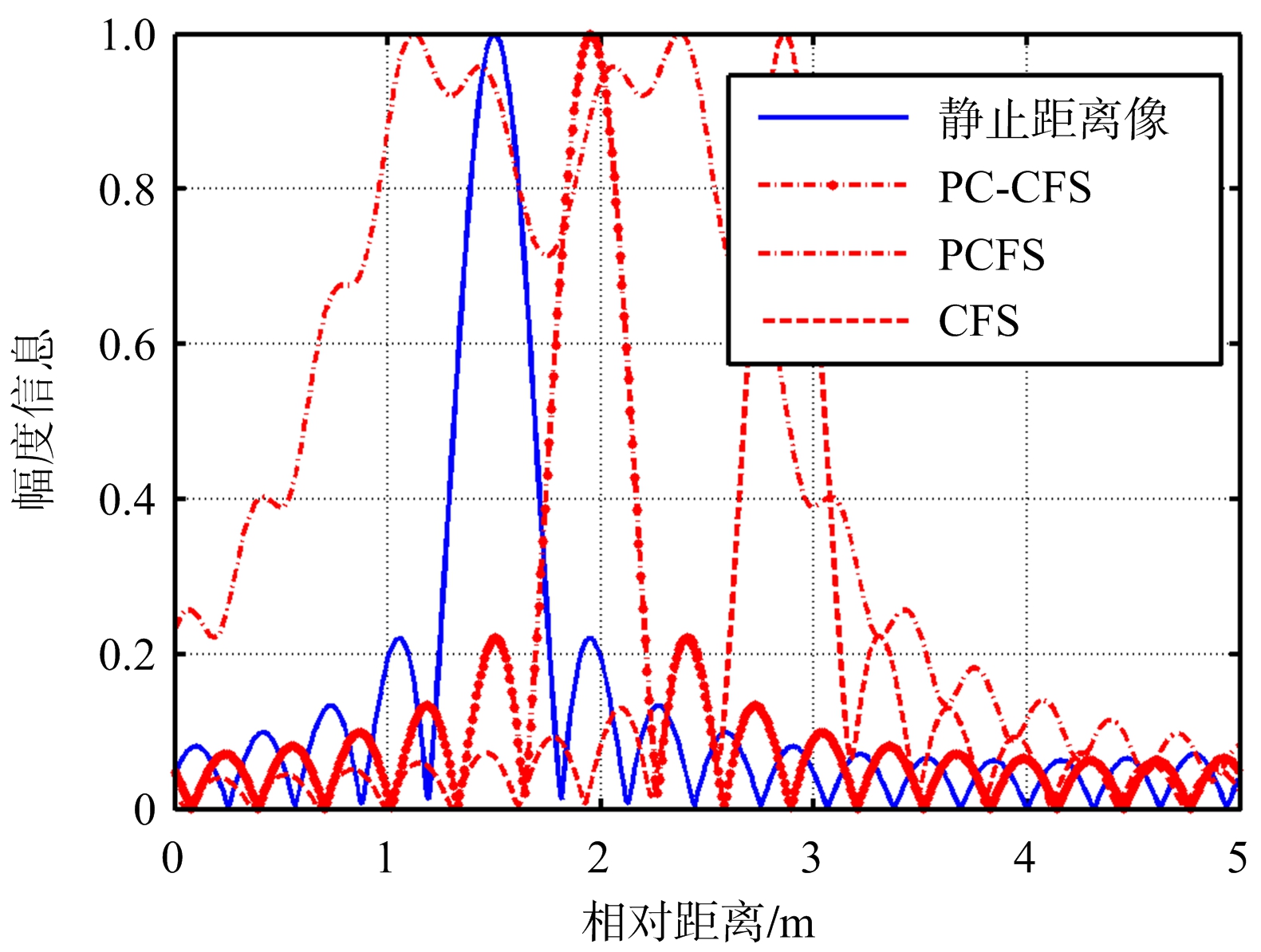
图12 V=10 m/s时不同信号距离像成像结果
本文提出了一种新的步进频率波形:相位编码调频步进信号。基于模糊函数分析了信号的距离、多普勒分辨性能,给出了相应的距离像成像方法。通过比较得出:1)在相同的合成带宽条件下,新信号所需的子脉冲数较少,因而提高了信号的数据率;2)新信号同时具有调频步进信号低旁瓣以及相位编码信号低距离多普勒耦合的特性,具有较高的距离多普勒联合分辨能力;3)进一步降低了速度补偿难度。随着信号数据率的提高,信号的不模糊距离窗将减小。因此,下一步将开展新信号的距离像合成方法研究,使得在提高信号数据率的同时克服因距离窗变小带来的距离混叠问题。
参考文献 :
[1] 卢再奇,曾祥桂,夏阳. 频率步进雷达距离旁瓣抑制自适应脉冲压缩算法[J]. 国防科技大学学报, 2016, 38(6):154-160.
[2] 吕明久,李少东,杨军,等. 基于随机调频步进信号的高分辨ISAR成像方法[J]. 电子与信息学报, 2016, 38(12):3129-3136.
[3] TEMPLE M A, SITLER K L, RAINES R A, et al. High Range Resolution(HRR) Improvement Using Synthetic HRR Processing and Stepped-Frequency Polyphase Coding[J]. IEE Proceedings: Radar, Sonar and Navigation, 2004, 151(1):41-47.
[4] 霍凯,姜卫东,黎湘,等. 一种新的OFDM相位编码频率步进雷达信号及其特性[J]. 电子与信息学报, 2011, 33(3):677-683.
[5] 王杰贵,张鹏程. 对相位编码步进跳频雷达的MCPC调制转发干扰[J]. 电子学报, 2017, 45(1):89-97.
[6] 吕明久,李少东,杨军,等. 基于全局最小熵的随机稀疏调频步进信号运动补偿方法[J]. 系统工程与电子技术, 2016, 38(8):1744-1751.
[7] BERIZZI1 F, MARTORELLA1 M, BERNABO M. A Range Profiling Technique for Synthetic Wideband Radar[J]. IET Radar, Sonar & Navigation, 2008, 2(5):334-350.
[8] 林厚宏. 基于波形捷变的雷达抗干扰技术研究[D]. 成都: 电子科技大学, 2016.
[9] 胡朗,薛广然,杜自成. 多载频相位编码雷达信号分析[J]. 火控雷达技术, 2015, 44(2):65-68.
HAN Jun, LU Xiaofei, LYU Mingjiu, FENG Mingyue
( Air Force Early Warning Academy , Wuhan 430019, China )
Abstract : Considering the problem that stepped-frequency waveform has low data rate and great difficulty in motion compensation, a novel phase coded chirp frequency-stepped signal(PC-CFS) is proposed. The novel signal is based on phase coded frequency-stepped signal with each sub-code chirp modulated. As a result, with the same sub-pulse width, the step size of carrier frequency is increased, the number of sub-pulses is reduced and the data rate is increased. Then the paper analyses the range resolution and Doppler resolution performances of the novel signal by deducing its ambiguity function. Analysis results show that the novel signal has better range resolution and Doppler resolution and lower difficulty in motion compensation. What’s more, the novel signal also has low probability of interception and good anti-jamming ability.
Key words : phase coded chirp frequency-stepped signal (PC-CFS); range resolution; Doppler resolution; ambiguity function; imagery processing
基金项目: 湖北省自然科学基金(No.2016CFB288)
修回日期: 2017-12-11
DOI: 10.3969/j.issn.1672-2337.2018.04.004
收稿日期: 2017-11-13;
文献标志码: A
文章编号: 1672-2337(2018)04-0371-07
作者简介 :
中图分类号 : TN957.52

韩 俊 男,1983年生,安徽合肥人,博士,讲师,主要研究方向为电子对抗信息处理、雷达信号处理。
E-mail:duj81@163.com

陆晓飞 男,1993年3月生,江苏江阴人,空军预警学院雷达兵器工程运用重点实验室硕士研究生,主要研究方向为阵列信号处理。
吕明久 男,1985年生,安徽泸州人,博士研究生,主要研究方向为目标检测与识别技术。
冯明月 男,1988年生,河北保定人,博士研究生,主要研究方向为电子对抗信息处理。
E-mail:fengmingyue2005@136.com