图1 机载单基雷达几何关系
岳 琦 1,2,3 , 吕晓德 1,2 , 杨璟茂 1,2,3 , 杨鹏程 1,2,3
(1.中国科学院电子学研究所, 北京 100190;2.微波成像技术国家重点实验室, 北京 100190;3.中国科学院大学, 北京 100049)
摘 要 : 机载双基雷达杂波空时分布具有严重的距离依赖性,即其分布随距离(俯仰角)的变化而变化,给杂波抑制带来困难,使传统的二维空时自适应处理(2D-STAP)性能变差。三维空时自适应处理(3D-STAP)利用俯仰维信息,将杂波谱分布由二维拓展至三维,通过在三维空间杂波谱分布的曲面上形成自适应凹口,来对杂波进行抑制。通过分析双基任意构型下的杂波在多普勒频率-水平空间频率-垂直空间频率三维空间中的分布特性,结合双基雷达体制特点,对传统3D-STAP算法进行了改进,使3D-STAP算法适用于双基情况,为双基雷达杂波抑制提供了一种新的思路。仿真表明,在典型双基构型下,与2D-STAP相比,该方法能使杂波脊附近的改善因子提高5 dB左右,有效提高了杂波抑制能力,有利于低速目标的检测。
关键词 : 机载双基雷达; 距离依赖; 三维空时自适应处理; 杂波抑制
机载双基地雷达 [1] 采用收发分置系统,通过将发射机和接收机分别放置在两个独立的平台上,大大提高了其抗电子干扰、抗隐身技术、抗反辐射导弹、抗超低空突防(四抗)的能力,近几年来受到了广泛关注。但与单基雷达相比,机载双基雷达下视工作将面临强杂波问题。由于收发平台的独立运动,使杂波特性会随着不同的双基构型而变化,且存在严重的距离依赖性,给杂波抑制带来很大困难。
空时自适应处理 [2] (STAP)是在时间和空间二维联合域进行自适应处理的技术,通过在空时二维平面的杂波脊处自适应地形成凹口来抑制杂波,能获得比一维空时级联处理更好的性能。但是STAP需要较准确地得到目标距离单元的杂波协方差矩阵,而用于估计杂波协方差矩阵的训练样本需要满足平稳且独立同分布的条件(IID)。在单基正侧视情况下,不同距离单元的杂波在空时二维平面上分布在同一条直线上,可以直接用STAP技术处理。但是机载双基雷达系统下,杂波谱在空时二维平面上的分布会随着距离的变化而变化,具有严重距离依赖性 [3-4] ,这会导致空时二维处理不能获得足够的独立同分布样本,使得杂波的协方差矩阵估计不准,严重降低了STAP的性能。
针对单基前视雷达杂波存在距离依赖性的问题,Corbell提出了一种利用阵列俯仰维信息的三维空时自适应处理(3D-STAP)技术。不同于传统的减少样本需求类方法 [5] 和杂波多普勒补偿类方法 [6-8] ,3D-STAP方法的特点是把与距离有关的俯仰维信息 [9-10] 加入到杂波谱分布的描述中,使杂波谱分布由二维拓展至三维,从杂波描述的本质上消除了杂波的距离依赖性 [11] 。但是在双基任意复杂结构下,3D-STAP方法是否依然适用还有待研究。本文首先验证了存在距离依赖性的单基前视杂波在多普勒频率-水平空间频率-垂直空间频率构成的三维空间中分布于同一曲面上,杂波分布特性不随距离而改变,3D-STAP方法在此杂波分布曲面形成凹口,即可实现杂波抑制。然后在双基任意几何关系的前提下,发现由于双基雷达的体制特点,使得同一距离单元处俯仰角会随方位角发生变化,需要对3D-STAP算法作出相应改进。在引入俯仰角和方位角的依赖关系后,验证了双基的杂波分布特性在三维空间中不会随距离而发生变化,即在任意距离单元,描述三维杂波分布的3个频率之间都存在同一函数约束关系。因此,不同距离处的杂波在三维空间中分布于同一曲面,可以应用3D-STAP方法对杂波进行抑制。最后,通过仿真验证了该方法在双基构型下的有效性。
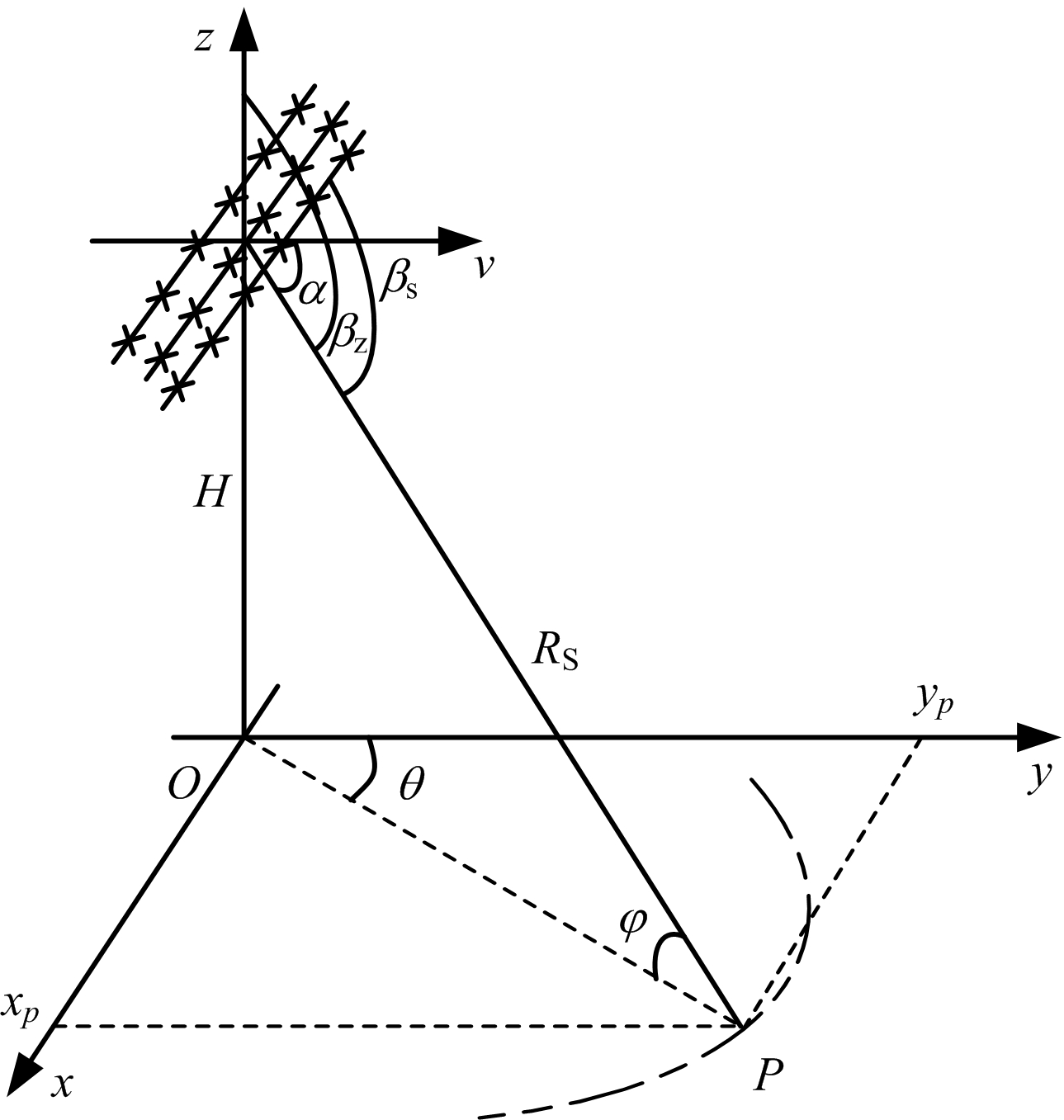
图1为机载单基雷达前视工作模式下的几何关系图,假设雷达平台沿 y 轴方向运动,速度为 v 。天线阵采用前视阵列,位于 xoz 平面, P 点为某一距离单元的一个杂波块,其相对于天线相位中心的俯仰角为 φ ,方位角为 θ , R S 为斜距, α 为视线方向与平台运动方向的夹角, β s 为视线方向和水平天线阵的空间锥角, β z 为视线方向和垂直天线阵的空间锥角。

图1 机载单基雷达几何关系
当天线阵采取等效线阵时,为二维空时自适应处理,此时杂波中不包含俯仰维信息,只与多普勒频率和空间频率有关。对于地面静止不动的散射体,其产生的杂波多普勒频率由平台的运动引起,为
(1)
式中, λ 为发射信号波长, f r 为脉冲重复频率。
空间频率,即回波的相位变化由天线阵元之间的间距所引起,二维STAP方法只考虑沿 x 方向的水平线阵。假设平台静止不动,以阵列中心作为参考相位中心,则位于 x i 处的一个阵元,其从一个地面静止散射体接收到的信号相对于相位中心的相位差为
Δ φ = ![]()
i =1,…, M
(2)
式中, M 为水平天线阵列单元数。
于是空间频率为
(3)
通常取天线阵元间距 d x = λ /2。
将多普勒频率和空间频率分别归一化,定义归一化多普勒频率为
f d =cos φ cos θ
(4)
归一化空间频率为
f s =cos φ sin θ
(5)
于是杂波的多普勒频率与空间频率满足如下关系:
(6)
可以看到在二维情况下,杂波的归一化多普勒频率 f d 与归一化空间频率 f s 的关系会随着俯仰角度 φ 变化,在平面上不同距离单元处的杂波分布表现为半径不同的同心圆,如图2所示。此时称杂波具有距离依赖性,不同距离的杂波分布不同,尤其是近距时不同距离单元的杂波分布相差很大,给杂波抑制带来困难。
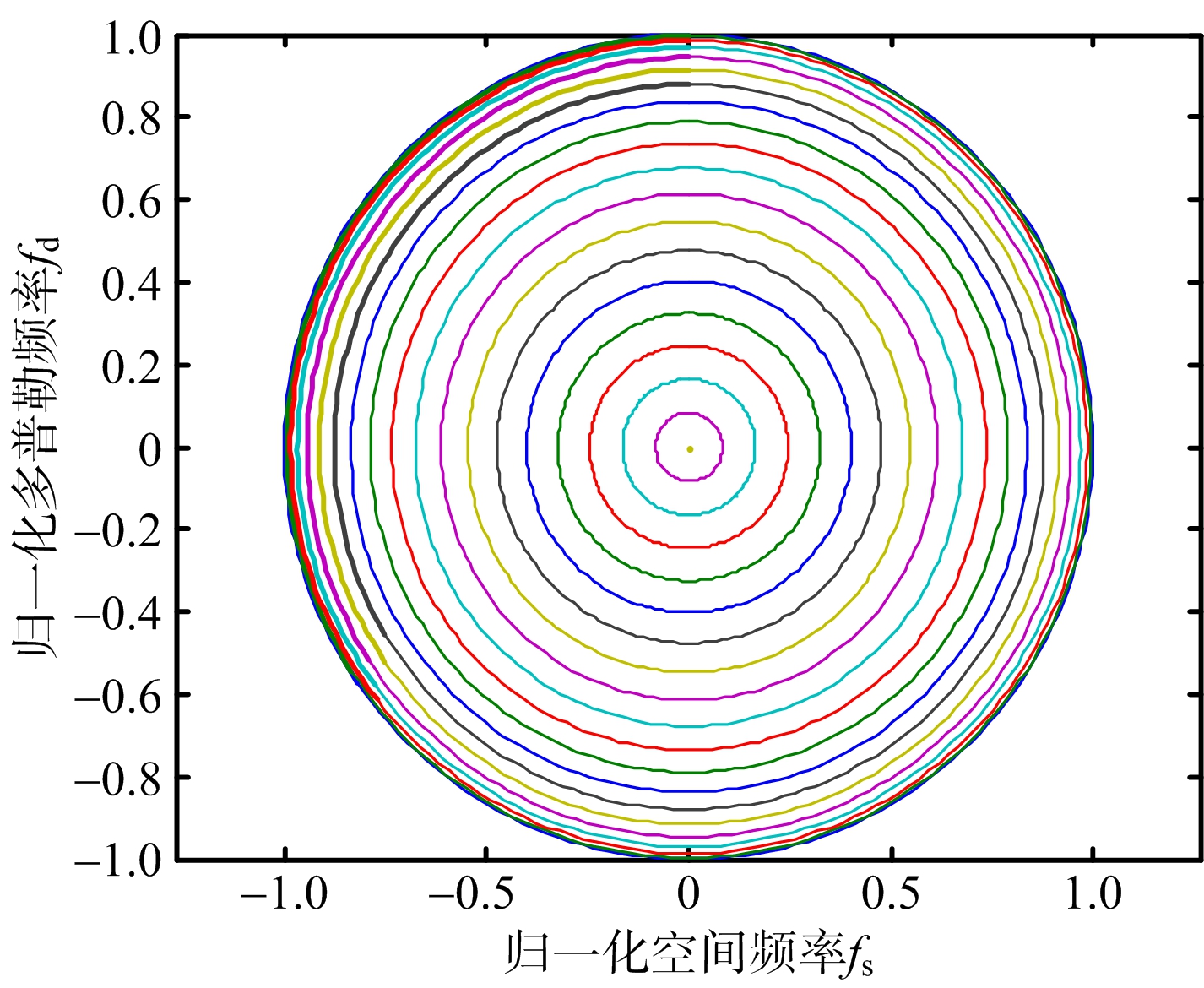
图2 单基二维前视杂波分布
3D-STAP以二维面阵为基础建立杂波模型。在对三维杂波分布的描述中,空间频率被分为水平空间频率和垂直空间频率,二维杂波分布中距离依赖性由不同距离处的俯仰角度不同而引起,3D-STAP将引起距离依赖性的俯仰角 φ 加入到了杂波描述之中,变成第三维信息。利用加入的垂直空间频率,从杂波描述的本质上消除了杂波的距离依赖性。
在加入垂直方向上的阵列单元后,对位于( x i , z i )处的一个阵元,其接收到的信号相对于天线阵相位中心的相位差为
i =1,…, M , j =1,…, N
(7)
式中, M 为水平阵元数, N 为垂直阵元数。
此时归一化水平空间频率仍为 f s =cos φ sin θ ,垂直空间频率 f z 为
(8)
归一化后 f z =-sin φ 。此时,多普勒频率 f d 与空间频率 f s , f z 之间满足如下关系:
![]() +
+ ![]() +
+ ![]() =
=
cos 2 φ +sin 2 φ =1
(9)
由式(9)可见,3D-STAP的杂波模型中,多普勒频率与水平空间频率和垂直空间频率之间满足确定关系,三者的平方和等于1,即不同距离单元的杂波在三维空间中分布在半径为1的球面上,如图3所示。这使得三维空间中杂波分布与距离无关,3D-STAP可以在 f d - f s - f z 三维空间中形成三维自适应权值,通过在球面上形成凹口来实现对杂波的有效抑制,从而消除杂波距离依赖性的影响。

图3 单基三维前视杂波分布
与机载单基雷达杂波分布相比,机载双基雷达由于接收机和发射机分置,彼此之间独立运动,会产生多种可能的几何场景,这使得双基杂波分布非常复杂,杂波特性会随着几何场景的不同而发生变化。此时无论是正侧视还是非正侧视情况,杂波分布均存在严重的距离依赖性。
要想将3D-STAP方法应用在机载双基情况,首先需要考虑双基体制带来的特殊问题。在单基情况下,等距离环均为以雷达为中心的圆环,一个距离单元处的俯仰角始终不变,但在双基情况下,发射机和接收机的分离使得等距离环表现为不规则椭圆,这意味着在一个距离单元处的俯仰角不再是固定不变的,而会随方位角的变化而变化。推导俯仰维信息时需要考虑其与方位向的依赖关系,接着再证明加入俯仰维信息之后,双基杂波在三维空间中的分布不会随距离而变化。
将接收机在地面的投影作为原点,双基基线 L 在地面的投影作为 y 轴建立直角坐标系,任意几何关系下的机载双基雷达示意图如图4所示。
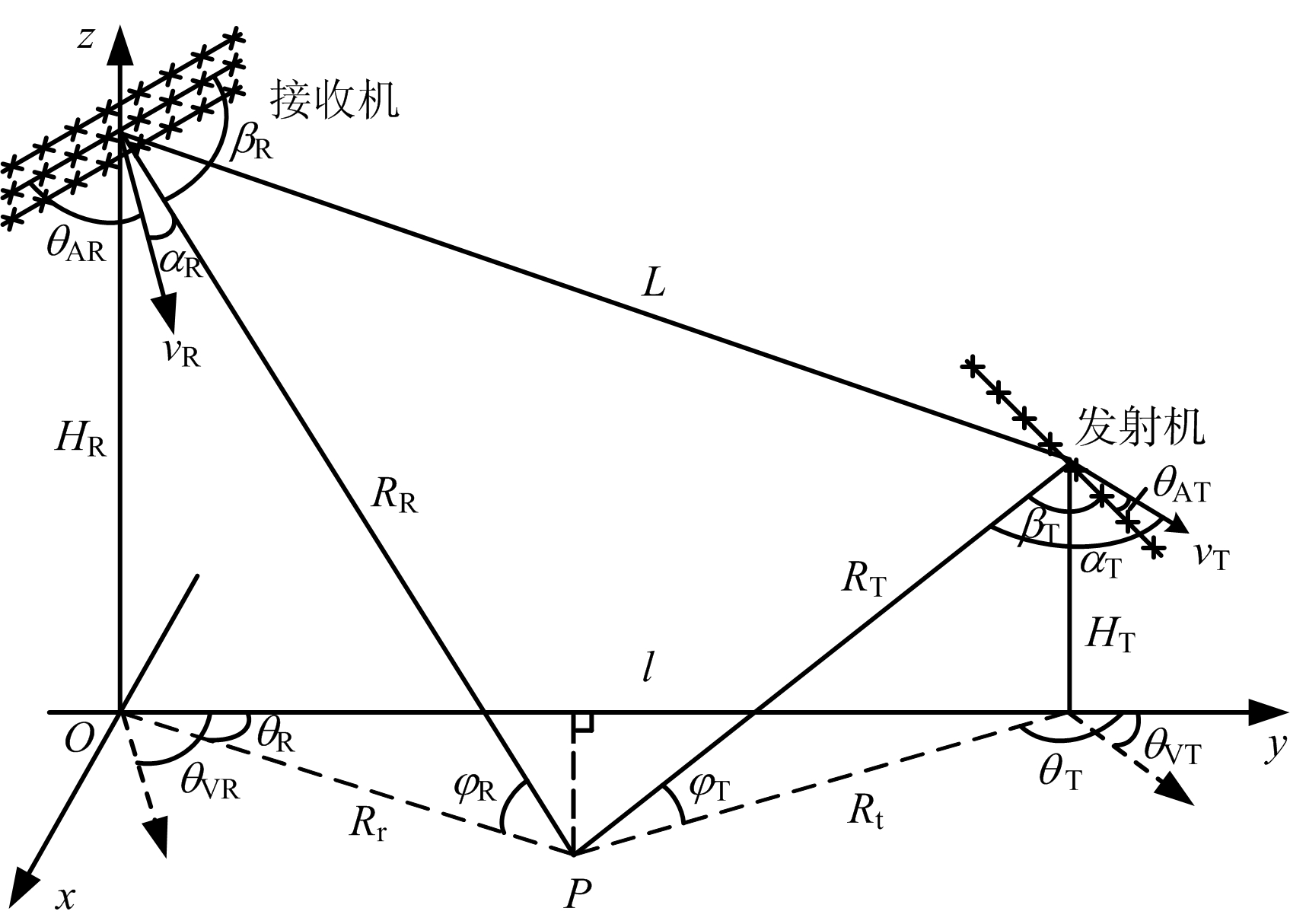
图4 机载双基地雷达几何关系
图中, H T 和 H R 分别为发射机和接收机的高度, V T 和 V R 为发射机和接收机的速度,接收机天线采用二维面阵, P 点为某一距离单元的一个杂波块, β T 和 β R 分别为发射机和接收机的视线方向与水平天线阵方向的夹角, α T 和 α R 分别为发射机和接收机的视线方向与载机运动方向的夹角, θ AR 为接收机运动方向与天线阵方向的夹角,前视模式时 θ AR =90°, θ VT 和 θ VR 分别为发射机和接收机相对于 y 轴的运动方向, φ T 和 φ R 分别为发射机和接收机的俯仰角度。
由此可写出多普勒频率 f d 、水平空间频率 f s 和垂直空间频率 f z 三者的表达式如下:
(10)
(11)
(12)
从图4可以推出如下关系:
(13)
(14)
(15)
(16)
(17)
(18)
(19)
由式(12)和式(13)可得
(20)
即 f z 与 R R 存在函数关系,记作 R R = F ( f z ),代入式(15),同理可得 R r = F ( f z )。
考虑空间角之间的关系有cos β R =cos( θ R - θ VR - θ AR )cos φ R ,代入式(11),可得
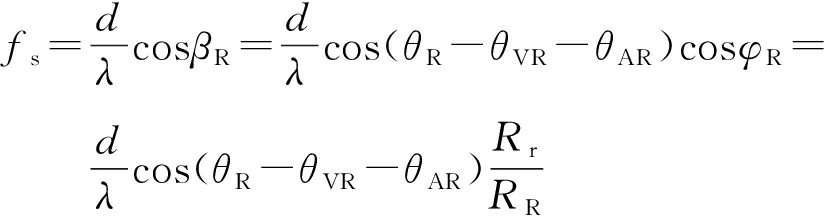
(21)
由于 θ VR 和 θ AR 为常数, R R 和 R r 为 f z 的函数,所以可得 f s 为 f z 和 θ R 的函数,即 θ R 也为 f s 和 f z 的函数,记作 θ R = F ( f s , f z )。
同样由空间角关系 f d 可推导如下:
f d = ![]()
![]() +
+
(22)
可见结果表达式中除去常数外, f d 只与 θ FR , R R 和 R r 有关,而 θ FR , R R 和 R r 均为 f s 和 f z 的函数,所以可得 f d = F ( f s , f z ),即3个频率之间存在特定的函数关系,表明不同距离单元杂波在三维空间中处于同一曲面,为抑制提供可能。当发射机和接收机均沿 x 轴运动,接收机采用前视模式时杂波的二维和三维分布如图5所示。

(a) 二维杂波分布
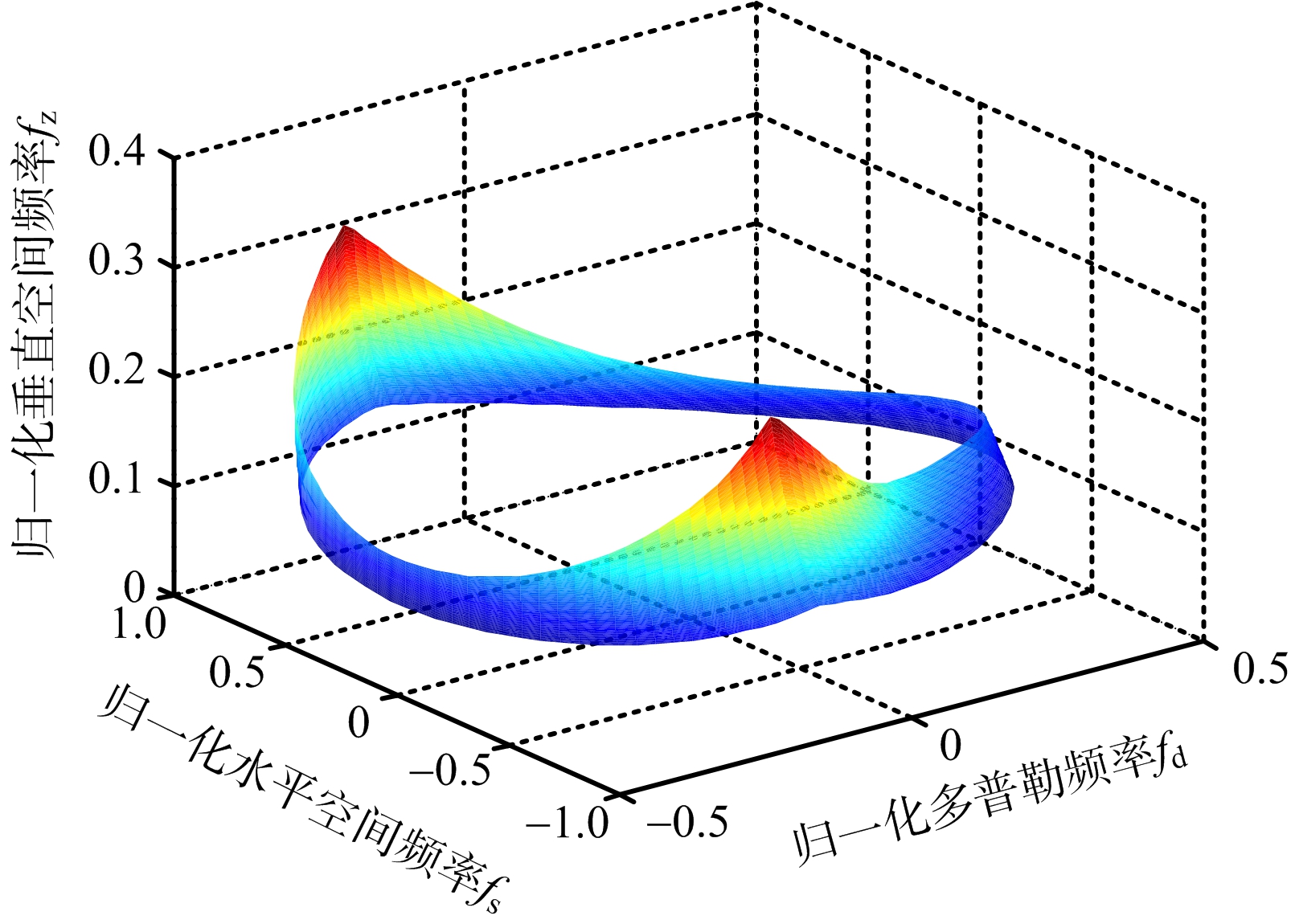
(b) 三维杂波分布
图5 机载双基杂波分布对比
由图5(a)可见,二维时不同距离处的杂波分布不能完全重合,具有距离依赖性,而图5(b)中杂波虽然有距离依赖性,但在三维空间中所有的杂波谱线均分布在一个近似圆环的曲面上,可以在三维空间中对曲面进行抑制。其他几何构型下的杂波分布情况与之类似。
3D-STAP算法的处理流程与二维基本一致,不同之处在于三维方法的空域是对 M × N 个阵元组成的面阵采样,空时导向矢量中加入了垂直方向的导向矢量。当垂直方向的通道数等效为1时,可退化为二维STAP处理。假设时域对 K 个脉冲采样,则三维空时采样矢量 X 可表示为
(23)
式中,
X k =[ x 11 k x 21 k … x M 1 k x 12 k x 22 k … x M 2 k …
x 1 Nk … x 2 Nk … x MNk ] T
(24)
式中, x mnk 表示第 m 行 n 列的阵元在第 k 次脉冲接收到的数据,所以矢量 X 为 MNK 维。在一个相干处理间隔内不同距离单元的三维采样数据的俯仰信息可以认为近似相同,所以杂波的三维空时协方差矩阵可以由如下统计方法计算:
R X = E [ XX H ]
(25)
协方差矩阵 R X 为 MNK × MNK 维,实际中 R X 一般由与待检测距离门相邻的若干距离门的数据估计得到,假设待检测距离门的数据为 X ,与其相邻的 L 个距离门的空时快拍数据则为 X ( l ), l =1,2,…, L ,因此协方差矩阵 R X 的估计式为
![]()
(26)
与二维空时处理相同,三维空时自适应处理的权矢量 W 同样由以下约束得到:
![]()
(27)
其最优解为
![]()
(28)
式中, S 为三维空时导向矢量。
S = S S ( ω x , ω z )⊗ S T ( ω f d )
(29)
式中,“⊗”表示Kronecker积, S S ( ω x , ω z )表示二维的空域导向矢量, S T ( ω f d )表示时域导向矢量,而空域的导向矢量由水平和垂直维的导向矢量得到,即
S S ( ω x , ω z )= S S X ( ω x )⊗ S S Z ( ω z )
(30)
3个导向矢量分别为
S S X ( f s )=[1 exp(j2π f s )…
exp[j2π( M -1) f s ]] T
(31)
S S Z ( f z )=[1 exp(j2π f z )…
exp[j2π( N -1) f z ]] T
(32)
S T ( f d )=[1 exp(j2π f d )…
exp[j2π( K -1) f d ]] T
(33)
式中,多普勒频率 f d 、水平空间频率 f s 和垂直空间频率 f z 三者的表达式见式(10)~式(12)。
分别用2D-STAP和3D-STAP方法对机载双基雷达典型构型下的杂波进行抑制,采用改善因子 IF 作为杂波抑制性能的评价指标。改善因子的定义为系统输出信杂噪比与输入信杂噪比的比值,用来反映自适应系统对数据信杂噪比的改善能力,可以有效表示自适应系统的性能。其表达式如下:
(34)
实验主要对仿真数据进行处理,实验的参数设置如表1所示。其中二维场景中的垂直通道由4个阵元通过波束形成得到。
表1 仿真参数
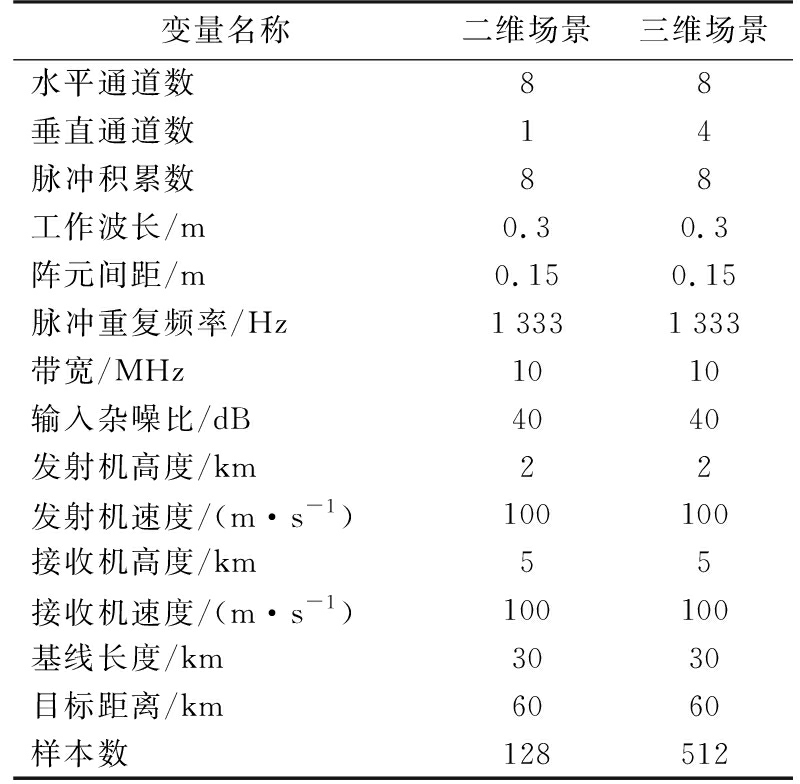
当发射机运动角度 θ VT =90°,接收机运动角度 θ VR =0°,接收机天线为正侧视时,目标距离处的杂波功率谱如图6所示。截取接收机方位角余弦值为0.05处的归一化改善因子进行对比,结果如图7所示。
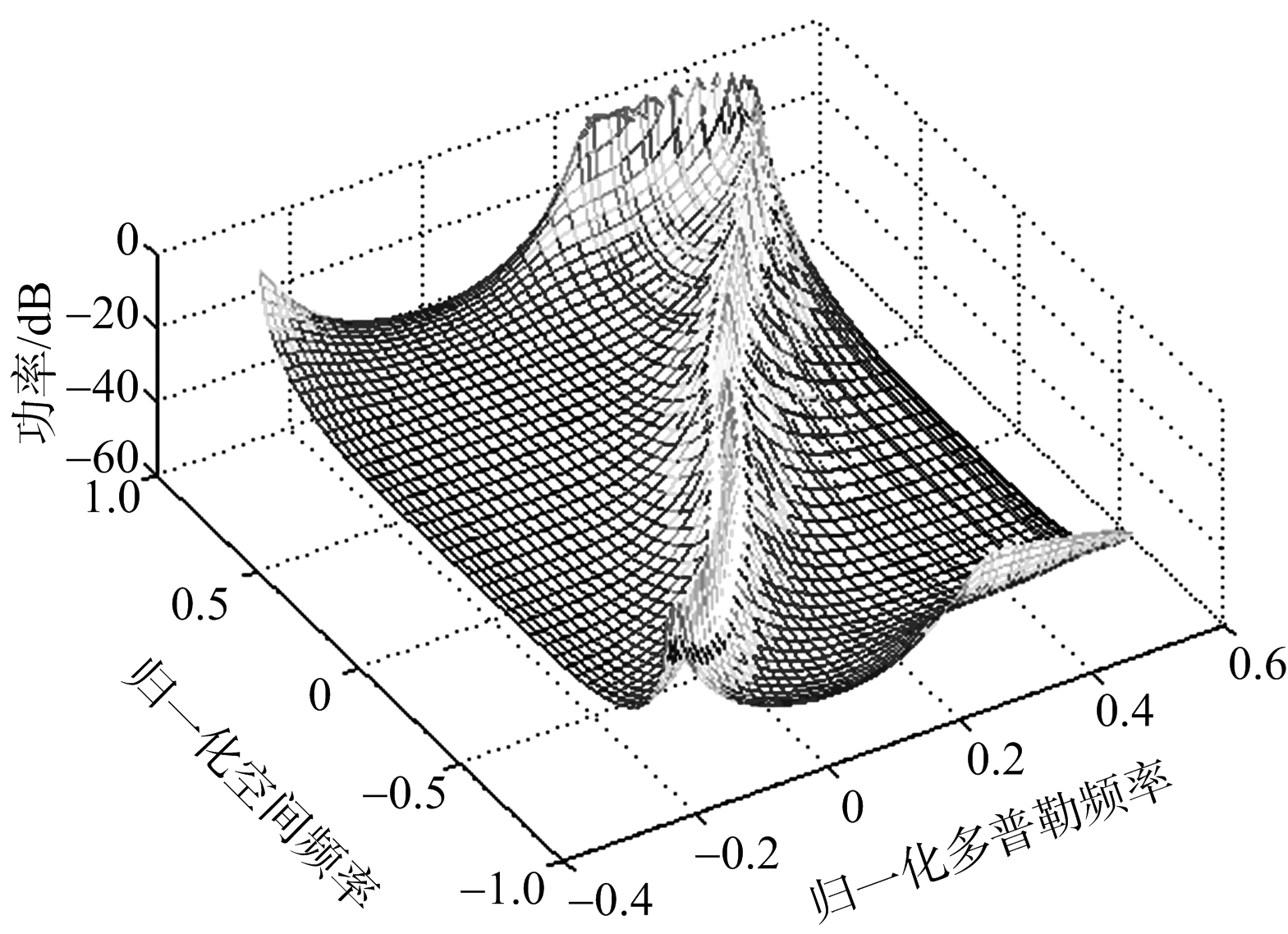
图6 构型一杂波功率谱
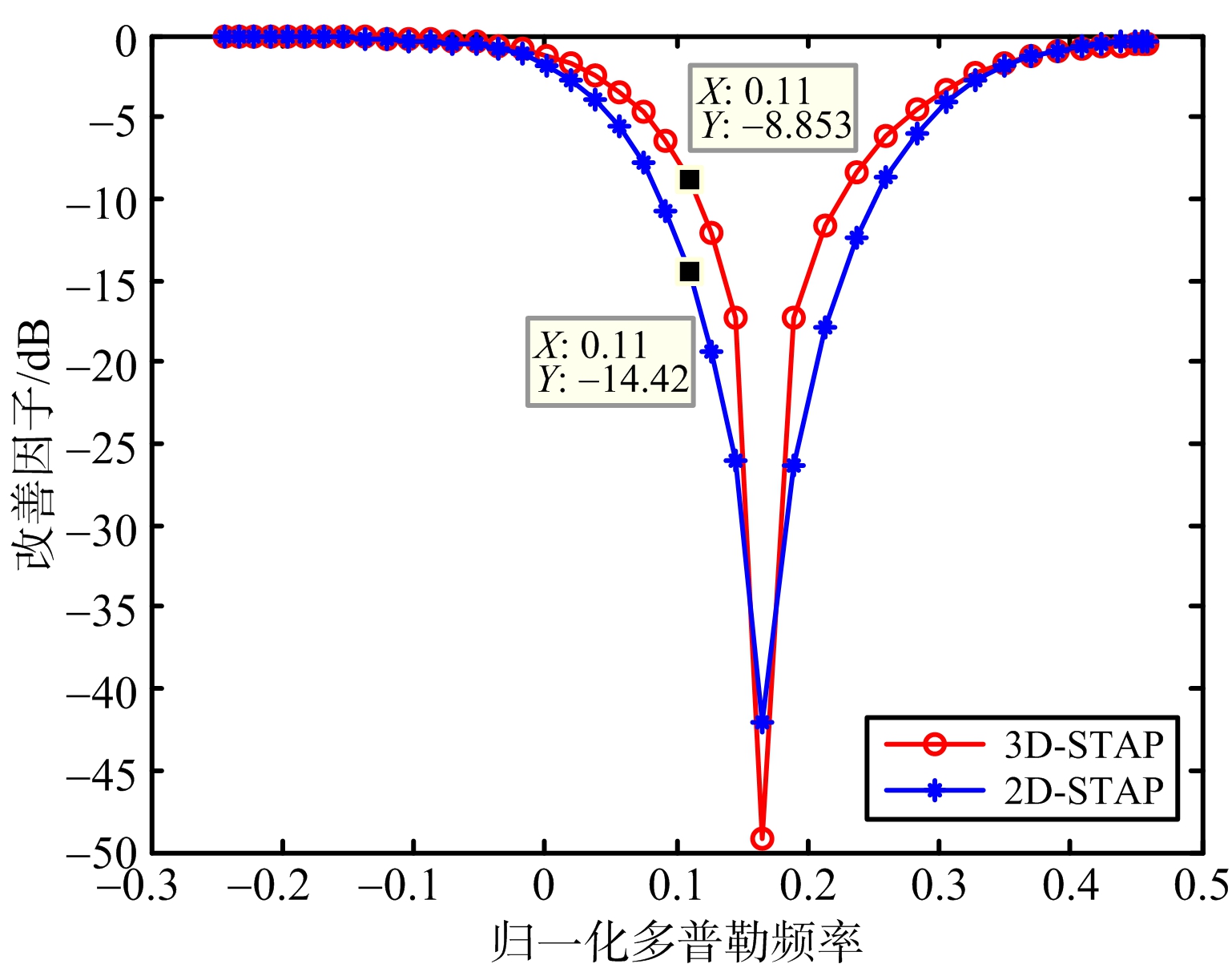
图7 构型一改善因子对比
对比图7中的改善因子可以看出,3D-STAP的改善因子凹口相对更窄,在靠近凹口处3D-STAP要比2D-STAP高5 dB左右,说明三维方法在靠近主杂波区时的性能改善明显。
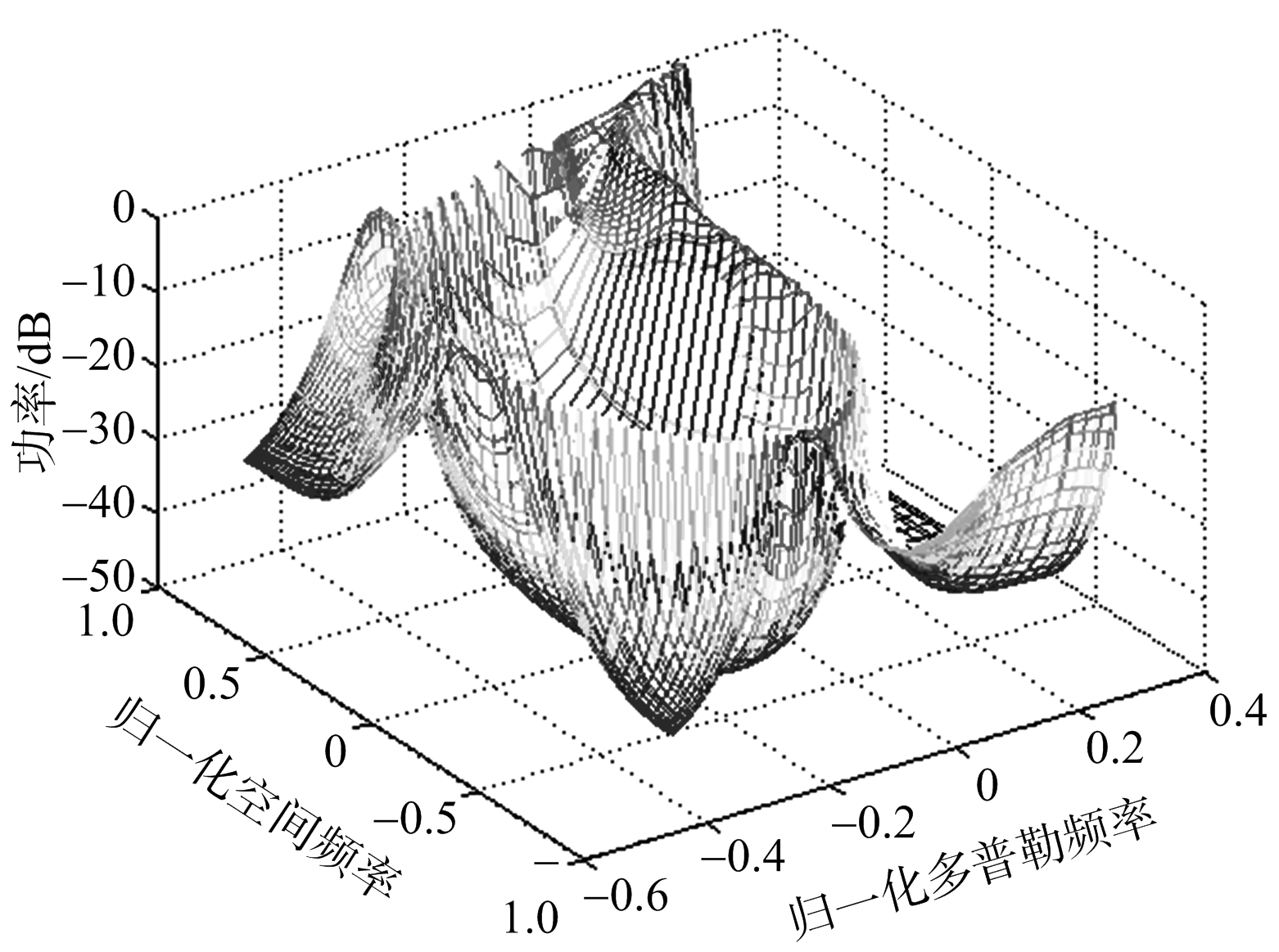
图8 构型二杂波功率谱
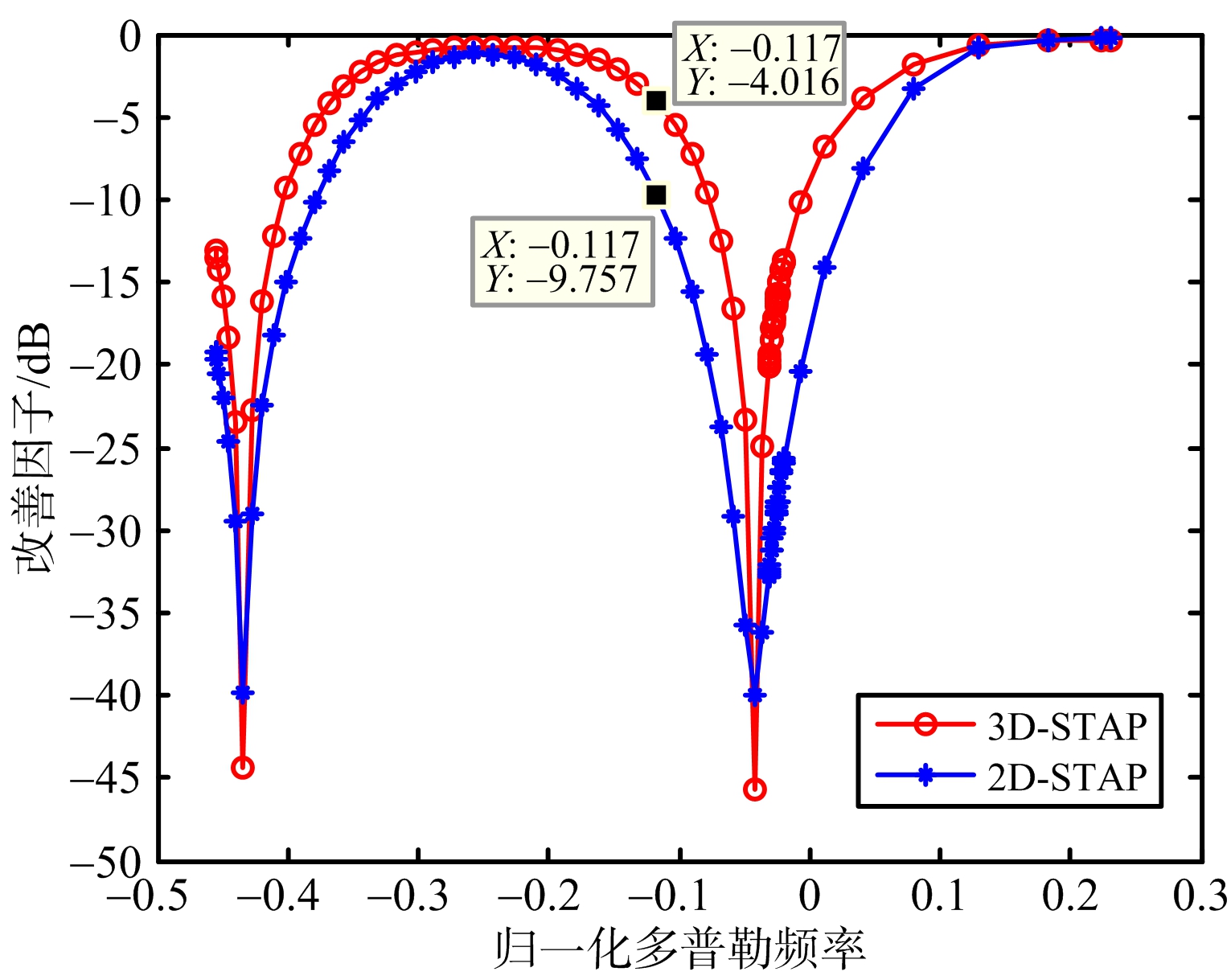
图9 构型二改善因子对比
在另一种较为复杂的几何关系下,发射机运动角度 θ VT =0°,接收机运动角度 θ VR =90°,接收机天线为前视时,杂波功率谱如图8所示,接收机方位角余弦值为0.54处的归一化改善因子对比结果如图9所示。由图中可以得到与之前相同的结果,3D-STAP在靠近主杂波区处的性能有所改善,证明了改进后的三维方法在双基不同几何关系下对杂波抑制的有效性。
在仿真过程中发现,虽然3D-STAP能够取得更好的杂波抑制效果,但是3D-STAP最优处理需要估计 MNK × MNK 维的协方差矩阵,并对其作求逆运算,相应的计算复杂度为 O ( M 3 N 3 K 3 ),与2D-STAP的计算复杂度 O ( M 3 N 3 )相比,计算量大大增加,并且处理中需要的样本数较大,实际中需要结合有效的降维方法,降低其运算量以实现实时处理。
针对机载双基雷达杂波分布在传统的二维模型下存在严重距离依赖性的问题,通过验证杂波分布特性在多普勒频率、水平空间频率和垂直空间频率构成的三维空间中不随距离而发生变化,其三维分布具有共面特性,提出可以利用俯仰维角度信息,从杂波描述上消除距离对杂波分布的影响。并充分考虑了双基特殊体制下,俯仰角和方位角的依赖关系,对传统3D-STAP算法作出相应改进,从理论上证明了改进后的3D-STAP方法在双基任意几何关系下对杂波抑制的可行性。并通过仿真与2D-STAP的改善因子进行对比,说明了3D-STAP方法结合了多普勒-方位向-俯仰向信息,使得改善因子在凹口附近提高了5 dB左右,改善了对目标的检测性能,特别是对接近主杂波区的低速目标的检测能力。
本文从理论上分析了机载双基雷达的特点及其杂波在三维空间中的分布特性,将3D-STAP算法扩展至双基情况,为双基雷达杂波抑制提供了一种更为有效的解决思路,推动了双基雷达系统杂波抑制和动目标检测技术的发展。
参考文献 :
[1] 段锐. 机载双基地雷达杂波仿真与抑制技术研究[D]. 成都: 电子科技大学, 2009.
[2] 王永良,彭应宁. 空时自适应信号处理[M]. 北京: 清华大学出版社, 2000:35-91.
[3] 彭晓瑞,谢文冲,王永良. 双基地机载雷达杂波建模及仿真分析[J]. 系统仿真学报, 2011, 23(2):257-261.
[4] 黄忠言,袁俊泉,王力宝,等. 天空双基地预警雷达非平稳杂波特性分析[J]. 空军预警学院学报, 2015, 29(4):235-238.
[5] 周宇,陈展野,张林让,等. 非均匀环境下利用雷达参数信息的STAP方法[J]. 电子科技大学学报, 2016, 46(6):905-910.
[6] 冯为可,张永顺,于伟洋. 基于杂波距离方位谱的机载非正侧MIMO雷达STAP方法[J]. 空军工程大学学报(自然科学版), 2016, 17(4):41-45.
[7] 杨鹏程,吕晓德,刘宇,等. 基于RDNLMS的机载外辐射源雷达杂波对消[J]. 电子与信息学报, 2016, 38(10):2488-2494.
[8] 许华健,杨志伟,廖桂生,等. 一种稳健的非均匀杂波协方差矩阵估计方法[J]. 电子与信息学报, 2017, 39(5):1036-1043.
[9] 段克清,谢文冲,陈辉,等. 基于俯仰维信息的机载雷达非均匀杂波抑制方法[J]. 电子学报, 2011, 39(3):585-590.
[10] 吴旭姿,刘峥,谢荣. 非正侧阵雷达距离模糊杂波抑制新方法[J]. 西安电子科技大学学报(自然科学版), 2017, 44(2):1-7.
[11] 高飞,谢文冲,王永良. 非均匀杂波环境3D-STAP方法研究[J]. 电子学报, 2009, 37(4):868-872.
YUE Qi 1,2,3 , LYU Xiaode 1,2 , YANG Jingmao 1,2,3 , YANG Pengcheng 1,2,3
(1. Institute of Electronics , Chinese Academy of Sciences , Beijing 100190, China ;2. National Key Laboratory of Science and Technology on Microwave Imaging , Beijing 100190, China ;3. University of Chinese Academy of Sciences , Beijing 100049, China )
Abstract : The space-time distribution of airborne bistatic radar clutter is of serious range dependence, that is, the distribution varies with the range or elevation angle, which degrades the performance of the conventional two-dimensional space-time adaptive processing (2D-STAP) and thus brings difficulties to clutter suppression. The three-dimensional space-time adaptive processing (3D-STAP) extends the distribution of the clutter spectrum from two dimensions to three dimensions by introducing the array elevation angle. Clutter is then suppressed by forming an adaptive notch on the entire 3D clutter plane. In this paper, 3D-STAP in the monostatic radar is improved to the bistatic situation by analyzing the clutter distribution characteristics in the 3D space, that is, the Doppler frequency, the horizontal spatial frequency, and the vertical spatial frequency. It provides a novel idea for the bistatic radar clutter suppression. Simulation results show that the proposed method can improve the improvement factor near the clutter ridge by about 5 dB in the typical case compared with 2D-STAP, which effectively improves the performance of clutter suppression and is beneficial to the detection of low speed targets.
Key words : airborne bistatic radar; range dependence; three-dimensional space-time adaptive processing (3D-STAP); clutter suppression
修回日期: 2017-10-27
DOI: 10.3969/j.issn.1672-2337.2018.04.011
收稿日期: 2017-08-29;
文献标志码: A
文章编号: 1672-2337(2018)04-0416-07
作者简介 :
中图分类号 : TN959.73

岳 琦 男,1992年生,河北人,硕士研究生,主要研究方向为机载双基雷达杂波抑制。
E-mail:yueqi_1992@163.com

吕晓德 男,1969年生,河北人,研究员、博士生导师,主要研究方向为基于阵列技术的新体制雷达系统及其应用。
杨璟茂 男,1992年生,甘肃人,硕士研究生,主要研究方向为机载双基雷达杂波抑制。
杨鹏程 男,1989年生,河南人,博士研究生,主要研究方向为外辐射源雷达信号处理。