0 引言
合成孔径雷达(Synthetic Aperture Radar, SAR)是现代遥感技术中微波遥感的重要发展。SAR用作主动成像传感器,可提供足够高分辨率的图像,并且能够在不受天气影响的情况下日夜工作。由于这个优点,它被用于许多不同的应用,例如图像分类、三维重建、快速映射、变化检测和图像融合等。
自动SAR图像匹配[1]是有效利用SAR数据的重要步骤。与光学图像匹配类似,SAR图像匹配是从不同视点、在不同时间、利用相同/不同的传感器拍摄的同一场景的两个或更多个图像之间找到对应/同源部分(例如区域、特征、点、像素等)的过程。 当匹配了几个关键点时,可以计算空间变换以最小化两个图像之间的不相似度量。SAR图像匹配的核心是自动找到一些不变特征点(Invariant Feature Points, IFP)并匹配它们。匹配的不变特征点用于通过使用几何或使用强度最小化某些成本函数来估计最佳变换。
为了获得足够高质量的不变特征点,在过去10年中已经进行了大量的研究工作。通常现有的SAR图像匹配技术可以分为两类:基于强度的方法(也称为基于区域的方法)和基于特征的方法。在基于强度的方法中,仅当要匹配的图像的辐射特性相同并且从相同类型的传感器获得图像时表现出较好的性能。相比之下,研究表明基于特征的方法更适合于在空间变化的辐射特性和不同的频带/平台/极化下的SAR图像匹配。在该方法中,提取并匹配来自两个图像的共同结构特征,包括点特征、边缘特征或线性特征(例如道路和河流)和区域特征等。
在基于特征的图像匹配方法中,基于局部不变特征的匹配方法,特别是尺度不变特征变换(Scale Invariant Feature Transform, SIFT) [2]及其框架模式下的改进算法[3]在光学图像匹配中取得了很好的结果。然而,由于SAR图像固有的斑点噪声和局部变形的影响,当直接用于SAR图像匹配时,这些方法的性能显著降低。为了使基于SIFT框架的方法能够适用于SAR图像匹配,国内外学者研究提出了有效的改进方法,包括SIFT-OCT[4],BF-SIFT[5],SAR-SIFT[6],NDSS-SIFT[7]等等。在尺度空间构建方面,Wang等[5]提出使用双边滤波器(Bilateral Filter,BF)建立尺度空间并采用双匹配策略来改善匹配结果;Fan等[7]将相位一致性和非线性扩散滤波(Nonlinear Diffusion Filter,NDF)结合在一起,以提高SAR匹配性能。在特征点检测方面,Dellinger等[6]提出了一种新的梯度定义,它通过均值比率(Ratio of Averages,ROA)来计算,以抑制SAR图像中高对比度区域特征检测的误报,从而获得良好的性能。
为了抑制相干斑噪声的影响并获取高质量的不变特征点,本文针对SIFT框架进行了以下改进: 首先,在尺度空间构建阶段,引入滚动引导滤波(Rolling Guidance Filter,RGF) [8],充分利用其在去除斑噪和保持边缘方面相对于双边滤波和非线性扩散滤波的优势,来解决相干斑噪声的影响。其次,在特征点检测阶段,采用指数加权均值比率算子(Ratio of Exponentially Weighted Averages,ROEWA)与Harris-Laplace检测算子相结合的方法用于检测稳定和准确的不变特征点,同时去除虚假特征点。
1 算法基本流程
本文算法的总体流程图如图1所示。

图1 本文算法总体流程图
2 算法分析
2.1 基于滚动引导滤波的非线性尺度空间构建
本文所提出的尺度空间策略受非线性尺度空间策略和滚动引导滤波算法的启发。常见的SIFT算法使用高斯滤波器来构建尺度空间(线性尺度空间),其缺点是它平滑整个图像,但是不能够有效地抑制SAR图像固有的相干斑噪声,同时模糊了边缘或者边界。滚动引导滤波与先前的边缘保留滤波器算法不同,是在规模上下文中的感知平滑,并且以快速收敛的迭代方式实现,通过分离不同的比例结构来减少伪影。RGF算法过程如下:
1) 第一步是使用高斯滤波器来去除相干斑噪声和细小的结构,表达式为
(1)
式中,J1(p)表示通过第一次迭代的高斯滤波计算后像素p的灰度值,N(p)表示像素p的邻域,q表示邻域N(p)中的像素点,kp表示归一化系数:
(2)
2) 第一步之后的后续迭代过程是利用引导的方式来加强边缘和明显的结构调整,表达式为
Jt(p)=![]()
Jt-1(q)
(3)
式中:Jt(p)表示通过第t次迭代的双边滤波计算后像素p的灰度值; Jt-1(p),Jt-1(q)分别表示通过第t-1次迭代后像素点p和q的灰度值;I(p)表示像素q的灰度值;δs和δr分别表示空间和距离的尺度。
本文提出将滚动引导滤波算法引入尺度空间构建策略,图像金字塔通过以下等式获得:
(4)
式中:J0(p)表示输入SAR图像;JN(p;δs)和 JN(p;kδs)表示经滤波后的图像,即多尺度空间金字塔中的某一层图像,N表示迭代次数;RGF(i,j;δs,δr)和RGF(i,j;kδs,δr)表示滤波核,由式(3)求得;k表示保证连续尺度空间的常数乘因子。
SAR图像的不同滤波算法的性能比较如图2所示。图2表明RGF在斑点噪声消除和边缘保留方面都比其他滤波算法(在相同尺度下)具有更好的性能。

(a) 原始图像

(b) 双边滤波

(c) 引导滤波

(d) 非线性扩散滤波

(e) 滚动引导滤波
图2 不同滤波算法的效果对比
本文使用等效视数(Equivalent Number of Looks,ENL) [9]和边缘保持指数(Edge-Preserving Index,EPI) [10]来估计建立规模空间时的性能过滤。ENL和EPI的计算方法如下:
ENL=μ2/δ2
(5)
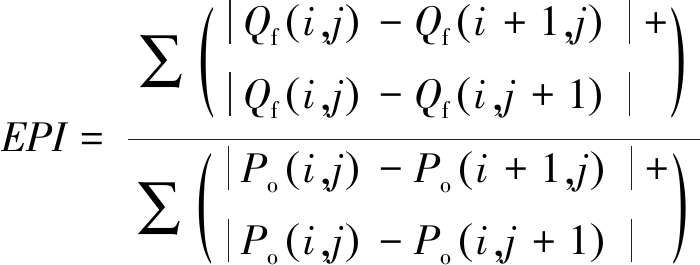
(6)
式中,μ和δ分别表示该窗口均匀区域内像素的均值和标准差。均匀区域内等效视数越大,说明去噪效果越好,反之,去噪效果越差。Qf(i,j)是滤波后图像的灰度值,Po(i,j)是原始图像灰度值。Qf(i,j)与Po(i,j)都在边缘区域内,(i,j)为像素点坐标。边缘区域内边缘保持指数越大,边缘保持效果越好,反之,边缘保持效果越差。
实验结果如图3所示。图3表明基于RGF的方法在综合ENL和EPI评估方面优于其他滤波方法。

(a) 均匀区域
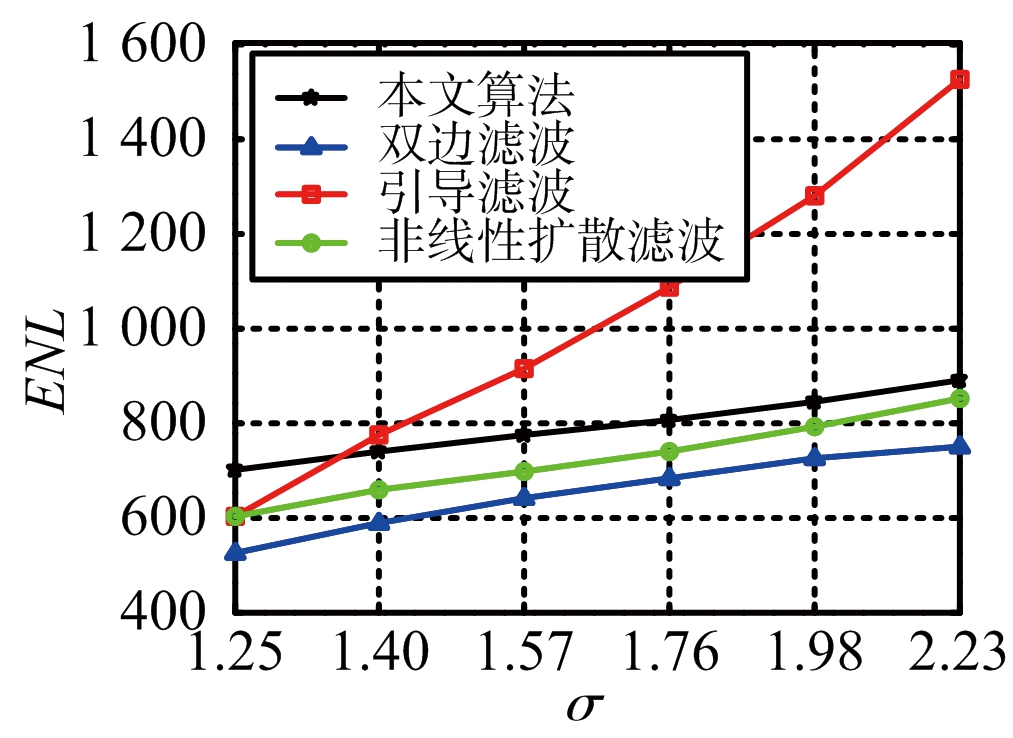
(b) 均匀区域等效视数曲线

(c) 边缘区域
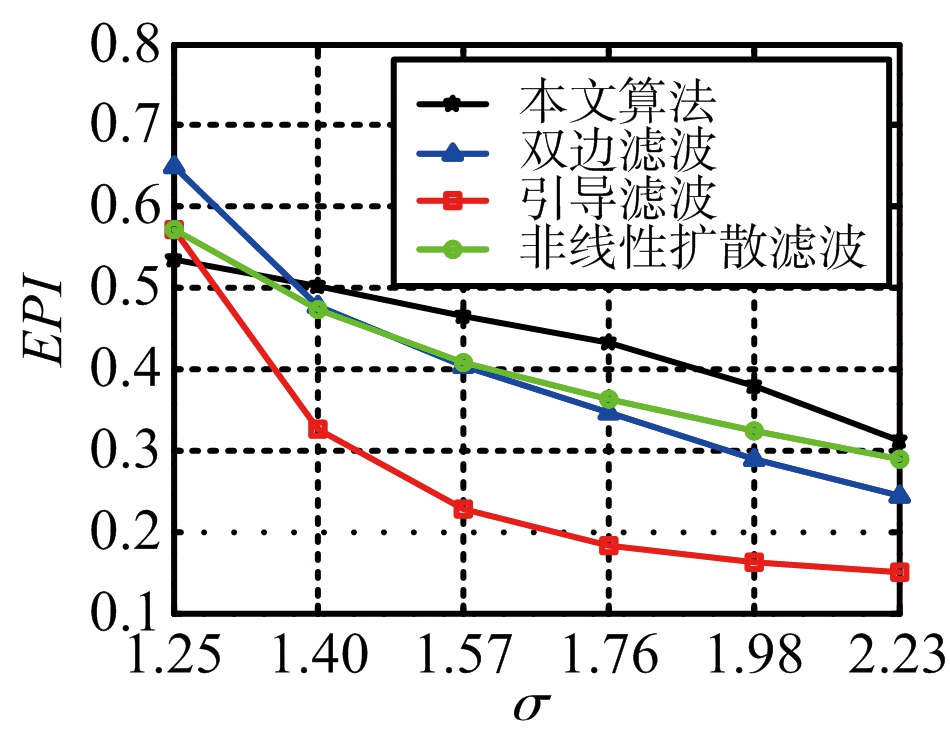
(d) 边缘区域保持指数曲线
图3 不同多尺度空间构建算法的效果对比
图4给出了基于不同滤波器的尺度空间的性能比较。从图4可以看出,本文所提出的基于RGF的尺度空间策略在多尺度上的斑噪去除和边缘保持方面具有比其他滤波方法更好的性能。
2.2 ROEWA结合Harris-Laplace的特征点检测
基于多尺度SAR图像,检测高质量的不变特征点是关键,但在SAR图像匹配中该问题尚未完全解决。

(a) 双边滤波 δs={1.25,1.4,1.57,1.76,1.98,2.23;δr=0.2}

(b) 引导滤波 γ={5,6,7,8,10,11;ε=0.2}

(c) 非线性扩散滤波 t={0.78,0.98,1.23,1.55,1.96,2.48}

(d) 本文方法 δs={1.25,1.4,1.57,1.76,1.98,2.23;δr=0.2}
图4 不同多尺度空间构建算法的实验结果
国内外学者已经提出了许多用于光学图像的特征检测算子,例如Harris,Hessian等。一个共同的特征是它们都依赖于基于梯度差分(Gradient by Difference,GD)的图像梯度计算方式。它们在光学图像中的匹配和物体识别方面表现良好,但是直接用于SAR图像匹配时则性能相对较差。由于相干斑噪声的影响,特别是在高对比度区域,上述的基于梯度差分的检测算子在SAR图像中的强散射纹理区相对于低散射纹理区会出现很高的错误检测率。
为了解决这个问题,国内外学者引入了梯度比率(Gradient by Ratio,GR)的概念。均值比率(ROA)算子首先作为梯度比率算法提出来计算梯度。指数加权均值比率(ROEWA)算子是ROA算子的改进版本,旨在提出一种在SAR图像中的更加高质量的梯度表示方法。ROEWA算子将局部区域的窗口角度划分为0,π/4,π/2和3π/4四种方式,计算沿着4种方式划分的局部窗口中像素的指数加权均值,并求出相对侧的指数加权均值的比率,其原理如图5所示。
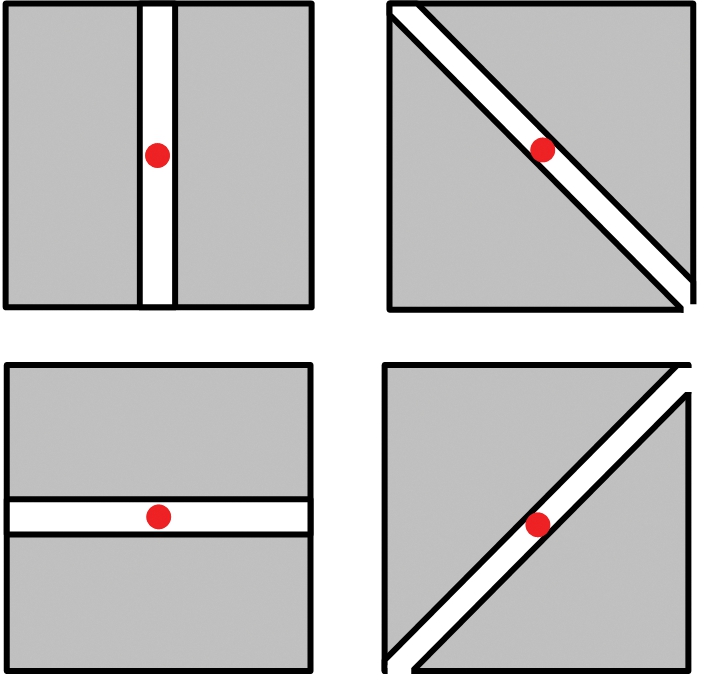
(a) 4种方向区域划分方式
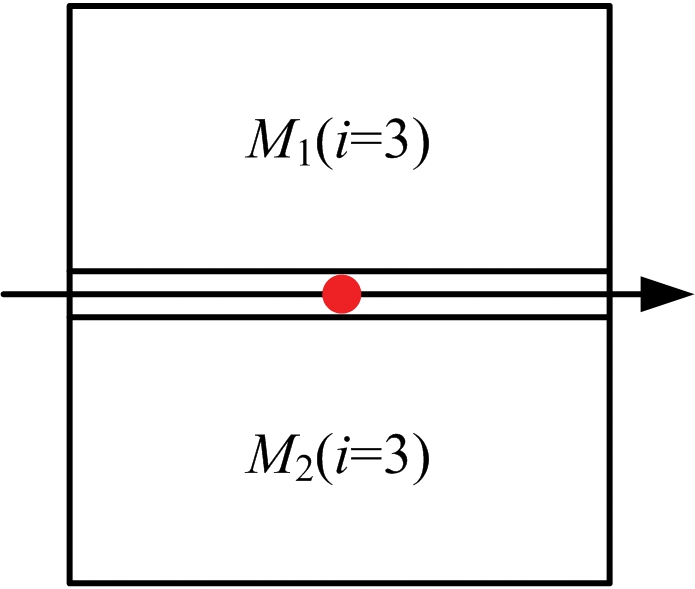
(b) 第i种局部窗口指数加权均值计算
图5 ROEWA算子的原理图
计算的方程式如下所示:
Ri,α=![]() =
=
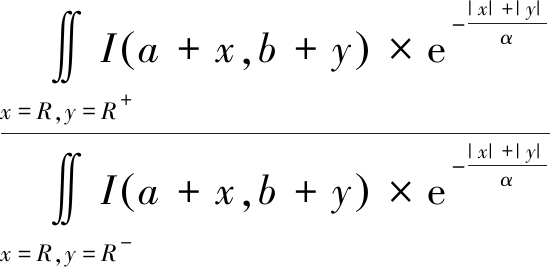
(7)
式中,(a,b)为给定点的坐标,α为指数权重参数,M1,α和M2,α为在第i种方向区域划分方式的相对侧局部窗口中统计出的指数加权均值。
图6比较了不同梯度计算方式的性能,从图中可以看出,传统的基于梯度差分的方法无法有效抑制SAR图像强散射纹理区斑点噪声,而改进的基于梯度比率的方法相比之下产生更少的虚假边缘或拐角特征。

(a) 原始图像

(b) 梯度差分

(c) 梯度比率
图6 基于梯度差分和梯度比率的检测算法在SAR图像上的对比
文献[6]提出的SAR-Harris检测算子通过将传统的Multi-Harris特征点检测算法中,基于梯度差分的梯度计算方式改进为基于梯度比率的ROA或ROEWA算子,极大地提高了在SAR图像中的强散射纹理区域特征点检测的准确率,如图7所示,在图6的原始图像中分别使用3种类型的特征点检测算法,其中Multi-Harris和Harris-Laplace均使用基于梯度差分的梯度计算方式,SAR-Harris则采用基于梯度比率的梯度计算方式。可以看出,使用基于梯度比率计算方式的SAR-Harris算法表现最佳,可以检测具有低误报率的特征点(如图中拐点)。

(a) Multi-Harris

(b) Harris-Laplace

(c) SAR-Harris
图7 3种类型的特征检测器在SAR图像上的对比
然而,由于SAR-Harris算法是对Multi-Harris特征点检测算法的改进,无法有效地确定特征尺度参数的大小,并且检测出的特征点位置不准确。 因此本文提出使用Harris-Laplace结合ROEWA的算法来检测SAR图像中的特征。传统的Harris-Laplace算法对于光学图像具有良好的尺度不变性,可以准确检测出特征点位置并且确定其特征尺度,其计算公式如下:
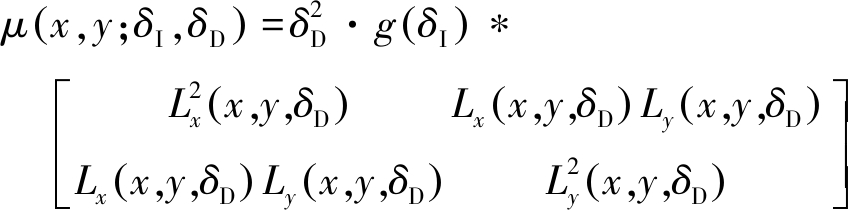
(8)
式中:g(δI)表示δ=δI的高斯卷积核,δI又称为积分尺度;Lα(x,y,δD)表示在α方向的微分核乘以δ=δD的高斯卷积核计算出的微分,微分核由梯度差分的方式计算得到,δD又称为微分尺度。本文针对SAR图像中强散射纹理区乘性斑点噪声的特点,对于Harris-Laplace算法中微分的计算方式加以改进,将Lα(x,y,δD)中微分核的梯度差分计算方式改进为对于SAR图像更为有效的基于梯度比率的ROEWA算子,从而得到Harris-Laplace-ROEWA特征检测算法,其方程式如下:
![]() *
*![]()
(9)
(10)
式中,δI和δD分别表示积分和微分尺度。Gx和Gy使用ROEWA以梯度比率的方式计算,其中R1,δD和R3,δD是水平方向和垂直方向的比率,它们在式(7)中计算。有关计算过程的更多细节可以在文献[6]中找到。我们将SAR-Harris检测方法与提出的方法进行了比较,实验结果如图8所示。
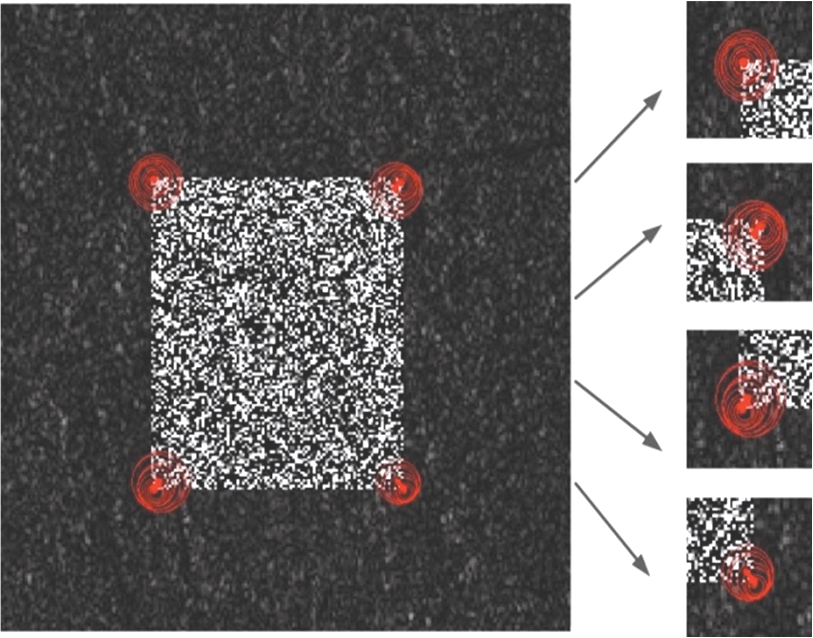
(a) 上述效果最好的方法SAR-Harris

(b) 本文方法Harris-Laplace-ROEWA
图8 SAR图像的角点检测效果对比
从图8可以看出,与其他方法相比,本文提出的特征检测方法可以准确地提取具有高位置精度和低误差率的不变特征点,特别是在高对比度区域。同时,本文所提出的方法可以抑制散斑噪声并选择真实的特征尺度。
2.3 描述符构建与特征搜索匹配策略
描述符构建阶段,标准SIFT算法采用SIFT描述子构建描述符,本文则采用KAZE算法[11]中的M-SURF描述符进行描述符构建:对于尺度参数为δD的特征点,在其梯度比率图像Gx(x,y)Gy(x,y)上以本文提出的Harris-Laplace-ROEWA算法提取的特征点为当前中心设置一个24δD×24δD的窗口,然后再将窗口划分为4×4的小子区域,每个小子区域大小为9δD×9δD,则相邻子区域有4δD重合部分,每一个子区域的梯度比率微分以子区中心为当前响应,取通过高斯核 (δG=2.5δD)进行加权,计算出长度为4的子区域描述向量dV:
dV=(∑Gx,∑Gy,∑|Gx|,∑|Gy|)
(11)
然后,每一个子区的向量以梯度比例获取特征点为中心进行另一个高斯窗口4×4(δG=1.5δD)对当前子区区域向量dV进行加权算术操作,最后统一归一化处理获取64维的描述符。
特征搜索匹配阶段,标准SIFT算法采用欧式距离进行特征点对的相似性评估,并采用随机KD树空间划分对描述子的特征点信息快速搜索,并通过最近邻方法进行粗匹配,最近邻方法通过比较两个向量的最近邻与次近邻之比的比例参数与设定初始阈值的判断准则来完成图像粗匹配过程。本文则通过KNN算法[12]进行特征搜索,并通过使用RANSAC算法剔除粗匹配过程中的错误匹配点,求取的几何变形参数来完成SAR图像匹配。
3 数据结果处理与分析
为了验证提出方法的性能,本文采用3种类型的SAR图像进行实验:1)不同斑点噪声的仿真SAR图像;2)不同仿射变换的多视角仿真SAR图像;3)不同频带/平台/极化/空间分辨率的真实SAR图像。其中第1类仿真SAR图像由原始SAR图像添加不同方差的乘性斑点噪声获得;第2类仿真SAR图像由原始SAR图像经过不同的仿射变换获得;第3类真实SAR图像分别为不同波段、不同分辨率TerraX-SAR与RadarSat2图像。
为了评估所提方法的性能,验证提出算法的有效性与稳定性,本文将所有实验的测试结果分别与BFSIFT(双边)方法和NDSS-SIFT(非线性扩散)方法进行了比较,并且使用以下3个指数定量评估所提出方法的性能:均方根误差(Root Mean Square Error,RMSE) [13]表示匹配的精确度,内联点比率(Inliers Ratio)表示匹配的准确度,以及算法耗时。Inlier比率和RMSE计算式如下:
(12)
(13)
式中:(xi,yi)和![]() 分别表示来自参考图像和输入图像的匹配的内联点的坐标; Ninliers为内联点的数量,Nall为所有匹配的总数量。较大的内联点比率表明获得高质量的特征点和正确的匹配的可能性更大。较小的RMSE表明估计的变换矩阵所求误差较小,即所求的变换矩阵较为精确。
分别表示来自参考图像和输入图像的匹配的内联点的坐标; Ninliers为内联点的数量,Nall为所有匹配的总数量。较大的内联点比率表明获得高质量的特征点和正确的匹配的可能性更大。较小的RMSE表明估计的变换矩阵所求误差较小,即所求的变换矩阵较为精确。
3.1 定性分析
首先为了验证本文算法对相干斑噪声和不同视角的SAR图像的有效性与稳定性,图9、图10分别显示了不同噪声影响、不同视角的仿真SAR图像配准算法对比实验结果。从图中可以看出,在斑点噪声和仿射变换导致的多视角的影响下,本文算法提取特征点分布较均匀,匹配特征点较准确、误差较小,整体有效性与稳定性表现较好。

(a) BFSIFT

(b) NDSS-SIFT

(c) 本文方法
图9 不同斑点噪声的仿真SAR图像实验结果

(a) BFSIFT

(b) NDSS-SIFT

(c) 本文方法
图10 不同仿射变换的仿真SAR图像实验结果
其次为了验证本文算法对真实SAR图像的普适性,图11显示了不同波段、不同分辨率TerraX-SAR与RadarSat2图像匹配算法的匹配效果。从图中来看,RadarSat2和TerraX-SAR存在大量相干斑噪声;同时由于采用不同的波段成像,图像灰度体现出较大的偏差。从图中可以看出,在不同平台的SAR造成的图像差异的影响下,本文算法仍然能够提取出数量稳定分布均匀的特征点,并达到良好的匹配效果。

(a) RadarSat2-SAR图像(左)和TerraX-SAR图像(右),0.7 m分辨率

(b) 图(a)的棋盘拼接图

(c) RadarSat2-SAR图像(左)和TerraX-SAR图像(右)

(d) 图(c)的棋盘拼接图

(e) RadarSat2-SAR图像(左)和TerraX-SAR图像(右),3 m分辨率

(f) 图(e)的棋盘拼接图
图11 不同频带/平台/极化/空间分辨率的真实SAR图像实验结果
3.2 定量分析
表1、表2分别显示了图9中添加斑点噪声和图10中进行仿射变换的仿真SAR图像的具体指数定量评估结果,图12~图15分别显示了15组测试真实SAR图像集的具体指数定量评估结果,本文所提出的改进SAR图像匹配方法分别从RMSE、检测内联点比率、尺度空间构造耗时和匹配算法总耗时四个方面验证本文算法的有效性与实时性。
表1 不同斑点噪声的仿真SAR图像定量评估结果
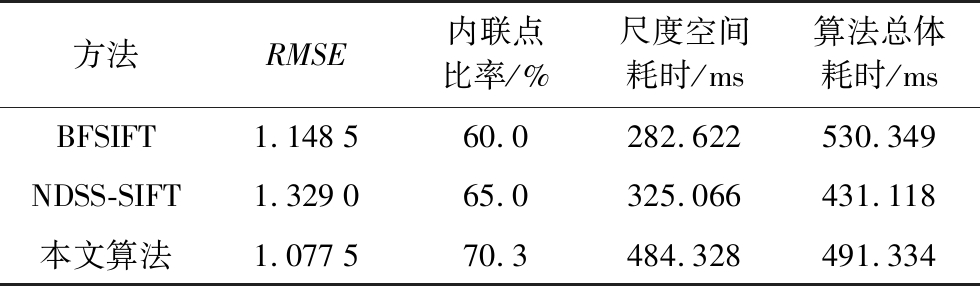
方法RMSE内联点比率/%尺度空间耗时/ms算法总体耗时/msBFSIFT1.148560.0282.622530.349NDSS-SIFT1.329065.0325.066431.118本文算法1.077570.3484.328491.334
表2 不同仿射变换的仿真SAR图像定量评估结果

方法RMSE内联点比率/%尺度空间耗时/ms算法总体耗时/msBFSIFT1.110964.7259.418448.651NDSS-SIFT0.851872.4287.219429.077本文算法0.792279.2394.121398.996
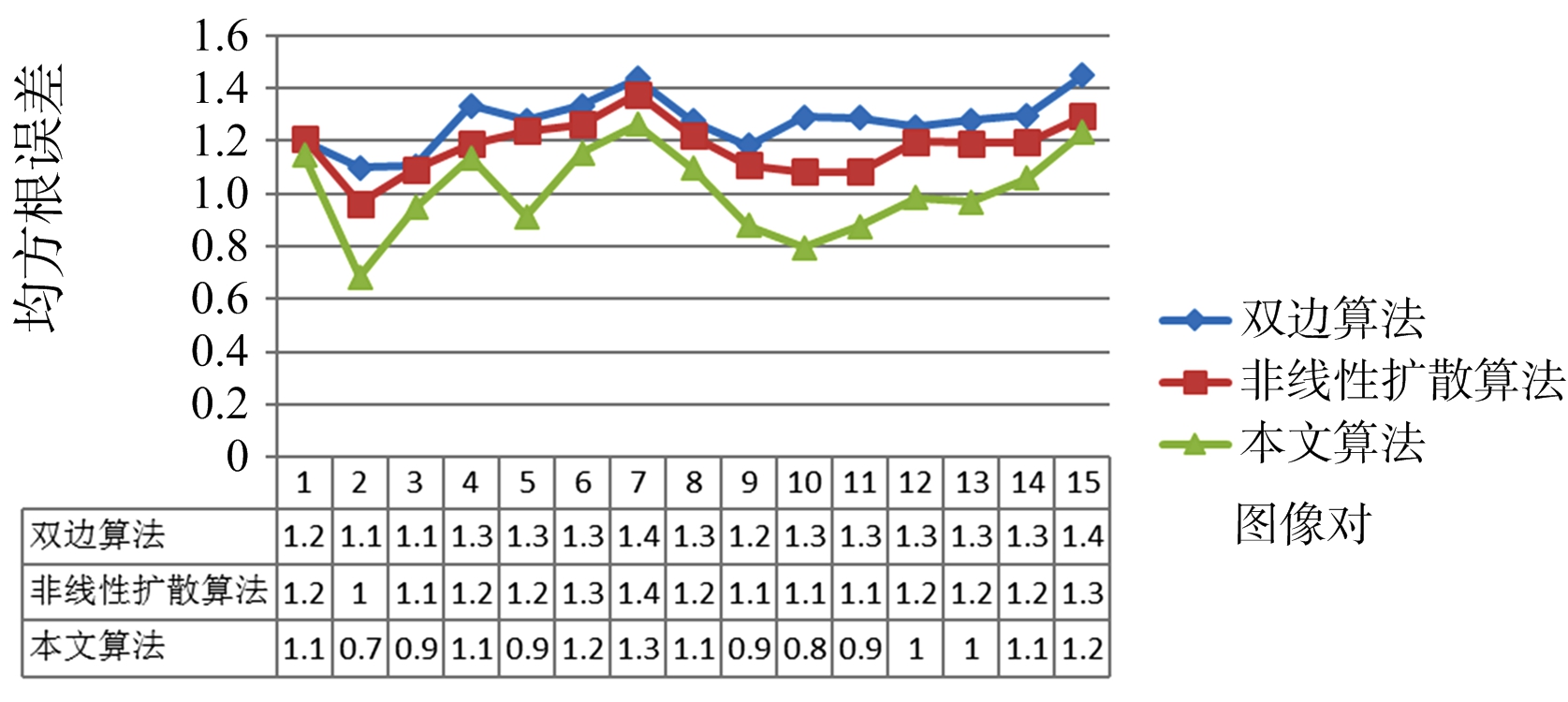
图12 均方根误差对比
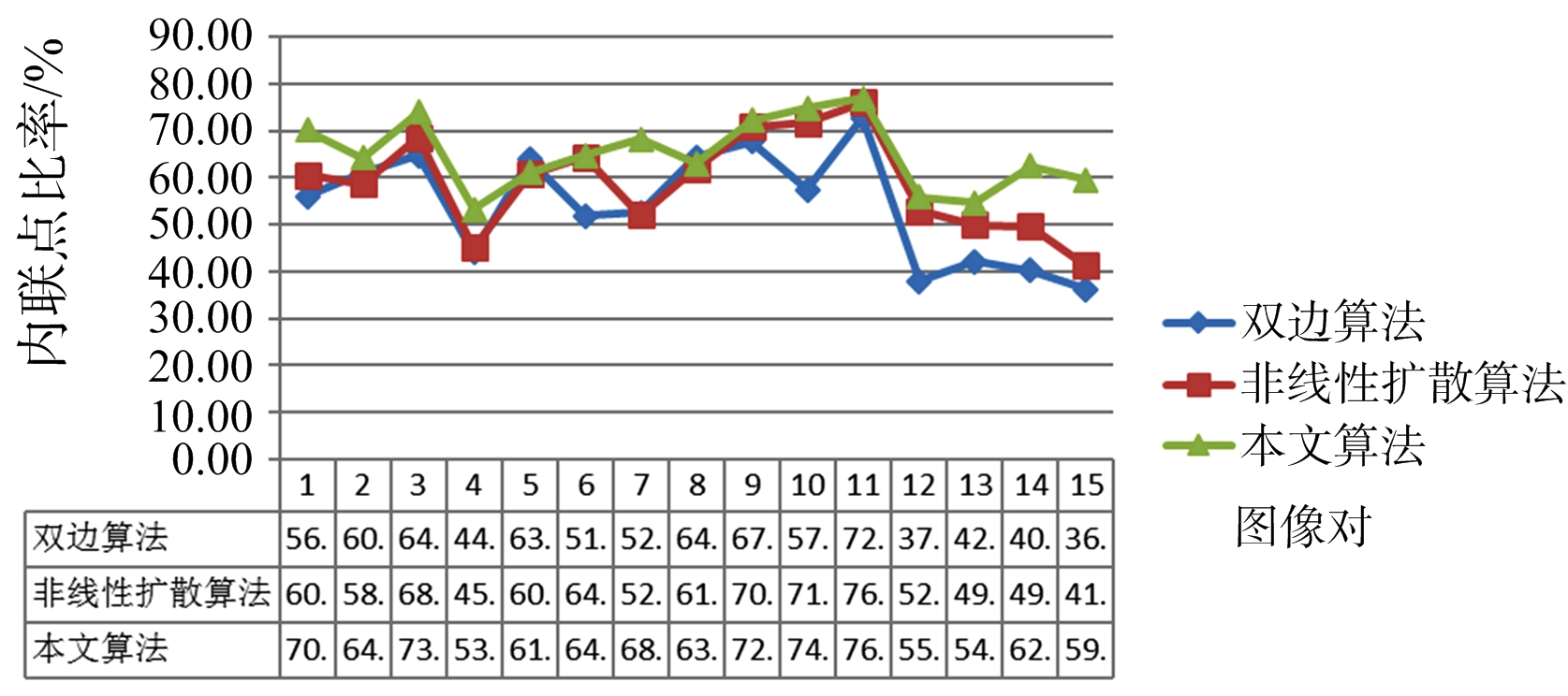
图13 内联点比率对比
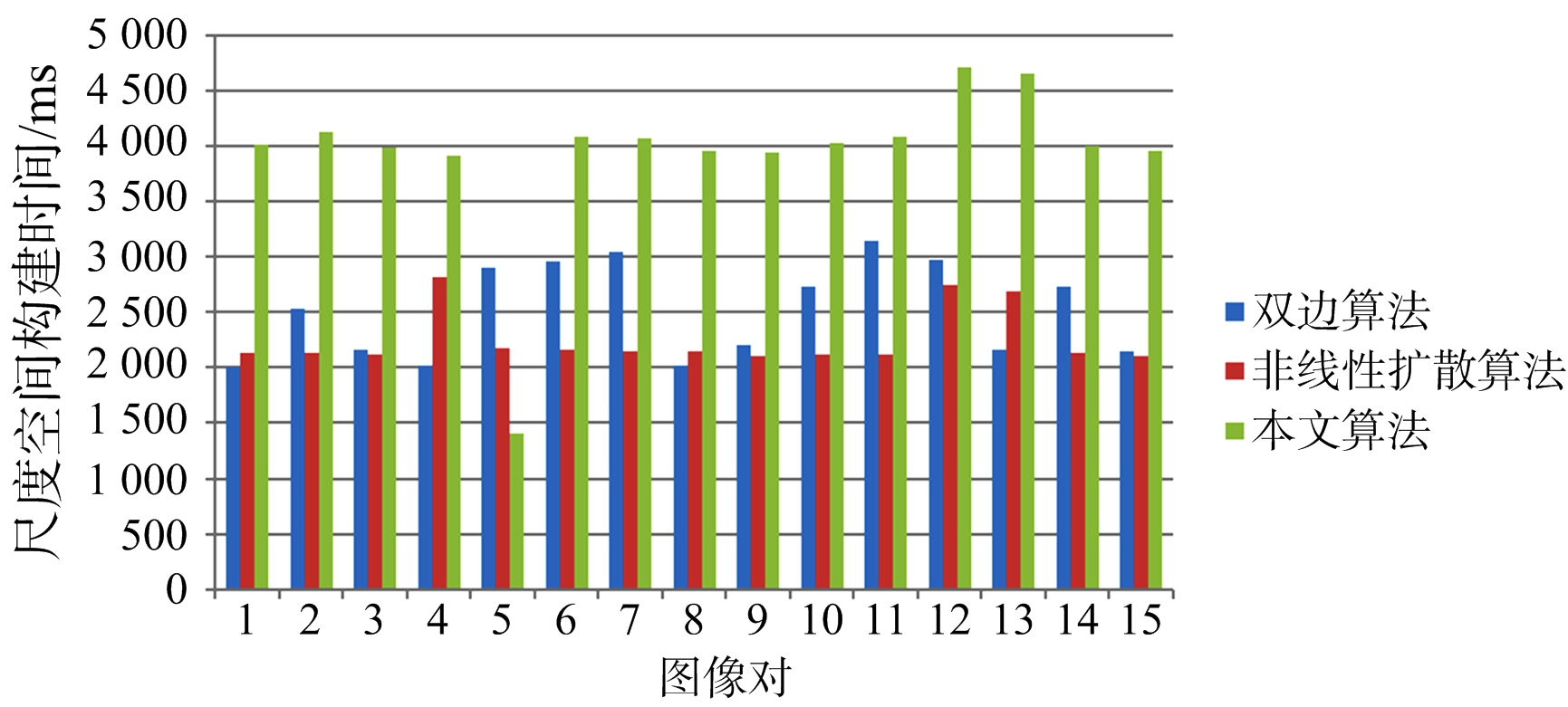
图14 尺度空间构建耗时对比
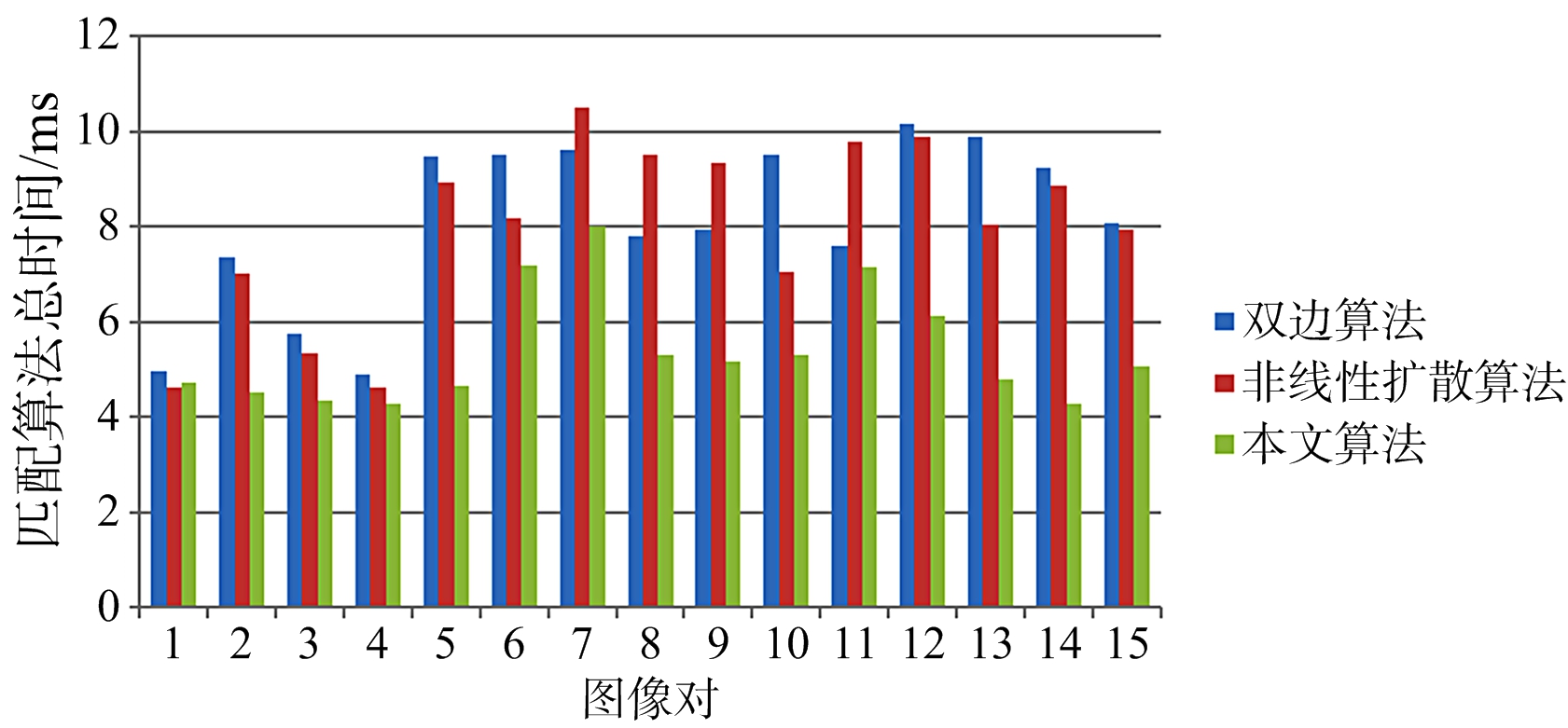
图15 算法总体耗时对比
针对SAR图像匹配:首先要获取足够多的稳定特征点数,其次是在稳定特征点局部区域构建鲁棒快速的描述符,最后将获得的特征点描述符进行高效准确的匹配。图12对比了BFSIFT算法、NDSS-SIFT算法和本文算法匹配点对的RMSE,本文算法的RMSE明显低于另外两种算法,由此可以看出本文算法在进行SAR图像匹配时具有更好的准确性。图13对比了两种算法和本文算法检测的内联比率,可以看出本文算法的内联比率略高于其他两种算法,主要由于本文采用的滚动引导滤波构建尺度空间时有效滤除了相干斑噪声,减少虚假特征点,并良好保存了真实边缘信息,增加有效特征点,并且利用ROEWA算子针对SAR图像处理的优越性,在特征点检测阶段进一步提高特征点的质量,在描述符构建阶段形成了鲁棒的描述符。图14对比了BFSIFT算法的双边滤波、NDSS-SIFT算法非线性扩散滤波与本文方法构建尺度空间耗时,本文方法耗时最多,接近于其他两种算法耗时的两倍,主要由于滚动引导滤波的迭代过程耗时。然而图15对比了两种算法与本文匹配算法总耗时,本文算法低于另外两种算法,最主要因为尺度空间构建阶段获取了高质量的滤波图像之后,特征点检测和描述符构建阶段检测出了准确的特征点并形成了鲁棒快速的描述符,所以特征搜索与匹配阶段极大地减少了搜索耗时与剔除错误匹配点对的时间消耗,算法的总体耗时相对减少。综合来看,本文算法在保证了算法时间复杂度的前提下,提高了匹配精度与匹配概率,在获取准确稳定特征点的同时,很大程度上保证了算法的实时性并提升了算法的有效性。
4 结束语
本文提出了一种基于改进SIFT框架的SAR图像匹配算法:为了减少斑点噪声的影响,本文算法利用去除相干斑噪声并且保持边缘的滚动引导滤波器来构造尺度空间;为了检测更准确的特征并减少错误匹配点,本文将ROEWA算子与Harris-Laplace检测算子相结合进行特征点检测。本文使用仿真和真实SAR图像进行相关算法的比较验证,实验结果表明,本文提出的算法针对不同噪声、不同视角、不同频带/平台/极化/空间分辨率的SAR图像优于其他SAR图像匹配算法的表现,并且算法总体耗时并未增加,在保证整体时间消耗一定的前提下对算法的性能产生了一定的提升。但尺度空间构建阶段耗时过长的问题仍然没有得到有效解决,后续工作需要考虑如何在保证算法性能的条件下,提高尺度空间构建阶段运算效率的问题。
[1] BENTOUTOU Y,TALEB N,KPALMA K,et al. An Automatic Image Registration for Applications in Remote Sensing [J]. IEEE Trans on Geoscience and Remote Sensing, 2005, 43(9):2127-2137.
[2] LOWE D G. Distinctive Image Features from Scale-Invariant Keypoints[J]. International Journal of Computer Vision, 2004, 60(2):91-110.
[3] KE Y, SUKTHANKAR R. PCA-SIFT:A More Distinctive Representation for Local Image Descriptors[C]∥Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Washington:IEEE,2004:506-514.
[4] SCHWIND P, SURI S, REINARTZ P,et al. Applicability of the SIFT Operator to Geometric SAR Image Registration [J]. International Journal of Remote Sensing, 2010, 31(8):1959-1980.
[5] WANG Shanhu, YOU Hongjian, FU Kun. BFSIFT:A Novel Method to Find Feature Matches for SAR Image Registration [J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(4):649-653.
[6] DELLINGER F, DELON J, GOUSSEAU Y, et al. SAR-SIFT:A SIFT-Like Algorithm for SAR Images [J]. IEEE Trans on Geoscience and Remote Sensing, 2015, 53(1):453-466.
[7] FAN Jianwei,WU Yan,WANG Fan,et al.SAR Image Registration Using Phase Congruency and Nonlinear Diffusion-Based on SIFT [J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(3):562-566.
[8] ZHANG Qi, SHEN Xiaoyong, XU Li, et al. Rolling Guidance Filter [M]∥Computer Vision-ECCV 2014, Germany:Springer, 2014:815-830.
[9] LEE J S, HOPPEL K, MANGO S A. Unsupervised Estimation of Speckle Noise in Radar Images [J]. International Journal of Imaging Systems and Technology,2005,4(4):298-305.
[10] 韩春明,郭华东,王长林,等.保持边缘的SAR图像滤波方法[J].高技术通讯,2003,13(7):11-15.
[11] ALCANTARILLA P F, BARTOLI A, DAVISON A J. KAZE Features [C]∥In European Conference on Computer Vision, Italy:Springer, 2012:214-227.
[12] ALTMAN N S. An Introduction to Kernel and Nearest-Neighbor Nonparametric Regression [J]. American Statistician, 1992, 46(3):175-185.
[13] LI Qiaoliang, WANG Guoyou, LIU Jianguo, et al. Robust Scale-Invariant Feature Matching for Remote Sensing Image Registration [J]. IEEE Geoscience and Remote Sensing Letters, 2009, 6(2):287-291.



