0 引言
相控阵天线能够以微秒级的速度捷变天线波束的指向,使得单部相控阵雷达在对指定区域搜索的基础上,还能同时跟踪多个目标[1]。这种强大的波束捷变能力使得相控阵天线在现代机载雷达中得到越来越广泛的运用[2]。
对于自卫电子对抗方而言,一旦敌方雷达进入跟踪状态,就意味着面临巨大的威胁,雷达告警器必须作出及时准确的告警;另一方面,对于雷达干扰而言,在作战过程中,实时根据所需对抗雷达的威胁程度来进行干扰资源分配才能最大限度地发挥电子对抗系统的作战效能[3-4]。通过对敌方雷达工作状态的识别可以实现威胁等级判别和辅助干扰样式选择[5],这样可以有效地防止干扰资源的浪费,提升干扰的针对性和有效性。因此,开展相控阵雷达工作状态识别具有重要意义。
当前关于相控阵雷达工作状态识别的研究大多使用频率、脉宽和脉冲重复频率等描述信号样式的常规参数,而较少关注波束扫描。例如,文献[6]研究了参数寻优LSSVM算法在机载火控雷达工作模式判定中的应用;文献[7]运用DS证据理论进行雷达工作模式识别;文献[8]从脉冲、脉冲组、工作模式三个层级运用多层次建模方法进行机载相控阵雷达工作模式识别。但是相控阵雷达,特别是相控阵机载火控雷达属多功能雷达,其功能的实现不单纯取决于信号样式。因此,仅通过信号样式分析工作状态是不完整的。
本文从相控阵雷达资源调度出发,分析了相控阵雷达波束调度的时序特征,然后引入了一种改进的统计直方图方法对雷达脉冲幅度(Pulse Amplitude, PA)进行分析,最后综合数据率和平均驻留时间实现工作状态识别。仿真结果表明:本文方法不仅能够在短时间窗内实现相控阵雷达工作状态快速识别,并且能够识别出雷达的目标跟踪个数。
1 相控阵雷达的资源调度
本文定义的工作状态主要指的是跟踪状态及搜索状态。而相控阵雷达实现工作状态转换的核心是雷达资源调度。对于搜索而言,其需要的数据率和波束驻留时间一般远低于跟踪,当发现目标后,雷达一方面要跟踪现有目标,另一方面还要继续空域搜索。因此,为了最大限度发挥相控阵雷达波束灵活的优势,实际中常采用搜索加跟踪(Track-and-Search, TAS)模式。图1是TAS模式的示意图。
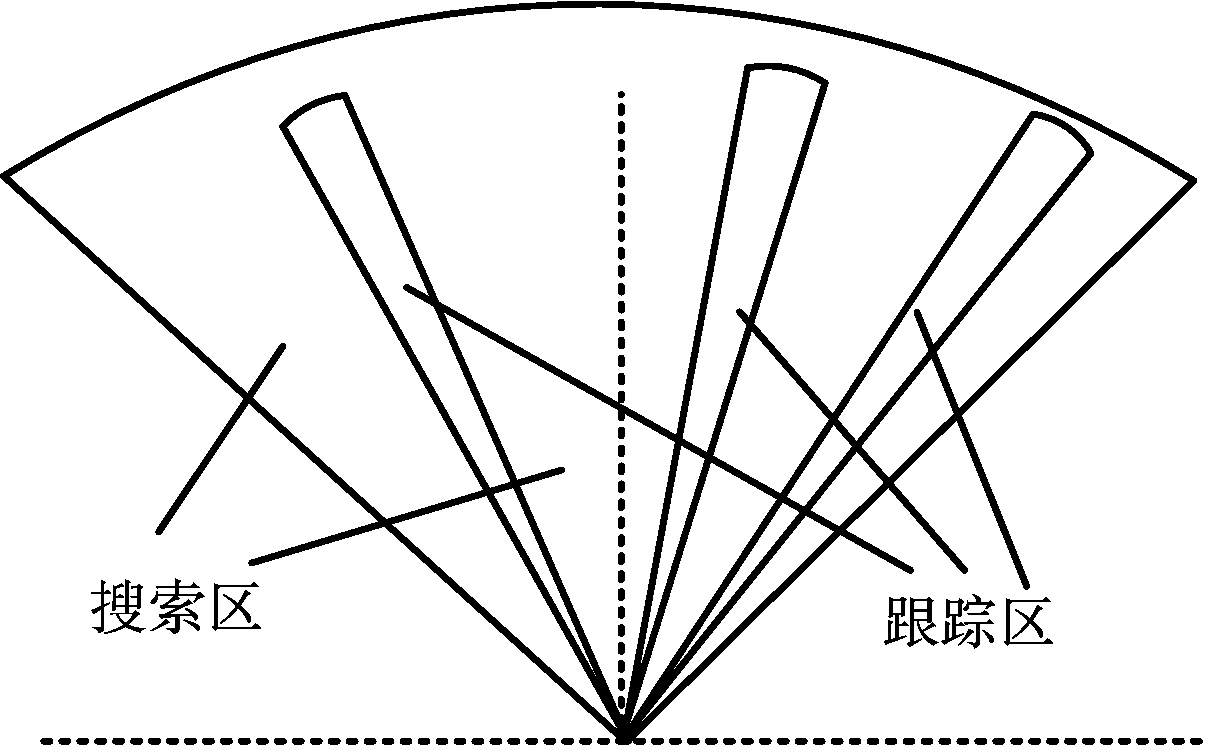
图1 TAS模式示意图
TAS模式下雷达区分搜索区域和跟踪区域,利用相控阵天线灵活的波束调度将搜索任务和跟踪任务分别对待,交替执行,使得不仅跟踪和搜索可以采用不同的数据率,而且对不同目标也可以采用不同的跟踪数据率。为了实现这一目的,通常在相控阵雷达系统设计时,会预先安排若干种跟踪状态,对不同的跟踪状态分配不同的跟踪间隔时间和跟踪波束驻留时间[9]。为了便于利用时间分割方法进行多目标跟踪,跟踪时间需集中在一起。因此各种跟踪状态对应的跟踪间隔时间ΔTn通常是最小跟踪间隔时间ΔTmin的整数倍。
ΔTn=k·ΔTmin,k∈N+
(1)
以3种跟踪状态为例,假设最小跟踪间隔为ΔTmin=0.5 s,那么3种状态的跟踪间隔时间可分别设计为ΔT1=0.5 s,ΔT2=1 s,ΔT3=2 s。若跟踪驻留时间分别为Ta,Tb,Tc,则其相应的波束调度时序如图2所示。

图2 TAS模式多目标跟踪波束调度时序关系
2 工作状态快速识别方法
2.1 侦察信号PA序列分析
雷达对抗侦察的一般模型可以表示为[10]
(2)
式中,Pr和Pt分别为侦收信号功率和雷达发射信号功率,Gr和Gt(θ,φ)分别为侦察天线增益和雷达天线增益,λ为发射信号波长,R为侦察机与雷达之间的距离,L为损耗因子。为简化模型,本文假设侦察天线采用全向天线,PtGrλ2/[(4πR)2L]为常数。这个假设在侦察机和雷达相对位置固定或采样时间很短而距离变化可以忽略的时候是合理的。那么式(2)可以简化为
Pr(t)=K·Gt(θ,φ)
(3)
式中,K为常数。由式(3)可以看出,接收机侦收到的雷达信号脉冲幅度完全取决于波束的指向,因此,可以认为当PA值相等(在一定容差范围内)时,波束指向相同。那么,通过对PA序列做统计直方图就可以得到雷达对不同方位的资源分配比例,从而判断雷达是否处于跟踪状态。
2.2 改进直方图方法
统计直方图概念清晰,实现简单,是数据分析中常用的一种方法。
设F是数据集合,数据长度为N,则定义于F上的直方图H可以表示为一个三元组{hi=(si,ti,vali)|i=1,2,…,m}。其中,[si,ti]称为直方图仓,是某一区间A的子区间;si和ti合称为hi的边界点;vali表示落入该区间的数据总个数。H必须满足以下3个条件:
1) ∀i≠j(i=1,2,…,m;j=1,2,…,m),[si,ti]∩[sj,tj]=∅;
2) [s1,t1]∪[s2,t2]∪…∪[sm,tm]=A;
传统的直方图分析方法一般采用等大小的仓宽度,并且宽度往往由人工进行选择。对于峰值检测来说,这种方法的一大弊端就是对数据抖动十分敏感。如图3(a)所示,它容易将处在边界点附近且存在抖动的数据分割到两个直方图仓内,从而导致峰值检测失败。因此,本文引入一种改进的直方图方法。如图3(b)所示,该方法可以根据数据情况自动设定每个仓的宽度和仓的个数,一定程度上克服了传统直方图的缺点。其计算方法如表1所示[11]。其中εr为用户参数,需要根据数据的稳定程度预先设定。
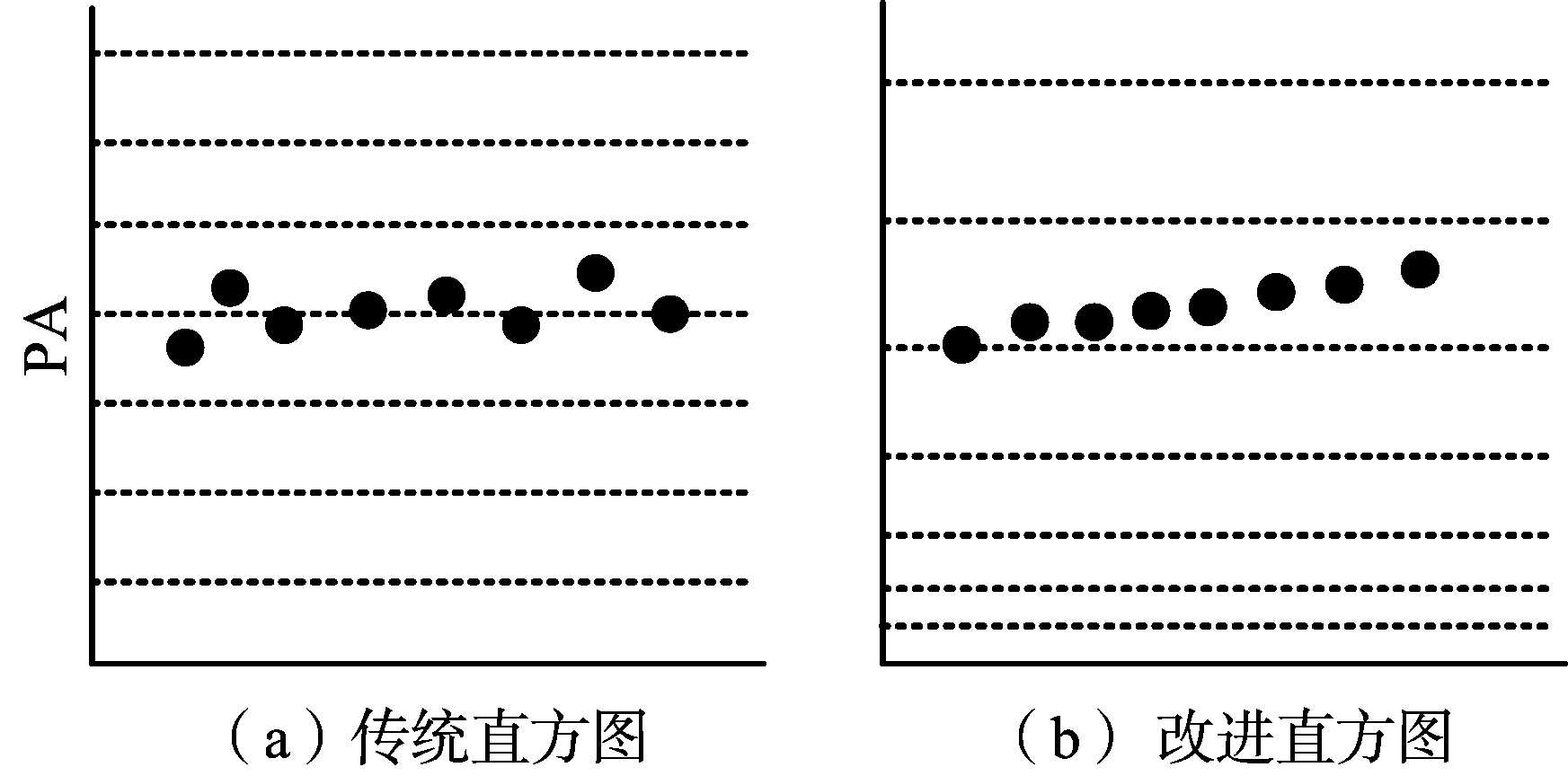
图3 两种直方图示意图
表1 改进直方图算法流程

变量说明: x(k)第k个数据N数据长度εr误差耐受值X(m) 第m个仓的起始值n(m)第m个仓内的计数值Step1:将所有数据升序排列;Step2:初始化;εr,k=2,m=2,n(1)=1,X(1)=x(1),X(2)=[(1+εr)/(1-εr)]·x(1)Step3:按照如下方法构造直方图。While(k
2.3 工作状态识别
对侦收信号的PA序列求直方图,实质上就是对雷达在不同方位上的发射脉冲数进行统计分析,反映的是雷达在不同方位上的能量资源分配。由前述相控阵雷达的资源调度可以知道,相控阵雷达在跟踪时所使用的数据率和波束驻留时间一般远大于搜索。因此,如果雷达在某一方位上进行目标跟踪,那么在相应的PA值附近就会侦收到大量脉冲,表现在直方图上就是出现一个比较高的尖峰。如图4和图5所示,图4为TAS模式下跟踪2个目标时的脉冲幅度值随时间变化规律,图5为其对应的统计直方图。从图中可以看出,通过设定适当的门限Th就可以检测出该尖峰,从而判断雷达是否处于跟踪状态,并且根据过门限的峰值个数还可以得到雷达的目标跟踪个数Nt。
(4)
(5)
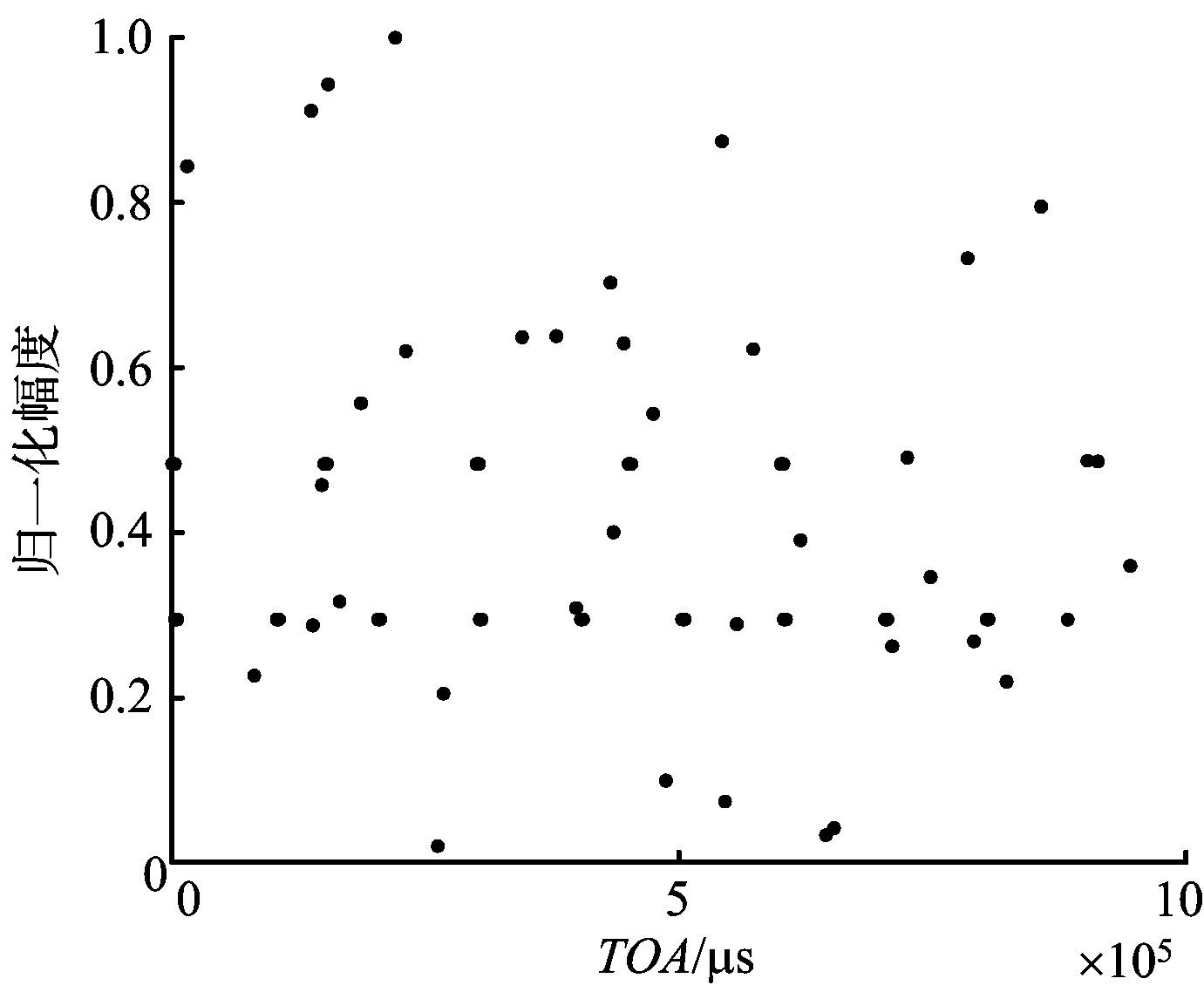
图4 脉冲幅度随时间变化规律
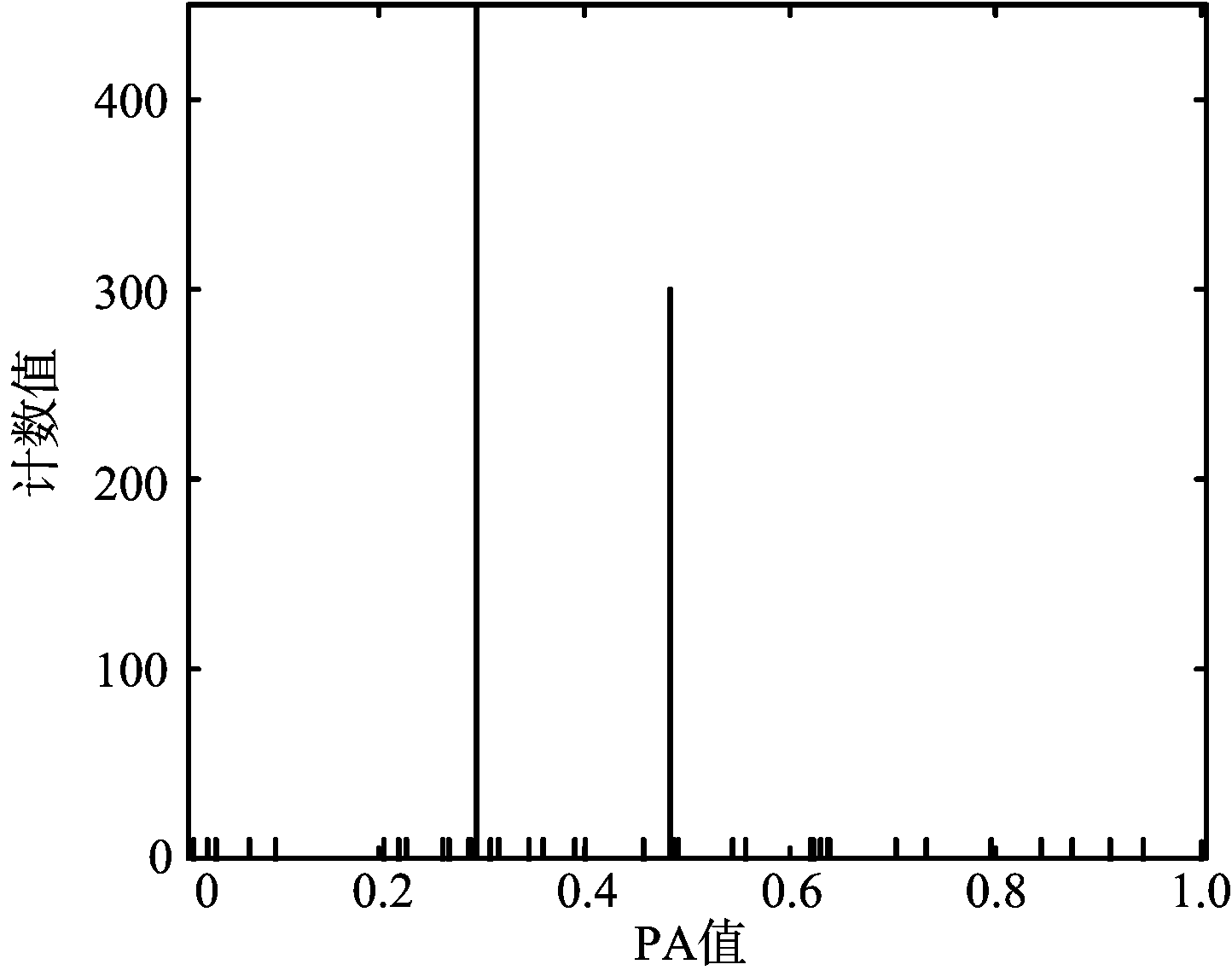
图5 脉冲幅度统计直方图
但是这种单一门限的峰值检测方法受门限设置的影响较大。如果门限设置过高,容易将跟踪误判为搜索而造成漏警;过低则会将搜索误判为跟踪,导致虚警。为了解决这个矛盾,可以先将峰值检测的门限设置得相对较低,防止漏警,然后再对过门限的PA范围进行数据率和单次驻留时间的检测,剔除不符合跟踪数据率和跟踪驻留时间的峰值,降低虚警。
3 仿真结果与分析
本节设计两个仿真实验,分别验证采样时间长度和测量误差对算法识别准确率的影响。仿真参数设置如下:雷达采用恒定脉冲重复间隔,PRI=50 μs;共设置4种跟踪状态,其跟踪间隔时间ΔT分别为[0.05, 0.1, 0.15, 0.2]s,单次驻留时间T分别为[2 500, 2 500, 3 000, 3 000] μs;搜索波束的单次驻留时间为500 μs。考虑到侦察机的侦收范围有限,设置侦收空域内雷达的目标跟踪个数为0~3个随机抽取,跟踪0个目标即为纯搜索状态;每个目标的跟踪状态也从4种状态中随机抽取。
3.1 采样时间长度对识别准确率的影响
不同应用场景对识别准确率和时效性的要求不同。为研究采样时间长度对算法识别准确率的影响。设置采样时间长度由0.1 s变化到2 s,变化步长为0.1 s,每个时间长度上做5 000次蒙特卡洛实验,得到仿真结果如图6所示。
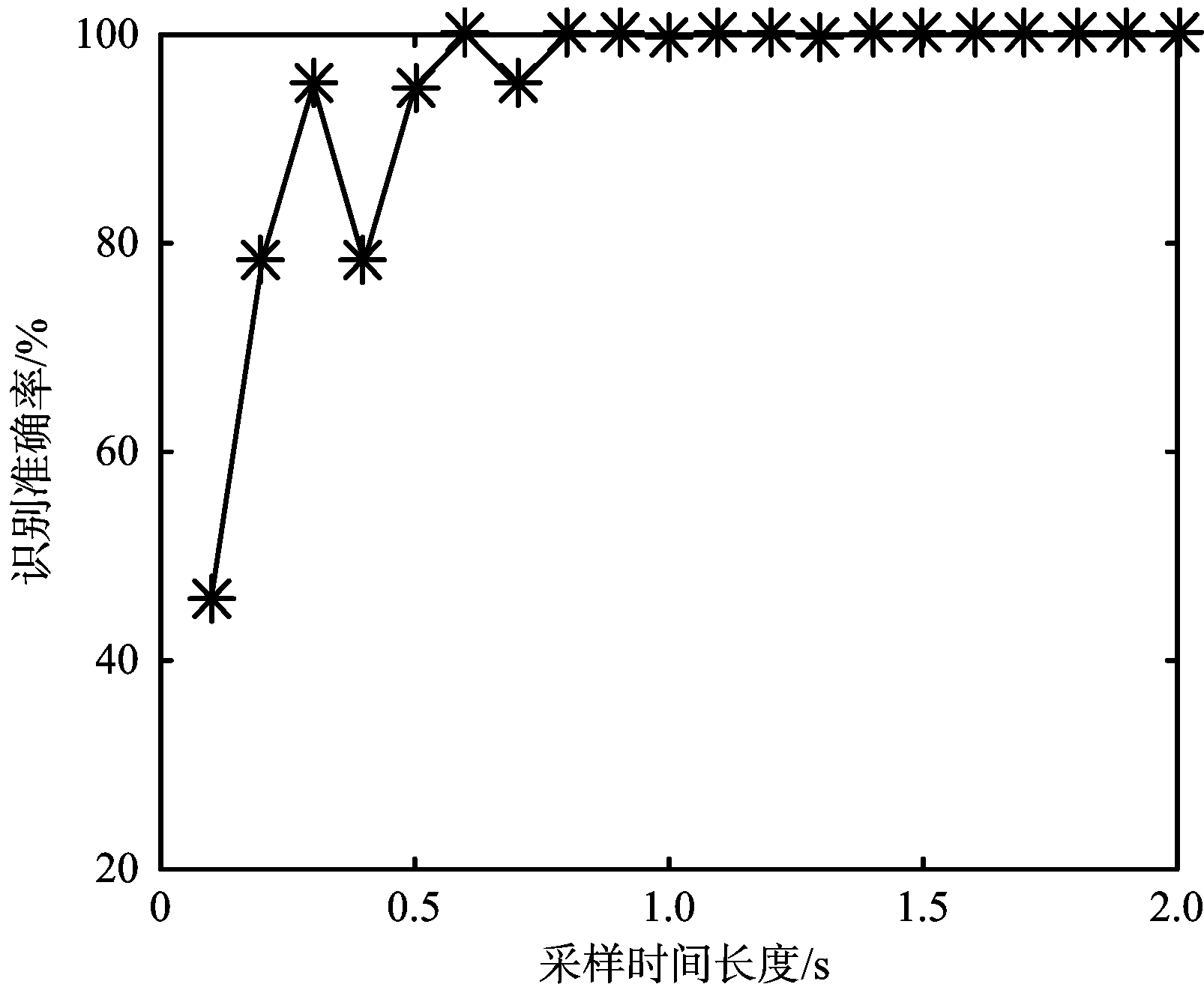
(a) 采样时长对工作状态识别准确率的影响
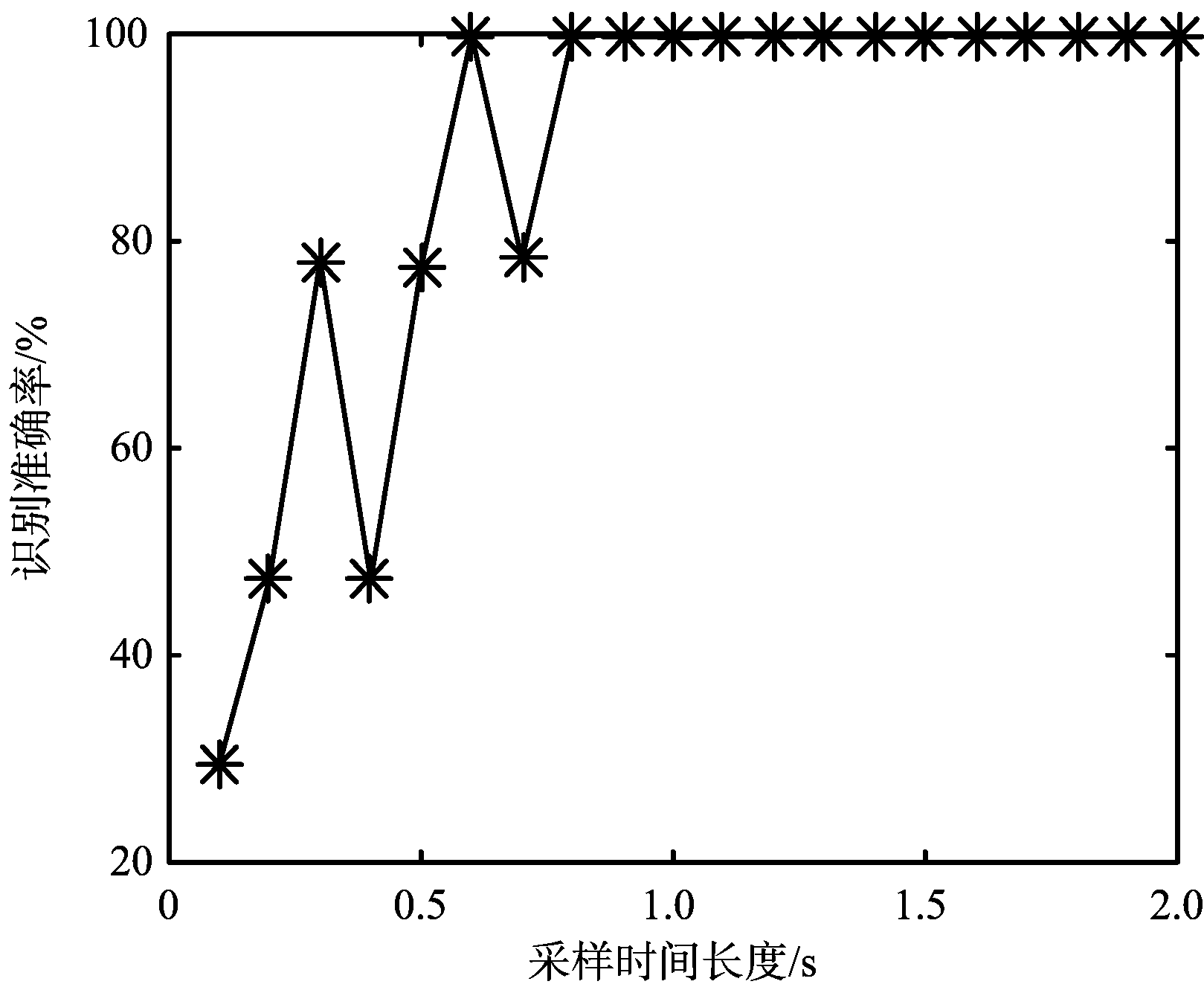
(b) 采样时长对目标跟踪个数识别准确率的影响
图6 采样时长对识别准确率的影响
由图6可以看出,当采样时间长度小于0.8 s时,雷达工作状态的识别准确率和目标跟踪个数的识别准确率均呈现波动上升的趋势。而当采样时长大于0.8 s以后两种识别准确率都已经稳定在了100%。这说明本文方法在短时间窗、小数据样本情形下具有较好的性能。并且由于算法简单,能够对数据进行实时处理,所以综合这两点可以得出结论,本文算法时效性较强,可以满足工作状态快速识别的要求。
3.2 测量误差对算法识别准确率的影响
实际侦察环境中,由于噪声等原因,雷达信号脉冲幅度的测量存在一定的随机误差。为检验算法的鲁棒性,在PA序列中加入高斯噪声以模拟测量误差。相对误差大小以1%为步长变化到10%。采样时间长度1 s。每种误差条件下进行5 000次蒙特卡罗仿真,得到识别结果如图7所示。
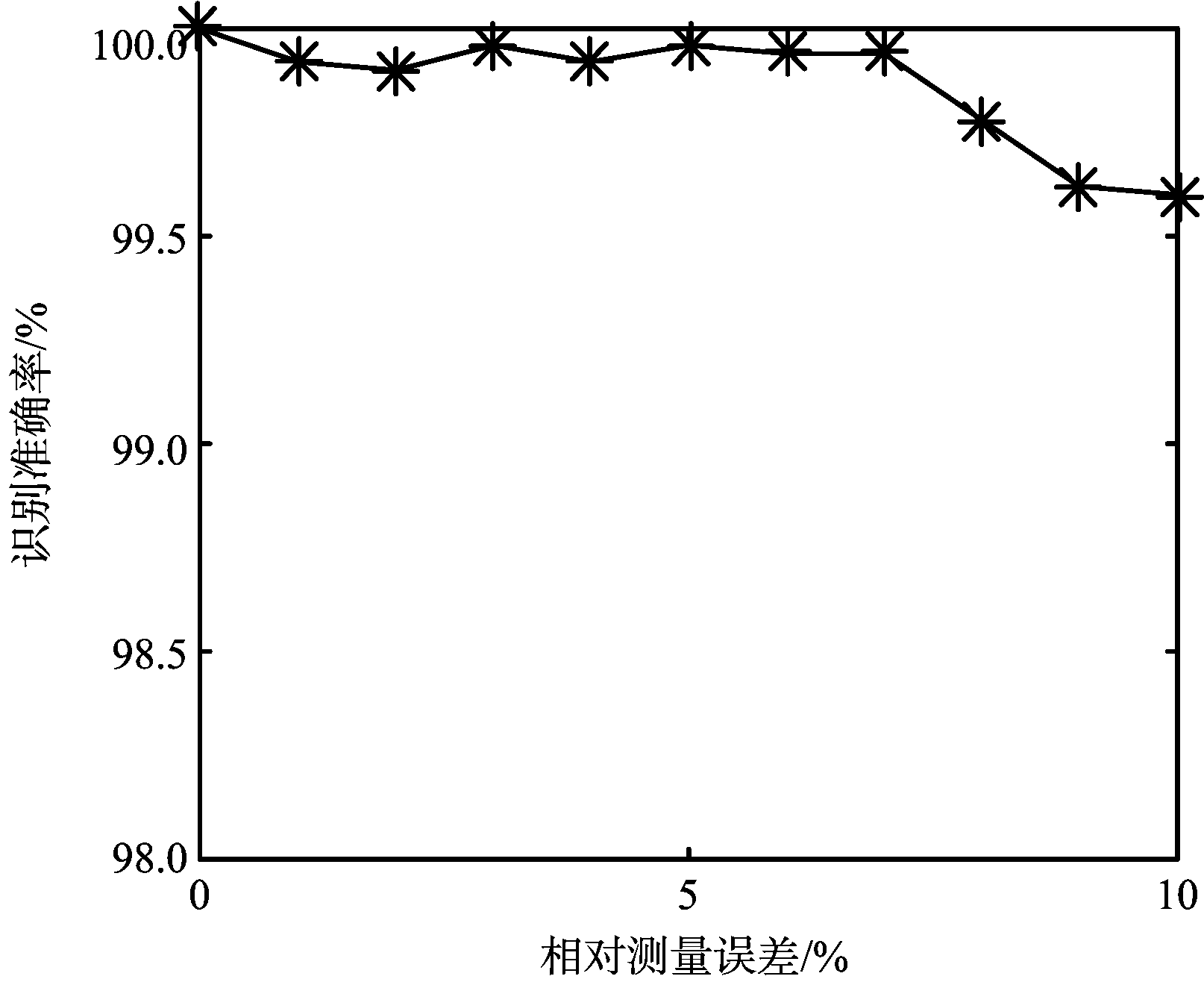
(a) 测量误差对工作状态识别准确率的影响
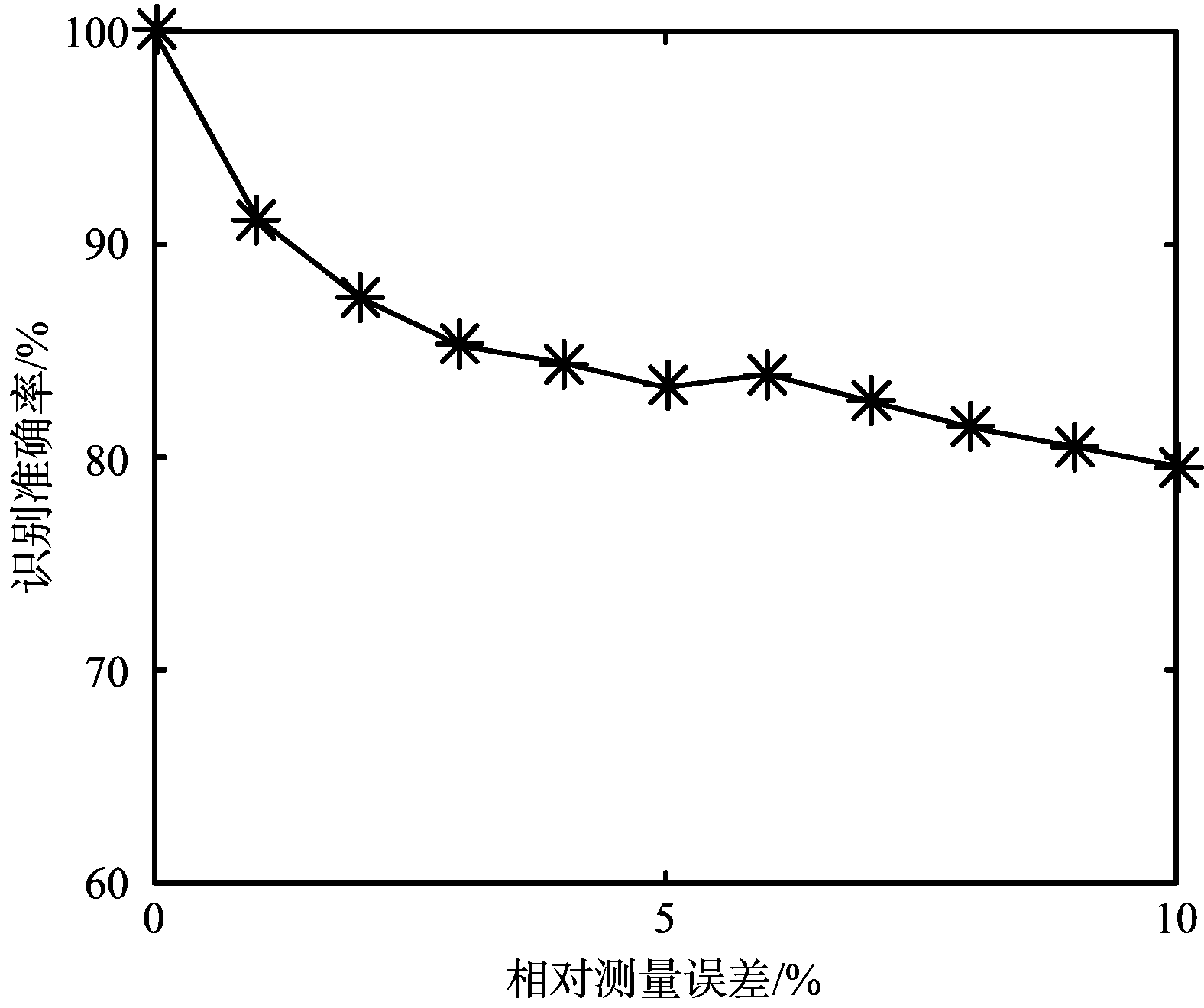
(b) 测量误差对目标跟踪个数识别准确率的影响
图7 测量误差对跟踪个数识别准确率的影响
从图中可以看出,随着测量误差的增大,工作状态识别准确率和目标跟踪个数识别准确率均有所下降。这是由于测量误差使得同一目标跟踪方位上的PA测量值出现抖动。尽管采用了改进的直方图方法,但是较大的抖动仍然可能使原本属于一个直方图仓的PA值被分散到不同的仓内,从而导致峰值检测失败,或者跟踪一个目标被当成跟踪两个目标而使得跟踪数据率和驻留时间降低,从而被当作虚警剔除。
尽管如此,由图7(a)可以看出,当测量误差高达10%的时候,雷达工作状态的识别准确率依旧可以达到99.5%以上。这说明本文算法在相控阵雷达工作状态识别应用上具有很强的鲁棒性。观察图7(b)可以看出,虽然当测量误差增大到10%的过程中,目标跟踪个数的识别准确率有所下降,但是总体上基本保持在了80%以上,说明算法在目标跟踪个数的识别上也具有较好的抗噪性能。
4 结束语
准确识别敌方雷达的工作状态对于威胁告警和电子对抗决策具有重要意义。本文以相控阵雷达为主要研究对象,从雷达资源调度分析出发,针对相控阵雷达工作状态识别展开研究,提出了基于脉冲幅度统计直方图的快速识别方法。首先,引入了一种改进的统计直方图方法,并对雷达脉冲幅度作统计分析,通过峰值门限检测的方法进行跟踪状态初判,然后综合利用数据率和平均单次驻留时间进行精确识别。仿真结果表明:本文方法对于短时间窗、小数据样本情况也能达到满意的识别准确率,并且具有较强的鲁棒性。可以为雷达告警器、电子情报(ELINT)侦察等多种应用场景提供参考。
[1] 胡子军,翟海涛. 基于任务驱动的机载相控阵雷达TAS调度算法[J]. 系统工程与电子技术, 2017, 39(3):536-541.
[2] 张洁,吴迪,朱岱寅. 一种机载/弹载阵列雷达前视超分辨成像算法[J]. 雷达科学与技术, 2018, 16(2):119-124.
ZHANG Jie, WU Di, ZHU Daiyin. A Forward-Looking Super-Resolution Imaging Algorithm for Airborne/Missile-Borne Array Radar[J].Radar Science and Technology,2018, 16(2):119-124.(in Chinese)
[3] 熊维毅,史小伟,余志斌,等. 量子遗传算法在对抗资源分配中的应用[J]. 电子信息对抗技术,2016, 31(4):52-57.
[4] 吴悦,张劲东,张杰,等. 认知雷达干扰和旁瓣均衡抑制的波形设计[J]. 雷达科学与技术,2018, 16(1):61-67.
WU Yue, ZHANG Jindong, ZHANG Jie, et al.Waveform Design for Equally Suppressing Interference and Sidelobes in Cognitive Radar[J]. Radar Science and Technology, 2018, 16(1):61-67. (in Chinese)
[5] 刘俊江. 机载火控雷达工作模式识别[J]. 电子测量技术,2016, 39(2):131-133.
[6] 王玉冰,程嗣怡,周一鹏,等. 参数寻优LSSVM算法在机载火控雷达工作模式判定中的应用[J]. 空军工程大学学报(自然科学版), 2017, 18(3):49-53.
[7] 王星,王志鹏,呙鹏程,等. 应用D-S证据理论的雷达工作模式特征层融合识别[J]. 空军工程大学学报(自然科学版),2016, 17(4):35-40.
[8] 李辉,郑坤,金炜东,等. 基于多层次建模的机载相控阵雷达工作模式识别[J]. 电子信息对抗技术, 2016, 31(4):1-5.
[9] 张光义. 相控阵雷达原理[M]. 北京:国防工业出版社, 2009:203-206.
[10] AYAZGOK S, ERDEM C, OZTURK M T, et al. Automatic Antenna Scan Type Classification for Next-Generation Electronic Warfare Receivers[J]. IET Radar Sonar & Navigation, 2018,12(4):466-474.
[11] KAUPPI J P, MARTIKAINEN K, RUOTSALAINEN U. Hierarchical Classification of Dynamically Varying Radar Pulse Repetition Interval Modulation Patterns[J]. Neural Networks,2010,23(10):1226-1237.
