0 引言
功率分配器简称功分器,作为一种无源微波器件,在相控阵雷达等微波系统以及微波电路中有着广泛的应用[1-3]。随着宽带、超宽带应用需求的日益迫切,宽带功分器也成为各种宽带电子系统中不可缺少的关键部件。
现有宽带功分器的研究主要集中在各输出端口等功率分配的宽带等分功分器。如文献[4]在分析了常规方法的缺陷后,提出了一种基于MATLAB程序的多项式化简方法,实现了任意带宽的切比雪夫阻抗变换器参数的快速计算,但该方法针对宽带等功分器,没有给出宽带不等功分器的设计。文献[5]通过ADS和HFSS软件联合仿真的方法,设计了一种1~18 GHz超宽带等分功分器,但没有给出传输线阻抗的计算方法。文献[6]采用粒子群优化设计方法得到了电路阻抗等参数,适用于阻抗变换级数较少的情况,当级数增多、同时要求不等功率分配时效果待斟酌。
目前,输出端口不等功率分配的宽带不等分功分器简洁有效的设计方法未见报道。为此本文提出了一种基于切比雪夫变换的超宽带功分器设计方法,可以根据功分器输出端口的功率分配比要求和工作带宽要求,采用切比雪夫多项式来计算得到电路各级阻抗参数,从而实现不同功分比要求和不同带宽要求的超宽带功分器的快速设计。
1 超宽带功分器阻抗变换设计方法
对于普通的两路Wilkinson功分器,如图1的单级两路功分器原理示意图,从总端口1进入的功率P1被分为P2和P3由两路输出端口2和3输出。其中,Z0是总口传输线阻抗,Za和ZA是端口2的两段传输线阻抗,Zb和ZB是端口3的两段传输线阻抗,R是隔离电阻。
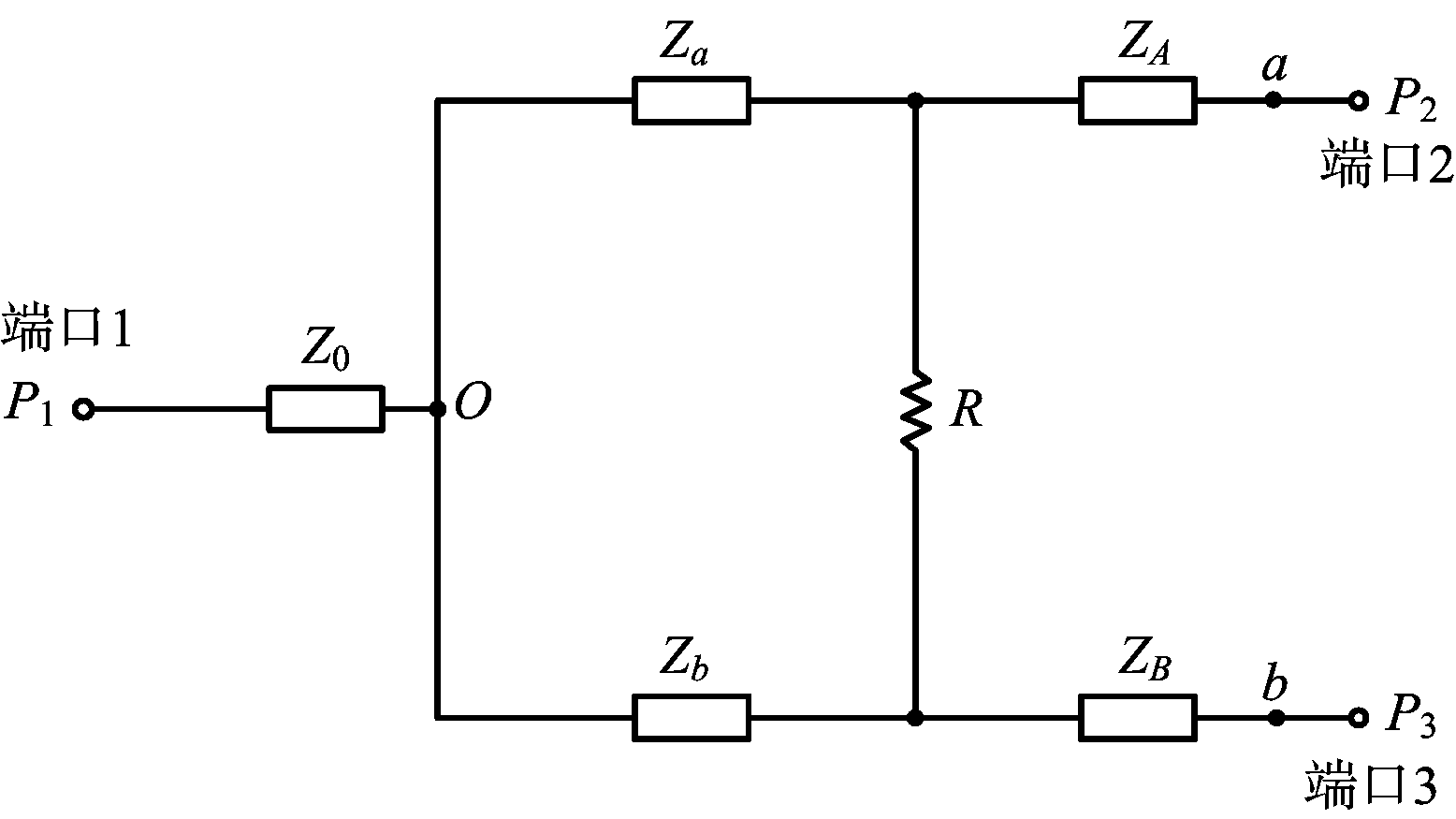
图1 单级不等分功分器原理示意图
对于图1中的单级不等分功分器,设a路传输线是从总端口1处的O点到输出端口2处的a点(即包含Za和ZA),b路传输线是从总端口1处的O点到输出端口3处的b点(即包含Zb和ZB)。当b和a两路之间的功率分配比为K2时,设P3=K2P2,则有ZA=K2ZB,Za=K2Zb。特别地,当K2=1时,即为等分功分器。
设由图1中的O点向a路看入的输入阻抗为Zain,由O点向b路看入的输入阻抗为Zbin,同样需要满足Zain=K2Zbin。则在O点位置有如下关系式:
![]()
(1)
将Zain=K2Zbin代入式(1),得
Zain=(1+K2)Z0
(2)
![]()
(3)
考虑到图1中的输出端口和外电路相连接,此时负载阻抗等于Z0,为使Z0变换到ZA和ZB,可分别通过一段1/4波长变阻器ZAT和ZBT来实现,因为ZA=K2ZB,为了使两个阻抗值较合理,可取ZA=KZ0,ZB=Z0/K。于是![]() 由此可得
由此可得![]()
为了满足宽频带的需求,基于切比雪夫阻抗变换,将输入阻抗Zain变换到ZA,或者将输入阻抗Zbin变换到ZB,阻抗变换比均为(1+K2)/K。为此采用了多级1/4波长阻抗变换,从阻抗ZaN和ZbN分别逐级变换到阻抗Za1和Zb1,以得到超宽带阻抗匹配,从而实现功分器的超宽带特性,原理示意图见图2。在两条支路之间相对应的每一级1/4波长阻抗变换连接处,跨接有隔离电阻Rn(n=1,2,…,N),以用于实现两条支路之间良好的隔离。
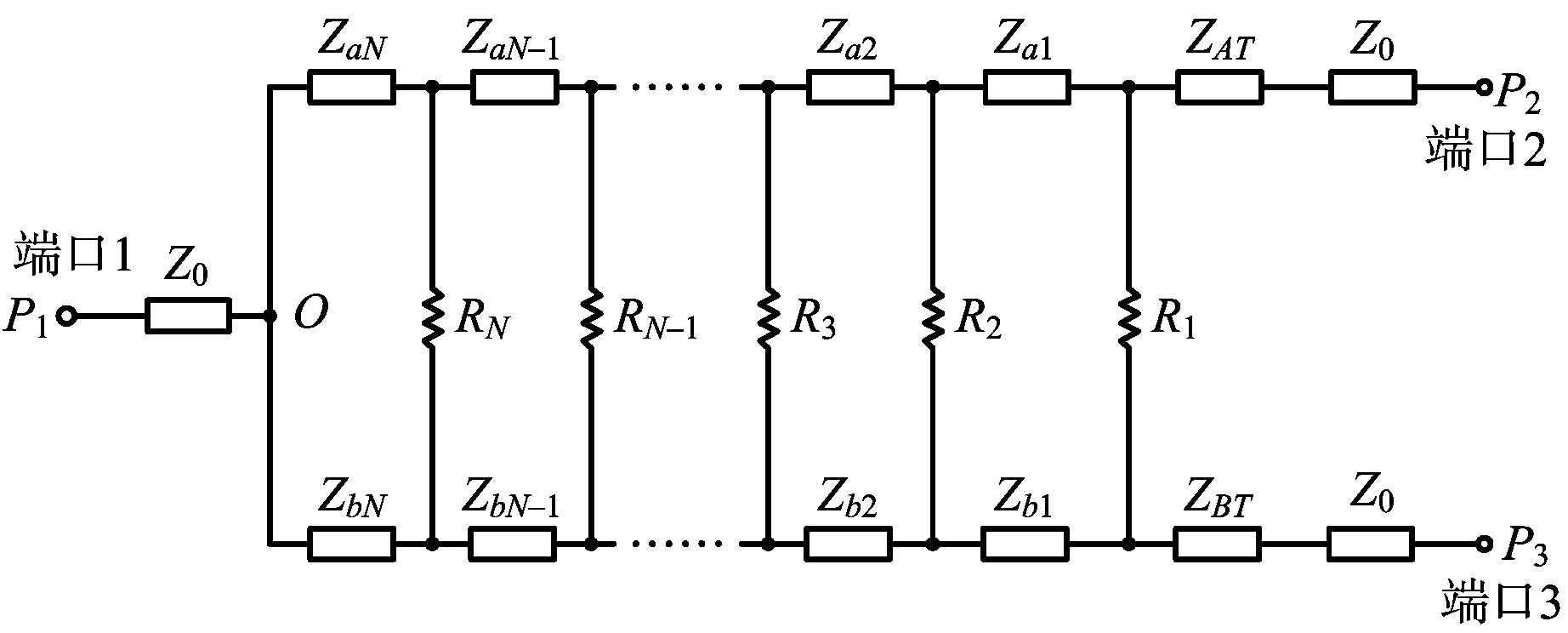
图2 N级超宽带不等分功分器原理示意图
这里考虑从Zain变换到ZA,另一路的计算推导步骤同理。对于多级阻抗变换后的原理图2,有ZaN=K2ZbN,ZaN-1=K2ZbN-1,…,Za1=K2Zb1。
对于N级变换,总的反射系数可表示为
Γ(θ)=2e-jNθ[Γ0cosNθ+Γ1cos(N-2)θ+…+
Γncos(N-2n)θ+…+0.5ΓN/2]
(4)
式中,N为偶数,或者表示为
Γ(θ)=2e-jNθ[Γ0cosNθ+Γ1cos(N-2)θ+…+
Γncos(N-2n)θ+…+Γ(N-1)/2cosθ]
(5)
式中,N为奇数。
使Γ(θ)正比于切比雪夫多项式TN(secθm·cosθ)来进行通带综合,即令
Γ(θ)=Ae-jNθTN(secθmcosθ)
(6)
这里N就是变换的级数。
式(6)中的系数A为
(7)
设通带内的最大反射系数幅值为Γm,则有
Γm=|A||TN(secθmcosθ)|max=|A|
(8)
结合式(7)和式(8),可得
(9)
于是,可以得到
(10)
另外,切比雪夫多项式Tn(secθmcosθ)有如下形式:
T1(secθmcosθ)=secθmcosθ
(11)
T2(secθmcosθ)=sec2θm(cos2θ+1)-1
(12)
其他高阶切比雪夫多项式可用式(13)求出:
Tn(secθmcosθ)=2secθmcosθTn-1(secθmcosθ)-
Tn-2(secθmcosθ)
(13)
式中,n=3,4,…,N。
用上述切比雪夫多项式对式(6)中的TN(secθmcosθ)进行展开,然后令其中的cos(N-2n)θ项与式(4)或式(5)中的对应项相等,可以得到各级反射系数Γn。另外,有关系式Γ0=ΓN,Γ1=ΓN-1,Γ2=ΓN-2,…。
又:
(14)
式中,当n=0时,Za0=ZA。
对于多级阻抗匹配,Γn较小,于是式(14)可以简化为
(15)
由此可以得到相邻各级阻抗变换之间的关系式:
Zan+1≈e2ΓnZan
(16)
由上式即可得到各级阻抗变换段的阻抗值。
2 超宽带功分器阻抗变换设计实例
采用上述方法,设计一个2~8 GHz频带范围的超宽带不等分功分器,两路输出端口之间的功率分配比为K2=1.5。
为了满足要求频段带宽要求,采用4级切比雪夫变换来设计超宽带功分器,即N=4,于是根据式(4)有
Γ(θ)=2e-j4θ[Γ0cos4θ+Γ1cos2θ+0.5Γ2]
(17)
根据式(6)、式(11)、式(12)和式(13)可得
Γ(θ)=Ae-j4θ[sec4θm(cos4θ+4cos2θ+3)-
4sec2θm(cos2θ+1)+1]
(18)
结合式(17)和式(18),令两式中的cos4θ和cos2θ对应项分别相等,可得
Γ0=0.5Asec4θm
(19)
Γ1=2A(sec4θm-sec2θm)
(20)
Γ2=A(3sec4θm-4sec2θm+1)
(21)
令Γm=0.03,于是根据式(7)、式(8)和式(9)有A=0.03。又,此时阻抗变换比为(1+K2)/K=2.041,根据式(10)可得secθm=1.330。
因此,根据式(19)、式(20)和式(21)有Γ0=0.047 0,Γ1=0.081 7,Γ2=0.099 5,Γ3=Γ1=0.081 7,Γ4=Γ0=0.047 0。
将Za0=ZA=KZ0代入式(16),然后由式(16)依次可得Za1=67.27 Ω,Za2=79.21 Ω,Za3=96.65 Ω,Za4=113.80 Ω。
根据Zan=K2Zbn关系式可得Zb1=44.85 Ω,Zb2=52.81 Ω,Zb3=64.43 Ω,Zb4=75.87 Ω。
根据![]() 可得ZAT=55.33 Ω,ZBT=45.18 Ω。
可得ZAT=55.33 Ω,ZBT=45.18 Ω。
3 超宽带功分器建模仿真
为了验证上述设计,建立了一个超宽带不等分功分器模型,如图3所示。设计时采用微带线这种传输线形式,微带板选用Rogers5880介质板,介电常数为2.2,介质板厚度为0.508 mm。根据上节计算得到的各级阻抗值建立模型,各隔离电阻值R1=680 Ω,R2=330 Ω,R3=200 Ω,R4=100 Ω。

图3 超宽带不等分功分器模型图
使用HFSS软件进行仿真,对模型中的各段阻抗线宽和线长进行微调,经仿真优化后得到各端口驻波比曲线、功分器输出端口的幅度曲线、相位一致性曲线和输出端口之间的隔离度曲线,分别见图4、图5、图6和图7。

图4 功分器各端口驻波比仿真曲线

图5 功分器输出端口幅度仿真曲线
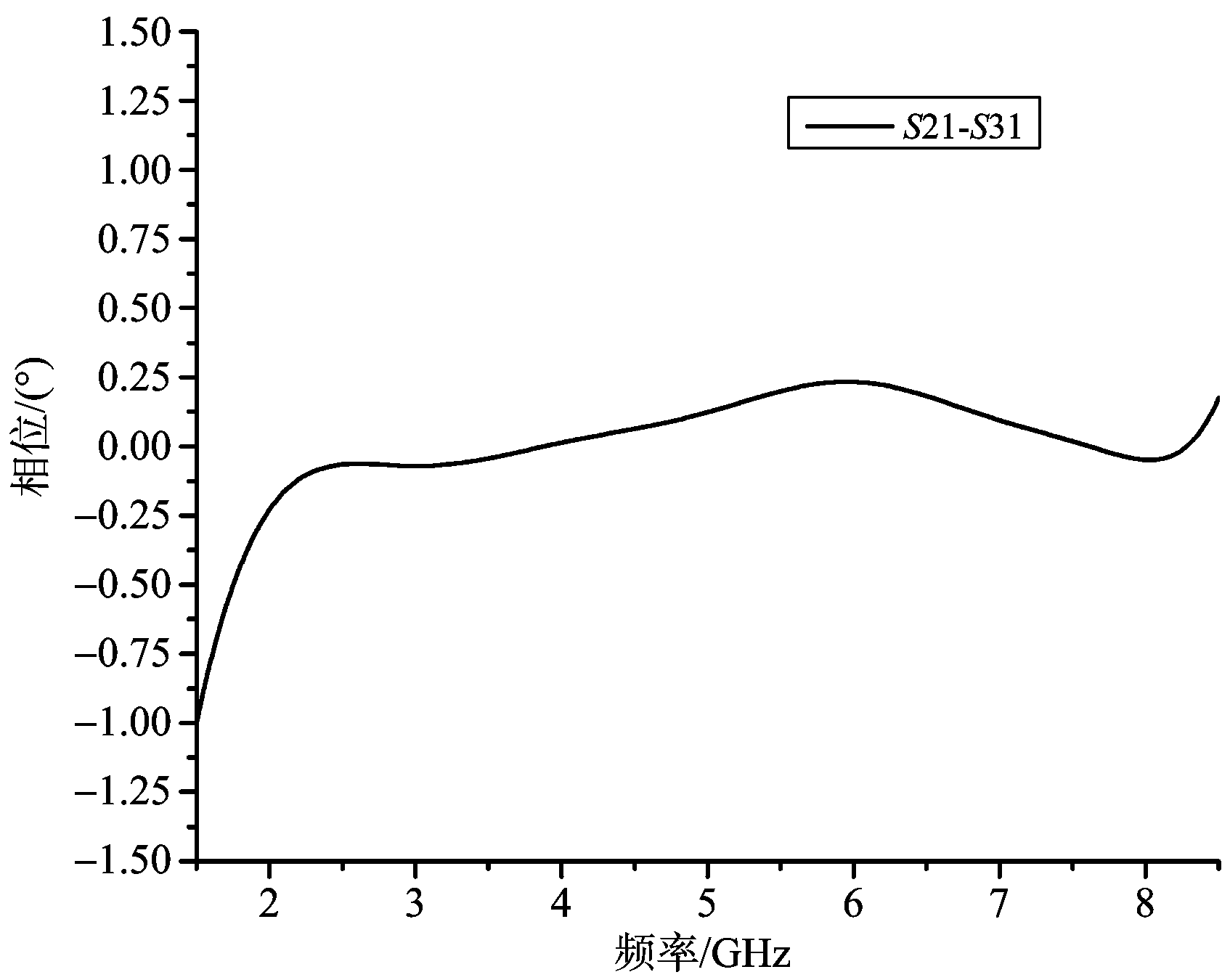
图6 功分器输出端口相位一致性仿真曲线
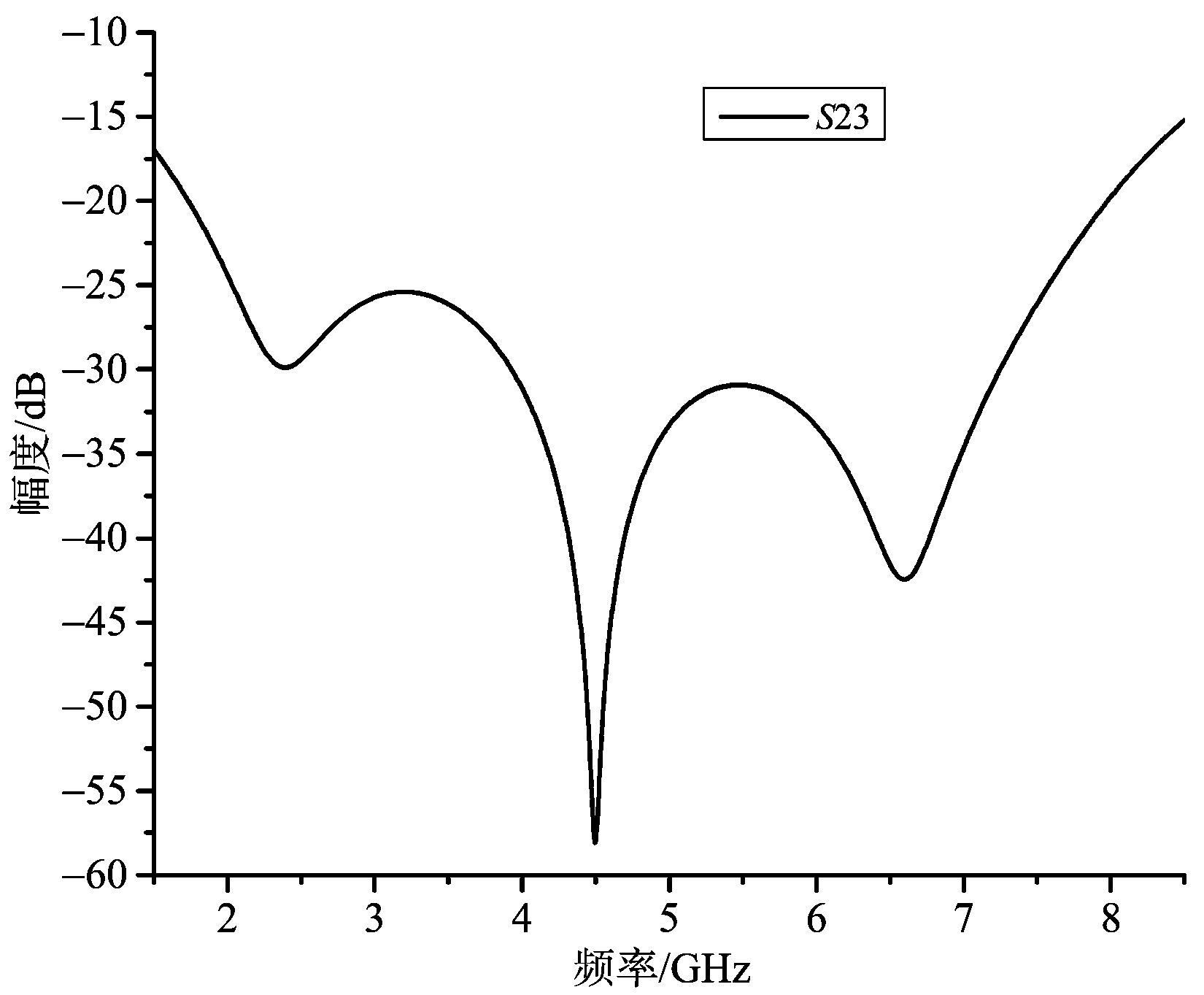
图7 功分器输出端口隔离度仿真曲线
根据仿真曲线,在2~8 GHz频段范围内,由图4可见,各端口的驻波比小于1.27;根据图5输出端口3的幅度S31和输出端口2的幅度S21结果可知,输出端口3和2之间的功率分配比在1.47~1.54之间,和设计要求的功率分配比1.5符合很好;同时由图6可知,输出端口3和2之间的相位一致性优于±0.3°;另外由图7可知,输出端口3和2之间的隔离度S23小于-19.7 dB。可见该超宽带不等分功分器在2~8 GHz的四倍频段范围内实现了较好的指标,验证了本文设计方法的可行性。
4 结束语
根据功分器输出端口的功率分配比,得到阻抗变换比,然后根据带宽要求选择变换的级数,再采用切比雪夫多项式来计算电路各级阻抗参数,实现超宽带功分器的快速设计。采用此方法设计了一个超宽带不等分功分器,两路输出端口之间的功率分配比为K2=1.5,在2~8 GHz宽达四倍频段范围内实现了较好的指标。另外,根据工作带宽要求,该设计方法可以灵活调整变换级数;与此同时,输出端口的功率分配比在一定范围内还可以连续设计。本文给出了一个解决超宽带不等分功分器难以设计的问题的方法,同样也适用于超宽带等分功分器的设计,具有一定的工程实用价值。
[1] WILKINSON E J. An N-Way Hybrid Power Divider[J]. IRE Trans on Microwave Theory and Techniques, 1960, 8(1):116-118.
[2] 卢晓鹏, 赵怀成, 赖清华. 一种X波段宽带低副瓣微带阵列天线设计[J]. 雷达科学与技术, 2013, 11(2):219-222.
LU Xiaopeng, ZHAO Huaicheng, LAI Qinghua. Design
of an X-Band Microstrip Array with Wideband and Low Sidelobe[J]. Radar Science and Technology, 2013, 11(2):219-222. (in Chinese)
[3] GUO Yingjiang, TANG Xiaohong, XU Kaida. Ultra-Wideband Power Divider with a Controllable Notched Band[J]. Electromagnetics, 2016, 36(3):214-223.
[4] 金辉, 羊恺, 张天良. 宽带Wilkinson功分器综合公式的缺陷与改进[J]. 微波学报, 2014, 30(2):65-69.
[5] 杜姗姗, 杨青慧, 张怀武. 1~18 GHz超宽带功分器的设计[J]. 压电与声光, 2017,39(4):498-500.
[6] 武欢欢, 陈明, 张延冬, 等. 宽带Wilkinson功分器的粒子群优化设计[J]. 强激光与粒子束, 2018,30(3):43-47.
