0 引言
脉冲压缩是现代雷达广泛采用的技术之一。线性调频(LFM)和相位编码是较常用的脉压信号形式,不过这些形式的信号有其固有的缺点,就是匹配滤波器输出的距离旁瓣太高。实际应用中为了压低距离旁瓣,常在脉冲压缩中进行加窗或其他预失真处理,但这引入了信噪比损失和主瓣展宽,将在一定程度上降低系统的灵敏度。而采用非线性调频可得到较低的旁瓣电平,又可避免因加权所引起的失配损失,这项损失的消除可以在相同的发射功率下获得更远的探测距离,因而在发射功率和探测距离要求比较苛刻的应用中具有重要的意义[1-3]。
1 窗函数法设计非线性调频信号
非线性调频信号的产生相比线性调频信号复杂,其模型众多,目前还不能通过精确的数学模型来设计非线性调频信号,实际中都采用近似的方法。目前比较经典的非线性调频信号设计方法有以下两种:一种是通过线性调频信号和正弦调频信号组合的方式形成S型调频曲线,然后根据公式求出非线性调频信号的群时延函数,再求群时延函数的反函数来得到非线性调频信号的频率调制函数;另一种更经典和常用的方法是窗函数法,它根据信号的自相关函数,运用相位逗留原理来设计非线性调频波形。衡量脉冲压缩雷达波形好坏的一个非常重要指标是信号的自相关性能,其要求是距离旁瓣越低越好,根据自相关函数设计波形就能保证这一点,而信号的功率谱和自相关函数存在一一对应的关系,所以问题就转化为根据信号的功率谱来设计非线性调频信号。假设所设计的非线性调频信号s(t)=a(t)[expjθ(t)],S(f)是其频谱函数,由匹配滤波理论知,经过脉冲压缩后输出信号的频谱为
So(f)=|S(f)|2
(1)
由相位逗留原理可知,信号频谱和调频斜率之间的关系如下:
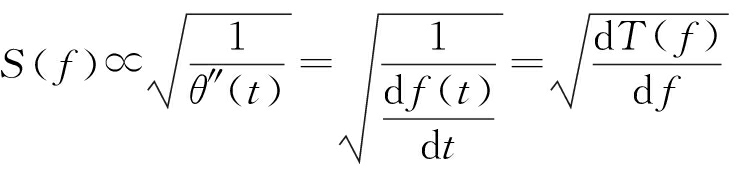
(2)
式中,T(f)为群延迟,它是f(t)的反函数。式(2)表明,若选定脉冲压缩后信号输出频谱函数为W(f),则![]() 因此,只需对W(f)积分便可得到群时延函数:
因此,只需对W(f)积分便可得到群时延函数:
T(f)=K![]() W(v)dv
W(v)dv
(3)
式中,K为常系数。当要求非线性调频信号带宽为B,时宽为T时,有
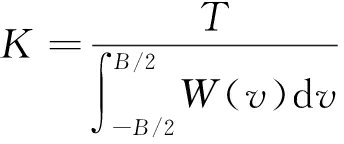
(4)
因为T(f)为f(t)的反函数,根据反函数定义得所设计的非线性调频信号的频率函数如下式:
f(t)=T-1(f)
(5)
根据信号瞬时频率和相位的关系得所设计非线性调频信号的相位函数为
θ(t)=2π![]() f(v)dv
f(v)dv
(6)
根据以上相位函数便可以设计出脉压后输出信号频谱为W(f)的非线性调频信号。
下面以blackman窗函数为例详细说明设计NLFM信号的具体步骤:
1) 选择blackman窗作为非线性调频信号脉压输出信号的频谱函数,窗函数表达式如下:
W(f)=0.42+0.5cos(2πf/B)+
0.08cos(4πf/B)
-B/2≤f≤B/2
(7)
2) 根据相位逗留原理,对上述W(f)积分得
T(f)=0.42Kf+(0.25KB/π)sin(2πf/B)+
(0.02KB/π)sin(4πf/B)
-B/2≤f≤B/2
(8)
由T(f)|f=B/2=T/2得常数K=(T/B)/0.42,代入式(8)得
T(f)=(T/B)f+(0.595 2T/π)sin(2πf/B)+
(0.046 7T/π)sin(4πf/B)
-B/2≤f≤B/2
(9)
3) 频率函数为群延时的反函数,求T(f)的反函数得到非线性调频信号的频率调制函数。
4) 求相位函数,对第3步求得的频率函数积分即可得到非线性调频信号的相位函数。
5) 完成非线性调频信号波形设计,由第4步得到的非线性调频信号相位函数可以直接得到所要设计的非线性调频信号,其实部波形及频谱如图1所示。
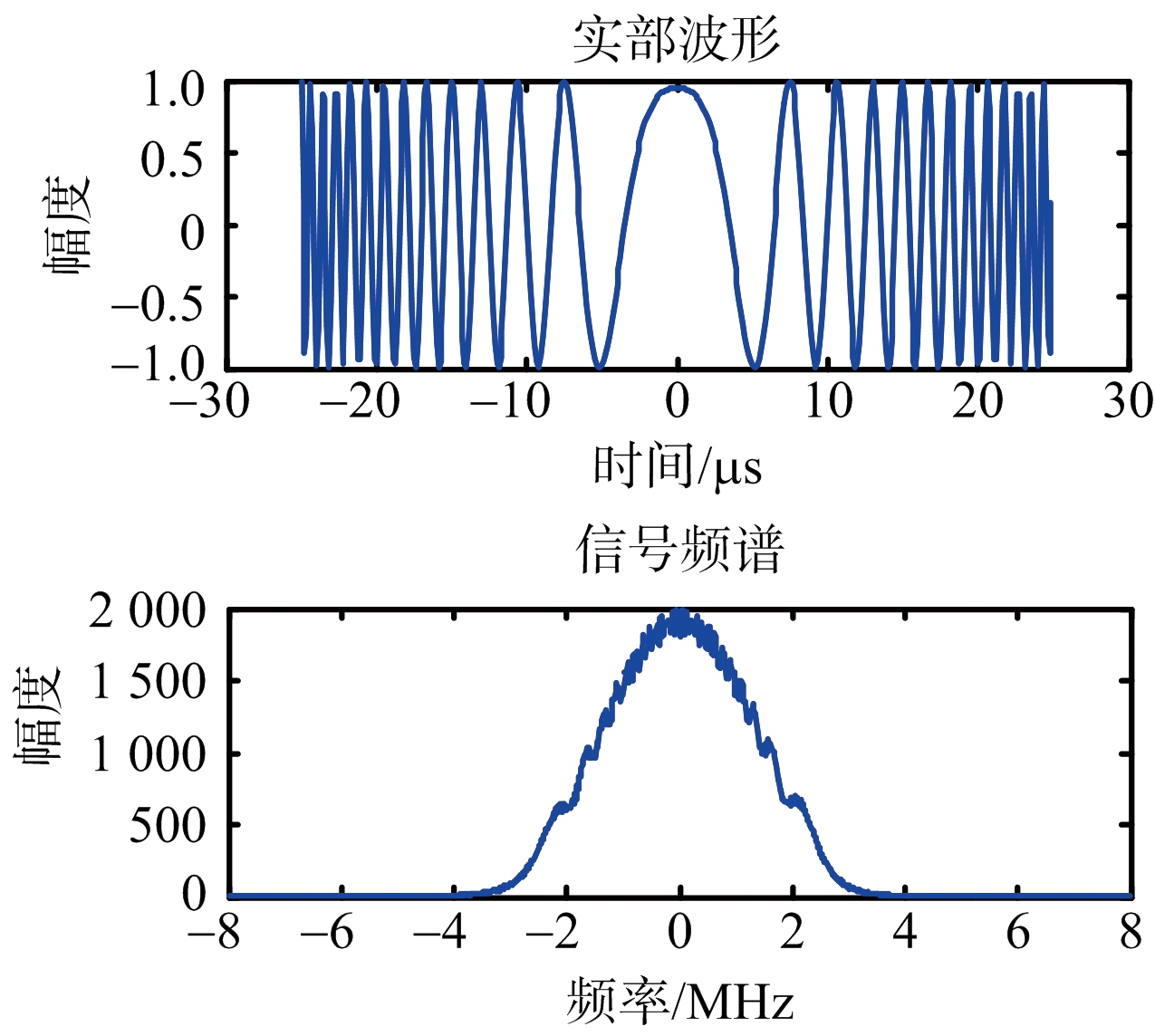
图1 非线性调频信号实部及频谱
该方法设计的非线性调频信号虽然没有因失配脉压引起的损失,但其第一副瓣电平较LFM信号加窗高很多。例如仿真参数分别为:信号时宽50 μs,信号带宽4 MHz,采样率8 MHz。采用布莱克曼窗加权线性调频信号的脉压结果的旁瓣为 -47 dB左右,而同样参数条件下,用布莱克曼窗函数设计出的非线性调频信号脉压结果其距离旁瓣却只有-37.76 dB,且在时带积低的情况下峰值旁瓣电平更高。究其原因,相位逗留原理本身存在近似,而且其调频函数很难得到显示函数表达式,一般只能通过插值或数据拟合的办法得到,通过数值方法解非线性方程和数值积分解求相位函数,这些过程都存在误差,故得到的波形质量不理想,有进一步提升的空间。
2 GASA优化算法
文献[4]提出了一种利用遗传算法优化设计非线性调频信号的方法,并与动态优化算法进行了比较,其调频函数的构造方法仍然基于泰勒窗函数,其迭代次数由动态优化算法的106数量级减少到102数量级,但其收敛性仍有较大的改进空间。
遗传算法和模拟退火算法是针对多参数非线性优化问题的有效方法。模拟退火算法因为是单点搜索,优化过程不具备并行性,每时刻仅保留一个优化结果,缺少历史信息,收敛速度比较慢,而且优化过程中容易因为温度控制不理想而得不到优良解。而遗传算法存在着早熟的现象,很容易收敛到局部最优解,或者在最优解附近震荡。针对上述遗传算法和模拟退火算法各自的缺点,同时兼顾了遗传算法并行搜索和模拟退火算法概率突变的优点,将模拟退火的思想应用于遗传算法中,文献[5]采用了改进的GASA算法,其流程框图如图2所示。
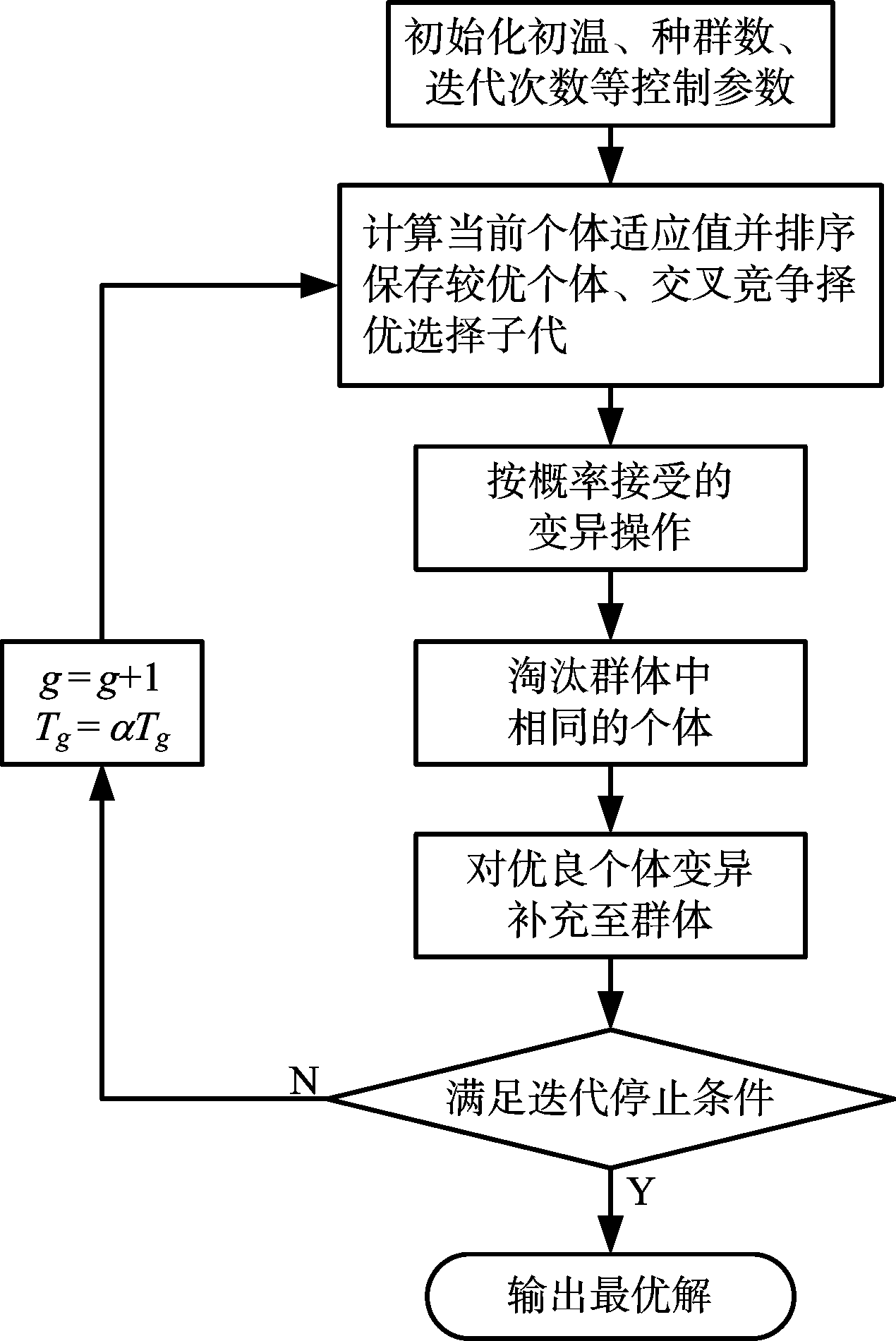
图2 GASA算法流程图
GASA优化算法的大体步骤描述如下:
1) 在优化参数初始化的时候选择大体经过优化筛选了的初始种群,而不是简单地随机产生初始种群,先随机产生大量个体,然后在其中挑选出一些适应度较大的个体作为初始种群。不同于传统的SA算法给出一较高的初始温度,以使得最初的随机搜索很充分,实际上进行了许多冗余的迭代,本算法按照下式确定优化的初始温度:
(10)
式中,fmin,fmax表示初始种群的最小和最大适应度值,pr0表示最差的接受概率。
2) 针对SA算法在选择复制操作过程中有可能丢失优良个体的可能,引入了一种最优保存机制,即把较优的个体直接送入下一代参与竞争,这里较优个体数为pk*popsize,其中popsize为种群总个数,通常取0.05≤pk≤0.2。
3) 针对遗传算法存在的选择压力,将模拟退火思想引入到GA算法,加入小范围择优竞争的机制。不同于遗传算法的按概率进行交叉和变异操作,GASA算法对所有个体平等参与交叉和变异,并且把交叉和变异产生的子代和父代竞争,如果子代适应度大于父代,则直接送入下一代队列,否则按一随机概率接收恶化解,进化初期的温度较高,接受一定数量的劣质解有助于保持优化种群的多样性,而且可以防止在局部收敛。随着进化过程的进行,温度可以逐渐降低以使接受劣质解的概率下降,这样有利于提高算法的收敛速度。
4) 在优化过程中,加入过滤相同个体的步骤,传统模拟退火算法在快接近最优解时,进化速度放缓或停止进化容易导致过早收敛的问题,因此在进化过程中过滤掉相同的个体有助于快速收敛到全局最优解。
5) 过滤掉相同个体后需要补充个体使种群总数保持不变,这里考虑从当代个体中较优的pk*popsize个个体中随机选择个体经过变异后,按照一定概率决定是否接受作为补充的新个体,直至个体数等于初始种群数,这样解决了种群缺乏多样性而陷入局部最优解的问题。
3 GASA算法优化设计NLFM信号
文献[6]指出泰勒函数调频曲线的特点,并将其推广到一般S调频函数,指出S调频函数应具有以下特点:它是以线性调频为基准上下摆动,以中心频率为原点的奇函数;此曲线的一阶导数为正,而二阶导数由负值向0再向正值单调连续增加;当接近脉冲的两个边界时,频率变化显著加快。
根据以上假设,文献[7]对参考函数f(α)=tan(πα)进行变形,构造出新的函数![]() 其中A,K1,K2为系数,并且满足0≤A<4,该函数满足S曲线的特点,可用于产生S曲线,当A=0时,即为常见的LFM信号,当A,K1,K2取得合适值时,令
其中A,K1,K2为系数,并且满足0≤A<4,该函数满足S曲线的特点,可用于产生S曲线,当A=0时,即为常见的LFM信号,当A,K1,K2取得合适值时,令![]() 再将整个函数乘以B,就得到时宽为T、带宽为B的S曲线函数f(t) 。脉压性能的3个重要指标是压缩后信号的距离旁瓣、主瓣展宽系数及信噪比损失,因此必须在A,K1,K2及BT四维空间搜索满足最佳脉压信号波形的参数。遗传算法虽然比较适合多参数的优化问题,但其迭代次数和收敛性仍有优化的空间。
再将整个函数乘以B,就得到时宽为T、带宽为B的S曲线函数f(t) 。脉压性能的3个重要指标是压缩后信号的距离旁瓣、主瓣展宽系数及信噪比损失,因此必须在A,K1,K2及BT四维空间搜索满足最佳脉压信号波形的参数。遗传算法虽然比较适合多参数的优化问题,但其迭代次数和收敛性仍有优化的空间。
4 算法仿真
1) 确定波形优化参数,本仿真取带宽B=4 MHz,脉宽T=50 μs,采样率fs=8 MHz,本仿真优化的目的为最小化最大副瓣电平,设最大副瓣电平为PSL,则优化的目标函数为E(X)= min(PSL),可取优化的适应度函数为![]() 约束条件为X∈D,其中Cmax为一较大常数,D为约束条件。
约束条件为X∈D,其中Cmax为一较大常数,D为约束条件。
2) 将![]() 中的A,K1,K2确定为优化参数,确定其取值范围为0≤A<4,-10<K1,K2<10,根据取值范围确定编码和解码规则,将3个参数量化为10位二进制表示,则可用30位二进制组合表示一组参数,称作一个染色体,其中的每位二进制编码作为一个基因,随机生成数量为1 000个染色体即30×1 000的二进制编码矩阵作为初始种群。种群数popsize=160,挑选适应度函数高的popsize个个体作为优化的初始种群,最差接受概率pr0=0.05,初始温度T0按照式(10)计算,温度控制系数α=0.99,停止迭代条件设为Tg=1,其中Tg=T0αg-1,g为进化代数,Tg为第g代的温度。停止条件也可以设置为达到最大迭代次数。择优保留比例pk=0.15,变异概率pm=0.08。
中的A,K1,K2确定为优化参数,确定其取值范围为0≤A<4,-10<K1,K2<10,根据取值范围确定编码和解码规则,将3个参数量化为10位二进制表示,则可用30位二进制组合表示一组参数,称作一个染色体,其中的每位二进制编码作为一个基因,随机生成数量为1 000个染色体即30×1 000的二进制编码矩阵作为初始种群。种群数popsize=160,挑选适应度函数高的popsize个个体作为优化的初始种群,最差接受概率pr0=0.05,初始温度T0按照式(10)计算,温度控制系数α=0.99,停止迭代条件设为Tg=1,其中Tg=T0αg-1,g为进化代数,Tg为第g代的温度。停止条件也可以设置为达到最大迭代次数。择优保留比例pk=0.15,变异概率pm=0.08。
3) 计算种群中每个染色体的适应度,按照从大到小排序,并选择前pk*popsize个较优个体直接进入下一代继续进化,对剩下的则采取交叉竞争进入下一代,大致过程为:随机选择当前种群中两个不同个体P1,P2,随机产生随机数2到29,执行单点交叉操作,记产生的子代个体为S1,S2, F(p)和F(s)分别表示父代和子代适应度的最大值,如果 F(s)大于F(p)则直接将子代中适应值大的个体送入下一代,否则按照概率: min(1,exp((F(s)-F(p))/T))>rand选择父辈中适应值较大的个体参与下一代进化。
4) 变异操作:对当前群体按变异概率pm=0.08变异(为了保证变异后仍然是满码集,变异操作在每个波形编码内部进行,即随机选择某个波形内的两个编码交换位置即可),变异后得到的个体按照概率min(1,exp((F(sm)-F(so))/T))>rand选择变异后个体,其中F(sm)和F(so)分别表示变异后和变异前个体的适应值。
5) 相同个体过滤删除操作:找当前群体基因相同的个体并从种群中淘汰。补充个体:因为删除操作,可能导致个体数小于初始群体数,按照上一步过滤的个体数自适应地补充新个体,使个体数等于初始群体数,其中补充的个体来源于当前较优个体通过变异得到,即对当前个体适应值排序后选择前J(J=pk*popsize=24)个较优个体进行变异。判断进化过程是否结束:若第g次迭代的温度Tg<1或进化代数g=G,则迭代结束,否则g=g+1,Tg=αTg继续进化过程。
图3为GASA算法随着迭代次数增加,每代不同个体适应度函数的平均值和最优值。
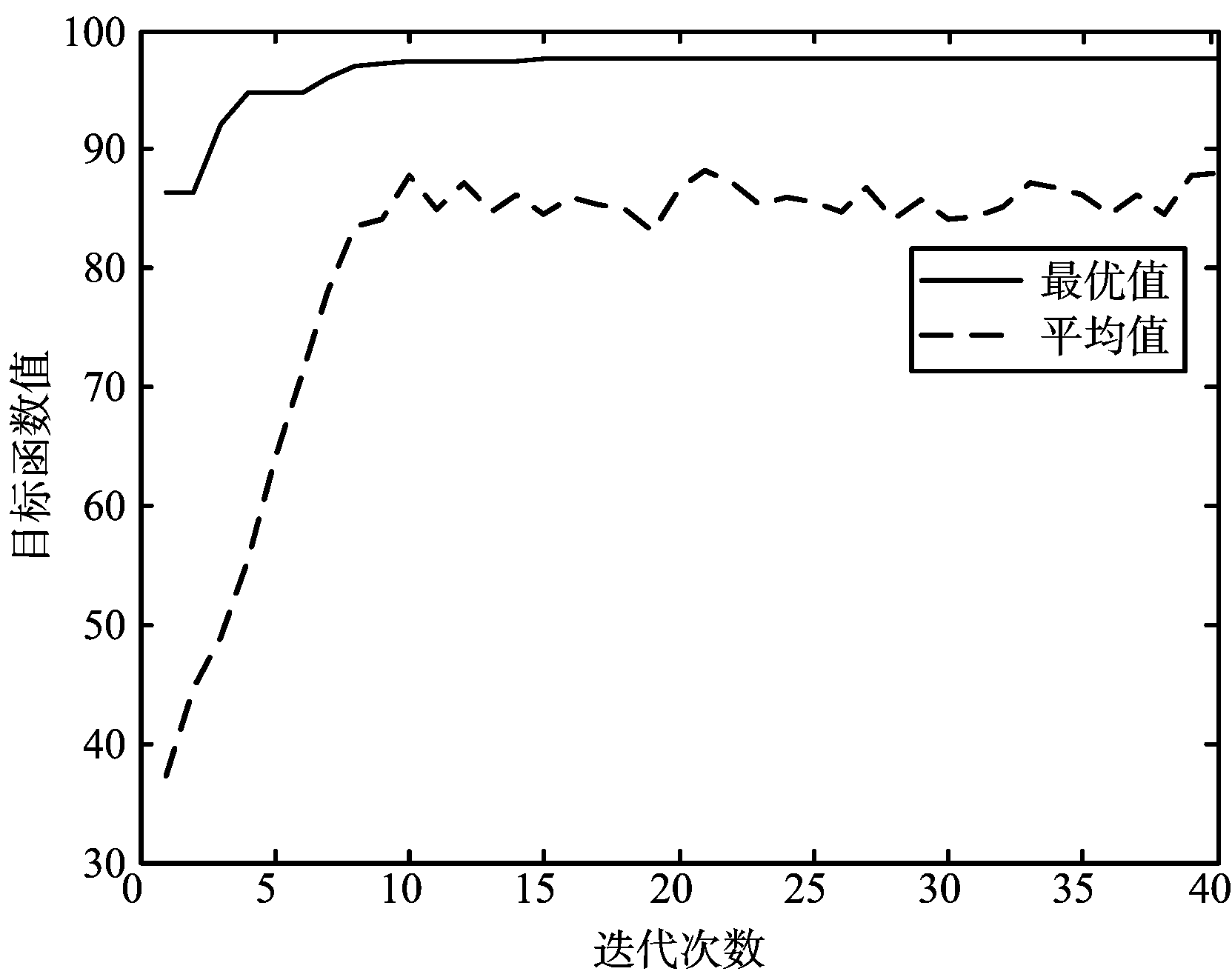
图3 适应度函数值收敛曲线
由图3可见,迭代次数10次左右优化的目标函数值已收敛,相比动态优化算法和遗传算法收敛速度有了明显提高。图4为通过优化得到的调频函数及其一、二阶导数的曲线。
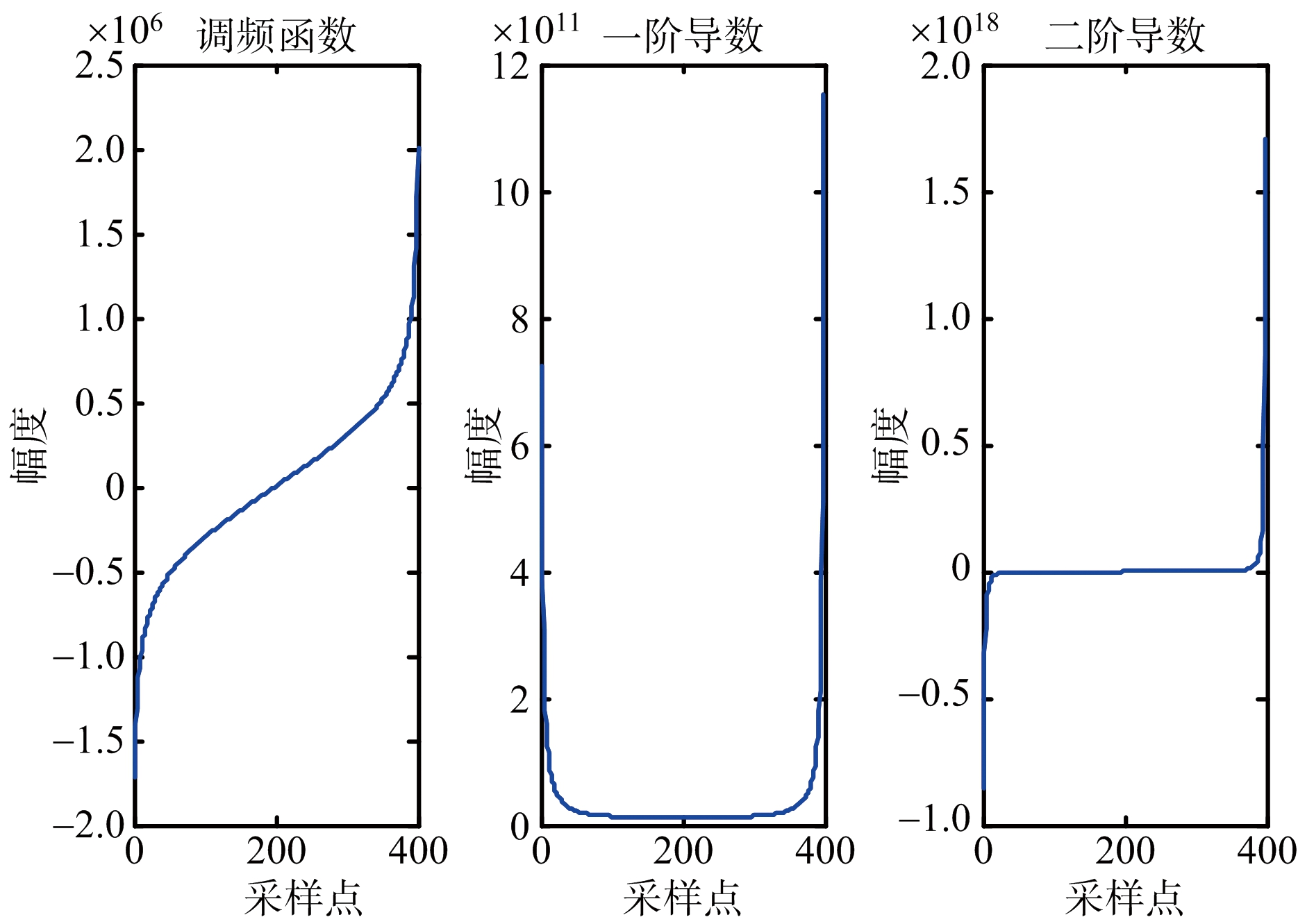
图4 调频函数及其一、二阶导数的曲线
由图4可知,经GASA算法优化得到的调频函数及其一、二阶导数满足上文提到的S曲线调频函数的特点。
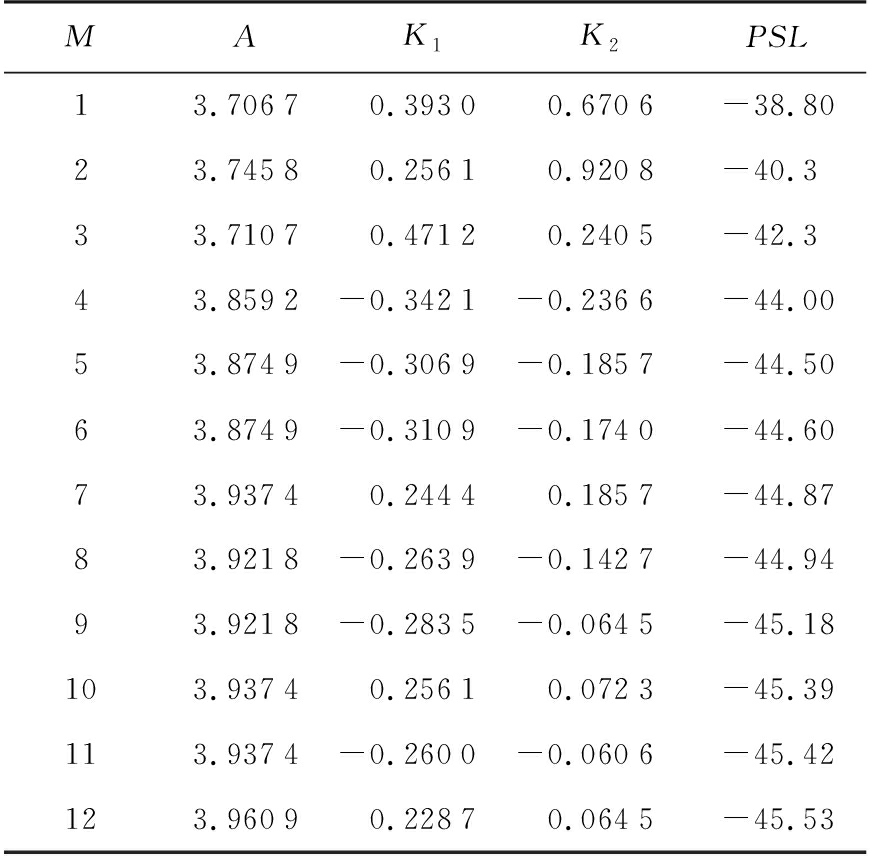
仿真中设信号带宽为4 MHz,采样率为8 MHz,信号时宽为50 μs,则信号点数为400点,脉压后信号共799点,设脉压后信号的模值为So,其中P是脉压后信号的峰值点,M表示主瓣底部的采样点数,因为非线性调频信号不存在线性调频信号的加窗损失,所以优化中只关心脉压后主瓣宽度和旁瓣电平的指标,则在优化![]() 过程中通过选择M值来折中决定主瓣宽度和旁瓣电平这两项指标。表1是选择不同M值时优化得到的A,K1,K2值以及PSL指标。
过程中通过选择M值来折中决定主瓣宽度和旁瓣电平这两项指标。表1是选择不同M值时优化得到的A,K1,K2值以及PSL指标。
在表1中当M=6时优化得到的NLFM波形和利用布莱克曼窗函数设计出的NLFM信号脉压后主瓣宽度相当,但峰值旁瓣电平可达-44.6 dB,较布莱克曼窗函数得到的-37.76 dB降低了约7 dB。而且其3 dB宽度内只存在3个采样点,在距离分辨率要求不是很严的场合,仍然可以满足要求。图5为采用GASA算法和窗函数设计的NLFM脉压波形对比。
表1 不同主瓣宽度下峰值旁瓣电平值
MAK1K2PSL13.70670.39300.6706-38.8023.74580.25610.9208-40.333.71070.47120.2405-42.343.8592-0.3421-0.2366-44.0053.8749-0.3069-0.1857-44.5063.8749-0.3109-0.1740-44.6073.93740.24440.1857-44.8783.9218-0.2639-0.1427-44.9493.9218-0.2835-0.0645-45.18103.93740.25610.0723-45.39113.9374-0.2600-0.0606-45.42123.96090.22870.0645-45.53
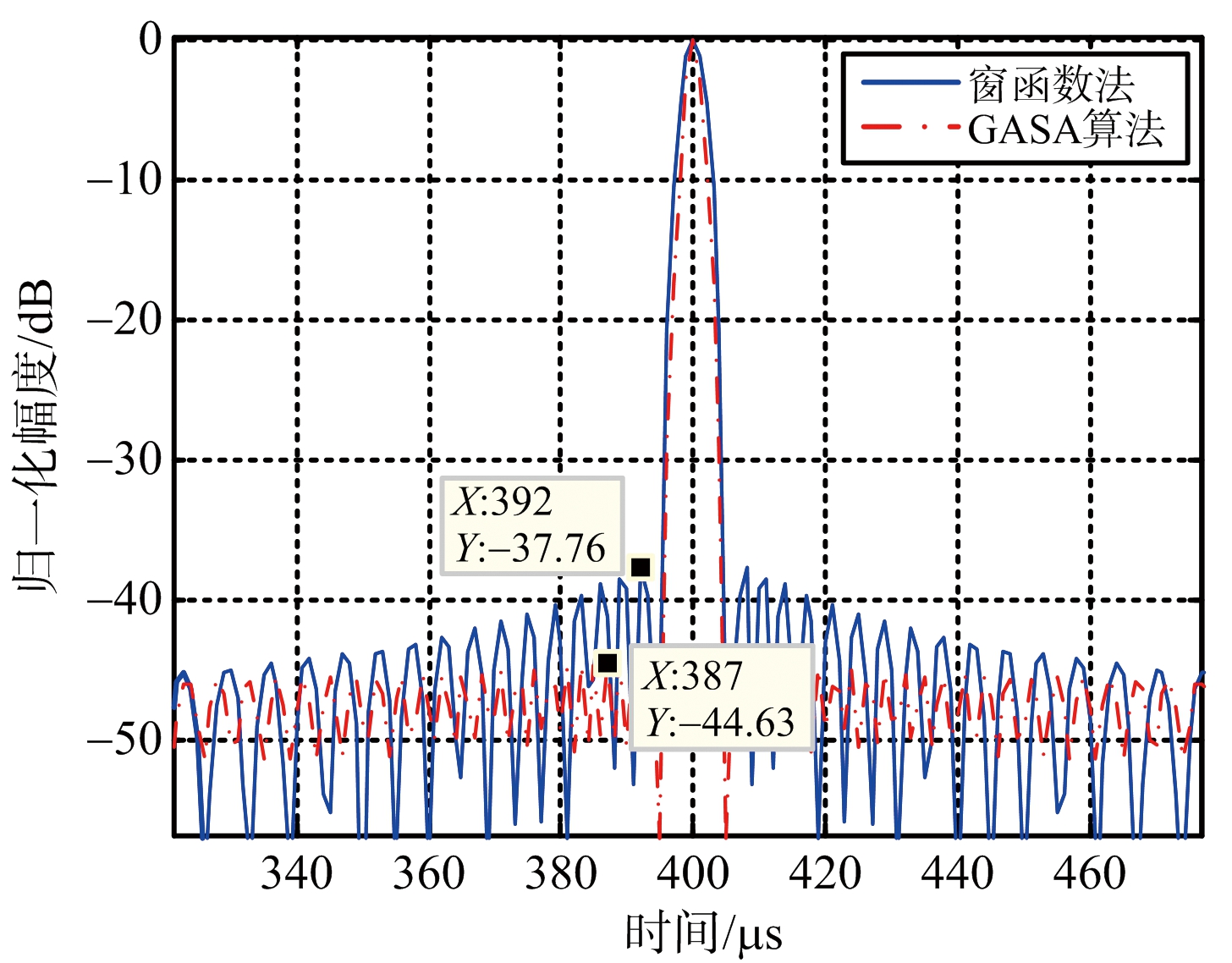
图5 两种方法设计的NLFM脉压结果
由图5可以看出,GASA算法设计的NLFM波形不但第一副瓣比传统窗函数法低,而且主瓣宽度更窄。
图6为经GASA算法优化设计的NLFM波形及其频谱,其幅度谱和线性调频信号加窗后频谱相似,但没有线性调频信号脉压时的加窗损失。
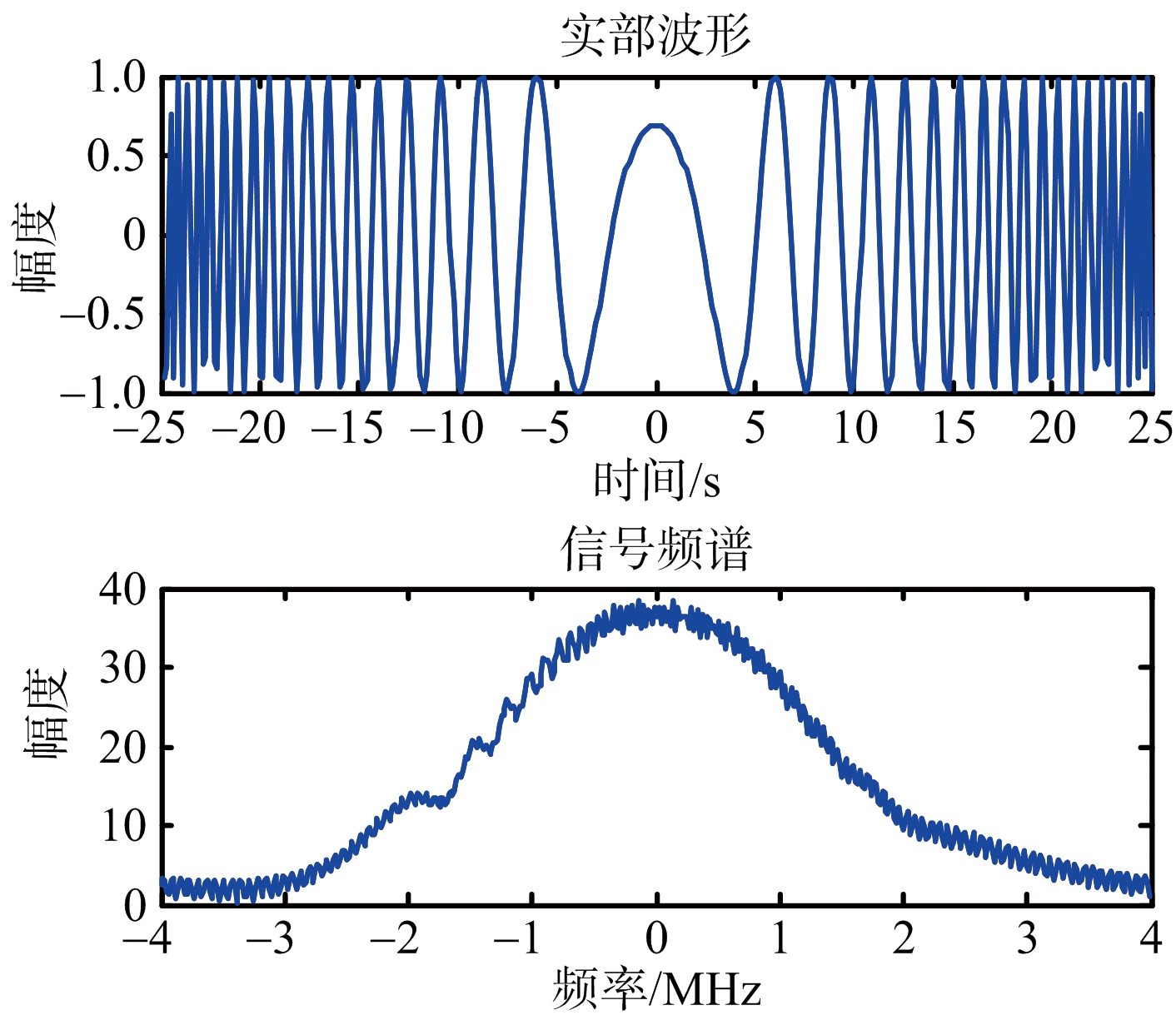
图6 NLFM实部波形及频谱
5 结束语
本文在讨论传统窗函数设计NLFM的基础上,分析了可用于设计NLFM波形的调频函数的特性,并用GASA算法优化设计了NLFM波形,与窗函数法相比其得到的波形脉压后峰值副瓣电平更低,与遗传算法及动态优化算法相比收敛速度更快。虽然设计的NLFM波形多普勒容忍性很低,但在跟踪雷达中,可以利用目标速度的先验信息,对被跟踪目标的多普勒进行补偿处理。
[1] 王传志,李学华,孙清,等.调频信号超低副瓣脉冲压缩算法[J].现代电子技术,2018,41(13):25-28.
[2] 王侠, 王进军, 杨战社. 基于三次样条插值的非线性调频雷达信号设计[J]. 山西大学学报(自然科学版), 2017,40(4):797-803.
[3] 张朝霞,刘杰,赵岩,等. 基于分段拟合的非线性组合调制雷达信号设计[J]. 计算机应用,2017,37(3):736-740.
[4] 杨志群,倪晋麟. 利用遗传算法优化非线性调频信号波形[J].现代雷达, 2000,22(1):44-49.
[5] 覃春淼.MIMO雷达波形设计[D].西安:西安电子科技大学,2013.
[6] 付启众,陈忠先. 一种超低副瓣非线性调频脉压信号的性能分析[J].雷达科学与技术,2007,5(1):60-64.
FU Qizhong, CHEN Zhongxian. Performance Analysis of an Ultra-Low Side Lobe Non-Linear Frequency Modulation Signal for Pulse Compression[J]. Radar Science and Technology, 2007,5(1):60-64. (in Chinese)
[7] 李康.非线性调频信号设计[D].西安:西安电子科技大学,2009.
