0 引言
无源雷达不需要特定的发射站,仅被动接收环境中已存在的机会照射源信号。由于不发射信号,无源雷达具有隐蔽性高、抗干扰能力强的优点;仅需接收装置,可以降低其成本,同时减小雷达系统的体积,使其配置更为灵活;利用其不产生电磁污染的优点,可以将其部署在大多数地区,扩大了无源雷达的应用场景[1-6]。近年来,随着机会照射源种类及数量的发展,无源雷达逐渐成为研究热点,相关研究工作日益增加[2,7-8]。
目前有研究的用于构成无源雷达的机会照射源可以分为陆地照射源与卫星照射源。其中,陆地照射源主要包括FM信号[9-11]、数字广播/电视信号(DAB/DVB-T)[12-15]、GSM信号[16-18]及WIFI信号[19-21]等。利用陆地照射源构成无源雷达的研究已较为成熟,已有包括美国的“沉默哨兵”系统[7,22-24]、德国的“PARADE”系统[25-26]及法国的“SINBAD”系统[27]在内的多种无源雷达系统被成功研制并投入实际应用。此外,由于卫星照射源覆盖范围广、不受地面疆界限制、工作状态稳定等的优势,国内外多家组织机构相继开展了以其作为机会照射源的无源雷达相关研究工作。其中,全球导航卫星系统(Global Navigation Satellite System, GNSS)由于其全球覆盖的特性,成为了研究重点[28]。
GNSS的发展为以此为照射源的无源雷达提供了客观条件。自从1958年美国军方开始研制全球卫星定位系统(GPS)以来,GNSS受到了全世界范围的广泛关注。目前主要的4个GNSS包括[29-32]:美国的GPS、俄罗斯的格洛纳斯系统(GLONASS)、欧盟的伽利略系统(GALILEO)以及中国的北斗系统。当这4个GNSS全部完成建设,实现全球范围的导航定位时,将为基于GNSS的无源雷达提供充分的信号来源,对其性能提供保障。
随着对海洋资源利用的增加,海面监视愈发受到重视。由于无源雷达全天时、全天候、代价低、隐蔽性好等优势,很适合被应用于岛礁、海上石油钻井平台或海面船只、低空气球上,实现对临近海域舰船等目标持续性监视。在选取适用于上述无源雷达的机会照射源时,陆地辐射源受其发射站位置的限制,发射信号不能完全覆盖海面区域,作为机会照射源是不适合的。而GNSS由于其全球覆盖的优势,能对海面目标进行照射。因此,以GNSS为机会照射源进行海面目标检测,是具有应用前景的。目前,国内外已有相关研究并取得相应的理论与实验研究成果。本文首先建立基于GNSS的无源雷达海面目标回波模型;然后介绍目前已有的基于GNSS的无源雷达海面目标检测的方法,并分析各方法的优缺点;最后对基于GNSS的无源雷达海面目标检测的应用方向进行展望。
1 海面目标回波模型
导航卫星的发射信号由“测距码+导航电文”调制到载波上构成,其典型结构可以表示为
s(t)=A·C(t)·D(t)·exp(j2πfct+φ)
(1)
式中,t为时间,A为信号振幅,C为信号测距码,D为调制在测距码上的数据码,fc为信号载波频率,φ为信号载波初相。
将基于GNSS的无源雷达应用于海面目标检测时,其构型如图1所示。发射站为导航卫星,接收站可以固定于海岸、岛礁或石油钻井平台,也可以置于海面船只或低空气球上,被动接收目标反射的机会信号。接收站具有两天线,其中,监视天线指向海面区域,接收海面目标反射回波;参考天线指向导航卫星,接收直达波,用于实现导航卫星与接收站之间的信号同步。所接收到的直达波与目标回波均为连续信号,对其进行正交解调,并根据等效脉冲重复频率(PRF)进行二维时域划分。提取直达波信号中的时延、多普勒、相位及导航码信息,用于构成参考信号。将目标回波与参考信号进行互相关处理,实现回波信号的距离向脉冲压缩,结果表示为[33]
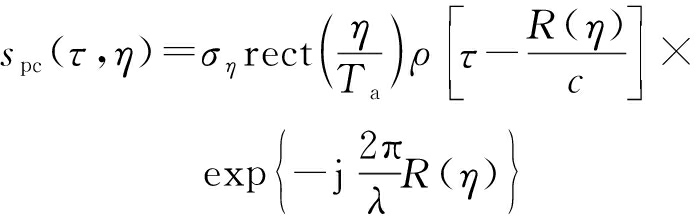
(2)
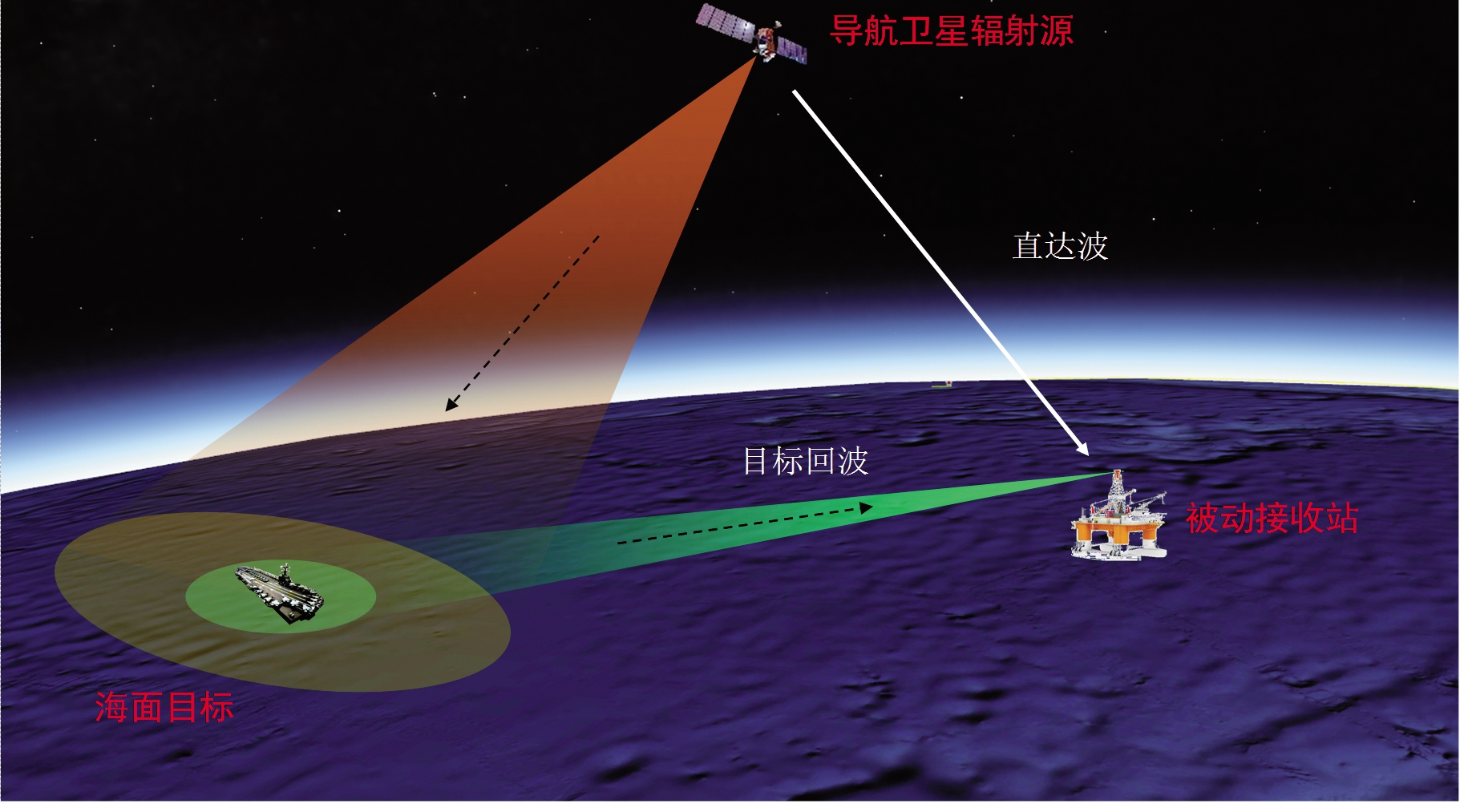
图1 基于GNSS的无源雷达构型图
式中:τ和η分别表示快时间与慢时间;ση表示目标的复散射率,其值随时间变化;Ta表示对目标的总观测时长;c表示光速;λ表示信号波长;R(η)=RT(η)+RR(η)-Rb(η)表示双基距离,RT(η),RR(η),Rb(η)分别为导航卫星距海面目标、海面目标距接收站、导航卫星距接收站的距离;ρ(·)表示回波信号脉冲压缩后的结果,其具体形式由接收的导航卫星信号中的测距码决定。
由于导航卫星运行能量来源于太阳能,其发射信号功率受限,通常其发射功率与天线增益之积为200 W[34]。同时,导航卫星位于中高轨道,与地球表面距离极远,以北斗系统中的中圆地球轨道(MEO)卫星为例,其轨道高度为21 528 km[35]。在上述参数条件下,可以计算得到GNSS信号在地球表面功率密度为-134.6 dBW/m2,极低的信号功率密度为无源雷达海面目标检测带来了挑战。当接收站接收到海面目标回波时,极低的信噪比使得目标被噪声所淹没,无法直接实现目标的检测。因此,基于GNSS的无源雷达海面目标检测的关键在于积累一段时间内的目标回波能量,以得到足够的回波信噪比。
目前已有多种回波能量积累方法被提出,包括Radon-傅里叶变换(RFT)[36]、Radon-分数阶傅里叶变换(RFRFT)[37]、Radon-分数阶模糊函数(RLCAF)[38-39]、相位差分-Radon吕变换(PD-RLVD)[40]、相邻互相关函数-吕变换(ACCF-LVD)[41]等。但上述方法主要针对常规雷达目标回波的较长时间相干积累,由于基于GNSS的无源雷达所需观测时间更长(通常为数十秒),海面目标在长观测时间条件下回波特性存在较大差异,将不满足相干等特性,无法直接利用上述方法进行处理。故针对以GNSS为机会照射源的无源雷达,仍需进行相关的海面目标检测方法的研究。
2 基于GNSS的无源雷达海面目标检测研究现状
目前,对基于GNSS的无源雷达海面目标检测的研究主要集中于英国、意大利以及中国。研究人员根据海面目标的回波特性,提出了多种积累回波能量以实现目标检测的方法,并通过仿真或实验验证了提出方法的有效性。下面将针对以单颗导航卫星为机会照射源的无源雷达,对现有海面目标检测方法进行介绍,并分析各自的优缺点。需要注意的是,由于下述方法均需要预先进行二维时域划分和距离向脉冲压缩处理,本节仅对距离向脉冲压缩后信号的进一步积累过程进行介绍。
2.1 基于距离-多普勒域的海面目标检测
针对海面大型目标和中小型目标,英国伯明翰大学的Ma,Antoniou, Cherniakov及意大利罗马大学的 Pieralice, Santi, Pastina等人分别提出了不同检测方法[42-44]。对于海面大型目标,由于其具有较大的雷达截面积(Radar Cross Section, RCS),目标回波功率相对较大,只需积累数秒回波信号,即可得到足够的信噪比,实现海面目标检测。将距离向脉冲压缩后的信号进行方位向傅里叶变换,并将快时间转换为对应的双基距离,即可将回波信号变换到距离-多普勒(RD)域。由于在受限的积累时间内,目标回波距离徙动及多普勒调频率较小,回波信号在RD域内可实现较为有效的积累。
为了验证基于GNSS的无源雷达海面目标检测的可行性及该检测方法的有效性,伯明翰大学进行了相关实验[42-43]。文献[43]中实验设置如图2所示,以一艘按照规定路线航行的渡轮作为海面大型目标,该目标如图2(a)所示,其尺寸约为184 m×25 m。接收系统如图2(b)所示,其置于英国普利茅斯港东海岸。两颗伽利略卫星GSAT0201和GSAT0203被选为机会照射源,其发射的E5a-Q信号作为机会信号被接收系统所接收,实验构型如图2(c)所示。实验中,接收系统对目标的总观测时长为145 s,图2(c)同时给出了对应的方位角及仰角范围。由于两颗卫星独立作为发射站,下面仅给出卫星GSAT0201得到的结果。由于目标RCS较大,不需要进行整个观测时间下的目标回波的积累。截取一段时长为2.5 s的目标回波,将其变换到RD域,结果如图3所示[43]。图中,零多普勒频率处的亮点为直达波和旁瓣,在RD域中 (2 000 m, 8.5 Hz) 处的强散射点为海面目标的渡轮。实验表明,利用GNSS作为机会照射源实现海面目标的检测是可行的。同时该实验验证了将短时间目标回波信号通过方位向傅里叶变换到RD域实现海面大型目标检测的有效性。

(a) 海面目标
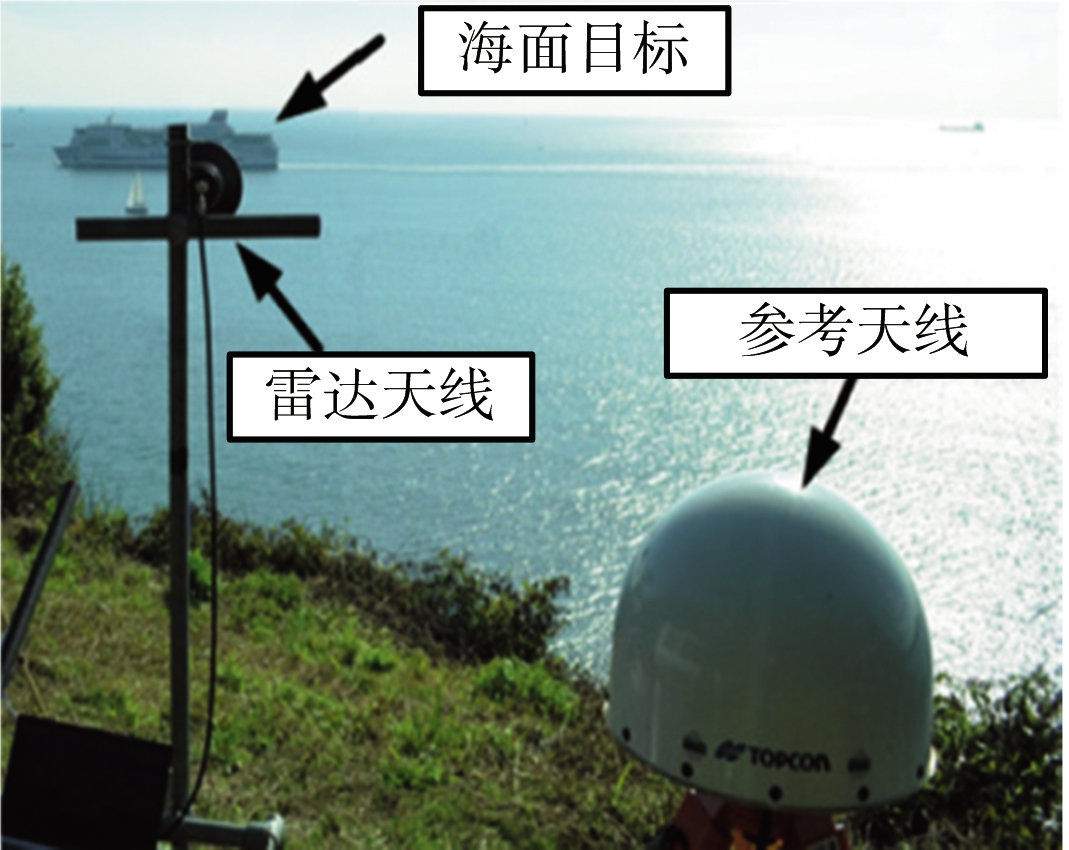
(b) 接收系统
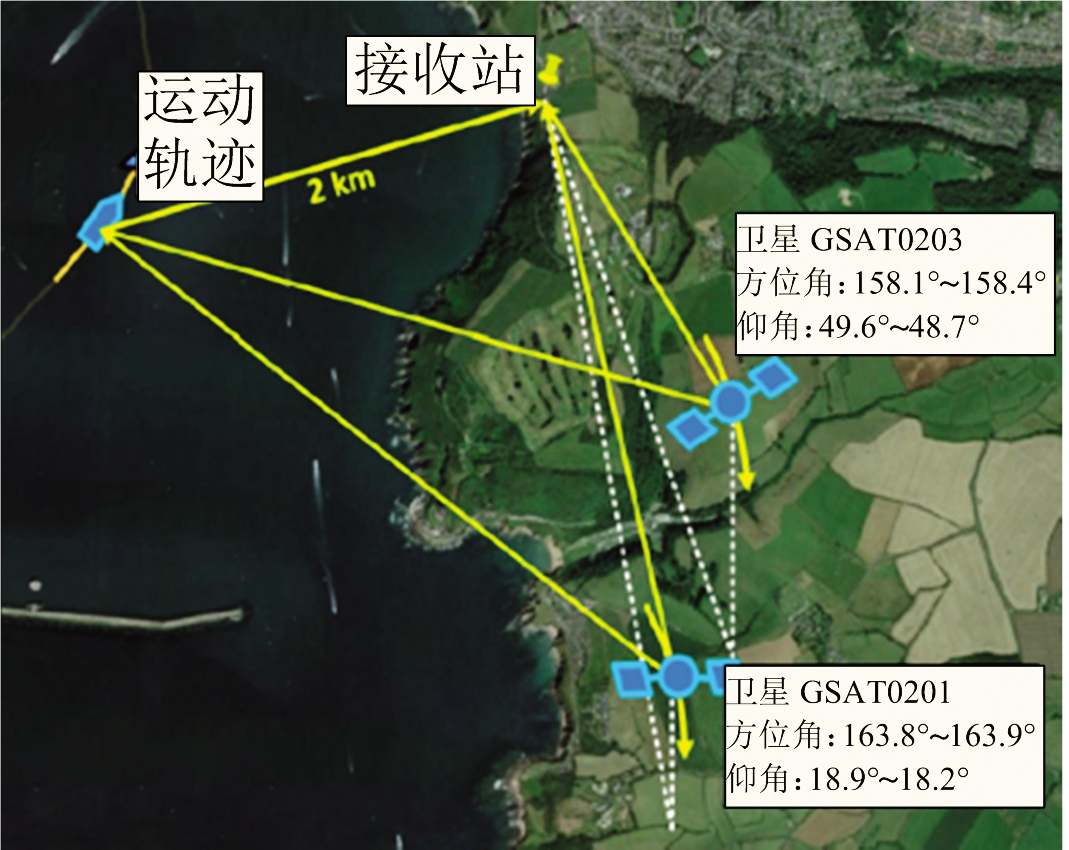
(c) 实验构型图
图2 基于GLONASS无源雷达海面实验
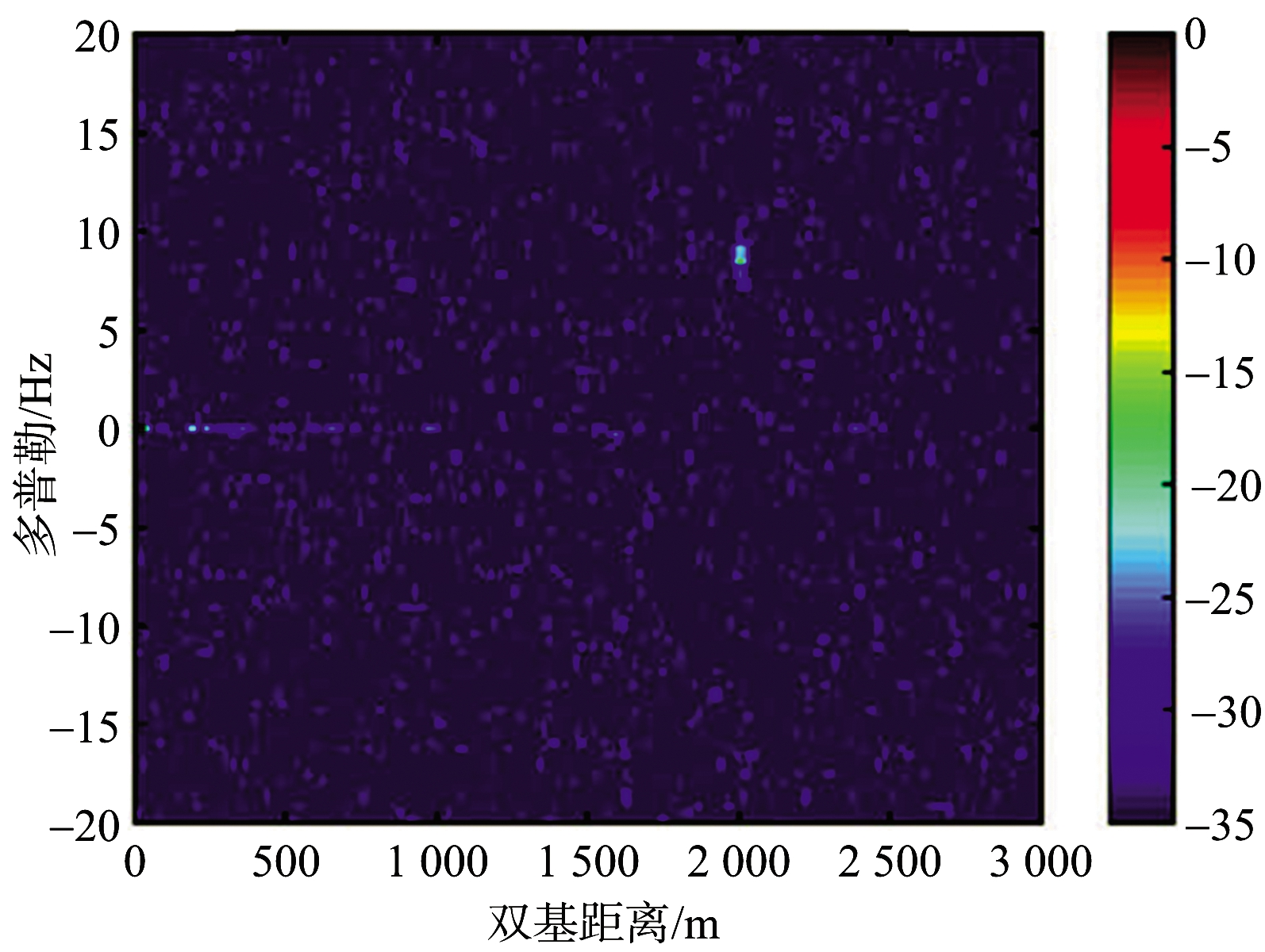
图3 短积累时间下RD域内实验结果
通过方位向傅里叶变换得到目标回波在RD域中的结果,处理流程简单,但该方法要求目标回波积累时间较短,使得其仅对海面大型目标的检测有效,适用范围受限。
对于海面中小型目标,由于目标RCS较小,接收系统处的目标回波功率较低,为了得到足够的回波信号能量,回波积累时间需要达到数十秒。但在数十秒的积累时间条件下,一方面,由于散射特性的变化,目标回波不再相干;另一方面,目标回波距离徙动和多普勒徙动不能忽略。因此,无法直接通过方位向傅里叶变换实现目标回波的有效相干积累。为了解决上述问题,相关研究人员提出一种分帧后距离和多普勒分别补偿的方法[44],该方法流程图如图4所示。整个积累时间Ta内的回波信号被分为N帧,每帧时长为Tf,帧内回波由于散射特性变化受限,可以认为是相干的。将各帧内信号分别进行方位向傅里叶变换,得到N幅RD图。由于目标的运动,在N幅RD图中,目标所在的距离和多普勒均不同。为了能有效积累这N幅RD结果,需要进行目标运动补偿(Target Motion Compensation, TMC)。双基距离与多普勒分别用R和fη表示,若以第0幅RD图作为参考,第n幅RD结果的距离补偿和多普勒补偿分别表示为
![]()
![]()
(3)
(4)
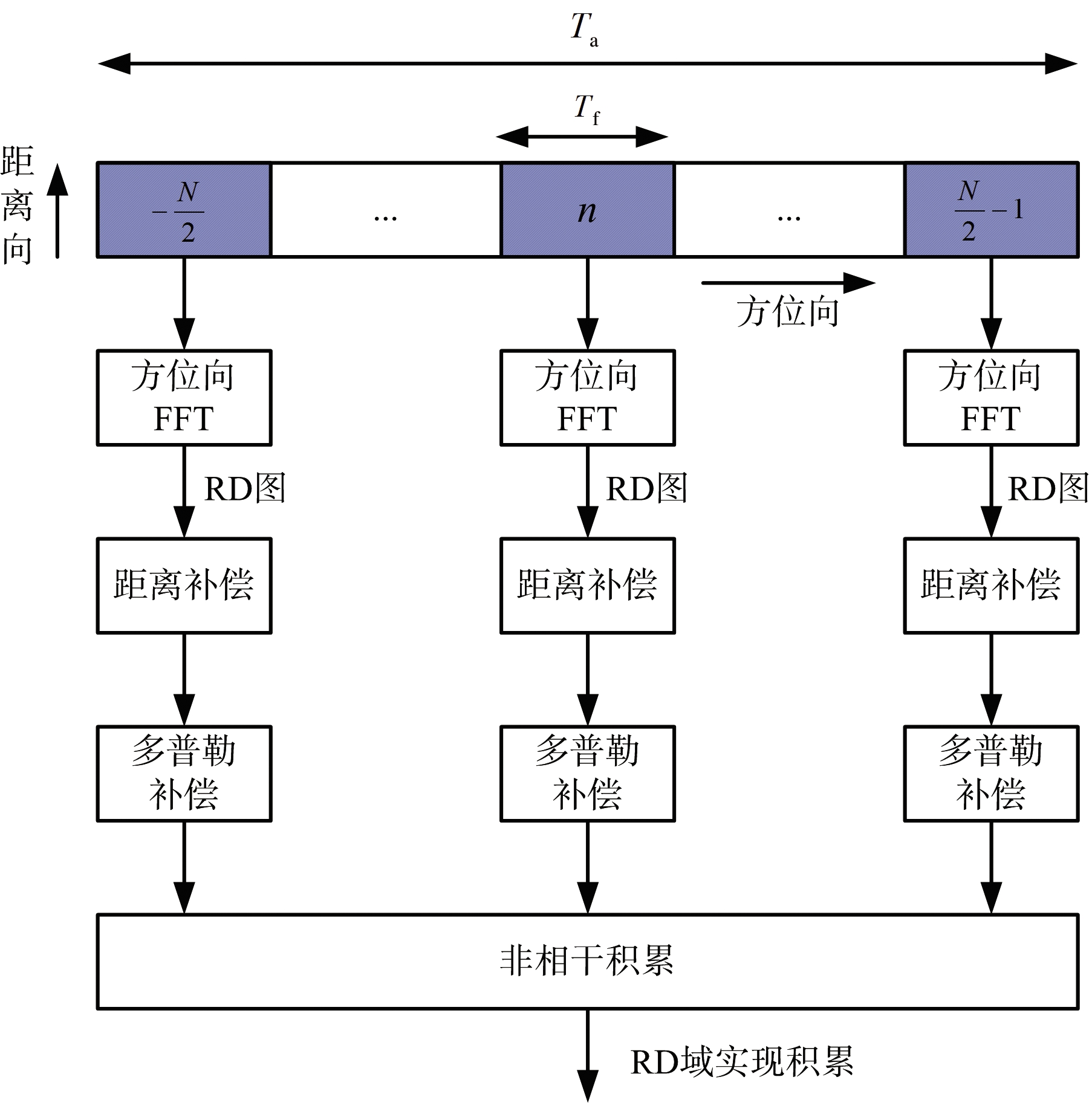
图4 基于距离多普勒域的长积累时间海面目标检测方法流程图
式中,fdr为多普勒调频率,其值未知。处理中,根据监视海面的范围及目标可能的运动速度,设置一组多普勒调频率组,通过自适应技术得到最优的多普勒调频率值。
在距离和多普勒补偿后,目标位于各幅RD图中的同一位置,再将各RD图幅值相加,实现非相干积累,最终在RD域内完成回波信号长时间有效积累。
罗马大学对相关实验数据进行了处理,验证了该方法的有效性。文献[44]中实验设置如图5所示,一艘长度约为10 m的渔船被作为海面小目标,该目标如图5(a)所示。如图5(b)所示为此实验的接收系统。选择GLONASS卫星作为发射站,实验构型如图5(c)所示。实验中利用渔船上的GPS接收机记录其位置,且渔船运动速度已知,故可以得到目标在RD图中的真实位置。图6为文献[44]中给出的实验结果。研究人员截取60 s目标回波进行积累,一帧时长设置为3 s,将整个积累时间分为20帧。每帧单独进行方位向傅里叶变换,得到20幅RD图,其中,单帧得到的RD图结果如图6(a)所示,图中白色×处为目标所在的真实位置。图中左下为目标实际位置的放大结果,无法明确检测到目标,证明对于海面中小目标,3 s的积累时长无法得到足够的信噪比。为了提高回波能量,非相干积累20幅RD图。若不经过TMC,得到结果如图6(b)所示,可以发现,非相干积累后噪声的起伏明显降低,但由于距离和多普勒徙动,该海面目标仍不能被有效检测。图6(c)为经过TMC后非相干积累的结果。图中存在明显可见的峰值,可以实现目标的有效检测,且在RD图中的位置与通过GPS接收机记录的位置相符,证明了所提出的检测方法的有效性。

(a) 海面目标

(b) 接收系统
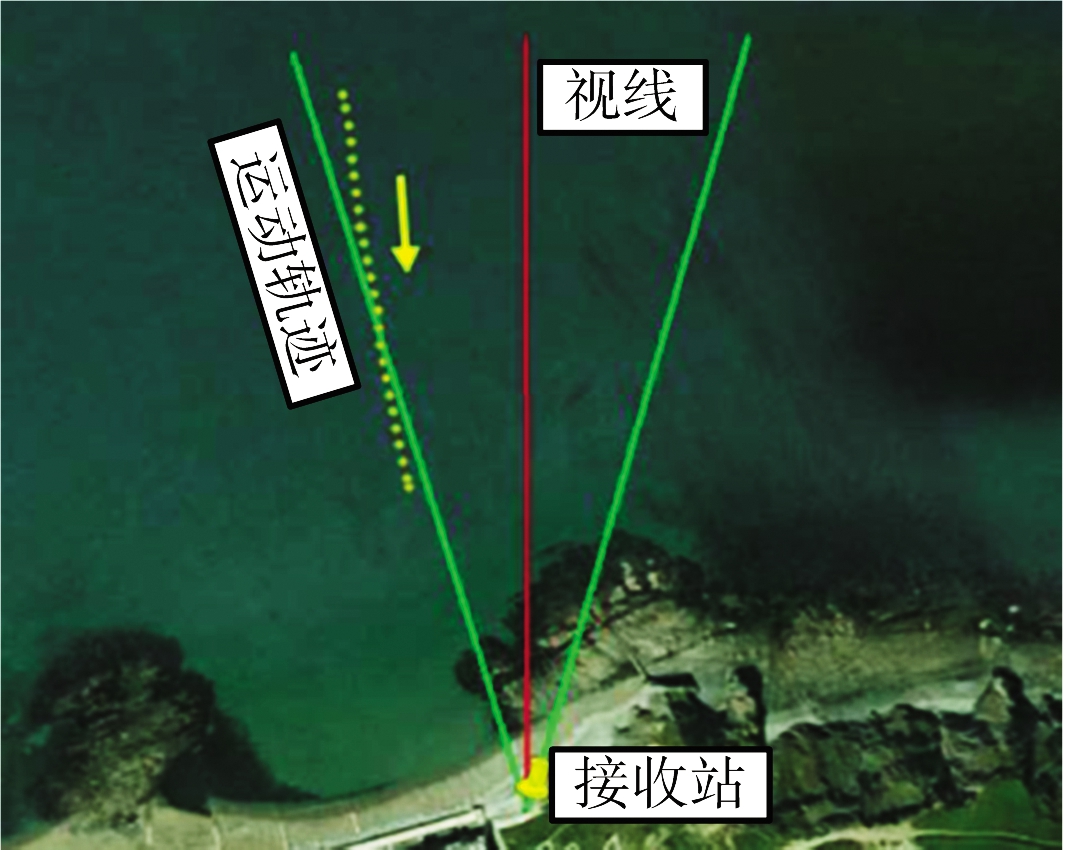
(c) 实验构型
图5 基于Galileo的无源雷达海面实验
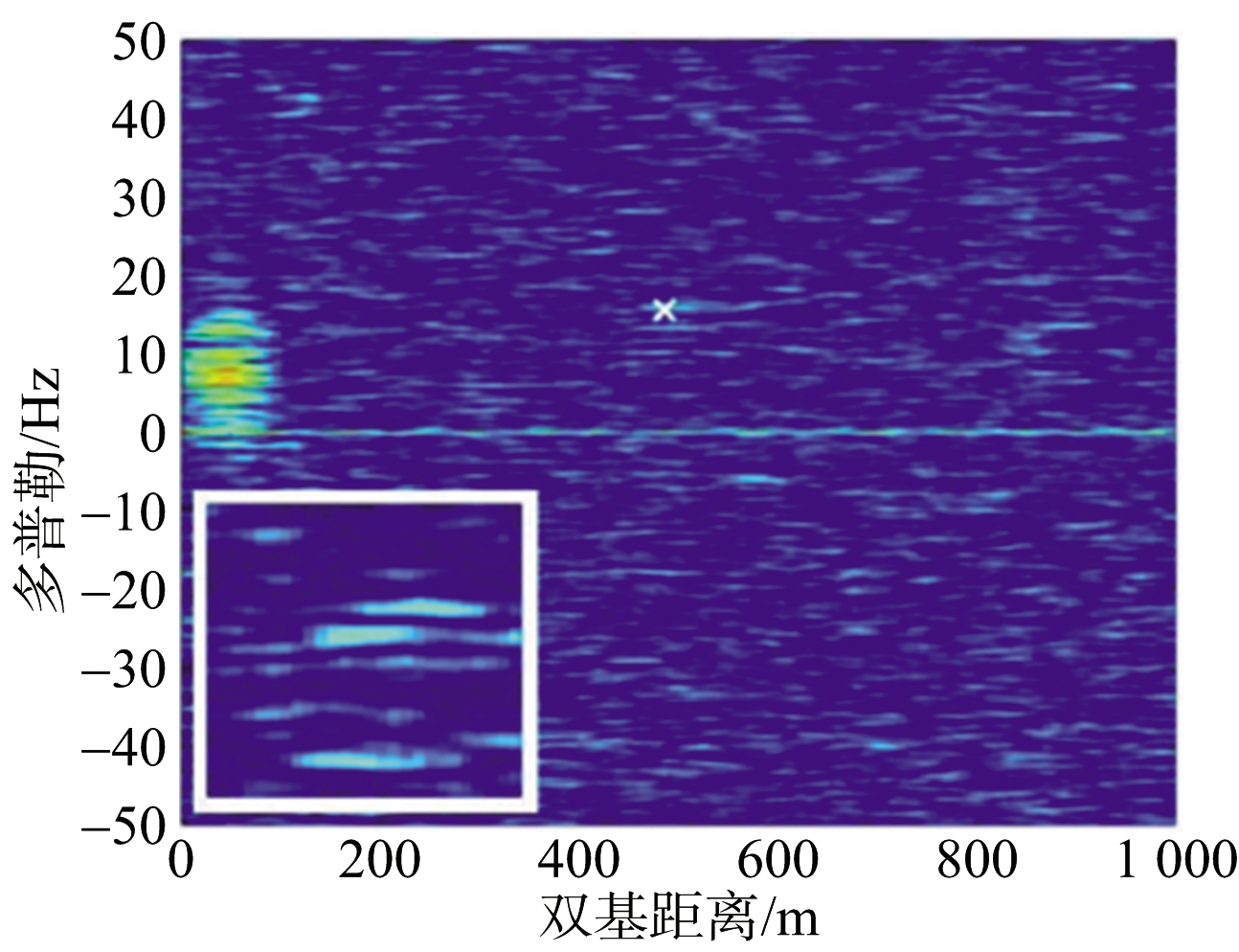
(a) 单帧
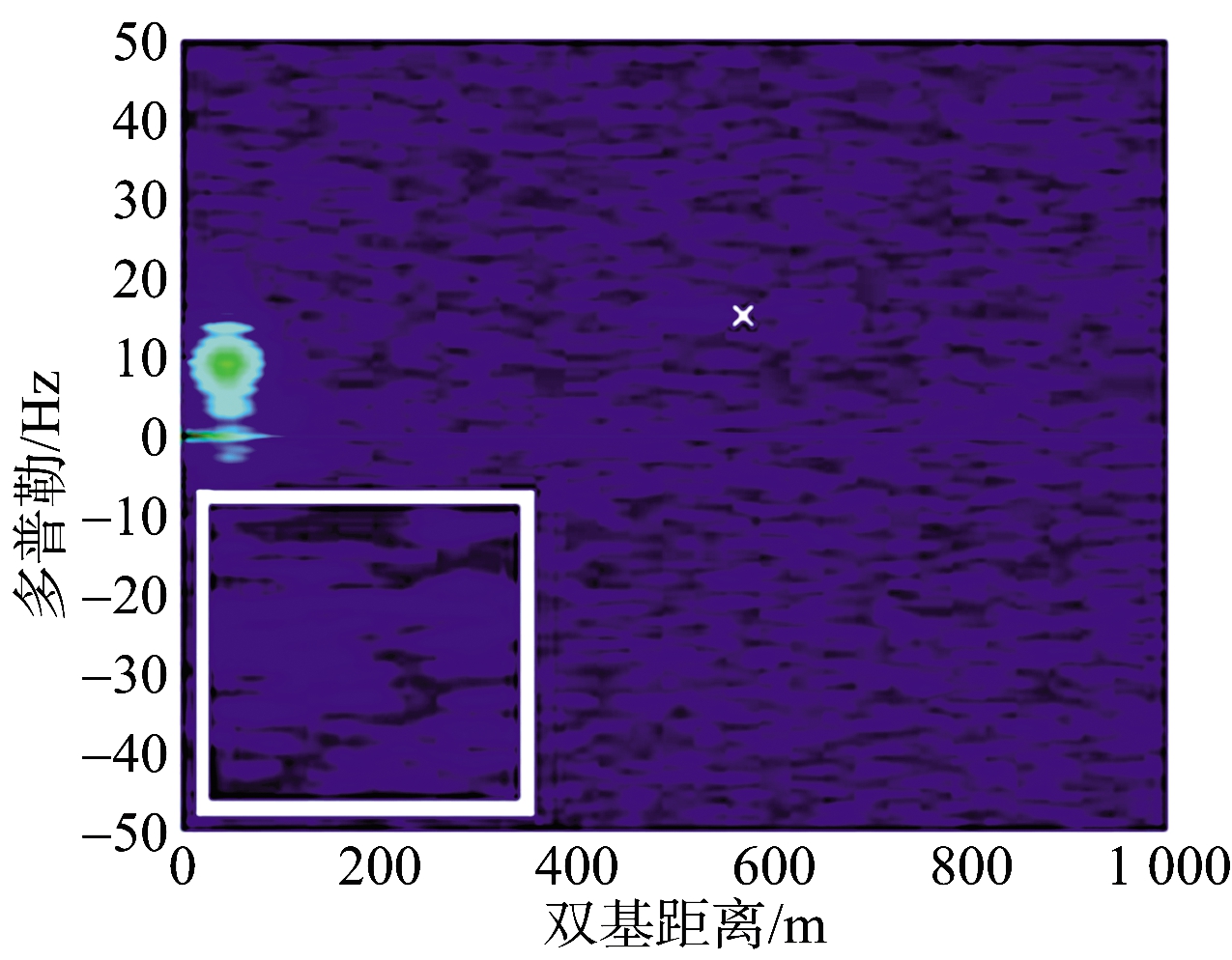
(b) 多帧,未经TMC
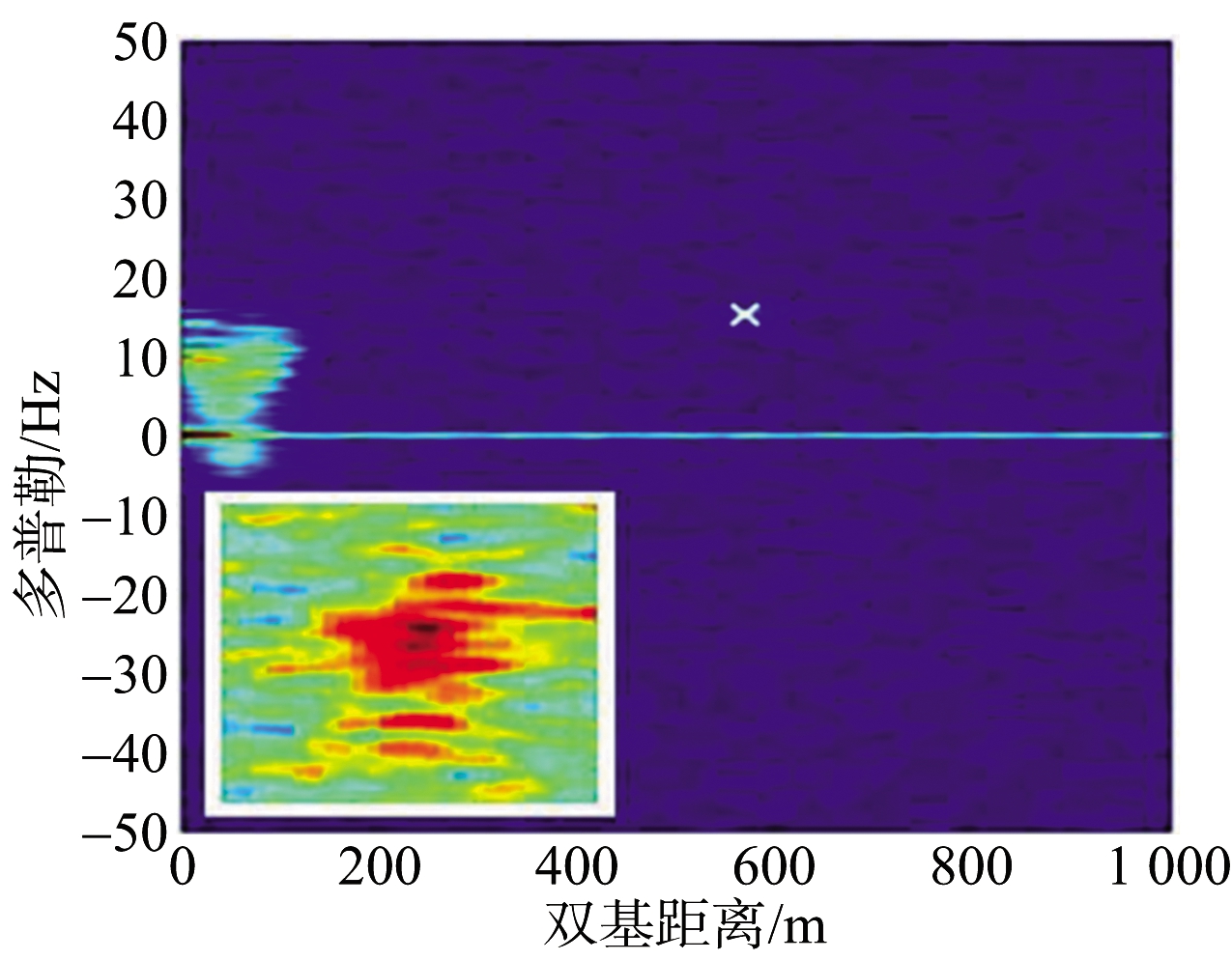
(c) 多帧,经过TMC
图6 长积累时间下RD域内实验结果
2.2 基于本地坐标系的海面目标检测
罗马大学的Santi,Pastina等人针对海面中小型海面目标,又提出了一种将RD域信号映射到本地坐标系的检测方法[45-46],其流程图如图7所示[45]。该方法同样先将长时间的目标回波分为N帧,并将帧内信号通过方位向傅里叶变换得到多幅RD图。接着将各RD图映射到本地坐标系内。由于目标在各RD图中的位置由其在空间坐标系下的参考位置矢量(x0,y0)和速度矢量(vx,vy)决定,在映射时需确定目标速度。由于其值未知,在处理中需要先根据目前可能的速度范围,给出M组待测试的目标速度矢量。对于本地坐标系内的点(x,y),以其作为目标的参考位置,在第m组测试速度条件下,可以得到第n帧回波理论上的距离和多普勒值,进而从实际得到的第n帧RD图中提取对应的值,记为In,m(x,y)。在N帧RD图均完成映射后,无需进行补偿,直接将本地坐标系内的结果进行幅值相加,即可完成各帧的非相干积累,从而在本地坐标系内实现目标回波的长时间积累。
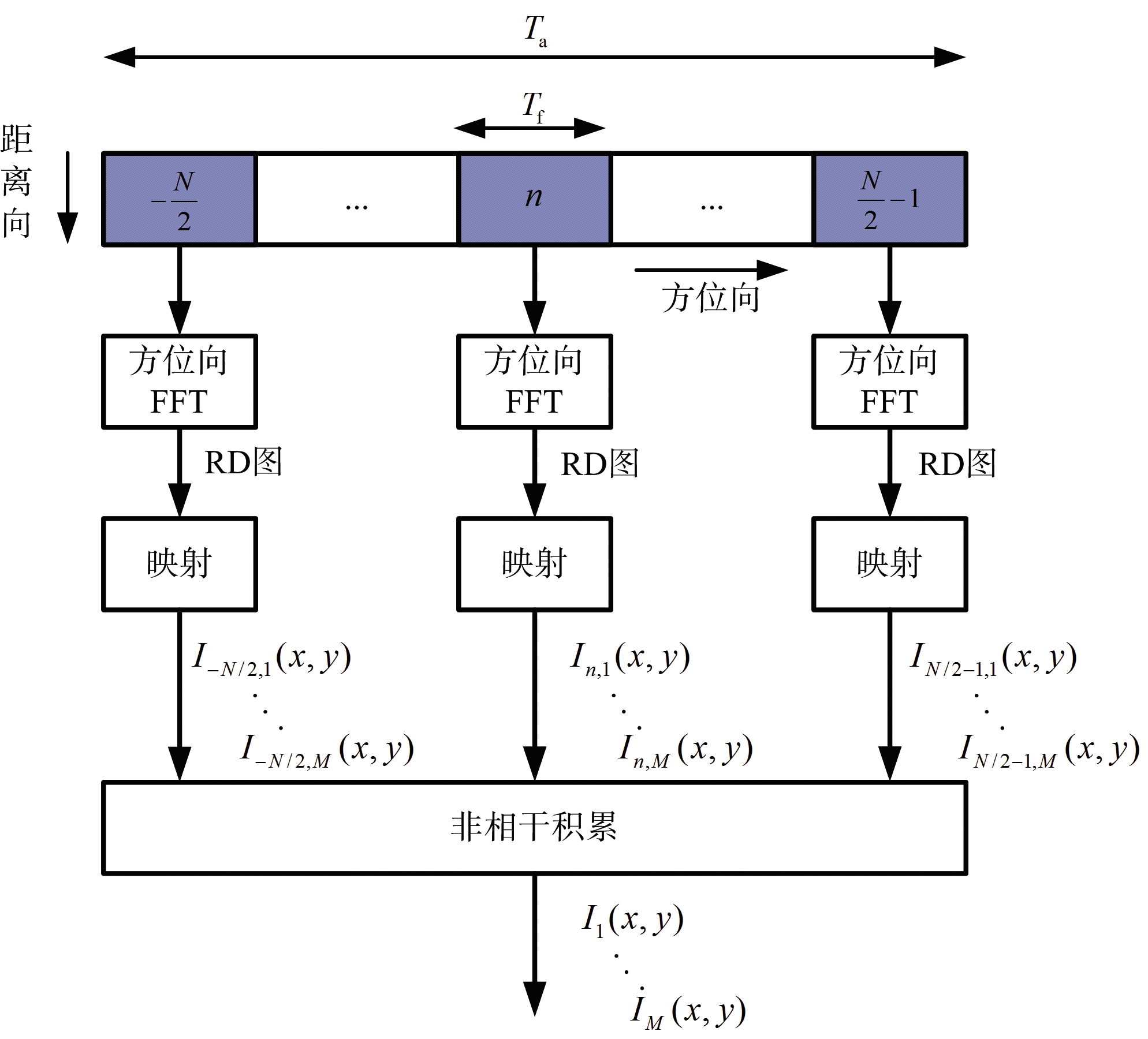
图7 基于本地坐标系的长积累时间海面目标检测方法流程图
相关研究人员通过仿真实验验证对该方法的有效性进行了验证,文献[45]中给出的仿真结果如图8、图9所示。仿真中,导航卫星发射信号带宽为1.023 MHz,目标在参考时刻的位置矢量为(1 300,0) m,速度矢量为(0,5) kn,加入高斯白噪声作为背景干扰,距离向脉冲压缩后回波信噪比为-24 dB,其值与真实情况下中小海面目标回波信噪比相符,要实现目标检测具有一定的难度。仿真中对目标回波的积累时长为30 s,每帧时长设置为1 s,将回波分为30帧。单帧RD结果如图8(a)所示,目标仍被噪声所淹没,无法检测到该目标。应用所提出的检测方法,假设估计的目标速度恰为准确的速度,则在本地坐标系内得到的最终积累结果如图8(b)所示。可以发现,在本地坐标系内实现了目标回波能量的积累,能有效检测到该目标。同时,目标所在的位置与实际目标参考时刻位置相符。
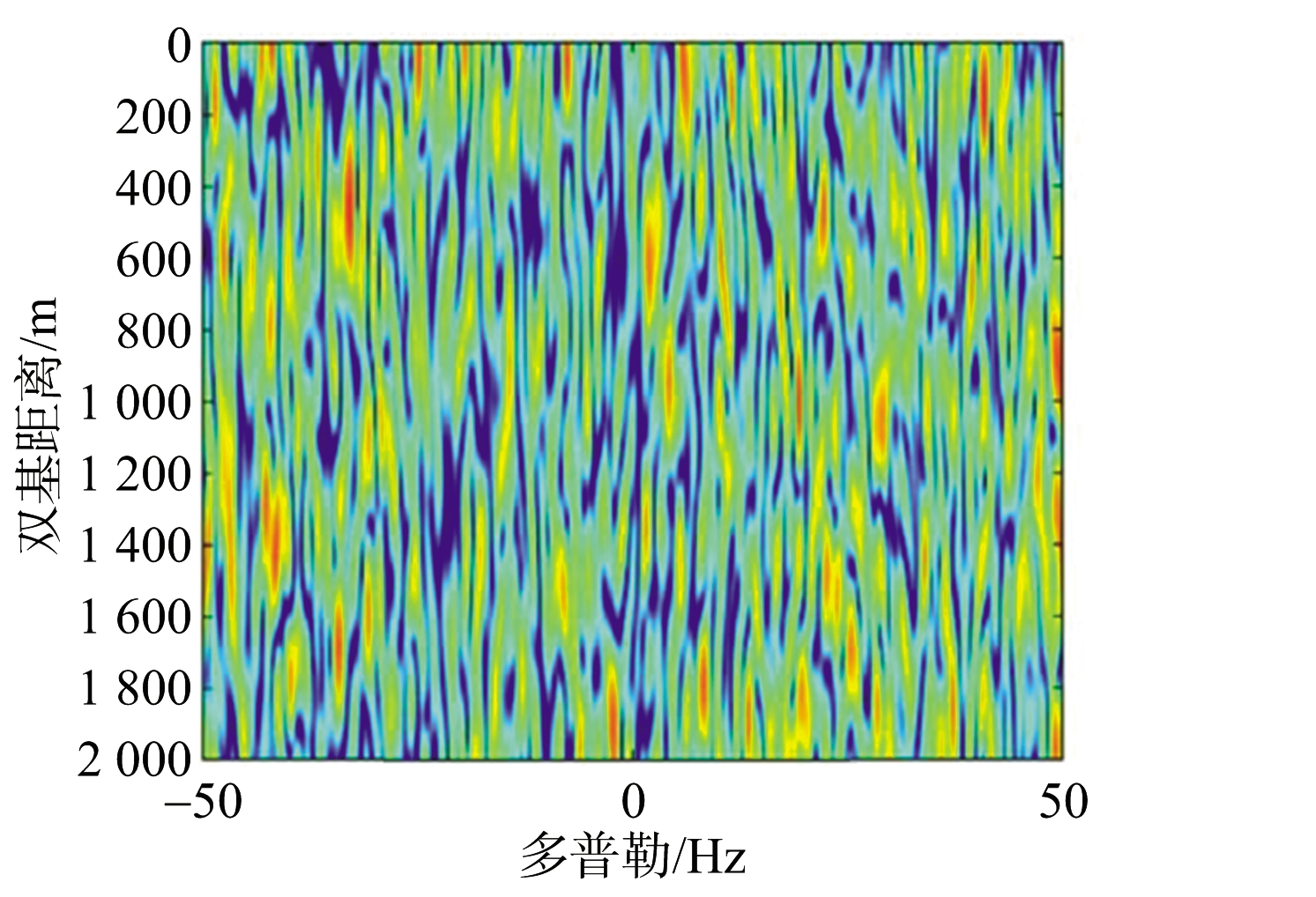
(a) 单帧RD图
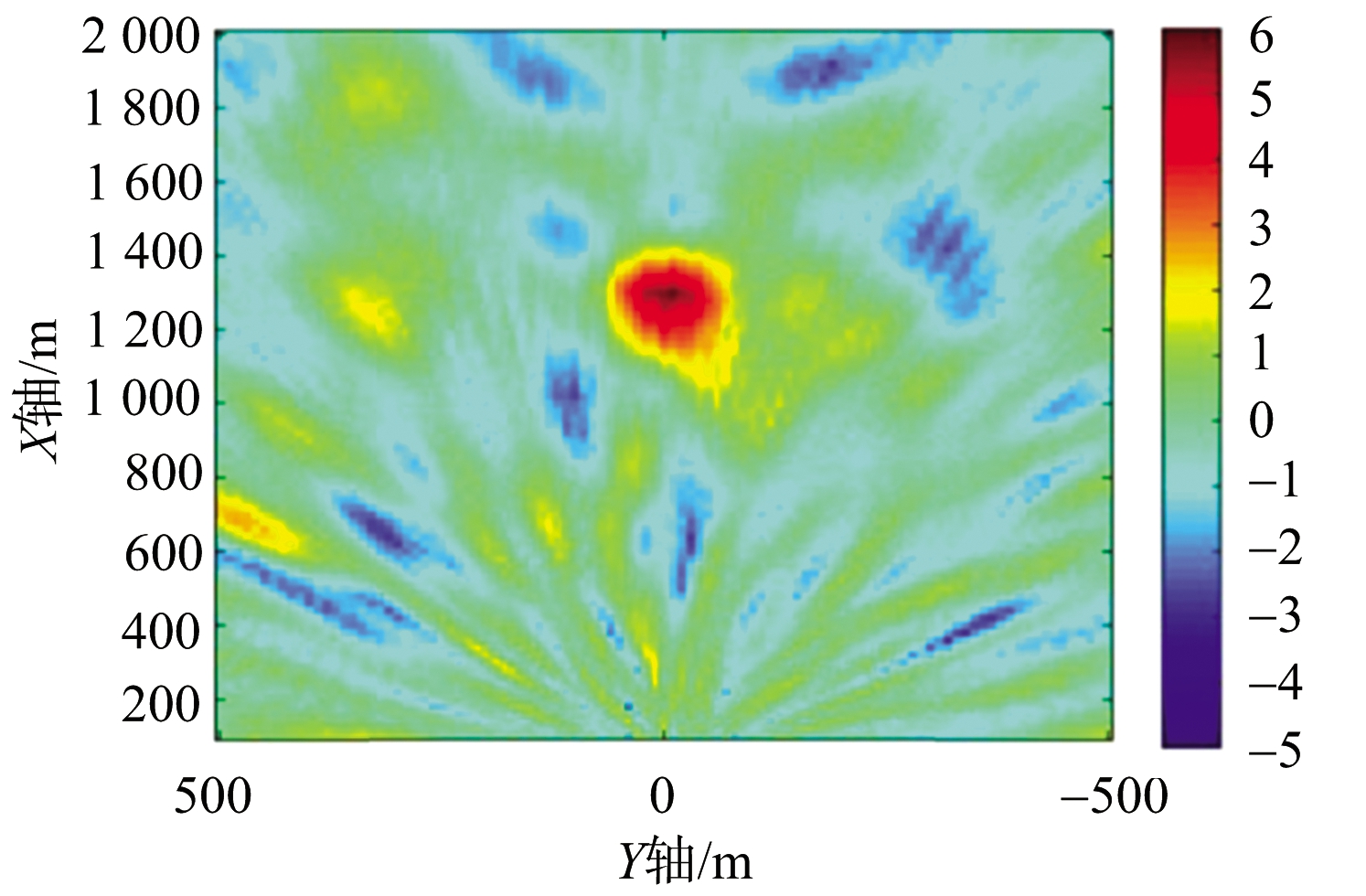
(b) 真实速度下本地坐标系内的积累结果
图8 本地坐标系中的仿真结果
但该方法由于本质上为一个四维搜索过程,处理中运算量极大。同时,对于单个机会照射源,不同的初始位置和速度的目标可能会存在相同的距离历史和多普勒历史,造成位置和速度估计的模糊。若将测试目标速度矢量变为(0,3) kn和(0,8.8) kn,在本地坐标系内,最终积累结果分别如图9(a)和图9(b)所示。可以发现,在错误的测试目标速度下,仍能实现目标的检测,但目标所在位置不再准确。
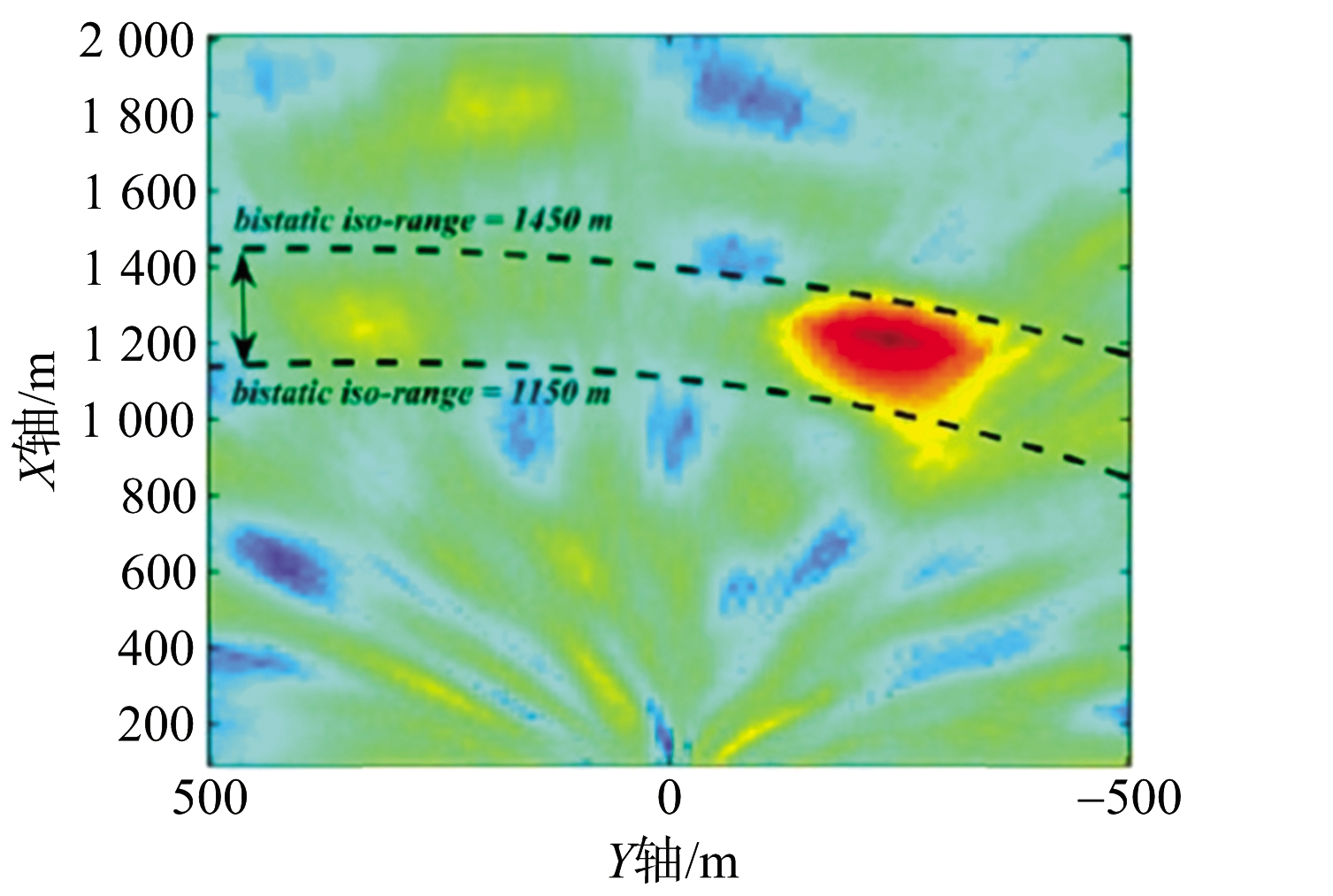
(a) (0,3) kn
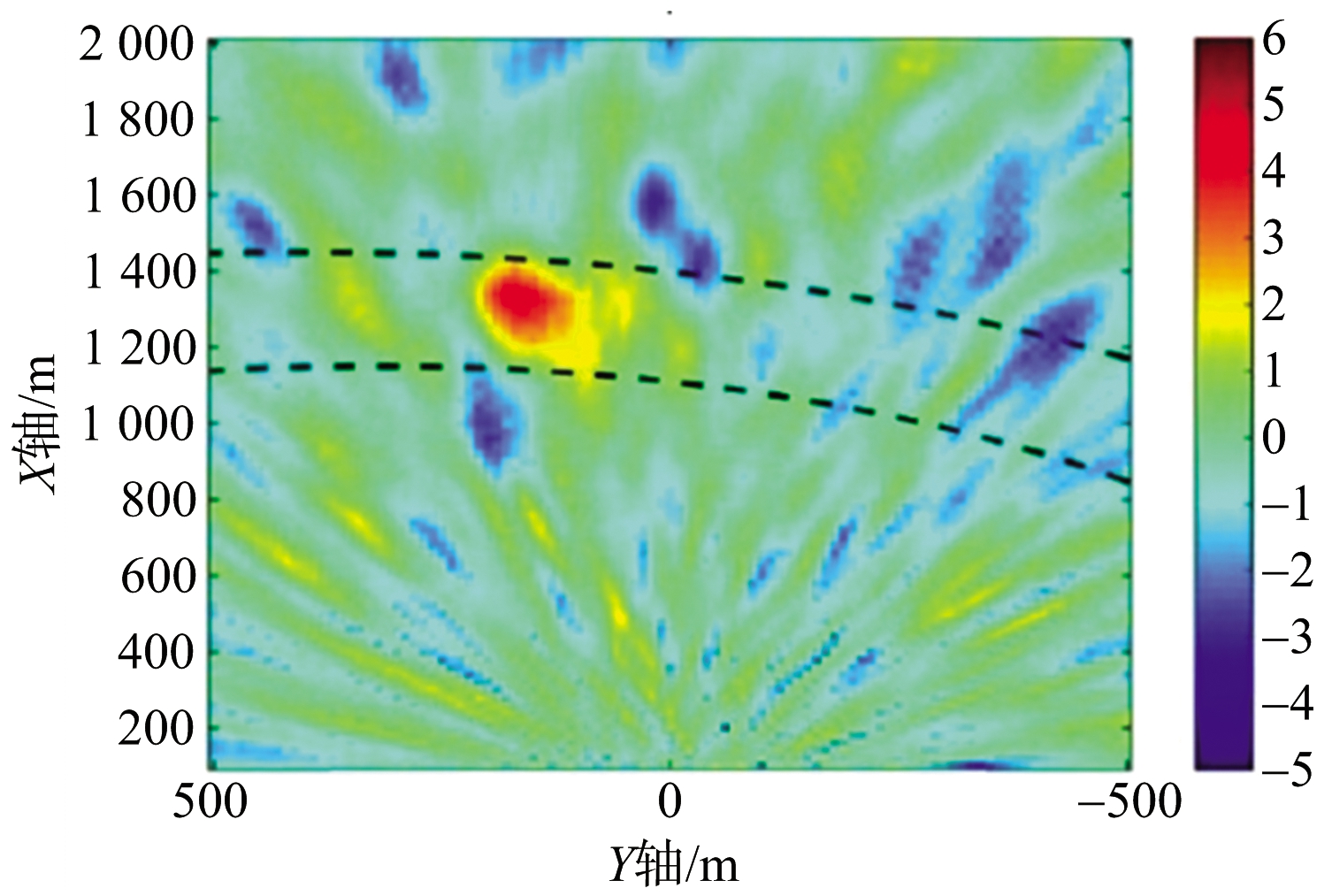
(b) (0,8.8) kn
图9 其他测试速度下本地坐标系内的仿真结果
2.3 基于DC-DFR域的海面目标检测
电子科技大学的李中余等人提出了基于多普勒质心-多普勒调频率(DC-DFR)域的海面目标检测方法[33,47-48],相较于上述直接将目标回波变换到RD域的方法,在多普勒参数域能实现更优的回波能量积累效果。该方法仍可针对海面大型目标和中小型目标两种情况进行不同处理。
对于海面大型目标,同样仅需数秒的回波积累时间。首先利用Keystone变换对距离向脉冲压缩后的结果进行距离徙动校正。对于徙动校正后的结果,取出同一距离单元的方位信号。若该方位信号包含目标,则其为线性调频(LFM)信号。忽略幅度及常数相位,该方位信号表示为
(5)
式中,fdc和fdr分别表示目标回波的多普勒质心(DC)和多普勒调频率(DFR)。
接着对方位信号进行分数阶傅里叶变换(FrFT)[49-51]。对于LFM信号,一个合理的旋转角度α可以在对应旋转频率fα轴上得到一个波峰。因此,含有目标的方位信号可通过FrFT实现在fα-α域的有效积累。由于最优积累时的旋转角度α与方位信号的DFR相对应,投影到fα轴上的位置与方位信号的DC相对应,因此,通过代换将回波能量积累到DC-DFR域,相关代换关系为
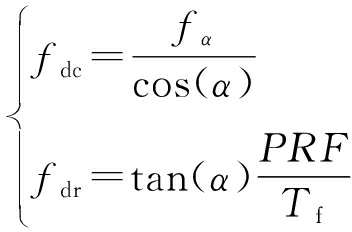
(6)
式中,PRF为脉冲重复频率。
相关研究人员通过仿真验证了该方法的有效性,图10给出了文献[47]中的仿真结果。仿真中,回波积累时间为5 s,在DC-DFR域的回波积累结果如图10(a)所示,图10(b)为目标DC剖面图,仿真结果中存在一个独立可见的峰值,因此能有效实现目标的检测。
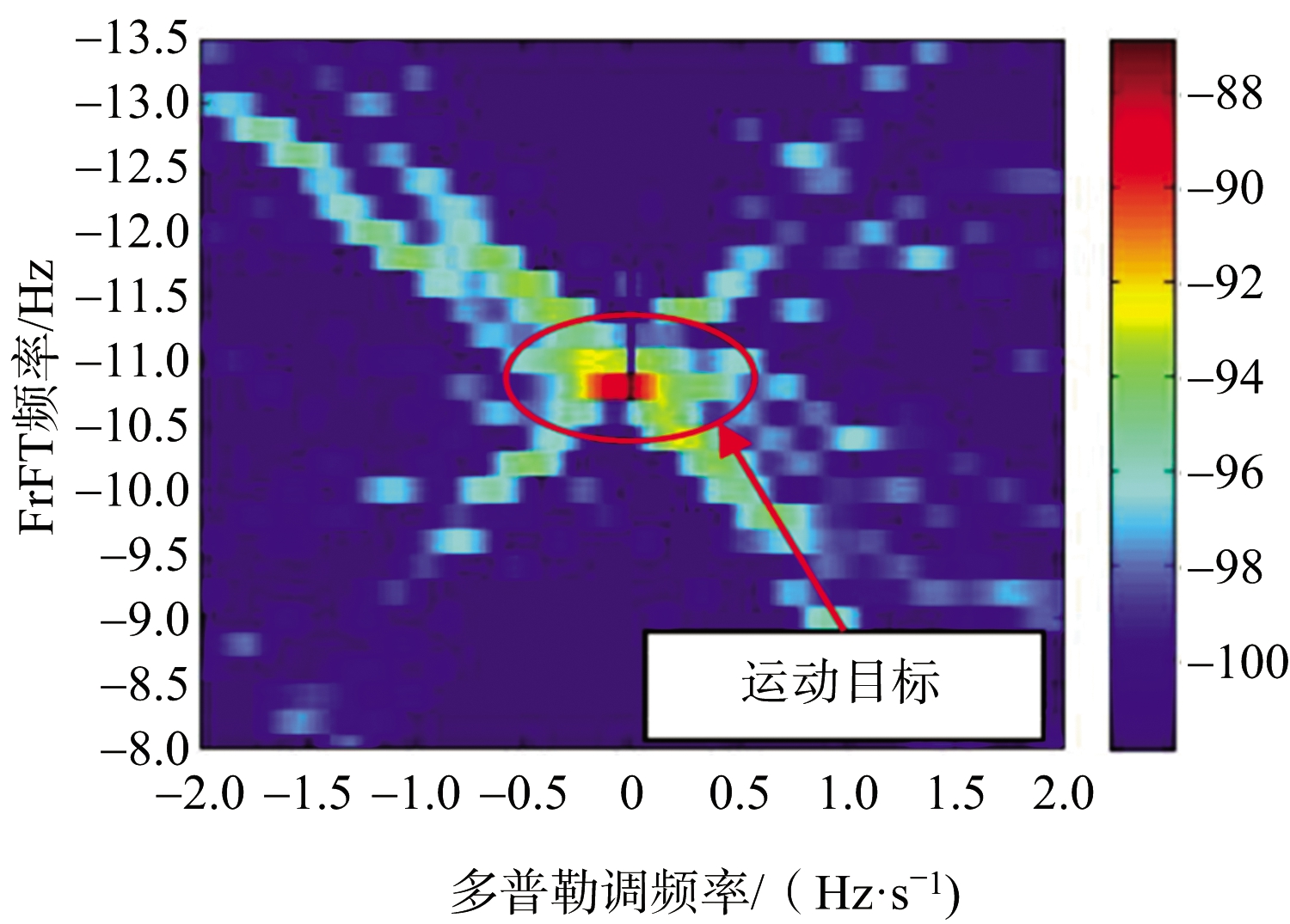
(a) 多普勒质心-多普勒调频率域
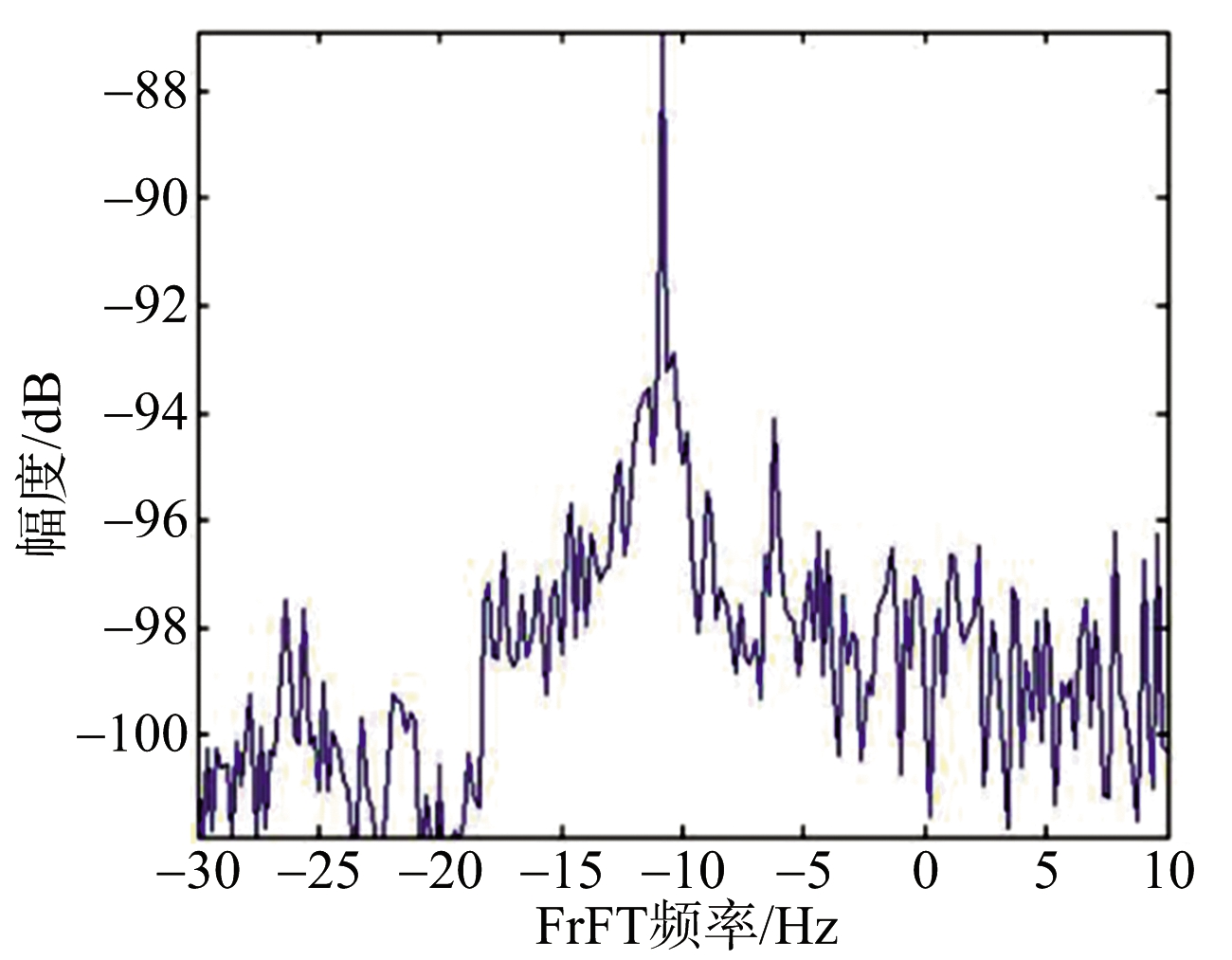
(b) 多普勒质心剖面
图10 短积累时间下DC-DFR域内仿真结果
为检测海面中小型目标,同样需要进行长时间目标回波的积累。在多普勒参数域内实现目标回波长时间积累的流程图如图11所示[47]。对于整个积累时间内的目标回波,同样先利用Keystone变换实现距离徙动校正,并将距离徙动校正后的信号取出同一距离单元内的方位信号。由于海面目标运动较为简单,包含目标的方位信号在长时间下仍可视为LFM信号。接着对方位信号进行分帧处理,利用FrFT得到各帧信号在DC-DFR域的结果。若取出的方位信号包含目标,则该目标在各帧DC-DFR图中位于相同的DFR处,但DC不同,因此在多帧非相干积累前需要进行DC补偿。各帧方位信号DC的差异与多普勒调频率及单帧时长有关,若以第0帧结果作为参考,则第n帧结果的需要补偿的DC表示为
Δfdc=n·Tf·fdr
(7)
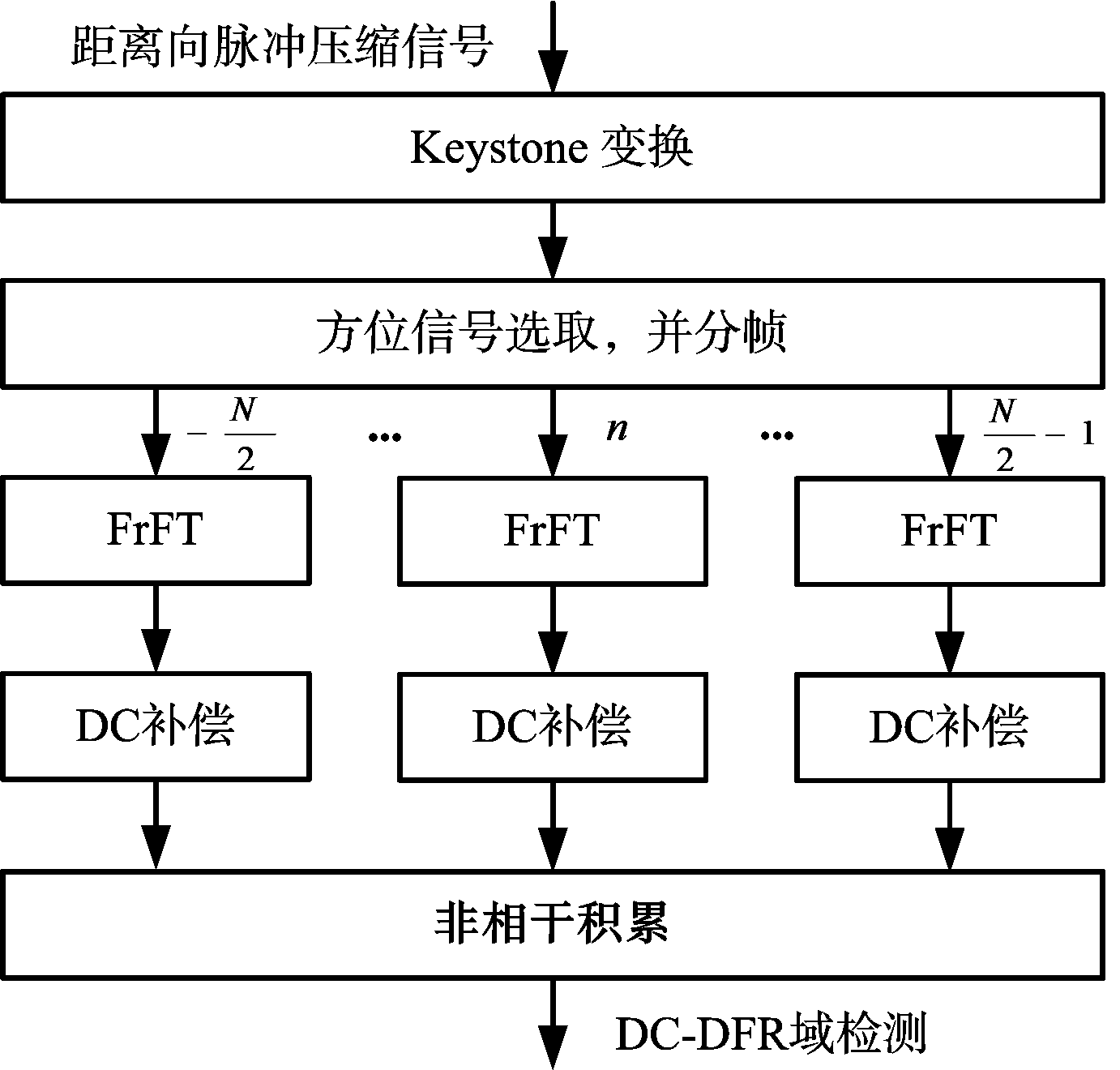
图11 基于多普勒参数域的长积累时间海面目标检测方法流程图
DC补偿后,目标在各帧积累结果中位于同一位置。最后进行多帧非相干积累,即可完成目标回波的长时间积累,在DC-DFR域实现对海面中小型目标的检测。
该方法的有效性通过仿真得到了验证。仿真中,加入高斯白噪声作为背景干扰,目标回波信号在距离向脉冲压缩后信噪比为-24 dB,为了有效检测该目标,对该目标回波的积累时间为60 s。Keystone变换后,取出同一距离单元的方位信号,以2 s作为一帧时长,将该方位信号分为30帧。假设所取方位信号包含目标,文献[33]中给出的DC-DFR域仿真结果如图12所示。图12(a)为中间帧通过FrFT得到的结果,目标仍被噪声所淹没,无法实现有效的海面目标检测。若不进行DC补偿,直接进行多帧非相干积累,结果如图12(b)所示。可以发现,噪声起伏降低,但由于各帧DC的差异,目标回波无法实现有效积累,仍不能检测到该目标。进行DC补偿后,多帧非相干的积累结果如图12(c)所示,目标在补偿后的各帧结果中位于同一位置,最终DC-DFR域的积累结果中存在一处明显的峰值,据此能有效实现该海面目标的检测。
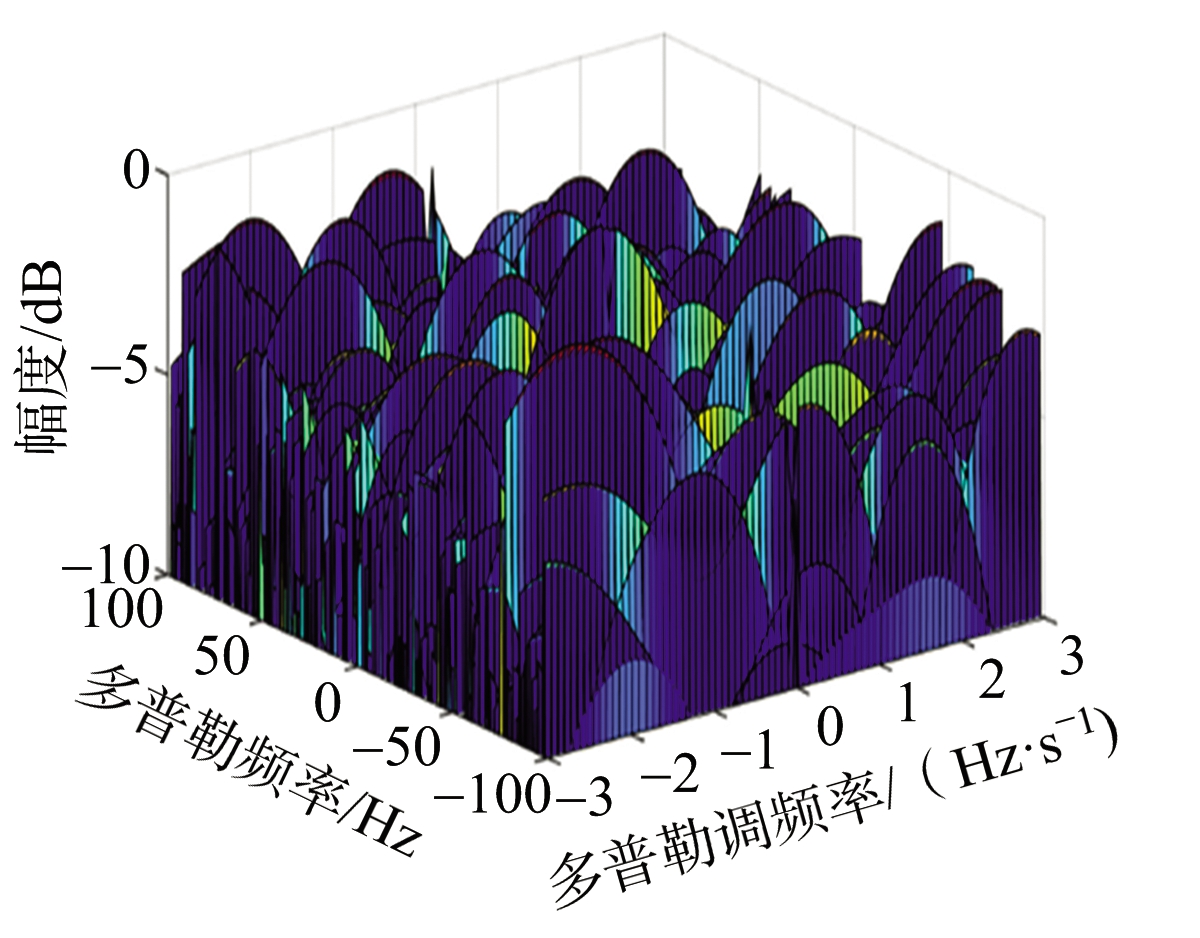
(a) 单帧
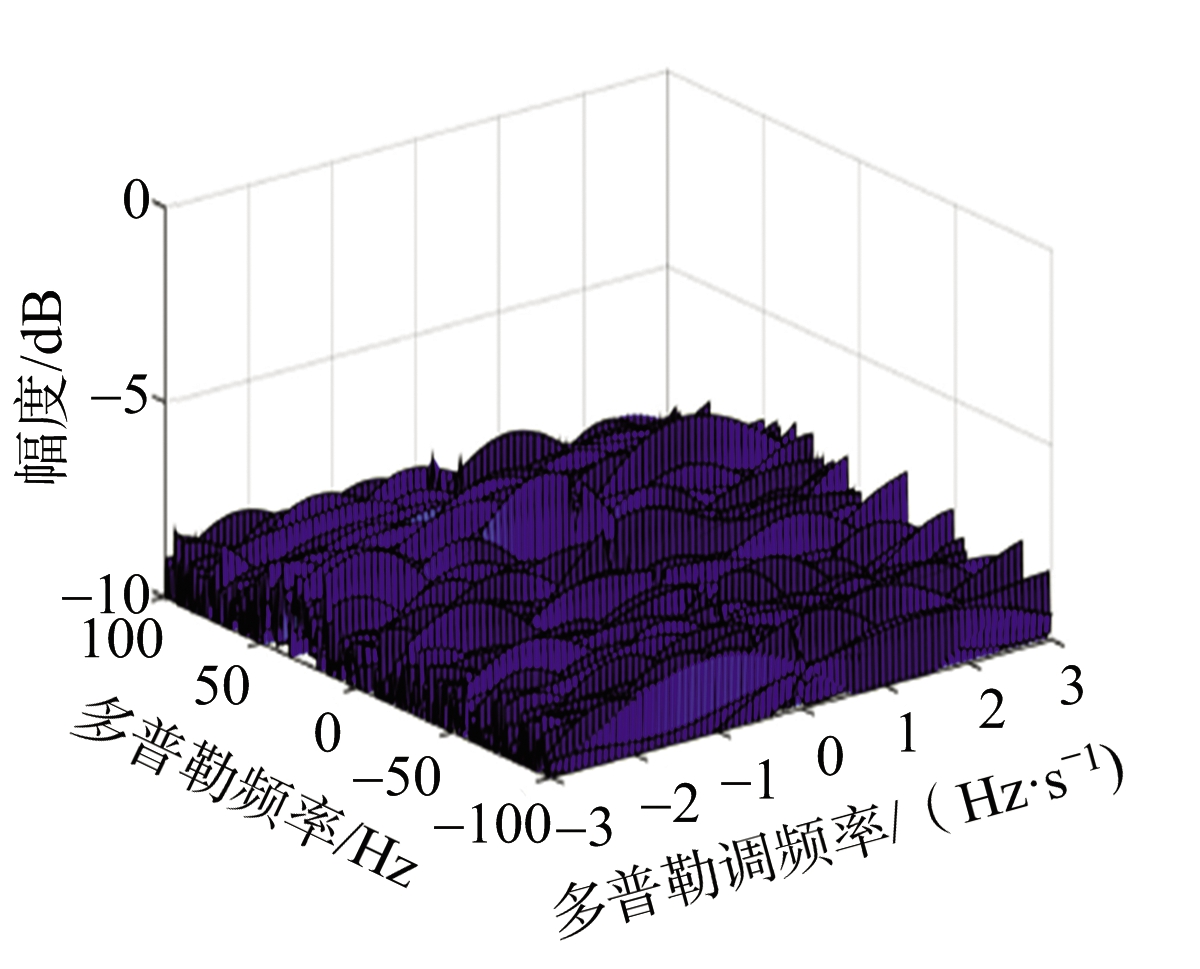
(b)多帧,未经DC补偿
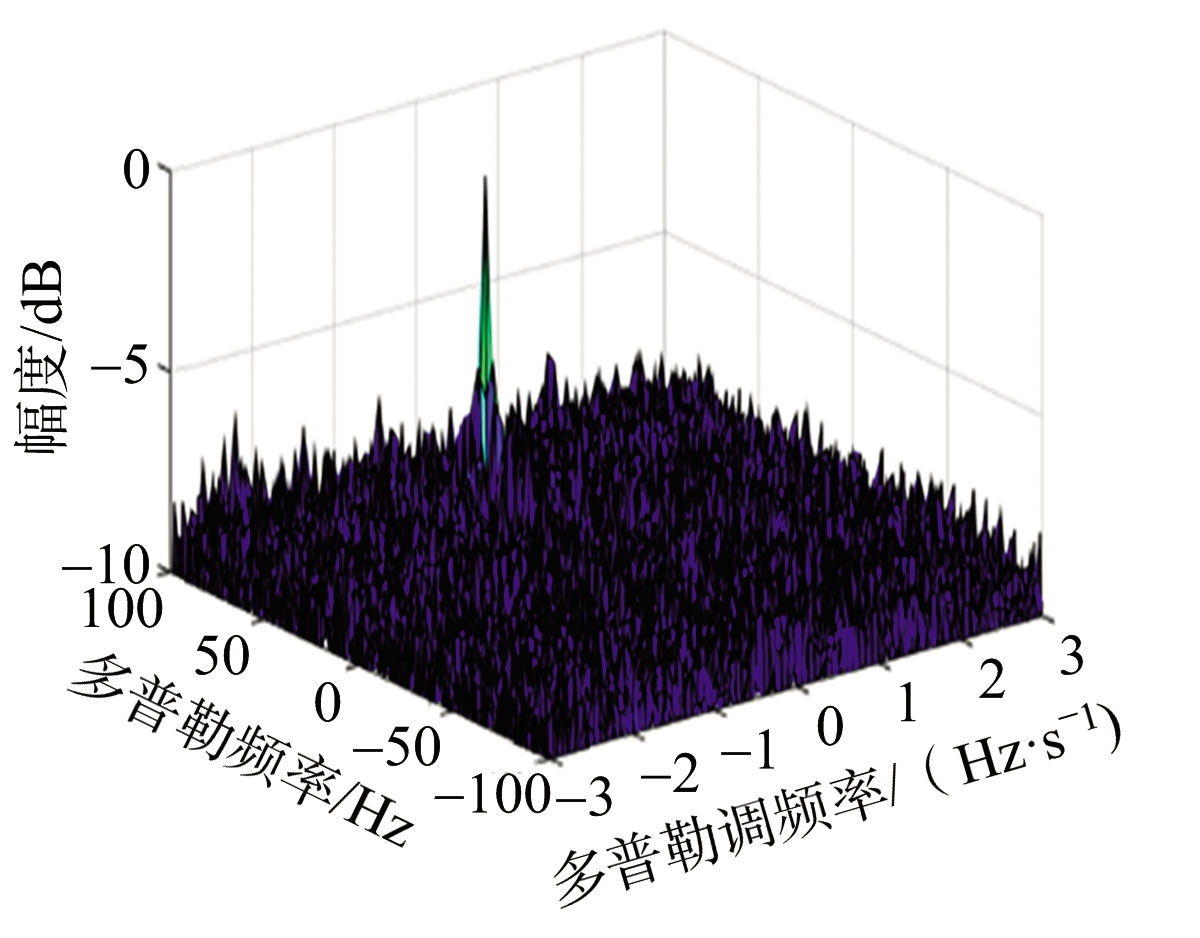
(c) 多帧,经过DC补偿
图12 长积累时间下DC-DFR域内仿真结果
在上述研究的基础上,研究人员将无源雷达系统中的单个接收单元扩展为接收天线阵列,并提出了一种对应的海面目标检测方法[48],相较于单个天线,多接收天线能获得更多的目标回波能量,可以实现更优的海面目标检测效果。用相邻通道间隔为d的K个天线接收海面目标反射的信号,构成系统的俯视图如图13所示[48],图中,p(η)为目标的瞬时位置,θ(η)为瞬时波达方向(DOA)。对应的海面目标检测方法流程图如图14所示[48]。 该方法同样先将每一天线单元所接收到的长时间目标回波通过Keystone变换实现距离徙动校正,并进行分帧处理。接着每一帧信号均通过FrFT相干积累到DC-DFR域。然后对不同天线相同帧的信号进行相干积累。由于位置的差异,不同天线单元所接收到的目标回波具有不同的DC及相位,相干积累前需要对其进行补偿。若要相干积累第n帧信号,对于第k个接收天线,DC补偿及相位补偿分别表示为
(8)
φk,n=![]()
(9)
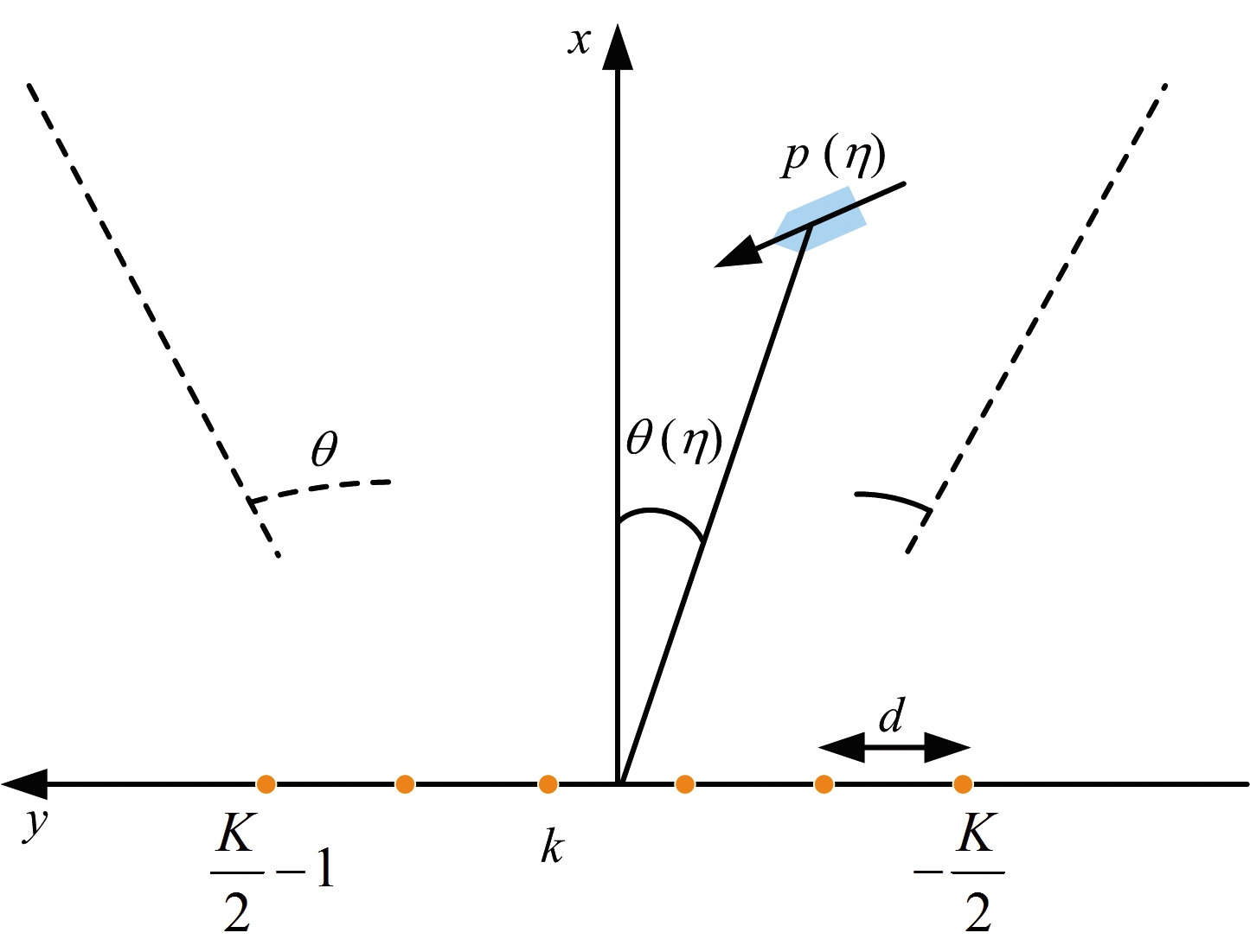
图13 系统构型俯视图
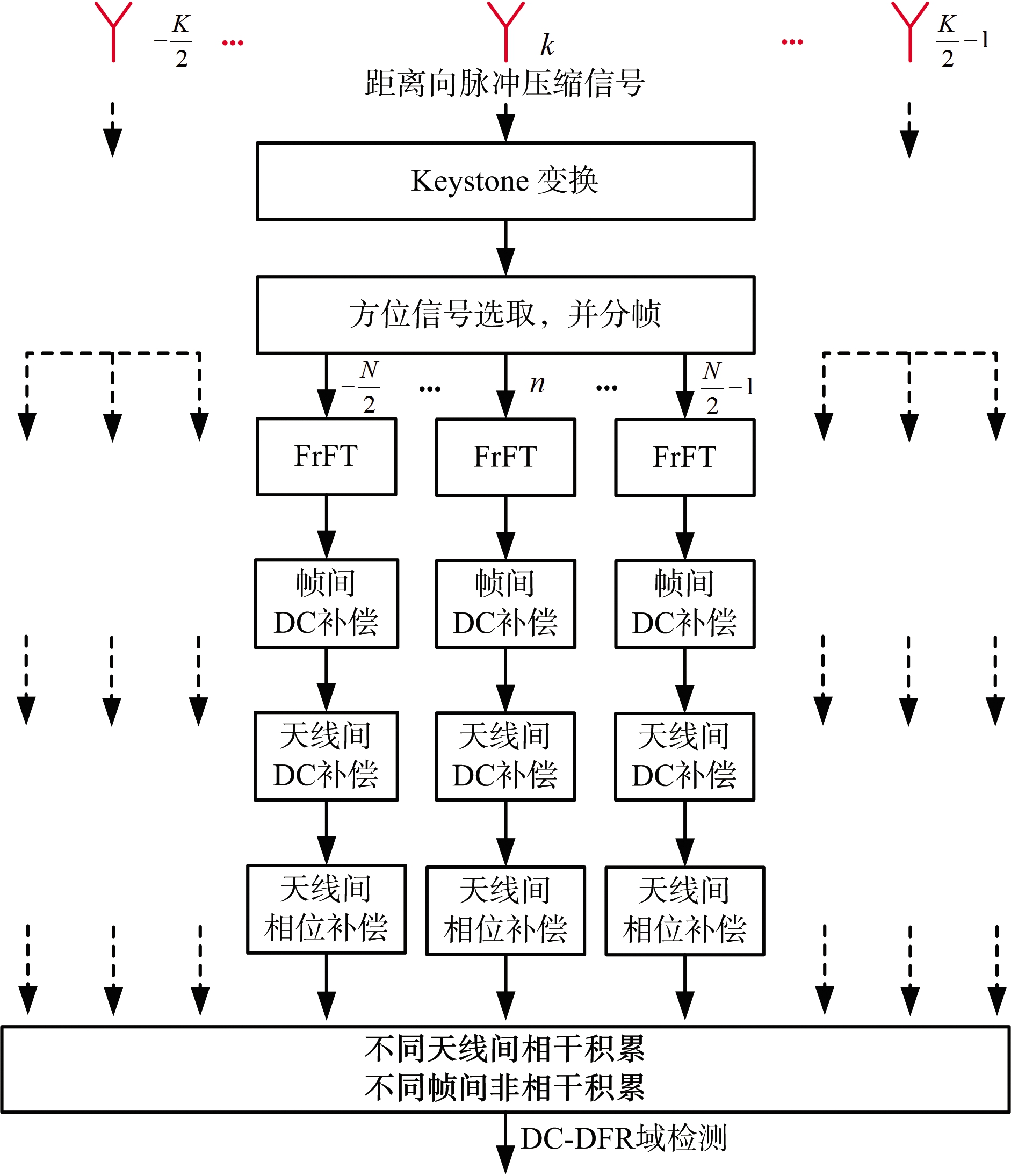
图14 基于多天线的长时间海面目标检测方法流程图
式中,θ0为参考时刻的波达方向,r0为参考时刻目标与接收站之间的距离,vp为参考时刻目标的切向速度,其值与DFR相对应,相关表达式为
(10)
由式(7)~式(9)可知,在进行天线间DC补偿与相位补偿时,实质上的未知参数仅为θ0。通过补偿多组与θ0有关的DC及相位,实现K幅DC-DFR图的积累,当估计的DOA与真实值相符时,可以得到最大的相干积累增益。
最后,与单天线情况相同,多帧信号在帧间DC补偿后进行幅值相加,最终实现多天线、长时间回波信号能量的有效积累。
该海面目标检测方法的有效性通过仿真得到了验证,仿真结果如图15所示[48]。仿真中的参数设置与上述单天线时的仿真参数相同,仅更改接收设备为具有14个接收单元的阵列天线。单帧信号进行多天线相干积累后的结果如图15(a)所示,可以发现,相较于单天线,多天线提高了目标回波的信噪比。图15(b)为多帧非相干积累后的结果,DC-DFR域中存在一处明显的峰值,可以实现该海面目标的有效检测。
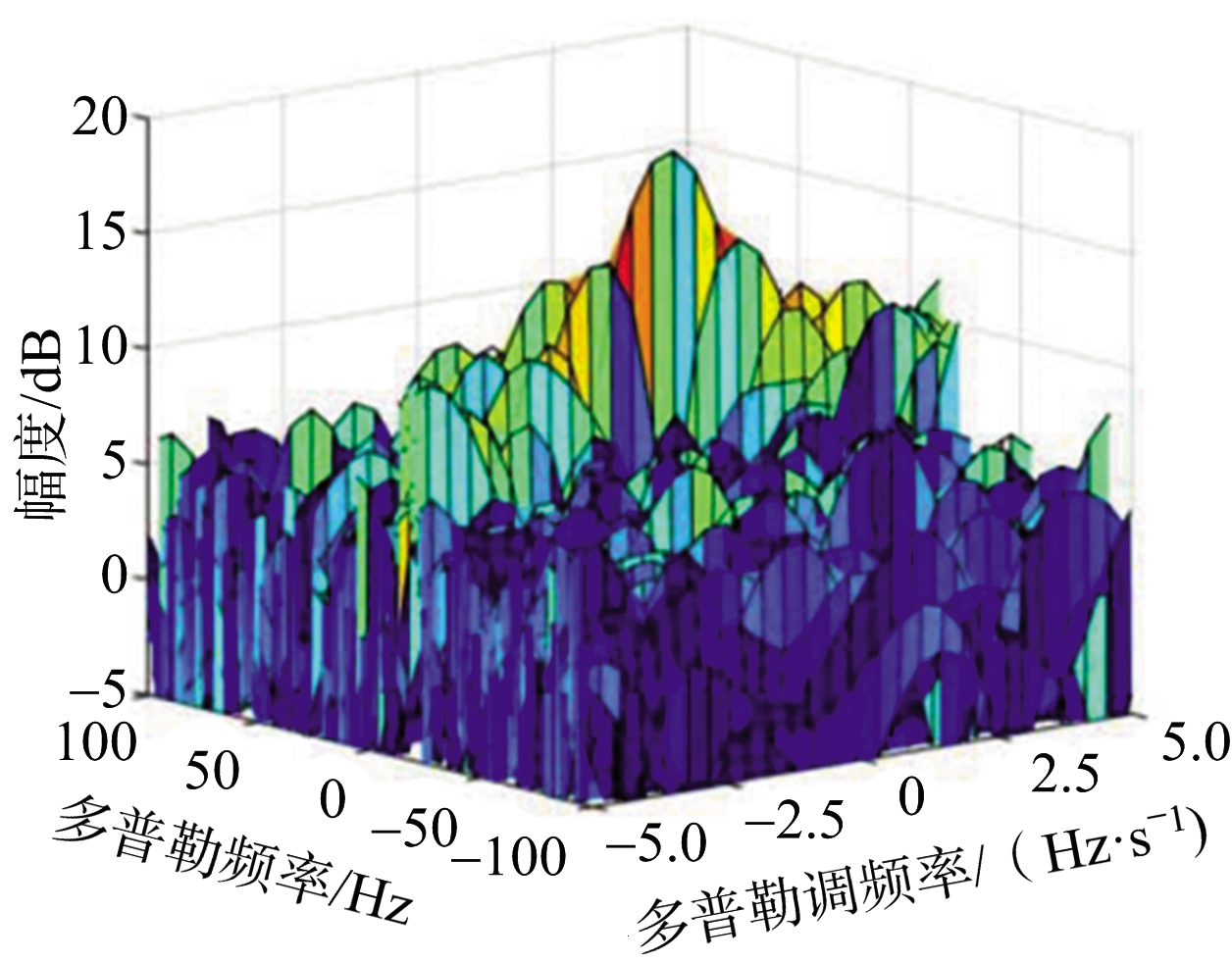
(a) 单帧,多天线

(b) 多帧,多天线
图15 多天线、长积累时间下的仿真结果
上述方法中的FrFT相较于直接的傅里叶变换能得到更优的积累结果,但FrFT自身计算量较大,且本方法需要依次取出不同距离单元的方位信号,增加了处理复杂度。并且,FrFT会造成较高的旁瓣,不利于目标检测。为解决这个问题,电子科技大学的李中余等人又提出一种基于改进的Wigner-Ville分布(M-WVD)的海面目标检测方法[52],用M-WVD替换FrFT实现帧内信号的积累。M-WVD同样能将LFM信号的能量积累到其调频率-中心频率处[53],故该方法仍是在DC-DFR域实现对海面目标的检测。相较于FrFT,由于M-WVD将LFM信号能量全部积累到一点,不存在旁瓣,故该方法更利于海面目标的检测。下面通过公式对M-WVD的流程及原理进行说明。
将LFM信号表示为
sLFM(η)=exp(j2πf0η+jπγ0η2)
(11)
式中,f0和γ0分别表示中心频率与调频率。
对该LFM信号进行相关处理,即
WVD(η,t′)=![]()
(12)
式中,t′为对应的时延,(·)*表示共轭。
对式(12)进行尺度变换η=η′/t′,得到
MWVD(η′,t′)=exp(j2πf0t′+j2πγ0η′)
(13)
对式(13)进行二维傅里叶变换,得到
MWVD(fη′,ft ′)=δ(ft ′-f0)δ(fη′-γ0)
(14)
因此,通过M-WVD能将LFM信号的能量积累到(f0,γ0)处。
相关研究人员通过仿真验证了该方法的有效性,文献[52]中的仿真结果如图16所示。仿真中,海面目标回波在距离向脉冲压缩后信噪比为-24 dB,对该目标回波的积累时间为60 s。对回波信号以2 s为一帧时长进行分帧处理,将目标回波分为30帧。帧内利用M-WVD进行帧内信号的相干积累,单帧信号的相干积累结果如图16(a)所示,目标仍被噪声所淹没,无法实现检测。将30帧M-WVD后的结果在DC补偿后,进行非相干积累,其结果如图16(b)所示,图中存在一处明显的峰值,能实现对该海面目标的有效检测。
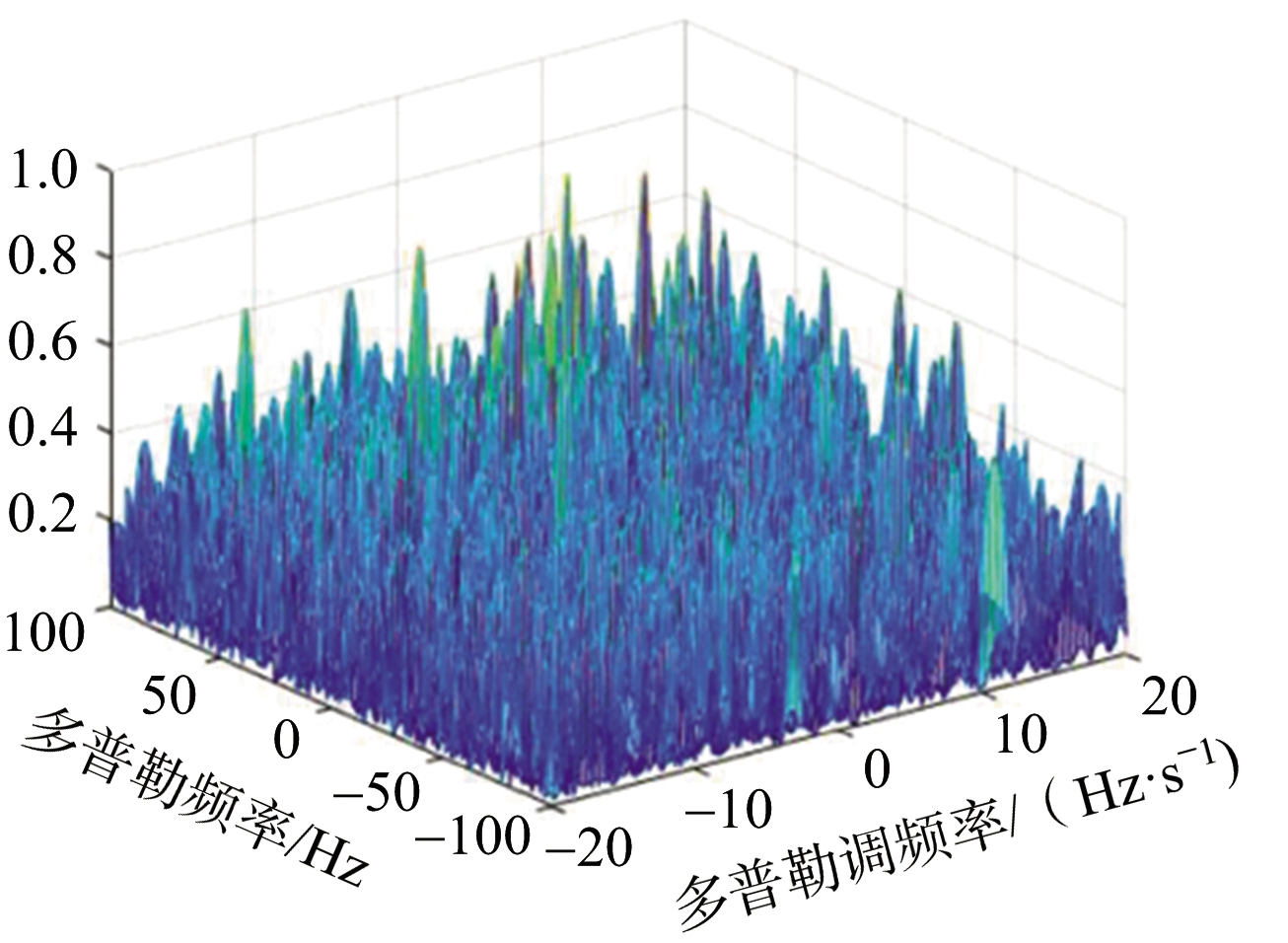
(a) 单帧
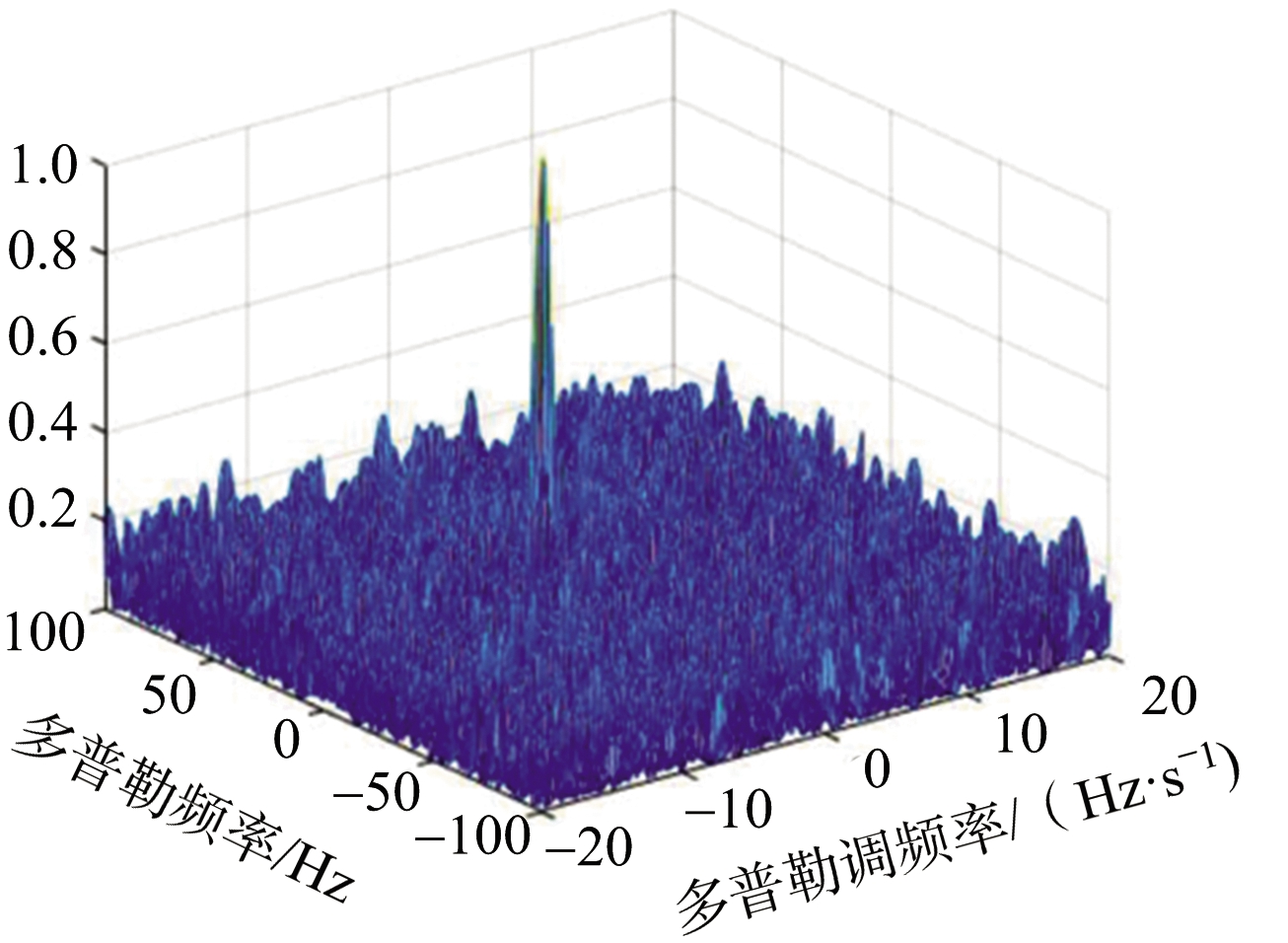
(b) 多帧,经过DC补偿
图16 基于M-WVD的长积累时间仿真结果
3 基于GNSS的无源雷达海面目标检测展望
对于地球表面上任一点,在任意时刻能被同一导航卫星星座中的6~8颗卫星所覆盖[54]。当目前的4个导航卫星系统均完成建设时,地球表面任一点可以被24~32颗卫星所照射,为基于GNSS的无源雷达提供了丰富的信号来源。且导航卫星发射信号采用码分多址(CMDA)或频分多址(FDMA)的复用方式,可以在不增加接收设备的前提下实现对多颗卫星信号的接收。因此,在利用基于GNSS的无源雷达进行海面目标的检测时,可以充分综合不同卫星和不同星座照射下的目标回波信号,实现多站多系统之间的目标回波信息融合,更利于有效实现海面目标检测。同时,由于不同卫星位于不同位置,且该位置是精确已知的,故可以考虑根据多点定位技术,研究利用多颗GNSS卫星作为机会照射源实现海面定位的方法。
但不同导航卫星之间位置的差异,也为海面目标的检测带来了更多挑战。以多颗GNSS卫星作为机会照射源,共同实现对海面目标的检测与定位,所带来的困难主要包括以下两个方面:
1) 不同GNSS卫星照射下的目标回波双基距离历史不同。在对目标的观测时间内,不同GNSS卫星运动轨迹的差异,使得多组目标回波具有不同的距离历史。且由于目标参考时刻的位置与运动状态未知,相关的多组距离历史及其差异是不可知的。若利用基于RD域的海面目标检测方法,分别对多颗GNSS卫星照射下的目标回波进行积累,则目标在多组RD图中将位于不同双基距离处,而该双基距离的差异无法直接进行补偿。若利用基于DC-DFR域的海面目标检测方法,由于无法确定目标在距离徙动校正后所在的距离单元,故不能直接同时取出包含目标的方位信号。
2) 不同GNSS卫星照射下的目标回波多普勒历史不同。双基距离历史变化的差异使得多组目标回波具有不同的多普勒历史,其多普勒参数(主要为DC)不同。同样,相关的多组多普勒历史及其差异是不可知的。若利用基于RD域的海面目标检测方法,分别对多颗GNSS卫星照射下的目标回波进行积累,则目标在多组RD图中将位于不同多普勒频率处。若利用基于DC-DFR域的海面目标检测方法,对多组目标回波进行积累,包含目标的方位信号在DC-DFR图中仍会位于不同DC处,且该差异无法直接进行补偿。
而基于本地坐标系的海面目标检测方法由于最终能量积累所在的平面与距离历史和多普勒历史均无关,在多颗导航卫星照射条件下,仍能应用该方法实现海面目标检测。但在多颗导航卫星作为照射源的条件下,其四维搜索过程的运算量更加庞大,使其使用范围受限。因此,对于多颗导航卫星构成无源雷达,若将其应用于海面目标检测,相应的检测方法还需进行进一步的研究。
4 结束语
本文对基于GNSS的无源雷达海面目标检测技术进行了综述。GNSS由于其全球覆盖的特性,在无源雷达海面目标检测方面受到了广泛的关注,具有广阔的研究与应用前景。GNSS信号到达地球表面的功率密度极低,为以GNSS为信号源的无源雷达海面目标检测带来了困难。为提高目标回波信噪比,实现海面目标的有效检查,国内外均进行了相关研究,并提出了多种目标回波能量积累方法。本文详细介绍了现有基于单颗GNSS卫星与单接收天线的无源雷达海面目标检测方法,并给出了相应的仿真或实验结果,同时分析了不同方法的优缺点。同时,本文指出,利用多颗GNSS卫星构成无源雷达实现海面目标检测将是下一步的发展方向,而本文给出的现有方法在此情况下不再适用或存在一定问题,故仍需要进行相关研究并提出新的海面目标检测方法。
[1] GRIFFITHS H D ,BAKER C J. Passive Coherent Location Radar Systems. Part 1: Performance Prediction[J]. IEE Proceedings - Radar, Sonar and Navigation,2005,152(3):153-159.
[2] 王俊, 保铮, 张守宏. 无源探测与跟踪雷达系统技术及其发展[J]. 雷达科学与技术, 2004,2(3):129-135.
[3] 唐小明, 何友, 夏明革. 基于机会发射的无源雷达系统发展评述[J]. 现代雷达, 2002,24(2):1-6.
[4] BROWN J, WOODBRIDGE K, STOVE A, et al. Air Target Detection Using Airborne Passive Bistatic Radar[J]. Electronics Letters, 2010,46(20):1396-1397.
[5] 陶建义. 基于外辐射源的无源雷达技术[J].现代电子, 2002(3):5-9.
[6] 万显荣. 基于低频段数字广播电视信号的外辐射源雷达发展现状与趋势[J]. 雷达学报, 2012,1(2):109-123.
[7] KUSCHEL H, O'HAGAN D. Passive Radar from History to Future[C]∥ 11th International Radar Symposium, Vilnius, Lithuania:IEEE,2010:1-4.
[8] WANG Jun, ZHANG Shouhong, BAO Zheng. Passive Cogerent Detection via Exploiting Illuminator of Opportunity [C]∥ 6th International Conference on Signal Processing, Beijing, China:IEEE, 2002:1415-1418.
[9] PAINE S, O'HAGAN D, INGGS W M, et al. Evaluating the Performance of FM-Based PCL Radar in the Presence of Jamming[J]. IEEE Trans on Aerospace and Electronic Systems, 2019,55(2):631-643.
[10] PARK G, KIM D, KIM H J, et al. Maximum-Likelihood Angle Estimator for Multi-Channel FM-Radio-Based Passive Coherent Location[J]. IET Radar, Sonar & Navigation, 2018,12(6):617-625.
[11] FU Yan, WAN Xianrong, ZHANG Xun, et al. Side Peak Interference Mitigation in FM-Based Passive Radar via Detection Identification[J]. IEEE Trans on Aerospace and Electronic Systems, 2017,53(2):778-788.
[12] KULPA K, OSINSKI B, GROMEK D, et al. Ground Clutter Stability Analyses in DAB based Passive Radar[C]∥ 2019 Signal Processing Symposium, Krakow, Poland:IEEE, 2019:146-149.
[13] SCHUPBACH C, PATRY C, MAASDORP F, et al. Micro-UAV Detection Using DAB-Based Passive Radar[C]∥ 2017 IEEE Radar Conference, Seattle, WA:IEEE, 2017:1037-1040.
[14] BOURNAKA G, UMMENHOFER M, CRISTALLINI D, et al. Experimental Study for Transmitter Imperfections in DVB-T Based Passive Radar[J]. IEEE Trans on Aerospace and Electronic Systems, 2018,54(3):1341-1354.
[15] BOLCARDI H, DERAKHTIAN M, SHEIKHI A. Dynamic Clutter Suppression and Multitarget Detection in a DVB-T-Based Passive Radar[J]. IEEE Trans on Aerospace and Electronic Systems, 2017,53(4):1812-1825.
[16] KRYSIK P, KULPA K, BACZYK M, et al. Ground Moving Vehicles Velocity Monitoring Using a GSM Based Passive Bistatic Radar[C]∥ IEEE CIE International Conference on Radar, Chengdu, China:IEEE, 2011:781-784.
[17] KNOEDLER B, BROETJE M, KOCH W. A Particle Filter for Track-before-Detect in GSM Passive Coherent Location[C]∥ 2019 IEEE Radar Conference, Boston, MA, USA:IEEE, 2019:1-6.
[18] KRYSIK P, SAMCZYNSKI P, MALANOWSKI M, et al. Velocity Measurement and Traffic Monitoring Using a GSM Passive Radar Demonstrator[J]. IEEE Aerospace and Electronic Systems Magazine, 2012,27(10):43-51.
[19] MARTELLI T, MURGIA F, COLONE F, et al. Detection and 3D Localization of Ultralight Aircrafts and Drones with a WiFi-Based Passive Radar[C]∥ International Conference on Radar Systems, Belfast:IEEE, 2017:1-6.
[20] LOSITO A, STENTELLA M, MARTELLI T, et al. Automatic Vehicles Classification Approaches for WiFi-Based Passive Forward Scatter Radar[C]∥ International Conference on Radar Systems, Belfast:IEEE, 2017:1-6.
[21] FENG W, FRIEDT J, GOAVEC-MEROU G, et al. Passive Radar Delay and Angle of Arrival Measurements of Multiple Acoustic Delay Lines Used as Passive Sensors[J]. IEEE Sensors Journal, 2019,19(2):594-602.
[22] NORDWALL B D. “Silent Sentry” A New Type of Radar[J]. Aviation Week & Space Technology, 1998,149(22):71-72.
[23] OLSEN K E , ASEN W. Bridging the Gap Between Civilian and Military Passive Radar[J]. IEEE Aerospace and Electronic Systems Magazine, 2017,32(2):4-12.
[24] 朱庆明, 吴曼青. 一种新型无源探测与跟踪雷达系统——“沉默哨兵”[J]. 现代电子, 2000(1):1-6.
[25] EDRICH M,SCHROEDER A. Multiband Multistatic Passive Radar System for Airspace Surveillance: A Step Towards Mature PCL Implementations[C]∥ 2013 International Conference on Radar, Adelaide, SA, Australia:IEEE, 2013:218-223.
[26] SCHROEDER A, EDRICH M. CASSIDIAN Multiband Mobile Passive Radar System[C]∥ 12th International Radar Symposium, Leipzig, Germany:IEEE, 2011:286-291.
[27] MILLET N, KLEIN M. Passive Radar Air Surveillance: Last Results with Multi-Receiver Systems[C]∥12th International Radar Symposium, Leipzig, Germany:IEEE, 2011:281-285.
[28] CLEMENTE C,SORAGHAN J J. GNSS-Based Passive Bistatic Radar for Micro-Doppler Analysis of Helicopter Rotor Blades[J]. IEEE Trans on Aerospace and Electronic Systems, 2014,50(1):491-500.
[29] 舒天开. 基于GNSS照射的双基SAR成像方法[D].成都:电子科技大学, 2018.
[30] FAN Xuezhen, LIU Feifeng, ZHANG Tian, et al. Passive SAR with GNSS Transmitters: Latest Results and Research Progress[C]∥ 2017 IEEE International Geoscience and Remote Sensing Symposium, Fort Worth, TX, USA:IEEE, 2017:1043-1046.
[31] ZHENG Yu, YANG Yang, CHEN Wu. Analysis of Radar Sensing Coverage of a Passive GNSS-Based SAR System[C]∥ 2017 International Conference on Localization and GNSS, Nottingham, UK:IEEE,2017:1-6.
[32] WANG T, LIU B, QIANG W, et al. GNSS Passive Radar Imaging Based on Differential Aperture[C]∥ 2019 18th International Conference on Optical Communications and Networks, Huangshan, China:IEEE,2019:1-3.
[33] LI Zhongyu, SANTI F, PASTINA D, et al. Multi-Frame Fractional Fourier Transform Technique for Moving Target Detection with Space-Based Passive Radar[J]. IET Radar, Sonar & Navigation, 2017,11(5):822-828.
[34] WILLIAM L M,JAMES A S. Principles of Modern Radar: Radar Application[M]. NJ, US:SciTech Publishing Inc, 2012:509-519.
[35] ZHANG Yun, TIAN Luman, MENG Wanting, et al. Feasibility of Code-Level Altimetry Using Coastal BeiDou Reflection (BeiDou-R) Setups[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015,8(8):4130-4140.
[36] XU Jia, YU Ji, PENG Yingning, et al. Radon-Fourier Transform for Radar Target Detection, I: Generalized Doppler Filter Bank[J]. IEEE Trans on Aerospace and Electronic Systems, 2011,47(2):1186-1202.
[37] CHEN Xiaolong, GUAN Jian, LIU Ningbo, et al. Maneuvering Target Detection via Radon-Fractional Fourier Transform-Based Long-Time Coherent Integration[J]. IEEE Trans on Signal Processing, 2014,62(4):939-953.
[38] CHEN Xiaolong, GUAN Jian, HUANG Yong, et al. Radon-Linear Canonical Ambiguity Function-Based Detection and Estimation Method for Marine Target with Micromotion[J]. IEEE Trans on Geoscience and Remote Sensing, 2015,53(4):2225-2240.
[39] 关键, 陈小龙, 于晓涵. 雷达高速高机动目标长时间相参积累检测方法[J]. 信号处理, 2017,33(S1):1-8.
[40] CHEN Xiaolong, GUAN Jian,LI Xiuyou,et al. Effective Coherent Integration Method for Marine Target with Micromotion via Phase Differentiation and Radon-Lv’s Distribution[J]. IET Radar, Sonar& Navigation, 2015, 9(9):1284-1295.
[41] LI Xiaolong, CUI Guolong, KONG Lingjiang, et al. Fast Non-Searching Method for Maneuvering Target Detection and Motion Parameters Estimation[J]. IEEE Trans on Signal Processing, 2016, 64(9):2232-2244.
[42] MA H, ANTONIOU M, CHERNIAKOV M, et al. Maritime Target Detection Using GNSS-Based Radar: Experimental Proof of Concept[C]∥ 2017 IEEE Radar Conference, Seattle, WA, USA:IEEE,2017:464-469.
[43] MA H, ANTONIOU M, PASTINA D, et al. Maritime Moving Target Indication Using Passive GNSS-Based Bistatic Radar[J]. IEEE Trans on Aerospace and Electronic Systems, 2018,54(1):115-130.
[44] PIERALICE F, SANTI F, PASTINA D, et al.GNSS-Based Passive Radar for Maritime Surveillance: Long Integration Time MTI Technique[C]∥ 2017 IEEE Radar Conference, Seattle, WA, USA:[s.n.], 2017:508-513.
[45] SANTI F, PASTINA D, BUCCIARELLI M. Maritime Moving Target Detection Technique for Passive Bistatic Radar with GNSS Transmitters[C]∥ 18th International Radar Symposium, Prague, Czech Republic:IEEE, 2017:1-10.
[46] PASTINA D, SANTI F, PIERALICE F, et al. Maritime Moving Target Long Time Integration for GNSS-Based Passive Bistatic Radar[J]. IEEE Trans on Aerospace and Electronic Systems, 2018,54(6):3060-3083.
[47] LI Zhongyu, SANTI F, PASTINA D, et al. Satellite-Based PCL for Moving Target Detection Using Keystone Transform and FrFT[C]∥ 2016 CIE International Conference on Radar, Guangzhou, China:IEEE,2016:1-4.
[48] LI Zhongyu, SANTI F, PASTINA D, et al. Passive Radar Array with Low-Power Satellite Illuminators Based on Fractional Fourier Transform[J]. IEEE Sensors Journal, 2017,17(24):8378-8394.
[49] MENDLOVIC D, OZAKTAS H M, LOHMANN A W. Fractional Correlation[J]. Applied Optics, 1995,34(2):303-309.
[50] 陈小龙, 关键, 黄勇, 等. 雷达低可观测动目标精细化处理及应用[J]. 科技导报, 2017,35(20):19-27.
[51] 陈小龙, 关键, 何友, 等. 高分辨稀疏表示及其在雷达动目标检测中的应用[J]. 雷达学报,2017,6(3):239-251.
[52] LAN Y, LI Z, LI W, et al. Maritime Moving Target Detection with Space-Based Passive Radar Based on Multi-Frame Modified Wigner-Ville Distribution[C]∥ 12th European Conference on Synthetic Aperture Radar, Aachen, Germany:IEEE, 2018:1-4.
[53] XING M, WU Renbiao, LI Yuanmeng, et al. New ISAR Imaging Algorithm Based on Modified Wigner-Ville Distribution[J]. IET Radar, Sonar & Navigation, 2009,3(1):70-80.
[54] SANTI F, ANTONIOU M, PASTINA D. Point Spread Function Analysis for GNSS-Based Multistatic SAR[J]. IEEE Geoscience and Remote Sensing Letters, 2015,12(2):304-308.




