0 引言
在强地物杂波、气象杂波和仙波等复杂干扰环境下,雷达回波在目标检测后,仍会包含大量的杂波剩余点迹,严重影响杂波环境下雷达正常的探测和跟踪性能[1]。而且,雷达回波信号在目标检测后,其点迹数据中除了包含目标尺寸、运动等本身固有物理属性外,还蕴含着可以鉴别目标点迹的特征参数。通过分析雷达点迹数据所反映的目标特征,可发掘出稳定用于区分目标点迹与杂波点迹的特征参数,再通过设计好的分类器进行分类判决[2]。因此,目标检测后借助目标点迹特征参数,进一步区分目标点迹与杂波剩余点迹是非常必要和可行的。
目前,一些国内外的专家学者利用雷达回波特征,针对此问题做了一些相应的研究。文献[3]针对雷达信号处理后较多的杂波剩余问题,通过对信号处理后的杂波剩余信号和目标信号提取杂波图迭代方差、高阶累积量、信噪比和归一化幅度方差等特征参数,运用K近邻算法对真实目标点迹和剩余杂波点迹进行鉴别,经过目标点迹鉴别处理后,剩余杂波点迹抑制率接近68.5%。但该方法在抑制剩余杂波的同时也滤除了较多的目标点迹。文献[4]针对航管雷达,提出利用最近邻分类器,根据多普勒速度、功率谱、波束驻留时间等特征区分目标与杂波,但是鉴别准确率不是很高。以上几种研究方法为区分雷达目标点迹和杂波点迹提供了一定的技术参考,但都相应地存在一定缺陷,也都没有应用到雷达点迹形成过程中所生成的特征参数。
本文针对目标检测过后过多的杂波剩余点迹对雷达探测和跟踪性能的影响,利用雷达点迹中的特征参数,提出了一种基于PSO-SVM算法的雷达点迹真伪鉴别方法。本方法将PSO算法与SVM算法结合在一起,选取雷达点迹形成过程中所生成的特征参数,先利用PSO算法对SVM参数进行优化选择,再利用优化参数后的SVM算法对雷达点迹进行真伪鉴别,测试点迹鉴别准确率,并与传统SVM算法进行对比分析。
1 支持向量机
支持向量机(SVM)是90年代中期发展起来的基于统计学习理论中VC维理论和结构风险最小原理的一种机器学习方法,根据有限的样本信息在模型的复杂性和学习能力之间寻求最佳折中,以获得最好的推广能力,其最终的目的是根据输入数据样本寻找到一个最优分类超平面,用于模式分类和非线性回归[5]。
支持向量机主要分为:线性可分支持向量机,通过硬间隔最大化处理是严格线性可分的数据集;线性支持向量机,通过软间隔最大化处理线性不可分的数据集;非线性支持向量机,通过引入核函数处理非线性数据集。本文中用到的是非线性支持向量机[6]。
非线性支持向量机针对非线性问题,使用核函数将训练样本从原始空间映射到一个更高维度的空间,使得样本在这个空间中线性可分,从而转化为线性可分问题,具体形式如下[7]:
假设已知训练集Z={(x1,y1),(x2,y2),…,(xn,yn)},xi为特征向量,yi为属性标签。令Φ(x)表示将x映射后的特征向量,于是,在特征空间中划分超平面所对应的模型可表示为
f(x)=ωTΦ(x)+b
(1)
式中,ω和b为模型参数。由软间隔最大化可得
s.t. yi(ωTΦ(xi)+b)≥1-l(yi(ωTΦ(xi)+
b)-1), i=1,2,…,n
(2)
式中,l为损失函数,C为惩罚因子。
选取适当的和核函数,式(2)的对偶问题是

式(3)求解后可得到,其分类函数如下:
(4)
根据需要解决的不同的数据分类问题,核函数主要分为线性核、多项式核、Sigmoid核和高斯径向基核。本文选用了高斯径向基核函数,其表达式为
(5)
式中,σ为核函数参数。
由SVM的推导过程中可以看出,影响SVM分类器的关键因素是核函数参数σ和惩罚因子C。因此,本文将利用PSO算法对这两个参数进行优化选择。
2 粒子群优化算法
粒子群算法,也称粒子群优化算法或鸟群觅食算法粒子群算法,属于进化算法的一种。鸟类等生物在寻找食物的过程中,一方面是依靠自身的探索,另一方面则是依靠伙伴相互之间的经验交流,从而能快速准确地找到在搜索区域中最好的食物源。PSO算法正是以上述生物现象作为模型而提出的一种进化优化算法。每个寻优的问题解都是搜索空间中的一只鸟,即“粒子”。每个粒子都包含有位置和速度两种信息,通过位置信息,可以计算出粒子的适应度值,从而确定粒子的优劣;而速度信息决定它们飞行的方向和距离[8]。
假设D维空间中,有N个粒子[9]:
粒子i位置:Xi=(xi1,xi2,…,xiD),xid∈[Xmin,d,Xmax,d];
粒子i速度:Vi=(vi1,vi2,…,viD),vid∈[Vmin,d,Vmax,d];
个体最优位置:pbesti=(pi1,pi2,…,piD);
全局最优位置:gbest=(g1,g2,…,gD);
其中,1≤d≤D,1≤i≤N。
则粒子i速度和位置迭代公式如下:
(6)
(7)
式中,ω为惯性权重,c1为局部学习因子,c2为全局学习因子,r1,r2为区间(0,1)内的独立随机数。
3 基于PSO-SVM的雷达点迹真伪鉴别算法模型
本文利用PSO-SVM算法对雷达点迹进行真伪鉴别。定义粒子由二维参数向量(C,σ)所决定,群体中每个粒子的优劣通过适应度函数值的大小进行评价,适应度值由所选取的适应度函数和二维参数向量(C,σ)共同决定。本文选取雷达点迹真伪鉴别准确率作为适应度函数。
基于PSO-SVM算法的雷达点迹真伪鉴别具体步骤如下:
1) 对采集的雷达点迹数据进行预处理。通过分析雷达点迹数据所反映的目标特征,提取可有效区分目标点迹与杂波点迹的特征信息(多普勒速度、EP个数、距离跨度、方位跨度、原始幅度、EP等级、点迹质量和方位向凝聚点迹个数等特征参数),并分为训练集和测试集。
2) 初始化PSO算法参数。粒子群粒子数量n,粒子维度(待寻优参数个数)m,局部学习因子c1,全局学习因子c2,惯性权重ω,算法最大迭代次数Tmax,算法收敛精度ξ,参数惩罚因子的取值范围[Cmin,Cmax]和参数核函数参数的取值范围[σmin,σmax]。
3) 输入训练集,利用5折交叉验证计算适应度函数值的平均值,记录、比较每一个粒子遍历过的最优个体适应度函数值和全局最优适应度函数值以及对应的参数[8]。
4) 对粒子群中每个粒子计算后,判断是否满足迭代结束条件,若满足条件,则输出最优参数组合(C*,σ*);如不满足条件,则利用式(6)和式(7)对粒子的速度和位置进行更新,再返回步骤3)。
5) 利用输出的最优参数组合(C*,σ*)SVM模型对测试集的点迹进行真伪鉴别,计算点迹鉴别准确率。
4 实验仿真与分析
本次实验中用到的数据均是从X型空管雷达上采集的实测点迹数据。在点迹数据中选取了8 000个目标点迹,8 000个杂波点迹。
本次实验总共分为两个部分:实验1,利用PSO算法对SVM算法参数核函数参数σ和惩罚因子C进行优化选择,获得最优参数组合;实验2,利用最优参数组合下的SVM算法,对获取的雷达点迹数据进行真伪鉴别,测试点迹鉴别准确率。
4.1 PSO算法优化SVM参数
本实验利用PSO算法优化选择SVM核函数参数σ和惩罚因子C。利用5折交叉验证计算雷达点迹鉴别准确率的平均值,记录、比较每一个粒子遍历过的点迹鉴别准确率以及对应的参数组合,从中选取最优参数组合。
在本次实验中,SVM算法的参数设置为:核函数参数σ∈[0.01,100],惩罚因子C∈[0.01,100];PSO优化算法的参数设置为:粒子种群数量N=20,粒子维度D=2,惯性权重ω=0.8,局部学习因子c1=2,全局学习因子c2=2,算法最大迭代次数Tmax=50,算法收敛精度ξ=0.001。
实验结果如图1所示。
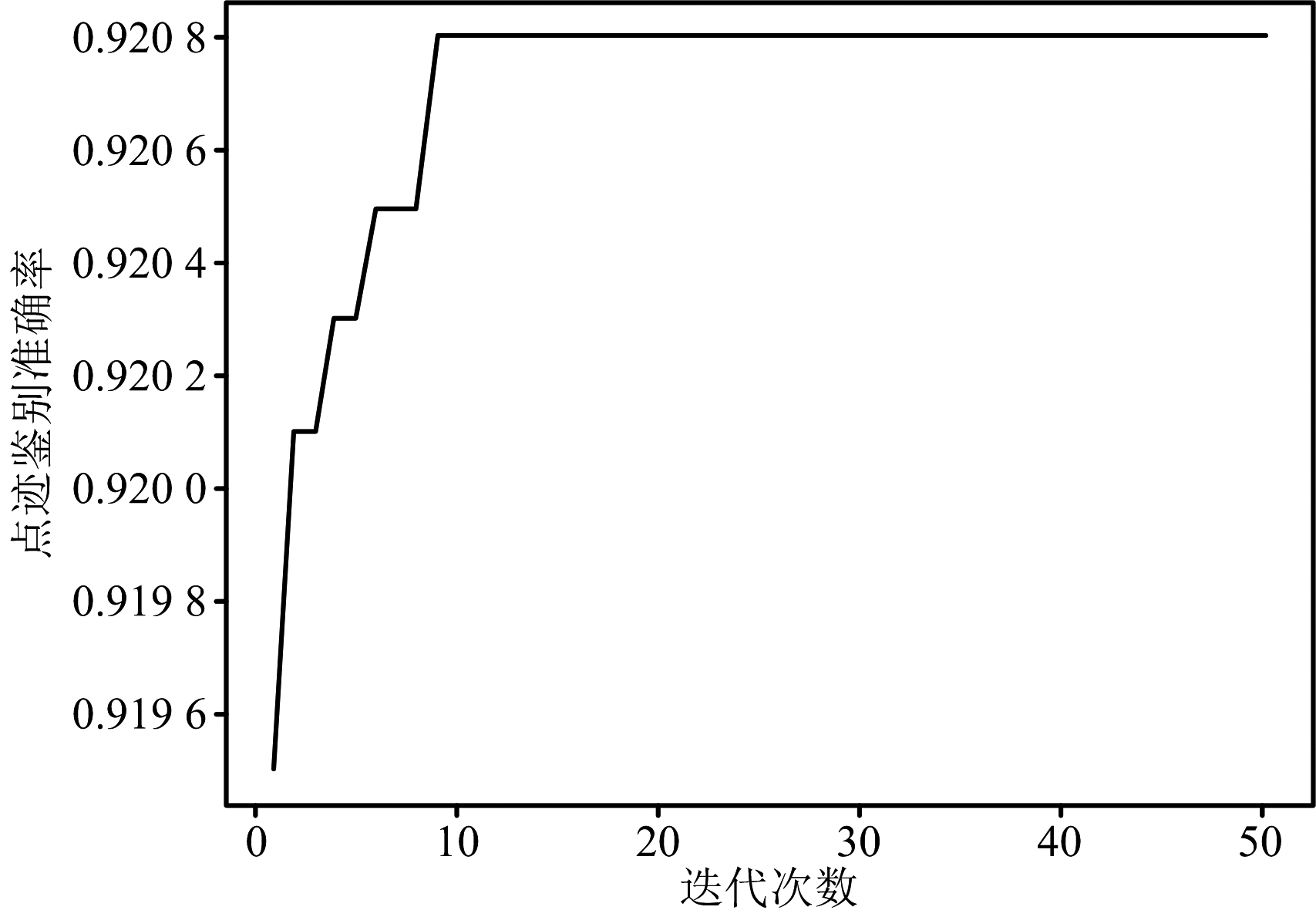
图1 点迹鉴别准确率图
由图1可以得出雷达点迹鉴别准确率最终稳定在0.921左右。其对应的最优参数组合为(15,22)。
4.2 最优参数下的SVM算法点迹鉴别分析
本实验对比了最优参数组合下的SVM与传统SVM两种算法的点迹鉴别准确率。对比结果如表1所示。
表1 点迹鉴别准确率对比
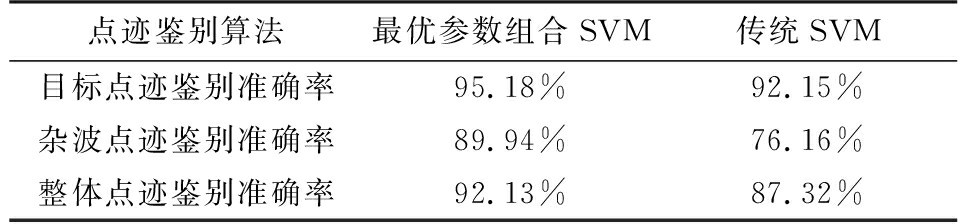
点迹鉴别算法最优参数组合SVM传统SVM目标点迹鉴别准确率95.18%92.15%杂波点迹鉴别准确率89.94%76.16%整体点迹鉴别准确率92.13%87.32%
由表1可知,最优参数组合下的SVM算法的目标点迹鉴别准确率达到了95.18%,杂波点迹鉴别准确率达到了89.94%,整体的点迹鉴别准确率达到了92.13%,在这三个方面均优于传统SVM算法。
另外,再从原本的8 000个目标点迹和8 000个杂波点迹中随机取2 000个目标点迹和2 000个杂波点迹作为测试数据。分别计算3种算法各自的所有点迹中鉴别出的目标点迹数、所有点迹中鉴别出的杂波点迹数、目标点迹中鉴别出的目标点迹数和杂波点迹中鉴别出的杂波点迹数,对比3种算法对目标点迹和杂波点迹的具体鉴别效果。
其中,所有点迹中鉴别出的目标点迹数和所有点迹中鉴别出的杂波点迹数是指从4 000个点迹中分别鉴别出目标点迹和杂波点迹的数量;目标点迹中鉴别出的目标点迹数是指从2 000个目标点迹鉴别出目标点迹的数量;杂波点迹中鉴别出的杂波点迹数是指从2 000个杂波点迹中鉴别出杂波点迹的数量。对比结果如表2所示。
表2 点迹真伪鉴别点数对比
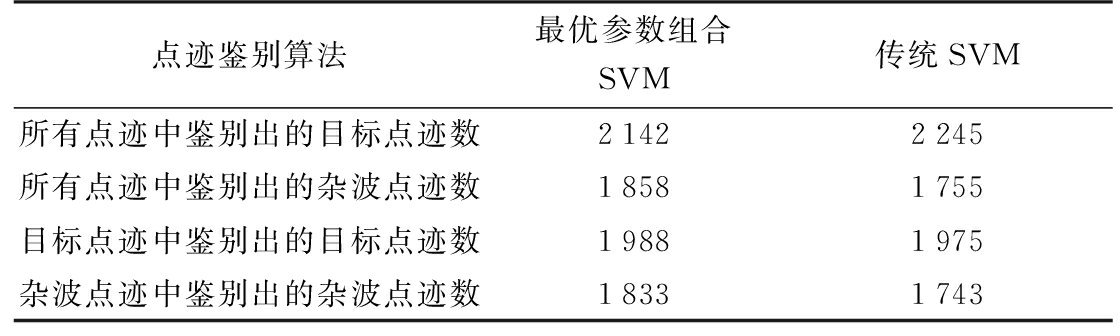
点迹鉴别算法最优参数组合SVM传统SVM所有点迹中鉴别出的目标点迹数21422245所有点迹中鉴别出的杂波点迹数18581755目标点迹中鉴别出的目标点迹数19881975杂波点迹中鉴别出的杂波点迹数18331743
由表2可知,最优参数组合下的SVM算法在所有点迹中鉴别出的目标点迹数、所有点迹中鉴别出的杂波点迹数、目标点迹中鉴别出的目标点迹数和杂波点迹中鉴别出的杂波点迹数四个方面均优于传统SVM算法。
另外从点迹数据中选取15 000个目标点迹和15 000个杂波点迹,对比最优参数SVM算法和传统SVM算法的杂波滤除效果。对比结果如图2所示。由图2可以看出,分别经过最优参数SVM和传统SVM进行点迹鉴别,再将鉴别出的杂波点迹滤除掉后,与原始点迹对比,大部分的杂波回波点迹被滤除掉,获得了较好的效果。对比图2(c)和图2(d)可以看出,最优参数下的SVM算法的杂波滤除效果要优于传统SVM算法。
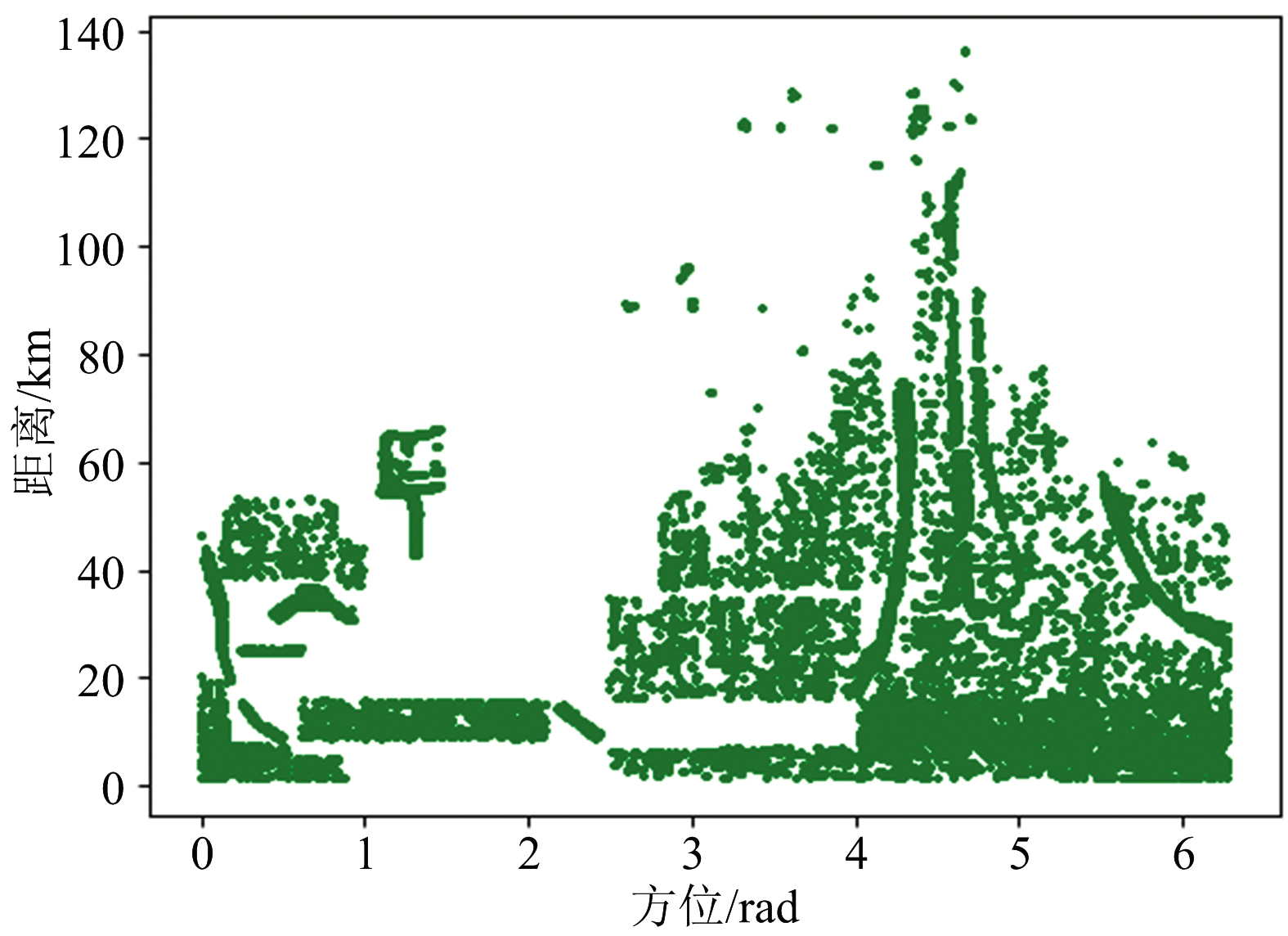
(a) 原始点迹图
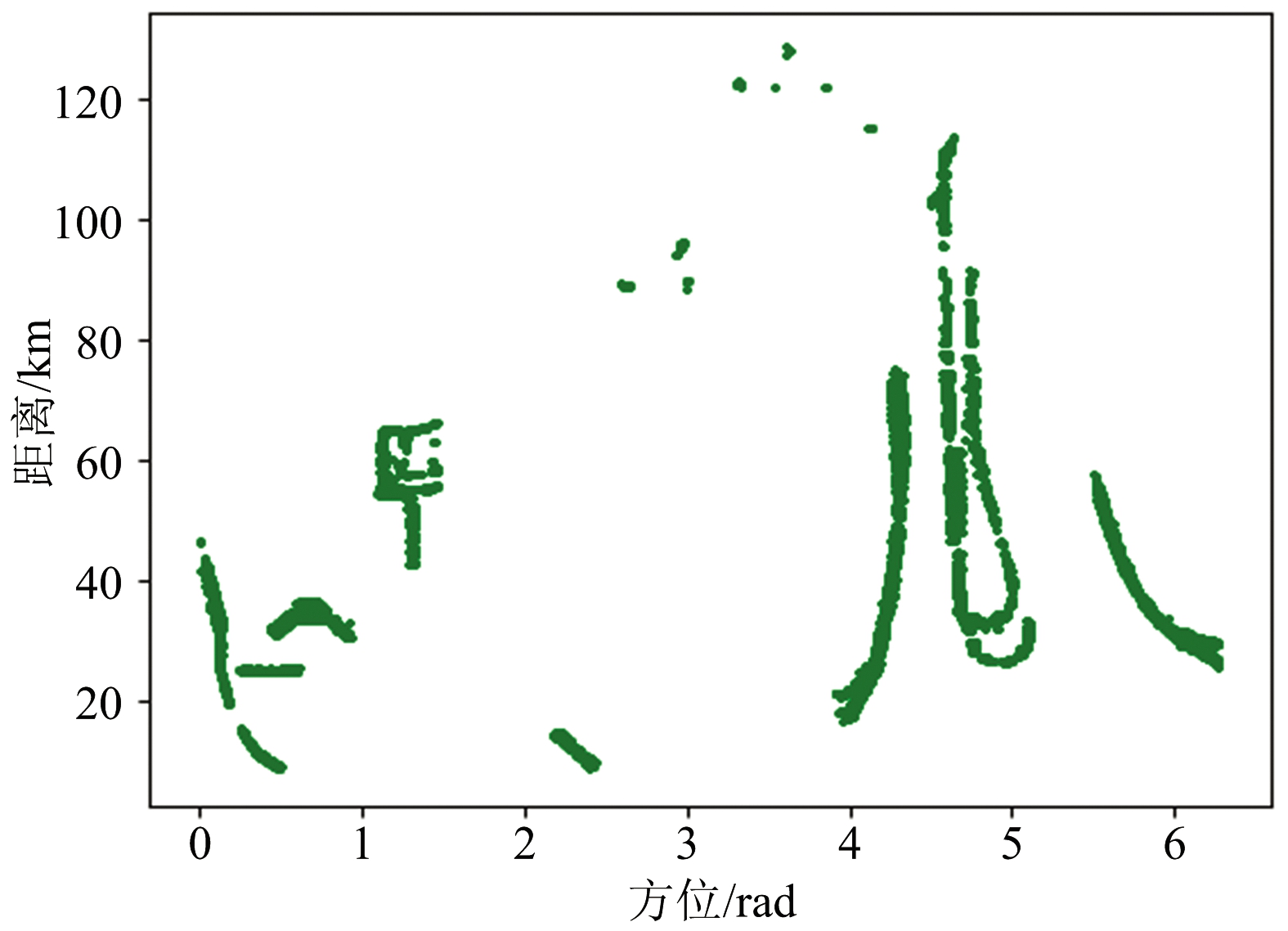
(b) 真实目标点迹图
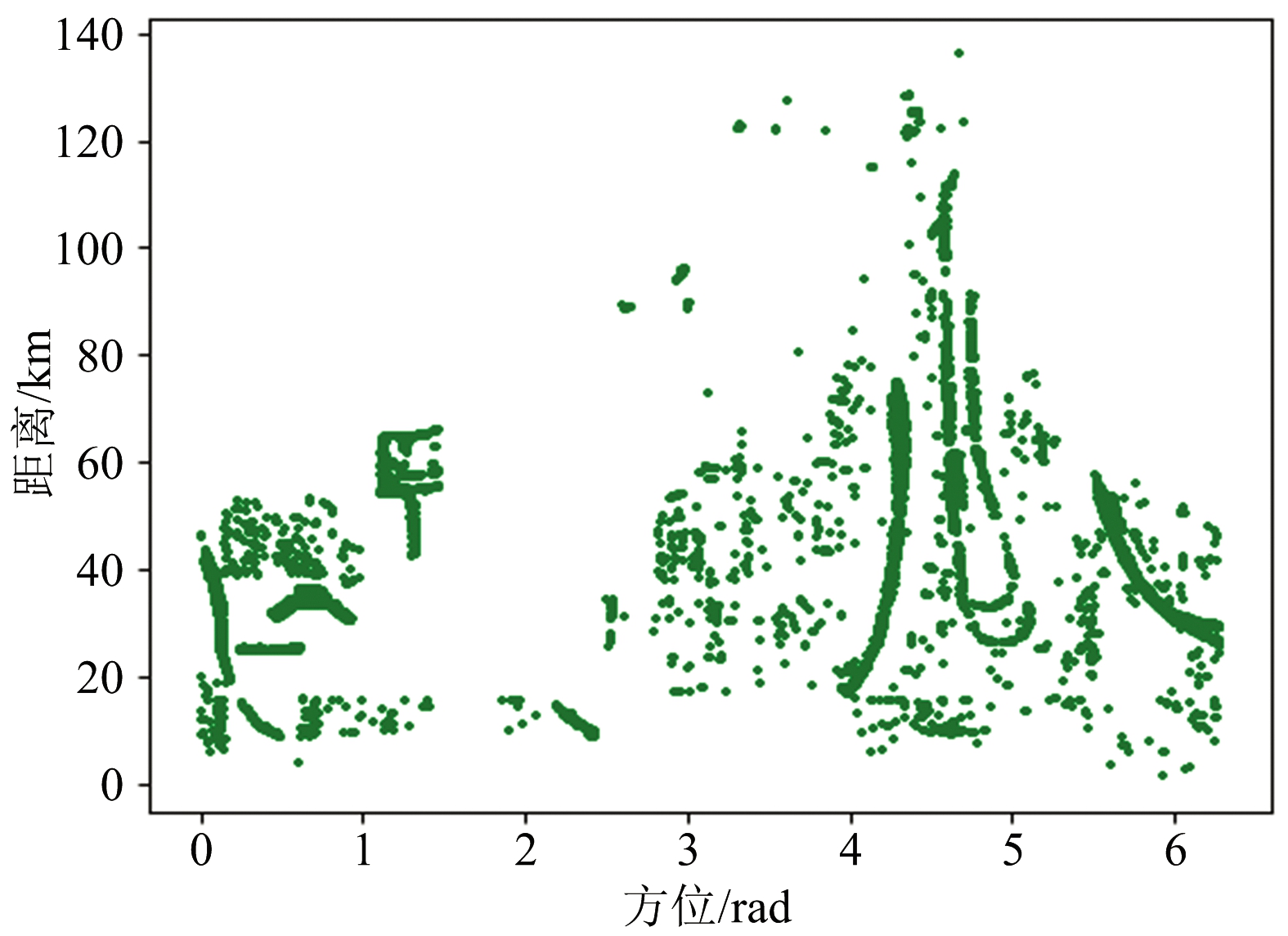
(c) 最优参数SVM处理后目标点迹图
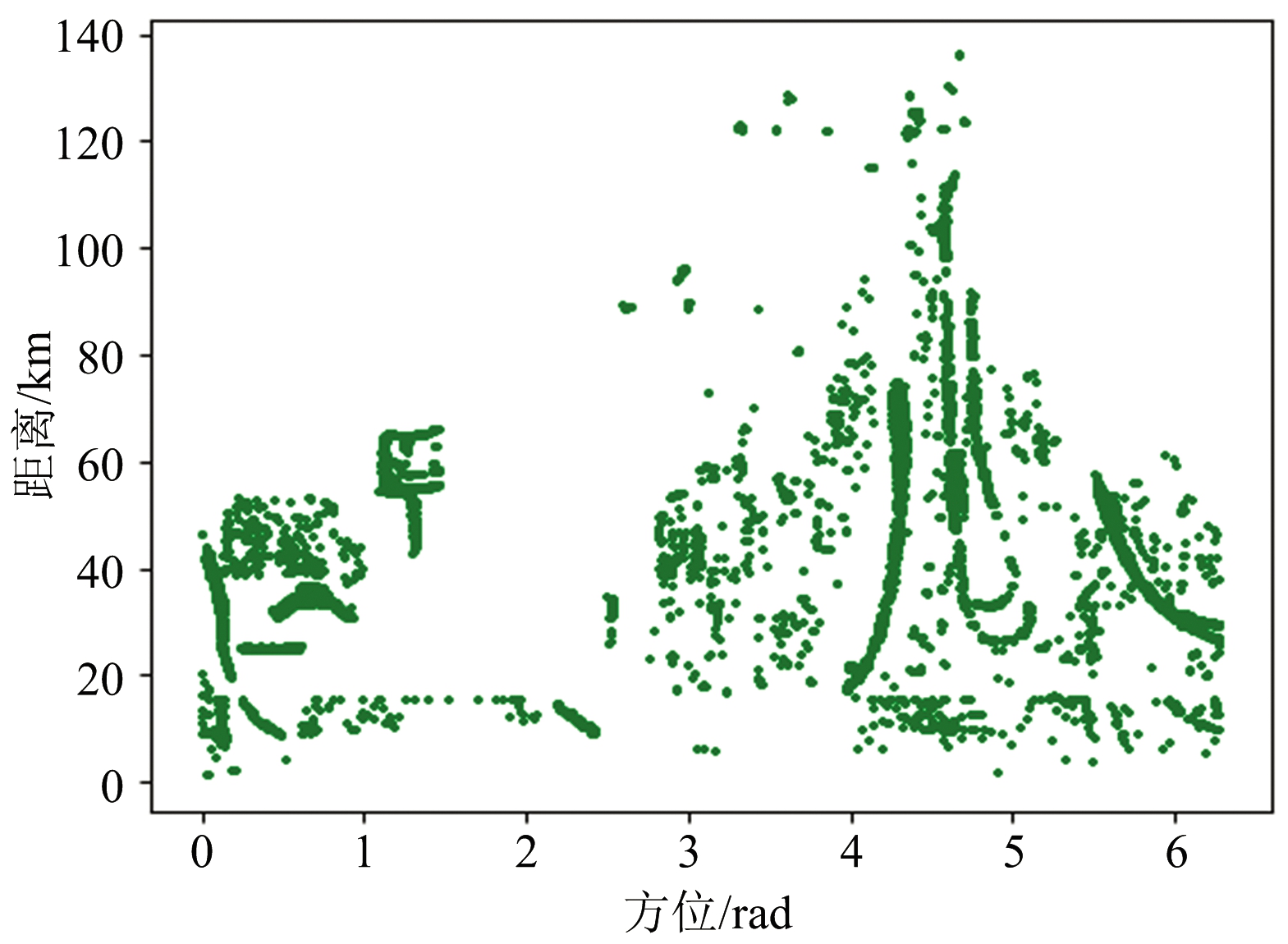
(d) 传统SVM处理后目标点迹图
图2 杂波点迹滤除效果对比
5 结束语
本文提出了一种基于PSO-SVM算法的雷达点迹真伪鉴别方法,该方法利用雷达点迹形成过程中所生成的特征参数,先利用PSO算法对SVM算法参数优化,获得最优参数组合,再利用最优参数组合下SVM算法对雷达点迹进行真伪鉴别,滤除杂波点迹。通过与传统SVM算法比较,验证了本文所提算法的可行性和有效性。实验结果表明,该算法点迹鉴别准确率达到了92.13%,杂波滤除效果均优于传统SVM算法。
[1] XU Shiyou,TANG Chaojing,JING Peiliang,et al. Efficient Centralized Track Initiation Method for Multistatic Radar[C]∥ International Conference on Information Fusion,Salamanca,Spain:[s.n.], 2014:132-138.
[2] 胡卫东,杜小勇,张乐锋,等.雷达目标识别理论[M].北京:国防工业出版社,2017:1-15.
[3] 韦涛.杂波抑制与真假目标判别[D].西安:西安电子科技大学,2017:15-34.
[4] NEUMANN C,SENKOWSKI H. Plot Based Target Classification for ATC Radars[C]∥2015 16th International Radar Symposium,Dresden,Germany:IEEE, 2015:254-259.
[5] 丁世飞,齐丙娟,谭红艳.支持向量机理论与算法研究综述[J].电子科技大学学报, 2011, 40(1):2-10.
[6] 周志华.机器学习[M].北京:清华大学出版社,2016:121-139.
[7] 王彩云,黄盼盼,李晓飞,等.基于AEPSO-SVM算法的雷达HRRP目标识别[J].系统工程与电子技术,2019,41(9):1984-1989.
[8] 张灿斌,段世忠,赵书敏.改进适应度函数的阵列综合粒子群算法[J].雷达科学与技术,2011,9(3):281-285.
[9] 满春涛,刘博,曹永成.粒子群与遗传算法优化支持向量机的应用[J].哈尔滨理工大学学报,2019,24(3):87-92.
