0 引言
挖掘窄带雷达对目标识别的潜力具有重要意义。期望利用窄带雷达能够对空间重点目标群和非重点目标类群(碎片等目标)进行初步分类识别和筛选[1-2]，雷达在此基础上可集中更多的时间和能量资源重点对重要目标进行跟踪，并为后续跟踪识别提供重点目标位置信息。目标雷达散射截面(Radar Cross Section，RCS)信息反映了目标的几何特征和电磁散射特征，还隐含了目标的运动特征，可以从中提取数学特征通过模式识别技术对目标分类识别[3-5]。
支持向量机(Support Vector Machines，SVM)作为一种常用来解决分类和回归问题的通用机器学习方法[6]，对小样本、非线性问题和高维问题等方面表现出良好泛化能力与预测能力，能够避免“维数灾难”的弊端，被广泛地应用于诸多领域，同样也适用于雷达目标识别[7-8]。SVM算法复杂度与训练样本数目成指数关系，而SVM增量算法需要用大数据集训练迭代，运算的存储空间和时间代价花费巨大[6, 9-11]。
基于RCS统计特征数据，SVM算法可以对空间目标进行分类识别。如果仅采用单次样本数据训练SVM分类器，样本数据全面性不足，很难保证未来的预测效果。因此，样本集需要进行初采样，以节省计算资源同时保证选出的样本子集能够实现全集合的SVM分类精度。基于此，本文提出并应用了一种用于RCS统计特征的支持向量机训练集约减方法，成功缩减了数据样本集规模，同时保持支持向量机训练分类的精度。
1 支持向量机算法
支持向量机是建立在结构风险最小化等严格坚实的统计学习理论基础上的。基本数学模型如下：
(1)
s.t.yi(wTXi+b)+δi≥1, δi≥0, i=1,2,…,d
式中：d为样本总数量；Xi为k维特征的样本向量；yi为类别标识变量，两类问题标志值默认取值为{-1,1}；ω为超平面法向量;b为偏置；δ为松弛变量，代表该样本点的分类误差；Csvm为惩罚系数。通过构造拉格朗日函数，对问题的模型进行转化，求解最优解
使得每一个样本都要满足优化问题的KKT条件：
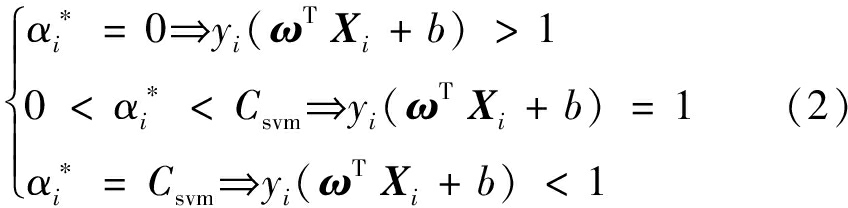决策函数的超平面法向量
偏置
决策函数表达式为
(3)
支持向量是拉格朗日系数不为0所对应的样本向量。从决策函数的表达式可以看出，最终分类超平面完全由支持向量决定。
2 本文SVM训练样本选取策略
通常来讲，SVM训练样本中非支持向量数目远大于支持向量的数目，而支持向量集就能够构造该训练样本集的最优分类超平面。Syed等最早开展SVM增量学习研究[9]，每次增量学习将新增样本集与原样本集的支持向量构成新样本集进行训练，依次不断循环迭代。曾文华等提出了一种利用KKT(Kaush-Kuhn-Tucher)条件互相检验的SVM增量学习方法[10]，分别对旧和新增样本集训练后，互相找出违反对方KKT条件的样本构成新的训练集。但是，上述方法完全筛选淘汰所有的非支持向量，而在全集训练条件下，原训练集的一些非支持向量可能转化为支持向量，而该部分样本被忽略将降低分类精度。因此，必须采取有快速高效的采样方法，淘汰掉每次样本集中的无用样本以提高训练的速度，同时保留重要信息来保证SVM训练的精度。
支持向量一定是分布在每一类训练集几何意义上边缘的样本点，而不可能是训练集内部的点。基于此，本文对每次试验的样本集进行初选样，选取两类边界样本和边缘样本构成样本子集。两类边界样本是两类样本的交际区中，那些靠得近却又不属同类的样本，支持向量常常被包含在其中。边缘样本是单类样本空间分布几何意义上边缘区域的样本集，代表了样本集空间分布的几何信息，常常包含了那些可能由非支持向量转化为支持向量的样本。
2.1 两类边界样本的抽取方法
中心距离就是样本到样本中心的距离。已知两类样本，那么根据类别就分别有两个中心点。某一样本点到所属类别中心距离称为自中心距离，到非属类别中心的距离称为互中心距离，定义中心距离比值为自中心距离和互中心距离的比值。一般地，两类边界向量样本的中心距离比值较大[11]。
Xi是k维特征的样本向量，p(Xi)是其多维高斯分布密度函数，表达式如下：
(4)
式中，μ为同类样本向量的均值向量，β为协方差矩阵。已知两类样本，那么根据类别就分别得到两个相应的多维高斯分布。定义某样本点高斯模型概率比值为非属类别与所属类别的高斯分布概率密度比值。一般地，两类边界向量样本的高斯模型概率比值较大。本文融合考虑中心距离比值和高斯分布概率比值，按照比值从大到小的顺序依次穿插排序，然后按所需样本数量再取样。
2.2 抽取单类边缘样本集
多维高斯分布模型在几何上根据特征向量维度不同呈现为椭圆或者超椭球体结构。首先对每类样本求解出其高斯分布模型，对样本分别沿所属类别的超椭球轴投影，选择轴投影轴两端的样本，最后按所需样本数量再取样。
2.3 直推式实验设计
直推式实验设计(Transductive Experimental Design，TED)是一种代表性的适用于无任何标签信息的无监督主动学习算法。根据无标注样本所包含的潜在结构分布信息设计合适的采样策略，来选择最能代表样本集结构分布的高价值样本。在最优实验设计算法的基础上，将给定数据集上的预测误差作为优化目标[12-13]。本文采取直推式实验设计的采样算法，对上述两类边界样本集和单类边缘样本集进行再采样，缩减样本集规模到指定水平。
3 实验结果与分析
本文使用包含有代表空间重点目标和非重点目标的RCS仿真数据，标记为目标1(Class 1)和目标2(Class 2)。利用上述RCS数据滑窗分段处理提取统计特征：计算每段时间窗内的RCS序列的统计特征，以每个数据段的一组多维特征构成一个特征向量(样本向量)，最终得到480个样本。
雷达目标RCS序列的常用统计特征有：(1)位置特征参数，描述了目标RCS时间序列的平均位置和特定位置，常用的有均值、极大/极小值、众数等；(2)散布特征参数，描述了目标RCS序列的离散程度，极差、方差以及变异系数等；(3)分布特征参数，描述了目标RCS序列统计分布的总体密度函数的特征，标准偏度系数、标准峰度系数、多阶中心矩等；(4)变换域特征，把RCS数据变换到其他特征域后重新进行特征统计，提取新的特征以突出目标特性，例如，采用傅里叶变换后的统计特征：频谱均值、熵、低频能量比等。
空间重点目标和非重点目标的RCS差异主要体现在群内部成员形状以及微运动特征上。例如，空间重点目标飞行过程中常常保持姿态稳定特性，而非重点目标(碎片等)会产生翻滚等较为剧烈的微动变化，此时统计特征方差所表述的RCS序列的变化离散特性差异性大，有助于目标分类识别。总之，目标状态差异可以由RCS统计特征的不同得以体现。本节实验提取了3组(A，B，C)二维特征(特征为：{A1，A2}，{B1，B2}，{C1，C2})向量构成样本集，所述特征进行了减去均值再除以标准差的标准化数据处理，避免某一特征值过大或过小。
3.1 两类边界样本的融合抽取实验
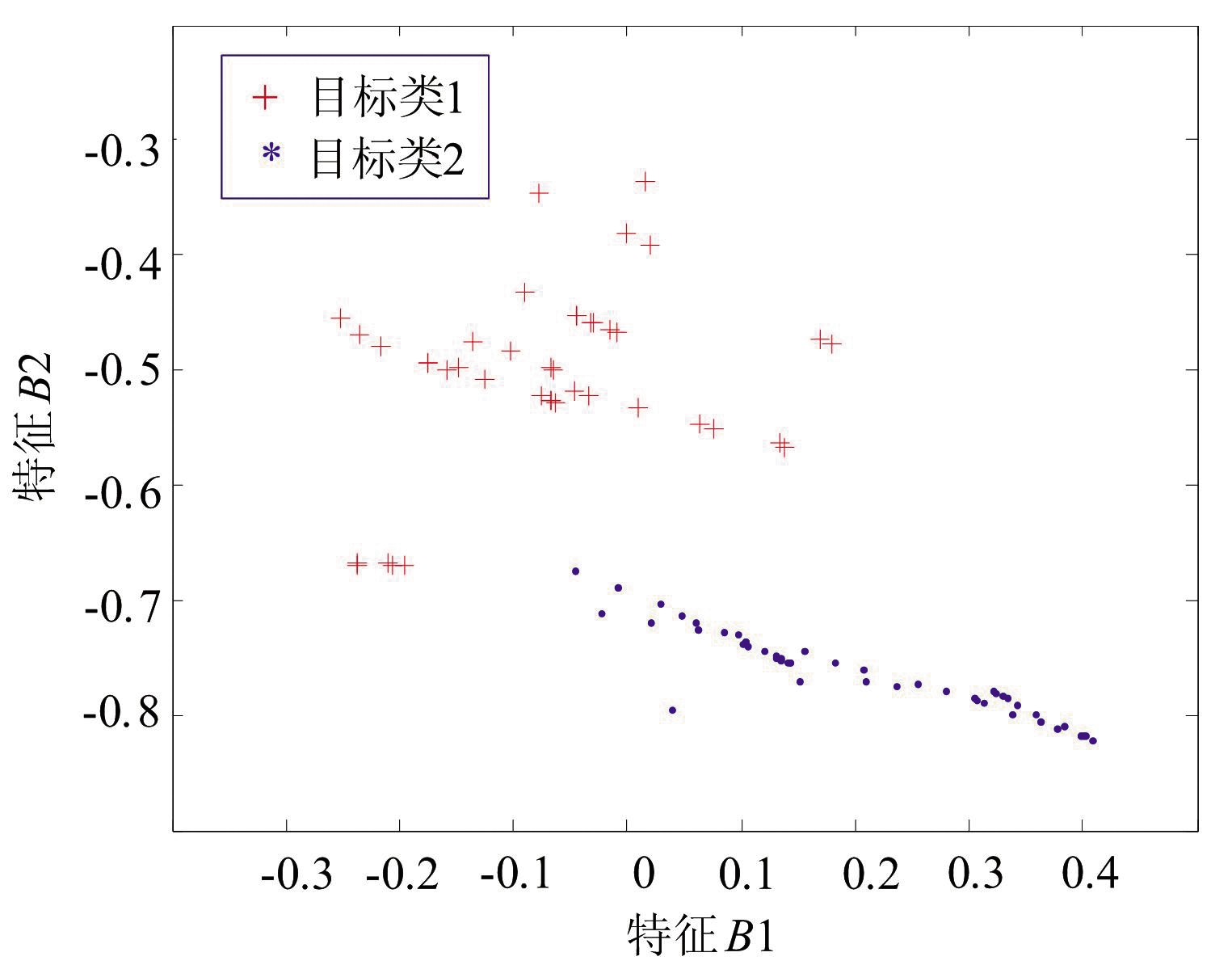
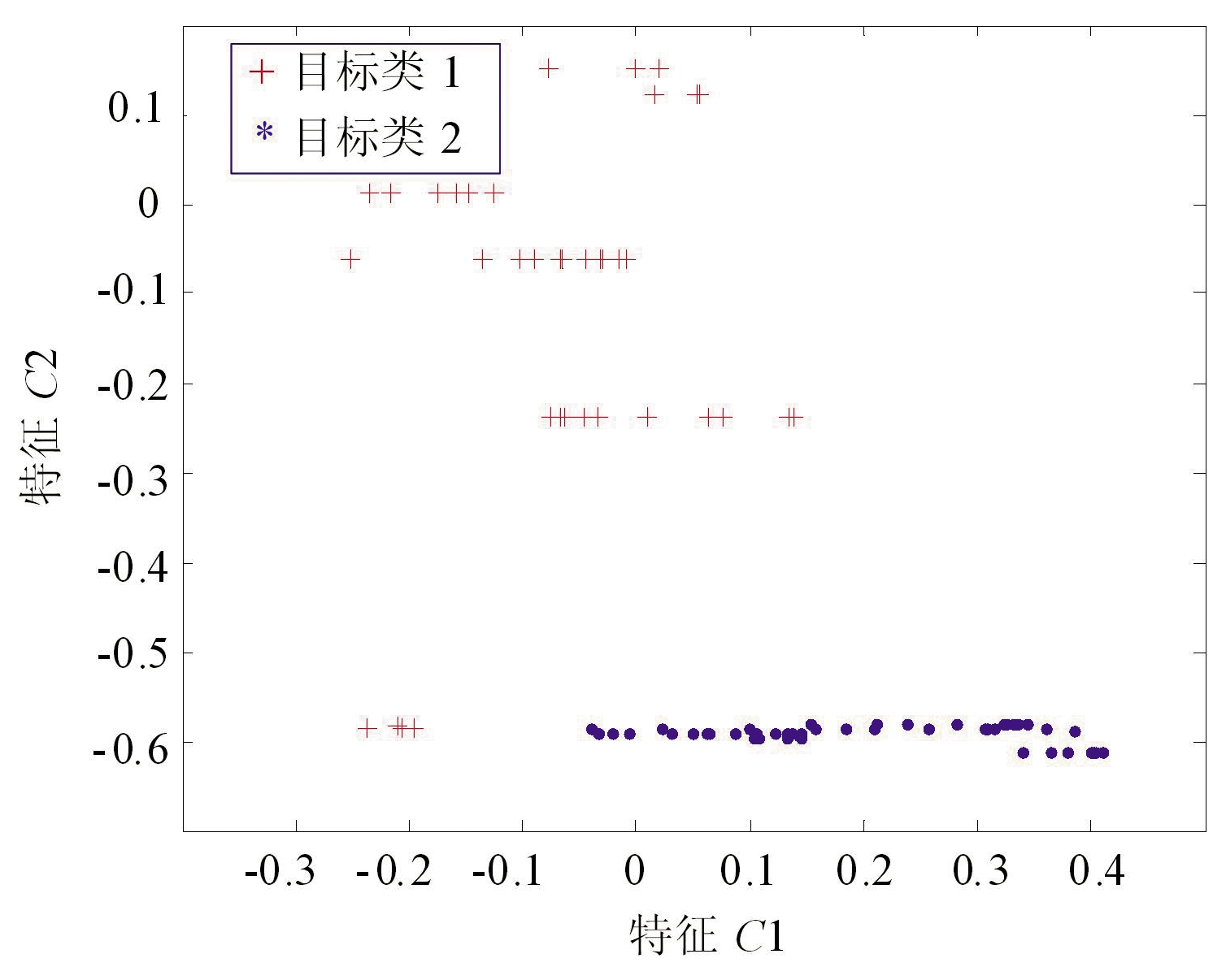
分别采用中心距离比值、高斯分布概率比值和融合方法，抽取训练集中两类边界样本，抽取样本的比例为20%。A样本集({A1，A2})，两类边界样本的抽取结果如图1所示。B样本集({B1，B2})情形下，两类边界样本的抽取结果如图2所示。C样本集({C1，C2})情形下，两类边界样本的抽取结果如图3所示。
(a)中心距离比抽样分布
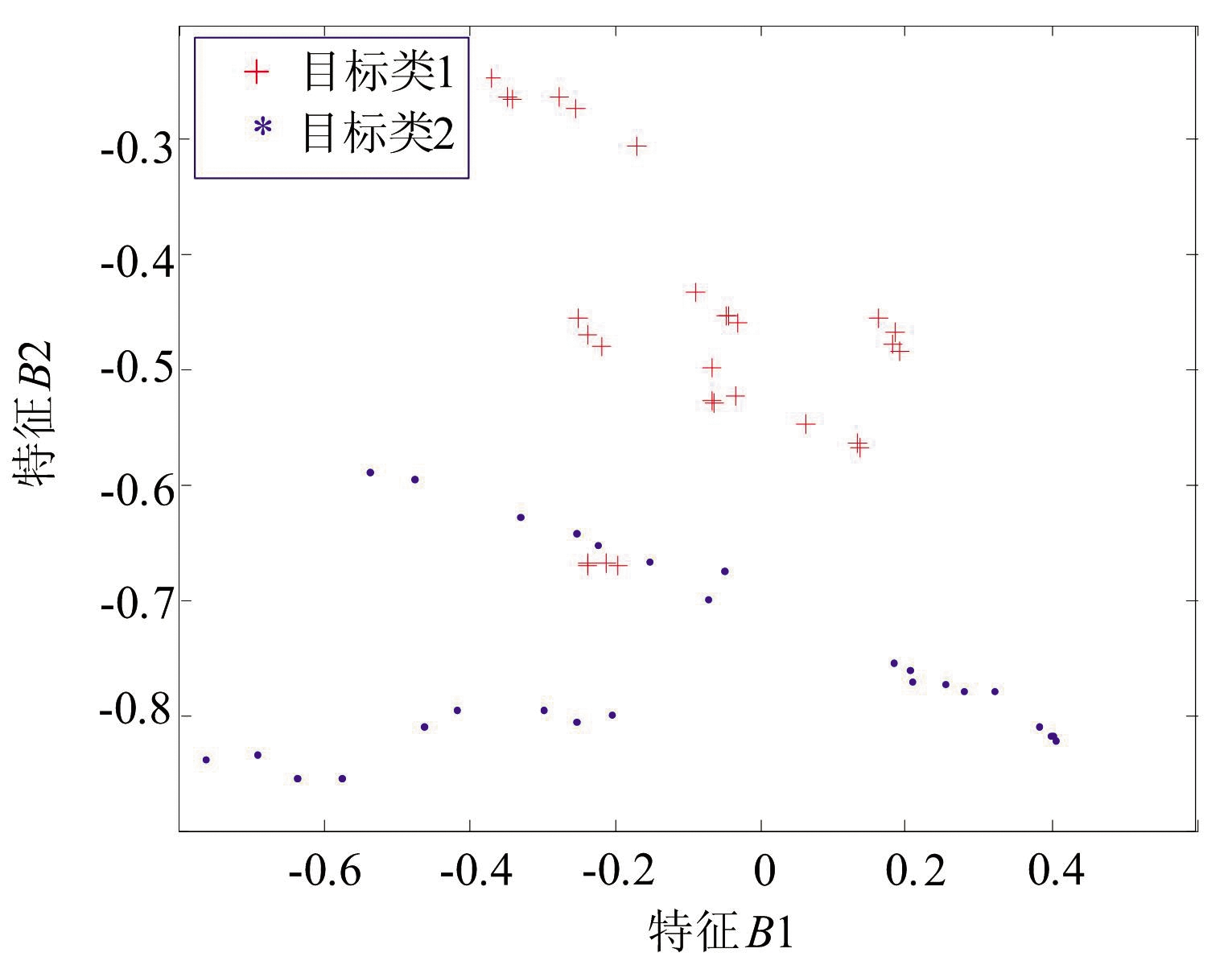
(b)融合方法抽样分布
图2 B样本集的两类边界样本抽取结果对比
(a)中心距离比抽样分布
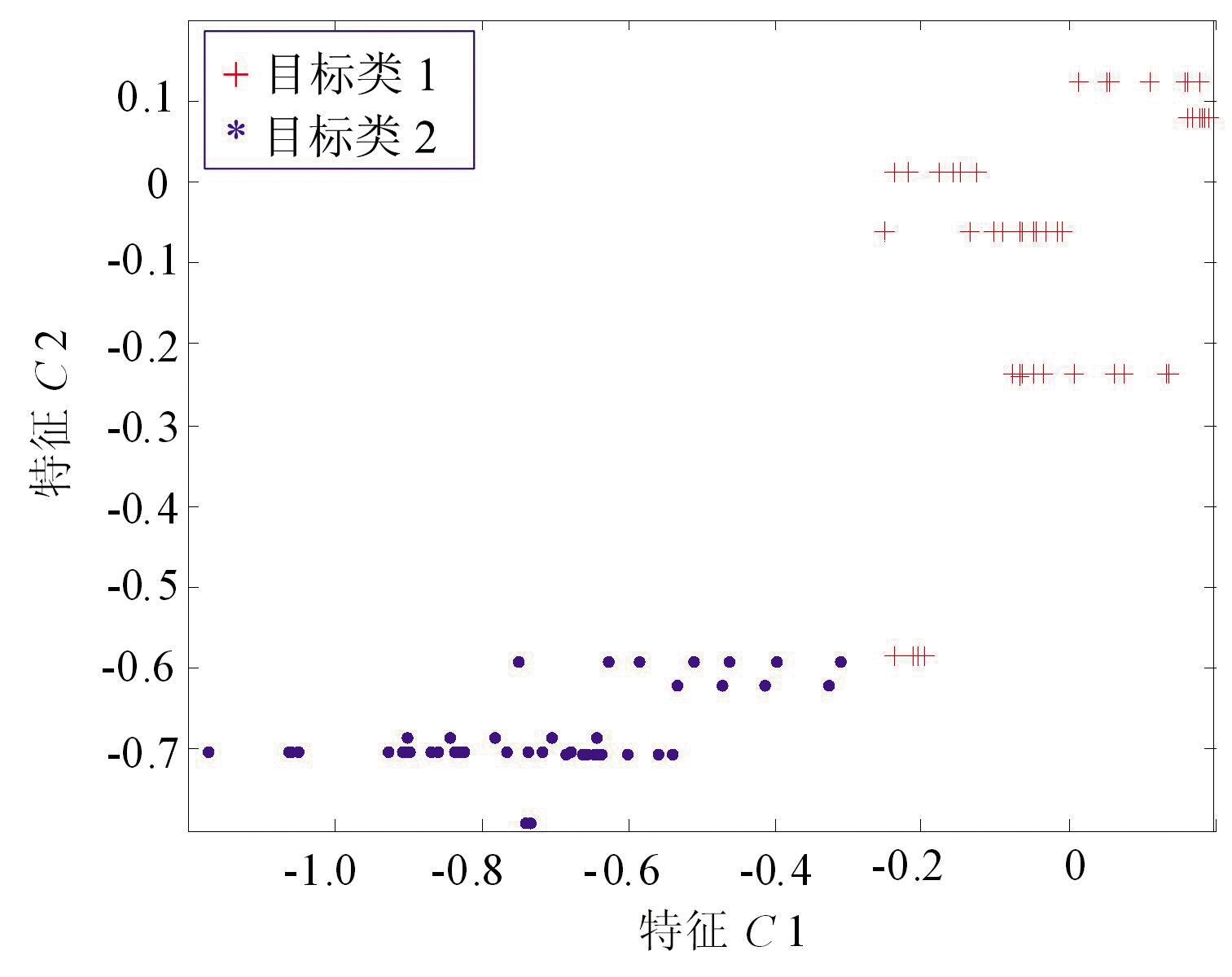
(b)概率比抽样分布
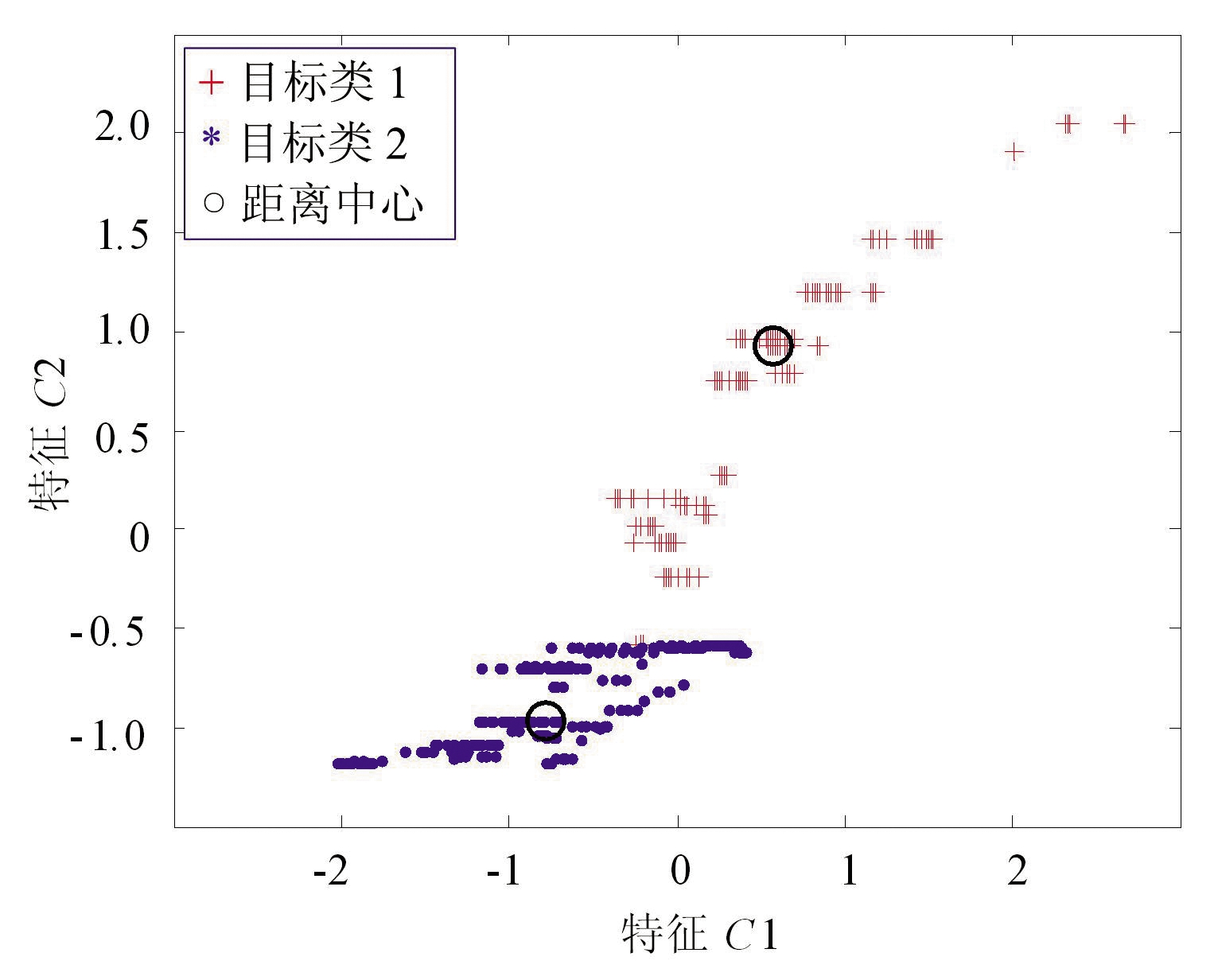
(c)样本全集与类别中心位置
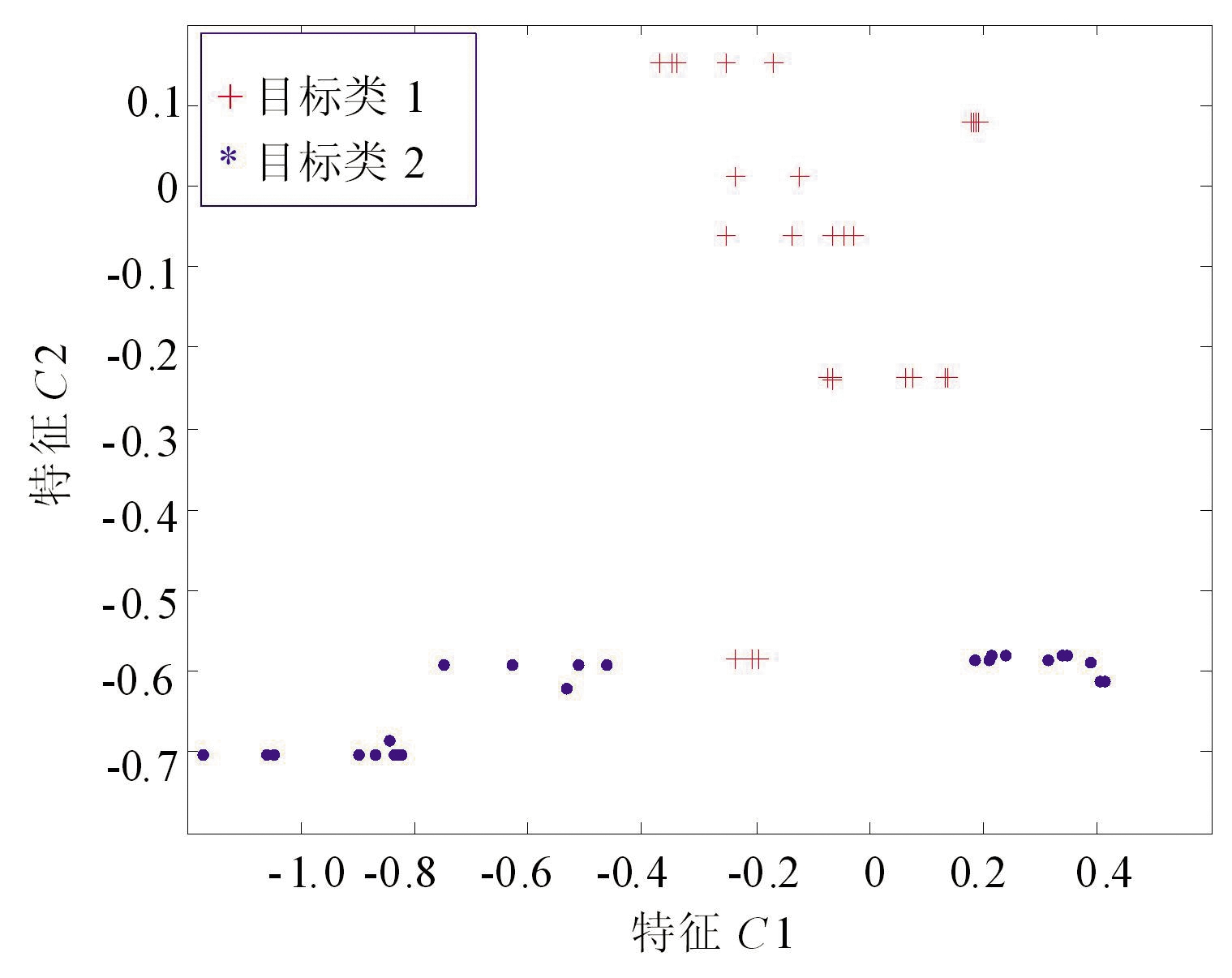
(d)融合方法抽样分布
图3 C样本集的两类边界样本抽取结果对比
图1(a)是采用概率比值方法抽取的样本分布图，图1(b)是本文所述将距离/概率比值融合抽取的样本分布图。比较图1(a)和(b)，图1(b)显然更能代表两类边界样本分布特性，图1(b)所示的融合方法抽取效果显著高于图1(a)。
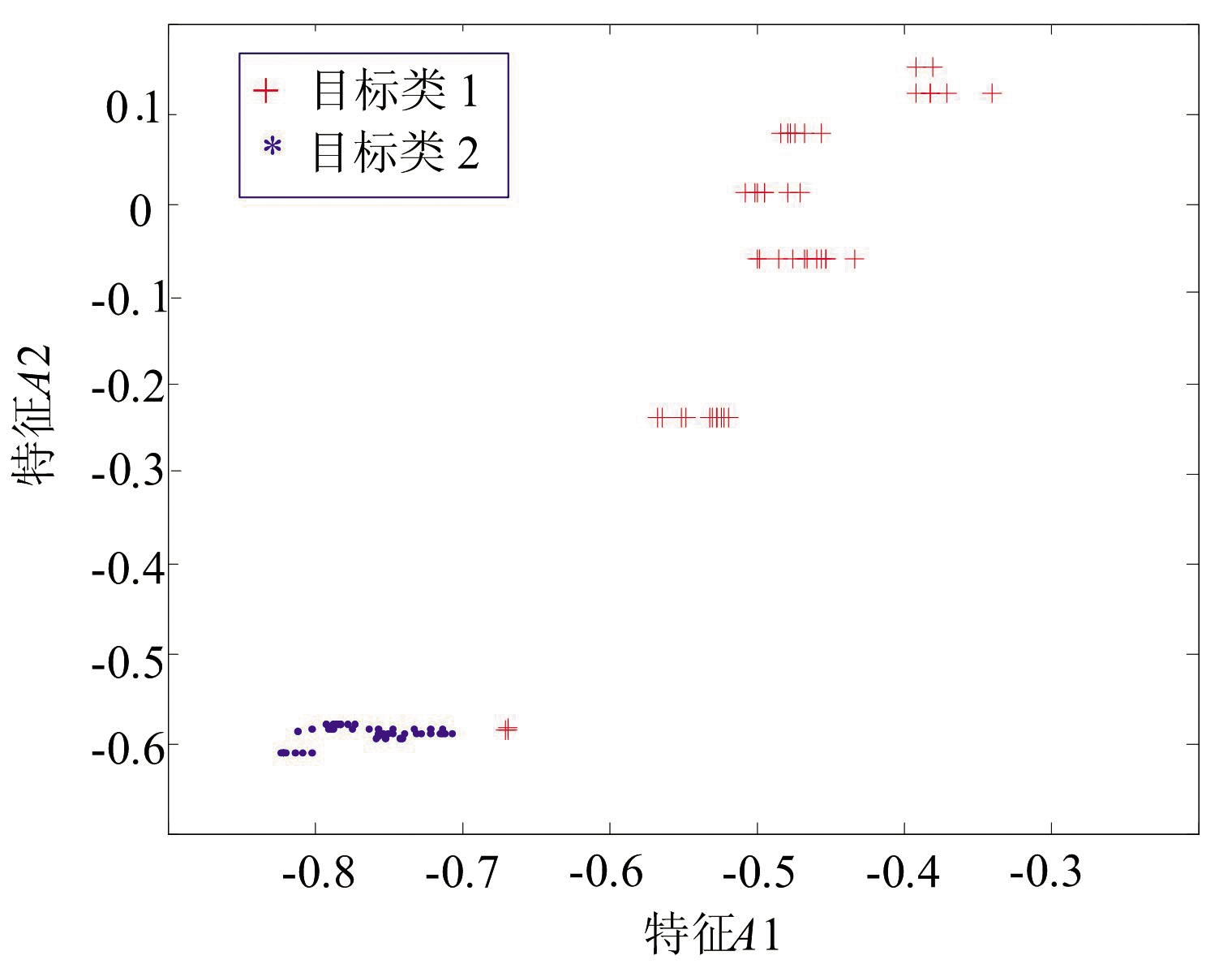
(a)概率比抽样分布
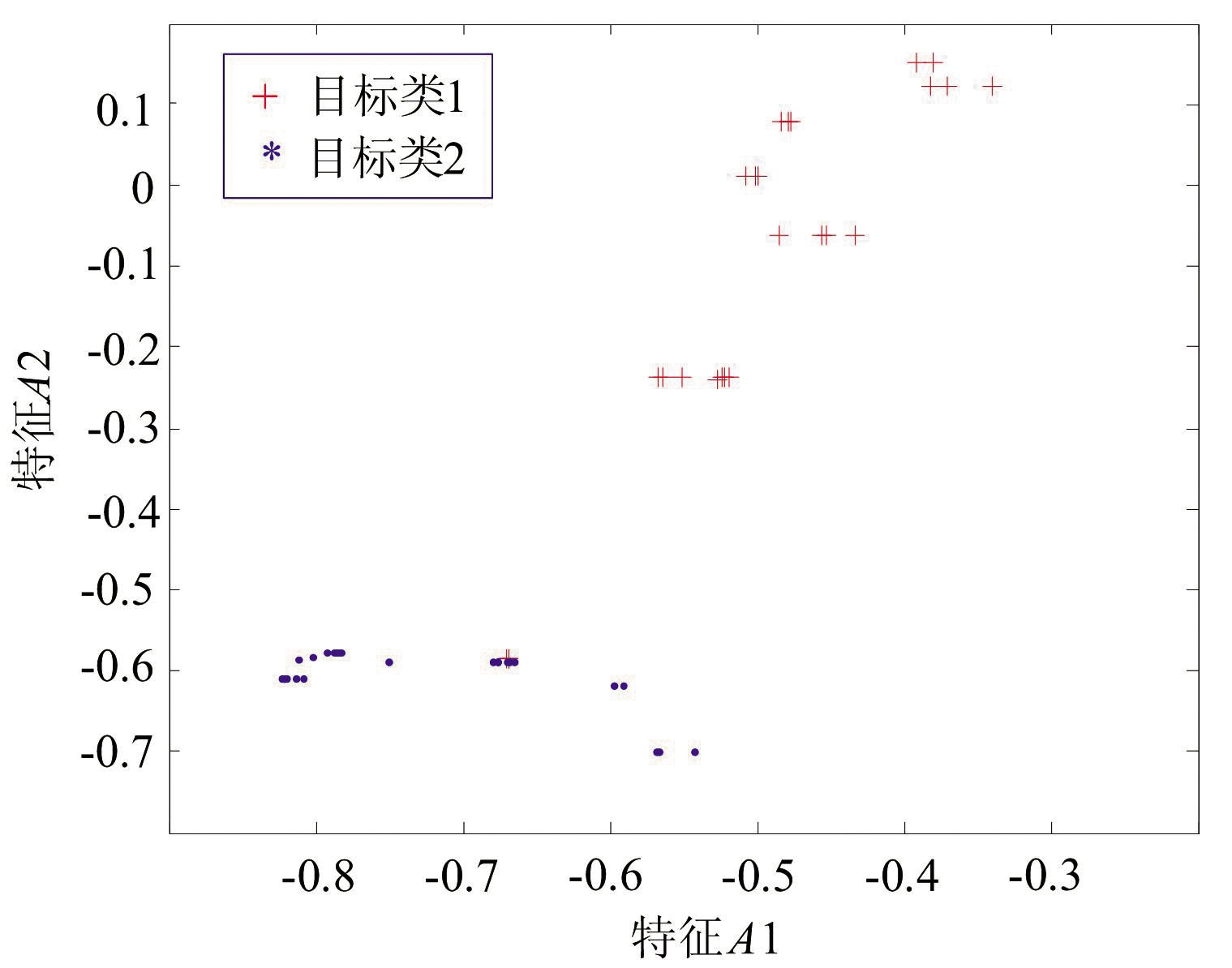
(b)融合方法抽样分布
图1 A样本集的两类边界样本抽取结果对比
图2(a)是采用中心距离比方法抽取的样本分布图。图2(b)是本文所述将距离/概率比值融合抽取的样本分布图。此时，图2(a)所示的采用中心距离比采样的效果不佳。
图3(a)和(b)结果表明：采用高斯分布概率比值方法和采用中心距离比值方法抽取的结果都有局限。图3(d)结果表明：本文所述的二者融合抽取的样本分布情况最佳。图3(c)是训练集样本全分布与两类别中心位置图。综上所述，与单独使用中心距离比或者概率比方法对比，本文所述的融合抽取的样本分布总能取得较好的抽样结果，融合方法具备更好的适用性。
3.2 单类边缘样本的抽取实验
实验分析单类边缘样本的抽取效果。对样本分别沿所属类别的椭圆轴方向投影，选择轴投影方向两端的样本，设抽取样本数目为134个；然后再使用直推式实验设计(TED)方法，抽取20个单类边缘样本，抽取样本的结果如图4所示。文字标号和圈点为TED法抽取样本的顺序与位置，TED法能够选择出最能代表样本集结构分布的样本。
(a)A样本集的边缘样本TED抽取结果
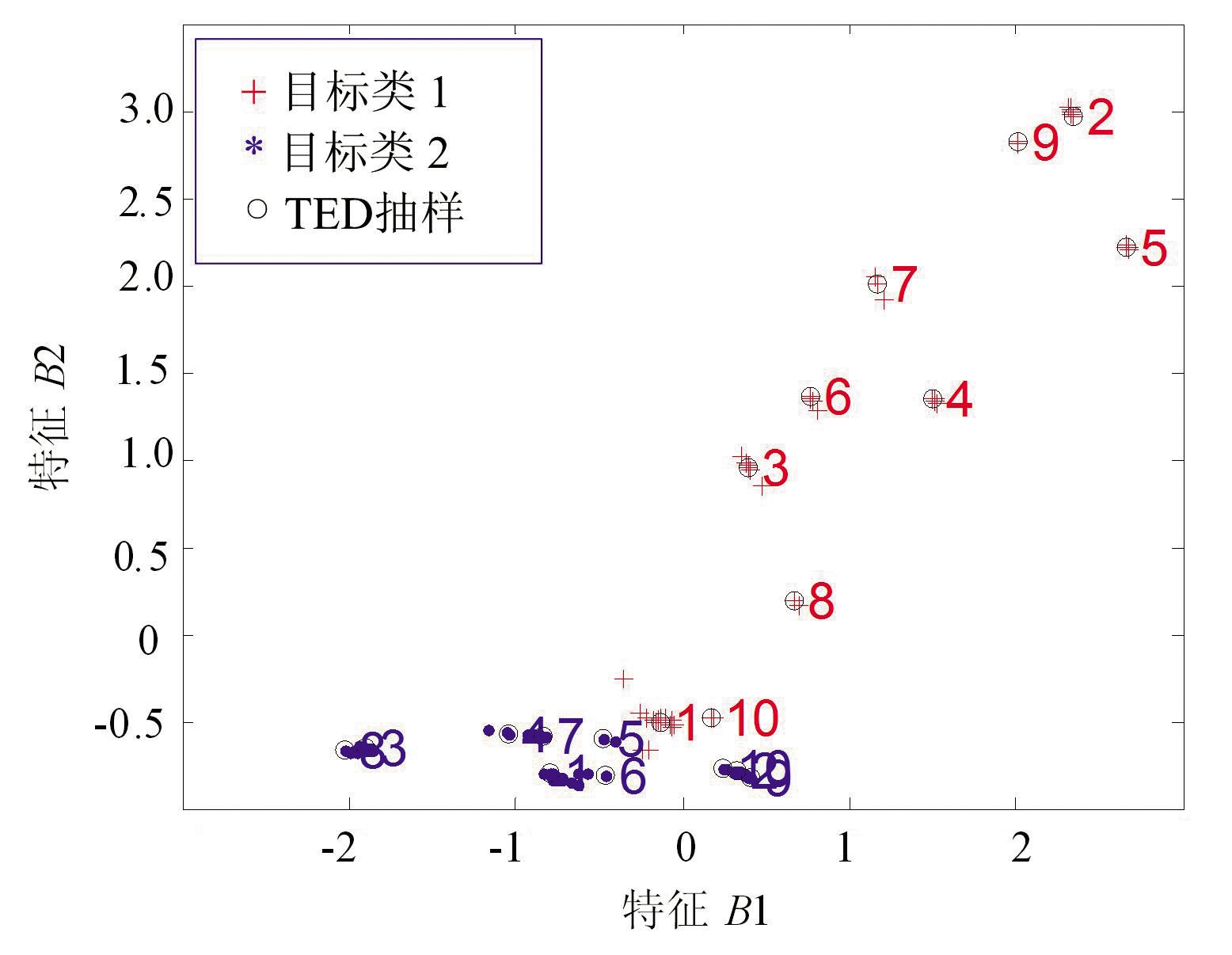
(b)B样本集的边缘样本TED抽取结果
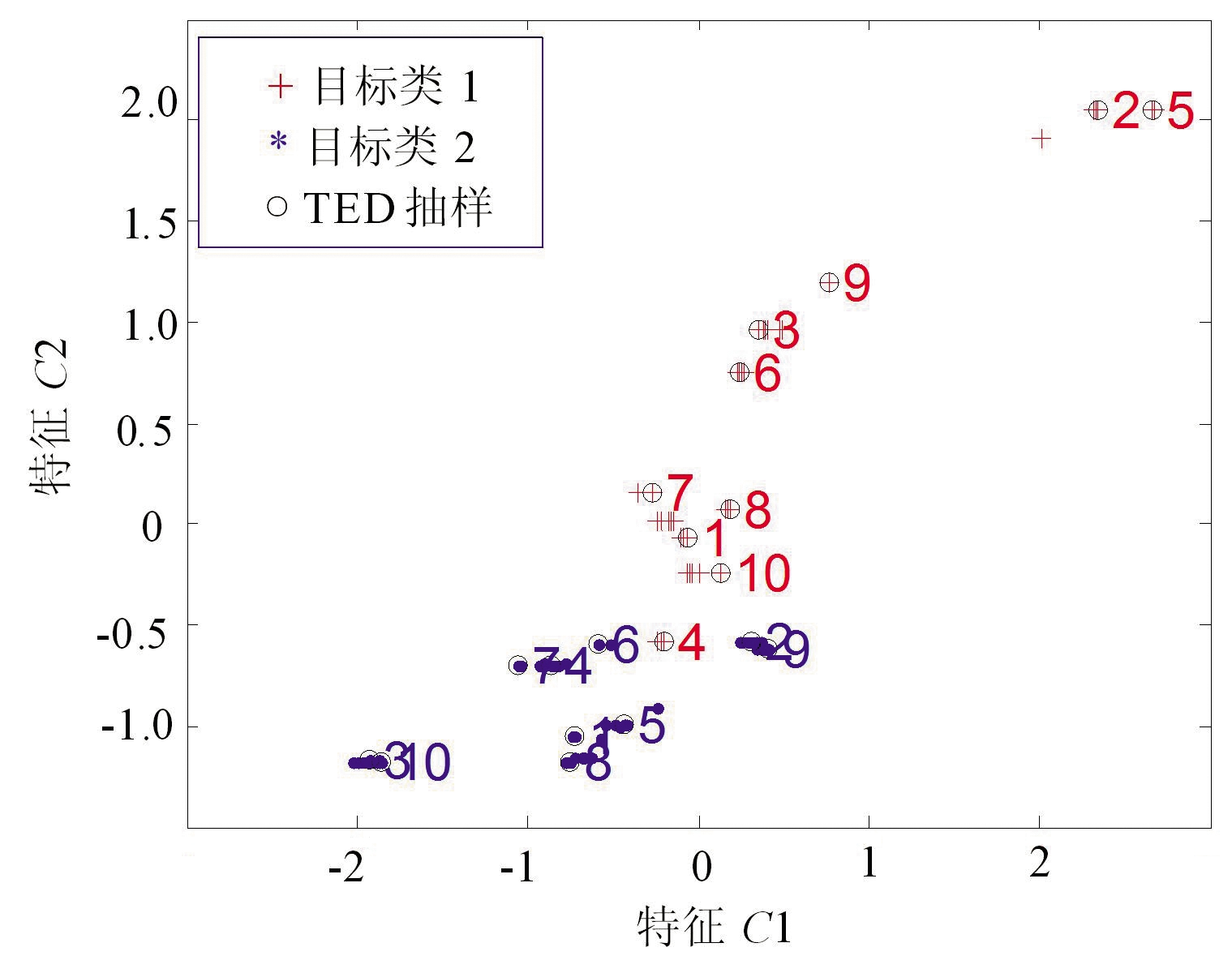
(c)C样本集的边缘样本TED抽取结果
图4 不同样本集的单类边缘样本抽取结果
3.3 不同约减方法下SVM训练的对比实验
采用Matlab自带的C-SVM数学模型，模型参数：Csvm=1，线性核和SMO算法求解。采用本文优化方法与随机抽样、TED法抽样方法，得到不同的样本子集，对比分析子集和全集之间SVM分类器精度的变化。首先，预设抽取样本比例，分别用本文优化方法、随机抽样与直推式实验设计方法抽取样本子集；然后，分别采用抽取的样本进行SVM训练，得到3条最优分类线，同时，采用样本全集也可以得到1条最优分类线。最后，对比分析不同样本集得到的4条最优分类线：以子集分类线与全集分类线的相似/贴近程度衡量抽样方法的性能，与全集分类线越相似/贴近的抽样方法对分类精度影响越小。
图5为B样本集下的SVM训练分类线对比：图5(a)、(b)、(c)和(d)分别对应10%，20%，30%和50%抽样比例；两类目标的全部样本都被绘制在图中；图中所示4条线分别为：中空圆形点线代表本文优化抽样方法得到的最优分类线，中空方形点线代表随机抽样方法得到的最优分类线，中空菱形点线代表TED法得到的最优分类线，虚线代表样本全集得到的最优分类线。
由图5知，纵向整体对比图5(a)、(b)、(c)和(d)的变化：随着抽样比例的提高，无论何种抽样方式，每种方法的分类线都会更加贴近全集的最优分类线，也就意味着分类精度越不受影响。
由图5(c)和(d)知，在较大样本采样比例下(>30%)，采用本文优化的采样方法得到的样本子集，其SVM训练得到的分类线与全集训练得到的分类线基本完全贴合。而此时，采用随机方法和TED法得到的分类线与全集训练出来的分类线尚有距离。
(a)10%抽样比例
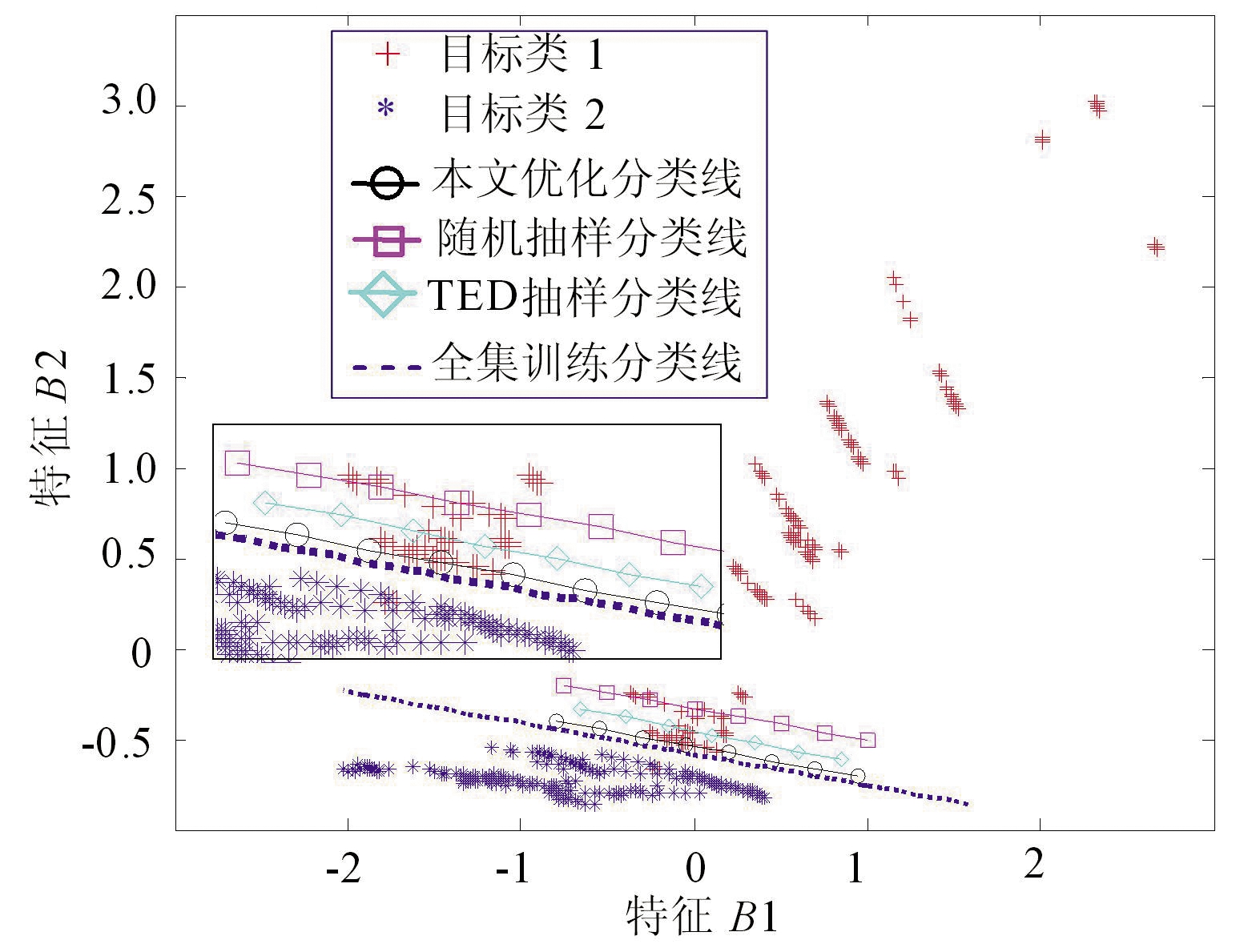
(b)20%抽样比例
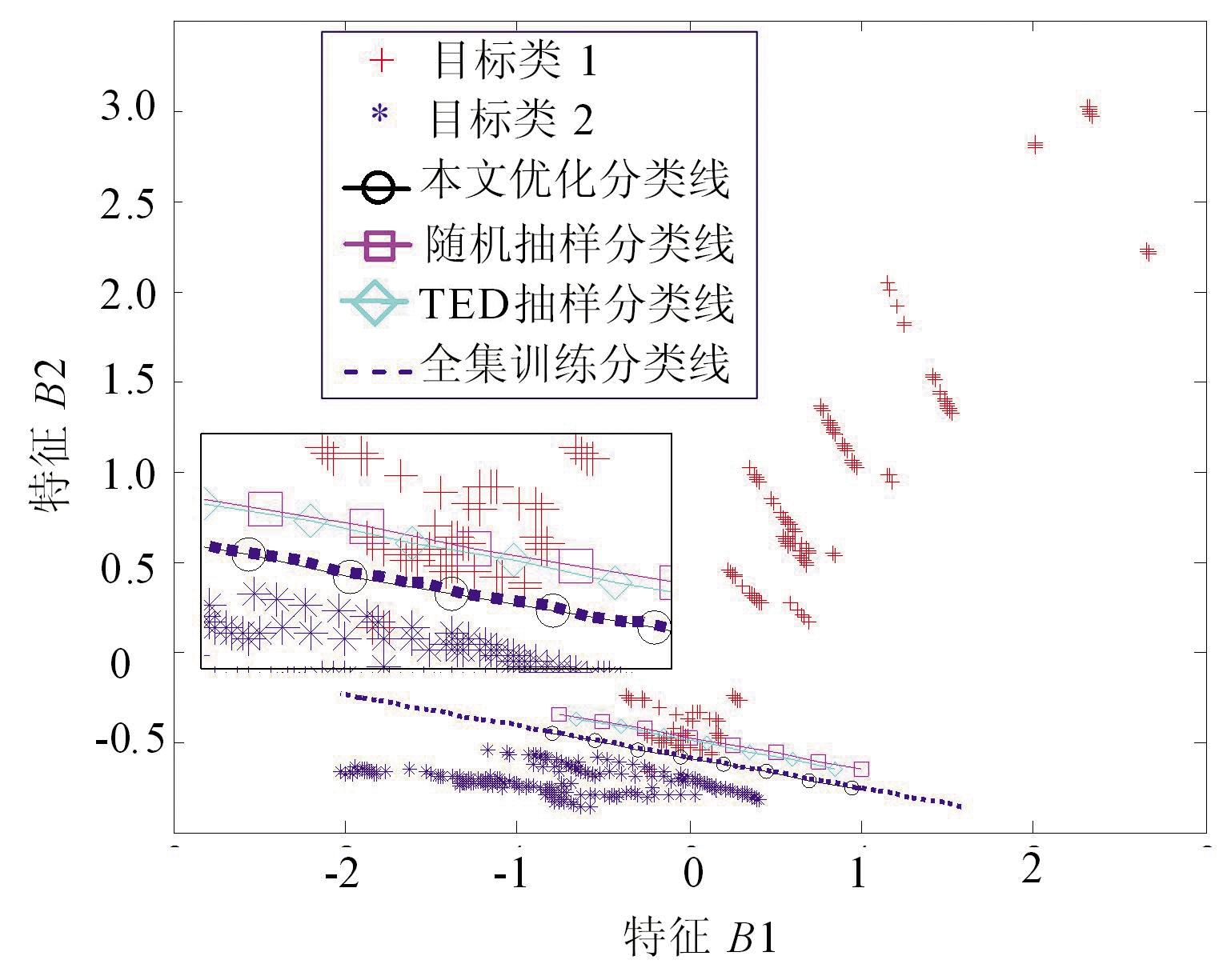
(c)30%抽样比例
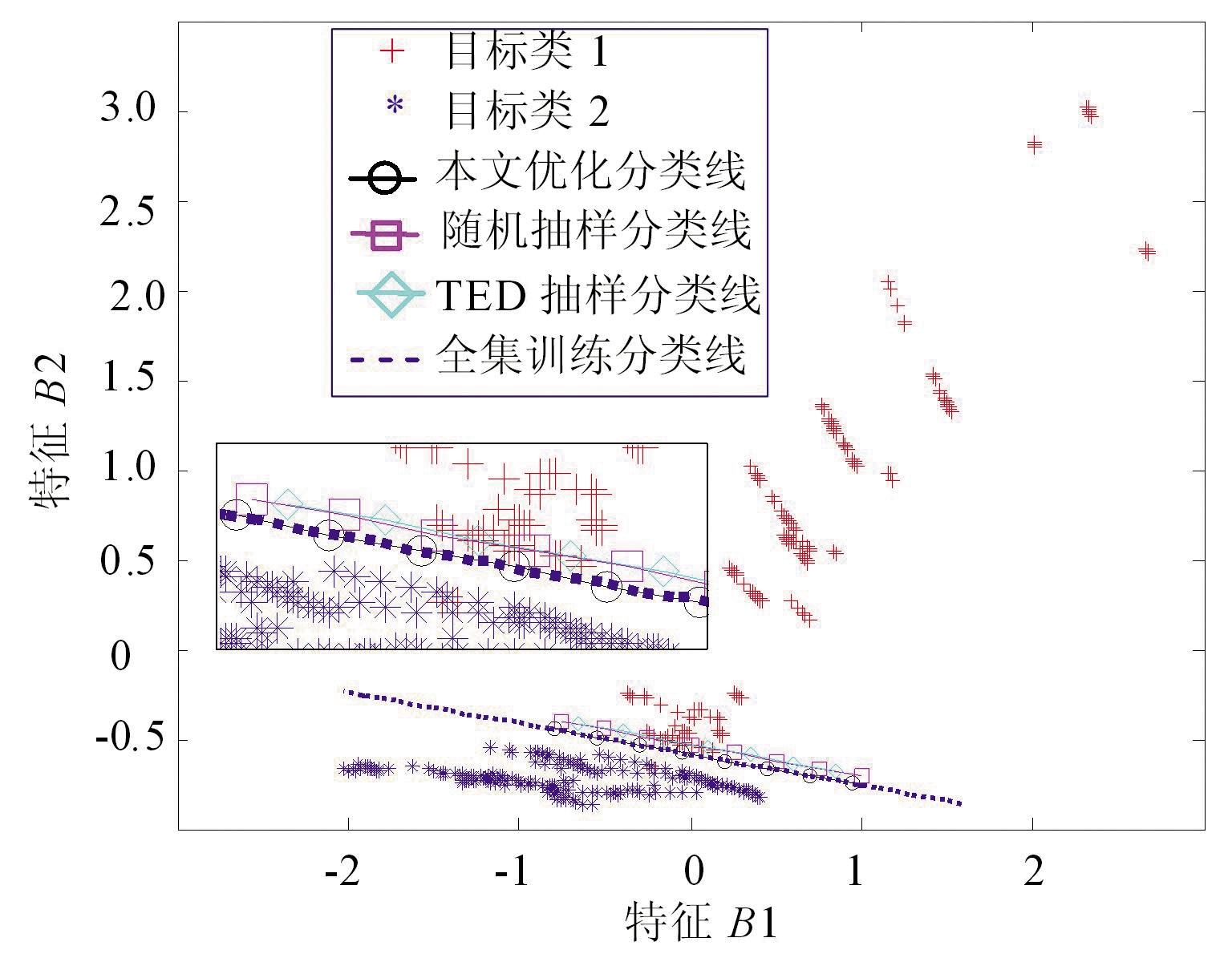
(d)50%抽样比例
图5 不同抽样比例下不同方法约减B样本集的SVM训练结果对比
由图5(a)和(b)知，在小样本采样比例下(<20%)，本文优化采样方法优势则更加明显。图5(a)为在采样比例10%下不同方法约减样本集的SVM训练结果：此时，随机方法和TED法得到的SVM分类线与全集分类线差距明显，还错分了许多样本，分类精度明显降低；而与之对比的本文优化采样方法的分类线则与全集得到分类线较为接近，分类精度降低不显著。
图6、图7分别为A、C样本集下的SVM训练分类线对比典型结果。
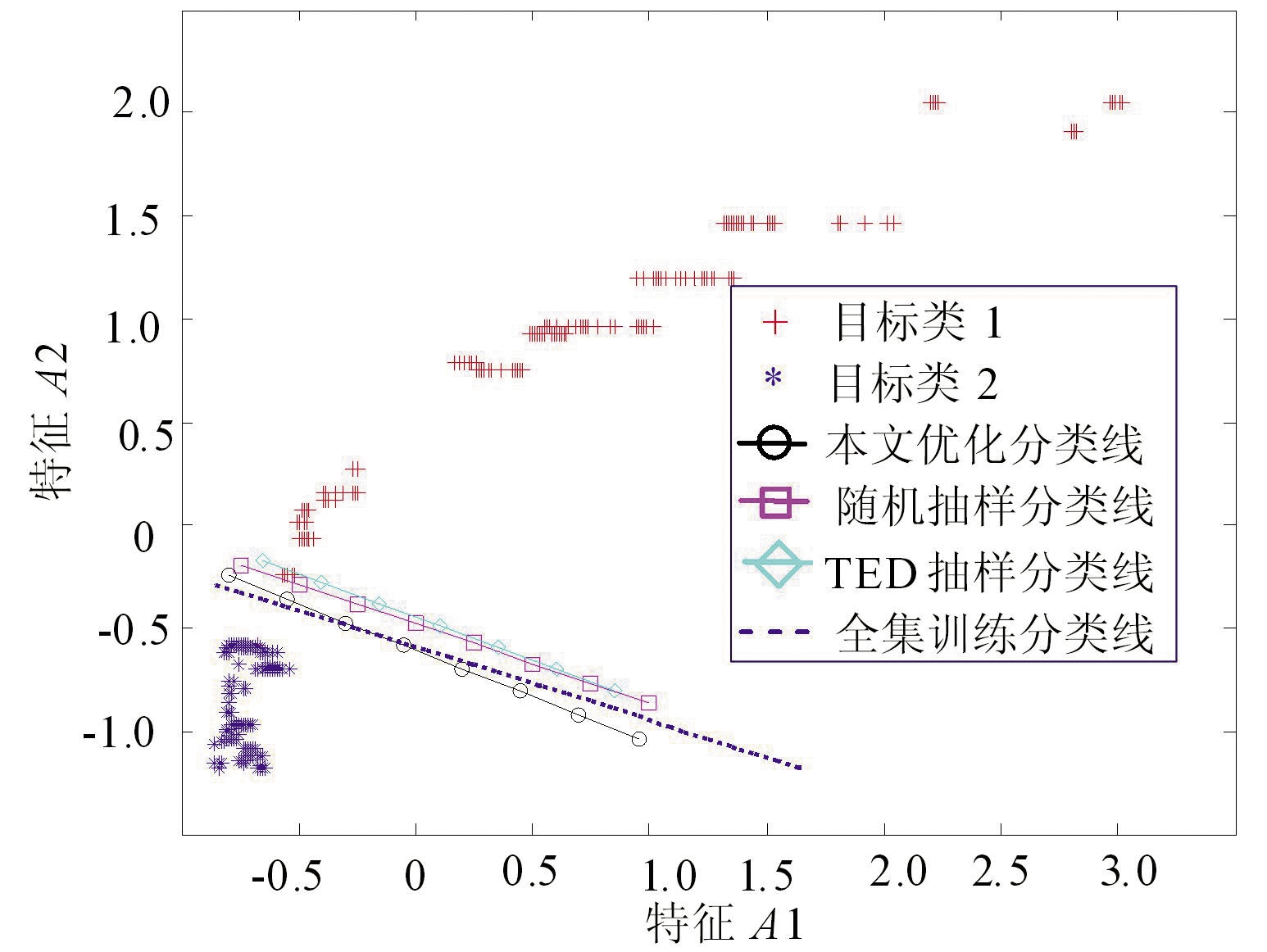
(a)10%抽样比例
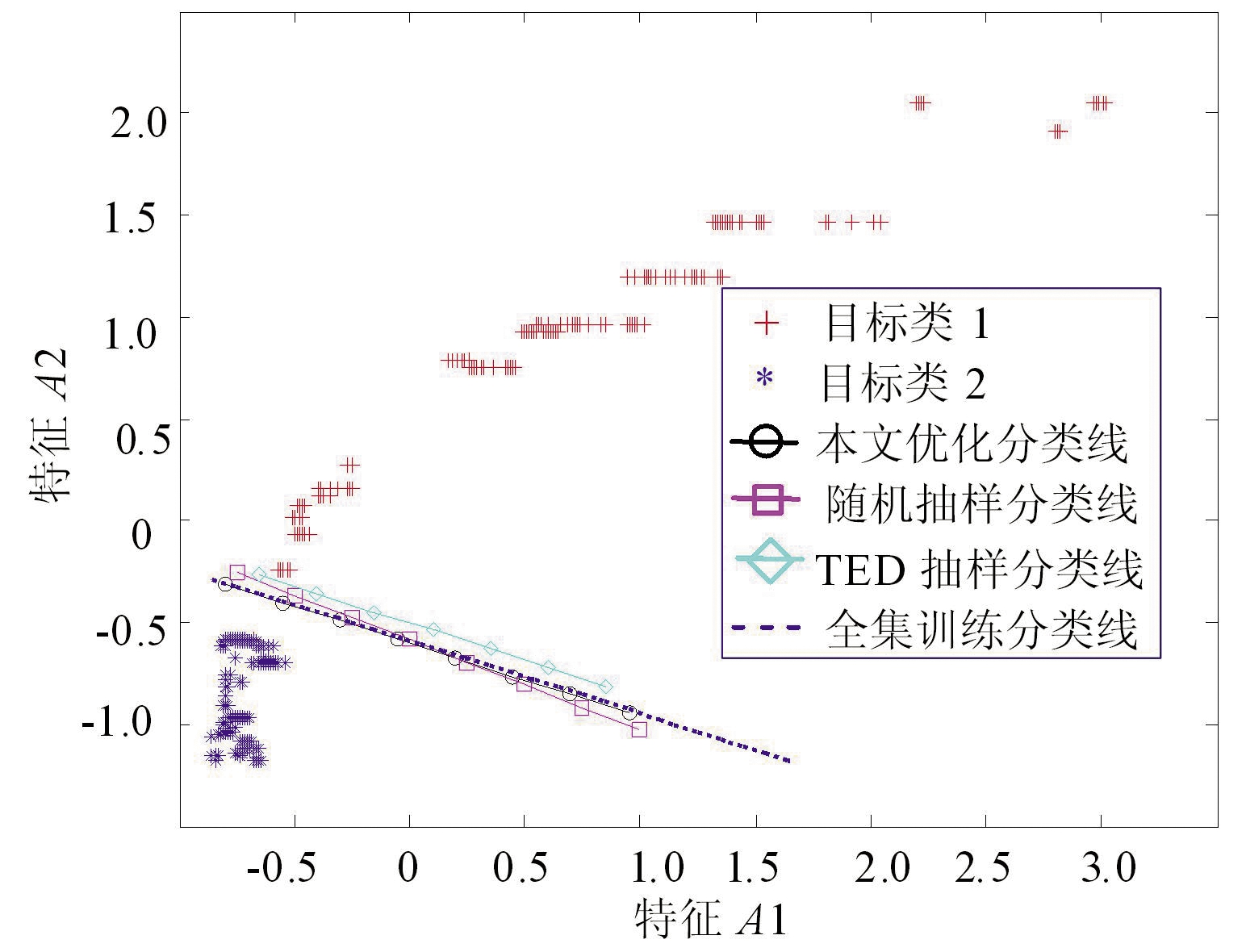
(b)30%抽样比例
图6 不同抽样比例下不同方法约减A样本集的SVM训练结果对比
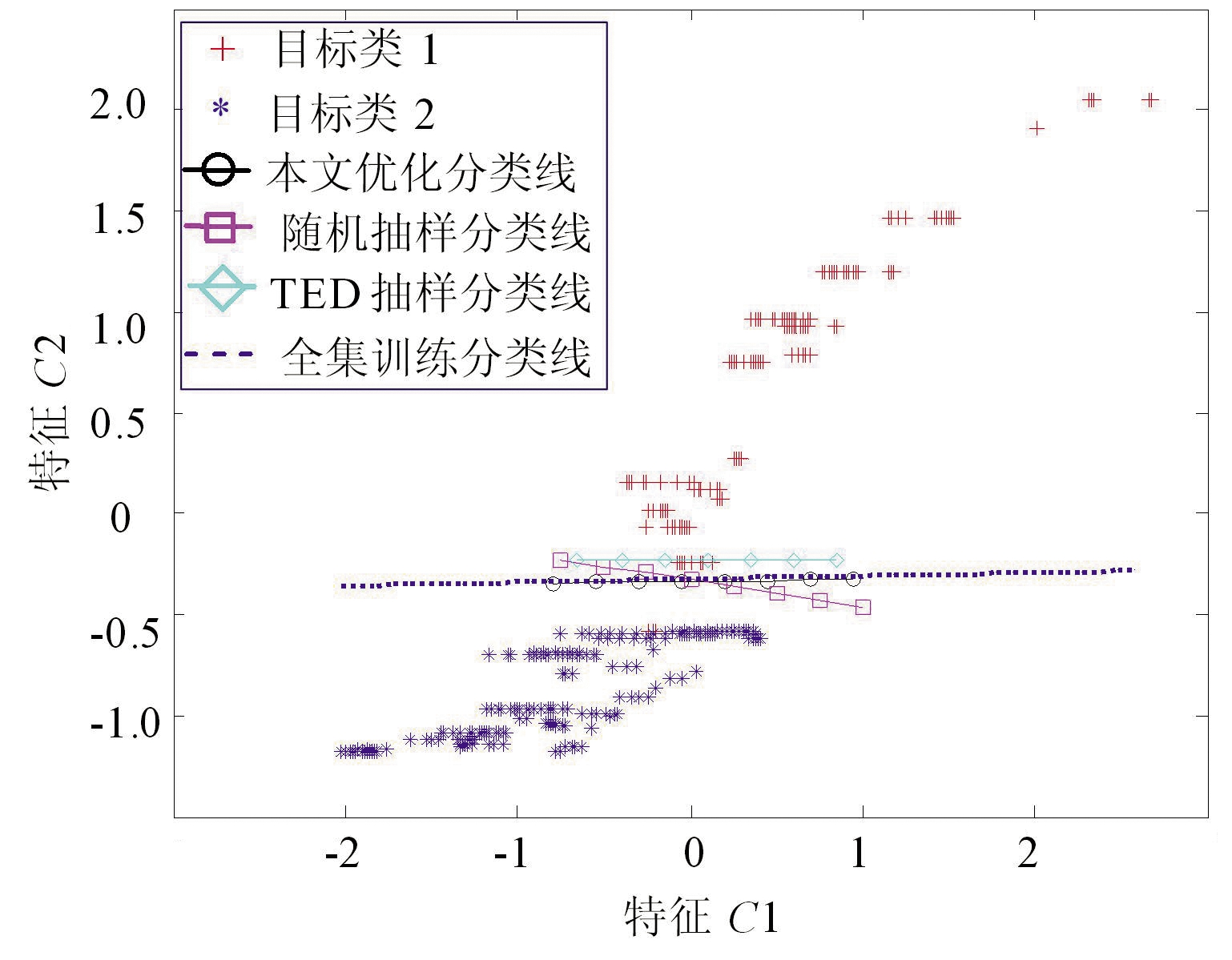
(a)10%抽样比例
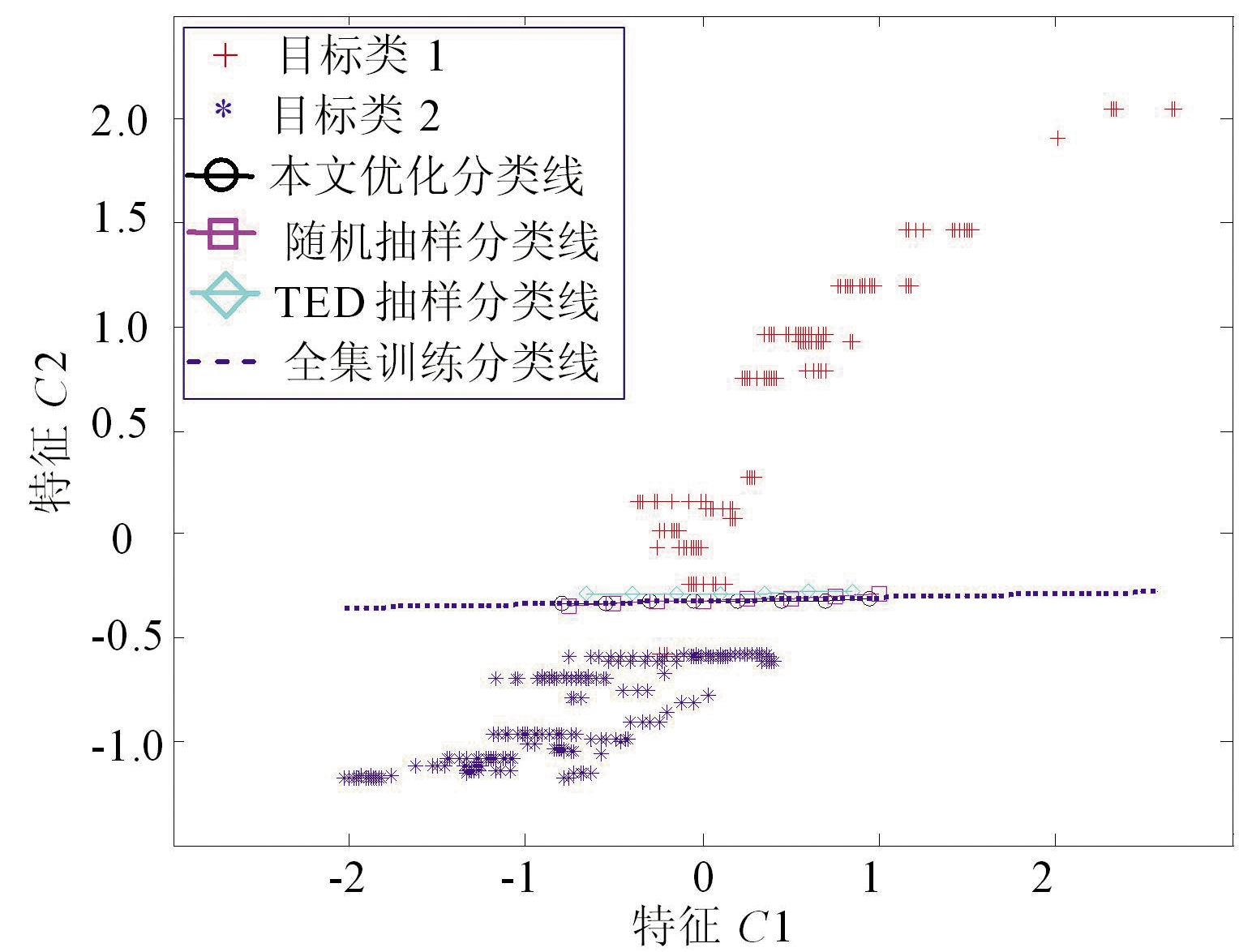
(b)30%抽样比例
图7 不同抽样比例下不同方法约减C样本集的SVM训练结果对比
总之，在本文所述3个样本集合的算法实验中，本文优化方法与随机抽样、TED法对SVM分类精度的影响规律与图5保持高度一致：在每个采样比例下，本文优化方法得到的SVM分类线与全集得到的分类线更加贴近。随着采样比例的提升，本文优化方法的分类线能够在更小的采样比例下与全集训练出的分类线贴合。在较低采样比例下(10%)，本文优化方法的分类线与全集训练的结果基本吻合，保持较高的分类精度。
4 结束语
本文提出了一种支持向量机训练集的约减方法，成功应用于基于窄带RCS统计特征的空间目标分类识别。基于支持向量一定是分布在每一类训练集几何意义上边缘的样本点的特点，本文用于SVM增量学习的样本初选方法不依赖于SVM分类界面选取样本向量，考虑样本簇的分布情况，不简单以距离量度决定样本向量的选取，使用高斯模型的方式，依赖样本向量的在两类高斯分布的概率比或者以高斯模型椭圆方向的两侧投影距离，选取边界支持向量和边缘支持向量，最后采用TED优化方法，在上述样本集中再优选出最能代表样本集结构分布的高价值样本。实验结果表明：通过对比抽取样本方法分析对SVM分类的精度影响，本文优化方法比随机抽样、TED法得到的SVM分类线更能贴近全集得到的分类线，特别是在小的采样比例下，采用本文优化方法得到的样本子集在SVM训练出的分类精度保持显著优于另两种抽样方法。综上所述，使用本文优化方法抽取样本子集，能够在保证SVM分类训练精度的同时，有效地降低样本集容量并保留原始样本集中分布在空间几何边缘的样本。
[1]王放.基于窄带RCS序列的低轨空间目标识别效果分析[C]∥ 第二届中国空天安全会议,辽宁大连:中国指挥与控制学会空天安全平行系统专业委员会,2017: 74-78.
[2]董会方, 卞磊, 杨广平.一种窄带雷达快速目标分类方法[J].国外电子测量技术, 2018, 37(2):105-111.
[3]FOSTER T.Application of Pattern Recognition Techniques for Early Warning Radar(EWR)Discrimination: ADA299735[R].[S.l]:[s.n.],1995.
[4]王曙光, 田西兰.一种窄带雷达舰船目标分类的决策方法[J].雷达科学与技术, 2016, 14(2):159-162.
WANG Shuguang,TIAN Xilan.A Decision-Making Algorithm of Ship Target Classification for Narrow Band Radar[J].Radar Science and Technology, 2016, 14(2): 159-162.(in Chinese)
[5]陈志仁, 顾红, 苏卫民, 等.改进的支持向量机低分辨雷达目标分类算法[J].系统工程与电子技术, 2017, 39(11):2456-2462.
[6]李妍坊, 苏波, 刘功申.一种基于组合保留集的SVM增量学习算法[J].上海交通大学学报, 2016, 50(7):1054-1059.
[7]王锦章, 徐冰超, 任 杰, 等.一种基于Gabor变换的HRRP目标识别方法[J].电子科技, 2017, 30(4): 19-21.
[8]易晓柯.支持向量机的全局局部特征融合目标识别[J].雷达科学与技术, 2011, 9(2):180-182.
YI Xiaoke.Target Recognition Based on Support Vector Machine(SVM)Features Fusion[J].Radar Science and Technology, 2011, 9(2):180-182.(in Chinese)
[9]SYED N A, SYED H, LIU K,et al.Incremental Learning with Support Vector Machines[C]∥ Proceedings of Workshop on Support Vector Machines at the International Joint Conference on Artificial Intelligence, Stockholm,Sweden:CiteSeerX,1999:272-276.
[10]曾文华, 马健.一种新的支持向量机增量学习算法[J].厦门大学学报(自然科学版), 2002, 41(6): 687-691.
[11]孔波, 刘小茂, 张钧.基于中心距离比值的增量支持向量机[J].计算机应用, 2006, 26(6):1434-1436.
[12]吕巨建, 赵慧民, 陈荣军, 等.基于自适应稀疏邻域重构的无监督主动学习算法[J].计算机科学, 2018, 45(6):251-258.
[13]CAI Deng, HE Xiaofei.Manifold Adaptive Experimental Design for Text Categorization[J].IEEE Trans on Knowledge and Data Engineering, 2012, 24(4): 707-719.
