0 引言
在雷达系统中，提高距离分辨率是改善杂波中目标检测的重要手段，也是目标分类识别、成像及距离测量的基础[1]。现代雷达发射大时宽带宽积信号，通过脉冲压缩提高距离分辨率，此时距离分辨率与雷达信号带宽成反比关系，若要进一步提高分辨率，则需要增加信号带宽，这在实际中有时难度较大或者代价过高，因此有必要研究不增加带宽情况下的距离超分辨问题。
以MUSIC谱估计为代表的空/时超分辨谱估计技术研究成果很多，后来学者们将其应用于雷达的距离超分辨中[2]，这些方法通常要求预估信源数目、较高的信噪比，以及需要较多的样本[3-5]，但是在实际中可能难以满足。近年来空域稀疏处理技术受到了很大关注，已有研究表明其具有角度超分辨能力，对样本数、信噪比的要求不高，也不需要预估信源数目[6-7]，因此只要能建立适当的距离维稀疏信号模型，利用该技术同样可实现距离超分辨。
雷达目标在观测空间中通常是稀疏的。当雷达发射线性调频信号时，目标回波的匹配滤波实际上是频域去斜脉压，回波信号在频域去斜后变成复正弦波。基于目标稀疏性和去斜回波的复正弦形式，本文提出了一种雷达距离超分辨方法，首先对雷达目标的线性调频回波信号进行频域去斜处理，然后建立多目标回波信号的距离维稀疏数学模型，最后构造关于目标距离的凸优化函数并求解，得到目标距离，同时实现雷达距离超分辨。
1 目标回波的频域去斜
设雷达发射线性调频(LFM)信号，表示为
(1)
式中：T为LFM信号的时宽；κ为LFM信号的调频斜率，κ=B/T，B为带宽；rect(·)为矩形函数，rect(t)=1,-1/2≤t≤1/2。
当乘积BT≫1时，易知匹配滤波器的频率响应函数近似为
(2)
考虑距离R1处的一个静止点目标，其回波信号为
se(t)=a1u(t-t1)=
(3)
式中，a1为回波信号的幅度，t1=2R1/c为双程时延，c为光速。
不难得到该回波信号的频谱为
Se(f)=
exp(-j2πft1)
(4)
利用式(2)对式(4)进行频域去斜，得到
S1(f)=Se(f)U*(f)=
(5)
式中,上标*表示取共轭。
式(5)表明，LFM回波信号经过频域去斜处理后变成了复正弦波信号的形式，是下文中用来构造距离维稀疏信号模型的基础。
同样地，若空间中存在M个静止点目标，则回波信号的频域去斜表达式为
SM(f)=
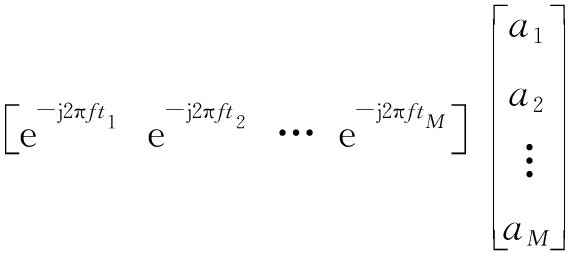
(6)
式中,am为第m个目标回波的幅度，tm为第m个目标回波的双程时延。
在[-B/2,B/2]上取N个离散频点，满足 N>M，代入式(6)得到去斜信号的矩阵形式，即
s=
Ea
(7)
2 距离维稀疏信号模型
通常情况下，对雷达某个探测波位而言，在感兴趣的距离范围内只有少数的几个目标，即只可能在少数几个距离点(对应时延t1,t2,…,tM)上存在目标，目标呈现稀疏性。如果对感兴趣的目标距离范围进行充分密集的离散化，得到离散时延点τ1,τ2,…,τK，K≫N，那么可以得到如下的稀疏性信号模型:
s=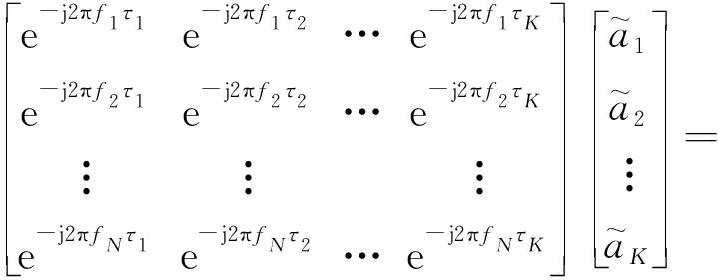
(8)
式(8)中，当且仅当τk=tm时
否则
即幅度矢量
是稀疏的，根据其非零元素的位置可以计算目标距离。
最后，考虑各种有源噪声的影响，有如下的距离维稀疏信号模型：
(9)
式中，n为N×1维噪声向量。
3 距离超分辨的凸优化实现
对于式(9)的稀疏信号模型，可以通过信号重构方法求解稀疏矢量
如前所述，其非零元素的位置确定了目标的距离，同时距离超分辨得以实现。这里我们通过构建如下的凸优化问题对式(9)进行求解[8]，即
(10)
式中：·F表示F-范数；λ为正则化因子，用于折中接收数据拟合误差和模型稀疏度；
的定义为
(11)
式中,0<p≤1。
4 实例与分析
本节中我们通过仿真实例来考察前述距离超分辨方法的性能。仿真条件为：LFM信号的时宽T=400 μs，带宽B=1 MHz，采样频率fs=4 MHz，因此常规匹配滤波脉压的距离分辨率为150 m；两个目标相距112.5 m，回波信噪比都是10 dB，静止、或者多普勒频率等于200 Hz。
图1 距离超分辨(目标静止)
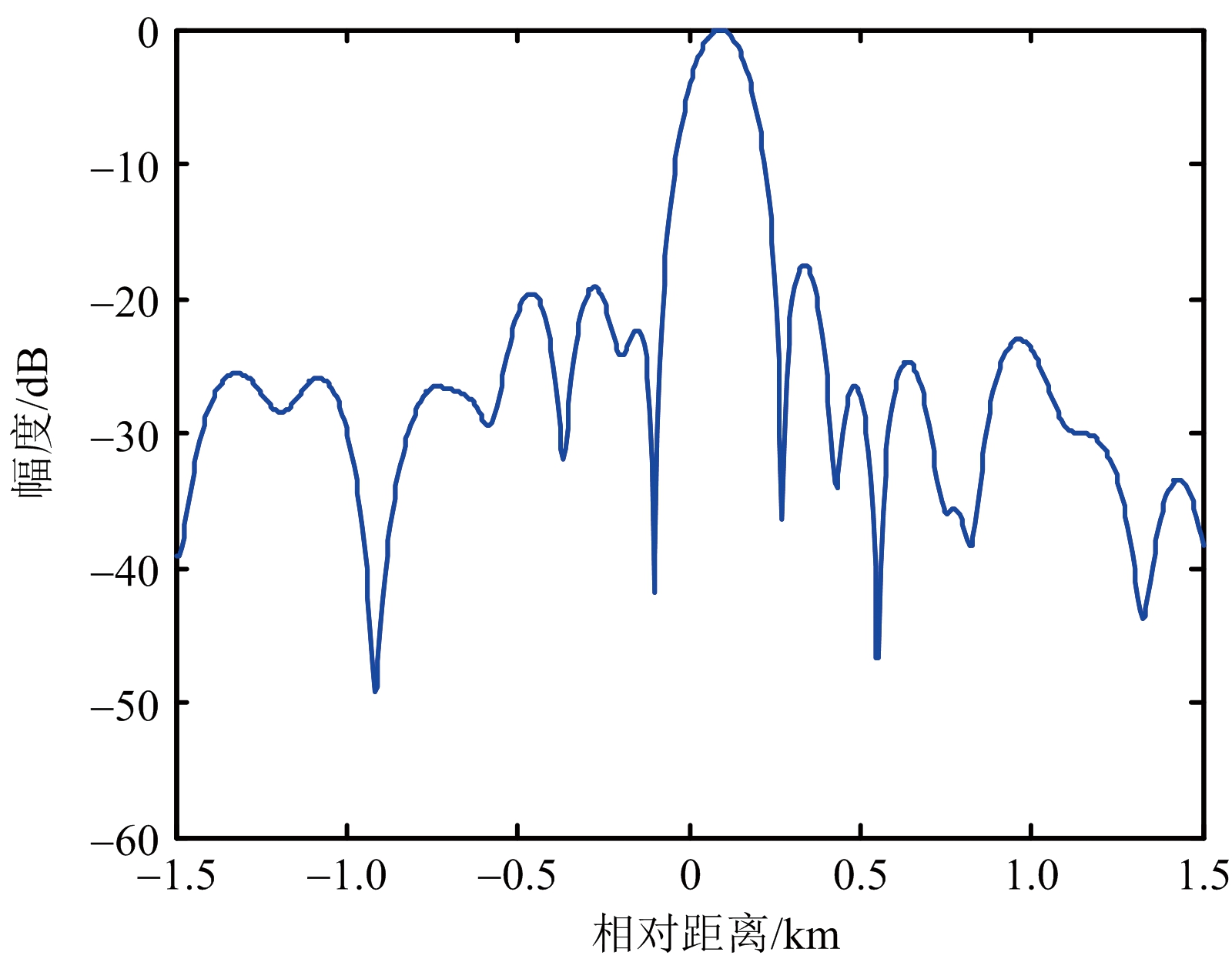
图2 常规脉压(目标静止)
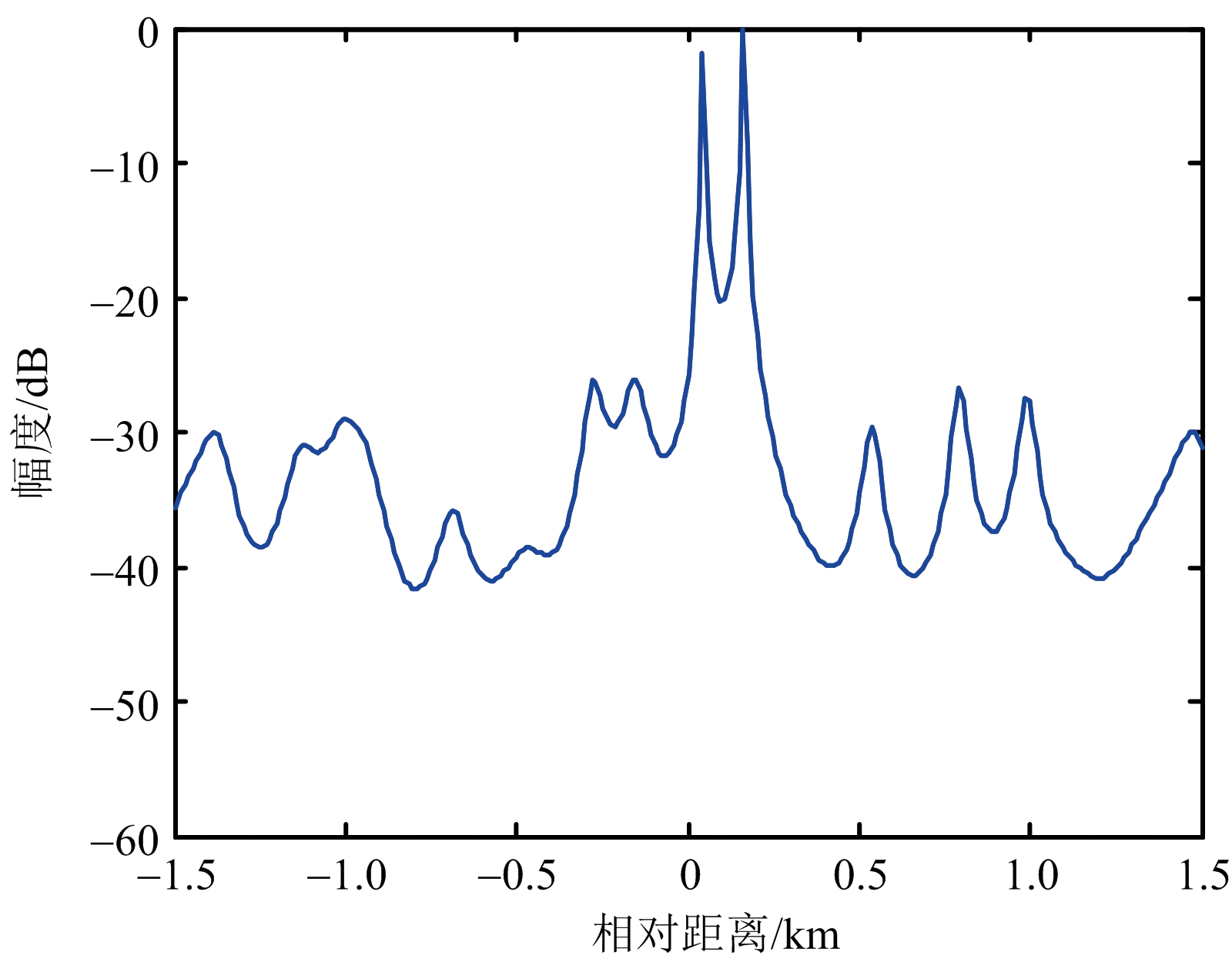
图3 距离超分辨(多普勒频率为200 Hz)
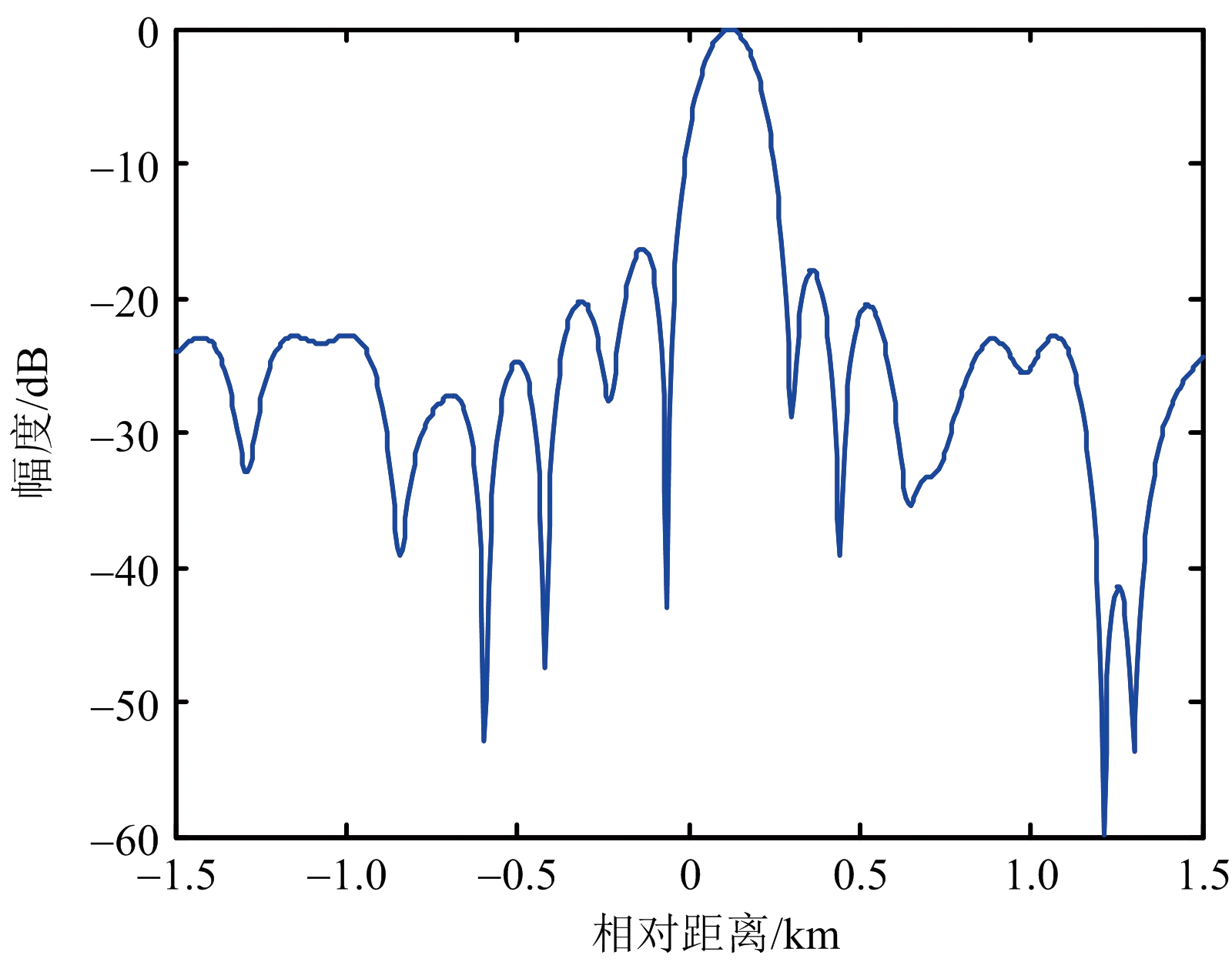
图4 常规脉压(多普勒频率为200 Hz)
对回波信号进行距离超分辨处理，结果如图1和图3所示，可以看到两个明显的尖峰，作为比较，还分别给出了常规匹配滤波脉压的结果，如图2和图4所示。从这些图中可以看到，由于两个目标靠得很近，在常规脉冲压缩处理中，两个目标的脉压主瓣重叠在一起，无法区分开来，但是经过本文的超分辨处理后，两个目标处出现两个尖峰，变得可以分辨了，即该方法具有超分辨能力。
5 结束语
众所周知，稀疏性是雷达目标的基本特征，而稀疏信号处理研究近年来广受重视，已有研究表明它可以实现雷达目标角度超分辨，因此只要构造适当的稀疏信号模型同样可以实现目标距离超分辨。基于这一思路，本文进行了有益的探索，构造目标回波的稀疏信号模型并求解，以实现距离超分辨，仿真结果表明这一思路是可行的。距离超分辨是雷达中很有意义的技术，本文的研究为此提供了一条新途径。本文的研究是初步的，关于采样率、信噪比等因素对超分辨性能的影响以及计算效率等更深入的问题将在后续工作中进一步探讨。
[1] 陈伯孝. 现代雷达系统分析与设计[M]. 西安:西安电子科技大学出版社,2012:323-333.
[2] 姚红梅,王军锋,刘兴钊. 最小熵谱外推技术及其在雷达超分辨中的应用[J]. 现代雷达,2005,27(3):18-19.
[3] 王永良,陈辉,彭应宁. 空间谱估计理论与算法[M]. 北京:清华大学出版社，2004：98-106.
[4] 刘小忠,闵威,张孟达，等. 宽带独立信号和相干信号的DOA估计[J]. 雷达科学与技术,2014,12(6):619-622.
LIU Xiaozhong，MIN Wei，ZHANG Mengda，et al. DOA Estimation for Wideband Independent and Cohe-rent Signals[J]. Radar Science and Technology，2014,12(6):619-622.(in Chinese)
[5] 李海,居梦琪,张喆. 基于PSO-MUSIC算法的分布式目标DOA估计[J]. 雷达科学与技术,2019,17(2):119-123.
LI Hai,JU Mengqi,ZHANG Zhe. DOA Estimation for Distributed Source Based on PSO-MUSIC[J]. Radar Science and Technology，2019,17(2):119-123. (in Chinese)
[6] 王秀红. 基于稀疏表示的波达方向估计方法研究[D]. 哈尔滨:哈尔滨工业大学,2017.
[7] 王鹏,邱天爽,金芳晓. 脉冲噪声下基于稀疏表示的韧性DOA估计方法[J]. 电子学报,2018,46(7):1537-1544.
[8] HUANG Tianyao,LIU Yimin,XU Xingyu. Analysis of Frequency Agile Radar via Compressed Sensing[J]. IEEE Trans on Signal Processing,2018,66(23):6228-6240.
