0 引言
随着电子信息技术的逐渐发展,当今电子侦察设备面临的电磁环境越来越复杂,一方面体现在脉冲流密度急剧增加,另一方面体现在雷达信号的调制方式越来越复杂多变[1-2]。如果能利用雷达数据库中的信息对脉冲流中的已知信号进行预分选,将大大提高雷达信号分选的效率,实现对雷达脉冲流的稀释,降低后续对未知雷达信号进行分选的复杂度[3]。
传统的模板匹配法使用雷达数据库先验信息进行匹配分选[4],分选速度较快,但无法适用于参数捷变的雷达信号。聚类方法将相似度高的雷达信号划分为一类[5-6],有较强的自适应能力,但是没有充分利用雷达数据库的先验信息进行准确识别。传统的神经网络层数较少,将其应用于雷达信号预分选时[7],存在学习速度慢、拟合精度不高、易陷入局部极小值,无法正确剔除未知雷达信号等问题。针对以上问题,本文同时将脉间和脉内参数[8]作为信号分选特征,使用基于深度学习算法实现的全连接神经网络作为分类器实现对已知雷达信号的分选,并且在全连接神经网络中引入了置信度神经元[9]来感知未知雷达信号并进行剔除。最后利用雷达数据库中信号的脉冲重复间隔(PRI)信息进行时域校验,进一步剔除未知雷达信号,进而提高分选准确率。
1 改进的全连接神经网络
基于深度学习算法实现的全连接神经网络是一种非线性数据建模工具,常用来对输入与输出间复杂的关系进行建模,具有独特的分布并行处理、非线性映射和自适应学习能力等特征[10]。该网络结构包含多个隐藏层,能以更少模型参数、更快收敛速度和更高拟合精度来逼近现实[11]。全连接神经网络的训练分为前向传播和反向传播两个过程,在前向传播过程中,通过输入特征得到分类结果。反向传播利用梯度下降法对损失函数进行优化,使损失函数减小,从而实现对神经网络参数的调整,不断提高神经网络的分类能力。
1.1 全连接神经网络输入特征
全连接神经网络的输入分别为雷达脉冲信号的载频、脉宽,以及文献[12]中提出的用以区分雷达脉内调制模式的维格纳熵和双谱熵。
维格纳分布是时频分析中常采用的方法,是一种典型的Cohen类时频分析方法。维格纳分布定义为信号的中心协方差函数的傅里叶变换,能充分体现信号在能量空间的瞬时功率谱密度特征。信号s(t)的维格纳分布定义为
(1)
双谱是最简单的高阶谱,运用双谱分析,可以达到有效抑制高斯噪声的目的。若随机序列{s(n),s(n+τ1),…,s(n+τk-1)}的k阶累积量满足
(2)
则其k阶谱分布为k阶累积量的(k-1)维离散傅里叶变换,信号的双谱即三阶谱,定义为
(3)
对变换后的信号沿时间频率对角面对空间X进行子空间划分为X1,X2,…,XN,则变换后的信号S在特征子空间Xi下的子空间分布概率可表示为
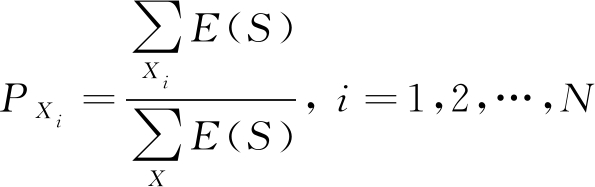
(4)
根据信息熵的定义,可以得到子空间分布概率下信号的信息熵:
(5)
对信号的维格纳分布和双谱分布进行式(4)与式(5)的计算可以得到信号的维格纳熵与双谱熵。
1.2 改进的全连接神经网络结构
本文使用的全连接神经网络结构如图1所示。
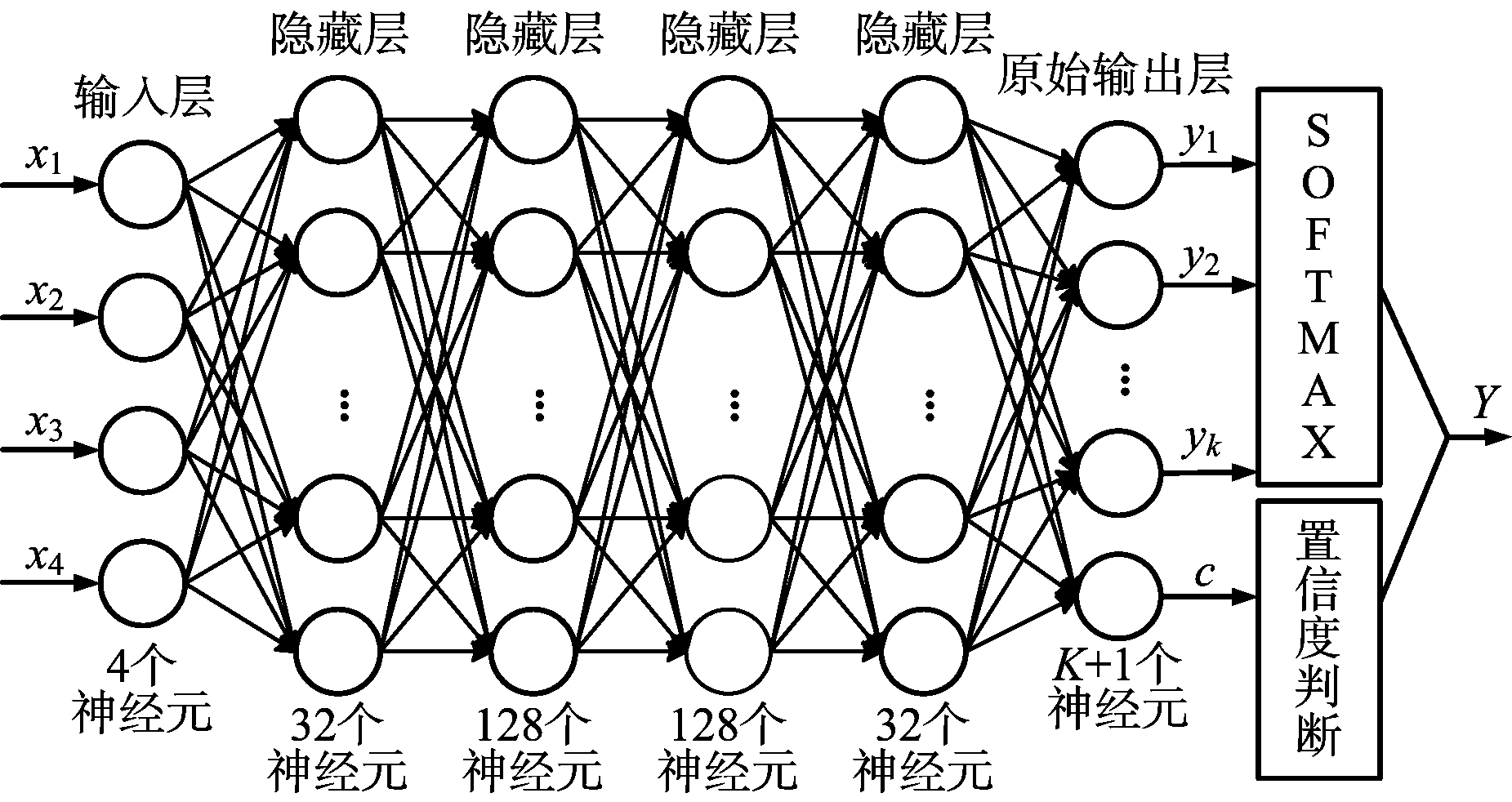
图1 全连接神经网络结构图
全连接神经网络由输入层、隐藏层和输出层组成。输入层有4个神经元,输入雷达脉冲的4种特征,分别为雷达脉冲信号的载频、脉宽、维格纳熵和双谱熵。
隐藏层一共有4层,分别包含32、128、128和32个神经元,每一层神经元将上一层输出数据作为输入,乘以权重W,再加上偏置b,最后通过ReLU激活函数得到下一层神经元的输入,公式如下:
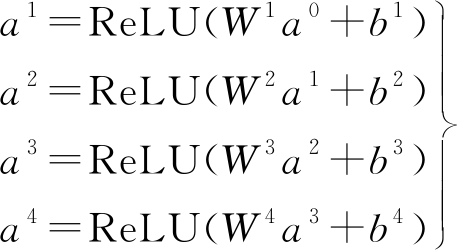
(6)
式中,a0为输入层数据,W1∈R4×32,W2∈R32×128,W3∈R128×128,W4∈R128×32,b1∈R32,b2∈R128,b3∈R128,b4∈R32。
输出层使用Softmax函数进行分类,分别输出各个类别的可能性(0.0~1.0),最后选择可能性得分最高的类别作为预测的类别。Softmax层的输出概率为
(7)
式中yi为原始输出层第i个神经元的输出值。为了实现全连接神经网络对未知雷达信号的剔除,在原始输出层的K个神经元的基础上增加了一个置信度神经元,并设置一个阈值判断层将置信度小于阈值的雷达信号判定为未知雷达信号。
1.3 置信度神经元设定
在雷达信号预分选问题中,假设雷达数据库中包含K部已知雷达。我们使用K部已知雷达信号样本对神经网络进行训练后,希望神经网络在准确识别已知雷达信号的同时,对未训练过的雷达信号具备感知能力,将其判断为未知雷达信号。对未知雷达信号的判定,在本质上是开集分类问题[13]。对于传统的全连接神经网络而言,使用已知雷达信号样本进行训练,神经网络只能分选出学习过的已知雷达信号,对于未知的雷达信号,会按照相似度分选为与其最相似的类别,这样会造成严重的分选错误。
在全连接神经网络中,Softmax层输出的预测概率和置信度的关联程度比较低[14],并且由于本文使用了ReLU激活函数,会使得神经网络对未训练过的雷达信号也输出较高的预测值[15],如果直接对Softmax层的输出结果设置阈值来判定是否为已知雷达信号,会造成严重的判别错误。因此本文参考文献[9]中的方法,在原始输出层中加入了一个置信度神经元。
置信度神经元连接前一层隐藏层,在神经元内使用Sigmoid激活函数生成置信指数c。改进后的全连接神经网络的输出概率为
P′j=c·Pj+(1-c)yj
(8)
式中,Pj为Softmax层输出概率,yj为训练样本原始标签。当c较大(置信度高)时,神经网络的预测结果主要取决于Softmax层的预测概率,当c较小(置信度低)时,神经网络的预测结果主要取决于样本原始标签的类型。
1.4 损失函数
由于雷达信号分选属于分类问题,所以本文采用了Softmax Loss函数用以计算当前迭代中的分类损失,损失函数如下:
(9)
全连接神经网络的训练过程,会不断将损失函数最小化,加入置信度神经元后,如果直接对式(9)进行优化,则神经网络会倾向于将置信指数c训练为0,以此来最小化损失函数,所以在原有的损失函数上需要加上置信指数c的损失,定义如下:
Lc=-log(c)
(10)
最终得到改进的全连接神经网络的损失函数为
L=Ls+λLc
(11)
在全连接神经网络的训练过程中,当λ设置为固定值时,如果Ls远远小于Lc时,神经网络会倾向于让置信指数c一直输出1,以此来减小损失函数,这样置信度神经元将失去判别未知雷达信号的能力。所以在实际训练中,需要设置动态的λ,用来平衡训练时的Lc和Ls,当Ls≥Lc时,减小λ,用来减小Lc所占比例,优先提高准确率。当Ls<Lc,增大λ,用以增大Lc所占比例,从而增加已知信号的置信指数。
这种方法在实际训练过程中还会导致强烈的正则化,在处理边界数据时,会将其置信度设置得很大,从而影响对边界区域未知雷达信号的判别。为了解决这个问题,在实际神经网络的训练过程中对一半数据使用新的损失函数,另外一半数据使用原始的损失函数。
2 时域校验
改进的全连接神经网络利用阈值判断层虽然在一定程度上剔除了未知雷达信号,但是当出现的信号和已知类信号非常相似时,全连接神经网络仍然有一定概率将其划分到与之最相似的已知雷达信号的类别中去,这样就会影响后续对未知雷达信号的分选工作。
为了进一步剔除未知雷达信号,本文利用雷达数据库里的时域信息(脉冲重复间隔)对全连接神经网络的分选结果进行时域校验。
对于不同PRI调制类型的信号采用不同的窗口校验方式,对时域校验窗口的定义如表1所示。
对雷达信号进行时域校验时,选择第一个脉
表1 不同PRI调制类型时域校验窗口参数

调制类型窗口类型窗口中心值窗口大小固定抖动滑变正弦调制单一固定窗口PRI中心值及其整倍数PRI容差PRI抖动范围PRI滑变范围PRI调制范围组变参差多个固定窗口每个PRI中心值及其整倍数PRI容差
冲作为基准脉冲,向后匹配窗口参数,若有脉冲出现在窗口内,则将第一个脉冲抽取出,并且将出现在窗口内的脉冲作为下一个基准脉冲,若连续3个脉冲没有出现在窗口内,则丢弃第一个脉冲,并且将第二个脉冲作为基准脉冲,继续进行窗口校验,直至脉冲抽取完成。抽取出来的脉冲判定为该已知类型雷达信号,剩余脉冲判定为未知雷达信号。
3 方法设计
本文设计的基于全连接神经网络与时域检验的方法(Fully Connected Neural Network and Time Domain Inspection,FNNTI)首先将雷达数据库已知雷达信号的单脉冲参数(脉宽、载频、维格纳熵、双谱熵)作为全连接神经网络的输入特征,雷达型号作为标签,对改进的全连接神经网络进行训练。分选测试时,将待分选的雷达信号单脉冲参数输入训练后的全连接神经网络,得到置信指数c和分类预测结果,置信指数c小于阈值的雷达信号判为未知雷达信号,对大于阈值的雷达信号进行时域校验,时域检验成功的判定为雷达数据库中已知信号,否则判为未知雷达信号。分选方法流程如图2所示。
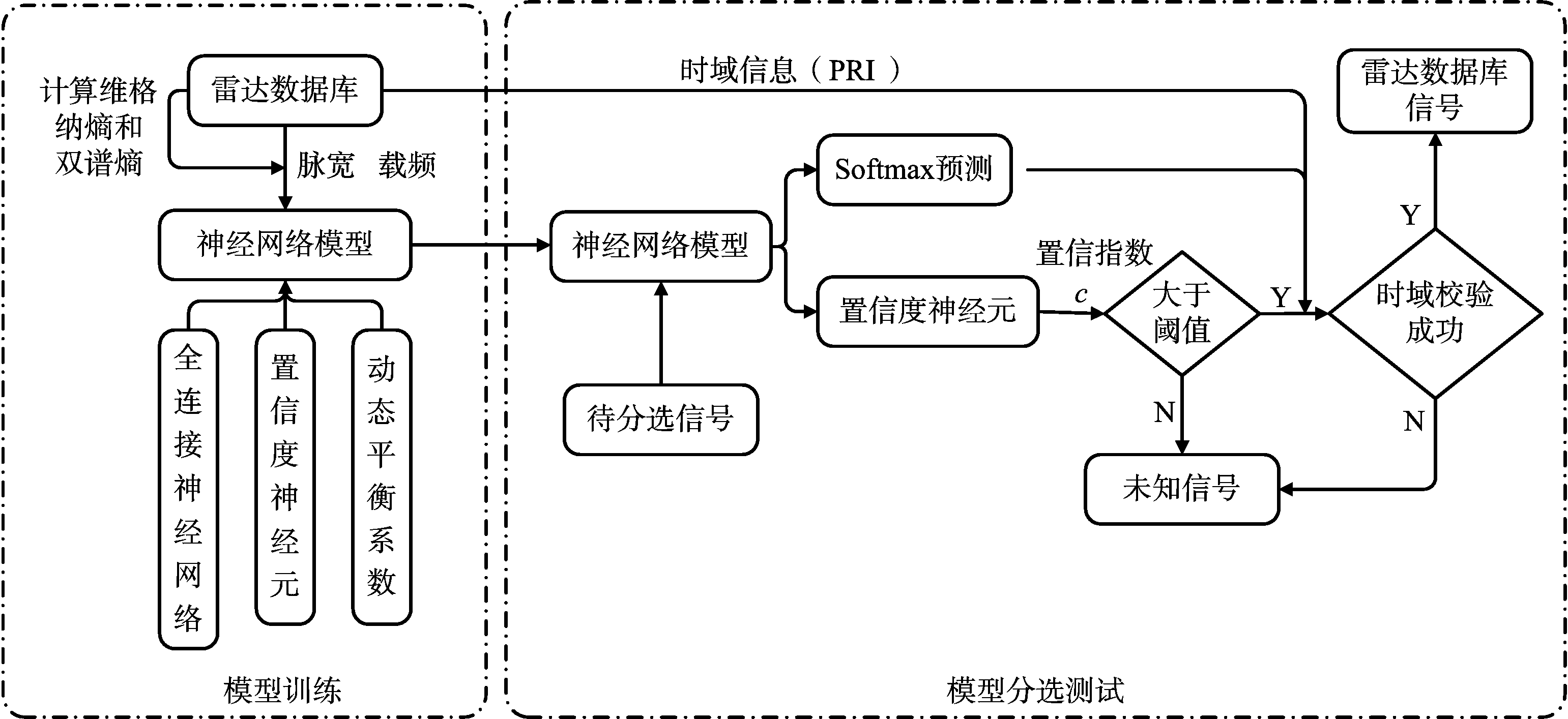
图2 FNNTI方法流程图
4 雷达信号预分选实验
本文设计的实验仿真环境:Window10,Intel CPU i7-4710HQ,8 GB内存,显卡为NVIDIA GeForce GTX 860 M。编程工具为:Matlab2014b,Python3.7.4,Tensorflow-gpu 1.14.0。
4.1 神经网络训练与测试
为了验证本文方法对参数捷变的雷达信号的分选效果,设定7部参数存在混叠并且有一定捷变的雷达信号作为雷达数据库中已知信号,对神经网络进行训练。雷达数据库已知雷达信号参数如表2所示。
表2 雷达数据库参数

雷达序号脉内调制类型载频/MHz及调制类型编码类型采样率/MHz脉宽/μsPRI/μs及调制类型已知1常规调制(CW)[20,22,24],载频捷变无6020150,固定已知2线性调频(LFM)20,调频带宽2,载频固定无6010100,抖动量1%已知3非线性调频(NLFM)20,调频带宽4,载频固定无6010[110,120,130],参差已知4二相编码(BPSK)[18,21],载频组变,每组10个[1,1,0,1,1,0,1,0,1,1]6020[160~180],滑变已知5四相编码(QPSK)20,载频固定弗兰克编码方式6010[200,300,400],组变每组20个已知6频率编码(FSK)[10,25],载频固定[1,1,1,1,1,0,0,1,1,0,1,0,1]6040250,抖动量1%已知7线性调频-二相编码(LFM+BPSK)25,调频带宽2,载频固定[1,1,1,0,0,1,1]6021250,固定
根据数据库中7部雷达信号的参数信息,使用Matlab对每种信号在信噪比5,10,15和20 dB的条件下分别生成500个仿真脉冲,即每种雷达信号生成2 000个脉冲,7种雷达信号合计14 000个脉冲,以雷达型号作为类别标签。
对全连接神经网络进行训练时,分别从每种信号的5,10,15和20 dB脉冲中随机取450个脉冲,划分为训练集,合计12 600个脉冲。将剩余脉冲划分为验证集,合计1 400个脉冲。将训练集中脉冲的载频、脉宽、维格纳熵和双谱熵作为输入特征,使用指数衰减型学习率,初始学习率设置为0.2,学习衰减率为0.99,迭代次数为7 000次,λ初始值设定为1.0,迭代7 000次之后,全连接神经网络在验证集上的准确率为99.64%,神经网络训练在验证集上的结果如图3所示,其中损失函数为无量纲值,其数值大小用来衡量预测值与真实值的差异大小。
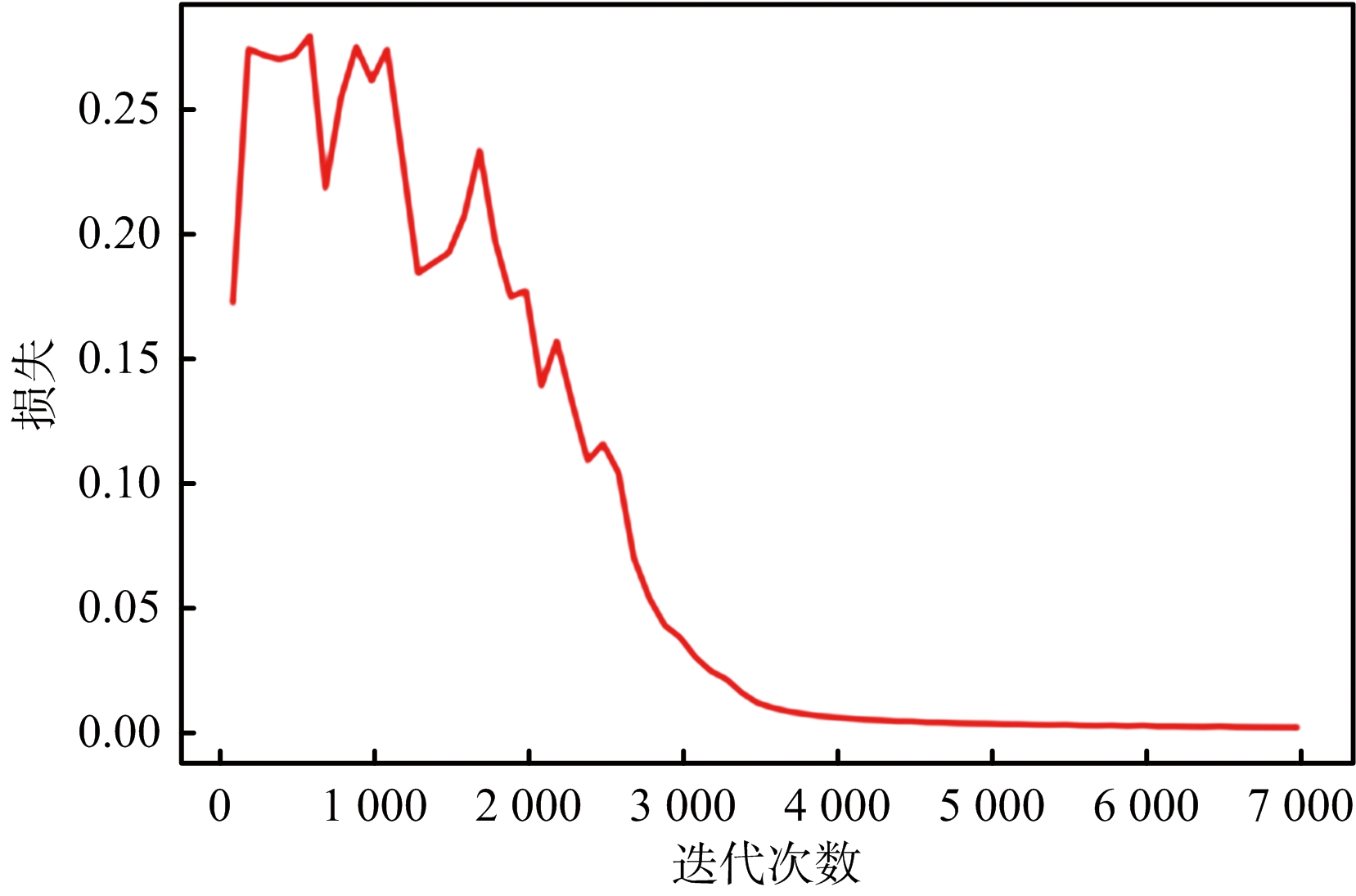
(a) 损失值随迭代次数变化曲线

(b) 准确率随迭代次数变化曲线
图3 改进的全连接神经网络训练效果图
由全连接神经网络的在验证集上的分选结果可以看出,全连接神经网络在雷达参数混叠且参数存在一定捷变的情况下具有很好的分选效果。
4.2 未知雷达信号判定测试
为了验证分选方法在同时具有已知雷达信号和未知雷达信号的混合脉冲流中的具体表现,设定11部雷达信号,其中7部为经过神经网络训练过的雷达数据库信号,参数如表2所示,另外4部为未知雷达信号。未知雷达信号的脉内调制类型与雷达数据库中已知雷达信号脉内调制类型相似,脉间参数存在一定混叠,未知雷达信号参数如表3所示。
表3 未知雷达信号仿真参数

雷达序号脉内调制类型载频/MHz及调制类型编码类型采样率/MHz脉宽/μsPRI/μs及调制类型未知1常规调制(CW)[15,16,17],组变,每组20个无6010200,抖动量1%未知2线性调频(LFM)15,调频带宽6,载频固定无6015[200,240,280],参差未知3二相编码(BPSK)[8,11,15],载频捷变[1,0,0,1,1,1,0,1,1,0]6010250,固定未知4四相编码(QPSK)15,载频固定弗兰克编码方式6010300,正弦调制,调制幅度40
11部雷达信号分别在5,10和20 dB的信噪比情况下各仿真300个脉冲信号,并且进行脉冲流合并,在信噪比为5 dB的环境下使用实验1中训练好的神经网络模型进行分选,对比神经网络输出的最大的Softmax预测值和置信度指数c,结果如图4所示。
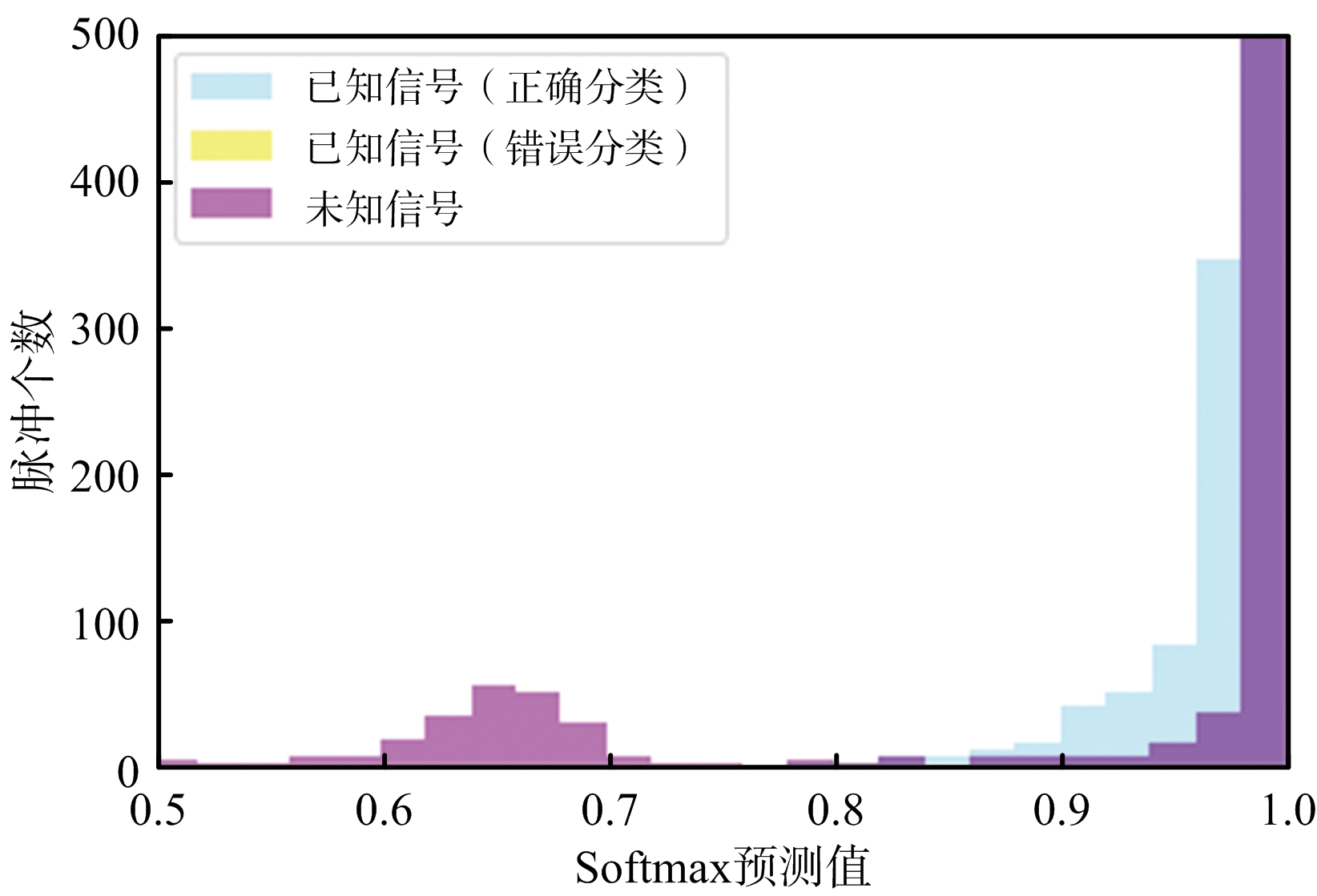
(a) Softmax预测值分布直方图
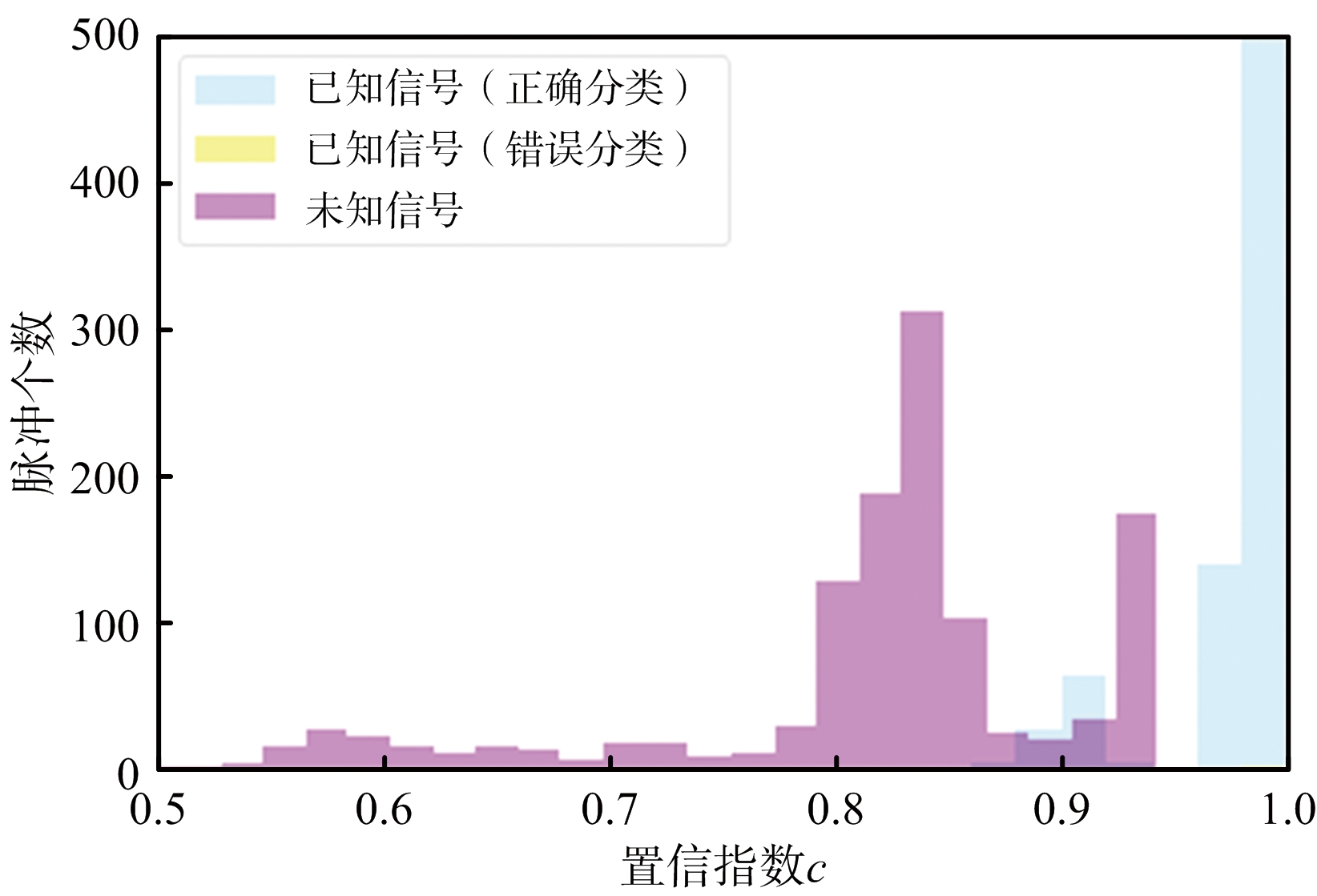
(b) 置信指数c分布直方图
图4 5 dB信噪比下置信度分布直方图
由图4可以看出,已知雷达信号和未知雷达信号最大Softmax的预测值出现严重混叠,直接对Softmax预测值设置阈值无法很好地分离已知雷达信号和未知雷达信号。未知雷达信号输出的置信指数c相对较小,已知雷达信号输出的置信指数c相对较大,两者具有一定的区分性,因此通过对置信指数c设置阈值能够剔除一部分未知雷达信号。
将实验1中验证集的最小c值作为置信指数阈值,小于阈值的判定为未知信号,大于阈值的使用Softmax层的预测结果进行类别判断,得到结果如表4所示。
由表4可以看出,使用改进的全连接神经网络,在不同信噪比环境下对已知雷达信号都有很好的分选效果,并且能够剔除一部分未知雷达信号。对全连接神经网络的分类结果进一步进行时域校验,得到结果如表5所示。
表4 不同信噪比环境下雷达信号分选准确率
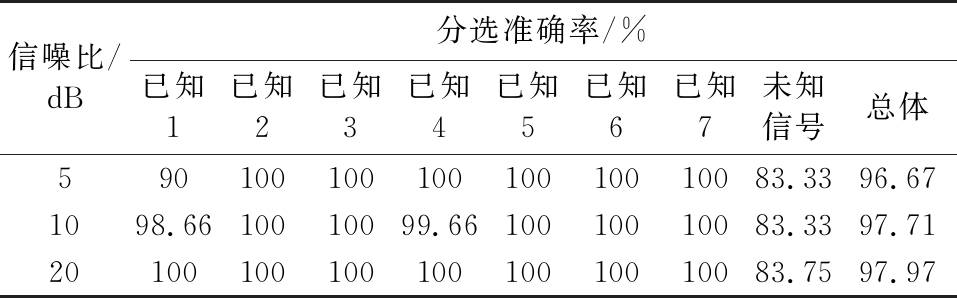
信噪比/dB分选准确率/%已知1已知2已知3已知4已知5已知6已知7未知信号总体59010010010010010010083.3396.671098.6610010099.6610010010083.3397.712010010010010010010010083.7597.97
表5 不同信噪比环境下时域校验后准确率
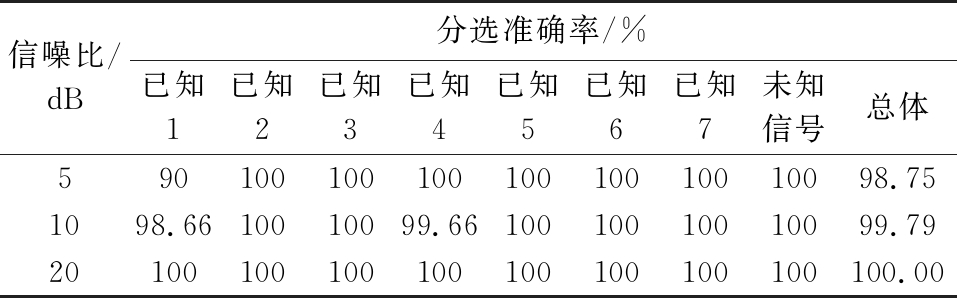
信噪比/dB分选准确率/%已知1已知2已知3已知4已知5已知6已知7未知信号总体59010010010010010010010098.751098.6610010099.6610010010010099.7920100100100100100100100100100.00
由雷达信号预分选的最终结果可以看出,时域校验利用雷达的时域关联特性,在一定程度上能进一步剔除未知雷达信号,提高分选准确率。
5 结束语
本文利用雷达数据库中雷达信号的脉内和脉间特征,对加入置信度神经元的全连接神经网络进行训练,在保证神经网络分选准确率的前提下,增加了其对未知雷达信号的判别能力。最后对神经网络的分选结果进行时域校验,进一步提高分选方法的准确率。仿真实验表明,在不同的信噪比环境下,本文提出的方法对参数捷变的雷达信号有较高的分选准确性,并且能很好地剔除未知雷达信号,具有一定的参考价值。
[1] 王杰贵,靳学明. 现代雷达信号分选技术综述[J]. 雷达科学与技术,2006, 4(2):104-108.
[2] 韩俊,陈晋汶,孙茹. 复杂体制雷达辐射源信号识别新方法[J]. 雷达科学与技术,2016, 14(1):76-80.
[3] 刘旭波,刘敬蜀,刘斌,等. 随机森林分类用于雷达信号预分选新算法研究[J]. 科技导报,2019,37(13):93-97.
[4] 王琨鹏,颜春林,杨辉. 基于模板匹配的雷达辐射源信号识别研究[J]. 舰船电子对抗,2014, 37(5):31-33.
[5] 吴连慧,周秀珍,宋新超. 基于改进OPTICS聚类的雷达信号预分选方法[J].舰船电子对抗,2018,41(6):95-99.
[6] SHENG Y,HOU C, SI W, et al. Extract Pulse Clustering in Radar Signal Sorting[C]∥2017 International Applied Computational Electromagnetics Society Symposium,Italy: IEEE,2017:1-2.
[7] 江涛,何明浩,翟卫俊. 小波神经网络在雷达信号分选中的应用[J]. 雷达科学与技术, 2004, 2(6):341-344.
[8] 袁泽恒,田润澜,王晓峰. 复杂体制雷达信号预分选的方法[J]. 电信科学,2018, 34(9):103-110.
[9] DEVRIES T, TAYLOR G W. Learning Confidence for Out-of-Distribution Detection in Neural Networks[J]. arXiv: Machine Learning, 2018:1-12.
[10] 陈格. 人工神经网络技术发展综述[J]. 中国科技信息,2009(17):88-89.
[11] 文茜. 基于神经网络的复杂雷达信号分类方法研究[D]. 西安:西安电子科技大学,2018:41-42.
[12] 梁华东,徐庆. 熵特征在雷达信号分选中的应用[J]. 空军预警学院学报,2015,29(1):7-12.
[13] 骆振兴,陈仕川,杨小牛. 通信辐射源个体开集识别中的二分类SVDD算法[J]. 通信对抗,2017,36(2):1-6.
[14] NGUYEN K, O’CONNOR B. Posterior Calibration and Exploratory Analysis for Natural Language Processing Models [J]. Empirical Methods in Natural Language Processing, 2015:1587-1598.
[15] HEIN M, ANDRIUSHCHENKO M, BITTERWOLF J, et al. Why ReLU Networks Yield High-Confidence Predictions Far Away from the Training Data and How to Mitigate the Problem[J]. Computer Vision and Pattern Recognition, 2019(7):41-50.
