0 引言
近年来，随着中国基础设施建设的振兴与发展，大型工程不断推进，雷达高精度测距技术在建筑物形变监测、湖泊液位测量、自动化汽车、目标高精度定位等方面被广泛应用。线性调频连续波雷达因具有结构简单、测距分辨率高、抗噪声能力强等特点被逐渐应用在高精度测距领域中。
线性调频连续波雷达对单个静止目标高精度测距的关键技术是准确得到回波信号与发射信号混频后差拍信号的频率，从而获得高精度的测距信息。现有的高精度频率测量方法主要有以下几大类：比值法、基于FFT的频谱细化算法、相位差法。典型的比值法有Rife算法[1]、Quinn算法[2-4]、Grandk算法等，这些算法利用频谱峰值附近多条谱线的幅度比值对频率进行校正，但接近量化频率点时误差较大，文献[5-7]都针对这个问题进行了改进,但运算量大幅增加,且精度提高有限。基于FFT的频谱细化算法首先使用少量点数FFT算法作粗估计，然后再用细化算法对频谱的局部进行放大作细估计，主要方法有补零FFT、CZT、Zoom-FFT[8]，FFT+FT连续细化法[9-10]等，但若要达到理论精度，需要牺牲指数倍的运算量和采样时间，对于工程应用非常不利。
上述两种测量方法均以信号谱线作为频率估计参数，没有引入相位信息作为参数，文献[1]分别给出了以信号谱线和相位两种参数测量方法的克拉美罗下界，后者的估计下界远低于前者。所以学者们开始对相位法测频进行深入研究，Tretter最早利用回波信号的瞬时相位实现了频率估计[11]，但在远距离测量时存在相位模糊。为了避免这个问题，Kay提出一种基于采样序列相邻点相位差的估计方法[12]，但其对信噪比要求较高，于是Fitz提出了利用自相关函数相位的方法实现频率估计[13]，这个算法降低了信噪比门限，但是测距范围很小，没有实际工程意义。文献[14]针对这个问题提出了改进Fitz算法，将自相关函数的相位进行解缠，估计范围扩大了M倍，且估计精度更高。文献[15]提出了一种利用补零FFT细化频谱的相位差测频方法，精度更加逼近理论下界，但低信噪比时容易出现相位模糊。近年来基于相位差法的频率估计算法不断被提出[16-18]，但估计精度都不及文献[15]。
综上所述，比值法实时性强但频率估计精度不足，频谱细化的估计算法运算量过大，实时性不足，相位差法兼顾了精度和实时性的要求，但对信噪比条件要求较高。基于此，本文针对静止目标的测距问题提出一种新的相位差改进算法，利用CZT消除相位模糊问题，再运用相位差法实现频率估计。与以往相位差方法相比，大幅降低了运算量并在低信噪比条件下精度更高。
本文第一部分介绍了雷达测距技术的研究背景，第二部分推导了传统相位差法测距的原理，第三部分给出了改进算法的原理和规避误差的方法，最后在仿真中将它与经典算法对比，证明了该算法的性能优势。
1 相位差法测距原理
线性调频连续波雷达将发射信号与接收信号混频，可以获得需要我们研究的差拍信号。以单调频斜率信号为例，雷达发射信号为
(1)
式中，a1为信号幅度，f0为中心频率，B为扫频带宽，
为调频斜率，T为扫频周期，φa为信号初始相位。经距离为r的静止目标反射后的回波信号为
R(t)=
τ≤t≤T+τ
(2)
式中，τ=2r/c为延迟时间。两个信号进行混频，在实际应用环境中，τ数值很小，故混频计算后可以忽略τ2项。得到差拍信号
(3)
由于τ≪T，后续计算可以忽略τ，所以差拍信号的定义域可以记为0≤t≤T。根据式(3)，信号频率fc由相位求导获得，fc=μτ，所以距离和频率的关系为r=cTfc/2B。
对差拍信号进行N点复采样，采样间隔T/N，无失真采样需满足奈奎斯特复采样定理，即采样频率fs=N/T≥fc，所以最大探测距离r≤cN/2B，得到离散信号表达式：
(4)
对其进行N点FFT变换，则距离分辨率ΔR=c/2B，变换后的表达式为
X(k)=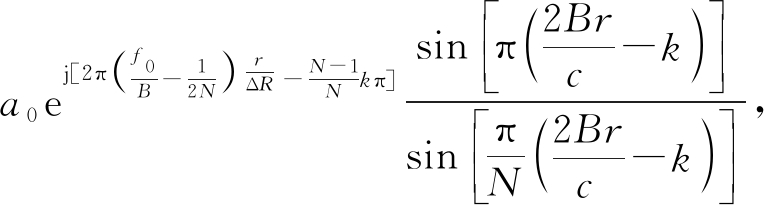
k=0,…,N-1
(5)
真实信号的频谱在k取最接近2Br/c的整数k0时幅值最大，最大值处的相位为
(6)
相邻谱线间的相位差
参考信号则假设r正好处于量化频点k0ΔR处，最大值点参考相位为
(7)
所以真实值与量化频点参考相位的相位差φr0=φk0-φk0， 距离估计就可以表示为
(8)
上述就是相位差法测距的过程，但是计算时忽略了相位模糊的问题。我们可以计算得到相邻谱线相位差Δφk0>2π，所以计算距离偏移量时会出现模糊，需要细化频谱使Δφk0<2π，从而消除模糊问题。
频谱细化的主流算法有3种，补零FFT、Zoom-FFT和CZT(Chirp-Z)。文献[16]就是利用补零FFT变换细化频谱后消除了相邻谱线的模糊，但其计算量较大且没有考虑误差导致的间隔谱线之间的相位模糊，所以在低信噪比条件下效果较差。Zoom-FFT所需要的原始数据较长，在工程瞬态过程中无法应用。CZT算法在Z平面对信号抽样细化，具有运算量小、实时性高的优点，但还没有学者利用CZT变换细化频谱后再运用相位差法实现距离测量，所以本文对这个方法进行深入研究。
2 基于CZT变换的改进相位差算法
CZT变换即将序列x(n)(0≤n≤N-1)沿Z平面的一段单位圆作等分角的抽样zk=AW-k (k=0,…,M-1),其中，A=A0ejθ0，W=W0e-jφ0，作CZT变换时A0=1,W0=1，θ0是起始采样角度，φ0是两相邻采样点之间的角度 [19]，设CZT细化倍数是δ，则抽样点在Z平面的周线如图1所示。
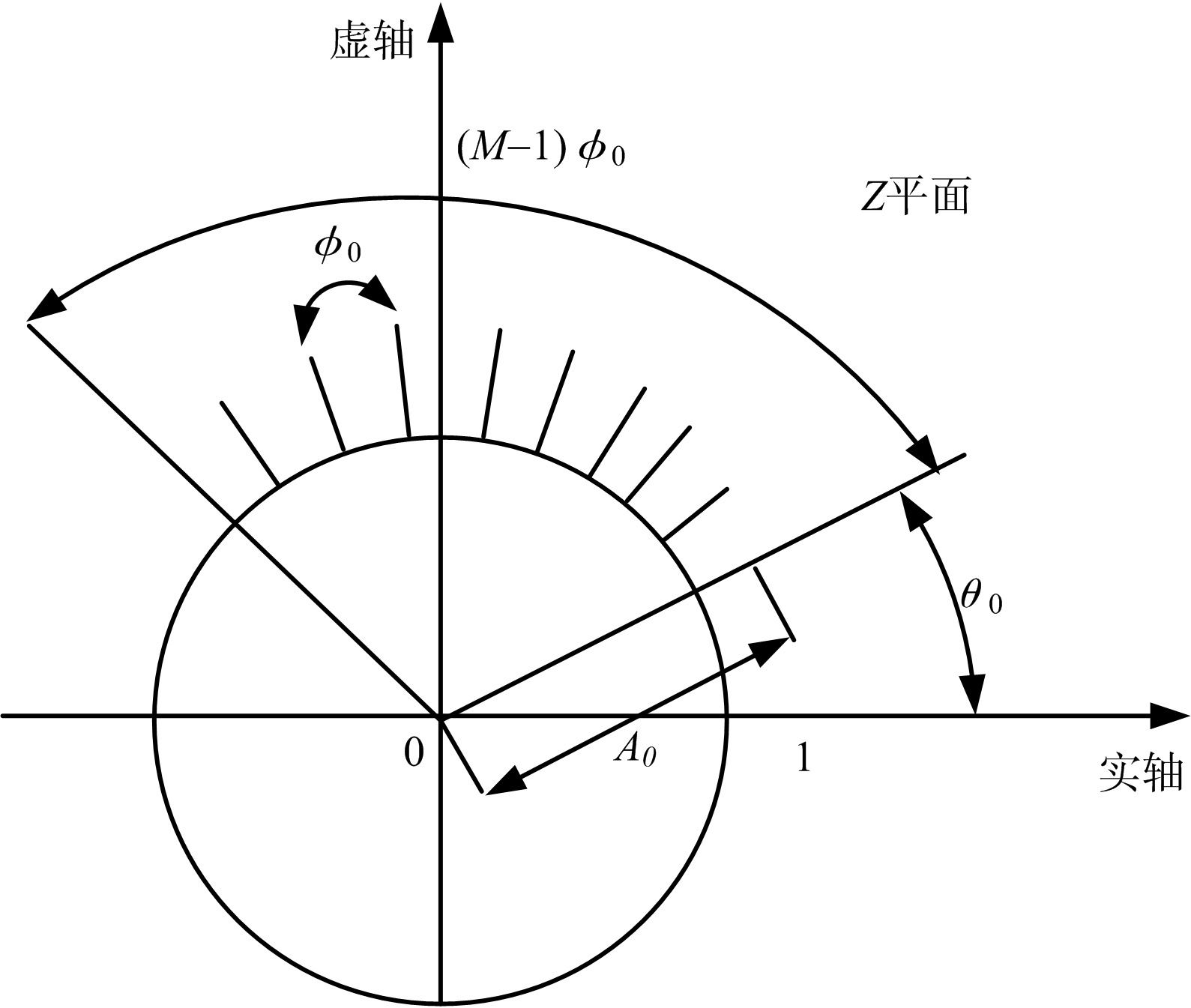
图1 CZT变换在Z平面抽样点的螺线轨迹
原信号的CZT变换表示为
X(zk)=
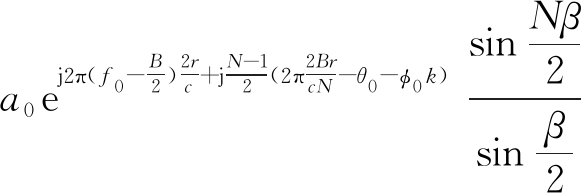
(9)
其中
故CZT变换后的信号最大值处k的相位为
(10)
我们设定细化频谱的起点为与最大谱线相邻的左谱线，终点为与最大谱线相邻的右谱线，则局部频谱细化为M=2δ点，频谱分辨率则为Δr=ΔR/δ，相邻谱线相位差
为避免相位模糊需满足Δφk1<2π，所以要求δ>f0/B。
由公式(5)可知，N点FFT后信号最大谱线的下标为k0，则θ0=2π(k0-1)/N，φ0=4π/MN，代入式(8)得
(11)
当r处于量化距离m1ΔR+m2Δr时(m2<δ)，参考相位为
(12)
式中，γ=δm1+m2。
当真实值偏移量化距离时，偏移值φr=φzk-φzk，则距离估计为
(13)
该算法利用CZT变换使频谱细化了δ倍，完成了相邻谱线相位去模糊的功能，但还需要进一步改进以获得低信噪比条件下更好的测量效果。
在低信噪比环境下，信号最大谱线位置可能发生偏移，产生误差。这时，我们会把第二大谱线m′2=m2±1当成m2来计算。当距离为r时，第二大谱线的相位为
而当r=m1ΔR+m′2Δr时，参考相位为
其中γ′=δm1+m′2。所以谱线偏移后计算得到的相位差为
(14)
将该结果计算距离，可以得到
(15)
理论上，即使噪声导致最大谱线位置偏差，还是可以获得正确的距离，但前提条件是上述相位值都是未解缠的，否则会出现模糊。例如φr-Δφzk<-π,m′2=m2+1时，计算得到的是解缠后的相位值，在-π～π区间，此时φ′r=φr-Δφzk+2π，这样就出现了Δr的误差。
为了避免这种情况，则必须满足下式：
(16)
我们已知-Δφzk<φr<Δφzk，所以
细化倍数与仅考虑相邻谱线相位模糊相差4倍，δ最小取32，这样就能避免谱线偏移时可能引起的模糊问题，极大提高抗噪声性能。
3 改进算法性能分析
3.1 改进算法与经典算法精度对比
采用Monte Carlo计算机模拟方法，对单一频率的有噪声差拍信号进行采样，运用改进Fitz算法、补零相位差算法、本文算法进行仿真，仿真参数如表1所示。
表1 仿真参数
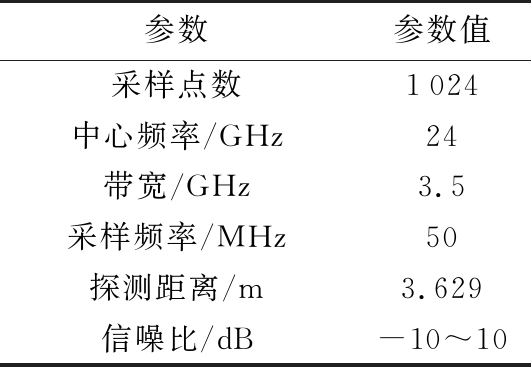
参数参数值采样点数1024中心频率/GHz24带宽/GHz3.5采样频率/MHz50探测距离/m3.629信噪比/dB-10^10
在不同信噪比条件下对不同算法进行仿真并利用如下公式计算归一化均方根误差。
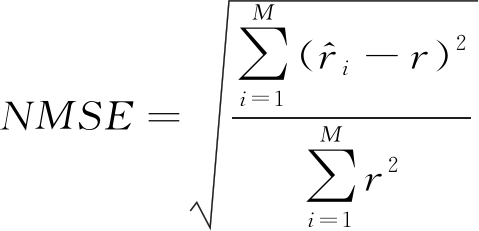
(17)
所得结果如图2所示。
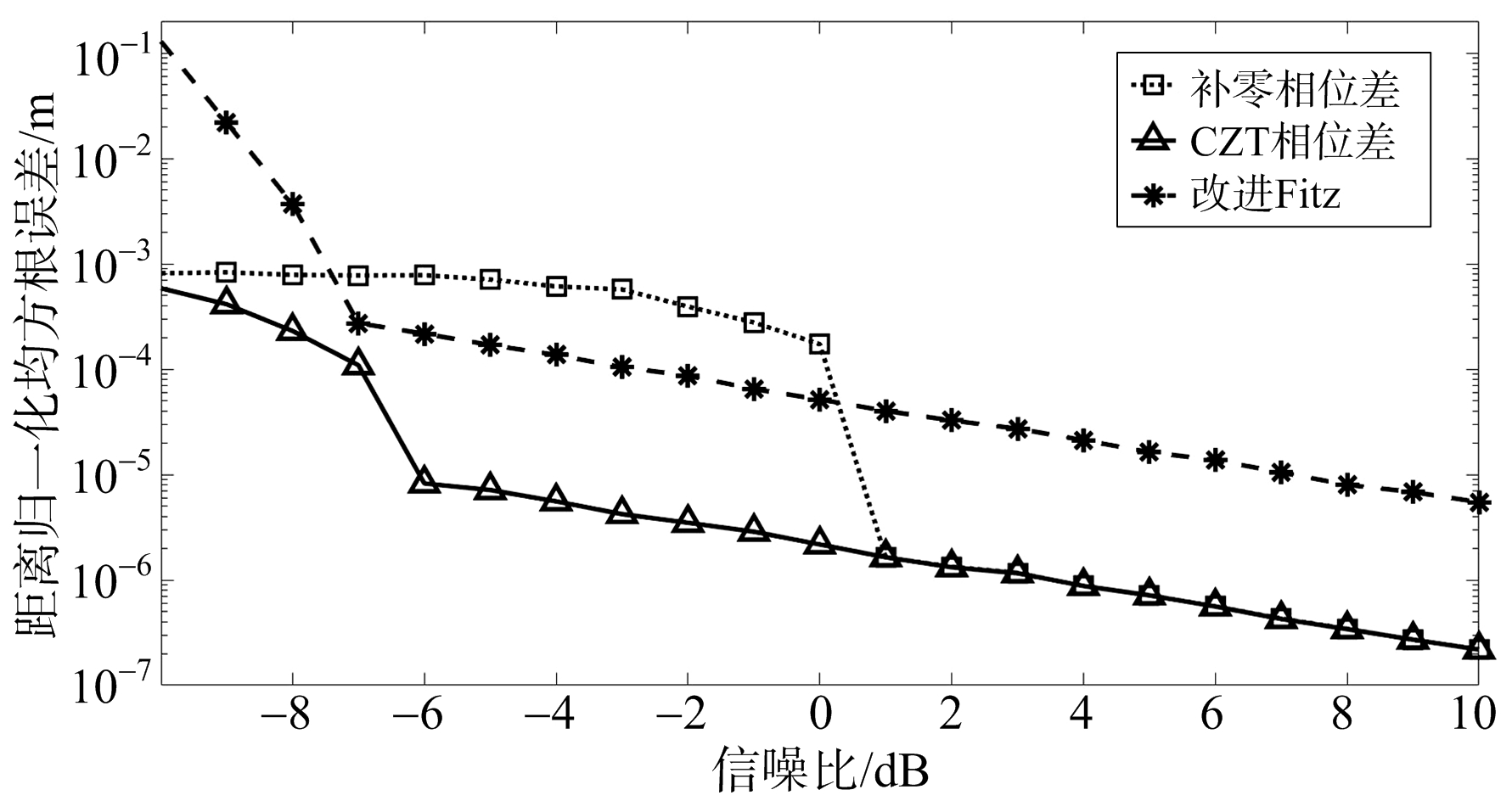
图2 各算法不同信噪比误差
图2表明改进后的Fitz算法在高信噪比条件下精度比相位差算法低一个数量级。补零相位差算法精度较高但信噪比门限也高，为1 dB左右，改进的相位差算法精度最高，抗噪声性能也最好，信噪比门限比补零相位差算法降低了7 dB。
3.2 改进算法与经典算法计算量对比
1) 改进Fitz算法
对N/2点信号作自相关运算，需要3N2/8次复乘，忽略复加运算。
2) 补零相位差算法
对输入信号作8N点FFT运算，需要4Nlog28N次复乘。
3) 基于CZT的相位差算法
对输入信号作CZT变换，使用基-2FFT法计算，M为细化点数，N为粗傅里叶变换点数，L为圆周卷积长度，L≥M+N-1，且L=2m(m为正整数)，则复乘次数为Llog2L+L+N+M[19]。
各算法计算量对比如表2所示。
表2 不同算法所需计算量对比
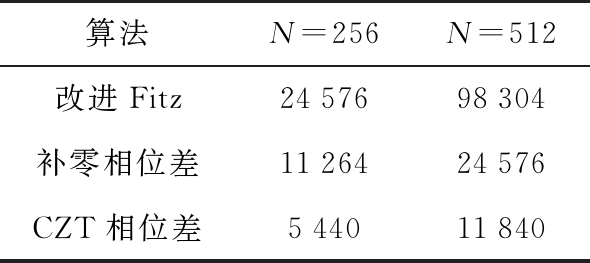
算法N=256N=512改进Fitz2457698304补零相位差1126424576CZT相位差544011840
可见改进Fitz算法的计算量远大于相位差算法，而CZT相位差算法又在补零相位差基础上减少了一倍以上计算量，点数越多减少量越大，其优势是显而易见的。
4 结束语
本文针对相位差法信噪比门限高的问题，研究了低信噪比条件下误差产生的原因，引入CZT算法，提出了能够避免由于误差导致的间隔谱线之间的相位差计算模糊的算法，提高了整体的抗噪声性能，降低了运算量。新算法在仿真中验证了其估计精度、抗噪声性能等方面较经典相位差算法都有较大改善，实现了低信噪比条件下的高精度距离估计，对实际工程应用有重要意义。
[1] RIFE D, BOORSTYN R. Single Tone Parameter Estimation from Discrete-Time Observations[J]. IEEE Trans on Information Theory, 1974, 20(5):591-598.
[2] QUINN B G.Estimation of Frequency, Amplitude, and Phase from the DFT of a Time Series[J]. IEEE Trans on Signal Processing,1997, 45(3):814-817.
[3] 周胜文,詹磊,廖春兰,等.基于改进的Quinn测频算法及其FPGA实现[J].太赫兹科学与电子信息学报, 2019,17(2):68-72.
[4] 李玲霞,贾帅,谢良波,等.基于改进Quinn算法的LFMCW雷达高精度测距[J].雷达科学与技术, 2018,16(5):465-470.
LI Lingxia， JIA Shuai， XIE Liangbo， et al. An Improved Quinn Algorithm for Improving the LFMCW Radar Ranging Accuracy[J]. Radar Science and Technology,2018,16(5):465-470.(in Chinese)
[5] 孙微涛,张志宝,罗文峰,等.基于Rife算法的跳频信号瞬时频率估计算法研究[J].计算机与数字工程,2018,46(5):870-873.
[6] 温兵会,毛卫宁.一种快速有效的正弦波信号频率估计方法[J].应用声学,2020,39(4):512-517.
[7] 孙宏军,王小威.基于幅值-相角判据的修正Rife正弦波频率估计算法[J].天津大学学报(自然科学与工程技术版),2018,51(8):810-816.
[8] 赵强,侯孝民,廉昕.基于Zoom-FFT的改进Rife正弦波频率估计算法[J].数据采集与处理,2017, 32(4):731-736.
[9] 刘畅,张丕状,姚金杰,等.基于FFT+FT的FMCW雷达高精度测距算法研究[J].国外电子测量技术,2019,38(10):65-69.
[10] CARBONI A , FERRERO A . A Fourier Transform-Based Frequency Estimation Algorithm[J]. IEEE Trans on Instrumentation and Measurement, 2018,67(99):1722-1728.
[11] TRETTER S. Estimating the Frequency of a Noisy Sinusoid by Linear Regression[J]. IEEE Trans on Information Theory,1985,31(6):832-835.
[12] KAY S . A Fast and Accurate Single Frequency Estimator[J]. IEEE Trans on Acoustics, Speech, and Signal Processing,1989,37(12):1987-1990.
[13] FITZ M P . Further Results in the Fast Estimation of a Single Frequency[J]. IEEE Trans on Communications,1994,42(234):862-864.
[14] QI Guoqing. A New Frequency Estimator of Single Sinusoid Based on Fitz’s Algorithm[C]∥Proceedings 7th International Conference on Signal Processing, Beijing: IEEE, 2004:1790-1793.
[15] QI Guoqing. High Accuracy Range Estimation of FMCW Level Radar Based on the Phase of the Zero-Padded FFT[C]∥Proceedings 7th International Conference on Signal Processing, Beijing: IEEE, 2004, 3:2078-2081.
[16] 廖烨,刘国峰,李康,等.基于相位差法和FRFT的Chirp信号参数估计算法[J].光通信研究,2020(3):73-78.
[17] 谢胜.基于Rife算法和相位差法的频率估计算法[J].水下无人系统学报,2018,26(3):263-266.
[18] XU Haitao, HAN Leng， HUANG Qingqing，et al. Frequency Estimator by Combination of Phase Difference Method and Interpolation Algorithm[J]. Journal of Algorithms & Computational Technology, 2019,13:1-10.
[19] 程佩青.数字信号处理教程[M].4版.北京：清华大学出版社,2013：235-241.
