0 引 言
现代空战的制胜机理是“OODA(Observe- Orient-Decide-Act)环”的高效运转,为夺取作战的主动权,必须提升OODA环运行的敏捷性和准确性,因此,基于无源侦察信号快速判断敌方机载火控雷达空空工作状态,是己方作战飞机有效规避威胁、实施抗击的基础。目前对敌方机载火控雷达的分析与研究,侧重于空空工作模式的反推。对工作模式的研究方面,文献[1-2]从信号波形和扫描特征入手,对机载火控雷达空空工作模式进行了全面的分析,说明了工作模式的繁杂现状。对工作模式反推判定的研究方面,贾朝文等[3]只提出了便于工程实践的识别思路;刘俊江等[4]主要针对机械扫描的PD体制雷达进行分析,不适用于相控阵体制雷达;王玉冰等[5-6]的分析局限于信号波形参数,且未考虑相控阵体制下的复杂工作模式。
随着数字阵列技术的应用,机载火控雷达的信号波形更趋复杂、工作方式的区分更加模糊,加之电子侦察系统侦获的全脉冲数据属于碎片化的采样信息,机载火控雷达工作模式的准确反推难以实现。本文从电子侦察系统获取的信息出发,对工作模式按状态分类,设计了信号波形模拟器,并提出了一种基于DS证据理论的空空工作状态识别方法,最后通过实验仿真验证了识别方法的实效性。
1 基于电子侦察视角的工作状态定义与分析
现役的机载火控雷达包含9种主要的空空模式[7]:速度搜索(VS)、边速度搜索边测距(VSR)、边搜索边测距(RWS)、边搜索边跟踪(TWS)、搜索加跟踪(TAS)、单目标跟踪(STT)、态势感知(SAM)、双目标跟踪(DTT)和多目标跟踪(MTT)。以TAS模式为例,该模式是相控阵体制雷达特有的工作模式,对搜索和跟踪能进行灵活的波束管控和时间资源调度,在发现目标后可即刻实施跟踪,且可以根据目标威胁程度增加跟踪数据率,极限情况下放弃空域搜索,变为STT或MTT模式。因此,在TAS模式下,被搜索和被跟踪的侦察机侦获的信号截然不同,信号时幅特征如图1所示。综上可知,随着相控阵体制、数字化技术的广泛运用,基于电子侦察数据的雷达工作模式反推不再适用。
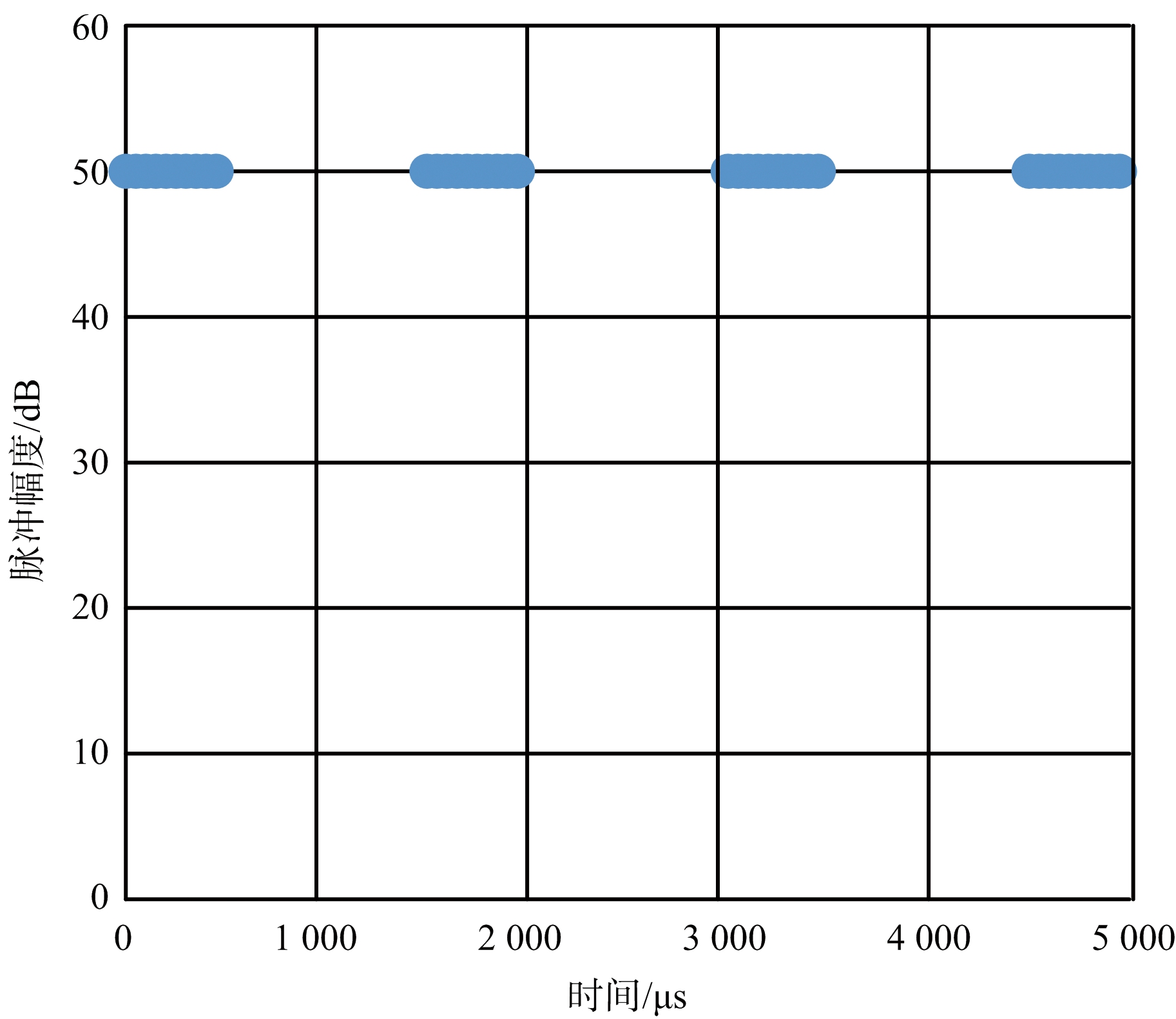
(a) TAS模式跟踪波形时幅图
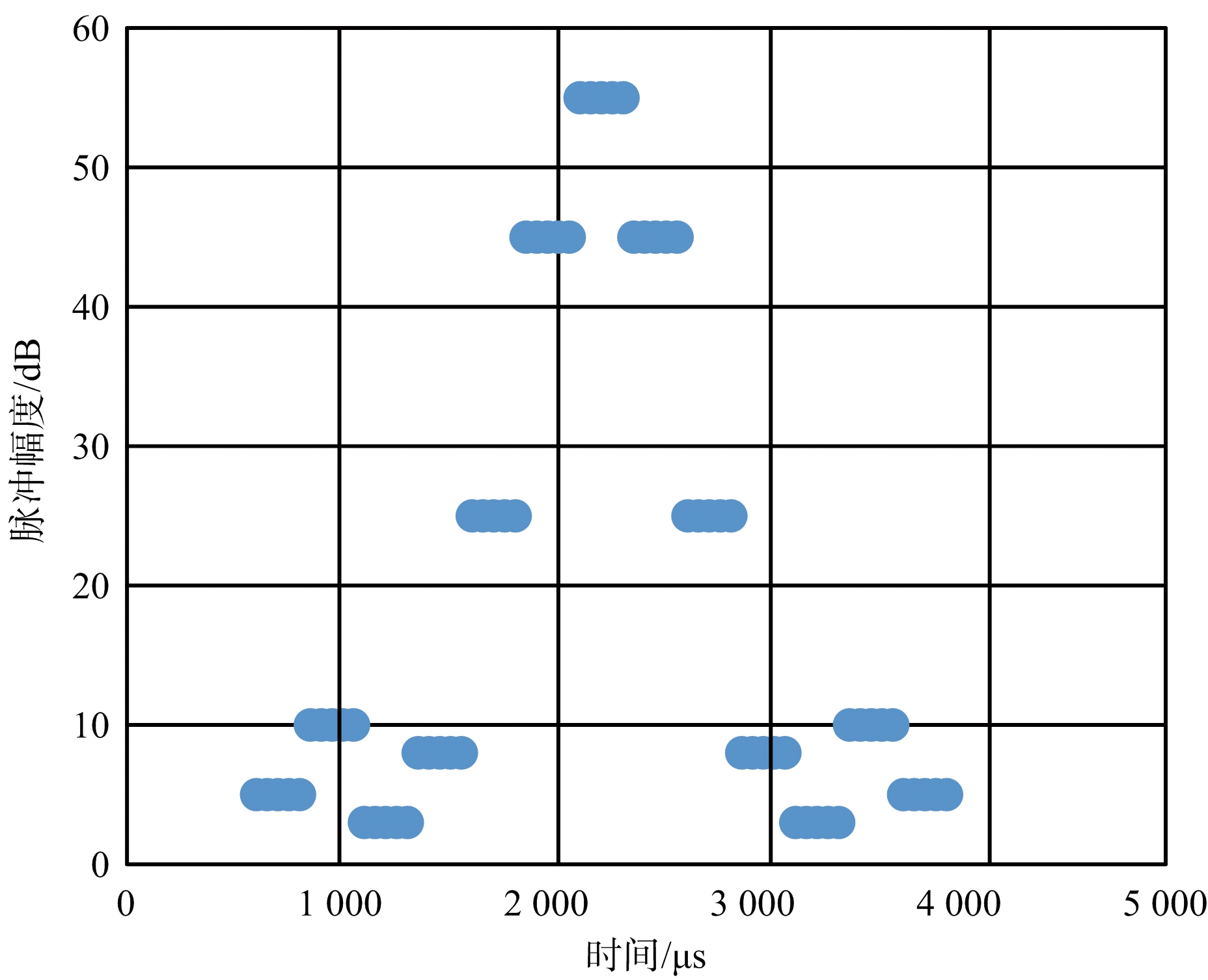
(b) TAS模式搜索波形时幅图
图1 TAS模式不同工作波形时幅图
1.1 空空工作状态定义
本文从电子侦察的角度出发,立足侦察接收机与雷达天线扫描的相对位置,综合雷达天线扫描特征和波性特征信息,定义如表1所示的8种机载火控雷达空空工作状态[8]。
表1 雷达空空工作状态分类表
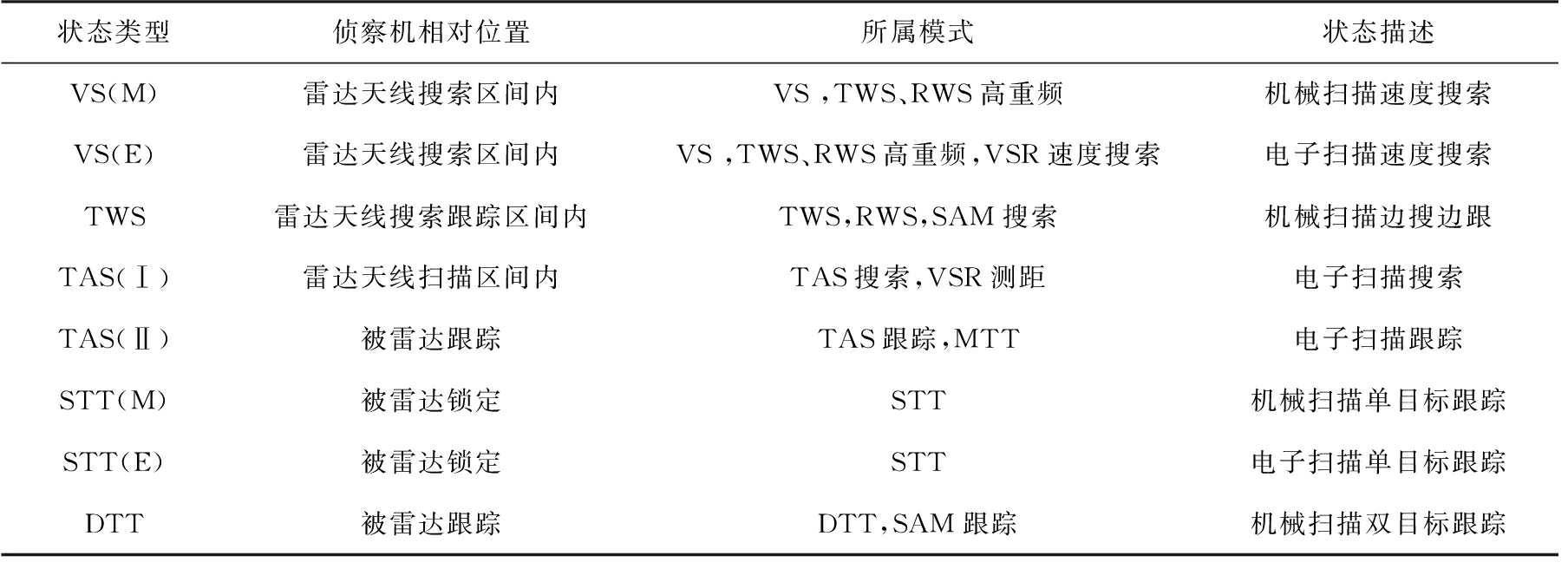
状态类型侦察机相对位置所属模式状态描述VS(M)雷达天线搜索区间内VS ,TWS、RWS高重频机械扫描速度搜索VS(E)雷达天线搜索区间内VS ,TWS、RWS高重频,VSR速度搜索电子扫描速度搜索TWS雷达天线搜索跟踪区间内TWS,RWS,SAM搜索机械扫描边搜边跟TAS(Ⅰ)雷达天线扫描区间内TAS搜索,VSR测距电子扫描搜索TAS(Ⅱ)被雷达跟踪TAS跟踪,MTT电子扫描跟踪STT(M)被雷达锁定STT机械扫描单目标跟踪STT(E)被雷达锁定STT电子扫描单目标跟踪DTT被雷达跟踪DTT,SAM跟踪机械扫描双目标跟踪
1.2 典型波形参数
不同空空工作状态的典型波形参数如表2所示[9]。其中,单个脉冲相参处理周期(CPI)内脉冲幅度趋势与雷达天线体制和扫描方式直接相关,相控阵体制雷达波位可灵活跳转,幅度包络呈“平顶”状,机械扫描雷达天线幅度包络保持变化趋势。因此,CPI周期内幅度包络平顶,变化趋势表示为“0”,否则表示为“1”。
表2 雷达空空工作状态典型波形参数
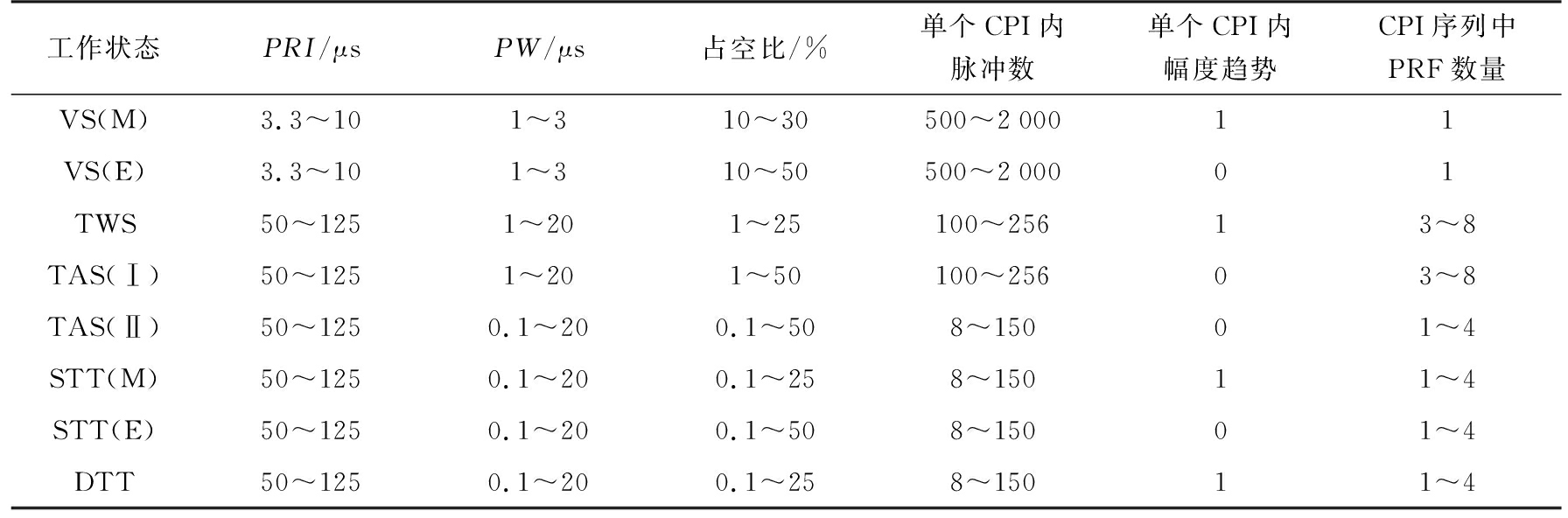
工作状态PRI/μsPW/μs占空比/%单个CPI内脉冲数单个CPI内幅度趋势CPI序列中PRF数量VS(M)3.3~101~310~30500~200011VS(E)3.3~101~310~50500~200001TWS50~1251~201~25100~25613~8TAS(Ⅰ)50~1251~201~50100~25603~8TAS(Ⅱ)50~1250.1~200.1~508~15001~4STT(M)50~1250.1~200.1~258~15011~4STT(E)50~1250.1~200.1~508~15001~4DTT50~1250.1~200.1~258~15011~4
1.3 信号波形模拟器设计
本文利用MATLAB软件开发了基于电子侦察视角的信号波形模拟器,可仿真8种状态的信号波形。此外,本文的信号波形模拟器可直观地呈现侦察机与雷达的相对位置、天线波束的运动轨迹和信号波形的幅度变化等。信号波形模拟器界面如图2所示。
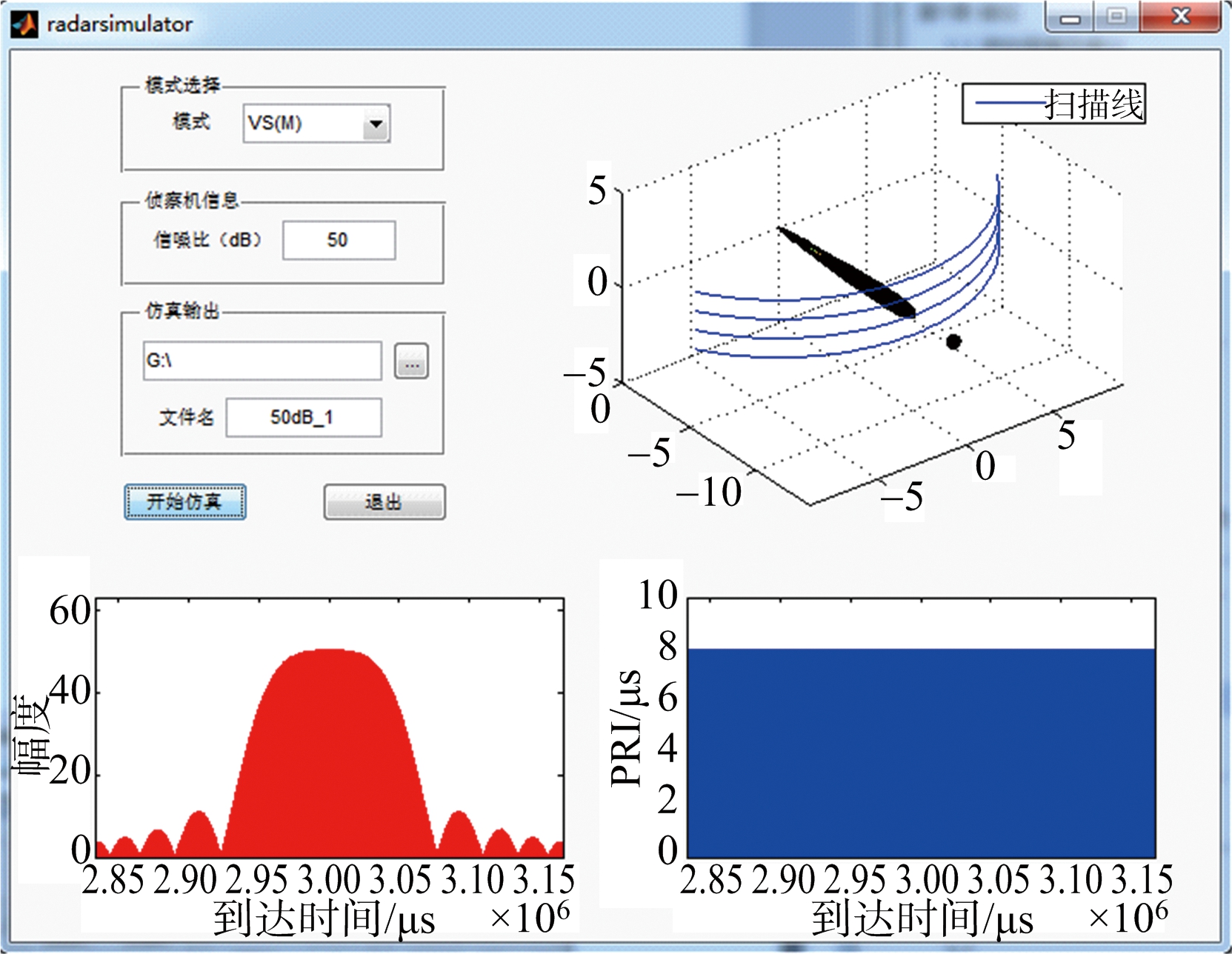
图2 信号波形模拟器
1.4 机载火控雷达特征参数集
电子侦察系统直接侦察得到的PDW(脉冲描述字),即雷达辐射源五大参数为DOA(到达角)、RF(载频)、PW(脉宽)、PA(幅度)和TOA(到达时间)。鉴于雷达波形日趋复杂多样,基于PDW的识别难度较大、准确性较低。本文的识别研究建立在有效分选的基础上,综合考虑波形参数和扫描特征,选取了5类识别特征参数:脉冲重复间隔(PRI)、PW、占空比(PWM)、单个CPI内脉冲数和单个CPI内幅度趋势,因此,雷达特征参数集可表示为P=(p1,p2,p3,p4,p5),具体含义如表3所示。
表3 雷达特征参数
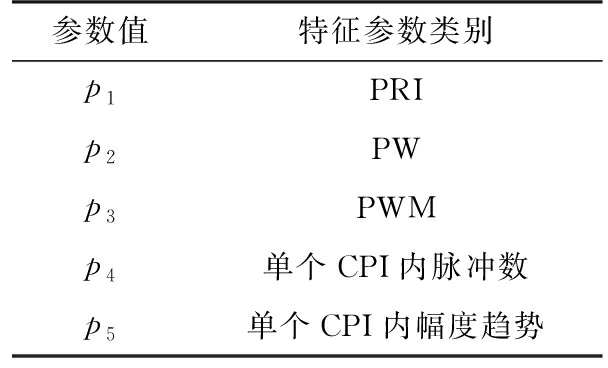
参数值特征参数类别p1PRIp2PWp3PWMp4单个CPI内脉冲数p5单个CPI内幅度趋势
2 DS证据理论的状态识别算法
2.1 DS证据理论
2.1.1 基本概念
证据理论[10]是由数学家Dempster及其学生Shafer为解决不确定性问题,通过定义基本分配概率、信任函数、似然函数和信任区间等概念,对不确定“证据”进行有效组合,形成较高准确率和可靠性推理结论的数学方法。该方法利用上下限概率,在识别框架内,依据信息论的理论支撑,有效地解决了多值映射问题,由于证据理论不需要知道先验概率,能够较好地应对“不确定”,因此,被广泛应用于目标识别、故障诊断、病理分析等领域。证据理论的基本定义如下:
1) 基本概率分配(BPA)。在识别框架Θ内,其子集表示命题,Θ的子集两两互斥,即任意时刻的识别选项唯一。证据是指对命题的支持程度,证据有其基本概率函数M,函数M是2Θ→[0,1]的映射。设A为2Θ的任一子集,即A⊆2Θ,且满足下列条件:
(1)
则称M为2Θ上的基本概率分配函数,也称为mass函数。M(A)为A的基本置信度值,表征证据对A的支持程度。
2) 信任函数(BF)。映射Bel:2Θ→[0,1],如果满足下列条件:
Bel(A)=∑B⊂AM(B)=1(∀A⊂Θ)
(2)
则称Bel(A)为信任函数。
3) 似然函数(PF)。映射Pl:2Θ→[0,1],如果满足下列条件:
(3)
则称Pl(A)为似然函数,其表示不否认A的信任度,也称A的非假信任度。
4) 信任区间。指事件发生上下限估计概率值的范围,如图3所示。A的信任区间[Bel(A), Pl(A)]。

图3 信任区间示意图
2.1.2 组合规则
在识别框架Θ内,对于∀A⊂Θ,有限个mass函数M1,M2,…,Mn的组合规则为
(M1⊕M2⊕…⊕Mn)(A)=
![]() ∑A1∩A2∩…∩An=AM1(A1)·
∑A1∩A2∩…∩An=AM1(A1)·
M2(A2)…Mn(An)
(4)
式中,K是归一化因子,表征证据的冲突程度,其表达式有两种形式:
K=∑A1∩…∩An=∅M1(A1)·
M2(A2)…Mn(An)
(5)
K=1-∑A1∩…∩An≠∅M1(A1)·
M2(A2)…Mn(An)
(6)
2.1.3 判决规则
若存在A0⊂Θ,满足下列条件:
1) (A0)=max {M(Ai),Ai⊂Θ};
2) M(A0)-M(Ai)>ε1;
3) M(θ)<ε2;
4) M(A0)>M(θ)。
则判定A0为最终结果,其中,θ为不确定集合,ε1,ε2为预设门限,通常由实验测试决定。
2.2 基本概率分配的确定
2.2.1 区间相似度
设两个正实数区间A和B,A=[amin,amax],B=[bmin,bmax],则定义两区间的相似度函数[11]为
(7)
式中,α为支持系数,α>0,α的作用是面对数据相似集中的情况时,增大数据的离散度,进而提高识别率。
D(A,B)是指区间A和B的区间距离,其表达式[12]为
![]()
(8)
通过上式的定义可以看出:
1) 0≤S(A,B)≤1;
2) A=B时,S(A,B)=1。
2.2.2 确定基本概率分配
1) 确定识别特征参数的区间范围。以CPI内脉冲个数为例,TAS(Ⅰ)状态的CPI内脉冲个数的取值区间为[100,256],TAS(Ⅱ)状态的CPI内脉冲个数的取值区间为[8,150],两种状态的区间范围示意图如图4所示。
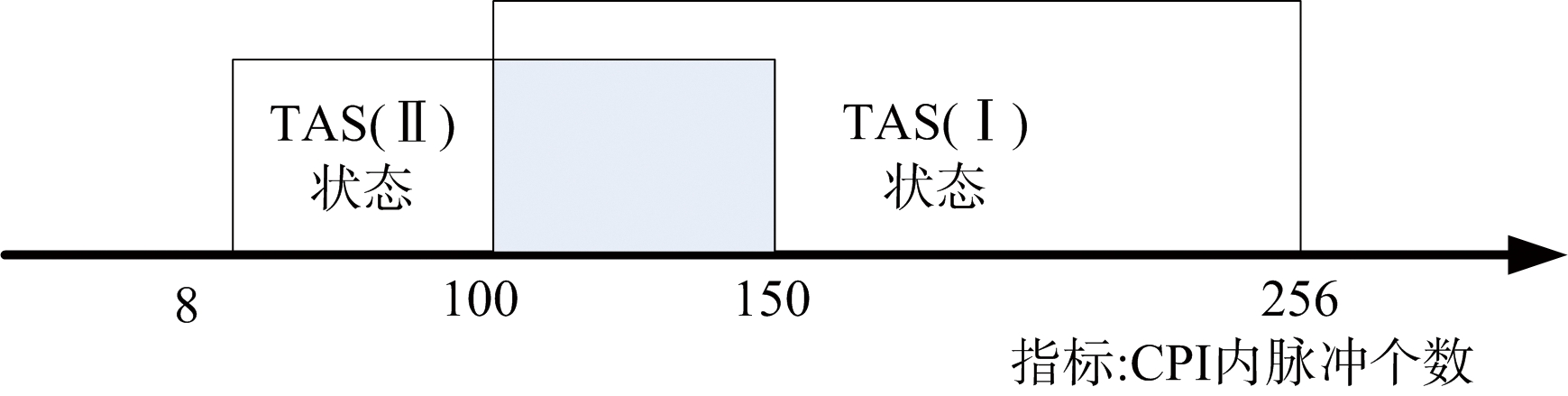
图4 特征参数的区间范围示意图
不同工作状态特征参数CPI内脉冲个数取值及交叠范围的取值p4如表4所示。
表4 特征参数p4的取值区间

工作状态p4TAS(Ⅰ)[100,256]TAS(Ⅱ)[8,150]{TASⅠ ,TAS(Ⅱ)}[100,150]
2) 求侦察样本值与各状态特征参数取值区间的距离D。例如,侦察信号的CPI内脉冲个数 p4=64,可认为p4=[64,64],进而根据公式(8),可求得侦察信号特征参数p4与不同工作状态的经验取值区间的距离D。计算结果如表5所示。
表5 特征参数p4与经验取值之间的距离

工作状态DTAS(Ⅰ)122.57TAS(Ⅱ)43.65{TASⅠ ,TAS(Ⅱ)}62.68
3) 计算基本概率分配。根据公式(7)的求解区间相似度,再对区间相似度进行归一化,进而可得不同工作状态单个特征参数的基本概率分配。计算结果如表6所示。
表6 特征参数p4的基本概率分配

工作状态MTAS(Ⅰ)0.1738TAS(Ⅱ)0.4867{TASⅠ ,TAS(Ⅱ)}0.3394
2.3 工作状态识别流程
对机载火控雷达8种空空工作状态的识别流程图如图5所示,具体步骤分为:
1) 建立雷达特征参数集。根据侦察信号分析得到的波形参数和扫描特征,建立雷达特征参数集。
2) 工作状态初始分类。当PRI值属于高重频范围,即p1∈[3.3~10]时,转到步骤3;当PRI值属于中重频范围,即p1∈[50~125]时,转到步骤4。
3) 单特征参数识别。当单个CPI内脉冲幅度值相对固定,即p5=1时,空空工作状态识别为 VS(M);当单个CPI内脉冲幅度值相对固定,即p5=0时,空空工作状态识别为VS(E)。
4) 多特征参数融合识别。先进行单相参周期分类,当p5=1时,工作状态为TWS、STT(M)或DTT;当p5=0时,工作状态为TAS(Ⅰ)、TAS(Ⅱ)或STT(E);再基于退化的特征参数集P*=(p2,p3,p4),使用前文的基本概率分配方法确定单个参数对应工作状态的概率;最后使用DS证据理论组合规则对不同工作状态进行多特征参数融合识别,根据判决规则得出识别结论。
5) 多周期融合识别。使用DS证据理论组合规则对多特征参数融合识别得到的信度值进行再融合,根据判决规则得出识别结论。
6) 补充判断。考虑到STT(M)与DTT, TAS(Ⅱ)与STT(E)的特征参数集P取值范围一致,无法有效区分,需从电子侦察角度引入“脉冲簇”的概念,脉冲簇是指侦察接收机稳定连续侦获敌方雷达信号的脉冲串。STT(M)与STT(E)状态下,雷达波束长时间锁定单个目标,脉冲簇时长通常为秒量级;DTT与TAS(Ⅱ)状态下,雷达波束对多个目标离散照射跟踪,脉冲簇时长通常为毫秒量级。因此,STT(M)与STT(E)的脉冲簇时长远大于DTT与TAS(Ⅱ),基于脉冲簇时长的判断,可实现对STT(M)与DTT,TAS(Ⅱ)与STT(E)的有效区分。
7) 输出空空工作状态识别结果。
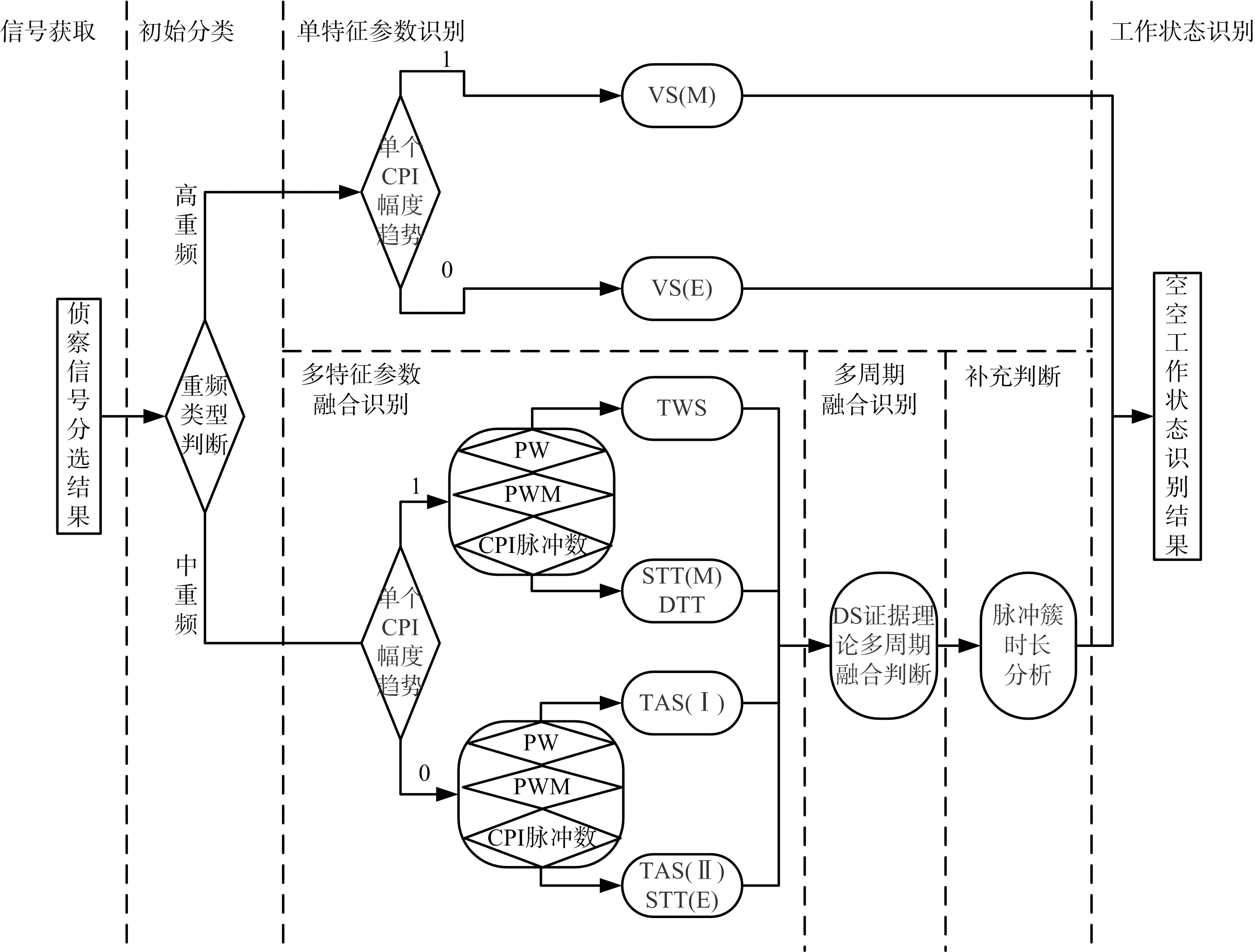
图5 空空工作状态识别流程图
3 仿真验证
使用信号波形模拟器仿真3种状态各4个CPI周期的信号,分析后得到雷达特征参数集,如表7所示。
表7 仿真信号特征参数
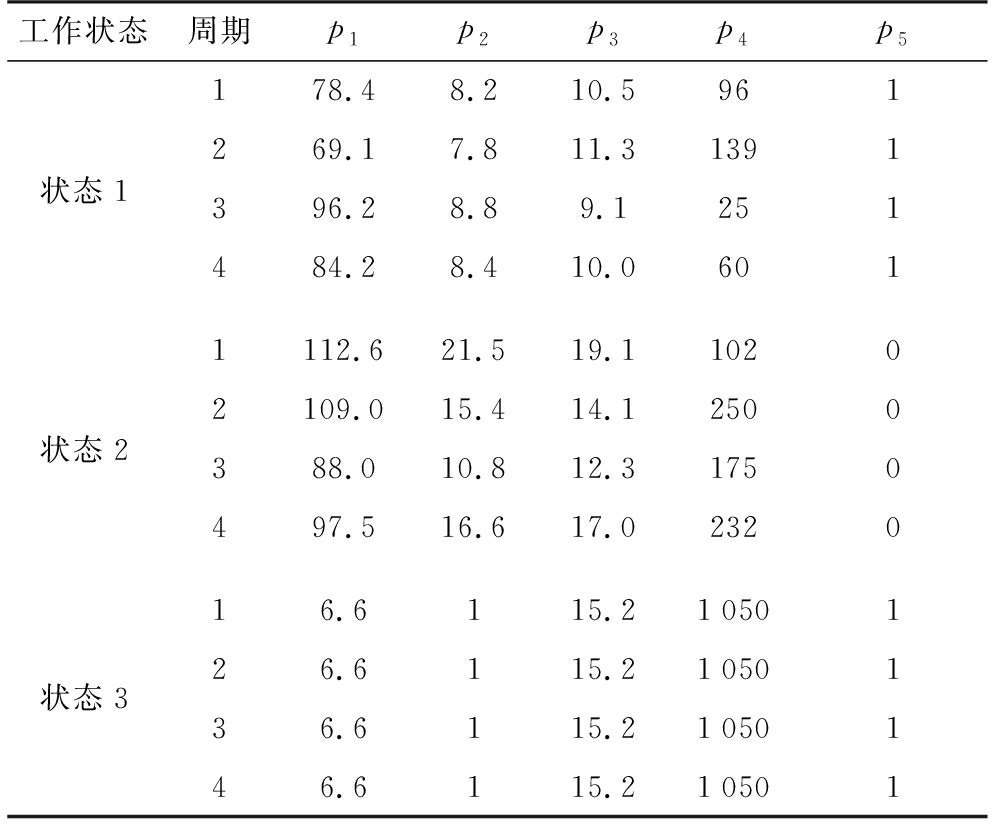
工作状态周期p1p2p3p4p5状态1178.48.210.5961269.17.811.31391396.28.89.1251484.28.410.0601状态21112.621.519.110202109.015.414.12500388.010.812.31750497.516.617.02320状态316.6115.21050126.6115.21050136.6115.21050146.6115.210501
3.1 单特征参数识别
根据工作状态识别流程,经工作状态初始分类可知,状态3的p1∈[3.3~10],属于高重频波形,且p5=1,可快速判定为VS(M)状态;状态1、2的p1∈[50~125],属于中重频波形,需要进行多特征参数融合识别。
3.2 多特征参数融合识别
状态1的p5=1,工作状态可能为TWS、 STT(M)或DTT。使用基本概率分配算法,计算单一参数对应工作状态的信度,如表8所示。在进行多特征参数融合识别时,M(η)表征参数交叠区域的置信度,为确保融合识别的准确度,经多次实验测试,确定判决规则中预设门限ε1=0.2,ε2=0.1。经计算,4个CPI周期中的单个参数对应不同状态的置信度值均不满足DS判决规则,无法有效识别具体的工作状态。对每个CPI周期内的多维特征参数进行融合,可发现第2、4 CPI周期中,M(STT(M)/DTT)-M(TWS)>ε1,M(η)<ε2,可判定状态1为STT(M)或DTT。考虑到4个周期中,仅2个周期有识别结果,识别结果可信度不高。
表8 状态1多特征参数融合识别情况
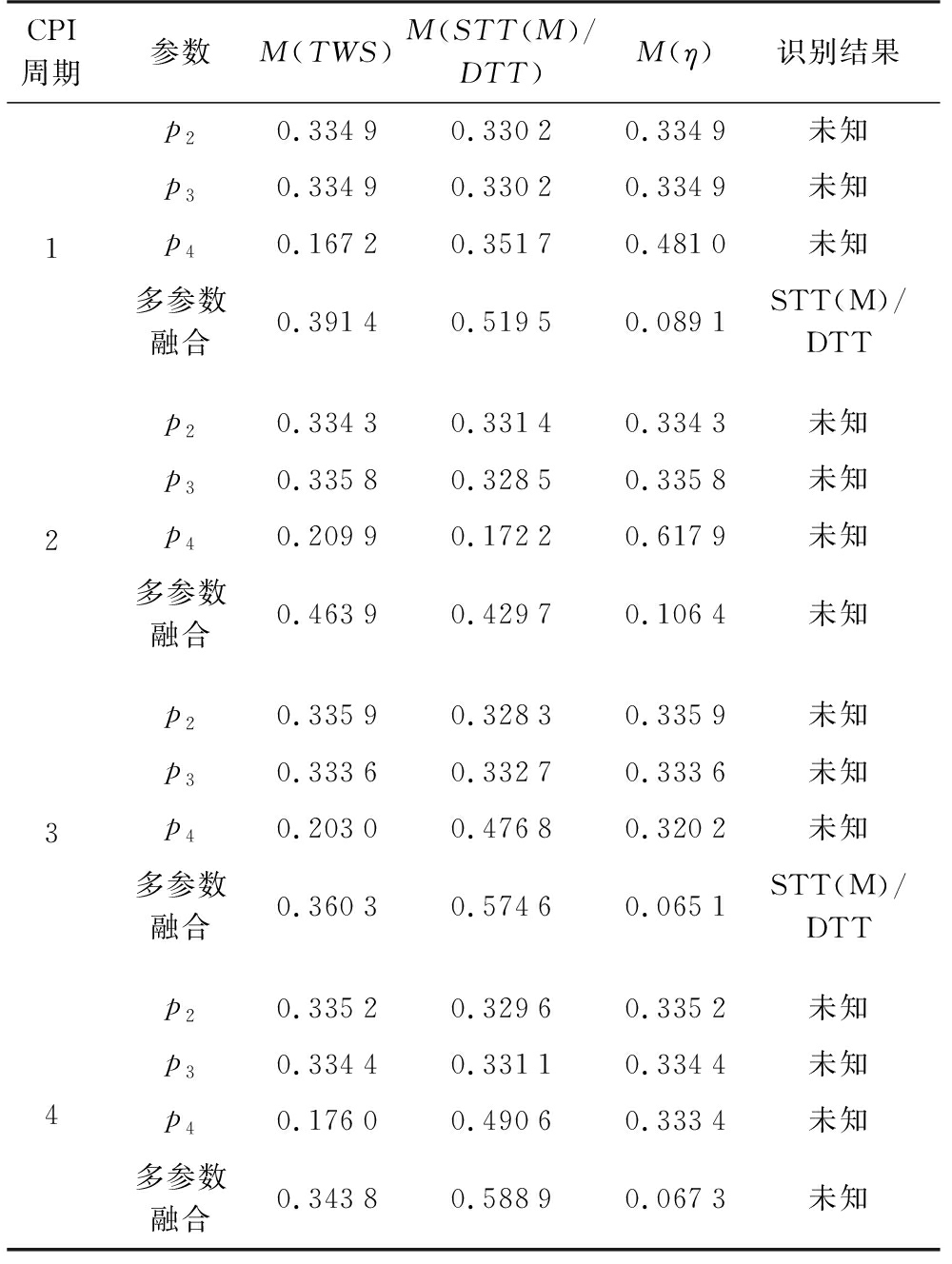
CPI周期参数M(TWS)M(STT(M)/DTT)M(η)识别结果1p20.33490.33020.3349未知p30.33490.33020.3349未知p40.16720.35170.4810未知多参数融合0.39140.51950.0891STT(M)/DTT2p20.33430.33140.3343未知p30.33580.32850.3358未知p40.20990.17220.6179未知多参数融合0.46390.42970.1064未知3p20.33590.32830.3359未知p30.33360.33270.3336未知p40.20300.47680.3202未知多参数融合0.36030.57460.0651STT(M)/DTT4p20.33520.32960.3352未知p30.33440.33110.3344未知p40.17600.49060.3334未知多参数融合0.34380.58890.0673未知
状态2的p5=0,工作状态可能为TAS(Ⅰ)、TAS(Ⅱ)或STT(E)。经多特征参数融合算法求解,如表9所示,可发现4个CPI周期中,仅第1个周期不满足DS判决规则,其余3个周期可识别为TAS(Ⅰ)状态。
表9 状态2多特征参数融合识别情况
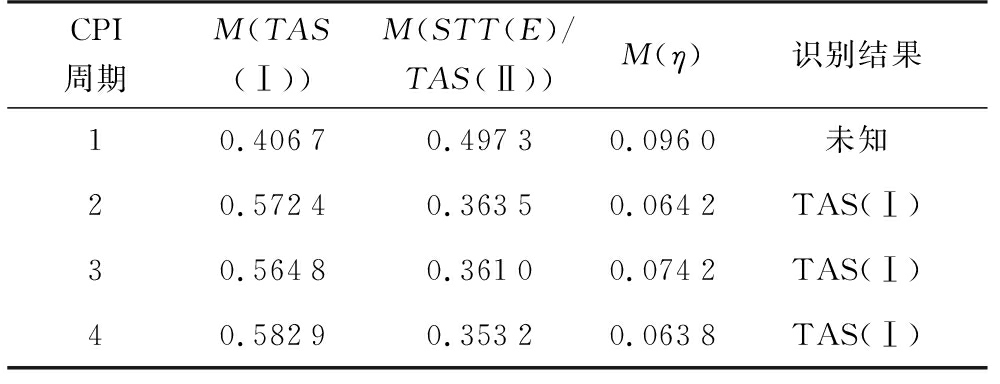
CPI周期M(TAS(Ⅰ))M(STT(E)/TAS(Ⅱ))M(η)识别结果10.40670.49730.0960未知20.57240.36350.0642TAS(Ⅰ)30.56480.36100.0742TAS(Ⅰ)40.58290.35320.0638TAS(Ⅰ)
3.3 多周期融合识别
经过多特征参数的DS融合可发现,当特征参数处于交叠区时,判定结果较为“模糊”,难以得到置信度高识别结果。对此,需要对状态1、2多参数融合结果进行多周期DS融合,计算结果如表10、表11所示。
表10 状态1多周期融合识别情况
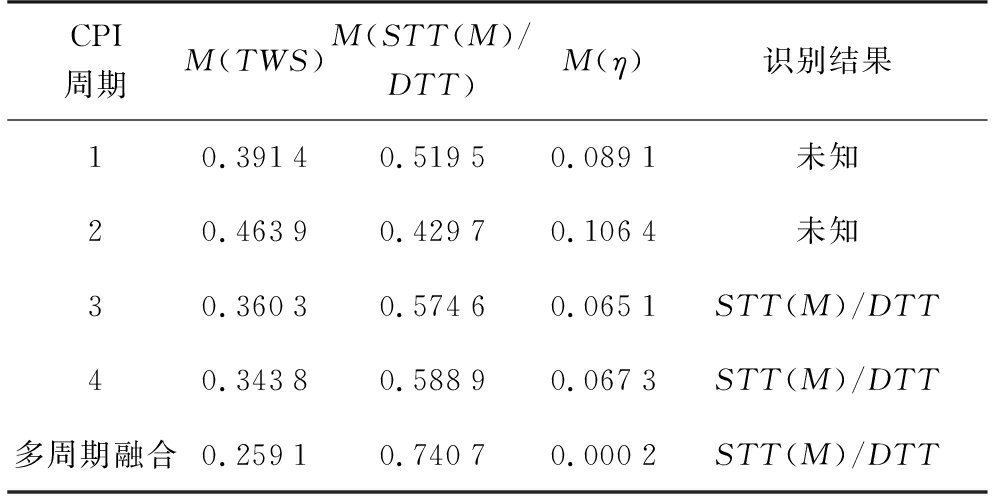
CPI周期M(TWS)M(STT(M)/DTT)M(η)识别结果10.39140.51950.0891未知20.46390.42970.1064未知30.36030.57460.0651STT(M)/DTT40.34380.58890.0673STT(M)/DTT 多周期融合0.25910.74070.0002STT(M)/DTT
表11 状态2多周期融合识别情况
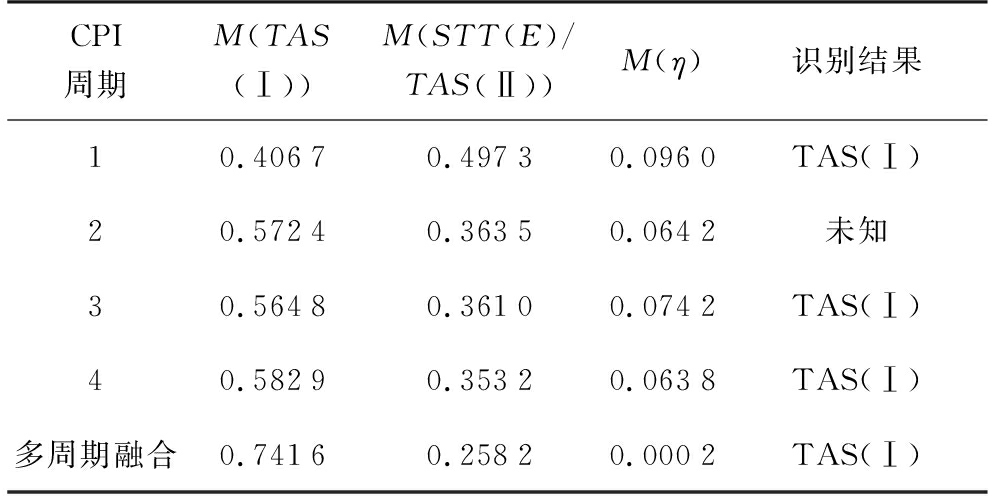
CPI周期M(TAS(Ⅰ))M(STT(E)/TAS(Ⅱ))M(η)识别结果10.40670.49730.0960TAS(Ⅰ)20.57240.36350.0642未知30.56480.36100.0742TAS(Ⅰ)40.58290.35320.0638TAS(Ⅰ)多周期融合0.74160.25820.0002TAS(Ⅰ)
多周期DS融合的结果显示,状态1的交叠区域置信度为M(η)=0.000 2,M(STT(M)/DTT)-M(TWS)=0.481 0,两项指标均大幅度优于预设门限,反映了多周期证据融合大幅减小单周期中交叠区域置信度较大带来的不确定性,同时能够有效避免单周期参数测量不准造成的不确定性,对支持证据进行了增强,表征了算法的有效性;状态2的融合结果同样反映了多周期DS融合的有效性。
3.4 随机样本测试
使用信号波形模拟器,生成8种工作状态 {VS(M)、VS(E)、TWS、TAS(Ⅰ)、TAS(Ⅱ)、STT(M)、STT(E)、DTT}信号各100组进行Monte Carlo测试。识别结果如表12所示,随着融合周期的增多,状态识别的准确性不断增大,多周期DS融合识别准确度变化趋势如图6所示。
表12 随机样本测试情况
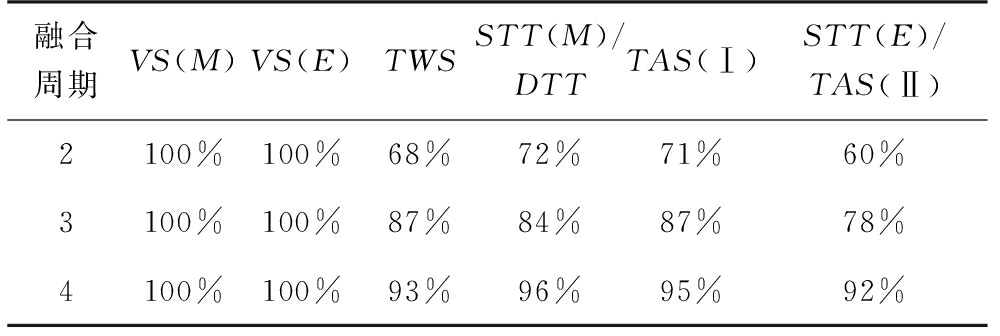
融合周期VS(M)VS(E)TWSSTT(M)/DTTTAS(Ⅰ)STT(E)/TAS(Ⅱ)2100%100%68%72%71%60%3100%100%87%84%87%78%4100%100%93%96%95%92%

图6 多周期DS融合准确度变化趋势图
4 结束语
为有效解决机载火控雷达空空工作模式反推识别难度大的问题,本文从电子侦察的角度定义了8种空空工作状态,并设计了信号波形模拟器,提出了基于DS证据理论的识别网络,进行了随机样本测试。仿真验证的结果表明,本文提出的方法能够从非合作方的角度,基于电子侦察数据对敌方机载火控雷达的空空工作状态进行准确识别,进而准确判断敌方雷达的行为状态和威胁等级,实用价值较高。
[1] 阳榴,朱卫纲,吕守业,等.多功能雷达工作模式识别方法综述[J].电讯技术,2020,60(11):1384-1390.
[2] 唐玉文,何明浩,韩俊,等.机载火控雷达典型空-空工作模式浅析[J].现代防御技术,2018,46(6):87-93.
TANG Yuwen, HE Minghao, HAN Jun, et al. Typical Air to Air Operation Modes of Airborne Fire Control Radar[J]. Modern Defence Technology, 2018, 46(6):87-93.(in Chinese)
[3] 贾朝文,周水楼.机载雷达工作模式识别[J].电子信息对抗技术,2011,26(1):14-16.
[4] 刘俊江.机载火控雷达工作模式识别[J].电子测量技术,2016,39(2):131-133.
[5] 王玉冰,程嗣怡,周一鹏,等.基于DS证据理论的机载火控雷达空空工作模式判定[J].现代雷达,2017,39(5):79-84.
[6] 王玉冰,程嗣怡,周一鹏,等.参数寻优LSSVM算法在机载火控雷达工作模式判定中的应用[J].空军工程大学学报(自然科学版),2017,18(3):49-53.
WANG Yubing, CHENG Siyi, ZHOU Yipeng, et al. A Parameter-Optimized LSSVM Method for Operation Modes Recognition of Airborne Fire Control Radar[J]. Journal of Air Force Engineering University (Natural Science Edition), 2017, 18(3):49-53.(in Chinese)
[7] 中航工业雷达与电子设备研究院.机载火控雷达[M].北京:国防工业出版社,2013.
[8] 马珂,毕大平,胡立群,等.基于ELINT的机载火控雷达空空工作状态识别[J].电子信息对抗技术,2019,34(4):35-39.
MA Ke, BI Daping, HU Liqun, et al. Air-to-Air Operation Statuses Recognition of Airborne Fire Control Radar Based on ELINT[J]. Electronic Information Warfare Technology, 2019, 34(4):35-39.(in Chinese)
[9] SKOLNIK M I. Radar Handbook[M].New York:Mc GrawHill Inc, 2008.
[10] 李捷,杨雪洲,周亮.基于改进DS理论多周期数据融合的目标识别方法[J].火力与指挥控制,2019,44(7):43-48.
LI Jie, YANG Xuezhou, ZHOU Liang. Research on Target Identification Based on Improved DS Evidence of Multi-period Fusion Method[J]. Fire Control and Command Control, 2019, 44(7):43-48.(in Chinese)
[11] 康兵义,李娅,邓勇.基于区间数的基本概率指派生成方法及应用[J].电子学报,2012,40(6):1092-1096.
[12] TRAN L T, DUCKSTEIN L. Comparison of Fuzzy Numbers Using a Fuzzy Distance Measure[J].Fuzzy Sets and Systems, 2002, 130(3):331-341.
