0 引言
2020年新冠病毒席卷全球,而预防病毒的有效手段之一就是在室内保持社交距离,而利用跟踪定位系统[1]可以监控密集人流。在密闭场所监测密集人流需克服以下几方面问题。1) 人流密集,目标较多,同时多个目标相距较近。2) 行人运动机动性高,目标易丢失,轨迹断裂等问题。3) 设备成本需相对较低。4) 设备需具备安全性。常规的室内跟踪设备包括摄像头、主动定位系统、超宽带雷达网络、通过WiFi等外部信号探测、连续波雷达等。
摄像头检测[2]成本低,得到的图像信息为用户提供更多目标细节便于识别,但是摄像头将三维空间物体映射到二维图像,导致部分空间信息缺失。同时摄像头探测易受光照影响,在光线较暗,目标反光,目标与背景颜色相近时工作性能并不理想,造成漏检。
主动定位系统[3]探测精度较高。但是室内人员需配置定位设备,对非合作目标无法探测。其次所配置的定位设备增添了硬件成本。
超宽带雷达网络[4-5]可对整个搜索区域成二维像。但是在室内条件下,杂物较多,由于多径效应,成像效果差。在多目标场景下容易产生较多的虚假像。
通过WiFi等外部信号[6]定位对不同场景迁移性差,且只适用于单个或者少量目标。当空间中存在多个目标或者目标相互临近时,难以区分检测。
连续波雷达[7]定位精度、分辨率均较高,但是在室内情况下,会有较严重的多径效应;而在多目标场景中,难以区分多径信号和弱目标信号。
本文讨论了一种使用激光雷达进行室内探测行人目标的检测方法。激光雷达[8]具有高精度、高分辨率、一次探测时间短、无多径效应和成本低的优点。
而在使用激光雷达对行人目标进行跟踪的算法中,需要满足5点要求。1) 由于行人目标远大于雷达分辨率,算法需适应扩展目标跟踪。2) 室内场景杂波环境复杂,需要区分静态非目标测量值与动态目标测量值。3) 行人目标运动无规律,算法应满足机动目标跟踪。4) 多个行人可能相距较近,算法区分不同轨迹。5) 算法应适应弱小目标的检测与跟踪。
本文介绍的激光雷达目标跟踪算法包括三部分。针对复杂的探测环境应用了基于时空杂波图[9-10]的固定物杂波去除算法,区分固定物与目标测量值。针对扩展目标[11]与弱小目标问题,应用基于权值三维映射的检测前跟踪算法。该算法通过多帧联合检测,解决了目标扩展问题与弱小目标问题[12]。针对密集多目标与目标机动问题,应用基于轨迹段关联检测算法,使得机动目标测量值可被正确关联。
综上所述,该激光雷达目标跟踪系统具有5个优势。第一, 利用时空杂波图抑制固定物杂波,提高目标检测概率。 第二,利用基于多帧检测的检测前跟踪算法,提高了弱小目标的检测率。第三,利用三维投影的思想避免了扩展目标量测集的划分[11],减少计算量。 第四,利用滑动时间窗和轨迹融合,对机动目标进行检测。第五,造价低,使用安全,易实现,通用性强。
1 模型与算法框架
1.1 杂波模型与目标模型
在激光雷达系统中,杂波点通常分为两类。第一类是由雷达内部和电磁干扰产生的随机噪声所引起的虚警点。通常均匀分布在整个监测区域,且在数量上服从泊松分布。由于背景噪声变化缓慢,因此可将该类虚警点的数量分布建模为参数为λa的泊松分布。
(1)
式中,![]() 表示由雷达内部和电磁干扰在第k帧中虚警点测量值的集合,运算符|·|表示集合中元素的数量。每个测量值包含二维空间信息与时间戳,即
表示由雷达内部和电磁干扰在第k帧中虚警点测量值的集合,运算符|·|表示集合中元素的数量。每个测量值包含二维空间信息与时间戳,即
(2)
第二类杂波为固定物杂波,通常由室内场景的墙壁等实际存在的固定物产生。固定物在每帧中被激光雷达探测得到测量值的概率恒定且较高,并服从固定的空间分布。在第k帧中,固定物杂波产生的测量值由集合![]() 表示。而前T帧中,未存在目标的“空房间”所得测量值均由两类杂波产生,即
表示。而前T帧中,未存在目标的“空房间”所得测量值均由两类杂波产生,即
(3)
测量值集合![]() 在本文算法中将用于估计固定物杂波的空间分布。而后续T+1至2T帧中,存在目标的测量值集合{z}T+1:2T。
在本文算法中将用于估计固定物杂波的空间分布。而后续T+1至2T帧中,存在目标的测量值集合{z}T+1:2T。
行人目标远大于激光雷达分辨率,因此单个行人在一次探测中会产生多个测量值,由此产生扩展目标问题。若第n个目标在第k帧中所产生测量值集合为![]() 则目标运动轨迹可表示为集合
则目标运动轨迹可表示为集合![]()
(4)
假设监视区域有K个行人目标,则用于目标检测与跟踪的测量集合{z}T+1:2T可表示为
{z}T+1:2T=
![]()
{(xi,yi,ti)|i=1,…,|{z}T+1:2T|}
(5)
而检测跟踪算法目的在于得到目标轨迹集合![]() 其中目标数K未知。针对该扩展目标跟踪问题,最常用算法为概率密度假设方法[11-12],但在该场景下有两点不足,其一是当目标生成较多点时使用随机分簇,而激光雷达系统中,一个行人产生测量点迹相对较多,枚举所有分簇情况计算量较大;其二是按时序逐帧关联检测,算法[11-12]对弱小目标的检测概率低于多帧联合检测方法。
其中目标数K未知。针对该扩展目标跟踪问题,最常用算法为概率密度假设方法[11-12],但在该场景下有两点不足,其一是当目标生成较多点时使用随机分簇,而激光雷达系统中,一个行人产生测量点迹相对较多,枚举所有分簇情况计算量较大;其二是按时序逐帧关联检测,算法[11-12]对弱小目标的检测概率低于多帧联合检测方法。
1.2 算法框架
本文整个数据处理流程包括三部分,其中输入为式(5)中的当前测量值与如式(3)中所示的历史测量值。算法三部分分别对应图1中红蓝绿三个方框。
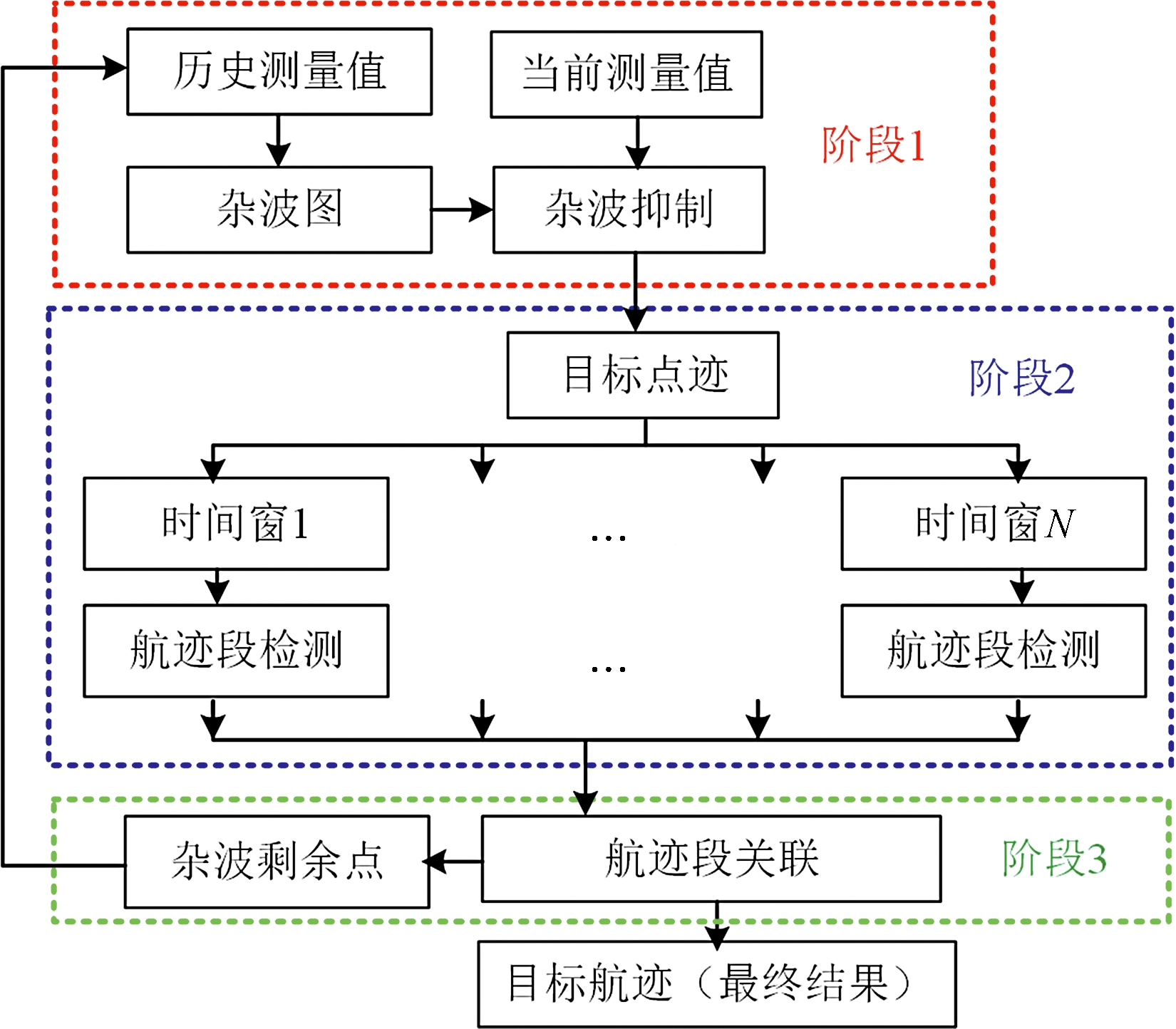
图1 算法结构框图
第一部分,利用时空杂波图进行杂波抑制。杂波图指的是将雷达监视区域进行网格划分。通过时空杂波图的建立,得出监视区域内的杂波空间分布,通过测量值所处位置杂波密度来估计其权值,将杂波区内的量测点给予小权值,将非杂波区内的量测点给予大权值,滤除权值过小的测量点,以此滤除大部分固定点杂波。
第二部分,轨迹段检测。将测量值集合按照时间顺序分为交叉时间窗,在每个时间窗内,通过基于权值的三维映射检测前跟踪算法得到目标轨迹段,这种检测前跟踪方法有利于抑制随机噪声,提升目标检测概率。
第三部分,轨迹段关联。将各个时间窗内所得轨迹段进行关联融合,同一目标产生测量值将关联为同一簇。由此使算法兼容机动目标跟踪同时提升相互临近多目标的跟踪性能。最后将去掉目标点迹的杂波测量值当作历史测量值更新固定物杂波的空间分布。
2 目标检测跟踪方法
2.1 时空杂波图
根据两种杂波变化十分缓慢这一时变特性,空间杂波密度可以用滤除行人测量值后的历史数据,即![]() 进行估计。而点迹的目标似然分数,可以通过杂波分布和高斯核密度来估计。其中每个量测点的分数即为“权重”。
进行估计。而点迹的目标似然分数,可以通过杂波分布和高斯核密度来估计。其中每个量测点的分数即为“权重”。
处理包括两步。第一步,利用过去时刻的量测估计搜索区域杂波空间分布。将二维监视区域划分为NA×NB个正方形单元格,利用各历史测量点集合{(xj,yj,tj)|j=1,…,|{z}1:T|}估计每个网格中心点(xn,ym)的杂波密度p0(xn,ym):
p0(xn,ym)=![]()
(6)
由此可得当前杂波图NX×NY个单元格的杂波密度{p0(xn,ym)|1≤n≤NA,1≤m≤NB}。
第二步,估计式(5)中N个当前测量点的权值。对于落入中心为(xn,yn)网格中的第i个测量点(xi,yi),其权值被定义为
(7)
此时权值取值范围为(0,1],权值越趋近于1,表示该点越可能由行人目标产生。同时将权值过低的测量值去除以降低计算量。经过该步滤除固定物杂波后的带权测量值集合可写作:
{(xi,yi,ti,qi)|i=1,…,Np}
(8)
式中,Np表示剩余测量值个数。此时剩余测量主要包括目标点迹与随机噪声产生的虚警点。
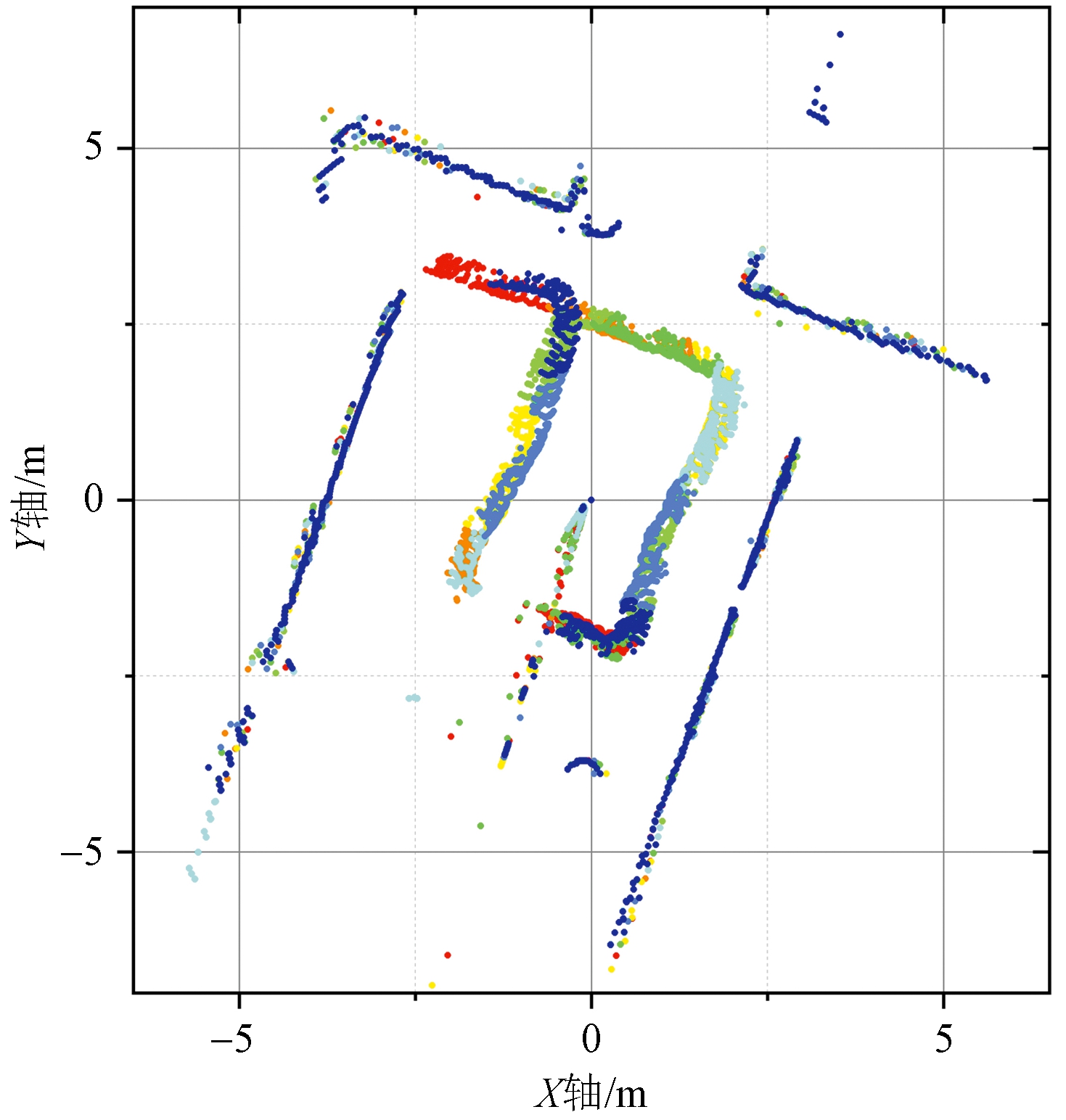
该部分处理效果如图2所示,图2(a)为式(3)中历史测量值,可以看出房间大致轮廓以及走廊。图2(b)为当前测量值即式(5),包含有目标轨迹的测量点,其中由红到蓝表示最初与最近所得测量值。图2(c)为目标测量值与静态杂波,其中红色表示静态杂波,蓝色表示目标点迹。图2(d)为滤除低权值点后的测量值,即式(8)。可以看出大部分固定物噪声已经被滤除,行人目标大致轨迹变得更加明显。同时,由于在后续检测中,使用目标测量值滤除后的固定物杂波估计当前杂波图,即
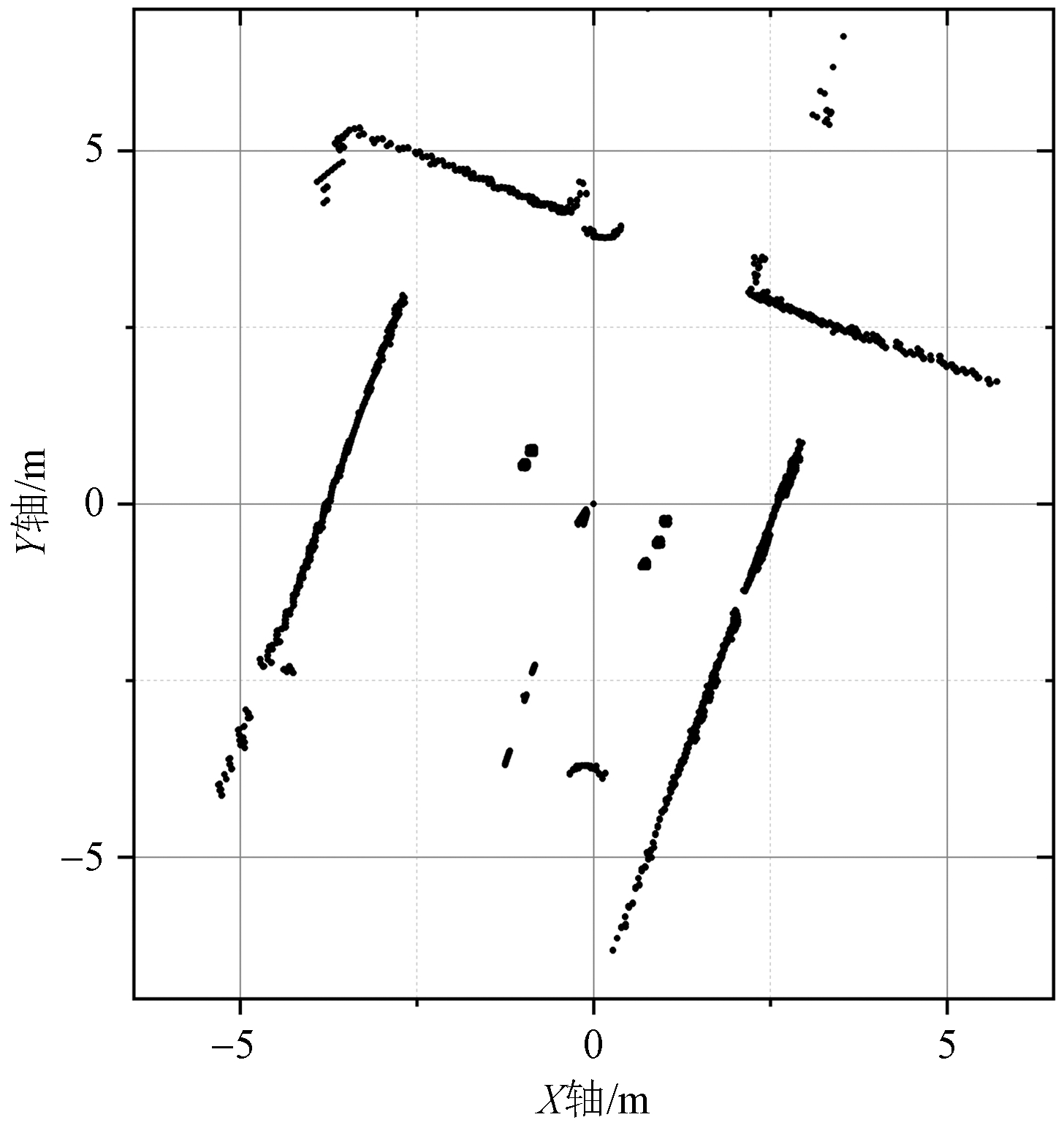
(a) 历史测量值
(b) 当前测量值
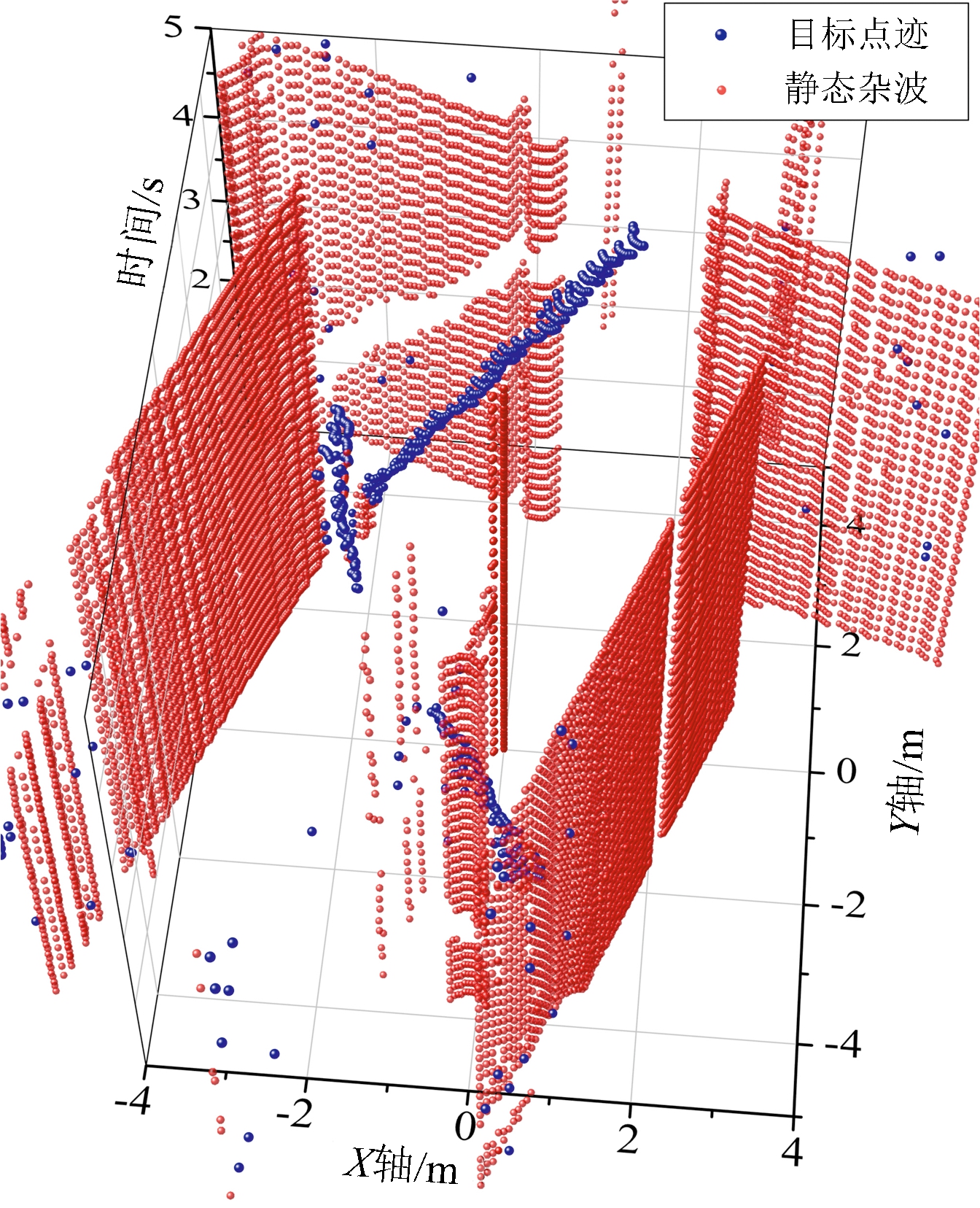
(c) 目标测量值与静态杂波
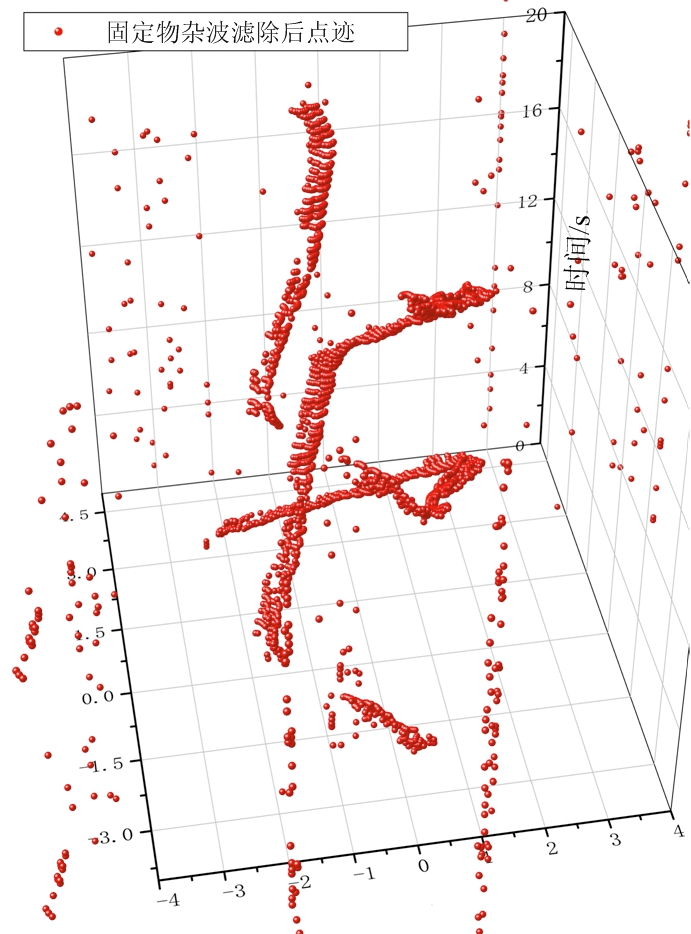
(d) 固定物杂波滤除后测量值
图2 固定物杂波滤除效果图
{z}T+1:2T-{(xi,yi,ti,qi)|i=1,…,Np}
(9)
式中减号为求集合元素的差集。因此杂波图可适应时间变化,自适应实时杂波图可以避免长时间探测后,杂波图与当前测量值不匹配问题。
2.2 基于权值三维投影的检测前跟踪算法
首先将式(9)中的测量集合按照时间划分为Nw个时间段,每个时间段长度为wt,即T=wtNw 。构建的每个时间窗包含d个时间段的点迹。在交叉时间窗中,第一个时间窗即为T到T+dwt的测量值,第w个时间窗为T+(w-1)·wt到T+(w-1+d)wt的测量值。对Nw个时间窗单独检测,由于dwt时间内包含多帧点迹,使用基于权值三维投影的检测前跟踪算法即可得到时间窗内的轨迹段。Nw个时间窗将得到Nw个轨迹集合。
假设某时间窗内,测量值集合为{(xi,yi,ti,qi)|i=1,…,N}。在dwt时间内行人可以近似为一条由二维空间坐标与时间信息组成的三维直线,而目标所产生的测量值(xi,yi,ti)通常分布在该三维直线附近。基于权值的三维映射可通过参数域累积得到经过最多量测点的三维直线,并将该直线检测为目标轨迹段,其原理如下。
若存在一个三维平面与目标轨迹的三维直线垂直,则该目标测量值在投影于该平面时会聚居在很小的一个区域甚至重合为一个点。然而该三维平面是未知的,因此我们构建一系列过原点的三维平面,若三维直线与其中某平面垂直,则该直线上的点投影到该二维平面就会呈现为距离较近的点簇。由此目标轨迹段检测问题将转变为两个子问题:1) 如何发现合适的三维投影平面,2) 如何在投影平面正确检测目标。
为了找到最优投影平面,我们建立Nb个涵盖各方向的三维平面,每个平面对应一个检测通道。 若其中某三维平面的法向量为b, b=(ex,ey,et), 则可确定过原点的三维平面:
exx+eyy+ett=0
(10)
若测量值(xi, yi, ti)映射到该平面,则其对应的投影点![]() 可由下式计算。
可由下式计算。
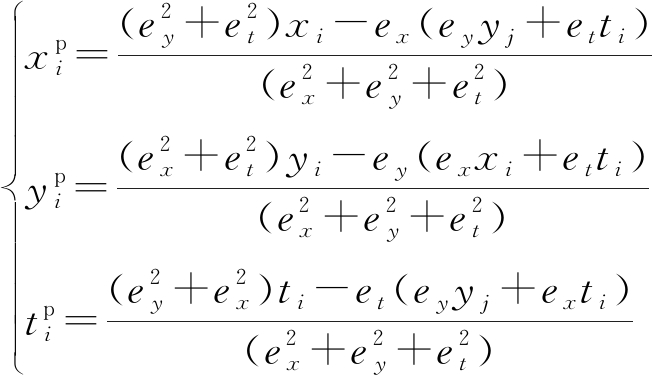
(11)
由集合{(xi,yi,ti,qi)|i=1,…,N}与平面(式(10))即可得到投影点集合:
(12)
式 (12)中投影点集合均位于平面(式(10)),因此接下来对平面(式(10))内投影点二维分布进行分析。
在第s个检测通道对应的三维平面(式(10))上,建立一个包含 (Nx,Ny)个网格单元的投票密度图Ms, Ms={Ms(c, d)|c=1,…, Nx; d=1,…, Ny},网格宽度分别为wx和wy。用(xc,yd)表示单元格Ms(c, d)中心,则一个投影点![]() 对单元格Ms(c, d)投票权值
对单元格Ms(c, d)投票权值![]() 为
为
![]()
(13)
由式(13)可知测量值权值qi较大或投影点与单元格距离![]() 较小时,单元格Ms(c, d)会得到一次较大的投票值。而若票值较小,认为单元格Ms(c, d)与投影点
较小时,单元格Ms(c, d)会得到一次较大的投票值。而若票值较小,认为单元格Ms(c, d)与投影点![]() 无关,强制使其投票值为0,即
无关,强制使其投票值为0,即
![]() ⟹
⟹
(14)
而一个网格单元中的投影点密度等于所有点在该网格单元上的投影密度的总和,即
(15)
根据总的投票数量,第s个检测通道内设置一个检测阈值Vs。若图Ms中有单元格的投影密度高于该阈值,则目标轨迹段可能存在于该单元格内。
(16)
其中检测阈值Vs被定义为
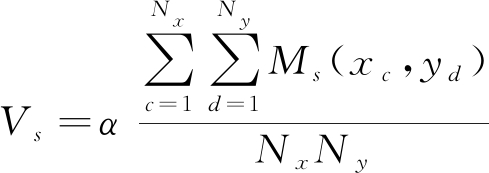
(17)
式中,α为控制检测阈值的常数。
若目标轨迹段存在于该检测通道,所投票单元格在图Ms上将聚为一个区域,通过区域生长法即可得到这些单元格所构成区域,检测通道s内得到的第u个区域![]() 可表示为
可表示为
(18)
通过回溯可以得到为单元格Ms(xci,ydi)投票的测量点集合![]() 该回溯过程可用函数B(·)表示:
该回溯过程可用函数B(·)表示:
(19)
该区域所对应的测量点,即为区域![]() 内每个测量点的集合,即
内每个测量点的集合,即
(20)
而这些测量点集合![]() 即被认为是某目标轨迹所产生的测量值,即时间窗中的一个轨迹段。
即被认为是某目标轨迹所产生的测量值,即时间窗中的一个轨迹段。
若场景中存在多个平行的三维直线,图Ms中可能存在多个检测区域,即在一条检测通道中检测出多个轨迹段。140个检测通道通过式(16)得到的轨迹段被放于集合。该轨迹段集合即为一个时间窗内通过检测前跟踪算法所得结果。第s个时间窗内得到的轨迹段集合用Γw表示,即
(21)
算法效果如图3所示,时间窗1中的点迹如图3(a)所示,有两个目标轨迹,但是其中一条轨迹由于部分测量时间内漏检而断为两段。图3(b)为检测通道内的投影点,其中蓝色点表示投影点,由于该检测通道对应三维平面与左侧轨迹垂直,因此这些投影点聚为一簇。图3(d)为此检测通道内映射投票图Ms,可以看出其对应区域权值远高于其他区域,因此很容易检测出左侧轨迹。即得到如图3(f)中蓝色轨迹段。在另一检测通道中,投影点如图3(c)所示,即使轨迹断为两部分,其投影点依然聚在一个区域,该通道投票图如图3(e)所示,该轨迹段投票区域明显大于其他区域,因此也可被完整检测,其检测结果为图3(f)中红色轨迹段。在其余检测通道中,由于对应三维平面法向量与目标轨迹段三维方向相差较大,投影点较为分散,便没有检测到轨迹段。综合图3(b)与图3(c)通道的轨迹段,即为该时间窗的检测结果,即图3(f)。
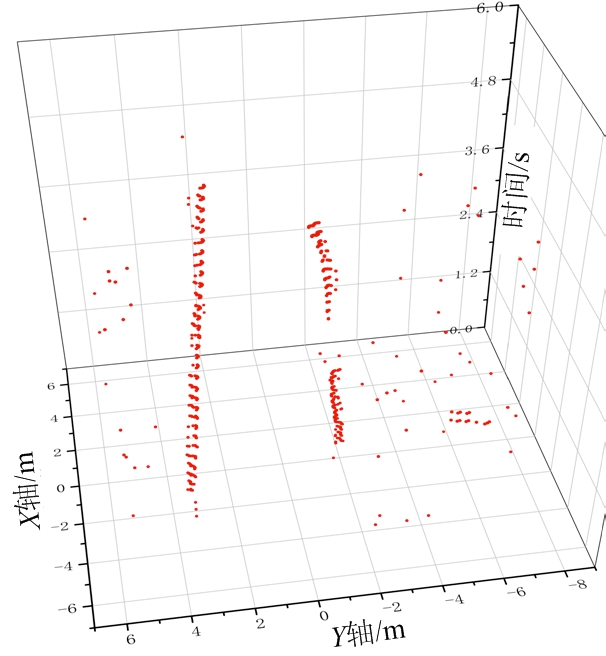
(a) 时间窗1内测量值
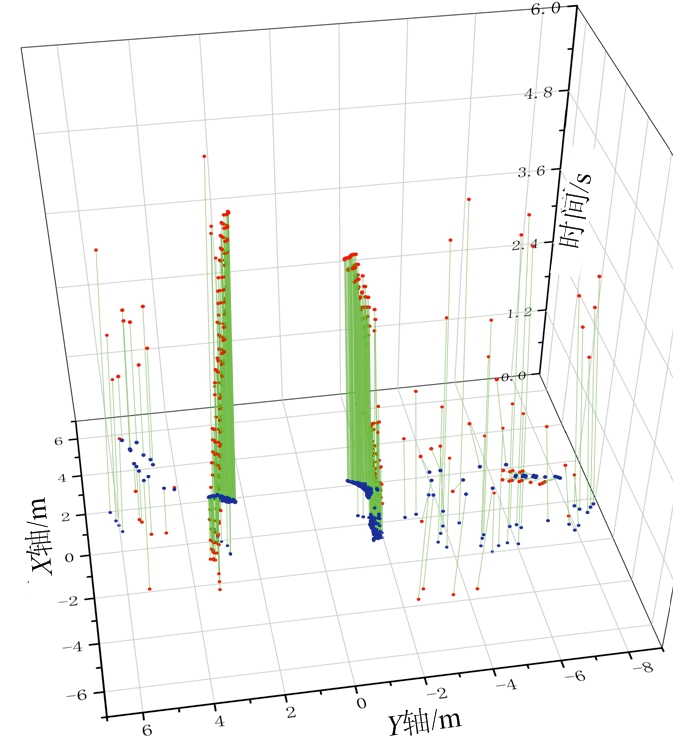
(b) 检测通道1内映射点
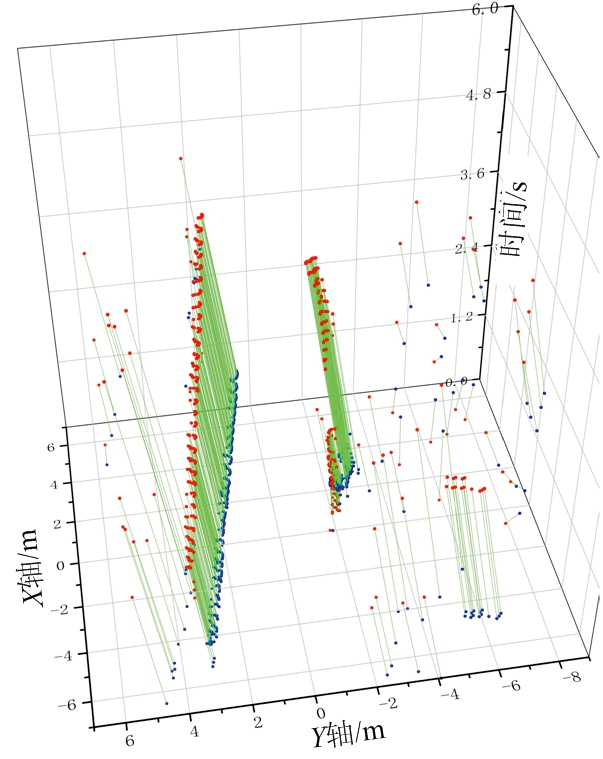
(c) 检测通道2内映射点
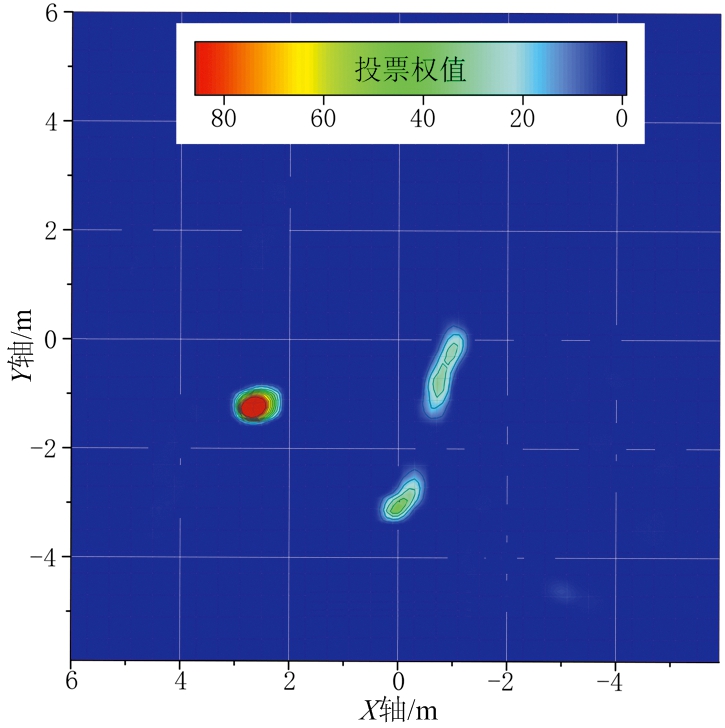
(d) 检测通道1内投票图
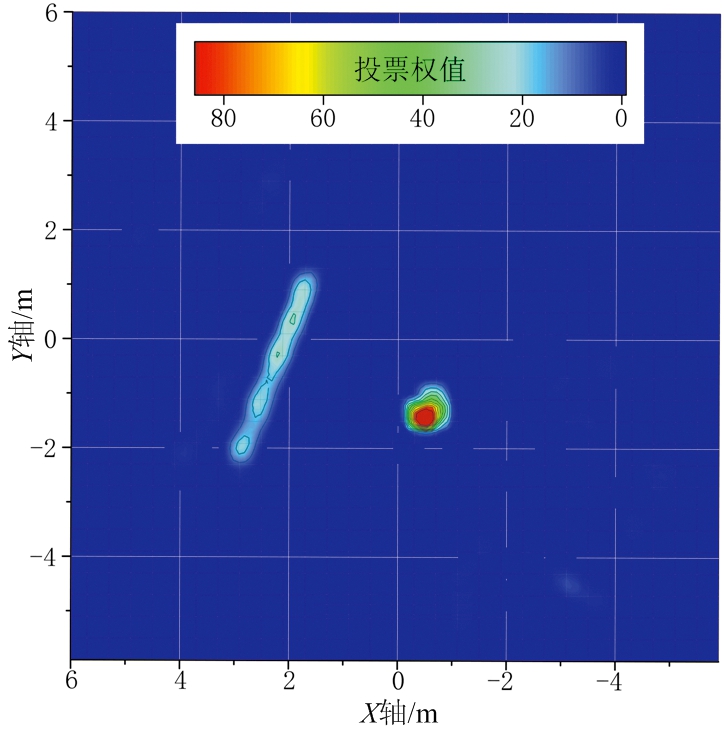
(e) 检测通道2内投票图
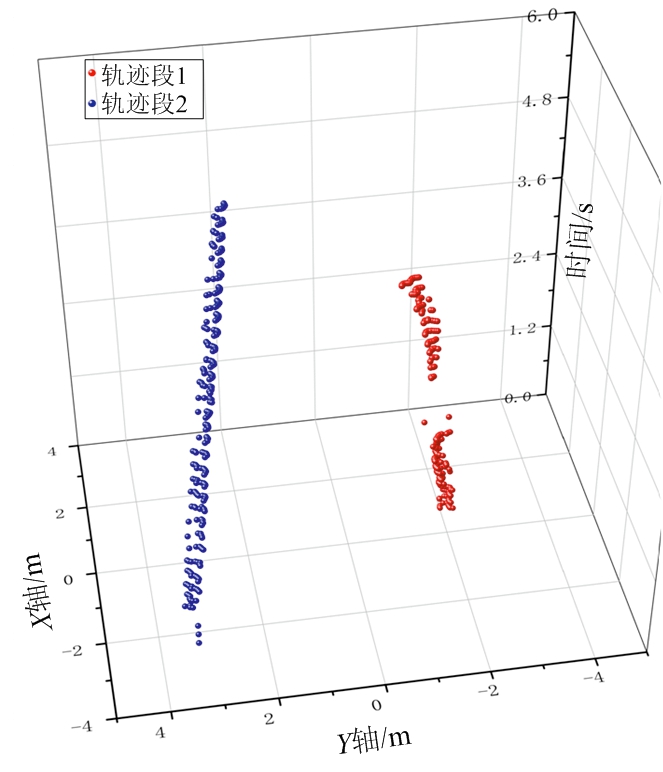
(f) 时间窗1所得轨迹段(2条)
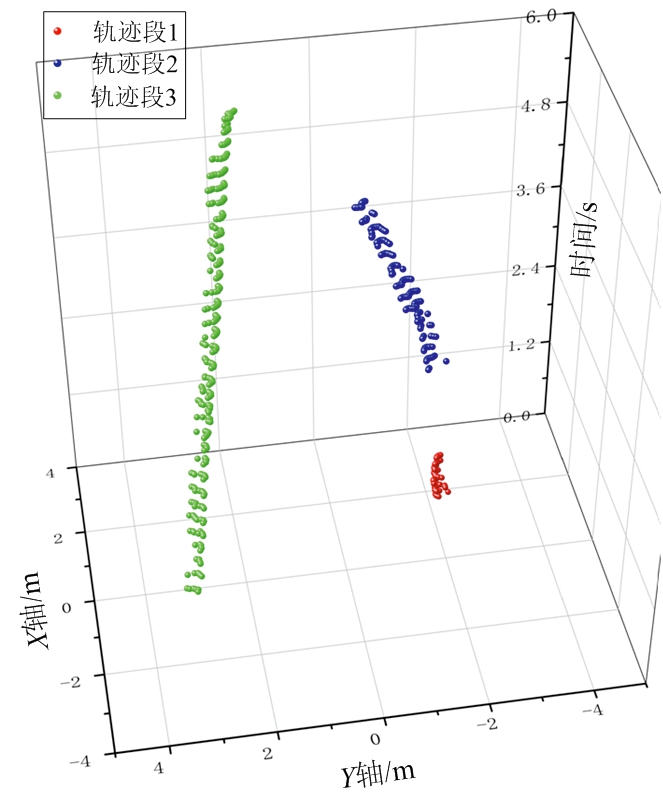
(g) 时间窗2所得轨迹段(3条)
图3 基于权值三维投影算法示意图
时间窗2的检测结果如图3(g)所示,两个时间窗复用了部分测量值,这使得不同时间窗中同一目标轨迹段具有关联基础。从图3(f)与图3(g)中可以看出,随机噪声点也已滤除。对图2(c)中测量值分时窗检测后得到如图4(a)所示的轨迹段集合,其中不同颜色轨迹段表示其来源于不同时间窗。
2.3 轨迹段关联
该阶段将不同时间窗内轨迹段, {Γw|w=1,…,Nw},相互关联,得到目标完整运动轨迹。将相邻两个时间窗所得轨迹段两两对比进行关联。时间窗轨迹段集合Γs中第i个轨迹段为![]() 轨迹段
轨迹段![]() 和轨迹段
和轨迹段![]() 之间的距离用dij表示。
之间的距离用dij表示。
(22)
(23)
其中,![]() 表示轨迹段
表示轨迹段![]() 中第a个测量点。
中第a个测量点。
![]() 表示两条轨迹的最优次模式分配(OSPA)距离[13]。在理想情况下,同一目标在连续两个时间窗中所得轨迹段有
表示两条轨迹的最优次模式分配(OSPA)距离[13]。在理想情况下,同一目标在连续两个时间窗中所得轨迹段有![]() 比例的测量值是相同的。当两条轨迹段的OSPA距离小于轨迹融合阈值Tf时,将两条轨迹融合为一条轨迹。融合准则如下:
比例的测量值是相同的。当两条轨迹段的OSPA距离小于轨迹融合阈值Tf时,将两条轨迹融合为一条轨迹。融合准则如下:
(24)
每个时间窗内的轨迹集合在轨迹融合的过程中及时更新。可将多个时间窗所得轨迹段放在一个集合,任意两两融合,轨迹段的总个数将越来越少,将同一目标所产生的轨迹段关联在一起。当轨迹段集合不再变化时,认为轨迹段关联已达到最优解。估计轨迹段![]() 的轨迹目标似然分数
的轨迹目标似然分数![]() 表达式详见文献[14]。滤除
表达式详见文献[14]。滤除![]() 值小与最终检测门限TF的轨迹,其余的连续性较好的轨迹即为最终确认目标轨迹,即
值小与最终检测门限TF的轨迹,其余的连续性较好的轨迹即为最终确认目标轨迹,即
(25)
对确认后的目标测量点进行野值去除与轨迹平滑,平滑后轨迹即为最终检测结果。
轨迹关联过程如图4所示,将图4(a)中各时间窗内所得轨迹段关联后结果如图4(b)所示,最终得到两簇测量值(红色和蓝色),即认为区域中存在2个行人目标。经野值滤除和轨迹平滑后的最终结果如图4(c)所示,即使有些时间目标没有产生测量值,但是依然能够将其正确关联,避免了目标丢失与轨迹断裂。与此方法相对应,若使用文献[4]中基于三维区域生长进行测量值分簇检测,对图2(c)测量值检测后可得如图4(d)所示的3条轨迹,其中2条原本属于同一目标。说明方法[4]在部分测量值缺失情况下会产生目标丢失问题,而本文方法避免了轨迹断裂。
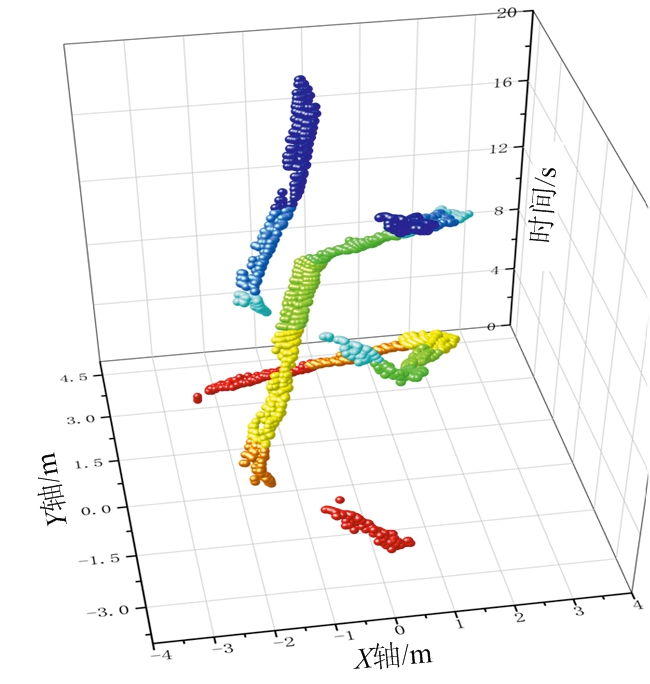
(a) 各个时间窗所得轨迹段
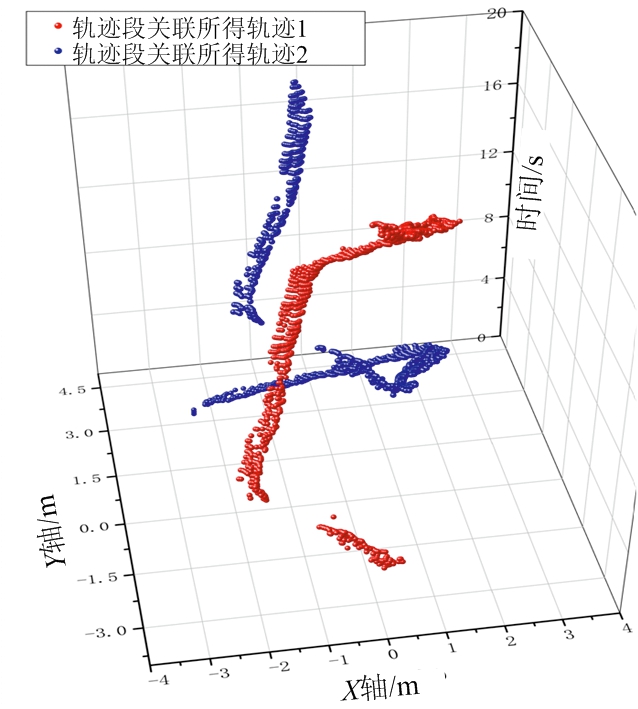
(b) 轨迹段关联结果
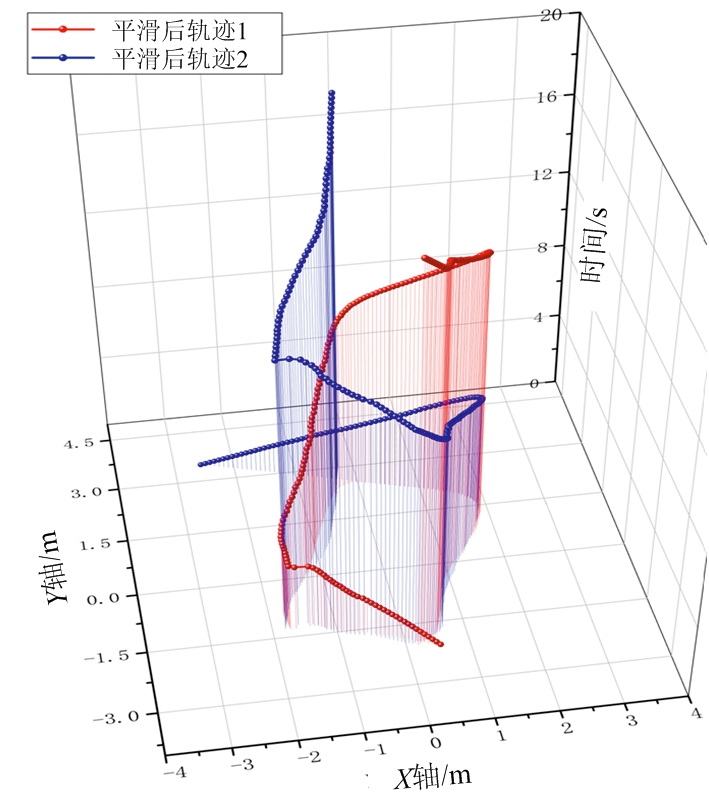
(c) 轨迹平滑后结果
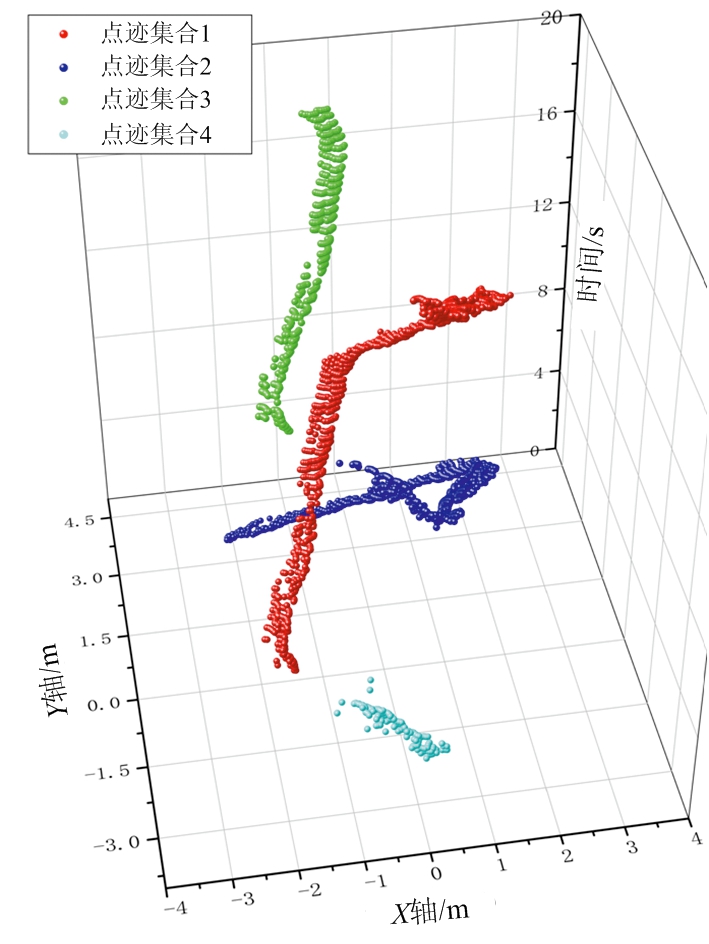
(d) 三维区域生长法[4]所得轨迹段
图4 轨迹关联过程
3 实验
为了验证该检测算法性能与激光雷达在室内跟踪定位中的精度,我们在两个不同场景中进行了多次跟踪实验。所用激光雷达测量半径为8 m;雷达天线转速为12.4π/s;激光波长为780 nm;方位分辨率为0.5°;距离分辨率为25 mm。
场景1中,激光雷达在室内带走廊的大厅中进行测试。雷达转速为6 r/s,探测半径为10 m,场景中有两个运动轨迹已知的目标,实验重复了4次。如图2(c)与表1所示,实验中测量值中大于98%的点为杂波值点,且绝大多数杂波值可由2.1节中杂波滤除方法滤除。
表1 杂波滤除效果 %
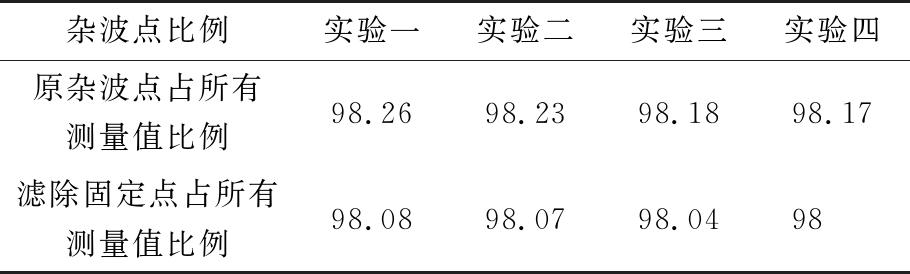
杂波点比例实验一实验二实验三实验四原杂波点占所有测量值比例98.2698.2398.1898.17滤除固定点占所有测量值比例98.0898.0798.0498
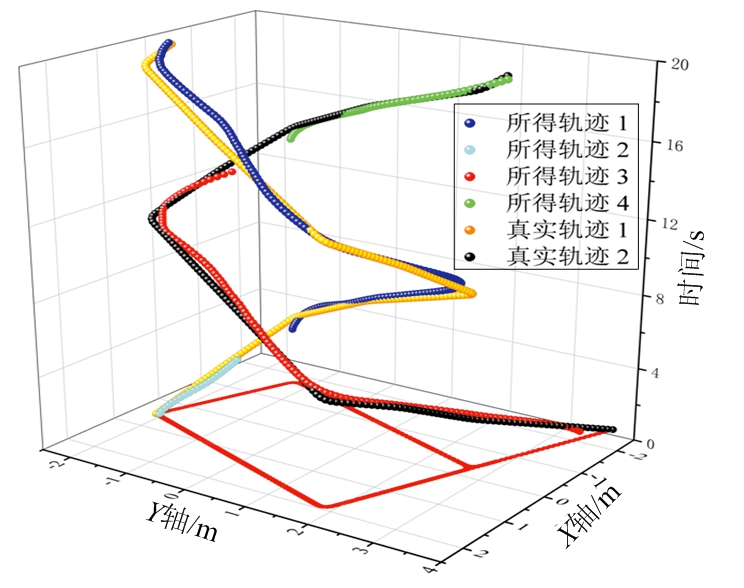
第一次实验中算法结果如图5(a)所示。获得的两条轨迹(绿色和蓝色曲线)与地面真实情况(黑色和红色曲线)匹配较好。
当雷达激光转向某方位时,由于强光干扰,在这些方位无法正常探测,测量值有明显缺失。而通过多帧联合检测轨迹段与轨迹段融合,缺失测量值并未造成轨迹断裂与目标丢失。在4次重复实验中均没有虚警轨迹或目标丢失。4次实验中两目标平均位置误差如图6(a)和图6(c)所示,位置误差始终小于35 cm。
使用文献[4]中基于三维区域生长所得轨迹如图5(b)所示。两个目标均断为2截,得到4条轨迹。在部分时间帧中目标漏检。在漏检时刻,将距离误差定为1 m。则4次实验中两目标平均距离误差如图6(b)和图6(d)所示,在丢失目标部分,误差明显增大。
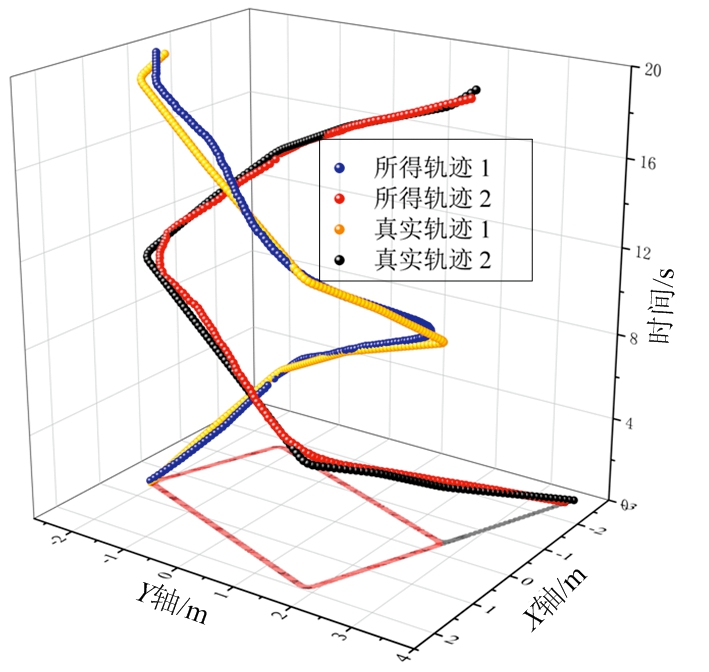
(a) 本文算法的真实轨迹与生成轨迹
(b) 文献[4]算法的真实轨迹与生成轨迹
图5 机动目标的真实轨迹与生成轨迹
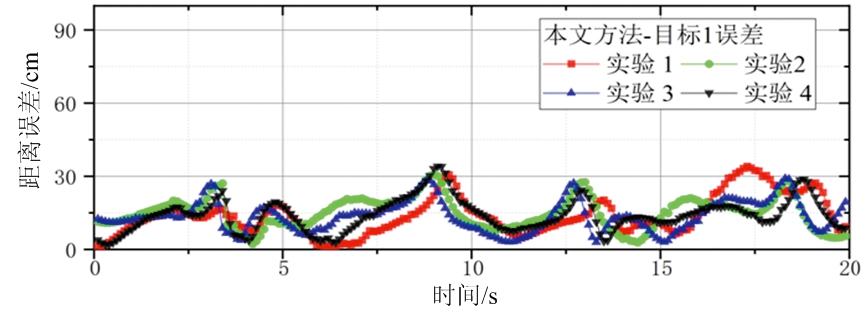
(a) 本文算法-目标1误差
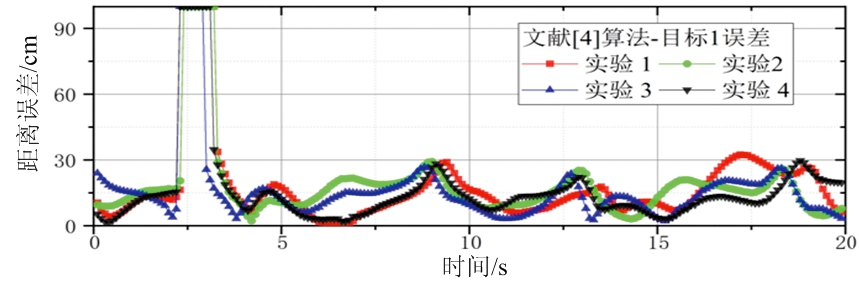
(b) 文献[4]算法-目标1误差
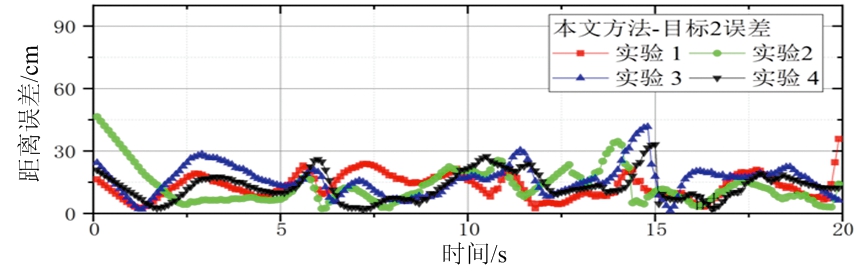
(c) 本文算法-目标2误差
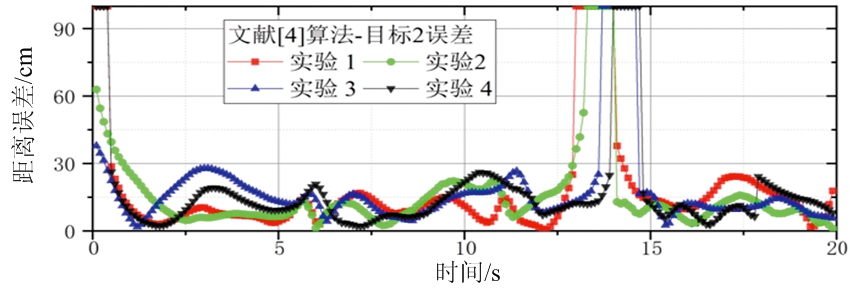
(d) 文献[4]算法-目标2误差
图6 机动目标的真实轨迹与生成轨迹的位置误差
场景1中两目标距离较远(总是大于3 m),因此在场景2中,激光雷达被放置在宽为2 m的走廊中,两目标并排行走,其间距为0.6 m左右,目标真实运动轨迹如图7(e)所示。图7(a)为场景2实验中固定物杂波;图7(b)为场景2中滤除固定物杂波之后的目标测量值。图7(c)为使用本文方法所得两目标轨迹,两目标被完整检测出且无虚警轨迹产生。图7(d)为使用ET-PHD[11]算法所得轨迹,所得结果存在2点问题。首先,存在部分虚警目标,由于固定点杂波并未被完全滤除,由此被检测为虚假的静止目标。其次,存在轨迹断裂,目标丢失的情况。在目标距离雷达较近时,目标所得测量点较多,检测概率较高,而当目标距离雷达较远时,得到测量点较少,甚至在有些帧中行人没有产生测量值。因此在这些位置出现目标丢失,轨迹断裂。而这两点也是多帧联合检测相较于单帧检测的优势。
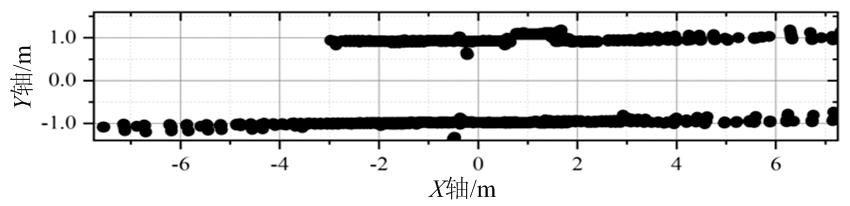
(a) 固定物杂波
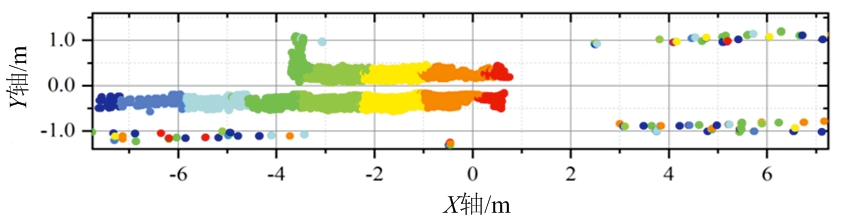
(b) 滤除固定物杂波
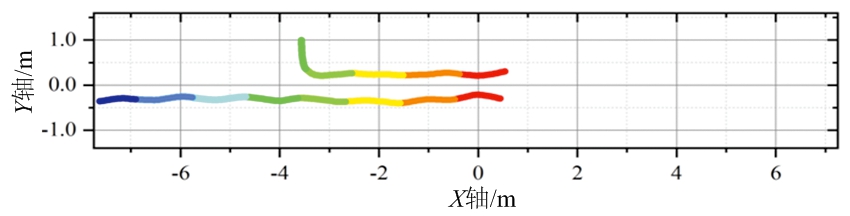
(c) 本文方法所得轨迹
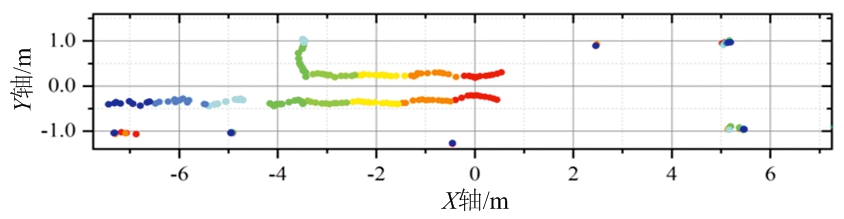
(d) ET-PHD[11]方法所得轨迹
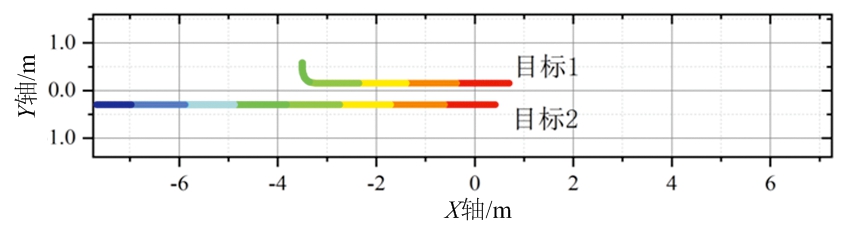
(e) 目标运动真实轨迹
图7 场景2下的真实轨迹与生成轨迹
场景2中的实验重复进行了3次,图8(a)为本文算法的位置误差,目标在距离雷达较近与较远时位置误差均较小,不高于25 cm。图8(b)为使用ET-PHD[11]算法距离误差,当目标距离雷达较近时,误差较低,而在距离较远(大于4 m)时,雷达产生对目标产生的测量点较少,此时目标可视为弱小目标,而ET-PHD[11]在跟踪弱小目标时,误差明显增大。
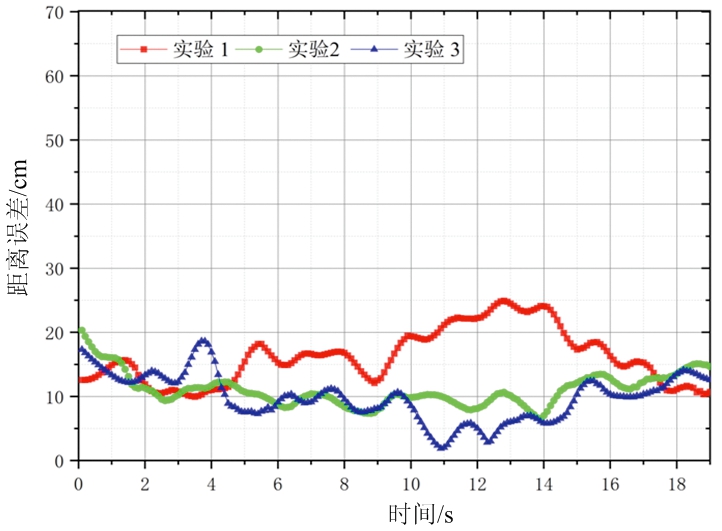
(a) 本文算法所产生的目标误差
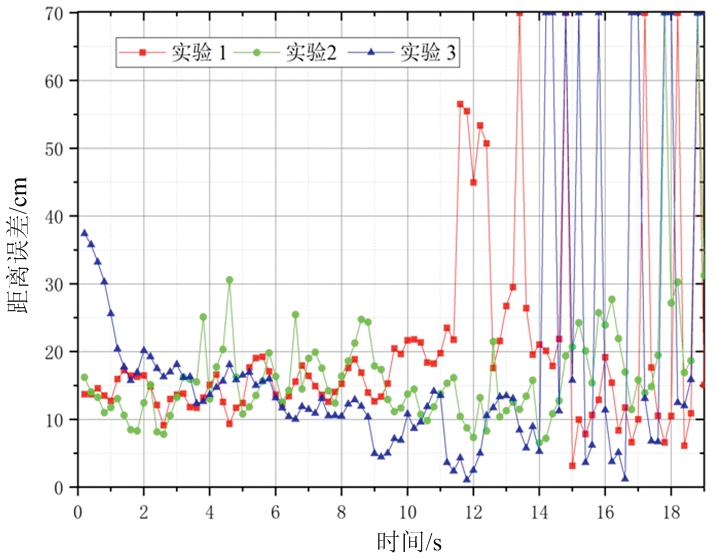
(b) ET-PHD[11]算法所产生的目标误差
图8 机动目标真实轨迹与生成轨迹的位置误差
实验总结如表2~5所示。表2为场景1中两目标4次实验距离误差。两算法最终平均误差分别为14.03和17.31 cm,相比之下,所提算法降低了18.97%的误差。
表2 场景1距离误差 cm
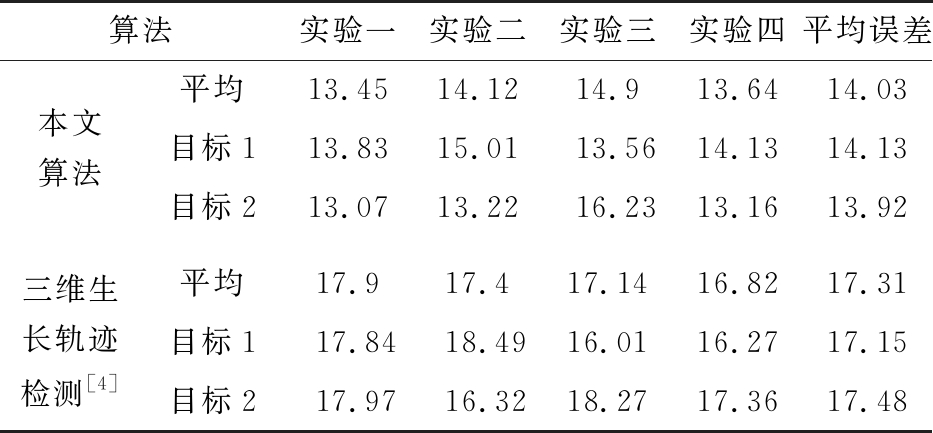
算法实验一实验二实验三实验四平均误差本文算法平均13.4514.1214.913.6414.03目标113.8315.0113.5614.1314.13目标213.0713.2216.2313.1613.92三维生长轨迹检测[4]平均17.917.417.1416.8217.31目标117.8418.4916.0116.2717.15目标217.9716.3218.2717.3617.48
表3为场景1中检测概率,相比之下,本文算法提升了7.32%的检测概率。两种方法均未建立虚假目标,故未作对比。
表3 场景1平均检测概率
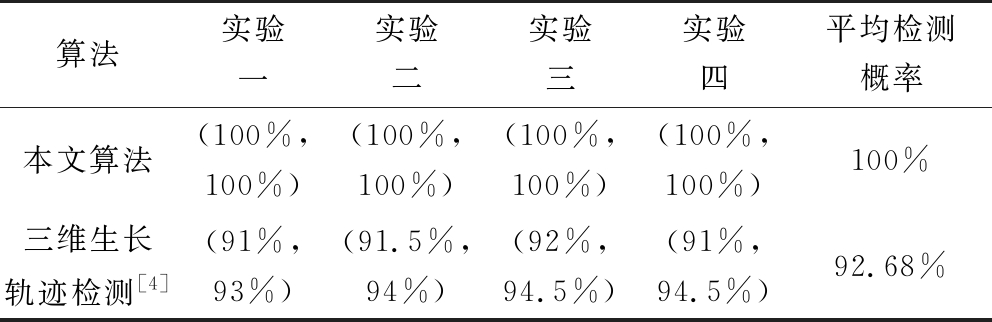
算法实验一实验二实验三实验四平均检测概率本文算法(100%,100%)(100%,100%)(100%,100%)(100%,100%)100%三维生长轨迹检测[4](91%, 93%)(91.5%, 94%)(92%, 94.5%)(91%, 94.5%)92.68%
表4为场景2中两目标3次实验距离误差,平均误差分别为12.38和20.67 cm,距离误差减少40.11%。表5为场景2中ET-PHD[11]方法的检测概率与虚假目标个数,由于本文算法在3次实验中,检测概率100%,无虚假轨迹,因此统计数据未列入表5。由表2~5可以清晰看出,本文算法在所有指标中均优于其他算法。
表4 场景2距离误差 cm
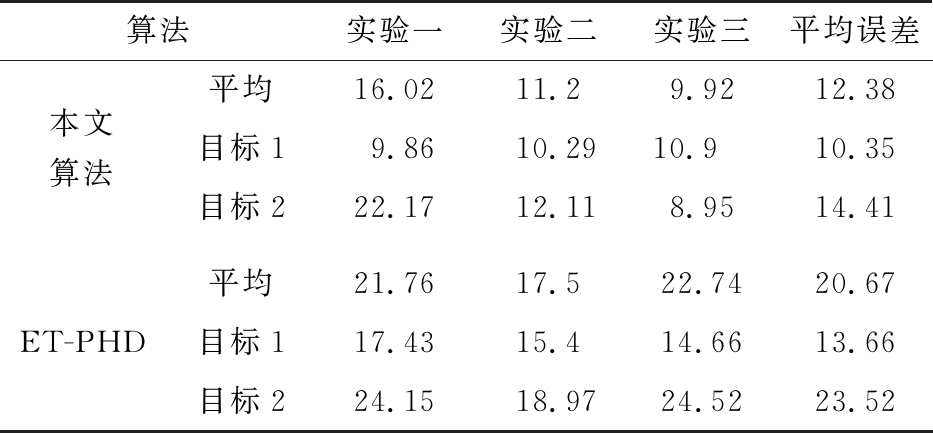
算法实验一实验二实验三平均误差本文算法平均16.0211.29.9212.38目标19.8610.2910.910.35目标222.1712.118.9514.41ET-PHD平均21.7617.522.7420.67目标117.4315.414.6613.66目标224.1518.9724.5223.52
表5 场景2 ET-PHD算法检测概率与虚假目标个数
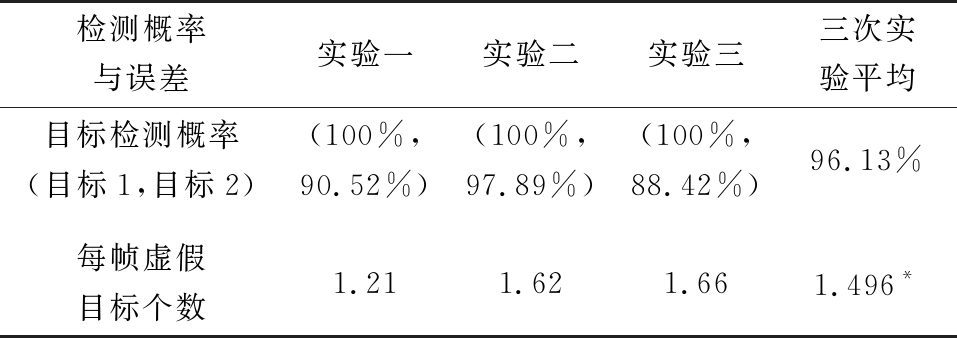
检测概率与误差实验一实验二实验三三次实验平均目标检测概率(目标1,目标2)(100%,90.52%)(100%,97.89%)(100%,88.42%)96.13%每帧虚假目标个数1.211.621.661.496*
同时应当指出,该实验位置误差也包含由非算法本身(外界因素)干扰所带来的误差。第一,在记录真实轨迹时本身便存有一定误差。第二,目标尺寸同样会带来误差。真实轨迹为目标中心位置,但激光雷达获得的距离是激光雷达与目标表面之间的距离,由此产生距离误差。
注:*1.496=(1.21+1.62+1.66)/3; 三次实验天线均转动为118圈。
因此算法实际测量误差将更低,10~15 cm的误差在室内定位监控社交距离时完全够用(通常室内社交距离应大于1.5 m)。在之前利用超宽带雷达目标跟踪行人的实验[4]中,定位精度约为50 cm。而在应用了本文检测前跟踪算法的激光雷达在精度上有较大提升,更加适用于室内行人检测,控制社交距离。
4 结束语
本文主要研究了利用激光雷达进行室内行人跟踪检测问题,较好地滤除了固定物杂波抑制了随机虚警点,可对多个机动行人产生的扩展目标进行较好的跟踪。两个场景下多次实验均无虚假轨迹,目标漏检出现。而且算法稳定有效,精度高。对比其他探测系统与检测方法,定位精度有较大提升。应该可以较好满足室内监视人群社交距离的需求。
[1] DARDARI D , CLOSAS P, DJURIC P M . Indoor Tracking: Theory, Methods, and Technologies[J]. IEEE Trans on Vehicular Technology, 2015, 64(4):1263-1278.
[2] 郑浩, 刘建芳, 廖梦怡. 室内视频监控下基于混合算法的人体异常行为检测和识别方法[J]. 计算机应用与软件, 2019, 36(7):224-230.
[3] 单广翠, 冯燕茹. 基于视频辅助的无源 RFID 室内跟踪技术[J]. 软件工程, 2016, 19(7):18-21.
[4] YAN B, GIORGETTI A, PAOLINI E. A Track-Before-Detect Approach for UWB Radar Sensor Networks[C]∥IEEE Radar Conference, Florence, Italy:IEEE, 2020:1-39.
[5] CHIANI M, GIORGETTI A, PAOLINI E. Sensor Radar for Object Tracking[J]. Proceedings of the IEEE, 2018, 106(6):1022-1041.
[6] SONG Xudong, FAN Xiaochen, XIANG Chaocan, et al. A Novel Convolutional Neural Network Based Indoor Localization Framework with WiFi Fingerprinting[J]. IEEE Access, 2019, 7:110698-110709.
[7] 李方敏, 夏雨晴, 马小林, 等. 基于速度差补偿的双频连续波雷达室内人体定位方法[J]. 电子与信息学报, 2017, 39(6):1432-1438.
[8] BEHROOZPOUR B, SANDBORN P A M, WU M C, et al. Lidar System Architectures and Circuits[J]. IEEE Communications Magazine, 2017, 55(10):135-142.
[9] YAN B, XU N, ZHAO W B, et al. An Efficient Extended Targets Detection Framework Based on Sampling and Spatio-Temporal Detection[J]. Sensors, 2019, 19(13):2912-2931.
[10] YAN B, PAOLINI E, XU N, et al. Multiple Maneuvering Extended Targets Detection by 3D Projection and Tracklet Association[J]. Signal Processing, 2020,179(4):107821.
[11] GRANSTROM K, LUNDQUIST C, ORGUNER O. Extended Target Tracking Using a Gaussian-Mixture PHD Filter[J]. IEEE Trans on Aerospace & Electronic Systems, 2012, 48(4):3268-3286.
[12] GRANSTROM K, ORGUNER U. On Spawning and Combination of Extended/Group Targets Modeled with Random Matrices[J]. IEEE Trans on Signal Processing, 2013, 61(3):678-692.
[13] RISTIC B, VO B N, CLARK D. Performance Evaluation of Multi-Target Tracking Using the OSPA Metric[C]∥13th International Conference on Information Fusion, Edinburgh, UK:IEEE, 2011:1-7.
[14] YAN B, XU N, WANG G, et al. Detection of Multiple Maneuvering Extended Targets by Three-Dimensional Hough Transform and Multiple Hypo-thesis Tracking[J]. IEEE Access, 2019,7: 80717-80732.
