0 引言
GaAs异质结双极晶体管器件具有线性度高、高频性能好、功率附加效率高和成本低等优点,在射频微波集成电路中,设计功率器件具有很大的优势。尤其是近几年,相比高电子迁移率晶体管,其优越的线性度和更低廉的成本越来越受到人们的关注,常被用来设计功率放大器[1-3]。而功率放大器的设计需要精确的非线性大信号模型,因此,GaAs HBT器件非线性大信号模型的建立非常重要,传统设计中基本使用的是经验模型,即利用复杂的经验公式拟合器件特性,如Gummel-Poon模型、VBIC模型、Aglient HBT模型等[4-8]。文献[5]中所提出的基于VBIC模型的GaAs HBT模型,使用改进的异质结效应的输运电流表达式,可以考虑到大电流下电子速度随集电极场的变化。但是由于VBIC模型是专门为硅双极技术开发的,对两个异质结的异质结构特性产生的效应模拟不佳,这导致HBT器件大信号模拟和电路设计性能受限。文献[6]使用基于Gummel-Poon模型的大信号分析方法来预测GaAs HBT器件的非线性行为,可以准确分析不同偏置条件下器件大信号本征元件随频率变化的情况,但是忽略了10-4级的B-C结和C-E结电导,只考虑了如跨导Gm、发射结电导Gbe、发射结电容Cbe等本征元件对大信号性能的影响。Aglient公司开发的Aglient HBT模型集众多经验模型的优点[4,8],文献[7]由于GaAs的衬底接近理想高阻,因此模型中忽略了衬底效应的影响,简化了模型,但是模型的简化会导致精度降低,性能变差。通过这些文献,我们发现经验模型为了准确预测器件的非线性行为,结构一般十分复杂,如 Gummel-Poon模型中常用的SPICE参数有30多个,Aglient HBT模型需要提取SPICE参数高达118个,提取公式也十分复杂。为了方便参数提取,往往会忽略一些参数,或简化公式,例如文献[7]所示的模型,但是这使得大信号模型的模拟性能变差。因此本文寻求一种更简单、更快速、更精确的建模方法来预测GaAs HBT器件的非线性行为。
许多电子科技领域的学者利用人工神经网络技术建立半导体器件的大小信号模型[9-25],在预测半导体器件特性,指导集成电路设计方面,相比经验模型,基于神经网络的器件模型建立迅速,简单且精确。目前,比较常见的应用于半导体器件建模的神经网络有很多种,如空间映射神经网络[14-16],在经验模型的基础上大大提高了模型精度;反向传播(Back-Propagation,BP)神经网络[13,17-19]和径向基函数(Radial Basis Function,RBF)神经网络[19-22],不需要了解器件的结构知识,也无需复杂的提取公式,只要有输入输出数据,就可以建立一个精确的模型;知识基(Know-ledge Based)神经网络[10,23],将神经网络与经验方程相结合的建模方法,比起纯粹的神经网络模型,它可以改善外推结果的可靠性;时间延迟(Time Delay)神经网络[24-25],有记忆功能,功能强大,训练过程很复杂,多用于人工智能领域。这些模型各有优劣,考虑到一些空间映射神经网络的文献[14-16]显示由于粗模型等效电路中的一些经验方程的简化或假设造成的误差,还是会影响到某些参数的精度,因此整个神经网络模型的大信号谐波特性精度不够高;知识基神经网络模型由于依赖先验知识,精度提高有限。时间延迟神经网络算法过于复杂。反向传播(BP)神经网络和径向基函数(RBF)神经网络 [12,18-21]因为训练过程简单,模型建立速度快,模型精度高,用于指导电路设计十分合适。
由于GaAs HBT器件已经广泛应用于集成电路设计,从业人员对其精确模型的需求越来越高,为了更好地使用HBT器件设计集成电路,对经验模型建立过程复杂困难,使用经验模型设计电路造成电路性能误差较大的问题,我们拟采用BP神经网络和RBP神经网络分别建立GaAs HBT器件的模型。通过对两种神经网络模型的分析和对比,综合考虑哪一个模型更值得选择。
1 人工神经网络
1.1 BP神经网络结构
BP神经网络是一种多层前向神经网络,它的核心就是通过调整权重逐步减小误差,原理图如图1 所示。在网络训练阶段用准备好的样本数据依次通过输入层、隐含层和输出层,比较输出结果和期望值,若没有达到要求的精度,即将输出结果与期望值的误差经过输出层、隐含层和输入层反向传播,并不断调节权值,使误差越来越小,直至达到我们需要的精度为止。
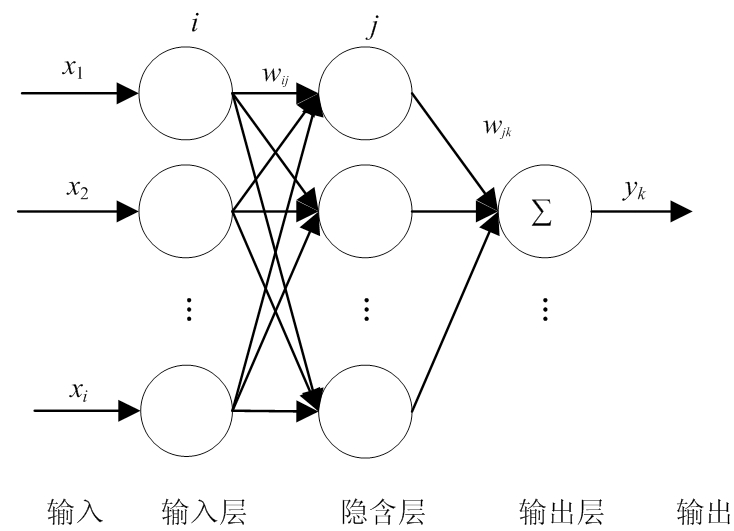
图1 反向传播(BP)神经网络结构原理图
如图1所示的BP神经网络,有三层结构,分别是输入层、隐含层和输出层,x1,x2,…,xi为神经元的输入,神经元之间靠权值连接,wij是输入层第i个神经元到隐含层第j个神经元的权值,wjk是隐含层第j个神经元到输出层第k个神经元的权值。神经元内部嵌入激活函数来处理神经元接收到的信息并产生输出,BP神经网络的创建使用的是MATLAB工具箱提供的newff函数,隐含层神经元激活函数采用的是非线性Sigmod函数,输出层神经元采用的激活函数是线性函数,Sigmod函数的表达式如下[18]:
(1)
式中,z是隐含层神经元的输入,隐含层第j个神经元的输入可表示为
(2)
神经网络的输出结果为
(3)
1.2 RBF神经网络结构
RBF神经网络的基本思想是:用径向基函数(RBF)作为隐藏神经元的基,构成隐含层空间,直接将输入矢量映射到隐含层空间,而隐含层空间到输出层空间的映射是线性的,即网络的输出是隐含层神经元输出的线性加权和,此处的权即为网络可调参数。隐含层的作用是将低维模式的输入数据变换到高维空间,使得在低维空间内的线性不可分问题在高维空间内线性可分。RBF神经网络原理图如图2所示[19-20]。
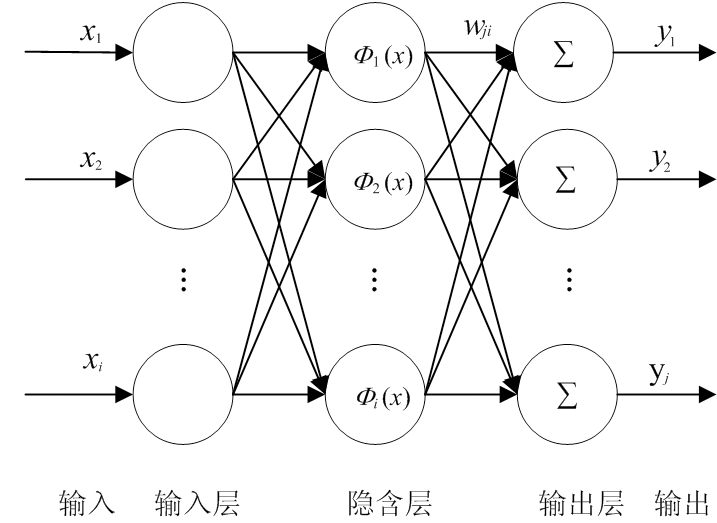
图2 径向基函数(RBF)神经网络结构原理图
RBF神经网络只有三层,第一层为输入层,第二层为隐含层,第三层为输出层。输入层到隐含层的神经元之间的权值全部为1。隐含层是使用径向基函数作为激活函数的神经元。隐含层与输出层之间就是普通的神经网络的连接关系,它们之间的权值可以训练而改变。
利用MATLAB工具提供的newrbe函数训练网络可设计一个精确RBF网络,这种网络隐含层神经元的数量是基于输入模式的数量,隐含层神经元内嵌的激活函数选取的是高斯函数:
(4)
式中μi是基函数的中心,σi是扩展常数,它决定了径向基函数下降的快慢,RBF神经元的宽度就是通过扩展常数来操纵的,在之后的训练和测试中可以调节扩展常数,使拟合结果达到最佳。输出层是隐含层输出的线性加权和,wji是第i个隐含神经元节点到第j个输出神经元节点的权值,RBF神经网络的输出可以用下式来表示:
(5)
2 GaAs HBT器件神经网络模型的建立
本文采用神经网络的直接建模法,不需要了解器件工作的知识,神经网络可以直接表征器件的外部电学特性,即黑匣子建模方法。BP神经网络建模的流程图如图3所示,首先建立GaAs HBT器件的直流模型,采用图1所示的BP神经网络结构,偏置电压VCE和基极电流Ib作为模型的输入变量,电流IC是输出变量,由于需要建立的模型结构比较简单,所以我们采用的BP神经网络结构隐含层只有一层,根据经验,选择隐含层神经元个数为9个,实际测量的GaAs HBT直流特性数据为VCE在0~5 V内变化,步进为0.05 V,Ib为10 ~50 μA,步进为10 μA时输出电流IC的结果,这些数据将作为神经网络模型的训练和测试数据。测试数据总共100组,从中随机选取50组进行训练,训练的过程如1.1节所述,即使用newff函数创建一个神经网络结构,精度设置为0.001,迭代次数900次,所用激活函数如公式(1),数据依次通过输入层、隐含层和输出层,比较公式(5)所示的输出结果y,即神经网络模型模拟出的IC值和测试的IC值,根据每一次的误差不断调整权值,直到使二者的最终误差小于0.001为止,这样一个BP神经网络模型就训练好了。另外50组作为测试数据,用来对比训练好的神经网络模型模拟结果是否精确。
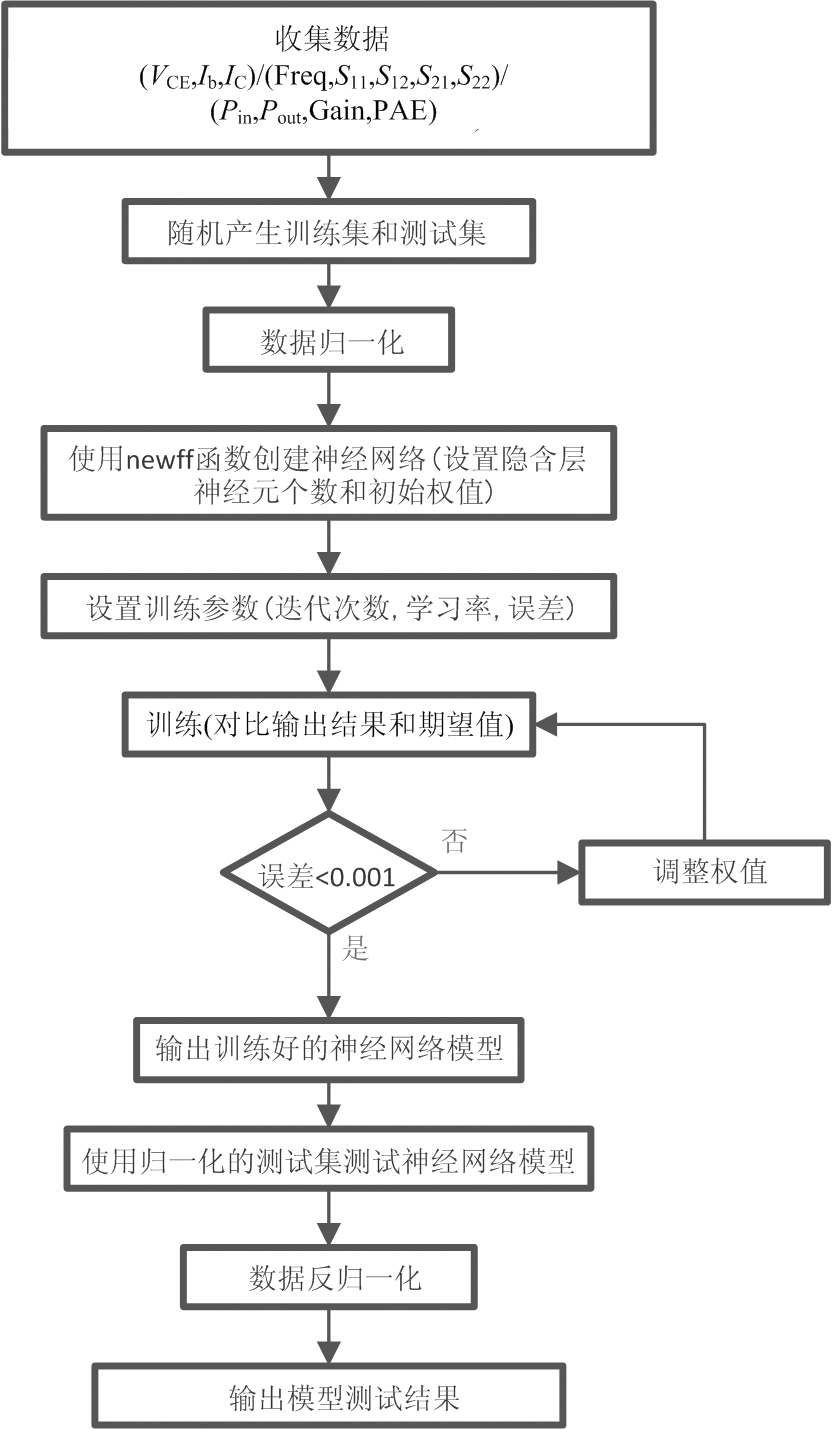
图3 BP神经网络模型建立流程图
再采用图2所示的RBF神经网络结构建立GaAs HBT器件的直流模型,使用同样的训练和测试数据,模型建立流程图如图4所示,首先利用MATLAB工具提供的newrbe函数创建一个RBF神经网络结构,随机选取50组数据,VCE和Ib作为输入变量,IC作为输出变量,隐含层神经元个数取决于输入变量的个数,所使用的径向基函数是公式(4)所示的高斯函数,它将输入变量变换到一个用高斯函数表示的线性空间,而不必像BP神经网络那样调节输入层到隐含层的权值。训练的过程如1.2节所述,扩展常数默认为1,而权值是在算法运行过程中自动调整的,newrbe函数创建神经网络的速度非常快,上述过程只要进行一次就可以得到一个零误差的径向基网络。通过不断调整扩展常数,最终的输出结果与测试结果拟合良好,一个RBF神经网络模型就建立好了。图5和图6分别是BP神经网络模型和RBF神经网络模型直流模拟结果和实测结果对比。
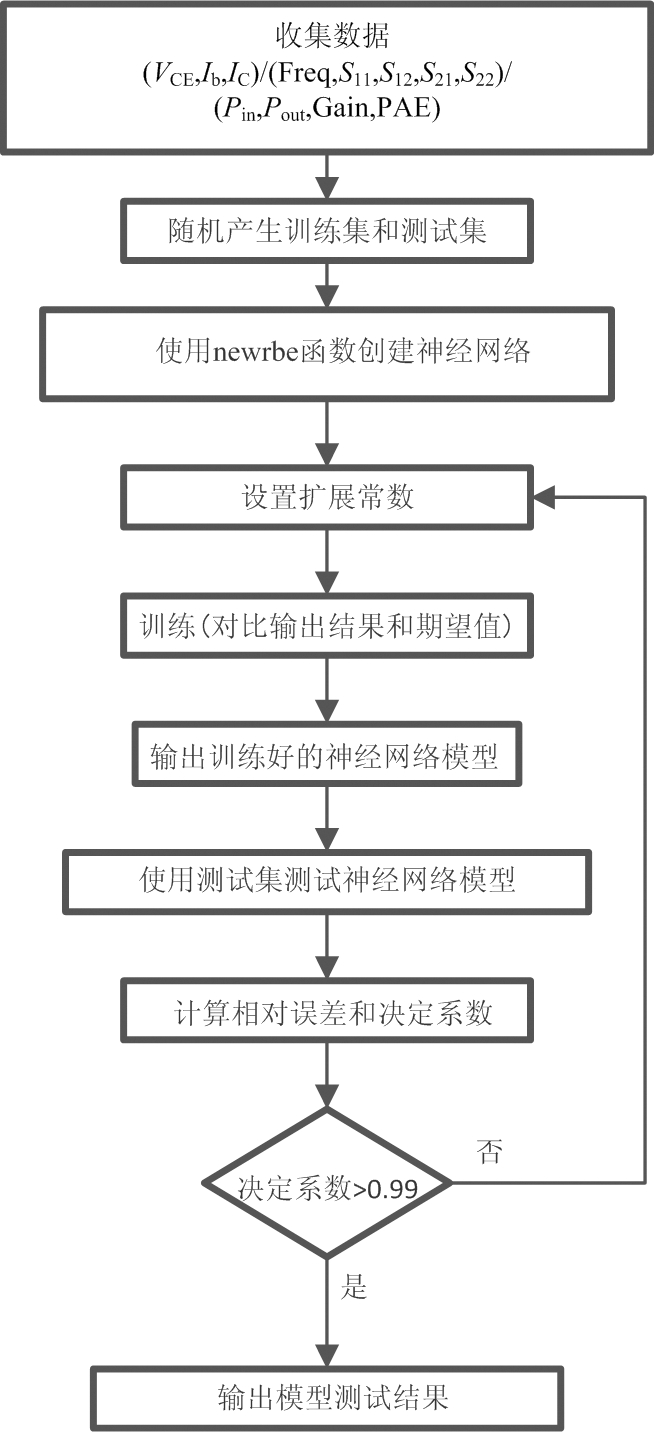
图4 RBF神经网络模型建立流程图
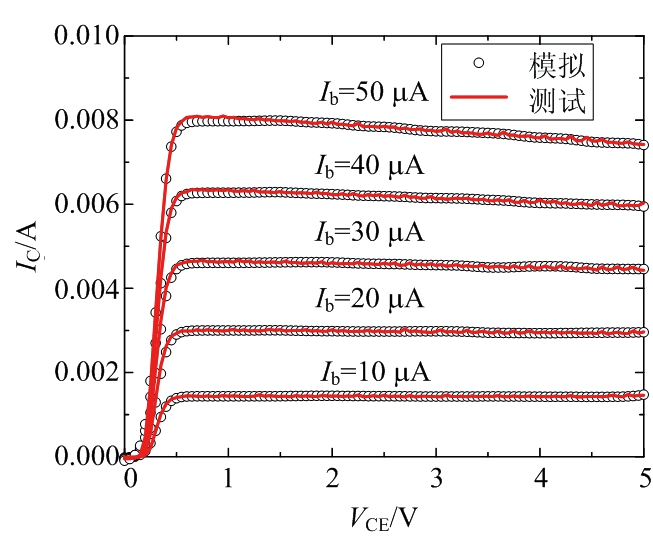
图5 BP神经网络模型直流模拟结果和实测结果对比
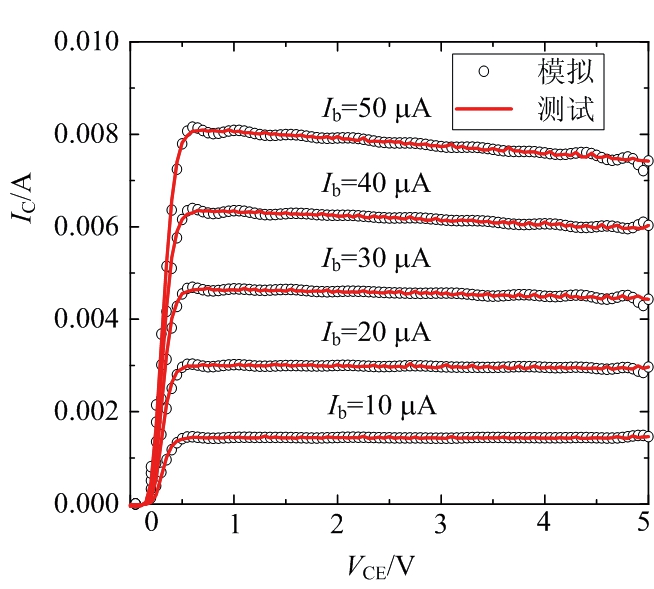
图6 RBF神经网络模型直流模拟结果和实测结果对比
GaAs HBT器件交流模型的建立,与直流模型一样采用图1和图2所示的神经网络结构分别建立GaAs HBT器件的S参数模型,建立流程分别如图3和图4所示。输入变量是偏置电压VCE,基极电流Ib和频率,S参数的归一化幅度和相位总共8个变量作为输出变量,S参数神经网络模型的建立过程与直流模型基本类似,仅输入输出变量不同,这也是神经网络模型相比经验模型的优越之处,方便又快捷,这里不再赘述。两个神经网络模型的训练和测试数据均来自于实际测试结果,这里选取偏置点为VCE=3.6 V,Ib=30 μA,频率0.1~40 GHz的GaAs HBT器件的S参数来验证神经网络模型的精确性,图7和图8分别是BP神经网络和RBF神经网络模型S参数模拟结果与测试结果的对比。
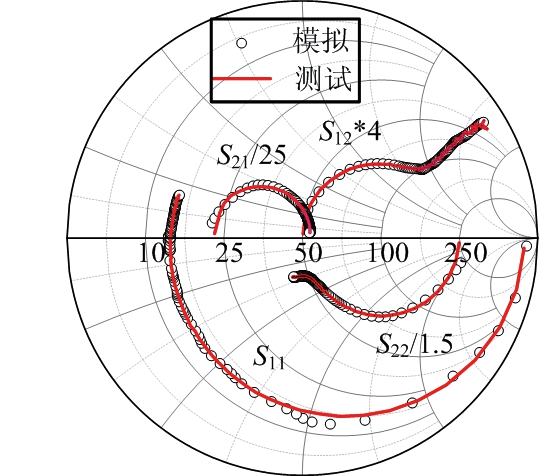
图7 BP神经网络模型S参数模拟结果与测试结果的对比
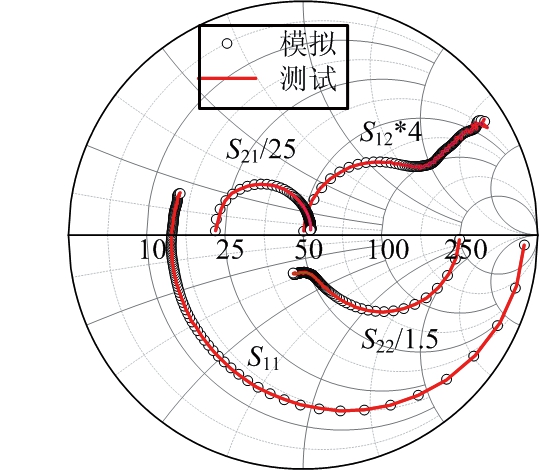
图8 RBF神经网络模型S参数模拟结果与测试结果的对比
谐波功率特性神经网络模型的建立与上述两个神经网络模型的建立过程类似,在VCE=3.6 mA,IC为2 mA,中心频率为3.5 GHz时,输入功率(Pin)作为模型的输入变量,随输入功率变化的输出功率(Pout)、增益(Gain)和功率附加效率(PAE)作为模型的输出变量,训练过程与直流模型基本一致,图9和图10分别是在VCE=3.6 V,IC=2 mA,中心频率3.5 GHz下,BP和RBF神经网络模型功率特性模拟结果与测试结果的对比。
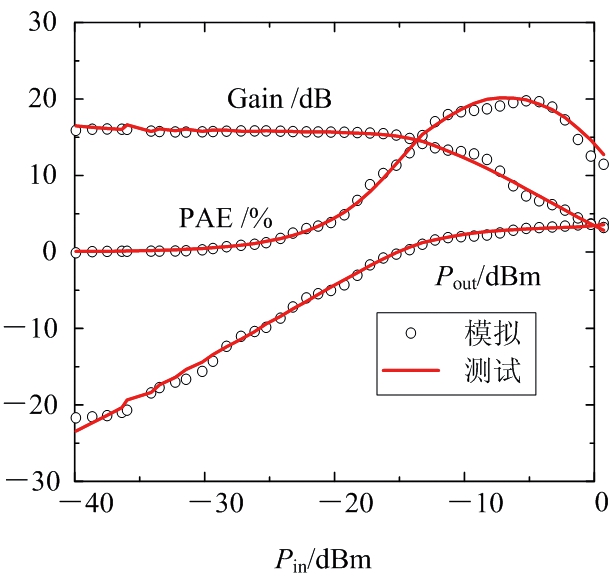
图9 BP神经网络模型功率特性模拟结果与测试结果的对比
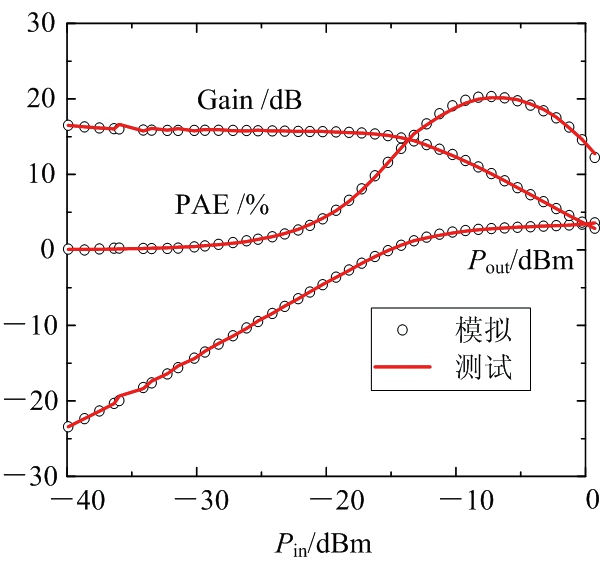
图10 RBF神经网络模型功率特性模拟结果与测试结果的对比
3 误差分析
从图5~10所示的神经网络模型模拟结果可以看出,神经网络模型模拟结果与测试结果拟合良好,GaAs HBT神经网络模型建立完成以后,两个模型的精度以平均相对误差来衡量,如表1所示。图11和图12是S参数模型的误差图,图13和图14是功率特性的误差图。
表1 两个神经网络模型的平均相对误差比较
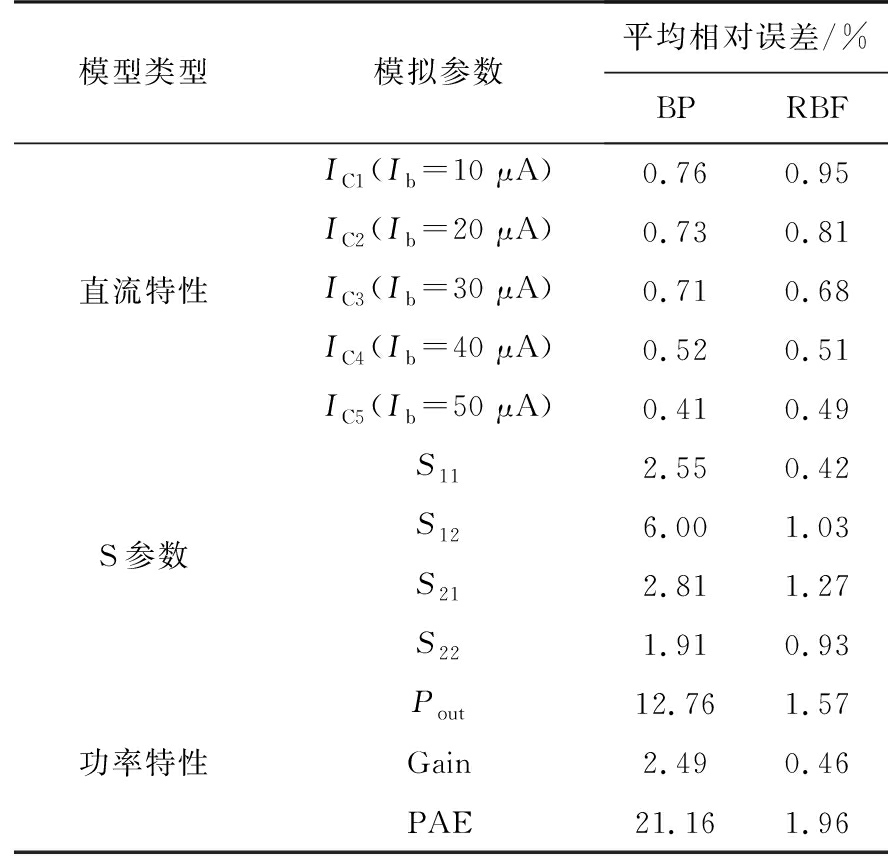
模型类型模拟参数平均相对误差/%BPRBF直流特性IC1(Ib=10 μA)0.760.95IC2(Ib=20 μA)0.730.81IC3(Ib=30 μA)0.710.68IC4(Ib=40 μA)0.520.51IC5(Ib=50 μA)0.410.49S参数S112.550.42S126.001.03S212.811.27S221.910.93功率特性Pout12.761.57Gain2.490.46PAE21.161.96
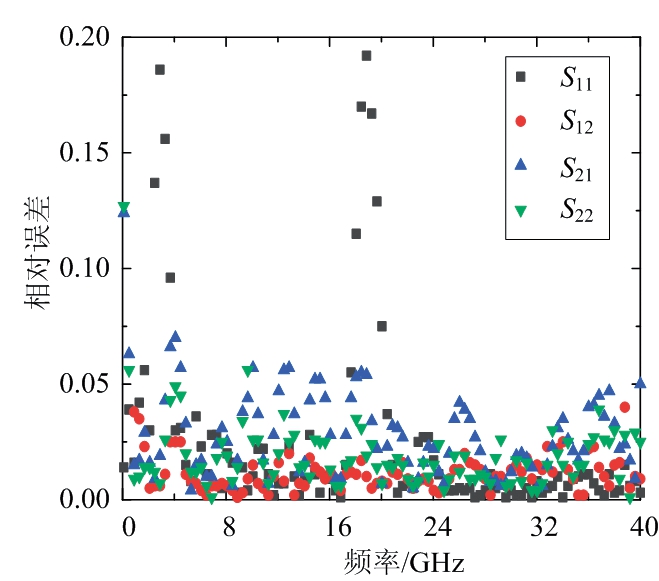
图11 BP神经网络S参数模型误差图
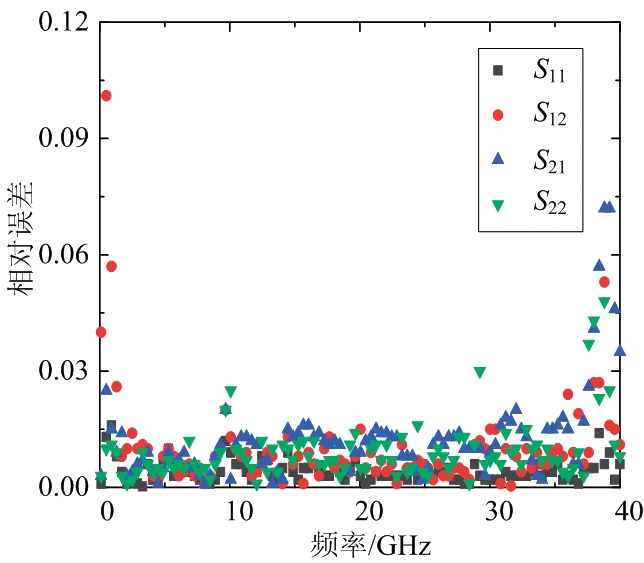
图12 RBF神经网络S参数模型误差图
对于直流模型,表中显示两个神经网络模型都具有较好的精度,平均相对误差均小于1%,BP神经网络直流模型总的平均相对误差为0.626%,RBF神经网络模型为0.688%,BP神经网络直流模型的精度略高。对于交流模型,从图7和图8可以看出,两个S参数模型模拟结果和测试结果都具有良好的一致性,但是BP神经网络模型在2 GHz以内有较大的误差,这一点从图11的误差图中也可以看出,如S12的平均相对误差高达6%,但是在2 GHz以上的频率范围内相对误差都低于2%。这是因为S12在100 MHz时,相对误差最大达到了4.52,使得平均相对误差比较高,去掉这个异常的数据,S12的相对误差在1.5%。图11误差图显示S21的相对误差相比其他S参数,较多分布在3%左右,是BP神经网络模型预测误差最大的S参数。RBF神经网络在S参数的预测上具有比BP神经网络更高的精度,如表1所示,4个S参数的平均相对误差都低于1.3%,图12的误差图中显示,在0.1~40 GHz内,S参数的相对误差绝大部分都在1%左右,但是参数S12在1.2 GHz以内的相对误差稍大,最大相对误差为10.1%,在1.2 GHz以上相对误差都在0.8%左右。S21是RBF神经网络模型预测的4个S参数相对误差较大的一个,如图12误差图所示,S21的相对误差集中在1.2%左右。
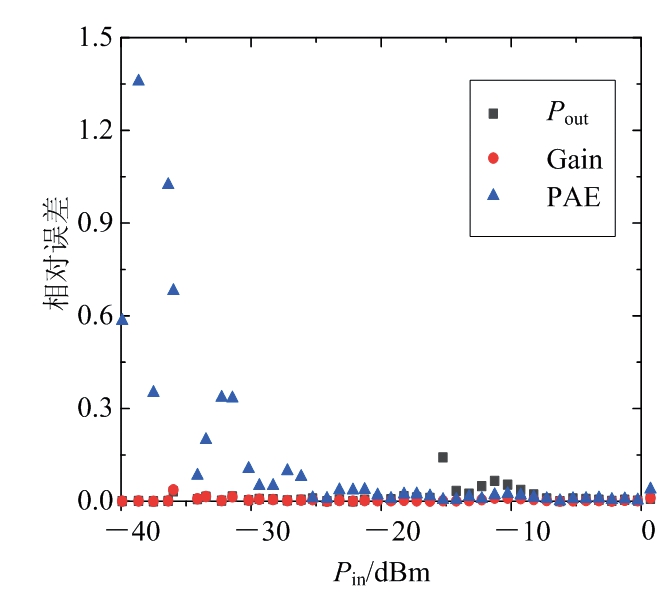
图13 BP神经网络模型功率特性误差图
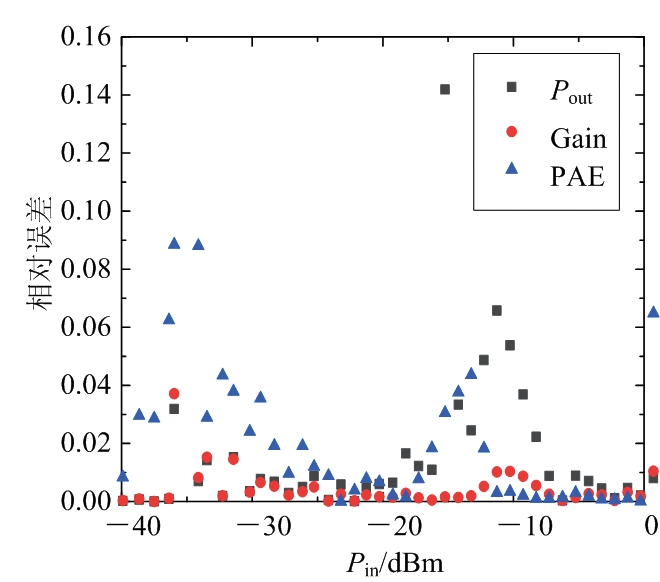
图14 RBF神经网络模型功率特性误差图
功率特性的模拟在经验模型中一直是一个难点,如GP模型、VBIC模型、Agilent HBT模型等,随着对模型精确度的要求越来越高,经验模型的建立越来越复杂,但是这会造成参数提取过程复杂繁琐,耗费研究人员更多时间。而神经网络模型可以精确模拟器件的功率特性。如图9和图10所示,BP神经网络和RBF神经网络模型模拟结果与测试结果都有良好的一致性,其中RBF神经网络模型的仿真结果精确度十分高。如表1所示,RBF神经网络的功率特性模拟结果的平均相对误差均低于2%,而BP神经网络模型功率特性的模拟结果的平均相对误差与RBF神经网络相比差距有点大,功率附加效率(PAE)的平均相对误差高达21.16%。从图13和图14的误差图中也可以看出,RBF神经网络模型的输出功率、增益和功率附加效率的相对误差都非常小,集中分布在0 ~ 0.02%这个区间内。BP神经网络模型的模拟结果不太好,尤其是功率附加效率,在较低的输入功率范围内,相对误差分布在0.4%~1.4%。因此,RBF神经网络模型在功率特性的仿真模拟中比BP神经网络更精确。
综上所述,通过对两个神经网络模型误差分析,RBF神经网络模型具有更高的准确性,而且在神经网络模型的训练中发现,RBF神经网络模型比BP神经网络模型具有更快的训练速度,这是因为BP神经网络属于全局输入网络,即网络的一个或多个可调参数(权值)对任何一个输出都有影响时,对于每次输入,网络上的每一个权值都要调整,从而导致网络训练速度很慢。如果对于输入空间的某个局部区域只有少数几个连接权值影响输出,则该网络称为局部逼近网络,RBF神经网络就属于局部逼近网络,训练速度比BP神经网络快得多。总的来说,RBF神经网络模型速度更快,精度更高,是建立HBT器件模型的良好选择。
4 结束语
本文研究了基于神经网络的GaAs HBT器件的模型,利用径向基函数(RBF)神经网络和反向传播(BP)神经网络分别建立了GaAs HBT器件的模型,并对两个神经网络模型进行分析和对比。研究结果表明,神经网络模型的模拟结果与测试数据具有良好的一致性。与经验模型相比,神经网络模型不必依赖器件内部结构知识,建模速度快,建模过程简单,节省了大量的时间,而且弥补了经验模型在预测功率特性方面的不足,可以更好地预测器件特性,方便研究人员进行电路设计。在模型的精度与速度方面,RBF神经网络模型因为训练速度更快、精度更高,比BP神经网络模型更具优越性,是建立HBT器件模型的良好选择。
[1] REFAI W Y, DAVIS W A. A Highly Efficient Linear Multimode Multiband Class-J Power Amplifier Utilizing GaAs HBT for Handset Modules[J]. IEEE Trans on Microwave Theory and Techniques, 2020, 68(8): 3519-3531.
[2] LIU M, XU P, ZHANG J,et al. A 4.2-to-5.4 GHz Stacked GaAs HBT Power Amplifier for C-Band Applications[J]. Circuit World, 2020, 46(4):243-248.
[3] LEE W, KANG H, LEEE H,et al. Broadband InGaP/GaAs HBT Power Amplifier Integrated Circuit Using Cascode Structure and Optimized Shunt Inductor[J]. IEEE Trans on Microwave Theory and Techniques, 2019, 67(12):5090-5100.
[4] WANG Z, XU Z, LIU J,et al. Scalable Agilent HBT Model for GaAs HBTs[C]∥ 2019 International Conference on Microwave and Millimeter Wave Technology (ICMMT),Guangzhou, China:IEEE, 2019:1-3.
[5] SHI Yuxia, WANG Yan. An Enhanced Model for InGaP/GaAs Heterojunction Bipolar Transistor[J]. Microelectronics Journal, 2013, 44(2):163-168.
[6] HU S, XU K, YU S,et al. Analysis of Nonlinear Large Signal Intrinsic Elements for InGaP/GaAs HBT Based on Gummel-Poon Model[J]. International Journal of Numerical Modelling-Electronic Networks Devices and Fields, 2018, 33(3):1-13.
[7] ROSS T N, CORMIER G, WIGHT J S. Development of a Model for a Microwave InGaP/GaAs HBT[J]. IEEE Microwave Magazine, 2015, 16(1):101-110.
[8] JIN R, CURTICE W R. Safe Operating Area of GaAs HBTs Based on Sub-Nanosecond Pulse Characteristics[J]. IEEE Trans on Microwave Theory and Techniques, 2010, 58(12):3996-4003.
[9] KUTUB S B, JIANG H J, CHEN N Y, et al. Artificial Neural Network-Based (ANN) Approach for Characteristics Modeling and Prediction in GaN-on-Si Power Devices[C]∥2020 32nd International Symposium on Power Semiconductor Devices and ICs ,Vienna, Austria:IEEE, 2020:529-532.
[10] IWAMOTO M, XU J J, ZHOU W F, et al. Know-ledge-Based Neural Network (KBNN) Modeling of HBT Junction Temperature and Thermal Resistance from Electrical Measurements[C]∥2017 IEEE MTT-S International Microwave Symposium (IMS), Honololu, HI, USA:IEEE, 2017:1065-1067.
[11] ZHONG Z, GUO Y X, WU W, et al. An Artificial Neural Network-Based Electrothermal Model for GaN HEMTs with Dynamic Trapping Effects Consideration[J]. IEEE Trans on Microwave Theory and Techniques, 2016, 64(8):2519-2528.
[12] MARKOVIC V, DORDEVIC V, PRONIC-RANCIC O, et al. Development and Validation of ANN Approach for Extraction of MESFET/HEMT Noise Model Parameters[J]. Electrical Engineering, 2018, 100(2):645-651.
[13] LEI N, JIANG F, SUN L. X-Parameter Modelling of GaN HEMT Based on Neural Network[J]. The Journal of Engineering, 2019(23):8955-8958.
[14] ZHAO Z, ZHANG L, FENG F,et al. Space Mapping Technique Using Decomposed Mappings for GaN HEMT Modeling[J].IEEE Trans on Microwave Theory and Techniques, 2020, 68(8):3318-3341.
[15] ELHAMADI T, BOUSSOUIS M, TOUHAMI N A,et al. Neuro-Space Mapping Modeling Approach for Trapping and Self-Heating Effects on GaAs and GaN Devices[J]. International Journal of RF and Microwave Computer-Aided Engineering,2017,27(6):1-10.
[16] WU H F, CHENG Q F, YAN S X, et al. Transistor Model Building for a Microwave Power Heterojunction Bipolar Transistor[J]. IEEE Microwave Magazine, 2015,16(2):85-92.
[17] KHUSRO A, HUSAIN S, HASHMI M S,et al. Small Signal Behavioral Modeling Technique of GaN High Electron Mobility Transistor Using Artificial Neural Network: An Accurate, Fast, and Reliable Approach[J]. International Journal of RF and Microwave Computer-Aided Engineering,2020,30(4):1-15.
[18] XUE M, SUN L, WANG S,et al. Nonlinear Equivalent Circuit Model Based on BPNN for GaN HEMTs[C]∥2019 IEEE International Conference on Electron Devices and Solid-State Circuits (EDSSC), Xi’an,China:IEEE,2019:1-5.
[19] HAYATI M, AKHLAGHI B. An Extraction Technique for Small Signal Intrinsic Parameters of HEMTs Based on Artificial Neural Networks[J]. International Journal of Electronics and Communications,2013, 67(2):123-129.
[20] WEATHERSPOON M H, MARTINEZ H A, LANGONI D,et al. Small-Signal Modeling of Microwave MESFETs Using RBF-ANNs[J]. IEEE Trans on Instrumentation and Measurement, 2007, 56(5):2067-2072.
[21] MA C T, GU Z H. Investigation on GaN HEMTs Based Three-Phase STATCOM with Hybird Control Scheme[J]. Micromachines, 2021, 12(4):464.
[22] LIU H W. Nonlinear Behavioral of GaN Doherty Power Amplifiers Using Neural Modeling[J]. Microwave and Optical Technology Letters, 2010, 52(2):307-309.
[23] ZHANG L, ZHANG Q J. Combined Genetic Programming and Neural Network Approaches to Electronic Modeling[C]∥2019 6th International Conference on Computational Science and Computational Intelligence, Las Vegas, NV, USA:IEEE,2019:1533-1536.
[24] LIU W, ZHU L, FENG F,et al. A Time Delay Neural Network Based Technique for Nonlinear Microwave Device Modeling[J]. Micromachines, 2020, 11(9):831.
[25] ZHAO Z H, NA W C, GONGAL-REDDY V M R, et al. Multi-Band Behavioral Modeling of Power Amplifier Using Carrier Frequency-Dependent Time Delay Neural Network Model[C]∥2017 IEEE MTT-S International Conference on Numerical Electromagnetic and Multiphysics Modeling and Optimization for RF, Microwave, and Terahertz Applications (NEMO), Seville, Spain:IEEE, 2017:82-84.


