0 引言
在机载气象雷达的天气信号检测、地杂波抑制等任务中,多普勒信息的获取非常重要[1-4]。一般来说,气象雷达需要的观测范围比较广,因此在设计系统时,通常选择较低的脉冲重复频率(Pulse Recurrence Frequency, PRF)来避免距离模糊。然而,低PRF会导致接收信号在多普勒域的混叠,造成多普勒信息的恶化,从而导致目前许多气象信号检测和地杂波抑制方法的失效[5-6]。因此,由于PRF的选择不能同时满足距离和多普勒的不模糊性要求,对机载气象雷达提出了挑战。因此,有必要探索有效的解决机载气象雷达多普勒模糊度的算法。
近几十年来,多普勒解模糊算法得到了广泛的研究,现有的多普勒解模糊算法可分为多种类型。在脉冲多普勒雷达中,可以使用单中脉冲重复频率下基于概率数据关联的解模糊算法[7]。在合成孔径雷达(Synthetic Aperture Radar,SAR)中,可以使用改进的二阶Keystone变换(MSOKT)和Keystone(KT)变换方法对多普勒模糊地面运动目标进行聚焦[8]。而对称三角线性调频连续波(LFMCW)雷达中,可以通过实现正确配对,得到真实目标,并解得最大模糊重数[9]。还有一些算法利用多方位子孔径的独立空间样本来补充低PRF导致的慢时样本不足。为了在不增加子孔径数目的情况下增加独立空间样本,以此引入了多输入多输出(Multiple-Input and multiple-Output, MIMO)技术[10-13]。多通道SAR高分辨率宽测绘带(High-Resolution and Wide-Swath, HRWS)成像中,采用了基于方位向数字波束形成(Digital Beam-Forming, DBF)的方法,即通过方位向多通道波束形成技术处理来重建清晰的多普勒频谱[14-15]。
现有的多通道SAR成像技术大多采用正侧视的工作方式,而机载气象雷达往往工作在前视的快速扫描下。因工作模式存在的差异,设计机载气象雷达多普勒解模糊算法是十分必要的。本文提出了两种多普勒解模糊算法。算法一基于方位向波束形成技术,利用每个多普勒频点中混叠信号的不同方位角特性,在每个多普勒频点中保留期望的多普勒频谱分量,并抑制其他非期望的多普勒频谱分量。在波束形成过程中采用了非期望信号协方差矩阵重构方法,进一步提高了算法的鲁棒性;并为了减少前视高速扫描模式下的角度估计误差,采用空间谱积分的方法估计出更准确的导向矢量。算法二利用导向矢量计算阻塞矩阵,将接收信号进行多普勒模糊相消预处理,阻塞每个多普勒频点的模糊多普勒分量。仿真结果表明,两种算法能有效地从混叠频谱重建出正确的多普勒频谱,而算法二与算法一在处理相同数据情况下,有更优良的性能,并有更小的运算量,对系统要求更低。
1 多通道回波模型
假设机载气象雷达方位多通道系统共有N个通道,垂直于航向均匀分布,如图1所示,Y轴为飞机速度方向,Z轴背向地球中心,X轴垂直于飞行方向,构成右手坐标系,其中φ为俯仰角,θ为方位角。
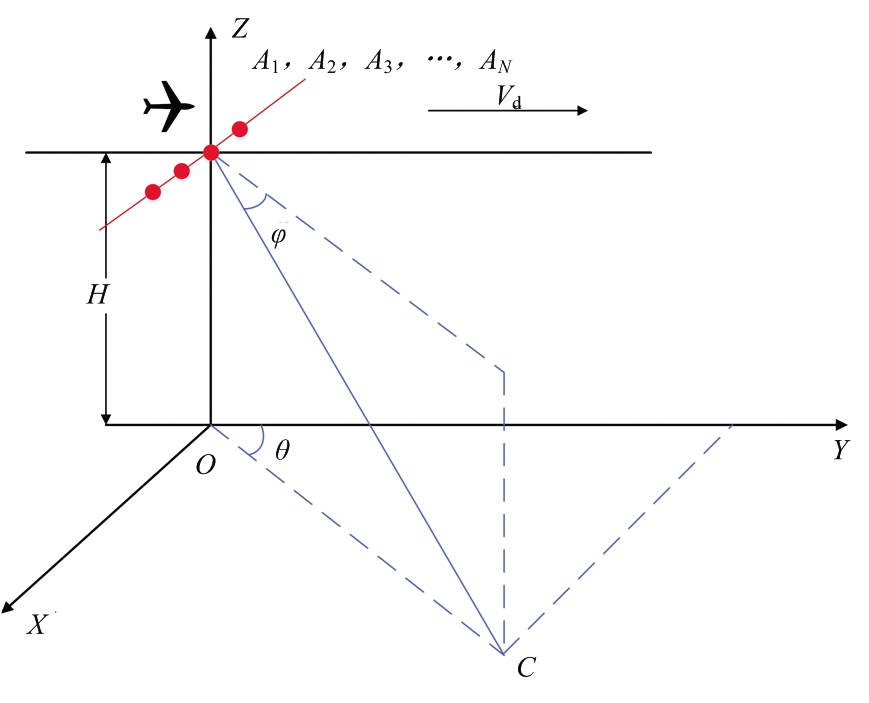
图1 三维空间几何接收模型
假设参考通道的起始坐标(等效相位中心坐标)为(0, 0, H),时刻t时为(0, vat, 0) (va为卫星速度),第n个(n=1, 2, …,N)通道的起始坐标(等效相位中心坐标)为(xn, 0, 0),时刻t时为(xn, vat, 0) 。对地面某个目标来说, 参考通道接收的回波信号为
s0(t,τ)=![]()
exp{jπKa(τ-r0(t)/c)2}·
exp{-j2πfc·(r0(t)/c)}+n(t,τ)
(1)
式中,Ka为线性调频信号的线性调频率,Tr为脉冲持续时间,c为电磁波传播速度,η为信号幅度,r0(t)/c表示电磁波从发射机传播到某一散射点再由该散射点反射回接收机的总时间,n(t,τ)为信号中的干扰成分。其中
r0(t)=![]()
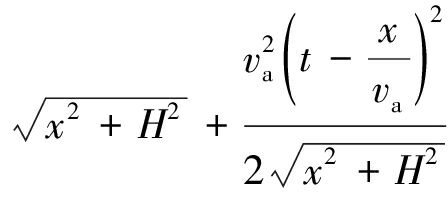
(2)
相应地,第n个通道接收的回波信号为
sn(t,τ)![]()
exp{jπKa(τ-rn(t)/c)2}·
exp{-j2πfc·(rn(t)/c)}+n(t,τ)
(3)
式中,
rn(t)=![]()
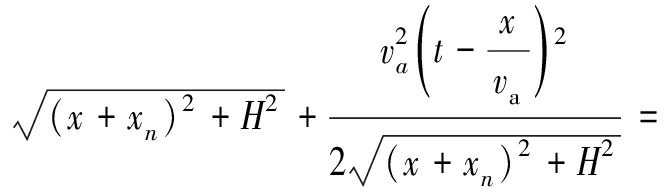
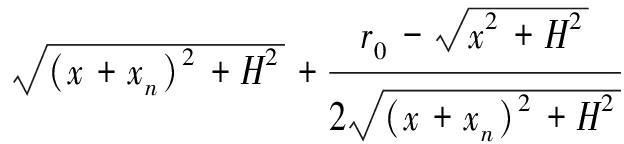
(4)
由此可见,对于某一点目标来说,不同通道接收的回波在时间上存在固定差异。但变换到多普勒域,与正侧视情况不同,前视情况下不同通道接收的回波在同一距离-多普勒单元上不仅仅相差一个线性相位项。假设fd为多普勒频率,每个多普勒单元均包含所有相同空间锥角下的回波,在多普勒不模糊的情况下,对于静止目标,其多普勒频率和角度的关系是
(5)
因此在前视条件下,多普勒频率和方位角的正弦值在空时平面上应该表现为椭圆曲线。如图2中的空时二维谱所示,图2(a)、(b)中,在无偏航角,即在飞机正前方处时,PRF的变化不会引起多普勒模糊;但在图2(c)、(d)中,在飞机具备一定偏航角时(图中为60°),较低的PRF会造成信号在多普勒域的混叠,由此每一个通道接收的回波都发生了多普勒模糊,无法利用信号中的多普勒信息,因此需要利用相关技术对该问题进行解决。
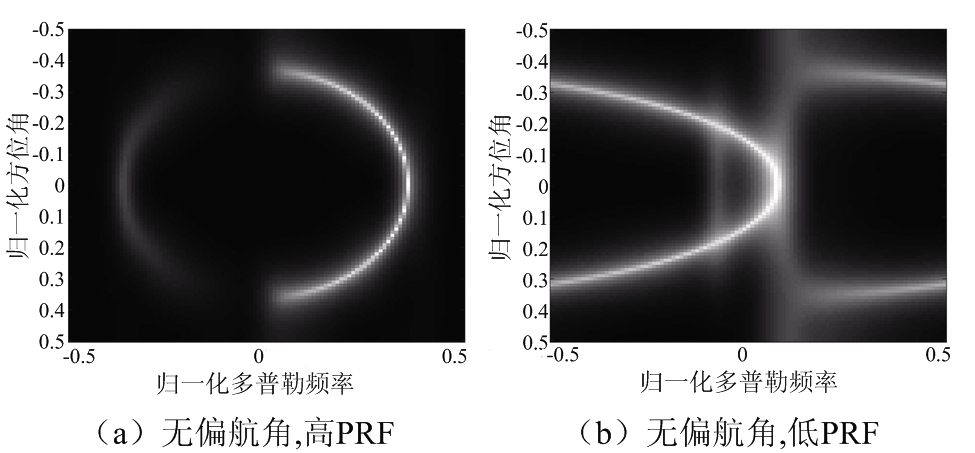
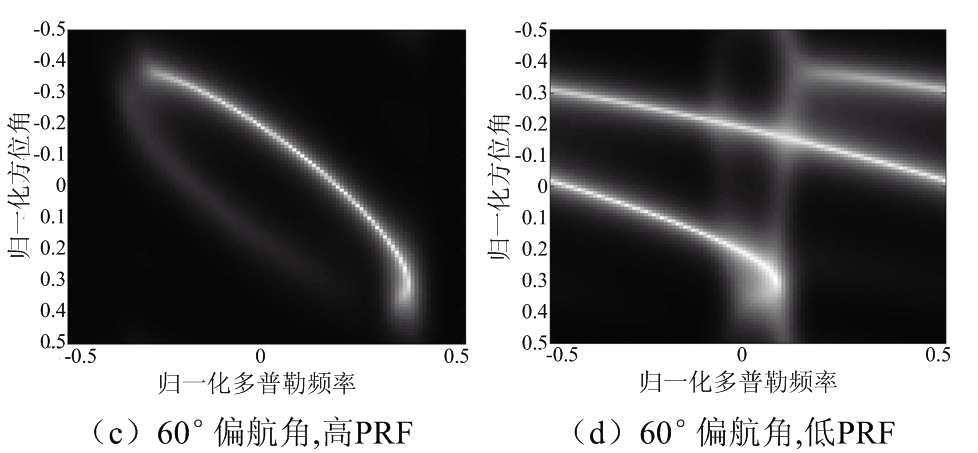
图2 不同偏航角不同PRF下的理论空时二维谱
2 多普勒解模糊算法2.1 传统Capon波束形成解模糊算法
在合成孔径雷达(SAR)中,通常采用Capon波束形成算法来解决多普勒模糊问题。利用方位多通道系统具有多个空间自由度的特性,将阵列响应的主波束指向期望多普勒频谱分量的方向,而波束零点则指向其他多普勒模糊分量的方向以此抑制非期望模糊分量。假设多通道机载气象雷达存在多普勒模糊,每个多普勒频率的回波信号来自多个不同的方向,每个频率单元包含K个模糊分量(K<N),导向矢量ak(θ)表示针对第k次多普勒模糊分量的导向矢量。因此,多普勒频率fd,方位角θ以及导向矢量ak(θ)之间的关系可以表示为
(6)
(7)
上标T表示转置运算符。因此,导向矢量ak(θ)也是关于fd的变量,即fd可以用来代替方位角θ表示导向矢量ak(θ)。为了提取第k个模糊度对应的多普勒频谱分量,Capon波束形成算法的最优权矢量由以下准则得到。
(8)
式中,上标H表示共轭转置运算符。R(τ,fd)是接收数据在多普勒频域的自相关矩阵。在实际处理中,接收信号的统计特性往往是未知的,因此在处理中通常由相邻的距离门数据来估计,可以表示为R(τ,fd)=E{x(τ,fd)x(τ,fd)H},其中x(τ,fd)是多普勒域中阵列的回波数据矢量。求解式(8)中的准则,Capon波束形成器的最优权向量可以描述为
(9)
所以,利用最优权矢量可以将对应于第k个模糊度的多普勒频谱分量提取为
(10)
然而,许多其他雷达不同于SAR,例如机载气象雷达,这些雷达工作在高速扫描模式下,使得机载气象雷达的相干脉冲数远小于成像雷达。另外,机载气象雷达的多普勒频率间隔远大于成像雷达的多普勒频率间隔。由于计算方位角需要利用多普勒频率,多普勒频率间隔越大,方位角计算误差越大,而传统的Capon波束形成算法对角度误差非常敏感,会在期望的多普勒频谱分量上形成零点,无法提取期望的多普勒频谱分量。为了提高Capon波束形成算法的鲁棒性,需要采用协方差矩阵重构和空间导向矢量估计算法。
2.2 基于改进方位向波束形成解模糊算法
当期望信号导向矢量失配或是期望信号包含在采样协方差矩阵中时,传统自适应波束形成器的性能会下降。而协方差矩阵重构可以有效地提高自适应波束形成算法的鲁棒性。根据协方差矩阵的表达式,进一步得到如下形式。
R(τ,fd)=E{x(τ,fd)x(τ,fd)H}=
Rs+Ri+n=
(11)
(12)
(13)
式中,Rs是期望信号的协方差矩阵,Ri+n是干扰和噪声协方差矩阵,![]() 是期望信号的功率,
是期望信号的功率,![]() 是干扰功率和噪声功率。在解决多普勒模糊问题时,期望的多普勒频谱分量可以看作是期望信号分量,而其他的模糊多普勒频谱分量可以看作是干扰或噪声分量。这样,Capon波束形成器的最优权向量可以满足
是干扰功率和噪声功率。在解决多普勒模糊问题时,期望的多普勒频谱分量可以看作是期望信号分量,而其他的模糊多普勒频谱分量可以看作是干扰或噪声分量。这样,Capon波束形成器的最优权向量可以满足
![]()
![]()
(14)
由于期望信号功率![]() 是恒定的,所以最优权矢量对采样协方差矩阵R(τ,fd)的约束等价于最优权矢量对干扰和噪声协方差矩阵Ri+n的约束,即Capon波束形成中第一个约束条件可以等价为
是恒定的,所以最优权矢量对采样协方差矩阵R(τ,fd)的约束等价于最优权矢量对干扰和噪声协方差矩阵Ri+n的约束,即Capon波束形成中第一个约束条件可以等价为![]() 在波束形成条件中只考虑Ri+n可以减少期望信号对求解最优权矢量的影响,所以需要对干扰和噪声协方差矩阵Ri+n进行重构。
在波束形成条件中只考虑Ri+n可以减少期望信号对求解最优权矢量的影响,所以需要对干扰和噪声协方差矩阵Ri+n进行重构。
在重构过程中,首先根据采样协方差矩阵R计算每个角度下的Capon空间谱。
(15)
式中,![]() 是采样协方差矩阵R的估计量,
是采样协方差矩阵R的估计量,![]() 是以θ为方位角的标称空间导向矢量,根据相应多普勒模糊成分下对应的多普勒频点值,可以推算出相应的方位角θ。因此干扰和噪声协方差矩阵Ri+n可以由以下积分式重构:
是以θ为方位角的标称空间导向矢量,根据相应多普勒模糊成分下对应的多普勒频点值,可以推算出相应的方位角θ。因此干扰和噪声协方差矩阵Ri+n可以由以下积分式重构:
(16)
其中积分范围![]() 是非期望模糊分量所对应的角度范围。经过协方差矩阵重构,最优权矢量的表达形式可以重写为
是非期望模糊分量所对应的角度范围。经过协方差矩阵重构,最优权矢量的表达形式可以重写为
(17)
在快速扫描工作模式下会产生较大的多普勒频率间隔,而较大的多普勒频率间隔会导致方位角计算误差和空域导向矢量失配,因此需要进行空域导向矢量估计。空域导向矢量估计的方法类似于协方差矩阵重构,首先需要Capon空间谱积分得到期望信号的协方差矩阵![]()
(18)
其中积分范围Θ是期望模糊分量所对应的角度范围。假设![]() 是通过多普勒频点计算出的方位角度,Δθ是一个很小的角度,则
是通过多普勒频点计算出的方位角度,Δθ是一个很小的角度,则![]() 在实际处理中,Δθ可以根据实际情况选择不同合适的角度值。
在实际处理中,Δθ可以根据实际情况选择不同合适的角度值。
根据子空间理论,对期望信号协方差矩阵![]() 进行特征值分解后,由最大特征值对应的特征向量所张成的信号子空间包含期望信号的导向向量。因此,取特征值分解后的最大特征值对应的特征向量作为估计的导向向量,即
进行特征值分解后,由最大特征值对应的特征向量所张成的信号子空间包含期望信号的导向向量。因此,取特征值分解后的最大特征值对应的特征向量作为估计的导向向量,即
(19)
其中ρ{·}表示计算协方差矩阵最大特征值对应的特征向量。因此,Capon波束形成器的最优权向量可以再次重写为
(20)
基于上述协方差矩阵重构和导向矢量估计方法,Capon波束形成算法将具有更好的性能。由此,可以利用如下数据处理流程进行多普勒解模糊处理。首先,需要确定一次处理的脉冲数和模糊数。然后,将原始数据按方位角进行分段。对于每段数据,需要利用多个距离门的数据估计原始样本协方差矩阵来计算Capon空间谱。对于不同的多普勒模糊度分量,可以通过计算最优权向量来恢复每个多普勒频谱分量。再将不同片段的多普勒频谱进行拼接,通过方位逆傅里叶变换并将数据按照顺序存储,即可得到解模糊后的数据。
2.3 基于阻塞矩阵的解模糊算法
阻塞矩阵通常被应用于阵列抗主瓣干扰中,其利用均匀线阵各阵元间存在均匀相位差的特点,通过构造阻塞矩阵阻塞预处理将主瓣干扰去除。当信号中存在主瓣干扰时,阻塞矩阵抗干扰方法首先对主瓣干扰进行方位估计,并构建阻塞矩阵对阵列接收信号进行预处理,抑制掉主瓣干扰。在多普勒解模糊任务中,非期望的多普勒频谱分量可以视为来自不同方位角的主瓣干扰,因此该方法的具体步骤如下:
首先需要确定模糊数K,然后以获取第k次模糊多普勒频谱模糊分量为例,需要确定其他非期望多普勒频谱分量在空间中所对应的方位角范围,设为Θ1,…,Θk-1,Θk+1,…, ΘK;根据上一小节介绍的导向矢量的估计方法,利用上述方位角范围作为积分范围,以式(18)为例对每一个非期望多普勒频谱分量进行空间谱积分即可得到非期望多普勒频谱分量的协方差矩阵,记为R1,…,Rk-1,Rk+1,…,RK。再对协方差矩阵进行主成分分析,通过协方差矩阵特征值分解,取最大特征值对应的特征向量,即为每一个非期望多普勒分量的估计导向矢量,记为a1,…,ak-1,ak+1,…,aK。以此可以确定除第k次多普勒模糊分量以外其他模糊分量的干扰方向。
然后根据干扰方向设计阻塞矩阵B。B可以由下式表示:
B=I-A(AHA)-1AH
(21)
式中,I是N×N的单位阵,A是非期望多普勒模糊分量特征向量组成的矩阵,即
A=[a1,…,ak-1,ak+1,…,aK]
(22)
因此对接收快拍信号x(τ,fd)进行阻塞处理后的信号为
yk(τ,fd)=Bx(τ,fd)
(23)
同理可以得到所有多普勒模糊分量的信号多普勒频谱y1(τ,fd),…,yk(τ,fd),…,yK(τ,fd)。根据理论的多普勒频谱位置对每一段频谱进行排序存储,再对整体进行方位向逆傅里叶变换,即可得到多普勒不模糊的时域数据。
3 实验结果与分析
在前一节中详细分析了两种多普勒解模糊算法的原理和处理流程,本节用仿真机载雷达数据对两种算法进行了验证。有关仿真数据的主要参数见表1。在验证过程中,分为两个实验:第一个实验通过扫描真实的雷达图像生成数据,这样得到的数据的频谱不是规律的,以对比解模糊前后多普勒频谱的细节。第二个实验对气象目标和地杂波数据进行了仿真,并用基于多普勒信息的检测方法对解模糊前后的数据进行气象目标检测,验证了算法的可行性。
在第一个实验中,通过扫描真实的雷达图像来生成仿真数据。首先,从数据中提取100个距离门和64个脉冲的数据,通过方位傅里叶变换进行处理,得到其多普勒频谱,其结果如图3所示。
为了构造多普勒模糊的数据,在上述数据的时域方位向上进行三抽一操作,即将数据的PRF降到原来的三分之一。然后可以得到抽取后数据的MVDR谱和多普勒频谱,如图4所示。
表1 两组仿真数据的主要参数
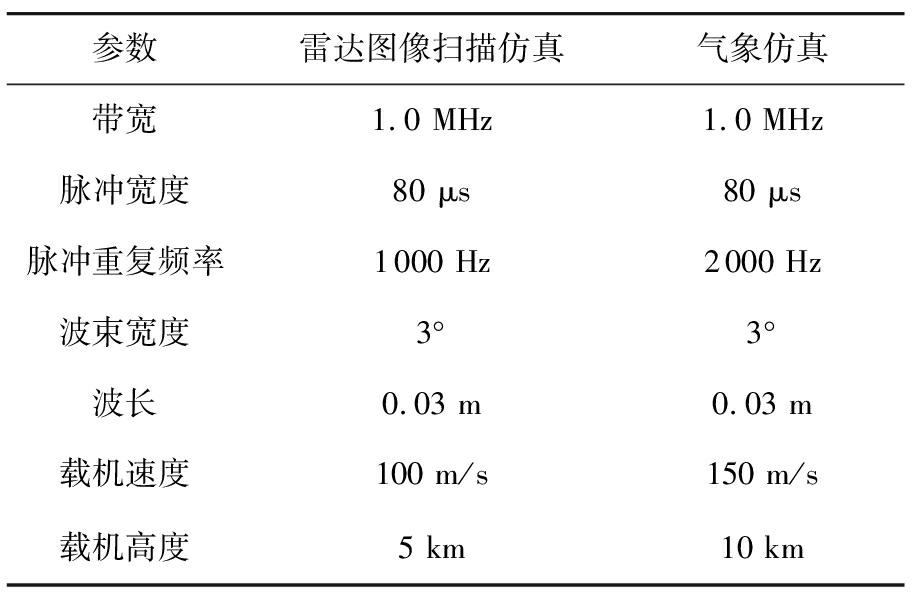
参数雷达图像扫描仿真气象仿真带宽1.0 MHz1.0 MHz脉冲宽度80 μs80 μs脉冲重复频率1000 Hz2000 Hz波束宽度3°3°波长0.03 m0.03 m载机速度100 m/s150 m/s载机高度5 km10 km
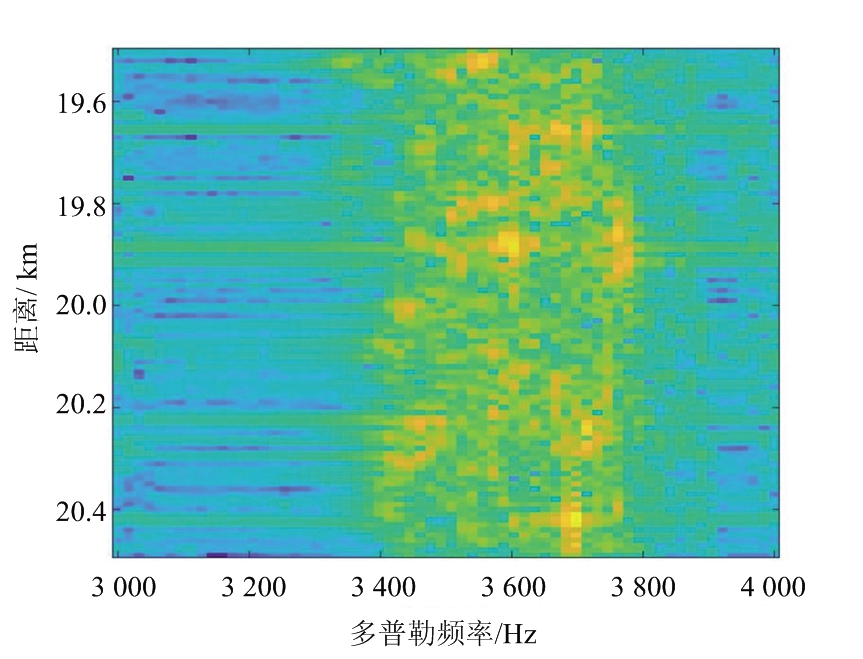
图3 原始数据的多普勒频谱

图4 进行方位向三抽一后的数据
通过对数据的MVDR频谱和多普勒频谱的分析,不难发现PRF降低后数据在多普勒域已经变得模糊。利用本文提出的两种算法可以恢复多普勒信息。对于改进的自适应波束形成解模糊算法,为了观察每组最优权矢量在不同方位角上的响应,使用每组最优权矢量来绘制自适应方向图;对于基于阻塞矩阵的解模糊算法,通过不同的阻塞矩阵可以抑制不同方位角上的模糊分量,因此在数据经过阻塞矩阵处理后也可以得到不同的自适应方向图。两种方法得到的自适应方向图分别由图5、图6所示。
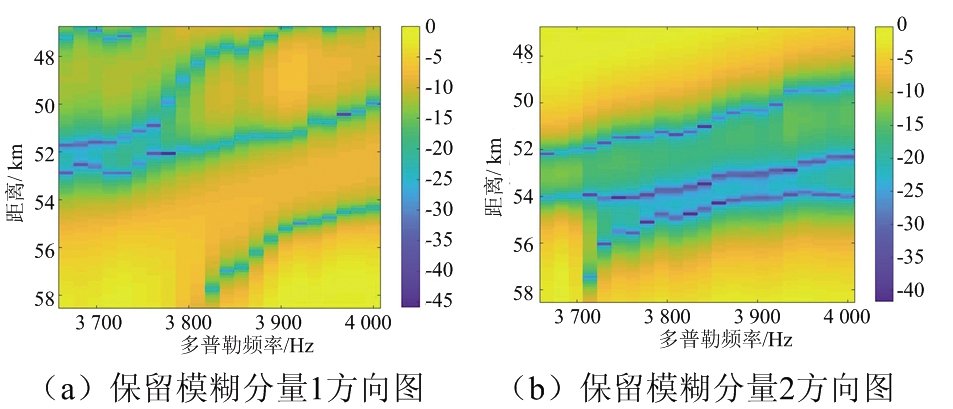
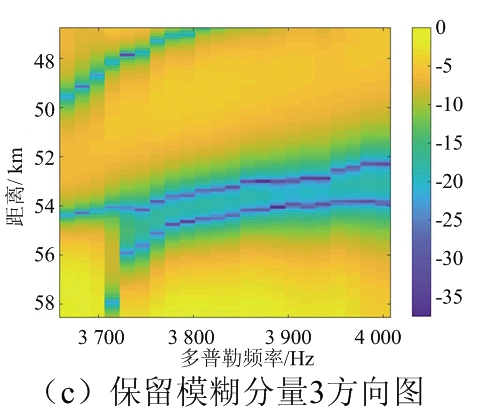
图5 改进波束形成算法最优权矢量的自适应方向图
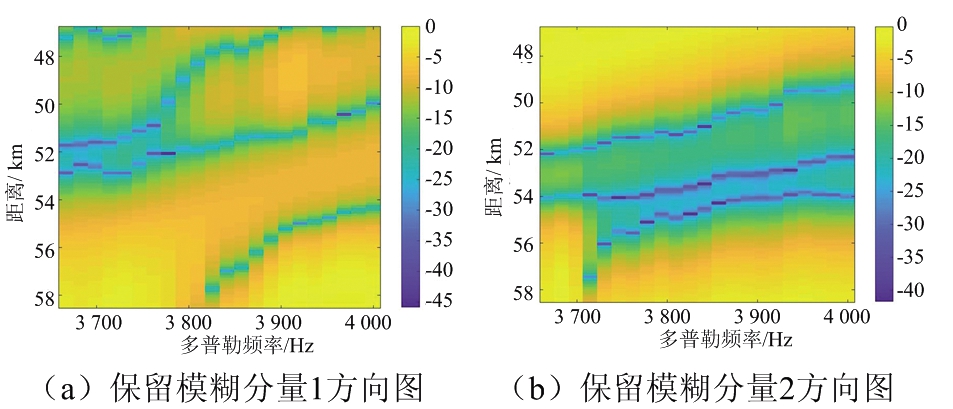
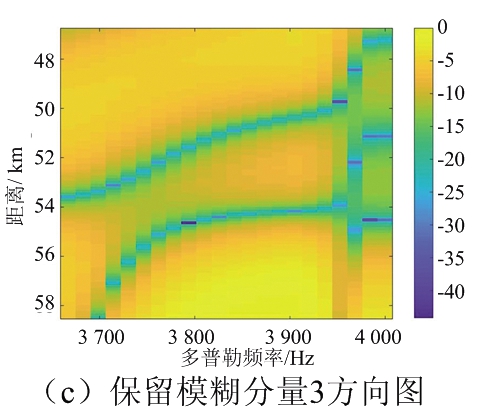
图6 阻塞矩阵算法处理数据后的自适应方向图
通过两种方法自适应方向图的观察,波束形成方法的权矢量和阻塞矩阵都可以按照设计要求在期望的方向上产生主瓣,在非期望的方向上产生零陷,因此可以按照要求抑制非期望的多普勒频谱分量并可以利用这些最优权值向量对数据进行空域滤波以及利用阻塞矩阵对频域快拍数据进行处理,恢复数据的多普勒频谱成分。再根据多普勒频率的实际位置对数据进行拼接,可以恢复原始的多普勒频谱。图7给出了两种不同的多普勒解模糊方法的结果,并作为对比,分别给出了将未进行导向矢量估计和未进行协方差矩阵重构的波束形成算法的解模糊结果。将图7(c)、(d)与图3原始数据频谱之间的比较,这两种算法均可以恢复信号的多普勒频谱;而图7(a)在导向矢量失配时,传统的波束形成算法失去了解多普勒模糊的能力;图7(b)在算法性能鲁棒性较差时,解模糊结果也会存在较大误差。
为了更加直观地比较两种算法解多普勒频谱模糊的性能,如图8所示,在原始数据,利用改进波束形成算法解模糊后的结果以及利用阻塞矩阵算法解模糊后的结果中分别取第50个距离门数据的归一化幅度进行对比。从图中曲线可以看出两种算法对多普勒模糊频谱均有一定的恢复能力,且在信号频谱能量较强的频率位置均有很好的重构效果;但对于信号频谱本应能量较弱的频率位置,基于改进波束形成解模糊算法的空域滤波效果不及基于阻塞矩阵解模糊算法。
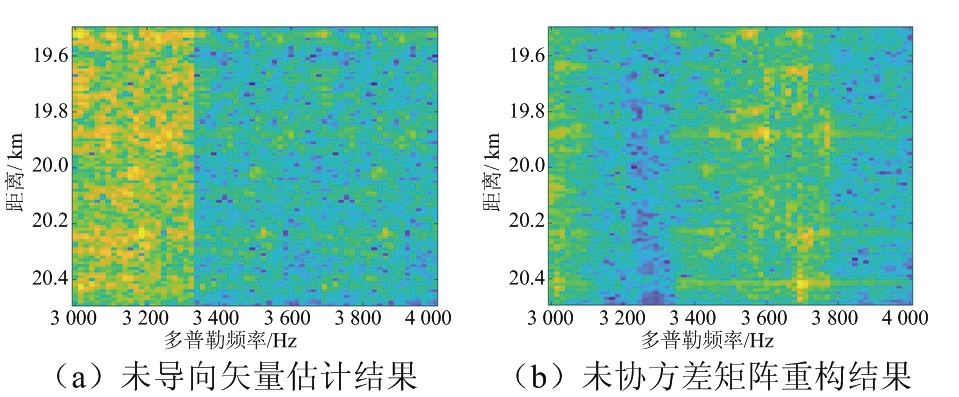
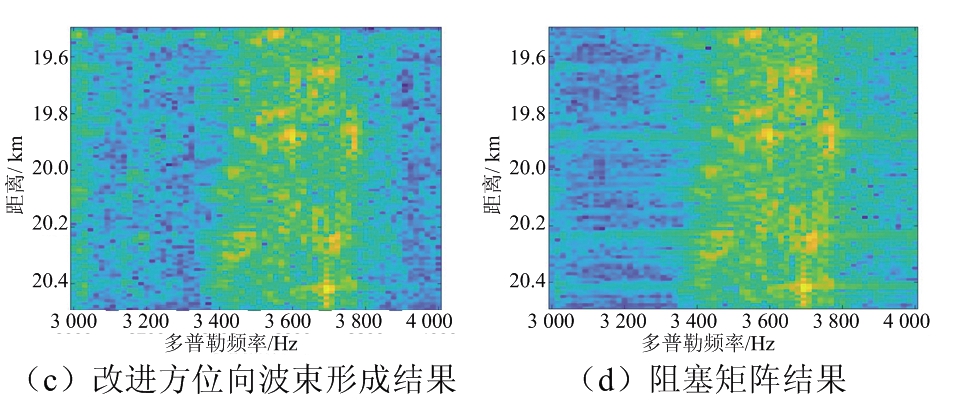
图7 传统算法的处理结果和本文两种算法的处理结果
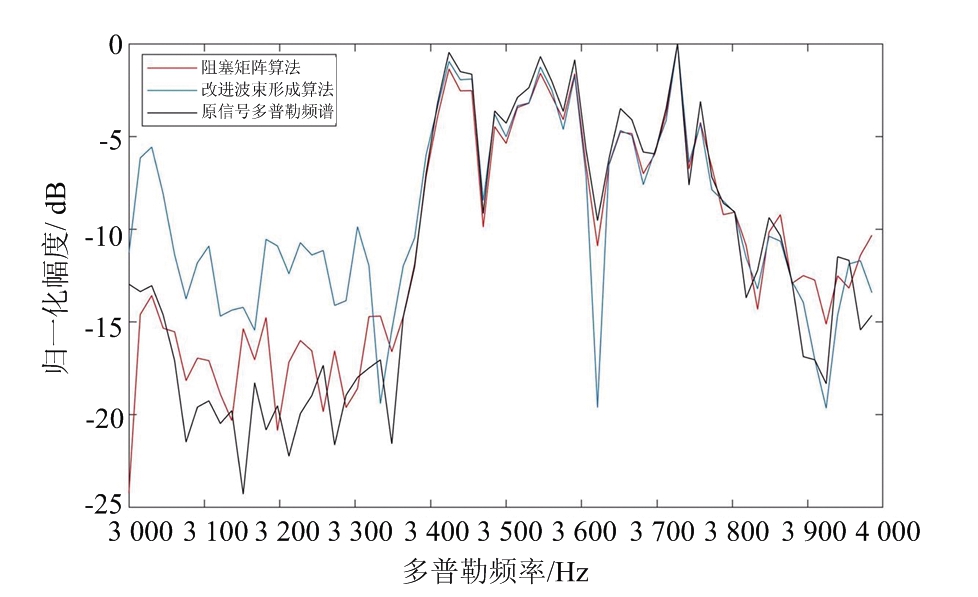
图8 两种算法处理结果性能对比
在第二个实验为了比较恢复多普勒信息的效果,产生了气象目标和地杂波的仿真数据,以用于对气象目标进行检测。首先采用基于多普勒信息的方法对气象目标进行检测,即杂波相位对准(Clutter Phase Alignment, CPA)[3],检测结果如图9(a)所示。CPA接近1意味着地杂波的概率非常高,CPA偏离1意味着这些分量是气象目标。然后将PRF减为原来的一半,并仍使用CPA检测气象目标,结果如图9(b)所示,此时因为多普勒模糊,气象目标和地杂波成分不能被明显地区分。然后使用本文提出的两种方法以恢复数据的多普勒信息。多普勒频谱恢复后的检测结果如图9(c)、(d)所示。对比图9(a)、(c)、(d),证明了本文的两种算法对多普勒频谱信息的恢复是有效的;但两种算法中从恢复的性能考虑,基于阻塞矩阵的算法的恢复效果更好;从工程实现的角度考虑,假设处理距离向Nr,方位向Na,通道个数N大小的数据,数据中出现了K次模糊,对于改进方位向波束形成算法,针对每个模糊成分,计算空间谱需要进行![]() 次矩阵求逆,计算最优权矢量需要
次矩阵求逆,计算最优权矢量需要![]() 次矩阵求逆,因此,总需
次矩阵求逆,因此,总需![]() 次矩阵求逆;但对于阻塞矩阵算法,针对每个模糊成分,估算导向矢量需要2*3*Na次矩阵求逆,计算阻塞矩阵需要Na次矩阵求逆,因此,总需7*K*Na次矩阵求逆,显然基于阻塞矩阵的算法在实现时大量减少了求逆和求和的次数,也就极大地提高了运算速度,便于工程实现。
次矩阵求逆;但对于阻塞矩阵算法,针对每个模糊成分,估算导向矢量需要2*3*Na次矩阵求逆,计算阻塞矩阵需要Na次矩阵求逆,因此,总需7*K*Na次矩阵求逆,显然基于阻塞矩阵的算法在实现时大量减少了求逆和求和的次数,也就极大地提高了运算速度,便于工程实现。
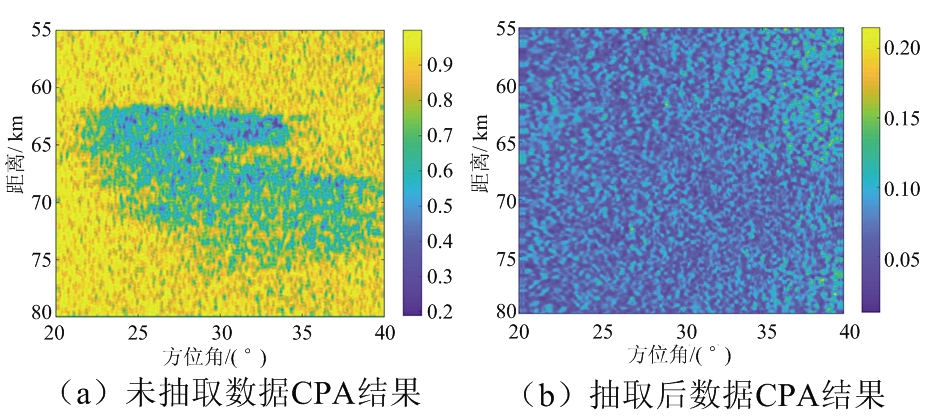
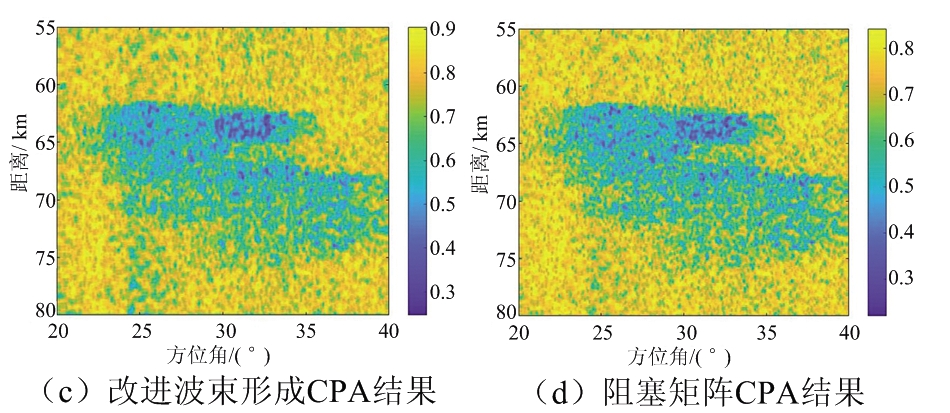
图9 两种算法处理后气象目标的检测结果
4 结束语
本文针对工作在前视快速扫描下的机载气象雷达系统,提出了两种多普勒解模糊算法,分别是:基于改进方位向波束形成的多普勒解模糊算法和基于阻塞矩阵的多普勒解模糊算法。针对两种不同的算法,本文分别给出了两种算法的原理和处理流程。仿真结果表明,这两种算法均可以在低PRF条件下恢复机载气象雷达数据的混叠多普勒频谱,且基于阻塞矩阵的多普勒解模糊算法从性能和工程实现上都要优于基于改进波束形成的多普勒解模糊算法。
[1] GOLBON-HAGHIGHI M H, ZHANG G, DOVIAK R J. Ground Clutter Detection for Weather Radar Using Phase Fluctuation Index[J]. IEEE Trans on Geoscience and Remote Sensing, 2019, 57(5):2889-2895.
[2] GOLBON-HAGHIGHI M H, ZHANG G. Detection of Ground Clutter for Dual-Polarization Weather Radar Using a Novel 3D Discriminant Function[J]. Journal of Atmospheric and Oceanic Technology, 2019, 36(7):1285-1296.
[3] HUBBERT J C, DIXON M, ELLIS S M, et al. Weather Radar Ground Clutter. Part I: Identification, Modeling, and Simulation[J].Journal of Atmospheric and Oceanic Technology, 2009, 26(7):1165-1180.
[4] 赵亮,张友辉. 基于SCI算法的雷达地物杂波识别技术[J]. 民航学报, 2018, 2(5):91-95.
[5] 王宇,吴迪,朱岱寅,等. 基于俯仰维信息的机载气象雷达目标检测[J].雷达科学与技术, 2020,18(6):672-681.
WANG Yu,WU Di,ZHU Daiyin,et al. Meteorological Target Detection Algorithm for Airborne Weather Radar Using Elevation Information[J]. Radar Science and Technology, 2020, 18(6):672-681.(in Chinese)
[6] 倪萌钰,陈辉,王晓戈,等. 星载雷达杂波多普勒特性分析[J].华中科技大学学报(自然科学版), 2021,49(3):46-51.
[7] 崔宏宇. 脉冲多普勒雷达解模糊方法研究[D]. 杭州:杭州电子科技大学,2019.
[8] WAN Jun,TAN Xiaoheng, CHEN Zhanye, et al. Refocusing of Ground Moving Targets with Doppler Ambiguity Using Keystone Transform and Modified Second-Order Keystone Transform for Synthetic Aperture Radar[J]. Remote Sensing, 2021,13(2):177.
[9] 宋健强, 刘云学. 一种基于24 GHz梯形调制LFMCW雷达解多普勒模糊方法[J].空间电子技术,2019,16(3):33-38.
[10] LI Shengyuan, LIU Nan, ZHANG Linrang,et al. Transmit Beampattern Synthesis for MIMO Radar Using Extended Circulating Code[J]. IET Radar, Sonar and Navigation, 2018, 12(6):610-616.
[11] GONZALEZ H A, LIU C, VOGGINGER B, et al. Doppler Ambiguity Resolution for Binary-Phase-Modulated MIMO FMCW Radars[C]∥2019 International Radar Conference, Toulon, France:IEEE,2019:1-8.
[12] 何团,唐波,张玉,等. MIMO-STAP稀疏字典降维方法[J].空军工程大学学报(自然科学版),2020,21(2):71-77.
[13] ROSSUM W V, ANITORI L. Doppler Ambiguity Resolution Using Random Slow-Time Code Division Multiple Access MIMO Radar with Sparse Signal Processing[C]∥ 2018 IEEE Radar Conference , Oklahoma City, OK, USA:IEEE,2018:441-446.
[14] WU Di, ZHANG Yudong, ZHU Daiyin,et al. A Channel Calibration Algorithm Based on Isolated Scatterers for Multi-Channel HRWS-SAR[J]. IEEE Access, 2019, 7:135665-135677.
[15] 郭子越. 多通道SAR高分辨率宽测绘带成像及地面动目标指示技术研究[D]. 南京:南京航空航天大学,2019.




