0 引言
逆合成孔径雷达（Inverse Synthetic Aperture Radar,ISAR）成像作为一种重要的侦测手段，可以全天候、全时段对非合作机动性目标进行成像［1-2］。但是，因为非合作目标的运动补偿建模比较复杂，积累转角和回波多普勒带宽受限，传统的ISAR 成像算法，如Range Doppler（RD）算法，其成像分辨率受到限制，因此研究超分辨ISAR 成像算法具有重要意义。
MUSIC 算法和ESPRIT 算法是两种传统的参数化ISAR 成像算法。但MUSIC 算法的分辨率不是很高，酉ESPRIT 算法是一种超分辨算法，但该算法只能在距离维或者方向维实现超分辨，无法在两个维度同时实现超分辨成像［3］。
压缩感知（Compressed Sensing,CS）理论适合于稀疏参数的高分辨重构［4］，并且ISAR 图像中的强散射点满足稀疏分布特性，所以CS 在超分辨ISAR成像中得到越来越多的研究和应用。稀疏信号恢复的出发点是在L0范数最小化的基础上进行参数重构，但这是一个NP 难问题，压缩感知理论在一定条件下，可以将L0范数最小化约束放宽为L1范数最小化约束，于是涌现出BP 算法［5］、梯度下降算法［6］以及迭代ISTA算法［7］等参数重构算法，但是这些算法在感知矩阵列相关性强的时候性能会出现下降，影响ISAR 成像效果。文献［8］采用光滑函数来近似L0范数并进行稀疏参数重构，但该算法中的正则参数需要人为手动设置，影响了算法的实用性。
文献［9］提出了基于稀疏贝叶斯学习（Sparse Bayesian Learning,SBL）框架的ISAR 成像算法，取得了不错的效果。相比于传统的SMV 模型［10］，MMV-SBL 模型避免了Kron 内积导致的感知矩阵尺寸过大问题，以及大尺寸逆矩阵计算问题［11］。文献［12］提出一种BI-MSBL 算法，该算法利用冗余信息的融合去除径向插值带来的条纹，获得更清晰的ISAR 图像。文献［13］则提出一种LS-SBL算法，利用目标自身的结构特征构建结构化先验模型和参数化字典，对旋转运动目标进行ISAR 成像，取得较为理想的成像效果。文献［14］引入LSM（Laplace Scale Mixture）尺度混合先验模型，并通过拉普拉斯估计（Laplace Approximation,LA）和变分贝叶斯（Variational Bayesian,VB）算法求解散射系数的后验分布，以此得到更稀疏更精确的ISAR图像。
为了在ISAR 成像中更好地压制噪声，消除条纹干扰，提高成像分辨率，本文提出一种基于双向插值处理（Bidirectional Interpolation Process）和频域信息融合（Information Fusion in Frequency Domain）的稀疏贝叶斯学习算法，简称BI-FF SBL 算法。该算法引入LSM 先验来为回波信号构建MMV SBL 模型，并采用LA-VB 算法进行目标散射系数的重构。首先对回波信号分别进行径向和横向插值预处理，将预处理得到的两份数据通过LAVB SBL 算法进行ISAR 成像；然后将得到的两幅ISAR 图像通过二维傅里叶变换进入频域，并将两个二维频谱进行信息融合处理，以消除噪声和条纹干扰的相关信息并保留目标结构信息；最后对融合处理后的频谱进行二维傅里叶逆变换，得到最终的ISAR图像。
1 信号模型
假设已对雷达回波信号作平动补偿，则ISAR成像模型可视为转台模型，ISAR 成像的原理图如图1所示，其中雷达向目标发射线性频率调制（LFM）脉冲。由于雷达到目标中心的距离远远大于目标的尺寸，因此雷达电磁波被视为以平面波的形式照射到目标上，并假定目标以恒定的角速度旋转。
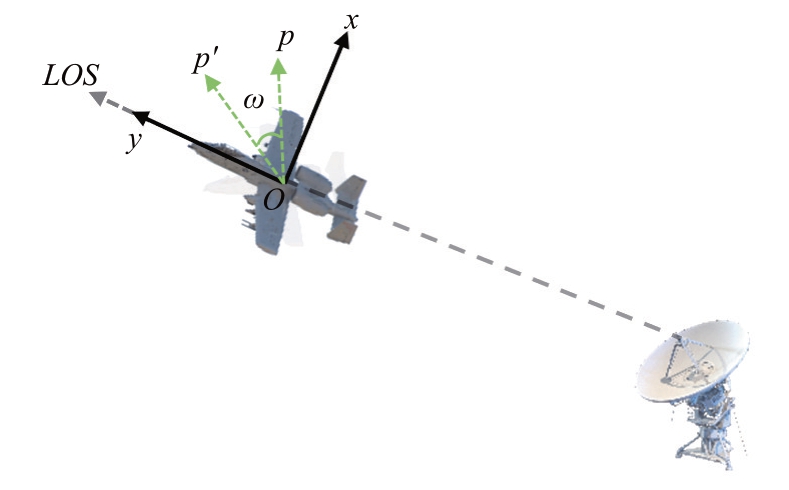
图1 ISAR转台模型
回波HRRP 数据是通过对接收信号进行径向脉冲压缩得到的，其理想点散射中心模型可以表示为
式中:s(θ,f)表示进行径向傅里叶变换后的HRRP数据，θ表示发收信号的目标转角，f表示脉冲发射频率；w(y,x)表示目标散射系数；c 表示电磁波速度；R0表示从雷达到目标中心的远场距离。
对成像的角度和频率，以及二维场景进行离散化处理。在以目标中心为原点的局部坐标系中，散射区域被离散为P行和Q列，得到
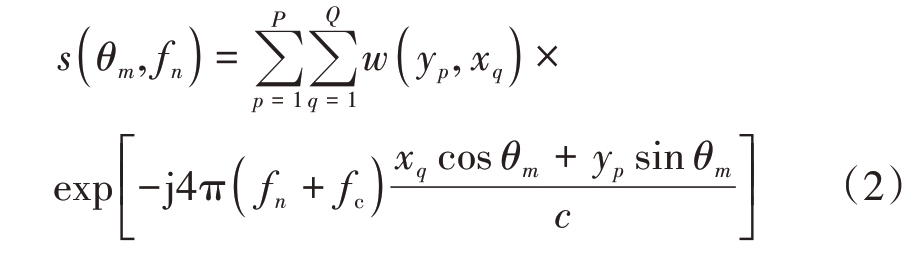
式中:fc 为载波频率；fn 为第n 个离散频率，n=1，2,…, N；θm 为第m 个脉冲对应的目标转角，m=1,2,…,M；w(yp,xq)代表坐标(yp,xq)处的散射系数，其中p=1,2,…,P，q=1,2,…,Q。
将上式经过一系列的推导和化简，并添加环境噪声U，可得到回波信号的矩阵表达式为
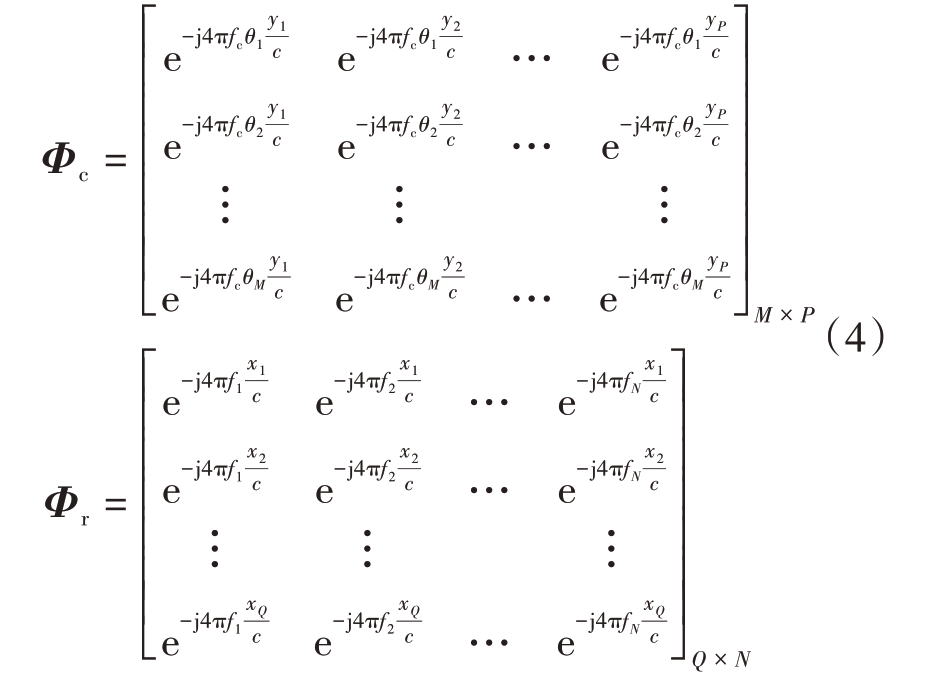
式中，S ∈CM ×N 表示回波信号矩阵，W ∈CP ×Q 表示散射系数矩阵，U ∈CM ×N 表示复高斯白噪声，Φc ∈CM ×P 和Φr ∈CQ ×N 分别表示方向维和距离维的部分傅里叶矩阵，可将其展开为
2 BI-FF SBL算法
本文提出一种基于双向插值处理和频域信息融合的稀疏贝叶斯学习算法，此处简称BI-FF SBL算法，并将其用于高分辨ISAR成像。
2.1 径向插值预处理
为了得到回波信号的MMV 模型，对式（3）两边同时右乘
矩阵（即对距离维作FFT 操作），回波方程改写为
式中，
事实上，式（5）的操作完成了对S 从N 列插值到Q 列的径向（频域）插值和傅里叶逆变换。从式中Y1 的表达可以发现，Y1 第q 列只来自于W 第q 列的回波叠加，所以Y1和W形成列与列的对应关系。
2.2 横向插值预处理
除此之外，对式（3）两边同时左乘
矩阵（即对方向维作FFT操作），回波方程改写为
式中，
式（6）的操作完成了对S 从M 行插值到P 行的横向（多普勒域）插值和傅里叶逆变换。将上式的等号两边均进行转置，得到
可以发现，Y2 的第p 行只来自于W 的第p 行的回波叠加，所以
的第p列对应于WT的第p列，二者形成列与列的对应关系。
2.3 基于LA-VB算法的参数重构
在传统的MMV-SBL算法中，回波信号的MMV模型可以表示为
式中，Y ∈CM ×Q，Φ ∈CM ×P，W ∈CP ×Q 与N ∈CM ×Q分别表示回波信号矩阵、感知矩阵、散射系数矩阵和噪声矩阵。
在稀疏贝叶斯统计模型中，令加性噪声n⋅q 服从零均值复高斯先验
，其中，n⋅q为矩阵N的第q列元素；β为方差的倒数（噪声精确度），服从伽马分布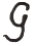
(β; a,b)，模型参数a，b一般设置为10-4。
令矩阵Y的列与列之间统计独立，则Y的似然函数可写为
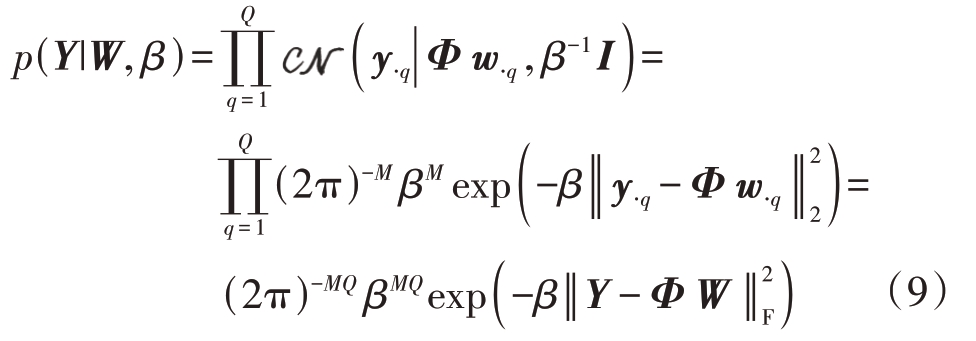
式中，w⋅q 为矩阵W 的第q 列元素
表示Frobenius范数。
由完全贝叶斯推导得出的近似后验概率分布的期望可以用来作为未知参数的后验估计，因此超参数λp,q和β的MAP估计可通过推导得出:
2.4 频域融合
在本文提出的BI-FF SBL 算法中，首先对回波信号矩阵S 分别进行径向插值预处理和横向插值预处理，得到Y1 和
然后利用LA-VB 算法对矩阵Y1 和
分别进行参数重构，得到散射系数矩阵
最后对
进行频域融合处理，得到最终的ISAR图像。频域融合算法的步骤如下:
（a）首先将
归一化处理，得到两幅归一化图像。
（b）然后将
分别进行二维傅里叶变换得到频域图像Z1 与Z2，并且通过平移变换将低频分量移动至图像中心。
（c）融合Z1与Z2而得到最终的频率图像Z:
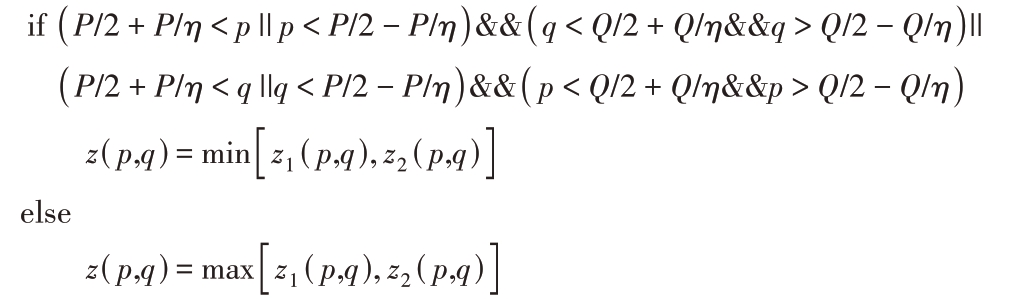
其中，z(p,q)、z1(p,q)和z2(p,q)分别为矩阵Z、Z1和Z2的第p行第q列元素，η为自适应稀疏，取值
。
（d）对频率图像Z 作二维傅里叶逆变换得到最终的ISAR图像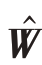
̂。
3 实验结果与对比分析
为了验证BI-FF SBL 算法的有效性，本文基于电磁仿真数据和实测数据完成了ISAR 成像实验。在实验中测试了4种不同的算法，包括R-D（Range-Doppler）算法、L1-BP算法、LA-VB算法以及本文提出的BI-FF SBL 算法，并将不同算法的ISAR 成像结果进行对比。
为了检验不同算法抑制噪声的能力，在仿真数据和实测数据中加入复高斯噪声，合成了信噪比分别为0，5和10 dB的实验数据。
3.1 仿真数据实验
在基于仿真数据的实验中，ISAR 成像目标是A-10攻击机，其CAD模型如图2（a）和（b）所示。回波信号由高频电磁仿真代码生成，入射频率为9.5～10.5 GHz，中心频率为10.0 GHz，带宽为1 GHz，共扫描128 个频率点。入射俯仰角为94°，入射中心方位角为135°，方位角宽度为5.729 6°，共扫描128 个方位角点。得到的回波信号矩阵尺寸为128×128。径向和横向分辨率均为0.15 m，成像面积为19.2 m×19.2 m。
图2 A-10攻击机CAD模型图
实验采用前文所述的4种算法，每种算法均在0，5 和10 dB 三个信噪比下进行ISAR 成像，成像结果如图3所示。
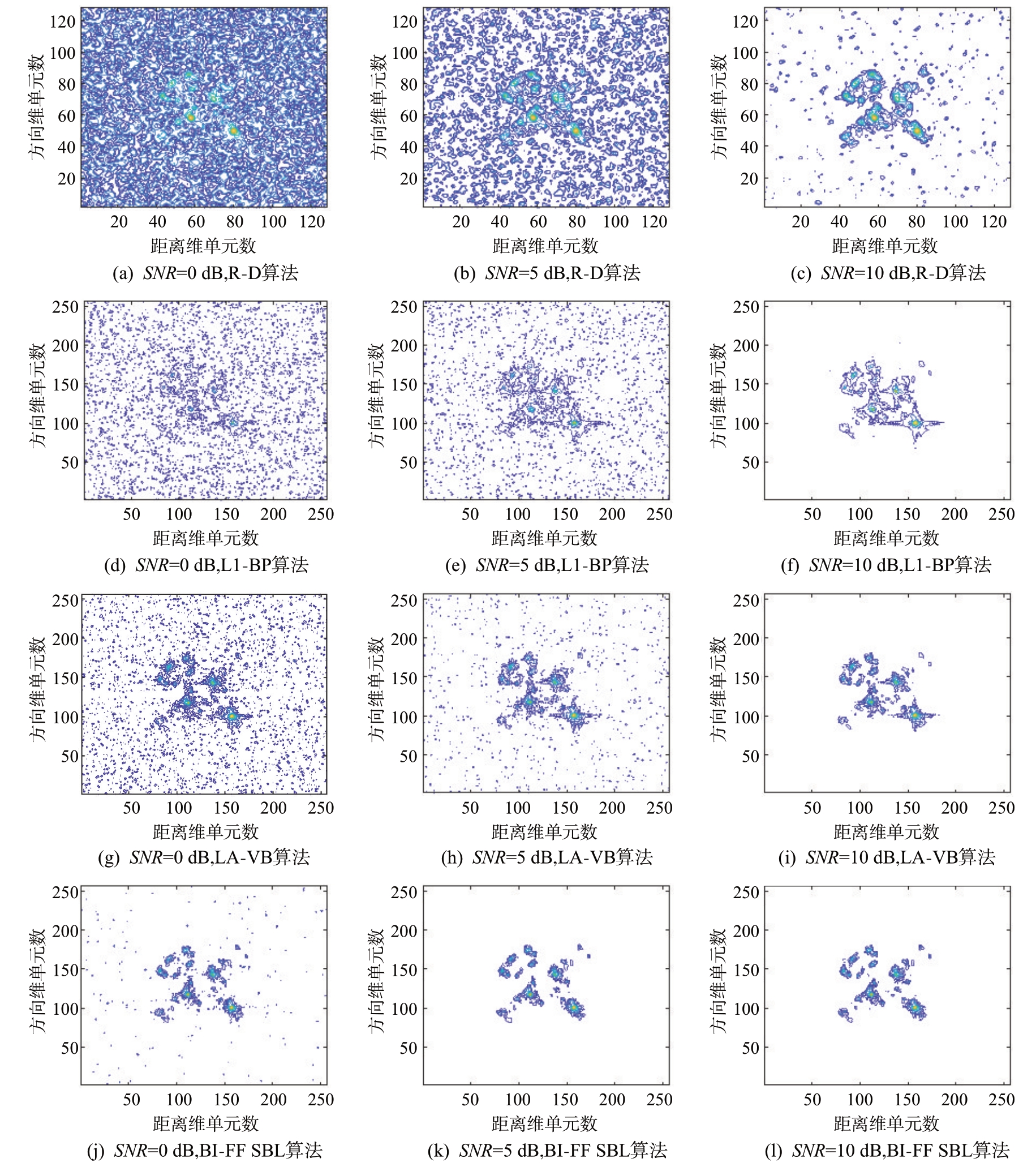
图3 不同信噪比下各类算法的仿真ISAR成像效果图
从图3 可以看出，在信噪比为0 dB 时，由于噪声的影响，传统R-D 算法和L1-BP算法已经近乎失效；LA-VB 算法虽然可以粗略重构出飞机的几何结构，但是ISAR 图像受噪点影响严重，只能模糊地重构出机头和机身处部分强散射点；本文的BIFF SBL 算法可以给出较为清晰的ISAR 图像，虽然图像中也分布有一些噪点，但仍然很好地保留了飞机的几何结构特征。
在信噪比为5 dB 时，各类算法的成像效果均有所提升，但R-D算法所成ISAR图像仍较为模糊，由L1-BP算法和LA-VB算法重构的ISAR图像中存在较多噪点，而BI-FF SBL 算法则可以给出清晰的ISAR图像。
在信噪比为10 dB 时，各类算法所成ISAR 图像均能清晰地体现飞机的几何结构特征。但是R-D算法所成图像分辨率很低，图中仍然存在较多噪点；L1-BP算法所成图像分辨率低于LA-VB 算法和BI-FF SBL算法。
3.2 实测数据实验
实测数据为ISAR 成像系统录取的Yak-42 飞机回波信号，中心频率为5.52 GHz，发射带宽为400 MHz，脉冲重复频率为400 Hz。实验采用的回波信号矩阵的尺寸为128×128，通过添加复高斯白噪声以获取信噪比分别为0，5 和10 dB 的实验数据。
实验采用前文所述的4种算法，每种算法均在0，5 和10 dB 三个信噪比下进行ISAR 成像，成像结果如图4所示。
图4 不同信噪比下各类算法的实测ISAR成像效果图
如图4所示，信噪比为0 dB 时，4 种算法的ISAR 成像结果中都存在不同程度的噪点，其中R-D 算法的成像效果最差；L1-BP 算法和LA-VB 算法所成图像受噪点影响严重，导致机尾处部分结构特征缺失；本文的BI-FF SBL 算法所成图像中虽然存在少量噪点，但依然能较好地体现飞机结构特征。
信噪比为5 dB 时，4 种算法的ISAR 成像效果都有所提高，L1-BP 算法和LA-VB 算法均好于R-D算法。BI-FF SBL 算法效果最好，图像中只有少量噪点且飞机结构特征清晰。
在信噪比为10 dB 时，4 种算法都能给出清晰的ISAR 图像，但3 种超分辨率算法的分辨率明显高于R-D 算法。在L1-BP 算法和LA-VB 算法结果中，均存在较明显的条纹干扰，而BI-FF SBL 算法则很好地去除了条纹干扰，在提高分辨率的同时很好地保留了飞机的几何结构特征。
3.3 图像重构误差实验
传统ISAR 成像算法，如R-D 算法和MUSIC 算法等，其回波数据的尺寸和ISAR 成像的尺寸是一致的，即M=P，N=Q。在超分辨ISAR 成像中，ISAR成像的尺寸可以远大于回波数据的尺寸，即M<P，N<Q。超分辨ISAR 成像可以重构出目标更多的几何结构特征，但也可能导致超分辨重构误差。
本文采用重构信噪比（Reconstruction Signal to Noise Ratio,RSNR）作为指标，来评价超分辨ISAR成像算法的重构误差，其定义如下:
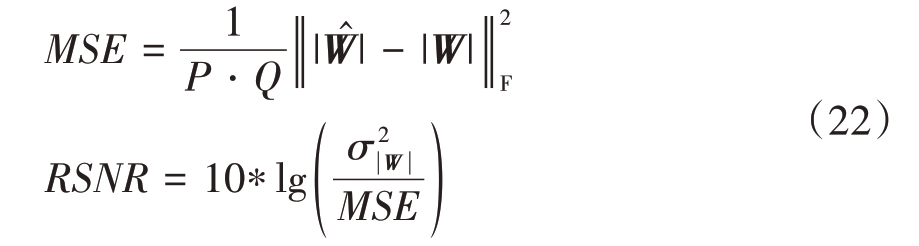
式中:W表示原尺寸ISAR图像，其尺寸与回波数据尺寸相同；
表示原尺寸图像W 的幅值方差；
表示超分辨算法重构的ISAR 图像，其尺寸大于回波数据尺寸。
在该实验中，以A-10 攻击机为ISAR 成像目标，通过高频电磁仿真得到相关回波信号。然后向回波信号中添加高斯白噪声，得到信噪比分别为0，5 和10 dB 的实验数据。该实验对比了BI-FF SBL 算法、L1-BP 算法和LA-VB 算法的RSNR，对比结果如表1所示。对于其中每一种算法，在获取原尺寸图像W 时，M=N=256，P=Q=256；在获取超分辨图像
̂时，M=N=128，P=Q=256。
表1 不同超分辨ISAR成像算法的RSNR对比
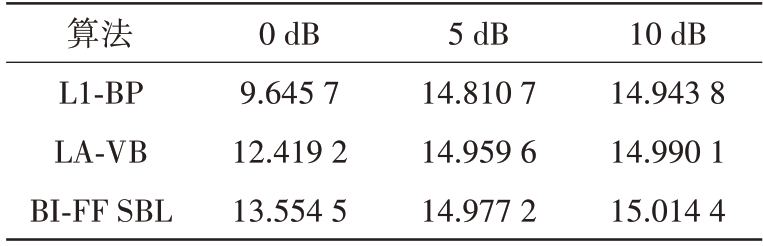
算法L1-BP LA-VB BI-FF SBL 0 dB 9.645 7 12.419 2 13.554 5 5 dB 14.810 7 14.959 6 14.977 2 10 dB 14.943 8 14.990 1 15.014 4
由表1可知，3种超分辨ISAR 成像算法在实验数据信噪比由5 dB降为0 dB时，RSNR 都有明显的下降，其中L1-BP算法最为明显，RSNR下降至10 dB以下。BI-FF SBL 算法在信噪比为10 dB 时，RSNR可以达到15.01 dB，且在信噪比下降至0 dB 时，RSNR 依旧可以保持在13 dB 以上。由此可见BIFF SBL算法的重构误差明显低于L1-BP算法和LAVB算法。
4 结束语
为了在ISAR 成像中更好地压制噪声，消除条纹干扰，提高成像分辨率，本文提出一种基于双向插值处理和频域信息融合的稀疏贝叶斯学习算法，即BI-FF SBL 算法。为了验证BI-FF SBL 算法的效果，本文进行了基于仿真数据和实测数据的ISAR 成像实验，并将实验结果与其他3 种ISAR 成像算法进行对比，发现BI-FF SBL 算法在压制噪声和去除条纹干扰方面具有明显的优势，且能提供更高的ISAR 成像分辨率。重构误差实验结果表明，相比于其他两种超分辨ISAR 成像算法，BI-FF SBL算法的重构误差更低。
本文BI-FF SBL 算法的不足是需要更多的计算时间。跟利用EM 算法进行参数重构的传统SBL 算法相比，LA-VB 算法在参数重构时，需要计算高斯一阶绝对矩，其中包括多次计算库默尔函数，导致运算量增加。本文的BI-FF SBL 算法为了增强压制噪声的能力，进行了两次插值预处理，再基于LA-VB 算法进行两次参数重构，导致计算时间增加。后续工作将探索计算复杂度更低的ISAR成像算法，在保留ISAR 成像效果的同时力求降低运算时间。
［1］曾涛，温育涵，王岩，等.合成孔径雷达参数化成像技术进展［J］.雷达学报，2021，10（3）:327-341.
［2］周子铂,王鑫奎,蔡万勇，等.联合时频分析和谱估计的机动目标ISAR 成像［J］.雷达科学与技术，2021，19（4）:393-402.
［3］冯德军，王雪松，陈志杰，等.酉ESPRIT 超分辨ISAR 成像方法［J］.电子学报，2005，33（12）:2097-2100.
［4］DONOHO D L.Compressed Sensing［J］.IEEE Trans on Information Theory,2006,52（4）:1289-1306.
［5］TANAY S,SHWETABH S,SWANAND K,et al.An Improved Algorithm for Basis Pursuit Problem and Its Applications［J］.Applied Mathematics and Computation,2019,355:385-398.
［6］RONG Jiajia,WANG Yong,HAN Tao.Iterative Optimization-Based ISAR Imaging with Sparse Aperture and Its Application in Interferometric ISAR Imaging［J］.IEEE Sensors Journal,2019,19（19）:8681-8693.
［7］ROSEBROCK F,ROSEBROCK J,CERUTTI-MAORI D,et al.ISAR Imaging by Integrated Compressed Sensing,Range Alignment and Autofocus［C］//13th European Conference on Synthetic Aperture Radar,Online:VDE,2021:1-5.
［8］YIN Zhiping,LU Xinfei,CHEN Weidong.Echo Preprocessing to Enhance SNR for 2D CS-Based ISAR Imaging Method［J］.Sensors,2018,18（12）:4409.
［9］LIU Hongchao,JIU Bo,LIU Hongwei,et al.Super-Resolution ISAR Imaging Based on Sparse Bayesian Learning［J］.IEEE Trans on Geoscience and Remote Sensing,2014,52（8）:5005-5013.
［10］WU Kejiang,CUI Wei,XU Xiaojian.Superresolution Radar Imaging via Peak Search and Compressed Sensing［J］.IEEE Geoscience and Remote Sensing Letters,2022,19:1-5.
［11］DING Yacong,CHIU Sungen,RAO B D.Sparse Recovery with Quantized Multiple Measurement Vectors［C］//2017 51st Asilomar Conference on Signals,Systems,and Computers,Pacific Grove,CA,USA:IEEE,2017:845-849.
［12］JIANG Zhongjin,ZHAO Shumin,CHEN Xing,et al.A Novel MMV Based SBL Algorithm for High Resolution ISAR Imaging［J］.Digital Signal Processing,2021,117（3）:103162.
［13］XU Gang,YANG Lei,BI Guoan,et al.Enhanced ISAR Imaging and Motion Estimation with Parametric and Dynamic Sparse Bayesian Learning［J］.IEEE Trans on Computational Imaging,2017,3（4）:940-952.
［14］ZHANG Shuanghui,LIU Yongxiang,LI Xiang,et al.Variational Bayesian Sparse Signal Recovery with LSM Prior［J］.IEEE Access,2017,5:26690-26702.
［15］ZHANG Shuanghui,LIU Yongxiang,LI Xiang.Fast Sparse Aperture ISAR Autofocusing and Imaging via ADMM Based Sparse Bayesian Learning［J］.IEEE Trans on Image Processing,2020,29:3213-3226.
