0 引 言
随着雷达系统的日益复杂,开展外场目标特性测量时存在干扰程度大、周期长、保密性差等一系列问题[1-2]。相比而言,室内场辐射式仿真通过将硬件设备和等效实物相结合,通过构建仿真系统,可以有效规避上述问题。但是,当采用长脉冲信号进行目标测量时,其脉宽对应的传播距离远大于暗室尺寸,发射信号与目标回波会在接收天线处发生耦合,无法准确提取目标的回波特征。
间歇采样理论的提出为解决这一问题提供了新思路[3-4]。目前,国内已有学者针对雷达脉冲信号实现暗室测量的相关方法展开了研究,文献[5-6]分析了均匀、伪随机两种间歇收发信号特性,较好地解决了产生虚假目标的问题。对于间歇收发造成的信号缺失,可以通过回波重构进行解决。目前主要的回波重构方法有两种:时频滤波法和压缩感知法。其中时频滤波法针对线性调频(Linear Frequency Modulation,LFM)信号,压缩感知法则是根据信号的稀疏特性,通过构造观测矩阵对脉冲编码调制(Pulse Code Modulation, PCM)信号进行重构[7-10]。但在噪声条件下,以上方法重构后的回波精度有所降低。因此,如何减弱噪声带来的影响,研究不稳定条件下的回波重构方法对目标特性测量具有重要意义。
在众多去噪算法中,小波变换不仅能够表征信号在时域和频域的局部特性,而且具备多分辨率分析的特点,在去噪方面表现出明显的优势。目前常用的小波去噪方法有:模极大值去噪法、相关性去噪法和小波阈值去噪法等。传统的小波阈值去噪主要采用软、硬阈值函数,但硬阈值函数存在不连续性的缺点,会产生伪吉布斯现象。软阈值函数虽然连续性、平滑性较好,但小波系数存在固定偏差,二者都会导致重构信号的精度有所下降[11-12]。文献[13-16]对传统阈值函数进行了优化和改进,但仍然存在不连续和固定偏差的缺陷。
针对上述问题,本文以室内场辐射式仿真为背景,首先分析间歇收发原理和LFM 信号的间歇收发特性,给出了小波阈值去噪的具体步骤。其次,基于软、硬阈值函数的缺点,对阈值函数进行了优化和改进。最后,阐述了雷达脉冲间歇收发回波的联合重构方法流程,并结合仿真及实验数据验证了该方法的可行性。
1 间歇收发基本原理
1.1 间歇收发流程
间歇收发处理过程如图1 所示,其实质是通过交替控制射频开关对原始信号进行采样,在脉冲信号开始发射一段时间后,将射频开关切换至接收通道,开始接收回波信号,待接收完毕后再次继续发射雷达信号,交替往复,直至信号发射完毕。
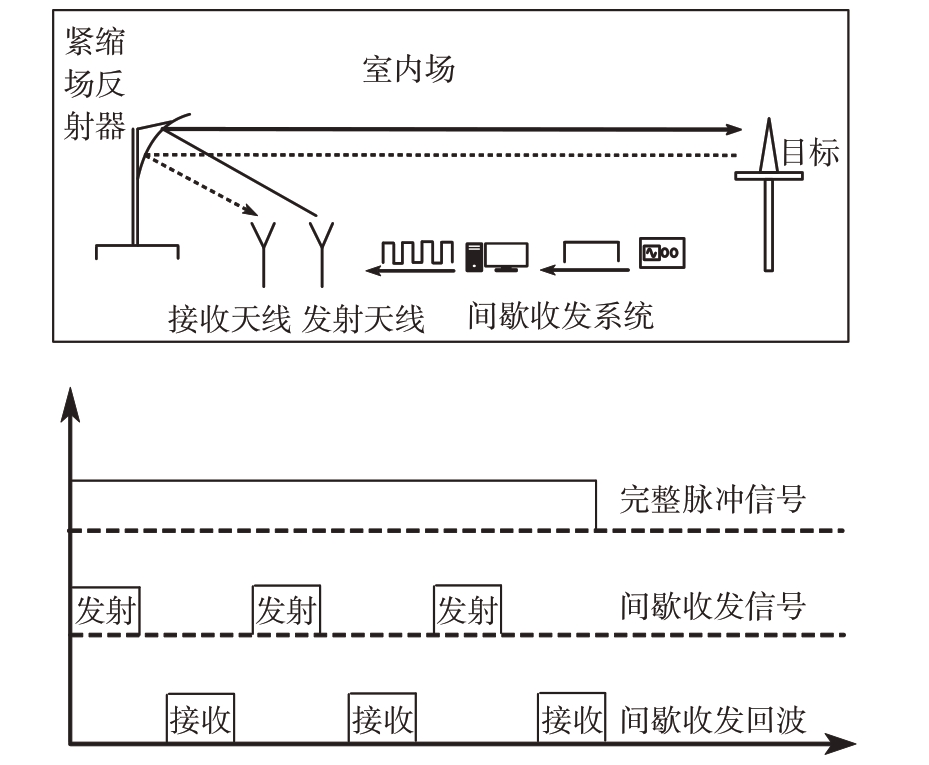
图1 间歇收发流程
间歇收发信号的数学模型可以等效为理想的周期矩形脉冲串,如图2所示。
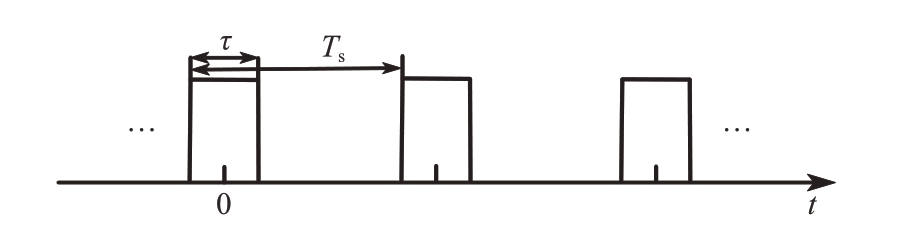
图2 间歇收发信号
其表达式可以写成
式中,τ 为间歇收发信号的脉宽,Ts 为间歇收发信号的周期,rect(·)为矩形脉冲信号,*代表卷积运算。对脉冲信号进行间歇收发处理,其实质为脉冲信号与p(t)相乘。
1.2 LFM信号间歇收发特性
LFM 信号因具备大时宽带宽积的特点而被广泛应用于雷达探测中。LFM信号的数学表达式为
式中,fc 为载波频率,K =(B/T)为调制斜率,T 为LFM 信号脉冲宽度,B 为信号带宽。经1.1 节分析可知,间歇收发处理后的LFM信号时域表达式为
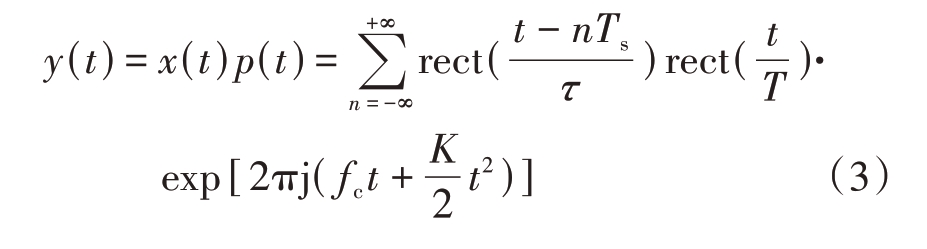
对式(3)进行傅里叶变换,可以得到y(t)的频域表达式为
式中,S( f)为LFM 信号频谱。由式(3)、(4)可以看出,在时域上,间歇收发处理相当于以Ts 为周期对原信号的波形进行采样。在频域上,其频谱是原信号频谱的周期延拓,但幅度大小受限于辛克函数的包络和间歇收发信号的占空比。
2 小波阈值去噪
2.1 小波阈值去噪原理
小波阈值去噪是通过构造不同的小波基函数对噪声信号逐步进行多尺度的细化分析,具有平移、伸缩的特性,是一种局部的时频分析方法。文献[17-18]提出了一种多分辨分析的算法,即Mallat 算法。采用此算法分解后的噪声信号在小波域上的数学特征可以区分为两部分:一部分是小波系数幅值较大的有用信号,另一部分是小波系数幅值较小的噪声信号。利用这一性质,选择适当的阈值和阈值函数对分解后的小波系数进行筛选,就可以有效地滤除噪声。最后对筛选后的信号进行小波逆变换,就可以达到消除噪声的目的。
小波阈值去噪的具体步骤为:
1)根据噪声信号特点选取合适的小波基函数和分解层数对待处理信号进行小波分解,得到分解后的小波系数。
2)确定阈值和阈值函数进行小波系数的阈值量化处理。
3)对处理后的系数进行小波逆变换,重构信号。
小波阈值去噪流程框图如图3所示。
图3 小波阈值去噪流程
2.2 传统阈值函数
常见的阈值函数最早由Donoho 等人提出[19],主要有硬、软阈值函数两种。其中硬阈值函数表达式为
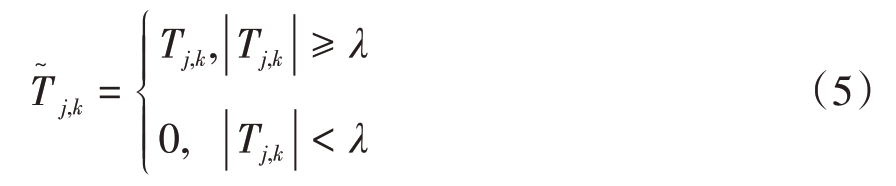
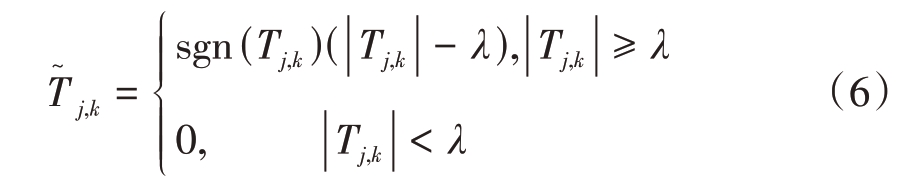
软阈值函数表达式为
式中,Tj,k 为含噪声信号的小波变换系数,T͂j,k 为阈值量化后的小波系数,λ为小波系数阈值。
硬阈值函数的基本处理思路是:通过设定阈值,将所有幅值小于阈值的小波系数全部置0,而幅度大于阈值的系数则全部保留。在软阈值处理中,则是将高于阈值的部分减去阈值后向0收缩。
传统的阈值函数虽然对去噪处理具有明显的效果,但二者本身存在着一些固有的缺陷。硬阈值函数在阈值处不连续,在信号突变的地方会产生较大的震荡。软阈值函数虽然连续性较好,但估计的小波系数存在有偏性,处理后的信号会可能出现失真。
2.3 阈值函数的优化与改进
针对传统阈值函数存在的问题,本文在软、硬阈值函数的基础上对其进行了优化和改进,优化后的函数表达式为
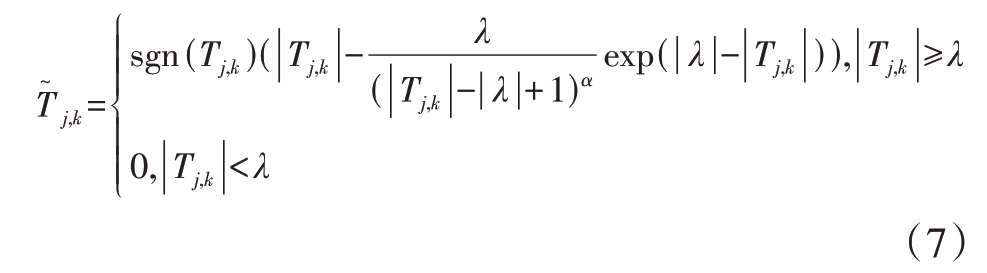
由式(7)可以看出,改进后阈值函数具有以下性质:
1)连续性:在阈值点处,![]() 因此函数是连续的,弥补了硬阈值函数不连续的缺点。
因此函数是连续的,弥补了硬阈值函数不连续的缺点。
2)奇偶性:在定义域范围内,改进阈值函数满足奇函数条件,对正负信号处理效果相同。
3)参数可调节性:优化后的阈值函数含有可调节参数α,通过改变参数的大小,能够使得阈值函数在![]() 的范围内渐近线更快地靠近硬阈值函数,克服了软阈值存在恒定偏差的问题,可以有效消除处理后信号的失真,提高去噪性能。
的范围内渐近线更快地靠近硬阈值函数,克服了软阈值存在恒定偏差的问题,可以有效消除处理后信号的失真,提高去噪性能。
3种函数图像如图4所示。
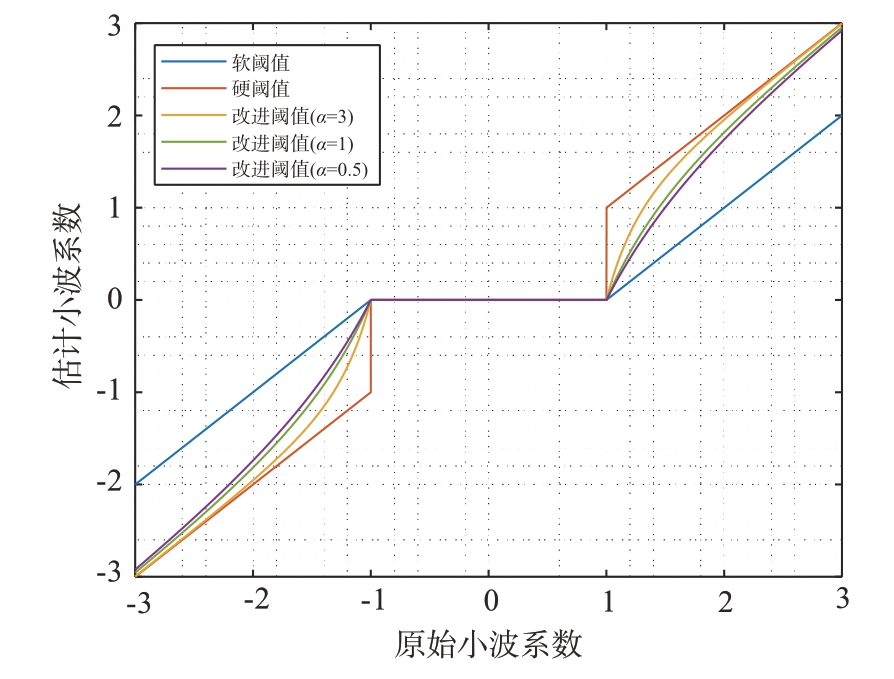
图4 不同阈值函数对比
3 间歇收发回波联合重构
3.1 噪声背景下的目标间歇收发回波
在室内场测量时,目标的回波信号中不可避免地存在噪声干扰。雷达接收机的噪声来源主要分为两种:内部噪声和外部噪声。对于噪声信号,可以等效为随机序列进行建模。由于内部噪声远大于外部噪声,且主要由热噪声构成。因此,含噪声的雷达回波信号具体表现为
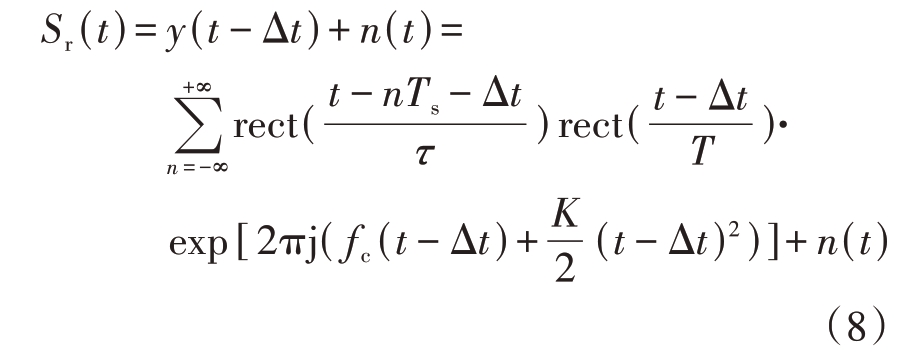
式中,y(t - Δt)为目标回波,n(t)为概率密度函数服从正态分布的高斯白噪声信号,Δt = 2R c 为回波时延,c为光速,R为目标到天线距离。
3.2 联合重构方法
间歇收发回波的联合重构方法具体步骤为:首先对含噪声回波进行小波分解,然后利用改进阈值函数进行去噪处理,最后根据回波信号的匹配滤波输出特性,将纯净信号进行回波重构。
将小波变换作用于式(8)可得
式中,TSr(j,k)为小波系数,ψ(2-jn - k)为小波基函数。式(9)中的小波基函数通常没有具体的解析表达式,所以通常采用Mallat 算法进行处理,Sr(t)的分解结果如图5所示。
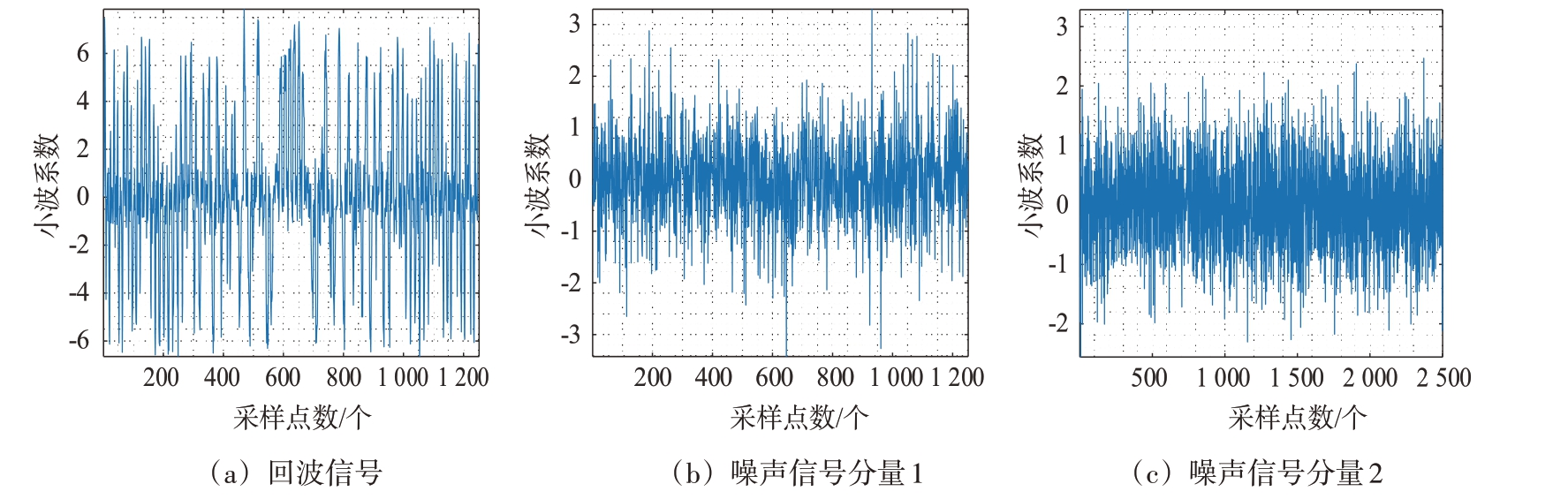
图5 小波分解结果
由于纯净信号中包含目标的有用信息,所以经小波分解后的小波系数较大,而噪声部分分解后的小波系数较小,且小于目标回波的分解系数。因此,通过选择合适的门限,对大于门限的分解系数进行保留;对小于门限的分解系数予以舍弃,最后将滤波后的结果进行小波逆变换,即可得到纯净信号,记为y'(t)。
由1.2 节可知,LFM 信号经间歇收发处理后,时域上相当于被部分采样,导致回波信号的能量和信息被截断,因此,从时域上进行回波重构的难度较大。在接收端对回波信号进行脉冲压缩处理,可以清晰观察到离散的距离像特性。对于完整的LFM 回波信号,匹配滤波器的时域形式为hT(t) = x*(t0 - t),经过匹配滤波后的输出回波表达式为
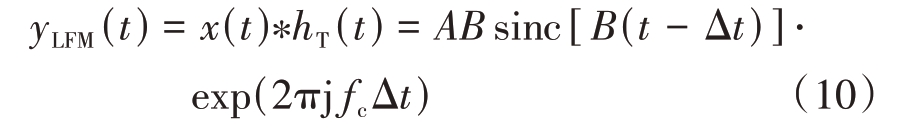
用相同的匹配滤波器对小波阈值去噪后的间歇收发回波进行脉冲压缩处理,可得输出表达式为
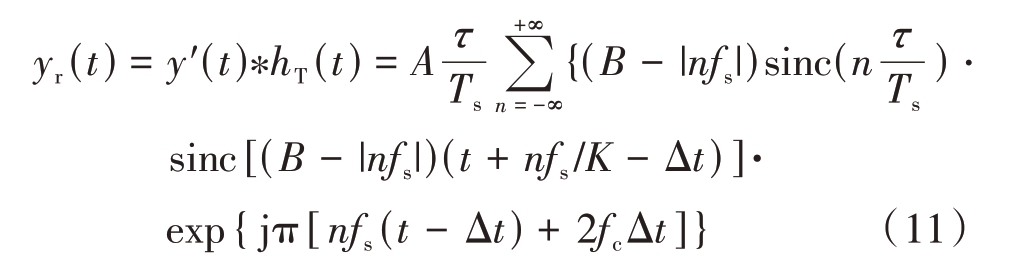
对比式(10)、(11)可以发现,去噪后回波信号的匹配滤波输出在幅度上表现为sinc 函数的加权求和,同时还受限于间歇收发调制参数τ和Ts。当n = 0 时,间歇收发回波与完整回波的脉压输出仅在目标位置峰值处存在差异,差值为τ/Ts。
通过时域加窗可以提取出间歇收发回波的匹配滤波输出主峰,加窗时还应注意窗函数的宽度应小于相邻脉压的间隔距离,由式(11)可推导出窗函数表达式为
此时,加窗后的匹配滤波结果为
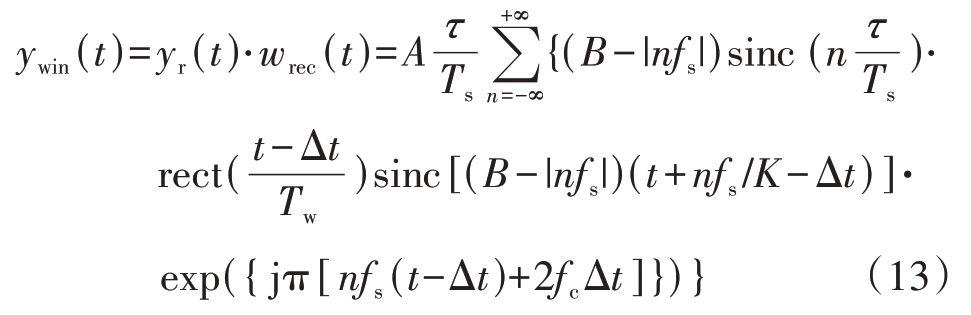
由于幅度上存在差异,式(13)的结果通过匹配滤波器的逆变换后,再经过能量补偿就可以实现对完整回波信号的重构,即
式中,H( f)为匹配滤波器的频域形式,F(·)代表傅里叶变换,E = Ts/τ为补偿的能量。
综上所述,基于小波变换的雷达脉冲间歇收发回波联合重构方法如图6所示。
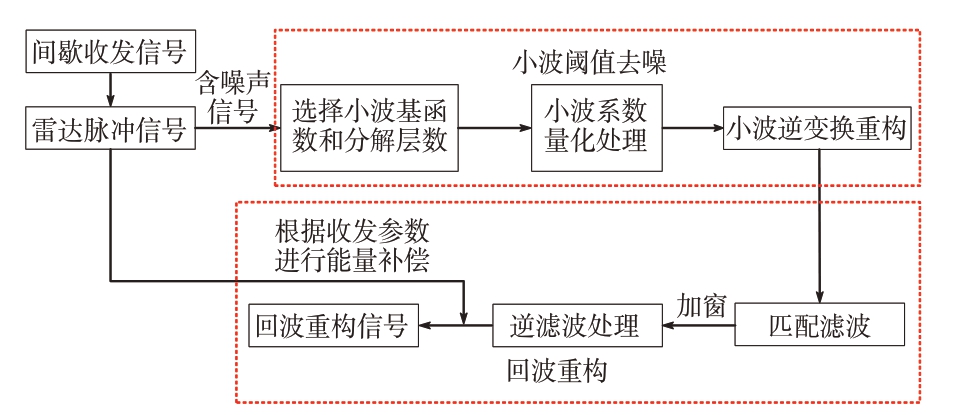
图6 联合重构流程图
4 仿真及实验结果
4.1 间歇收发回波去噪性能分析
本节设计含高斯白噪声的间歇收发回波信号进行仿真实验,以信噪比(Signal-Noise Ratio,SNR)和均方误差(Mean-Square Error,MSE)作为评价指标,测试不同阈值函数的回波去噪性能。目前,常用的小波基函数有Harr 小波、dbN 小波和Sym 小波。实验中选取对称性和正则性好,且不产生相位畸变的dbN 小波进行验证。仿真参数如表1 所示,仿真结果如图7所示。
表1 仿真参数设置

主要参数LFM脉宽T、带宽B ITR脉宽τ、周期Ts目标距离小波基函数分解层数信噪比量值50 μs、5 MHz 0.1 μs、0.5 μs 45 m db2 3-5 dB
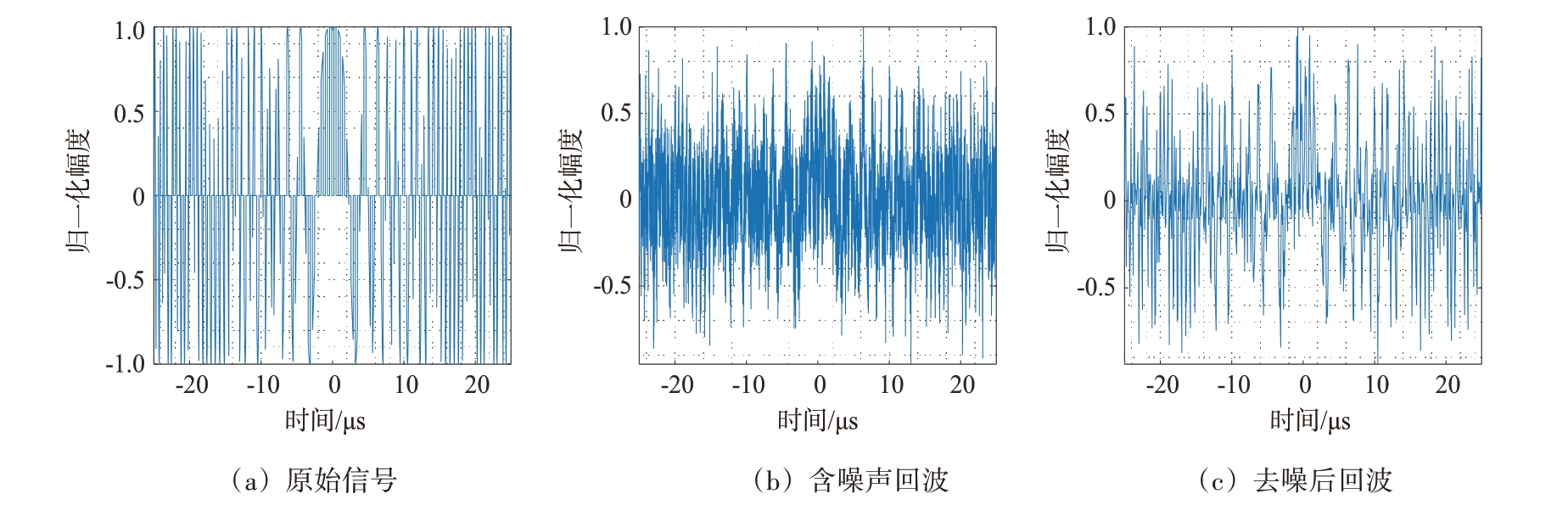
图7 去噪结果
图7为去噪前后回波的时域波形,对比图7(b)和图7(c)可以发现,改进阈值函数不仅能够有效减少间歇收发回波中产生的毛刺和震荡,而且去噪后的信号与原始信号的逼近程度较高。
为定量分析本文中改进阈值函数在不同信噪比条件下的回波去噪性能,用SNR 和MSE 作为评价指标进行对比,其表达式如下:
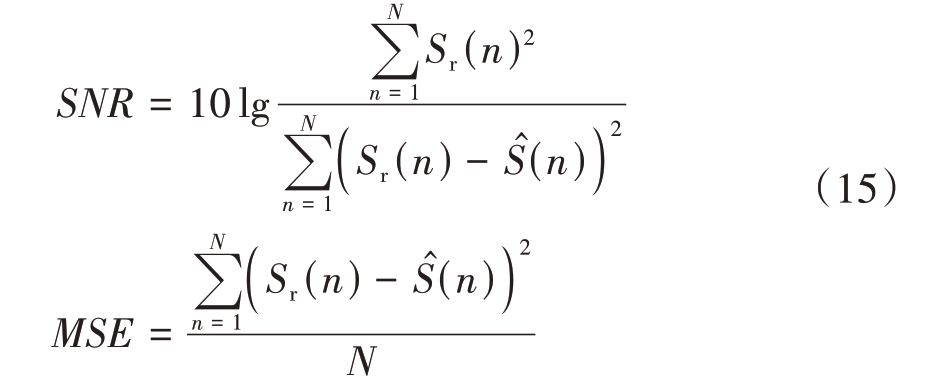
式中,Sr(n)为原始信号,![]() 为小波阈值去噪后信号,N为信号长度。
为小波阈值去噪后信号,N为信号长度。
由表2 和表3 数据可以看出,当输入信噪比在区间[-10 dB,0 dB]范围内变化时,3 种阈值函数均能达到较好的去噪效果。在相同条件下,相比传统阈值函数,改进阈值函数的SNR 最大,MSE 最小,去噪效果最优。
表2 去噪效果SNR对比 dB
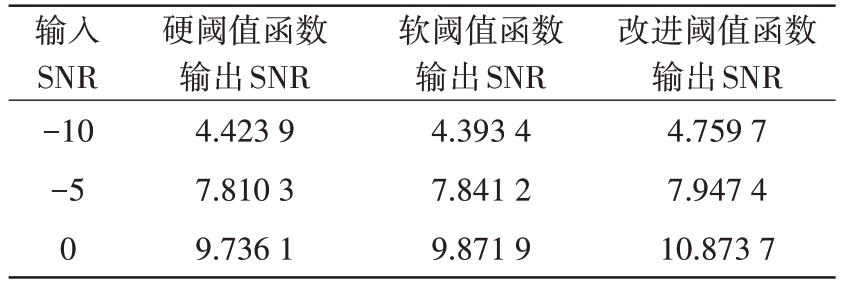
输入SNR-10-5 0硬阈值函数输出SNR 4.423 9 7.810 3 9.736 1软阈值函数输出SNR 4.393 4 7.841 2 9.871 9改进阈值函数输出SNR 4.759 7 7.947 4 10.873 7
表3 去噪效果MSE对比
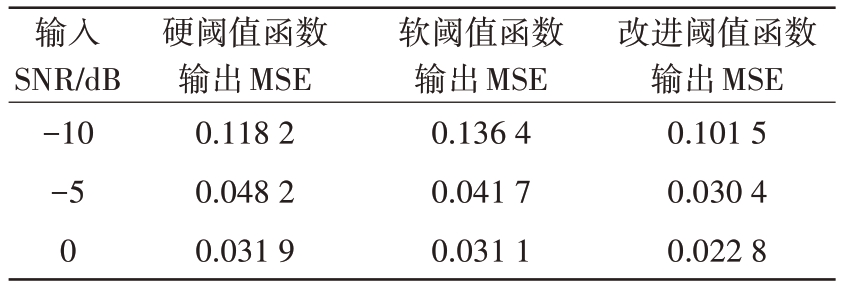
输入SNR/dB-10-5 0硬阈值函数输出MSE 0.118 2 0.048 2 0.031 9软阈值函数输出MSE 0.136 4 0.041 7 0.031 1改进阈值函数输出MSE 0.101 5 0.030 4 0.022 8
4.2 间歇收发回波联合重构方法分析
小波阈值去噪后的回波匹配滤波输出结果如图8(a)所示,与完整信号相比,二者主峰位置相同,仅存在幅度上的差异,其主峰与相邻虚假峰值之间的距离为ΔR = cfs/2K = 2 500 m,与式(11)结果一致。图8(b)为匹配滤波输出加窗结果,根据式(12)可以确定窗函数的宽度,在时域上对主峰进行截取。
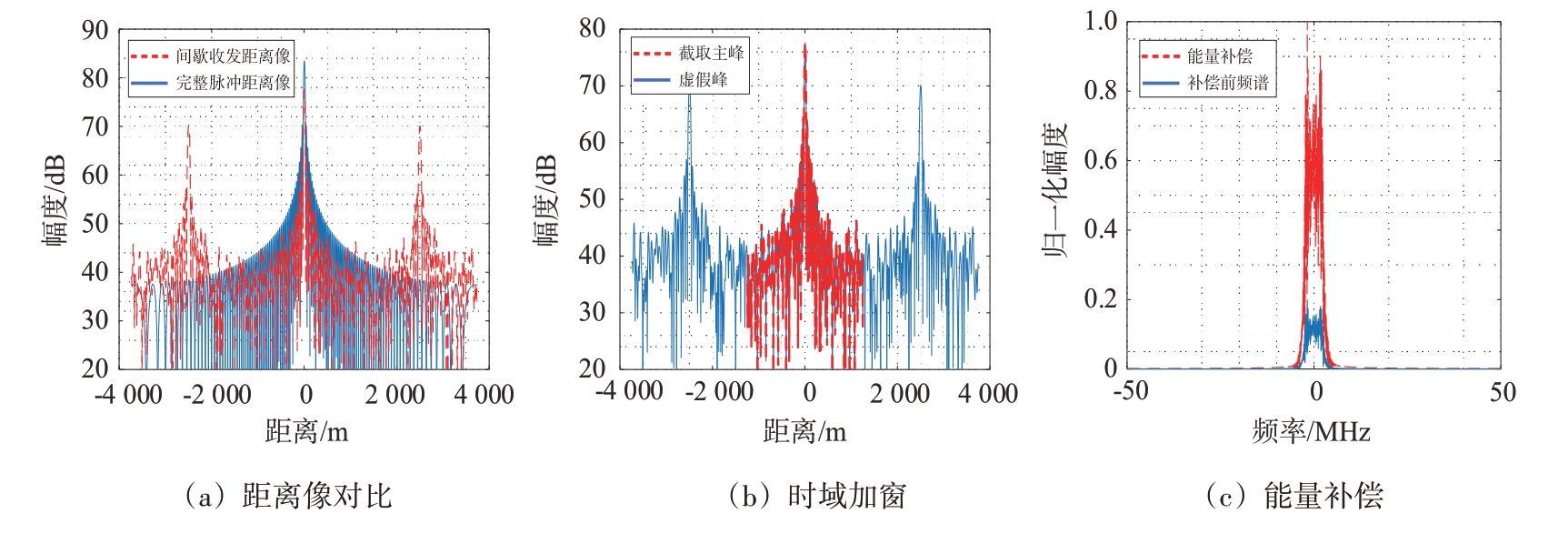
图8 联合重构结果
通过对提取后的主峰信息进行逆滤波可以恢复原始信号,由于间歇收发会导致脉冲信号的部分能量损失,重构时需要对损失的部分能量进行补偿,图8(c)为逆滤波和能量补偿后的频谱,其频谱与完整回波频谱基本一致。
经能量补偿后,利用傅里叶反变换对时域波形进行重构,图9(a)为联合重构回波的仿真结果。对比图9(b)可以发现,经小波变换处理后的重构回波包含完整回波的大部分信息,且与完整回波逼近程度更高,证明该联合重构方法对提升室内场间歇收发重构回波的相似度具有良好的效果。
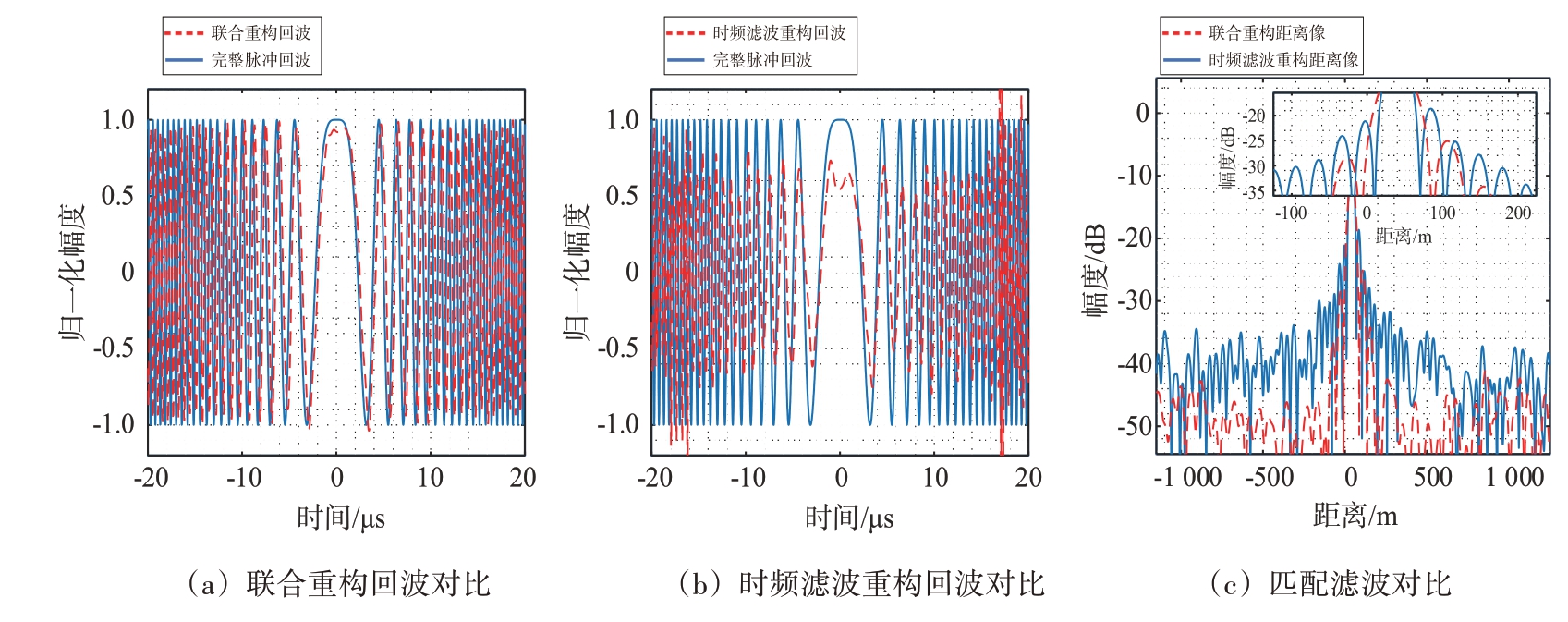
图9 回波和距离像对比
图9(c)为对重构回波进行匹配滤波的结果,从局部放大图中可以发现,联合重构回波的最高距离像旁瓣可以抑制到-25 dB 以下,有利于提升对弱目标的检测能力,但是会导致主瓣分辨率的损失以及峰值的降低。
4.3 重构性能分析
本文选取波形相似系数ρ 和均方误差MSE 作为评价指标。其中ρ 越接近1,MSE 越接近0,重构性能越好,具体表达式为
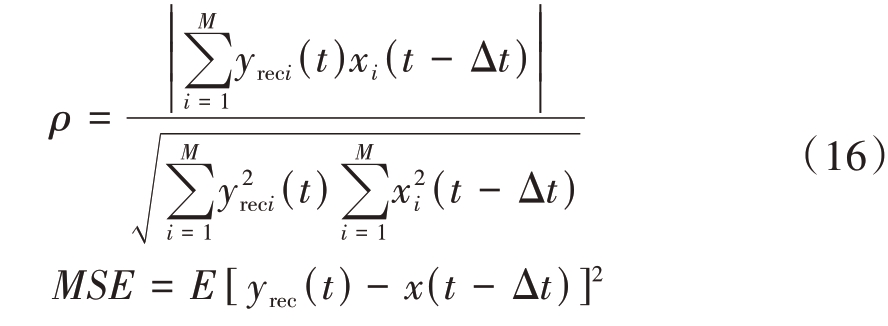
式中,yrec(t)为重构信号,x(t - Δt)为完整LFM 回波信号。
将联合重构法与时频滤波重构法进行对比,仿真结果如图10所示。图10(a)中,随着信噪比的增加,二者波形相似系数逐渐趋近于1。经小波变换处理后的波形相似系数整体上要高于时频滤波法的重构回波,且在低信噪比条件下,改进阈值函数的相似系数最高。由图10(b)可知,当信噪比在区间-20~0 dB 内变化时,联合重构回波的均方误差均小于时频滤波重构回波,且改进阈值函数效果最好。
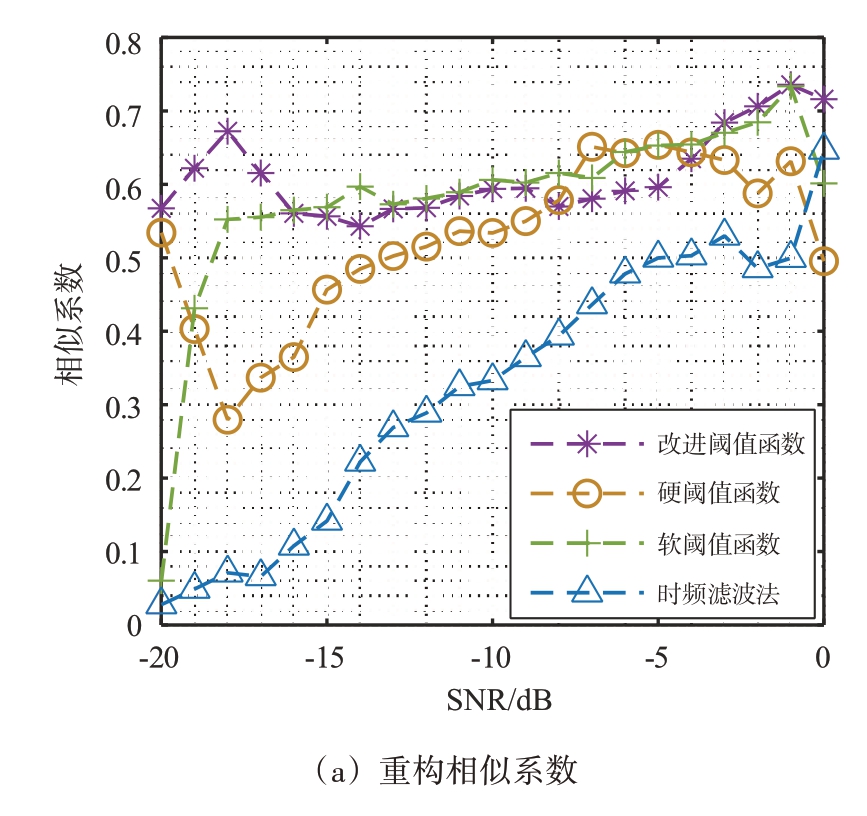
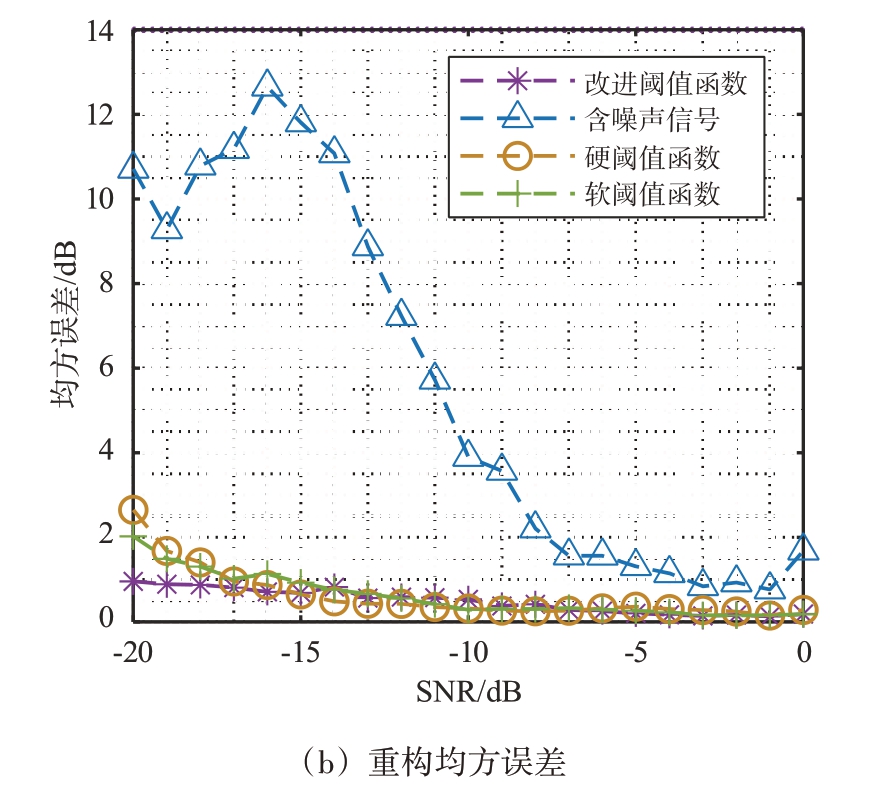
图10 回波重构性能
综上所述,本文提出的联合重构方法能提高重构回波与完整回波的相似度,减小重构误差,提升重构性能。
4.4 暗室实测数据分析
为模拟室内场间歇收发方法对雷达目标的探测过程,验证联合重构方法的有效性,设置实验场景如图11所示,实验参数如表4所示。
表4 实验参数设置

主要参数LFM脉宽T、带宽B ITR脉宽τ、周期Ts目标距离小波基函数分解层数量值50 μs、1 MHz 0.02 μs、0.1 μs 8.7 m db2 3

图11 实验场景
首先,利用Matlab 将间歇收发信号写入任意波形发生器中,经上变频器形成射频信号,并通过功放增加射频信号的发射功率。在接收端,使用天线对角反射器的回波进行接收,接收到的信号经下变频器进行下变频处理。最后,将示波器作为回波信号的采集设备,采集后导入电脑分析即可,完成雷达脉冲信号空间辐射的全过程闭环实验。
图12(a)为对示波器采集的回波进行小波阈值去噪后的中频信号,由于测试线缆及硬件仪器的不稳定性,虽然接收到的回波不是理想矩形脉冲串调制,但回波包络与LFM 信号包络起伏特性相同。由上文分析可知,相邻脉冲串之间除了包含目标回波信号,还包含发射天线到接收天线的直达波信号,因此需要在时域进行截断,滤除直达波保留目标回波。
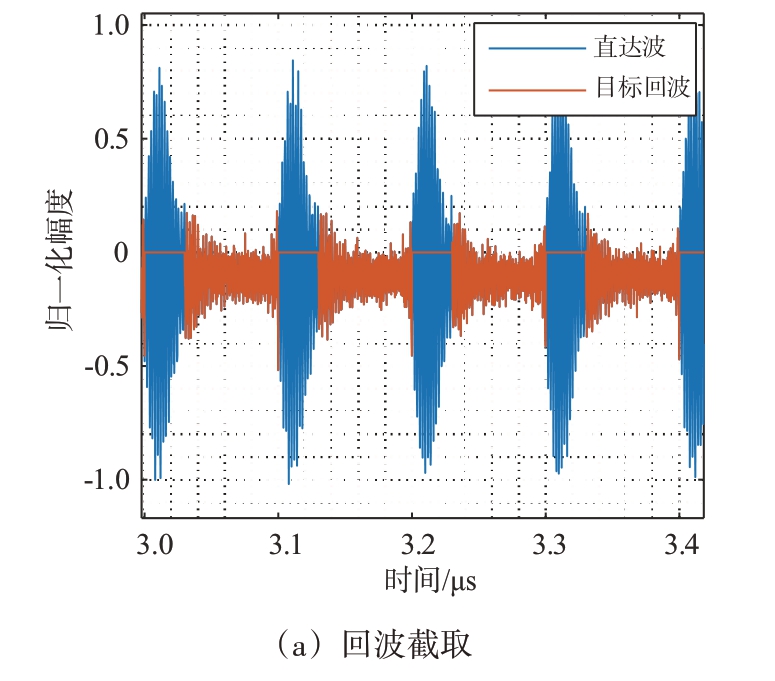
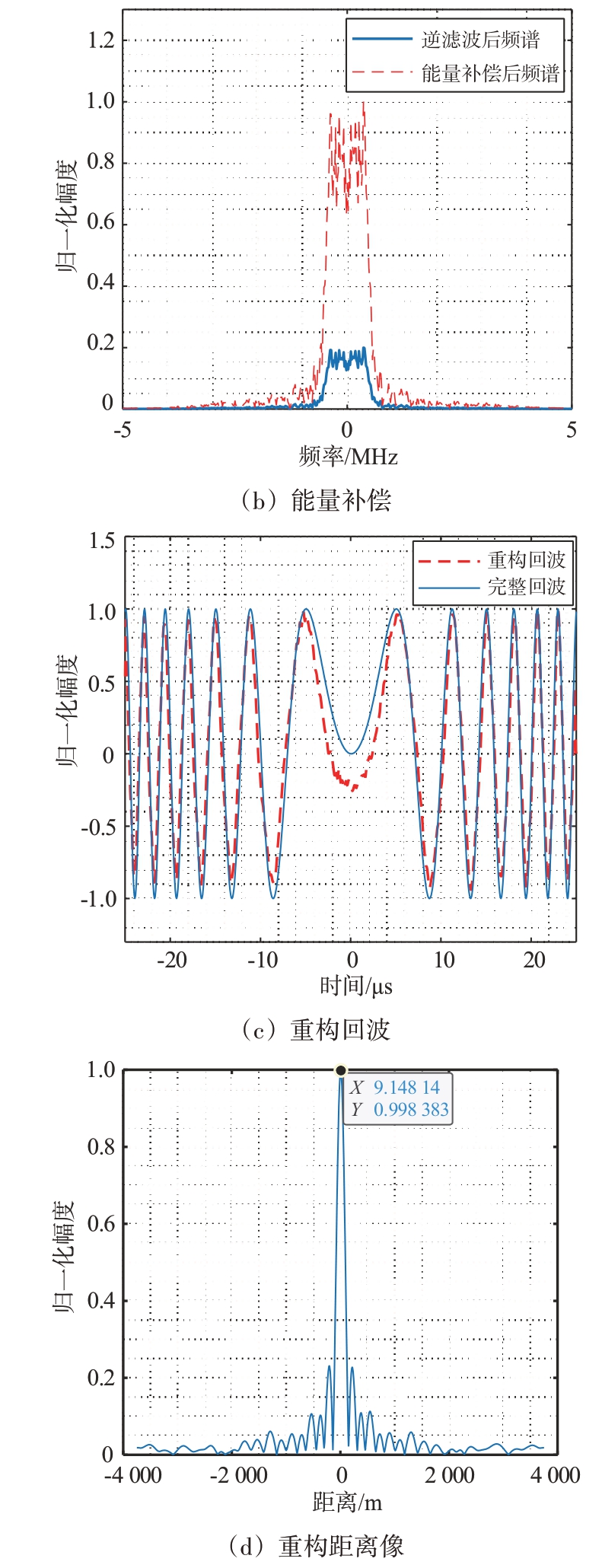
图12 实验结果
在实验中,由于设置的间歇收发采样频率为1/0.1 μs = 10 MHz,大于信号带宽1 MHz。因此,间歇收发回波的频谱在频域上没有发生混叠,且主频谱与相邻虚假频谱的延拓周期为10 MHz,滤除虚假频谱后通过能量补偿即可得到完整回波。由于去噪过程中小波基函数和分解层数的选择会造成信号部分失真,使得在起始处波形出现轻微震荡,能量补偿和重构结果如图12(b)、(c)所示。
通过对重构回波进行匹配滤波处理,能够得到目标的真实位置。从图12(d)中可以看出,目标真实位置为9.14 m,由于实验中发射信号设置带宽较窄,分辨率较低,可以认为与实际场景中设置的8.7 m 基本一致,证明该联合重构方法在雷达探测和目标特性测量中具有良好的应用价值。
5 结束语
针对噪声背景下室内场仿真中间歇收发回波的重构问题,本文提出了基于小波变换的联合重构处理方法。由于传统阈值函数存在的不连续性和恒定偏差等缺点,改进了阈值函数以优化小波阈值去噪算法。结合LFM 间歇收发回波的匹配滤波输出特性,构建了联合重构流程,并进行了仿真和实验分析,得到了重构后的完整回波与距离像图像。仿真和实验结果表明,经改进阈值函数处理后的回波重构性能效果更佳,证明了该联合重构方法的有效性,为噪声和杂波背景下的准确重构提供了理论和方法指导。
[1]XIE Ailun,LIU Xiaobin,ZHAO Feng,et al.Waveform Design and Processing Method of Pulse Signal in Anechoic ChamberMeasurement[J].Measurement,2022,203:111938.
[2]关键,刘宁波,王国庆,等.雷达对海探测试验与目标特性数据获取——海上目标双极化多海况散射特性数据集[J].雷达学报,2023,12(2):456-469.
[3]周凯,何峰,粟毅.一种快速抗间歇采样转发干扰波形和滤波器联合设计算法[J].雷达学报,2022,11(2):264-277.
[4]王栗沅,何华锋,韩晓斐,等.全极化雷达抗间歇采样转发式干扰的非匹配滤波方法[J].雷达科学与技术,2023,21(6):661-669.
[5]潘小义,刘晓斌,陈吉源,等.间歇采样转发干扰技术研究述评[J/OL].系统工程与电子技术,2024:1-21[2024-01-15].http://kns.cnki.net/kcms/detail/11.2422.TN.202401 04.1303.004.html.
[6]WU Qihua, ZHAO Feng, ZHAO Tiehua, et al. Stepped Frequency Chirp Signal Imaging Radar Jamming Using Two-Dimensional Nonperiodic Phase Modulation[J].Frontiers of Information Technology & Electronic Engineering,2023,24(3):433-446.
[7]FAN Qibin,JIA Cui,LIU Jin,et al.Robust Recovery in 1-Bit Compressive Sensing Via-Constrained Least Squares[J].Signal Processing,2021,179:107822.
[8]XIE Ailun, LIU Xiaobin, ZHAO Feng, et al. Pulse Radar Imaging Method in an Anechoic Chamber Based on an Amplitude Modulation Design[J]. Remote Sensing,2022,14(18):4560-4574.
[9]LIU Xiaobin, ZHAO Feng, XIE Ailun. Target Measurement in Radio Frequency Simulation Using Code-Interrupted Transmitting and Receiving of Pulse Signal[J].IEEE Trans on Antennas and Propagation,2023, 71(5):4451-4460.
[10]谢艾伦,刘晓斌,赵锋,等.辐射式仿真中PCM 信号间歇收发回波重构方法[J].系统工程与电子技术,2022,44(3):771-776.
[11]吴叶丽,行鸿彦,李瑾,等.改进阈值函数的小波去噪算法[J].电子测量与仪器学报,2022,36(4):9-16.
[12]YANG Haitao,TONG Yaonan,CAO Zhiqi,et al.Infrared Image Enhancement Algorithm Based on Improved Wavelet Threshold Function and Weighted Guided Filtering[J]. Journal of Physics: Conference Series,2023,2525:012017.
[13]LIN Haibo, CHEN Xuefeng, HUAN Wang, et al. Research on Wavelet Denoising Algorithm Based on Improved Threshold Function[C]//2022 IEEE 6th Advanced Information Technology, Electronic and Automation Control Conference,Beijing,China:IEEE,2022:179-182.
[14]杜诗强,宋宇鲲,张玄,等.一种改进的小波阈值去噪算法[J].微电子学与计算机,2021,38(2):40-46.
[15]GUO Hua, YUE Leihui, SONG Peng, et al. Denoising of an Ultraviolet Light Received Signal Based on Improved Wavelet Transform Threshold and Threshold Function[J].Applied Optics,2021,60(28):8983-8990.
[16]WANG Zili, ZHOU Hefeng. Study on GPS Observation Data Denoising Method Based on Improved Wavelet Threshold[J]. Advances in Applied Mathematics, 2019,8(11):1708-1715.
[17]MALLAT S G. A Theory for Multiresolution Signal Decomposition:the Wavelet Representation[J].IEEE Trans on Pattern Analysis and Machine Intelligence,1989, 11(7):674-693.
[18]SHENG Jing, ZENG Yuping, LIU Guoman, et al. Determination of Weak Knock Characteristics for Two-Stroke Spark Ignition UAV Engines Based on Mallat Decomposition Algorithm[J].Mathematical Problems in Engineering,2021(9):1-11.
[19]DONOHO D L, JOHNSTONE J M. Ideal Spatial Adaptation by Wavelet Shrinkage[J]. Biometrika, 1994, 81(3):425-455.