0 引 言
目前,雷达观测环境日趋复杂,杂波等外部干扰因素增加,目标运动模式呈现多样化,如何在复杂环境中实现高机动多目标的准确跟踪已经成为目标跟踪领域的热点。21 世纪初,Mahler 等人基于随机有限集(Random Finite Set,RFS)理论[1]提出了多目标Bayes 估计的次优解概率假设密度(Probability Hypothesis Density,PHD)滤波算法[2],为多目标跟踪提供了一种全新的理论工具和思路。为了解决PHD 算法高维积分无闭合解的问题,Vo 提出了高斯实现形式下的高斯混合PHD 滤波(Gaussian Mixing PHD,GMPHD)[3],并利用标签化[4]手段实现目标航迹区分。但该算法仅适用于线性系统,非线性场景下跟踪精度急速下降,甚至丢失目标。于是,文献[4]在PHD 算法基础上借助扩展卡尔曼(Extend Kalman,EKF)思路提出了适用于非线性场景下的EK-PHD 算法。然而,随着跟踪目标机动性不断增强,系统非线性程度加强,上述算法稳定性和跟踪精度均不理想,且无法显式区分不同目标航迹,尤其在目标轨迹存在交叉时容易出现航迹混乱问题,近些年来不少专家学者给出了优化方案。文献[5]提出了一种采用EKF 预测和更新高斯分量的EK-GMPHD 算法,实现了非线性交叉目标的准确跟踪,但该算法在目标发生机动突变时误差骤增且并未实现交叉航迹的显式区分。文献[6]在GMPHD 算法基础上引入强跟踪思想和机动变化率这一概念,实现自适应高机动目标的状态突变,但其自适应性强依赖于CS 模型依据先验知识设定的参数。文献[7]提出了基于容积卡尔曼的GMPHD 算法,提升了对多扩展目标的跟踪性能,但该算法缺乏对目标机动突变的自适应性。文献[8]对标准GMPHD 滤波算法进行改进后,可同时实现多目标高虚警环境下的目标数目和目标空间位置以及运动状态的估计,增强算法复杂环境下检测性能,但该算法对高机动目标跟踪能力较弱,且不具备显式区分航迹能力。文献[9]提出了自适应多模型GMPHD 估计机动多目标的全局状态,但其应用场景受到动态环境和点目标假设的限制,且并不具有显式区分航迹能力。文献[10]提出了一种基于量测驱动的标签化GMPHD,实现对多目标航迹的标识,但并未对非线性自适应性进行提升。文献[11]提出将最小可检测速度带入到交互式多模型广义标签多伯努利滤波器中,减少在跟踪机动多目标时由于多普勒盲区造成的量测消失现象,但该算法计算复杂度较高。以上算法均无法实现在较低计算复杂度下,自适应跟踪高机动性多目标,显式确定目标与航迹的对应关系,且其跟踪性能不受限于先验知识。
本文将在GMPHD 算法基础上引入标签演化过程和自适应CS模型,提出一种基于自适应CS模型的标签化GMPHD(ICS-LGMPHD)算法。该方法的创新之处在于借助标签化手段显式区分目标航迹的同时维持短时间漏检目标航迹,并利用滤波估计值实时调整多目标各自对应CS 模型参数,通过预测更新将目标机动性变化实时反馈到状态估计值上,在保证计算代价的情况下区分目标航迹、提升算法自适应能力与跟踪精度。文章首先阐述了GMPHD 多目标跟踪算法基本原理,然后介绍标签演化过程、自适应CS 模型原理和ICS-LGMPHD算法递推过程及算法流程图,最后通过仿真实验对比扩展GMPHD、平方根容积GMPHD 和自适应CS-GMPHD 算法,从跟踪精度与仿真耗时两个层面评估ICS-LGMPHD算法性能。
1 GMPHD多目标跟踪算法
1.1 随机集模型
二维平面内,设k时刻目标的状态方程和量测方程表示为
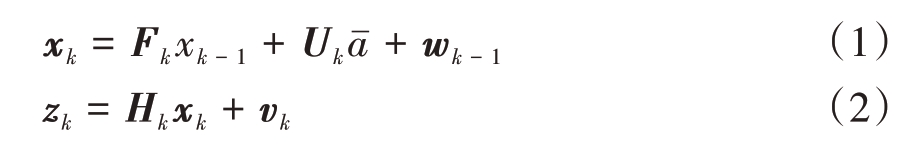
式中xk、zk分别为k时刻目标状态和观测值,Fk为系统转移矩阵,Uk为输入控制矩阵,aˉ为加速度均值,Hk为观测矩阵,wk - 1为过程噪声服从N(0,Qk - 1)分布,vk 为量测噪声服从N(0,Rk)分布,两者相互独立。
将Mahler 等人提出的RFS 理论应用到多目标跟踪问题中,以集合形式构建多目标状态模型和量测模型。设x1,…,xN(k)为k时刻N(k)个目标的状态向量,z1,…,zM(k)为k 时刻所有目标产生的M(k)个量测向量,以RFS形式表示为

采用RFS 形式充分体现出了多目标跟踪中目标个数及状态的不确定性。
1.2 GMPHD滤波算法
GMPHD 滤波算法将每个目标表示为一个高斯项Jk,服从高斯分布![]() 利用均值
利用均值![]() 、权值
、权值![]() 和协方差
和协方差![]() 来描述目标状态特性,其中i = 1,2,…,Jk,经过预测和更新,获取目标个数及状态信息,其均值与协方差的预测更新采用的是Kalman滤波。
来描述目标状态特性,其中i = 1,2,…,Jk,经过预测和更新,获取目标个数及状态信息,其均值与协方差的预测更新采用的是Kalman滤波。
1)预测
假设已知k - 1 时刻所有目标的高斯和,则k时刻的PHD预测方程Dk|k - 1(x)可表示为
式中,DS,k|k - 1(x)、Dβ,k|k - 1(x)和γk(x)分别表示存活目标、衍生目标和新生目标的预测PHD 函数。其中DS,k|k - 1(x)具体表示为
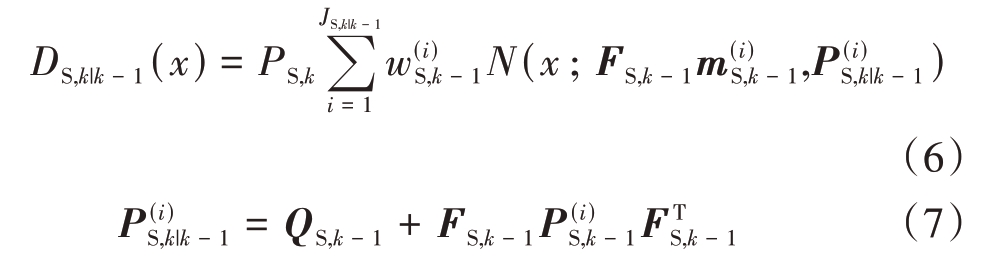
式中PS,k 为目标存活概率,JS,k|k - 1 为从k - 1 时刻到k时刻的存活目标个数。
k时刻衍生目标预测PHD为
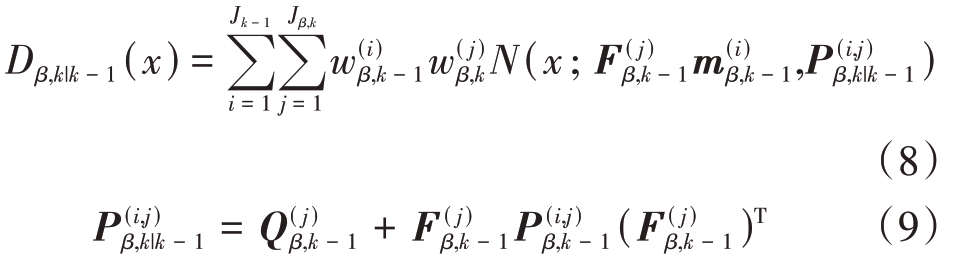
式中Jβ,k为从k - 1时刻到k时刻衍生目标个数。
k时刻新生目标预测PHD为
式中Jγ,k表示k时刻新生目标个数。
根据k - 1 时刻目标个数Nk - 1 预测k时刻目标个数Nk|k - 1为
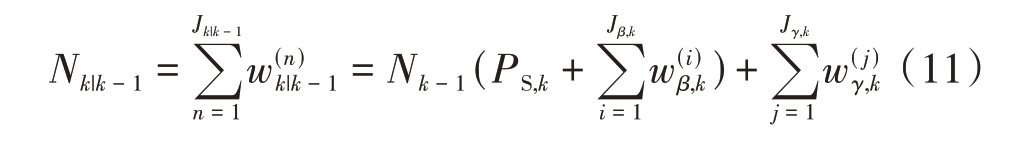
2)更新
依据量测信息对预测出的存活、新生、衍生目标的混合加权高斯和进行滤波更新,同时更新目标个数,GMPHD的更新方程表示为
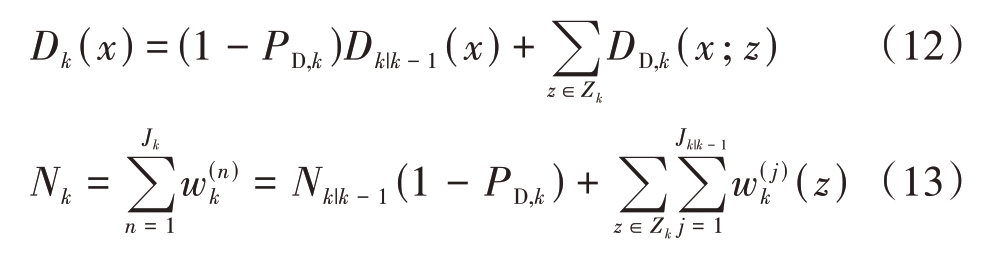
式(12)中PD,k 表示雷达的检测概率,第一项表示漏检情况下的采用预测PHD 作为更新结果,第二项表示目标被检测到后更新的PHD,目标状态参数更新过程如下:
其中
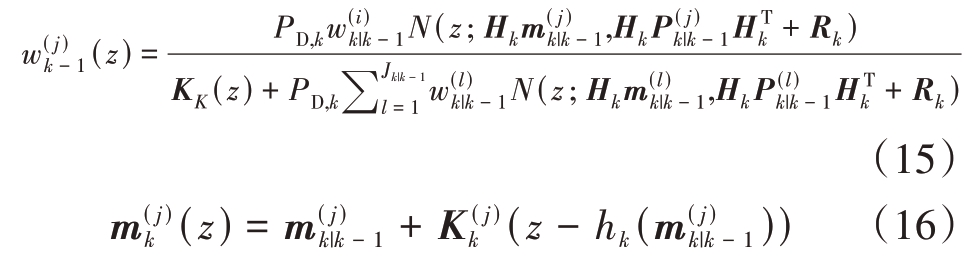
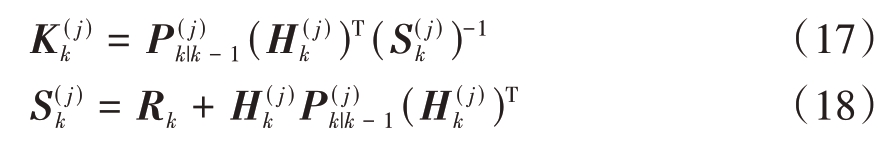
式中K为滤波增益,S为新息协方差。
2 基于自适应CS模型的标签化GMPHD算法
2.1 标签演化过程
初始阶段,为每个高斯项分配独特标签,在k = 0时刻,标签集合为
式中,J0表示k = 0时刻的高斯项个数,li表示第i个目标的标签,存放在标签集合L0 中。初始化漏跟标签集合![]() 为空。
为空。
预测:k时刻的预测标签集合为
在预测过程中存活目标的标签值固定不变,为每个新生的目标分配标签![]() 本文并未考虑衍生目标。
本文并未考虑衍生目标。
更新:在更新过程中,同一高斯项更新后的标签不变,也即li(li ∈Lk|k - 1)的高斯项更新后可能会重复![]() 次,其中
次,其中![]() 表示求集合的势。
表示求集合的势。
剪枝与合并:从标签集合Lk 中剔除被裁剪的高斯项对应的标签。若被合并的两个高斯项标签相同,则取其相同标签作为合并后高斯项的标签,若不相同,则取最大权值高斯项的标签。
状态估计:在状态提取时,为了保证标签的唯一性原则,需要对k 时刻目标估计状态进行裁剪,保证每一个标签只保留最大权值高斯项,其余丢弃。同时,对处于短时间漏检的目标进行航迹维持,具体流程如下:
1)提取标签集![]() k时刻的标签集为
k时刻的标签集为
式中状态提取的权值阈值wth = 0.5。将提取出来的标签进行裁剪,保证标签唯一性,利用标签对应的状态估计更新对应目标航迹,若目标为新生目标,则为其开启新航迹。
2)构建漏跟标签集![]()
检查k - 1 时刻漏检标签集![]() ,若标签
,若标签![]() 的标志量kj 与当前时刻差小于设定的最大漏检时间阈值Kn,则将标签l j 存入k 时刻的漏检标签集
的标志量kj 与当前时刻差小于设定的最大漏检时间阈值Kn,则将标签l j 存入k 时刻的漏检标签集![]() 中,保持其标志量kj不变。
中,保持其标志量kj不变。
将k - 1 时刻目标航迹存在而在k 时刻航迹未被更新的目标标签lm 存入漏检标签集![]() 中,设置其标志量km为k。
中,设置其标志量km为k。
3)漏跟目标航迹外推
借助目标运动状态方程预测k 时刻目标空间位置
最后利用预测值更新漏检目标航迹。
以上为改进算法的标签演化过程,算法迭代过程中标签按顺序产生,避免发生重复,且对于长时间漏跟目标或消亡目标,算法自动注销目标标签等信息,减少算法迭代数据量。与此同时,借助目标运动状态方程预测短时间漏检目标状态,实现漏检目标航迹维持,提高航迹连续度。
2.2 基于自适应CS模型的LGMPHD算法
CS模型的跟踪效果强依赖于机动频率值和加速度极限值,以上两个参数需要根据先验知识获取,一旦参数值设置不合理,其跟踪性能急速下降。为了避免CS 模型固有缺陷,提高对高机动多目标的跟踪精度,本文借鉴文献[12]中推导出的自适应的CS模型参数机动频率α和加速度方差![]() 计算方程:
计算方程:
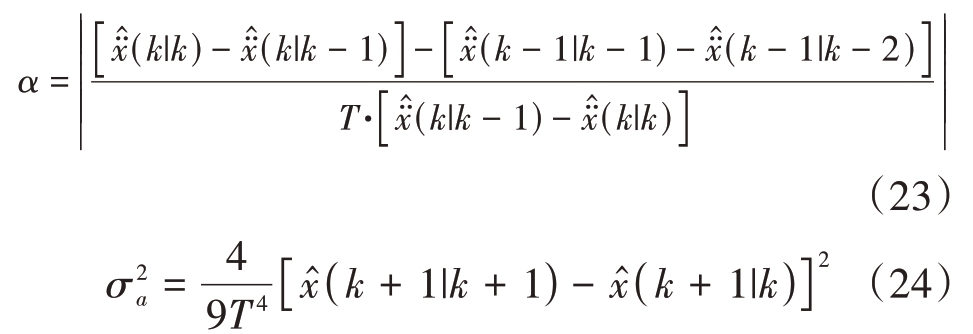
式中![]() 和
和![]() 分别表示目标在k 时刻加速度的滤波估计值和预测值,同理
分别表示目标在k 时刻加速度的滤波估计值和预测值,同理![]() 和
和![]() 分别表示k - 1 时刻加速度的滤波估计值和预测值
分别表示k - 1 时刻加速度的滤波估计值和预测值![]() 分别表示k + 1 时刻位置的滤波估计值和预测值。将文献[12]中适用于单目标的自适应CS模型扩展到多目标跟踪场景,在GMPHD 算法迭代过程中,利用当前时刻滤波值更新目标对应CS 模型参数,至下一时刻目标估计时,根据CS 模型预测目标状态,并将目标机动性变化实时反馈到过程噪声协方差矩阵上,进而在更新时通过滤波增益将目标机动性变化反馈到目标状态估计值上,降低目标状态估计值与真实值之间的误差。结合2.1 节的标签演化过程,ICS-LGMPHD 算法的具体流程如下:
分别表示k + 1 时刻位置的滤波估计值和预测值。将文献[12]中适用于单目标的自适应CS模型扩展到多目标跟踪场景,在GMPHD 算法迭代过程中,利用当前时刻滤波值更新目标对应CS 模型参数,至下一时刻目标估计时,根据CS 模型预测目标状态,并将目标机动性变化实时反馈到过程噪声协方差矩阵上,进而在更新时通过滤波增益将目标机动性变化反馈到目标状态估计值上,降低目标状态估计值与真实值之间的误差。结合2.1 节的标签演化过程,ICS-LGMPHD 算法的具体流程如下:
1)初始化
为目标状态集中每个高斯项分配独特标签,初始化漏检标签集![]() 根据经验初始化每个目标CS模型对应的机动频率αi和加速度方差
根据经验初始化每个目标CS模型对应的机动频率αi和加速度方差![]() 得到k = 0时刻的强度函数和标签集如下:
得到k = 0时刻的强度函数和标签集如下:
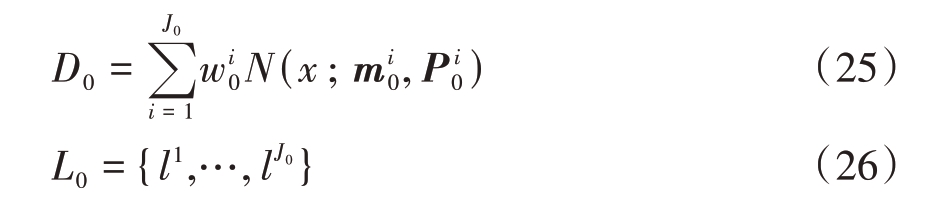
2)预测
根据k 时刻估计的CS 模型参数,修正对应目标xi 的状态矩阵![]() 输入控制矩阵
输入控制矩阵![]() 及参数
及参数![]() 具体计算方法可参考文献[13]。采用EKF 算法预测均值
具体计算方法可参考文献[13]。采用EKF 算法预测均值![]() 和协方差
和协方差![]() 为
为
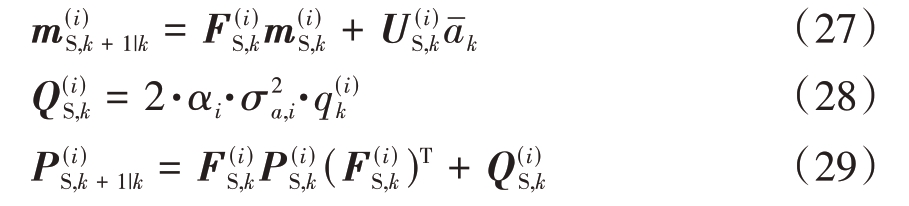
此时k + 1 时刻的预测强度函数和预测标签集表示如下:
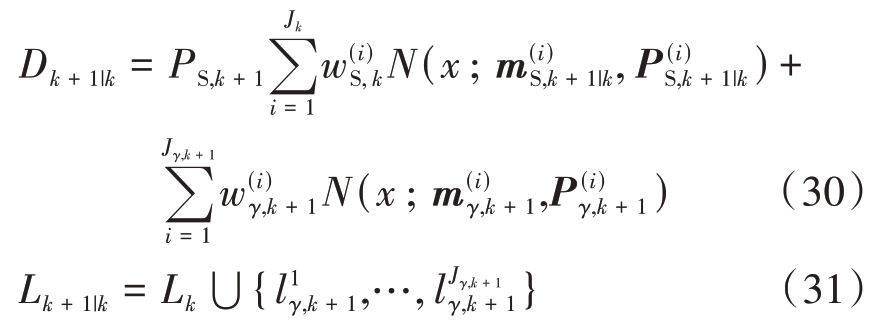
3)更新
将k + 1时刻预测强度函数写作高斯和形式为
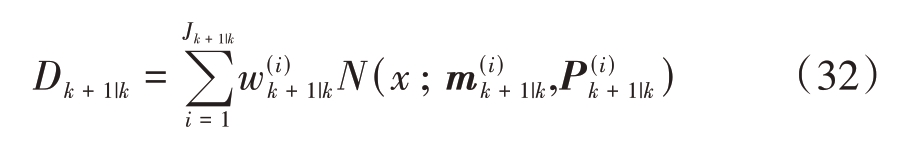
式中Jk + 1|k = JS,k + Jγ,k + 1 为预测高斯项的个数,则k + 1 时刻的更新强度函数和更新标签集表示如下:

式中![]() 的更新均采用EKF算法。
的更新均采用EKF算法。

且同一高斯项更新后的标签和CS 模型参数不变。
4)剪枝与合并
假设更新后的目标状态集中有Np个高斯项的权值![]() 小于裁剪阈值T_prun,这些高斯项被视为虚假目标,进行裁剪后的PHD 函数及权值表示为
小于裁剪阈值T_prun,这些高斯项被视为虚假目标,进行裁剪后的PHD 函数及权值表示为
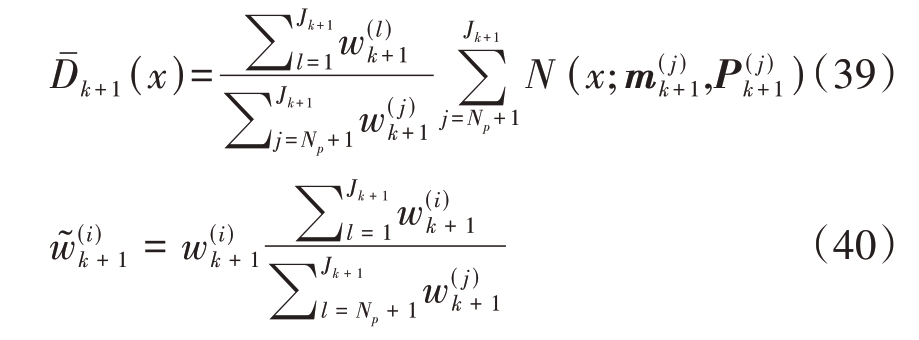
同时舍弃被裁剪高斯项对应标签、CS 模型参数。
假设两个高斯项![]()
![]() 之间满足状态的欧式距离小于合并门限U_merg,表示为
之间满足状态的欧式距离小于合并门限U_merg,表示为
则将两个高斯分量进行合并,合并方程如下:
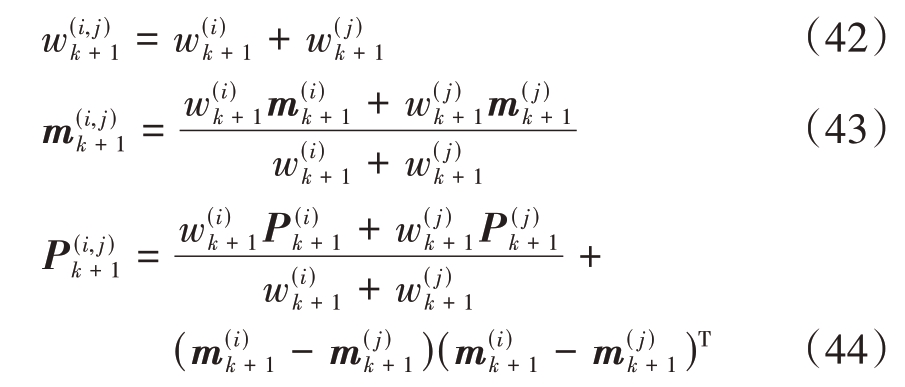
两个高斯分量在合并时,若对应的标签相同,则取其相同标签为合并后高斯项的标签,若不相同,则取权值最大的高斯项对应的标签为合并后高斯项的标签。合并时模型参数选择权重最大的。
5)自适应参数估计
任意目标xi属于多目标集合,利用该目标状态信息实时调整机动频率αi和加速度方差![]()
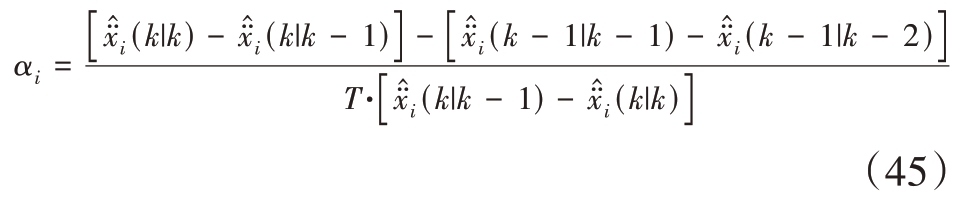
通过调整每个目标CS 模型参数,将目标机动变化实时反馈到目标状态估计上,提升模型与真实目标运动模式的匹配度。
6)状态估计
提取k + 1时刻的状态集和标签集

更新漏跟标签集合![]() ,并利用集合
,并利用集合![]() 及目标运动模型对漏检目标进行航迹预测。
及目标运动模型对漏检目标进行航迹预测。
2.3 ICS-LGMPHD算法流程图
基于ICS-LGMPHD 算法流程图如图1所示,本文并未考虑对衍生目标的跟踪。
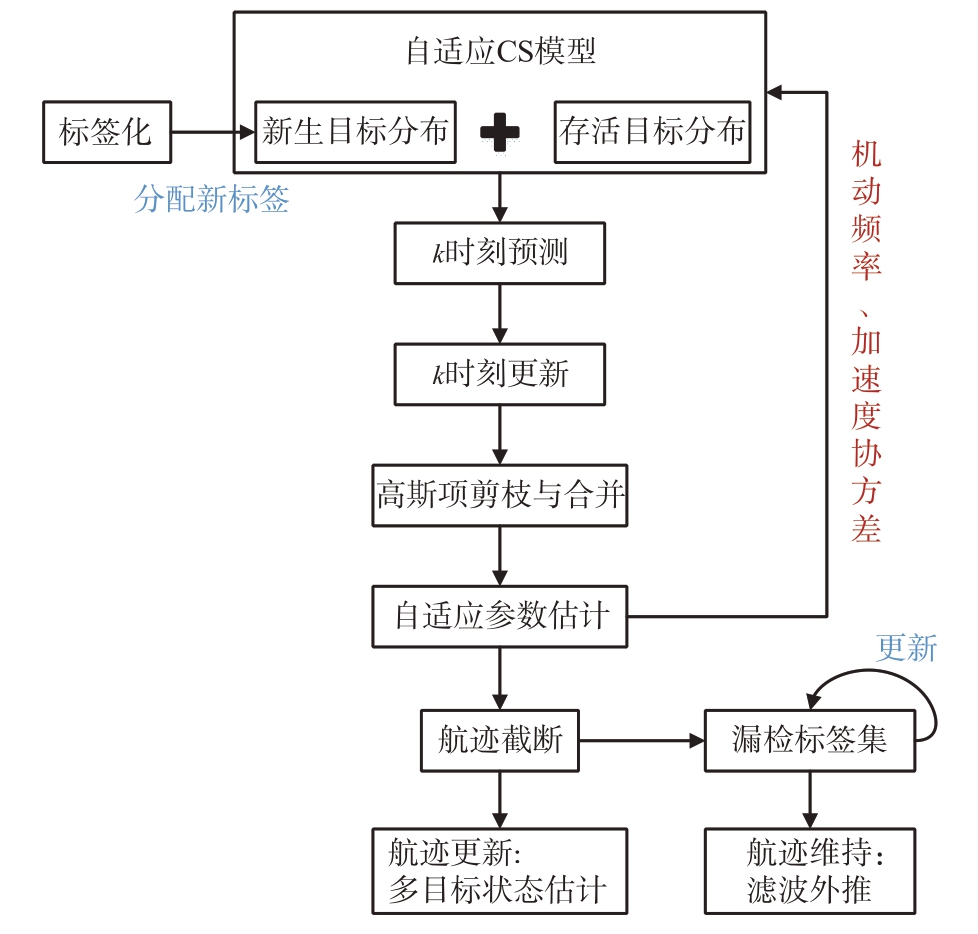
图1 ICS-LGMPHD算法流程图
初始化为当前目标分配唯一标签,跟随算法流程进行标签演化,跟踪过程中为新生目标分配新标签,确保航迹和目标的唯一对应关系,记录并更新漏检标签,利用目标运动方程外推漏检目标航迹。在每个时刻滤波结束后,利用滤波估计值及推导出的自适应机动频率和加速度方差计算方程实时修正当前存活目标各自对应的CS 模型参数,确保算法运动模型和目标真实运动模式实时统一。
3 仿真实验与分析
为了验证ICS-LGMPHD 算法跟踪高机动多目标的性能优势,本次仿真实验比较了扩展GMPHD算法、平方根容积GMPHD 算法和自适应CS-GMPHD 算法3 种不同的GMPHD 改进算法。仿真场景为[-6 × 104,6 × 104]×[-2.5 × 104,2.5 × 104]的二维空间,测量时间N = 120 s,设置了4 个分别在不同时刻出现且轨迹存在交叉的目标,其初始时刻的运动状态为

设定目标1 运动时间为1 ~110 s,目标2 为11~120 s,目标3 为16~120 s,目标4 为21~110 s。目标1 与目标2、目标3 分别于85 s、29 s轨迹交叉,目标2、目标3、目标4 先后在102 s 附近轨迹交叉。各目标发生机动变化时刻和加速度大小如表1~表4所示。
表1 目标1机动情况
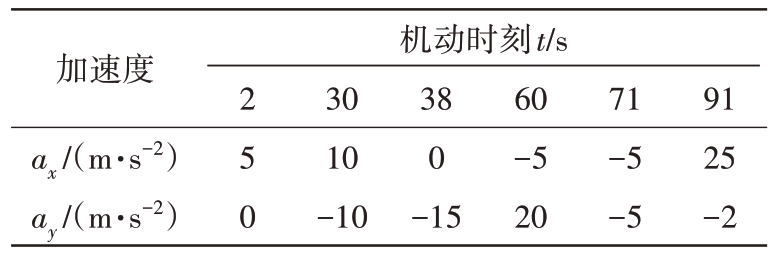
加速度ax/(m·s-2)ay/(m·s-2)机动时刻t/s 25 0 30 10-10 38 0-15 60-5 20 71-5-5 91 25-2
表2 目标2机动情况

加速度ax/(m·s-2)ay/(m·s-2)机动时刻t/s 20-5-5 30 8-18 45-10 20 60 30-10 80 2 23
表3 目标3机动情况
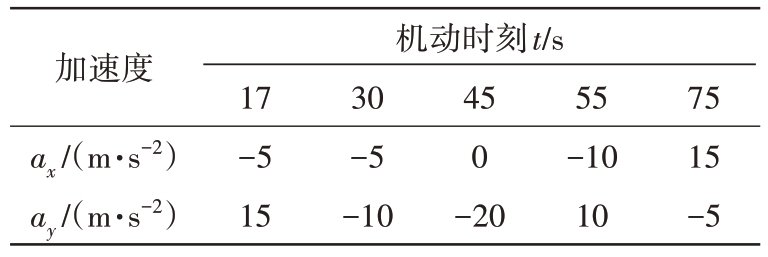
加速度ax/(m·s-2)ay/(m·s-2)机动时刻t/s 17-5 15 30-5-10 45 0-20 55-10 10 75 15-5
表4 目标4机动情况
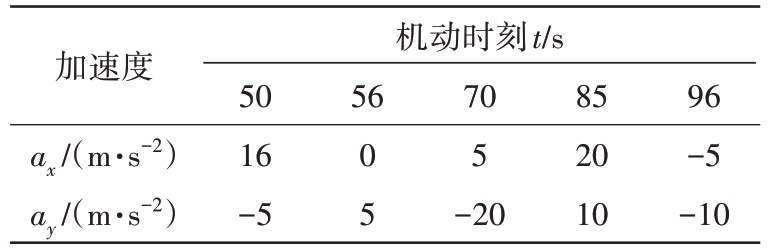
加速度ax/(m·s-2)ay/(m·s-2)机动时刻t/s 50 16-5 56 0 5 70 5-20 85 20 10 96-5-10
仿真条件下设定的状态转移矩阵Fk|k - 1、输入控制矩阵Uk - 1、过程噪声协方差矩阵Qk - 1 和量测矩阵Hk分别表示为
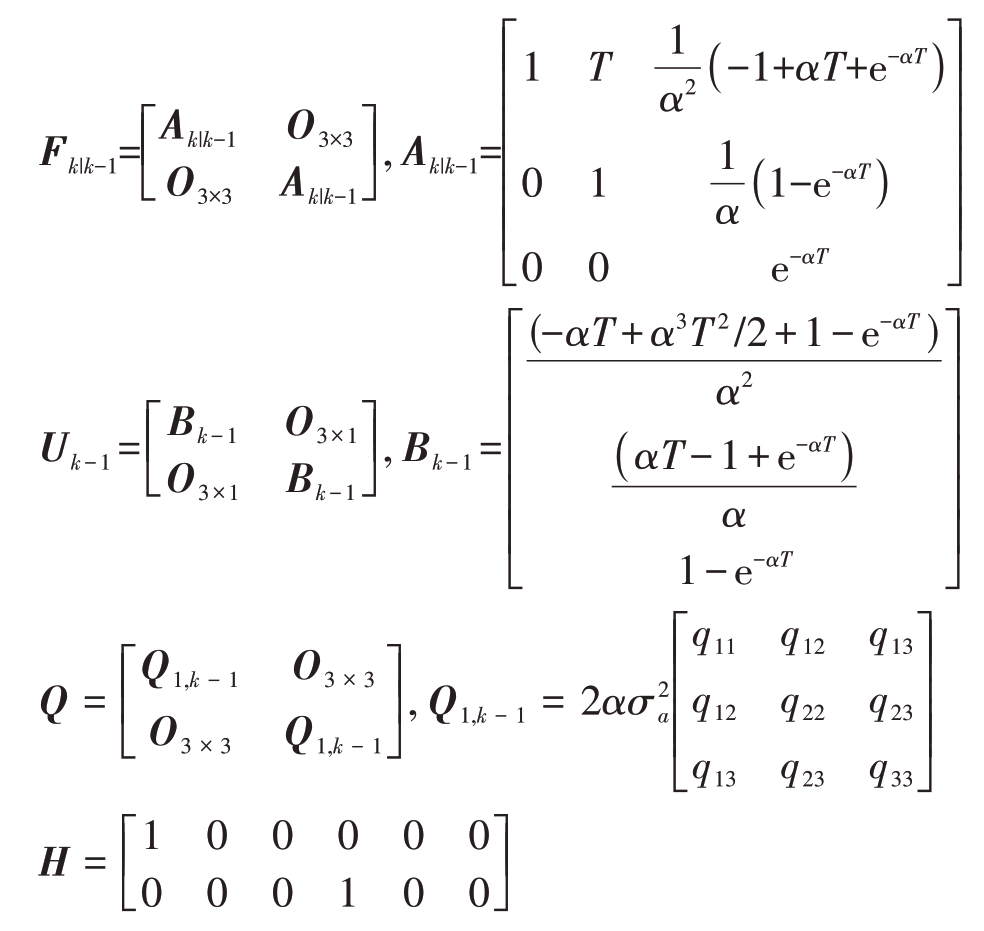
假设没有衍生目标,新生目标的PHD函数为
设置采样间隔T = 1 s,裁剪阈值T_prun = 10-4,合并门限U_merg = 4,目标检测概率pd = 0.98,杂波平均数rc = 5,最大高斯分量数Jmax = 100,状态提取的权值阈值wth = 0.5。本文采用最优子模式分配(OSPA)距离和仿真耗时两个指标对算法跟踪性能进行评价,OSPA距离定义为
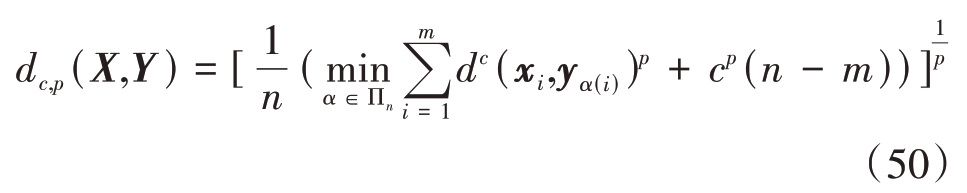
其中,势估计误差定义为
式中:X、Y 表示任意子集,维数分别为m、n;p 为阶数参量,无量纲;c 为截取参量,量纲为m。两个参数分别调节对目标状态和目标数目估计偏差的惩罚度,参数值设定越大,相应的误差影响越大。本实验中选取参数p = 1,c = 200 m。单次蒙特卡洛实验仿真结果如下,性能指标均是通过100次蒙特卡洛平均得出。
图2 为4 种滤波算法的滤波结果,其中图2(d)中不同颜色表示算法输出的航迹标签不同。由图2 可以看出,ICS-LGMPHD 算法可以显式区分不同目标航迹,而其余3种算法均无法确定目标航迹归属关系,尤其是当目标轨迹发生交叉时,ICS-LGMPHD 算法可以借助标签信息确定交叉前后时刻不同目标状态归属于哪一条航迹,明确目标与航迹的对应关系。此外,ICS-LGMPHD 算法还通过对漏检目标航迹外推,使得多目标跟踪航迹更加完整。
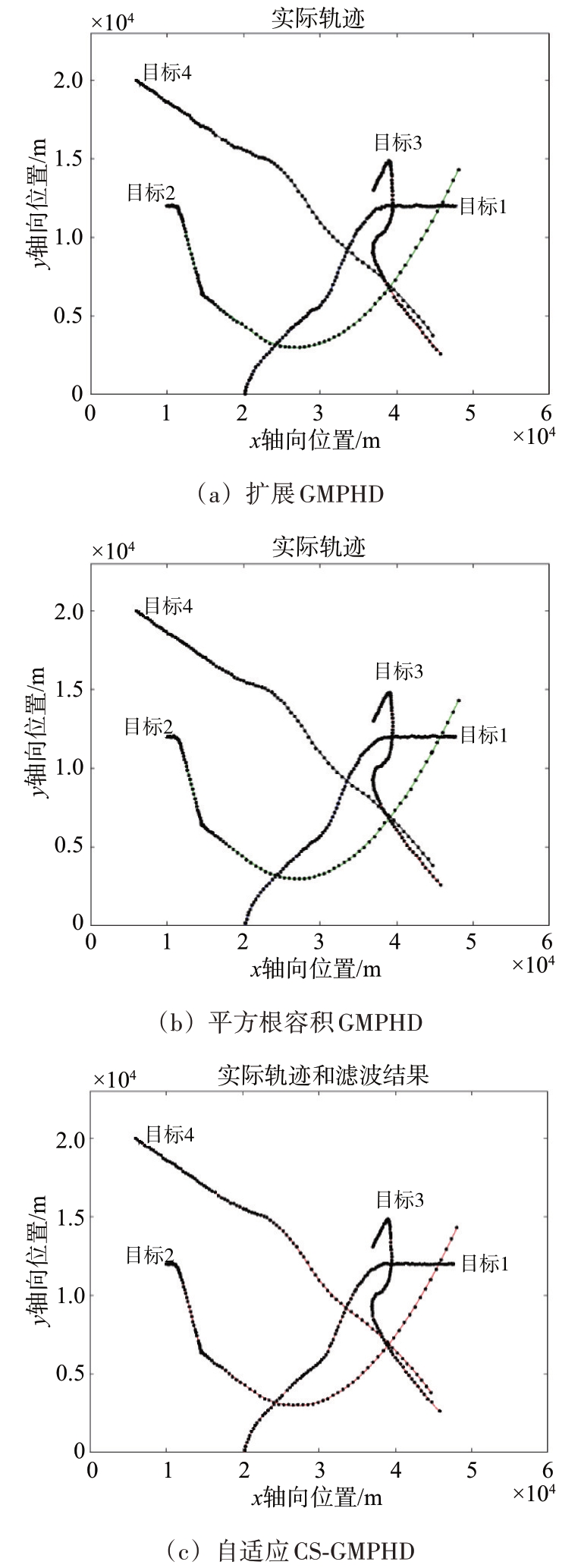
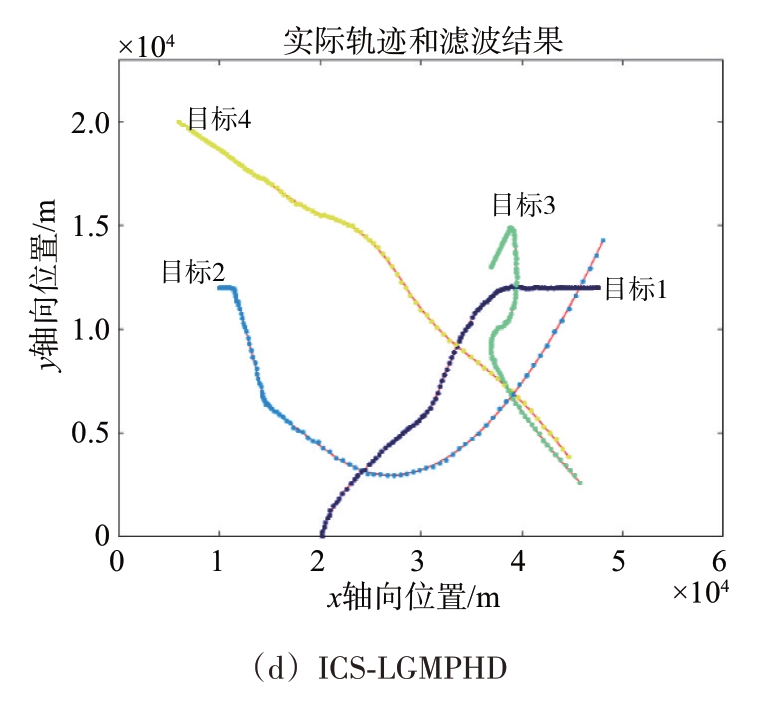
图2 4种滤波算法的滤波结果
图3 为4 种算法的目标个数估计。通过对比图3 中目标个数估计出错时刻与表1~表4 的4 种目标机动突变时刻可以看出,在目标个数估计出错时刻附近均存在不同程度的加速度机动突变,由此可知目标跟丢情况与目标发生强机动有直接关系。通过图3可知ICS-LGMPHD算法仅存在18 s和104 s 两个时刻的目标漏跟,相较其余3 种算法目标估计准确性更高,这是因为ICS-LGMPHD 算法通过自适应CS 模型实时调整目标对应的αi 和![]() 参数,将目标机动性变化实时反馈到状态估计上,进而提高了高机动多目标跟踪准确性。该实验结果验证了ICS-LGMPHD 算法对机动性突变的自适应性。
参数,将目标机动性变化实时反馈到状态估计上,进而提高了高机动多目标跟踪准确性。该实验结果验证了ICS-LGMPHD 算法对机动性突变的自适应性。
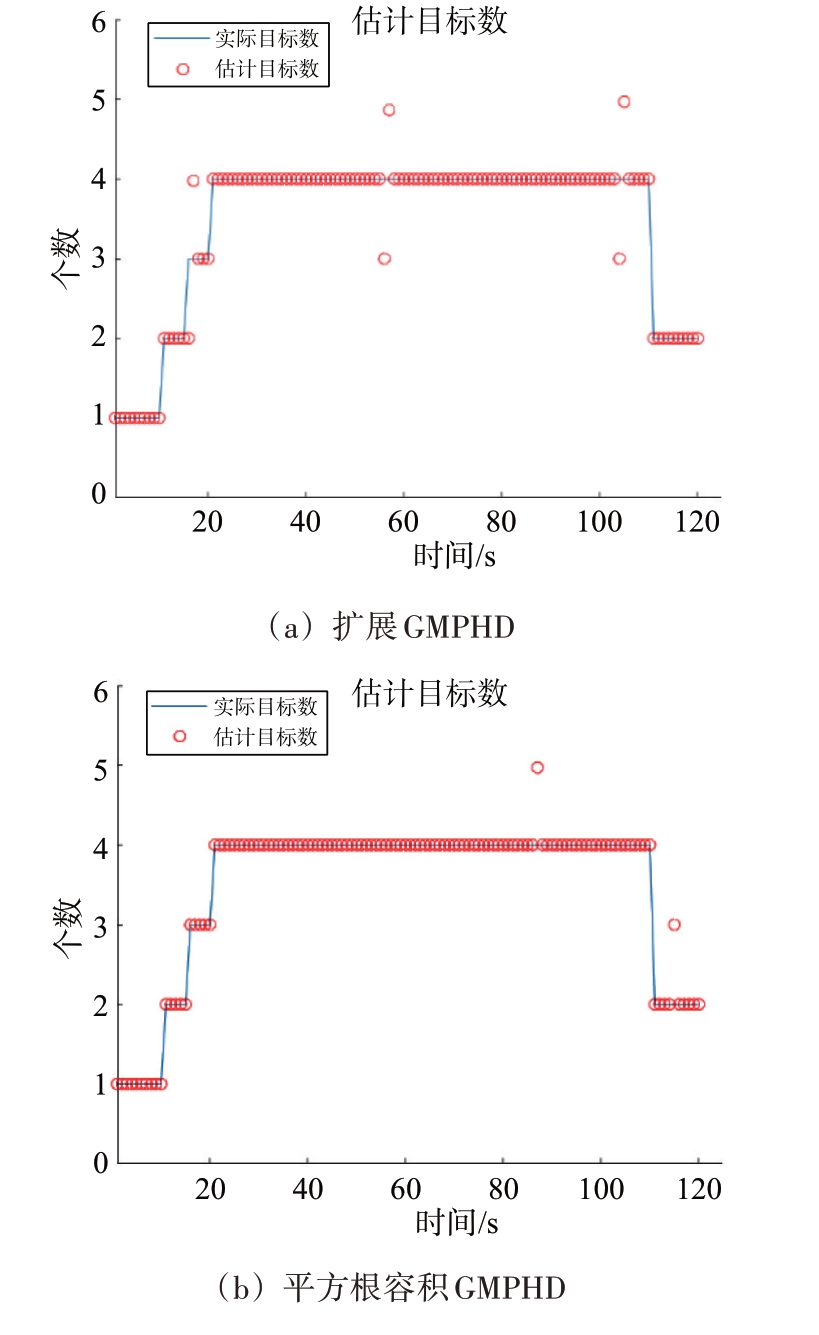
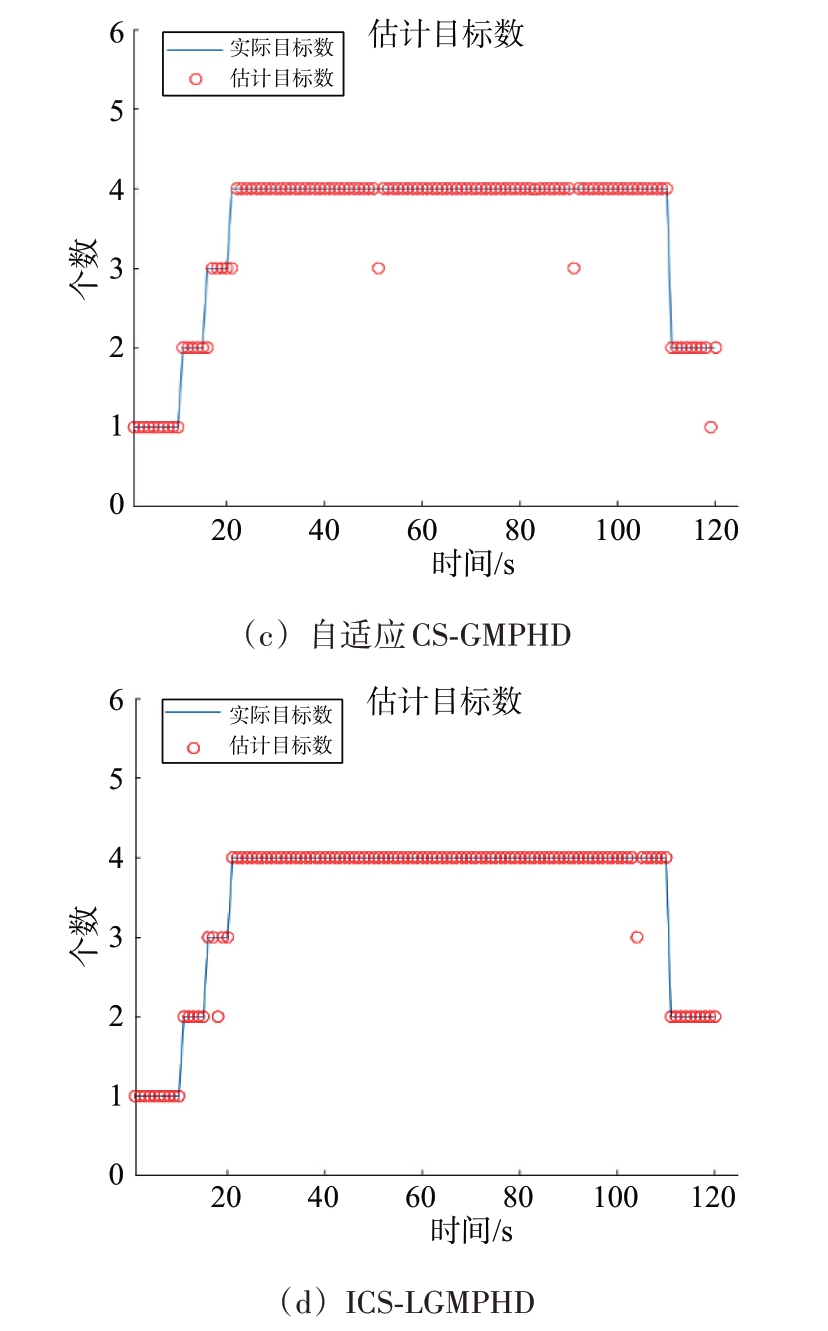
图3 4种滤波算法的目标个数估计
通过图2 和图3 可以看出,ICS-LGMPHD 算法在目标交叉的29 s、85 s 及102 s 并未出现航迹混乱或目标个数估计出错的情况,且在交叉时刻准确对应目标状态与航迹,于交叉结束后算法输出航迹正确对应了真实目标运动轨迹,较稳定地实现了交叉目标跟踪。
图4 为4 种算法的OSPA 距离误差对比。通过对比目标运动时刻可知,1~10 s仅存在单个运动目标、11~15 s 和111~120 s 有两个运动目标,此时4种算法的误差整体较低,22~110 s 存在4 个运动目标,此时OSPA 误差叠加后整体幅度上升。但在目标个数相同的时间段内可以看出ICS-LGMPHD 算法误差整体偏低且呈现稳定收敛趋势,其余3种算法的OSPA 误差波动较大,收敛趋势不明显。其主要原因是在多个目标随机发生机动性突变时,ICSLGMPHD 算法通过实时调整目标对应模型参数不断逼近其真实运动状态,快速降低OSPA 误差,从而呈现稳定收敛趋势。同时对比4 种算法的目标个数估计出错时刻,OSPA 距离均出现了较高尖刺,相比之下,ICS-LGMPHD 算法误差整体偏低,且收敛速度较快。其主要原因是ICS-LGMPHD 算法通过预测漏检目标状态实现漏检目标航迹维持,从而减少OSPA误差尖刺。
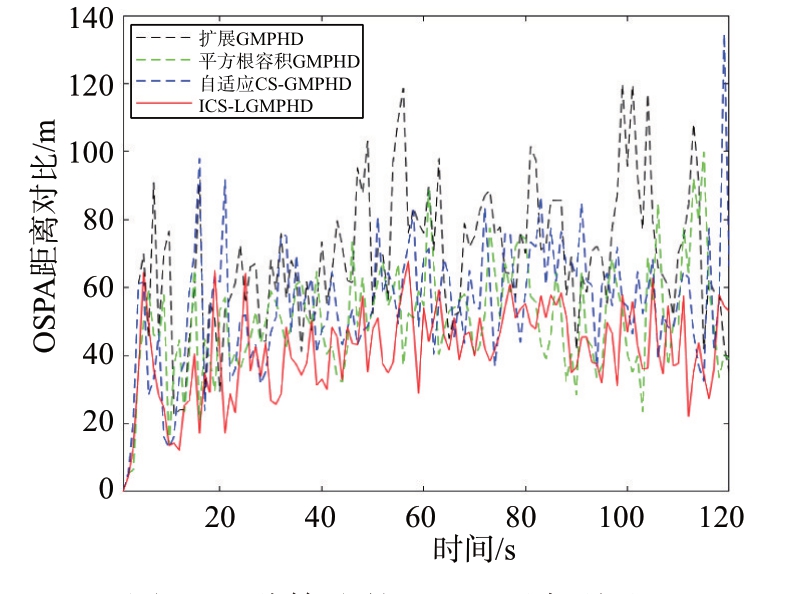
图4 4种算法的OSPA距离误差
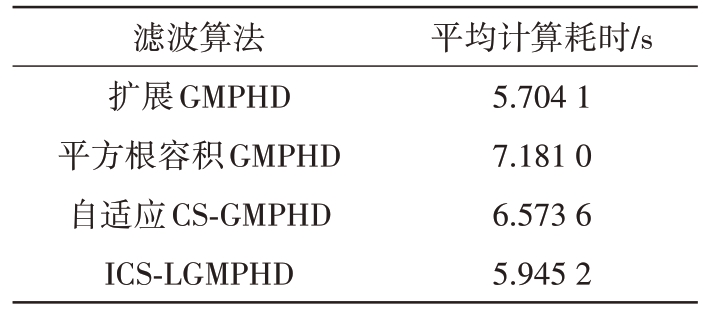
根据表5 的4 种算法平均计算耗时对比可知,ICS-LGMPHD 算法在扩展GMPHD 算法基础上引入标签化和自适应CS 模型仅增加了4.23%的计算损耗,与其他两种算法相比整体计算量较低。
表5 4种算法平均计算耗时对比
滤波算法扩展GMPHD平方根容积GMPHD自适应CS-GMPHD ICS-LGMPHD平均计算耗时/s 5.704 1 7.181 0 6.573 6 5.945 2
图5 为检测概率分别设置为0.98、0.95、0.90、0.85时,ICS-LGMPHD 算法的OSPA距离误差对比。由图5 可知,在检测概率为0.98、0.95、0.90 时,OSPA 误差整体变化并不明显,而当检测概率下降至0.85 时,此时OSPA 误差尖刺增多,且峰值较高。这说明随着检测概率的下降,ICS-LGMPHD 算法误差整体波动微弱,但误差尖刺增多,且误差尖刺值随着检测概率下降而增大。故ICS-LGMPHD 算法在系统检测概率较高时算法跟踪效果更佳。
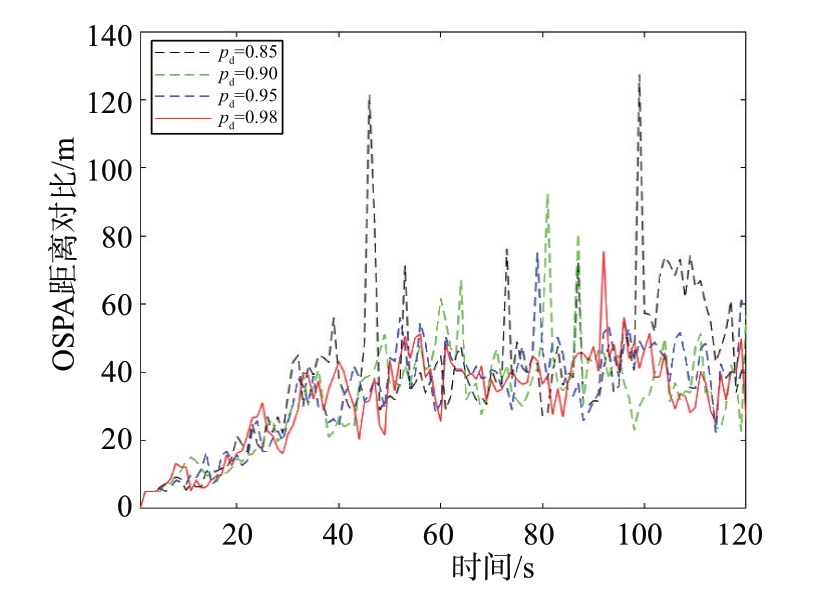
图5 不同检测概率下ICS-LGMPHD算法的OSPA距离误差
4 结束语
本文提出的ICS-LGMPHD 滤波算法,通过为每个高斯项加注标签,保证在低计算量的同时实现目标航迹的显式区分,并利用漏检标签集结合目标运动方程对漏检目标航迹外推,实现了高机动多目标跟踪场景下目标与航迹的准确关联。算法通过实时在线调整多目标各自对应模型参数,提升目标模型与其真实运动状态的匹配度,将目标机动性突变实时反馈在目标状态估计上,提高了对高机动多目标的跟踪精度。通过仿真对比扩展GMPHD 算法、平方根容积GMPHD 算法和自适应CS-GMPHD 算法,验证了本文所提算法以较低计算量实现显式区分目标航迹、自适应跟踪高机动多目标,且具有较高跟踪精度。
[1]GOODMAN I R, MAHLER R P, NGUYEN H T. Mathematics of Data Fusion[M].Netherlands:Springer,1997.
[2]MAHLER R P S. Multitarget Bayes Filtering via First-Order Multitarget Moments[J]. IEEE Trans on Aerospace and Electronic Systems,2003,39(4):1152-1178.
[3]VO B N,MA W K.A Closed-Form Solution for the Probability Hypothesis Density Filter[C]//The 7th International Conference on Information Fusion,Philadelphia, PA, USA:IEEE,2005:856-863.
[4]PANTA K,CLARK D E.Data Association and Track Management for the Gaussian Mixture Probability Hypothesis Density Filter[J].IEEE Trans on Aerospace and Electronic Systems,2009,45(3):1003-1016.
[5]覃俊慧.车载毫米波FMCW MIMO 雷达目标跟踪技术研究[D].桂林:桂林电子科技大学,2023.
[6]程瑾.雷达高机动多目标跟踪算法研究[D].西安:西安电子科技大学,2019.
[7]LIU Zhe, JI Linna, YANG Fengbao, et al. Cubature Information Gaussian Mixture Probability Hypothesis Density Approach for Multi Extended Target Tracking[J]. IEEE Access,2019,7:103678-103692.
[8]柳毅,张淑芳,索继东.基于GM-PHD 的目标空间分布感知算法[J].雷达科学与技术,2020,18(3):279-286.
[9]陈玲.基于贝叶斯滤波理论的多目标协同跟踪方法研究[D].镇江:江苏大学,2022.
[10]安思宇.基于随机有限集的多目标跟踪研究[D].哈尔滨:哈尔滨工程大学,2020.
[11]国强,卢宇翀,戚连刚,等.多普勒雷达下的机动多目标跟踪算法[J].西安交通大学学报,2023,57(9):174-184.
[12]鲁其兴,汤新民,周杨.基于双变量自适应“当前”统计模型的场面4D 轨迹跟踪预测[J].系统工程与电子技术,2024,46(2):675-683.
[13]韩清华,龙伟军,杨振,等.机动目标跟踪时组网机会阵雷达功率分配算法[J].雷达科学与技术,2023,21(1):16-23.