0 引 言
雷达已成为现代社会中不可或缺的工具，其应用范围横跨自动驾驶、健康监测等多个领域，能够为人们提供全天候的信息支持，增进人们生活的便利及保障公共健康安全。随着医疗技术的持续发展和人们对健康意识的日益提高，非接触式生命体征检测技术成为雷达领域备受关注的技术之一，并被应用于许多领域。在救援救灾活动中［1-4］，通过在无人机上搭载雷达，利用该技术搜索定位灾害现场的幸存者，从而提升救援效率；在动物医疗领域［5-6］，该技术允许医护人员在无需直接接触的情况下检测动物生命体征，从而减少对野生动物的刺激，同时降低了人员受伤的风险。此外，非接触式生命体征检测技术在驾驶安全监测方面同样展示出极大潜力［7-8］，它能实时监测驾驶员的身体状态，从而预防因疲劳或突发健康问题导致的交通事故。
在雷达非接触式生命体征检测技术的研究领域，多数现有研究聚焦于静态单一目标的检测。Hu 等人［9］提出集合经验模态分解（Ensemble Empirical Mode Decomposition，EEMD）算法进行生命体征检测信号分离，改进了传统经验模态分解算法（Empirical Mode Decomposition，EMD），有效解决了如基函数的选择和模态重叠等问题。Xia 等人［10］采用变分模态分解（VMD）算法进一步解决了端点效应和模态混叠等问题。杨路等人［11］进一步将VMD 和深度学习中的长短期记忆网络相结合，并利用粒子群算法优化参数，有效提高了生命体征信号的预测准确率。在面向多目标检测的研究中，Zhao 等人［12］提出了一种用于多目标生命体征检测的信号处理算法，但在相同距离的多目标情境下存在频谱混叠、目标识别困难的问题。Zhu等人［13］提出了基于Capon 的多目标生命体征检测算法，该算法能够区分相同距离的多个目标并测出目标的生命体征，但后续缺乏有效的抗干扰处理，使得信号易受噪声干扰。Dong等人［14］提出了一种基于完全噪声辅助聚合经验模态分解（CEEMDAN）联合独立成分分析（ICA）的生命体征检测算法，该算法能利用单根接收天线检测出相同距离单元内的多个目标的生命体征。然而，受限于天线数量，该算法无法准确区分出生命体征信号所属的具体目标。
针对上述挑战，本文提出了一种新型的基于FMCW 雷达的多目标生命体征检测算法。算法首先利用距离-方位维FFT 生成距离-方位图（RA图），然后通过方差法去除静态杂波和直流分量。随后通过设定阈值来筛选出目标位置，并提取这些位置上的目标回波在特定时间内的相位变化信息。接下来，运用VMD 算法对呼吸和心跳信号进行分离和重构，并通过奇异值分解与自相关方法去除噪声，获得干净的呼吸和心跳信号。最终，应用FFT 分析得出呼吸频率和心率，准确实现多目标生命体征检测。
1 理论分析
1.1 信号模型
雷达发射的线性调频连续波信号可以写为
式中，At 表示发射信号的振幅，fc 表示起始频率，μ = B/Tc 表示调频斜率。雷达发射信号经由目标反射回来到达接收机，总共经过时间τ，则回波信号可以表示为
式中，M 表示雷达发射信号返回时的大气损耗、目标截面积、接收天线增益等因素造成的振幅变化。将雷达回波信号与发射信号进行混频，并利用低通滤波器去除高频信号，余下的中频信号可以表示为
式中σ = AtM。由于残余视频相位是τ 的平方，其值非常小可以忽略不计，再代入时延τ的表达式：
式中，d 为目标胸腔振动带来的距离微动，可以简单表示为
Ab 和Ah 分别为呼吸、心跳引起的胸腔振动幅度，
分别为呼吸和心跳随时间变化的频率。将中频信号化简得
目标胸部微动较小，除以光速后可以忽略不计。除此之外，我们关心的就是与d 相关的相位ϕ的变化：
1.2 生命体征检测算法
本文使用的雷达在获取到回波数据后会先混频成中频信号再输出到信号处理端，本文算法对中频信号进行后续的处理。本文算法对生命体征信号处理的流程分为3 个主要步骤：目标检测、相位提取和信号分离去噪，详细流程如图1所示。
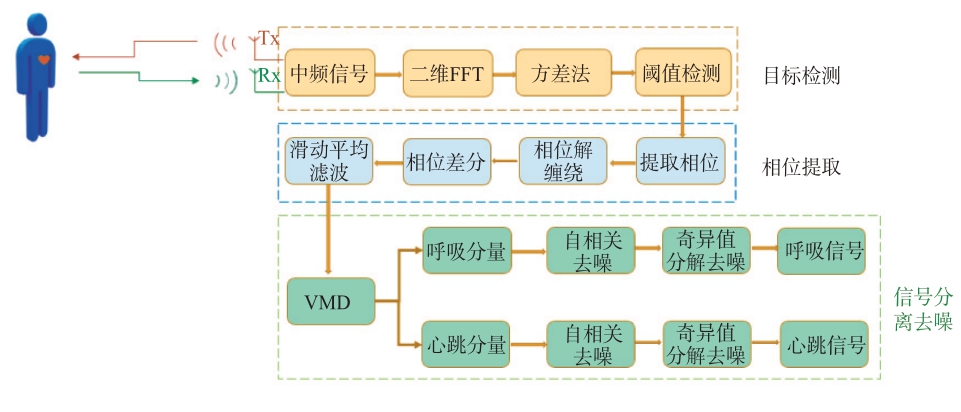
图1 生命体征信号处理流程图
1.2.1 目标检测
在获取目标胸部位移信号之前，需要确定目标的位置。雷达将回波信号进行混频处理，可以获得中频信号，该信号作为原始数据传输至信号处理单元。首先，采用距离-方位维FFT 生成包含目标位置信息的距离-方位图。然而，在雷达的探测范围内，可能存在其他物体反射的电磁波，形成静态杂波；同时，雷达硬件的固有问题和温度漂移可能产生直流分量，这两种因素均可能在RA 图中引起非目标点的干扰信号。
为了有效去除这些干扰并精确定位目标，本文算法采用方差法进行目标定位。此方法通过计算RA 图中各点的方差值来实现目标识别，其原理是人体的呼吸和心跳运动引起的胸腔起伏运动会导致目标位置处的方差值显著高于其他位置。与之相对的是，静态物体位置的方差值接近于零。因此，方差法能够有效降低由静态物体杂波和直流分量所引起的干扰，从而准确确定目标位置。目标位置处的方差计算公式如下：
式中，X(m,n)为位置
处的方差，xi 为该位置第i个啁啾（chirp）的值，
为该位置所有chirp 的均值，N为该位置的chirp数。
此时方差图中目标同一距离上依然会存在一部分干扰，但目标点的方差值远大于干扰值，因此只需要设置一个合适的阈值就能筛选出目标位置点。
1.2.2 相位提取
因为呼吸心跳引起的胸部起伏幅度非常微小，对于FMCW 雷达来说，在距离上难以分辨，但目标胸部起伏引起的雷达回波相位变化较为显著，因此需要对目标所在距离向进行相位提取。相位提取公式如下：
式中，
表示信号n 点的相位，
表示n 点的实部值，
表示n点的虚部值。
传统的arctan函数只能返回
的值，因此只能区分一、四象限的点，arctan 2函数在此基础上进行改进，能够区分4 个象限的点，arctan 2 公式如下：
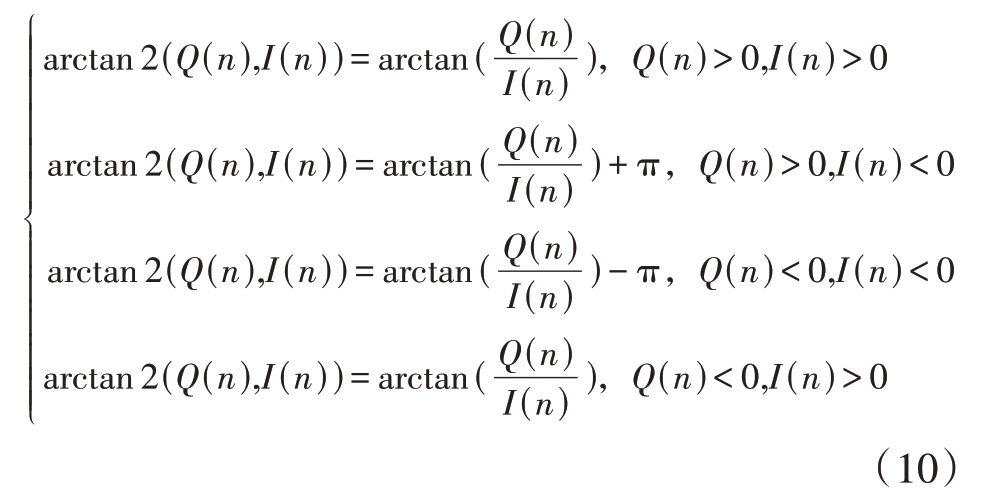
由于arctan 2 函数值的区间是
，当相位变化超过π 时，会导致相位折叠，因此需要进行相位解缠绕使得相位展开，相位解缠绕的表达式如下：
最后对相邻两点的相位作差，达到消除相位漂移的目的，得到的相位差信号可以表征胸部的振动。但此时信号包含着脉冲噪声，因此后续加入滑动平均滤波算法进行噪声滤除。
1.2.3 VMD分解
VMD 算法本质上是为了解决变分问题，它将信号分成多个本征模态函数（IMF），通过交替乘子法（ADMM）更新迭代每个IMF的中心频率及带宽，最终将每个IMF 解调到各自的基带，并提取每个IMF及其中心频率。
首先假设将胸部振动信号分解为k 个本征模态（
它们是中心频率为
的有限带宽信号，为了让每个模态的估计带宽最小，且模态的总和等于原始胸部振动信号，该约束变分问题可以表示为
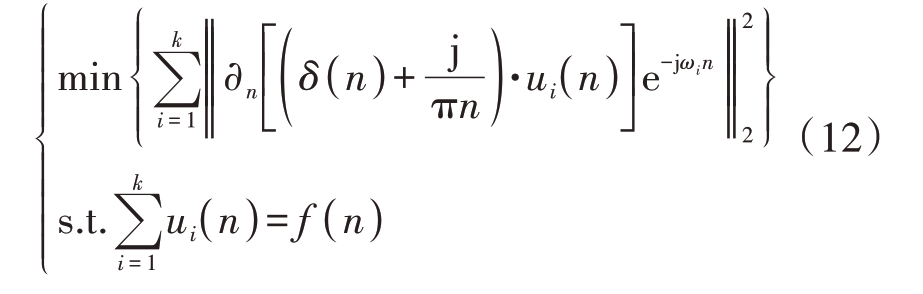
式中，
表示单位脉冲函数，
表示原始胸部振动信号。引入惩罚系数α和拉格朗日乘法算子λ可以将式（11）转化为无约束变分问题：
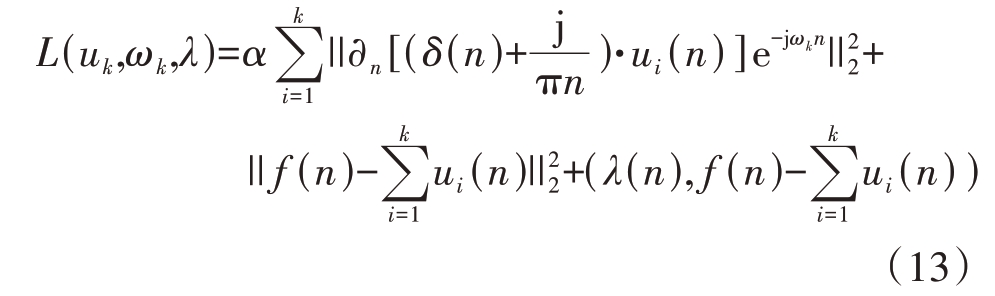
然后通过ADMM 交替迭代模态
中心频率
，拉格朗日乘数
，它们的迭代公式如下：
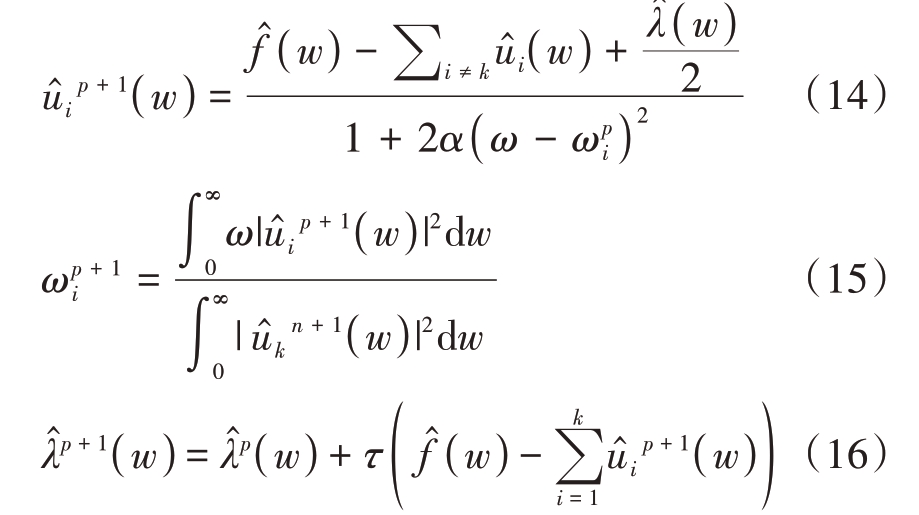
式中，p 表示迭代次数，
表示各自的FFT变换，τ表示噪声容限参数。
其中信号分解出的IMF 数量k 决定了信号的分解程度，合适的k值能够将原信号的不同分量较好地分离出来，但k 值选取过小时，会造成信号分解不够充分，IMF中依然含有多个分量；k值选取过大时，会造成信号分解过头，导致原信号中的一个分量分解成多个子模态。
惩罚系数α 决定了本征模态的带宽。α 越小，本征模态分量带宽越大，但带宽过大会使得一个本征模态分量包含原信号的多个分量；相反，α 越大，本征模态分量带宽越小，但带宽过小会使得分解后的信号不完全。
为了获取合适的
，本文采用融合鱼鹰和柯西变异的麻雀优化算法选取最优的参数组合。在将信号分解成多个IMF 后，选取呼吸和心跳频谱范围的IMF进行信号重构，摒弃无用分量。
1.2.4 奇异值分解与自相关去噪
自相关方法是利用信号的时域相关性降低噪声水平。假设离散信号序列长度为N，信号
的自相关估计的公式可以表示为
其中自相关也分为有偏估计和无偏估计，有偏估计（biased）和无偏估计（unbiased）的表达式可以分别表示如下：
有偏估计：
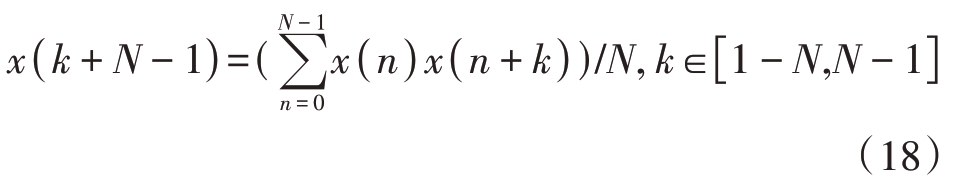
无偏估计：
信号进行自相关之后，信号的频率不变，噪声会被抑制。此时信号长度变成了2N - 1，点数增加了一倍，所以信号频谱的分辨率也增加了一倍。
奇异值分解是指对于一个m × n 阶的实矩阵A，一定存在m 阶正交矩阵U 和n 阶正交矩阵V，使得矩阵A能够分解为下式表示：其中Σ 为矩阵A 的全部非零奇异值组合成的对角矩阵
的前几个奇异值较大，包含了矩阵A的大部分信息。
对信号进行奇异值去噪，首先要将信号序列重构成一个大小合适的矩阵形式，然后对该矩阵进行奇异值分解，保留奇异值较大的部分，而将奇异值较小部分置为零，通过这种方式可以有效地移除信号中的噪声成分。需要指出的是，SVD 去噪方法在噪声水平相对较低时可能不会表现出显著的去噪效果，但在噪声较强的情况下，此方法能显著提高信号的信噪比。此外当噪声能量超过信号本身时，使用SVD 去噪存在信号丢失的风险。为了降低这种风险，本算法在执行SVD 去噪前，先对信号进行自相关去噪处理，为后续SVD 去噪提供一个更为干净的信号基础。
2 实验测试与结果分析
2.1 实验准备
本实验采用TI 旗下的型号为AWR1843 的77 GHz 毫米波雷达板进行数据采集，并利用Matlab R2022a平台进行数据处理。雷达参数值如表1所示。
表1 雷达参数配置
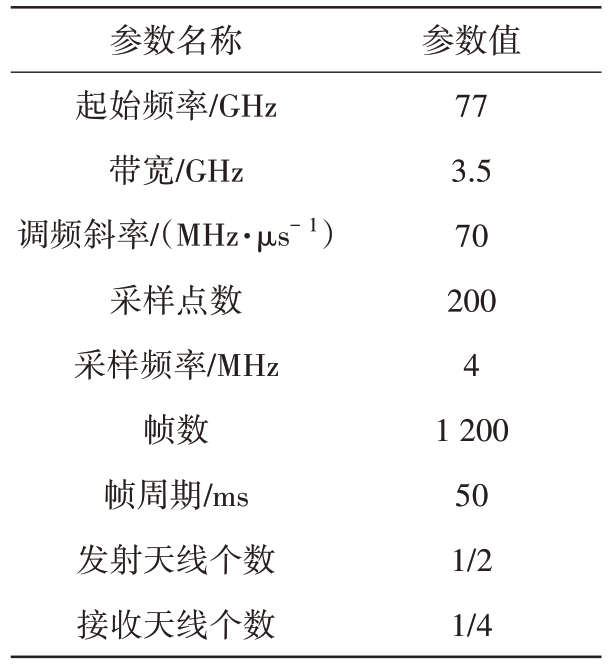
参数名称起始频率/GHz带宽/GHz调频斜率/（MHz·μs- 1）采样点数采样频率/MHz帧数帧周期/ms发射天线个数接收天线个数参数值77 3.5 70 200 4 1 200 50 1/2 1/4
实验场地选择了一间空旷的大教室，可以减少静态杂波的干扰，实验场地布置的斜视图和侧视图如图2和图3所示。
图2 实验场地斜视图
图3 实验场地侧视图
本次设计的实验分为两大类，以评估所提算法在不同情境下的性能表现。一是当受试者与雷达的相对位置跨越不同的距离单元时，雷达采用单发单收模式进行数据采集，此时仅使用单通道数据进行信号处理，并将算法中的距离-方位维FFT 简化为仅针对距离维的FFT。二是当受试者位于相同距离单元内时，雷达采用二发四收的MIMO 模式采集数据并对信号执行完整算法流程。为进一步评估算法性能，每种实验设置下又细分为双目标和三目标两种情况，共构成4个不同的实验场景，如图4和图5所示。
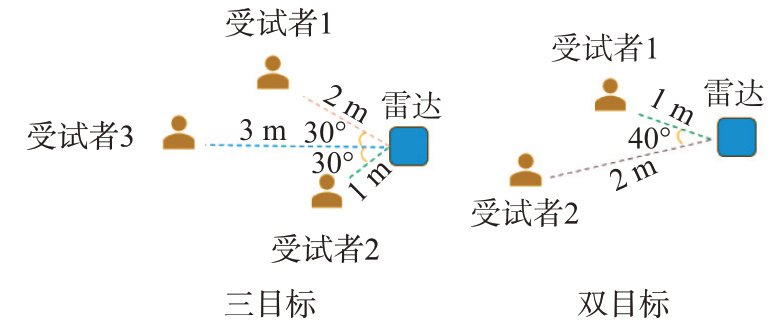
图4 不同距离目标示意图
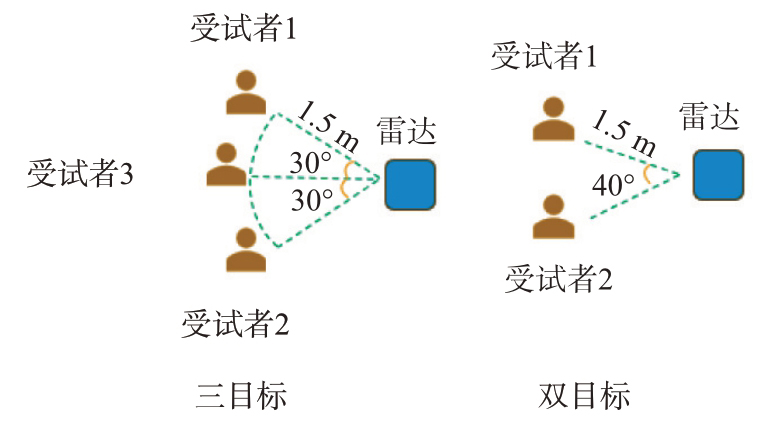
图5 相同距离目标示意图
本实验的参考设备使用ADS1292R 盾板心电采集传感器和指夹式脉搏血氧仪。设备示意图如图6 所示。其中ADS1292R 盾板心电采集传感器可以通过电极贴采集人体的心电信号，并能够导入Matlab 平台与实验信号进行对比；指夹式脉搏血氧仪可以较为准确地测得短时间内的心跳频率变化。图7 是ADS1292R 盾板心电采集传感器采集的心电数据所绘制的波形图。
图6 实验设备示意图
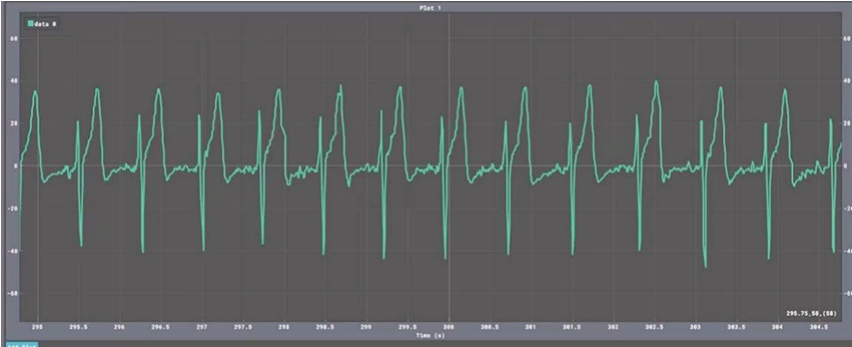
图7 心电数据波形图
2.2 实验结果
2.2.1 目标检测
图8 和图9 分别是对两种场景的原始信号进行距离维FFT 和距离-方位维FFT 得到的时距图和RA图，可以看出图中还存在直流分量和杂波。图10和图11 分别是进行方差法处理后的结果，直流分量和静态杂波已被去除，只剩下目标点存在较高的幅值，此外由图10 可以看出如果目标处于同一距离将无法分辨，图11 进行二维FFT 后则可以进行有效区分。实验结果表明，方差法可以有效地剔除直流分量和静态杂波干扰。经过方差法处理后，在目标同距离维度上仍然存在低幅度的频谱泄露，对目标检测造成干扰。常用的解决频谱泄露的方法如加汉宁窗会在一定程度上影响目标的定位，因此本文设置阈值进行筛选，确定目标位置，如图12所示。
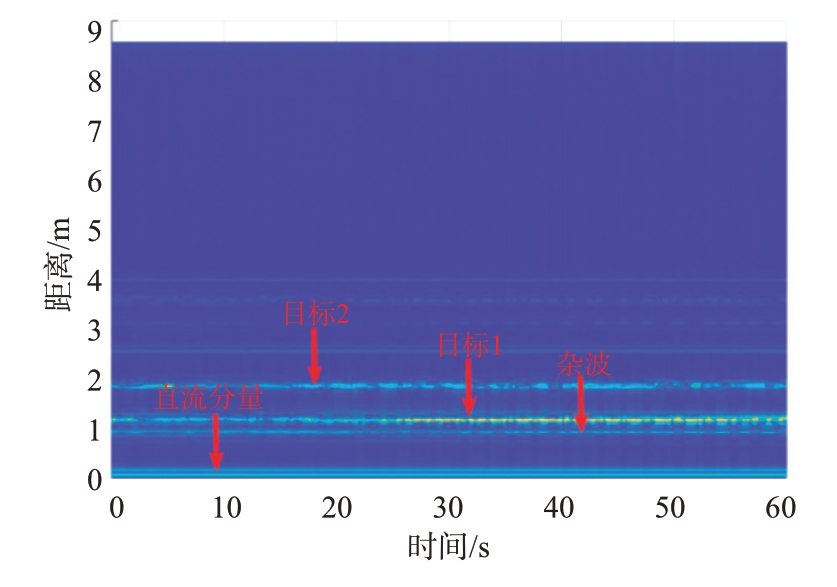
图8 不同距离目标时距图
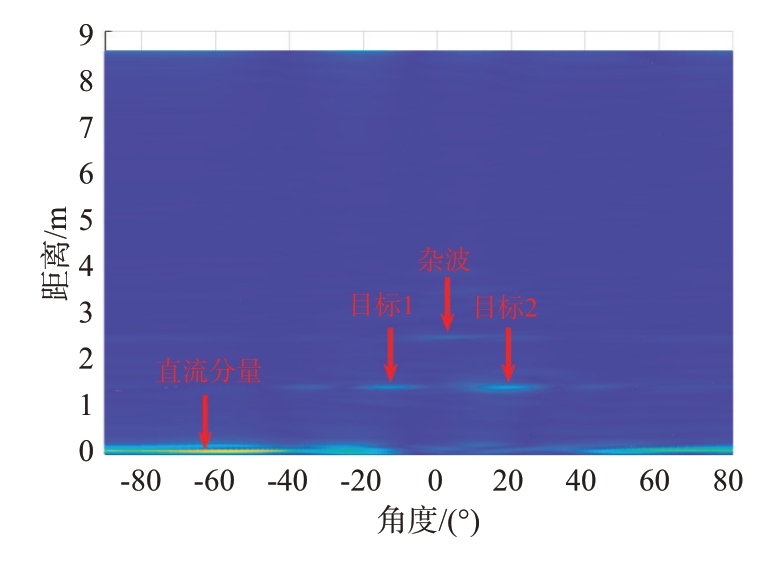
图9 相同距离目标RA图
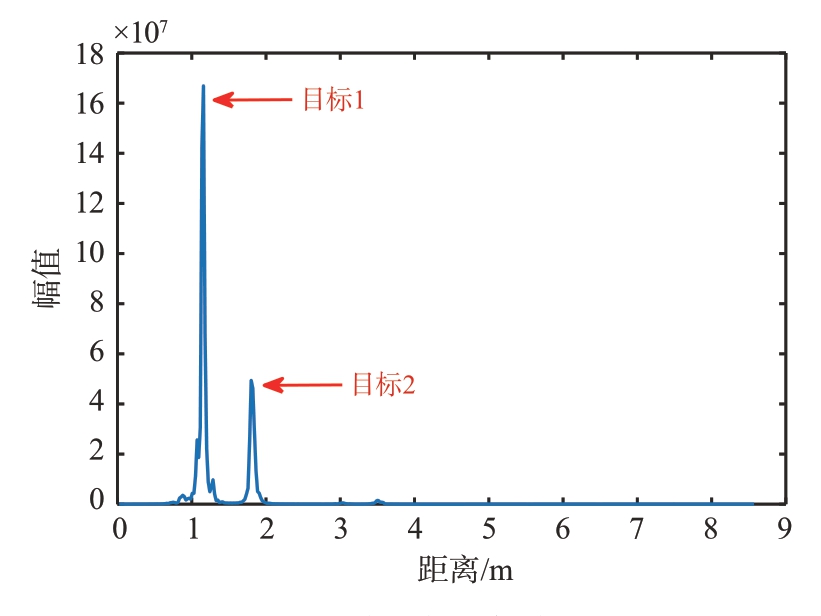
图10 不同距离目标方差图
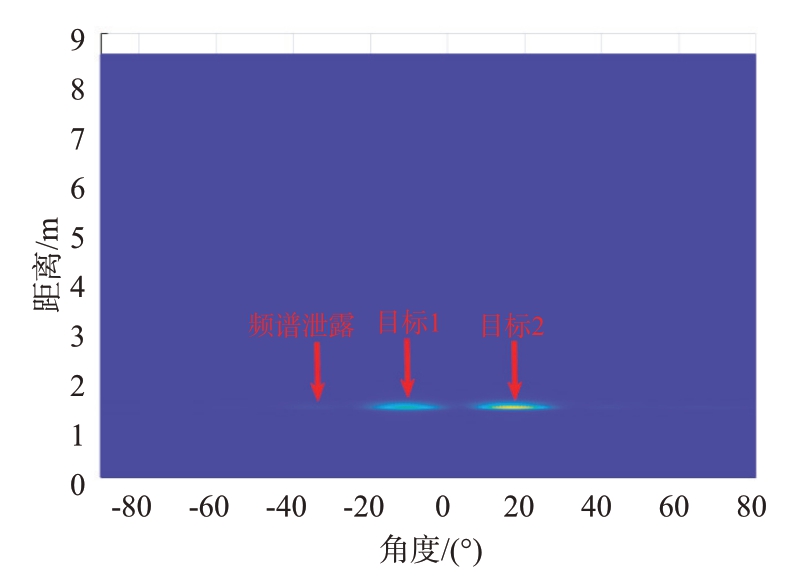
图11 相同距离目标方差图
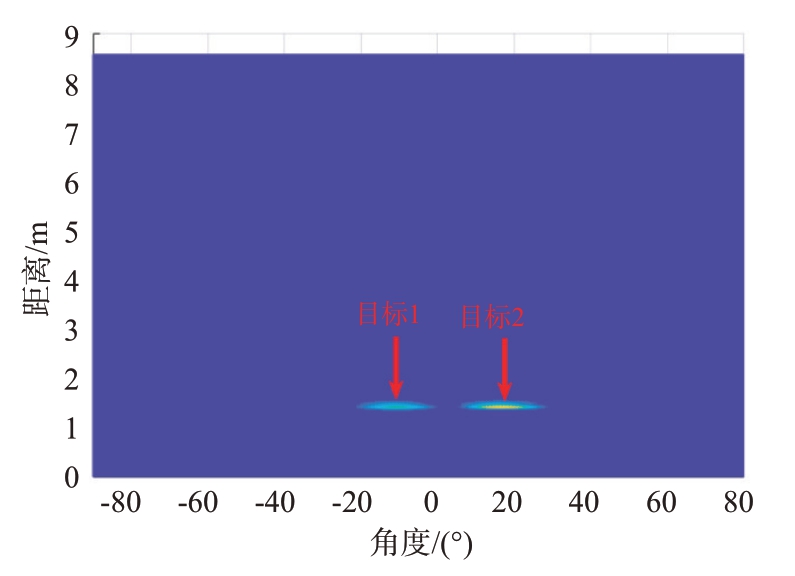
图12 阈值检测图
2.2.2 相位提取
确定了目标位置后，就可以提取相位信号。图13（a）展示了提取出的目标原始相位变化信息，图13（b）展示了相位解缠绕后的波形，然后进行相位差分，消除相位偏移得到图13（c）展示的相位波形。最后利用滑动平均滤波法滤除脉冲噪声，得到图13（d）的相位变化波形。
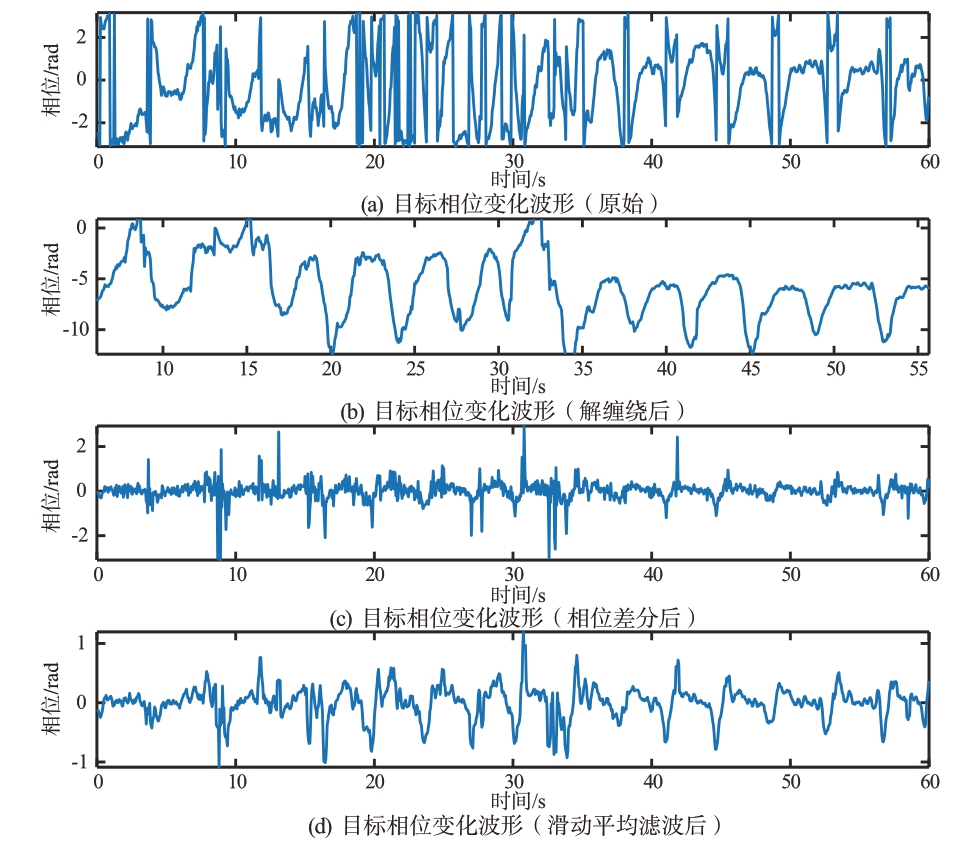
图13 相位波形图
2.2.3 信号分离
图14所示结果为采用融合鱼鹰和柯西变异的麻雀优化算法，以样本熵值作为判定依据，多次迭代确定的VMD惩罚系数及其分解层数。该优化算法展示了向期望值快速收敛的能力，表明其在参数优化方面的高效性。利用算法确定的惩罚系数和分解层数对信号执行VMD，进而获得图15 所示的各IMF。这些IMF 之间的频率重叠部分较小，分解完全。在获得这些子模态后，通过频谱筛选对它们进行了进一步的信号重构处理，得到了图16所示的重构信号。尽管该重构信号进行了初步的信号还原，但仍然存在较大的噪声。因此该重构信号需要经过进一步的降噪处理，以提高信号质量，确保分析结果的准确性。
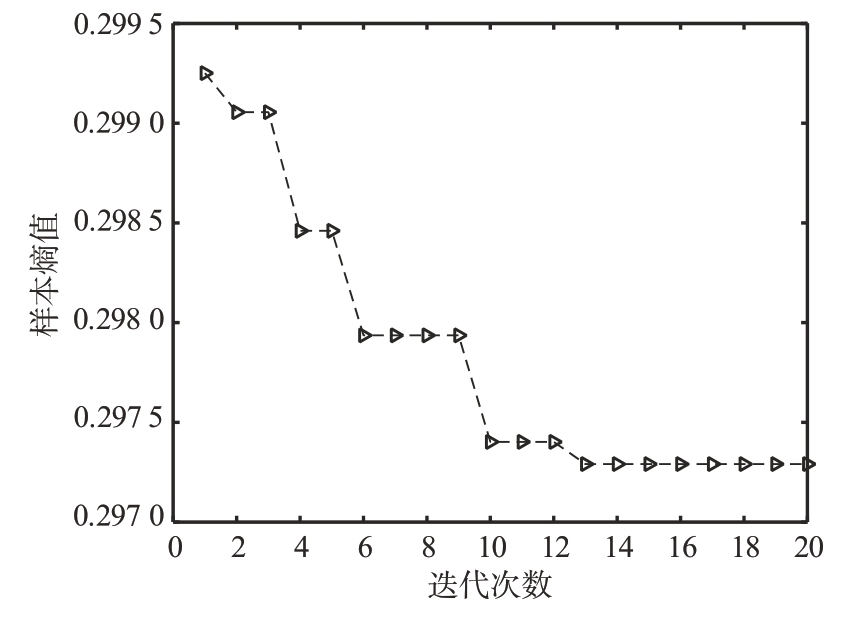
图14 融合鱼鹰和柯西变异的麻雀优化算法迭代图
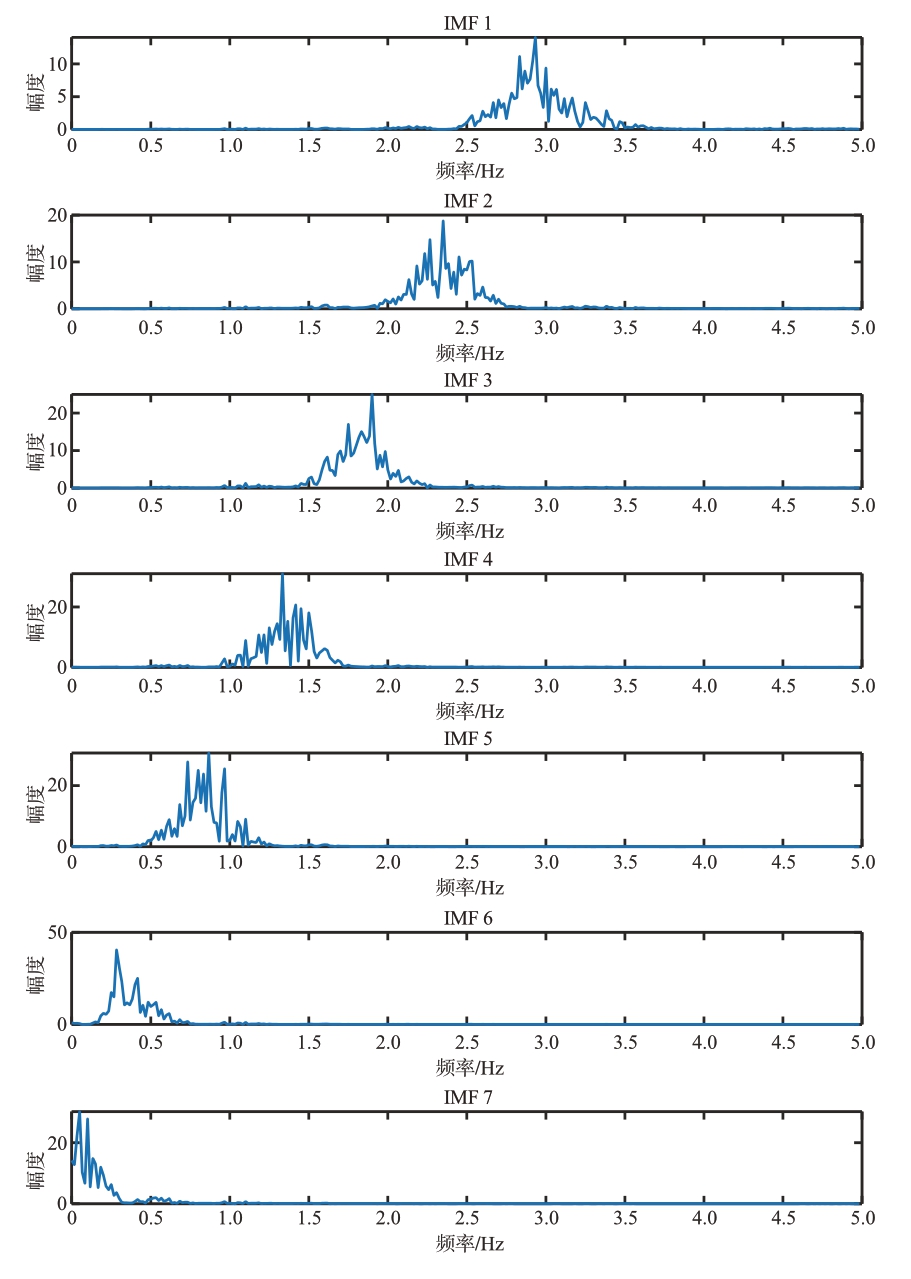
图15 VMD各子模态频谱图
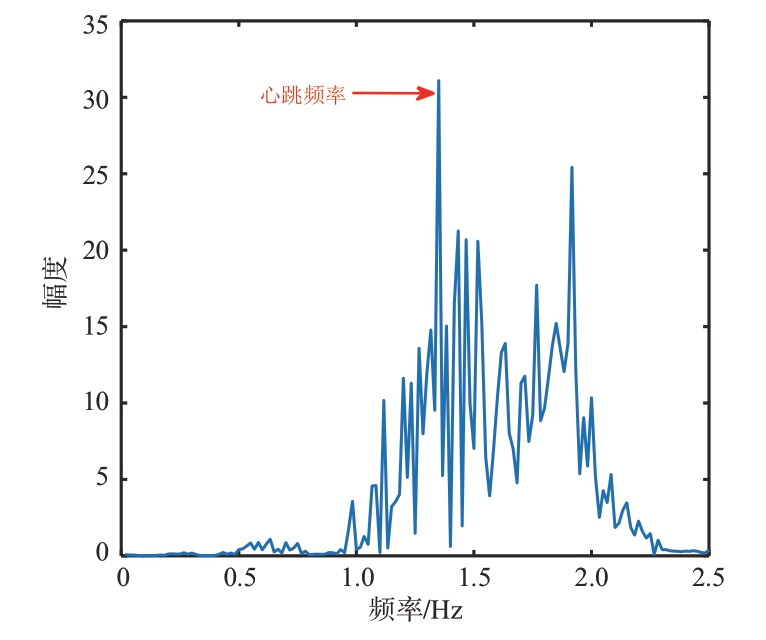
图16 VMD心跳重构信号频谱图
2.2.4 信号降噪与频率估算
对于图16 中经过初步重构的信号，首先采用自相关方法进行降噪处理以提升信噪比。处理后的信号频谱图如图17 所示，可以看出信噪比得到了一定程度的改善但信号仍受到了较为明显的噪声干扰。为了进一步提高信号质量，本算法随后采用SVD去噪方法，结果如图18所示，该方法以较小的频谱泄露为代价，基本上消除了剩余的噪声，显著提高了信号的纯净度。将分离去噪后的心跳信号与参考设备采集的ECG 信号进行对比，如图19 所示，两者在频率上展现了高度一致性，验证了算法的有效性。图20 和图21 是分离出的呼吸信号波形图和频谱图，可以看出呼吸信号在频域上能量非常集中。
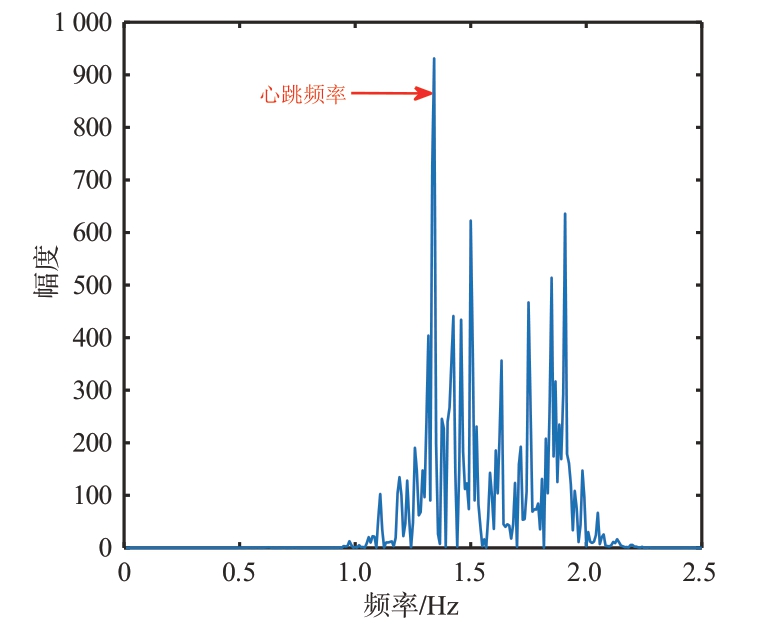
图17 自相关分解去噪效果图
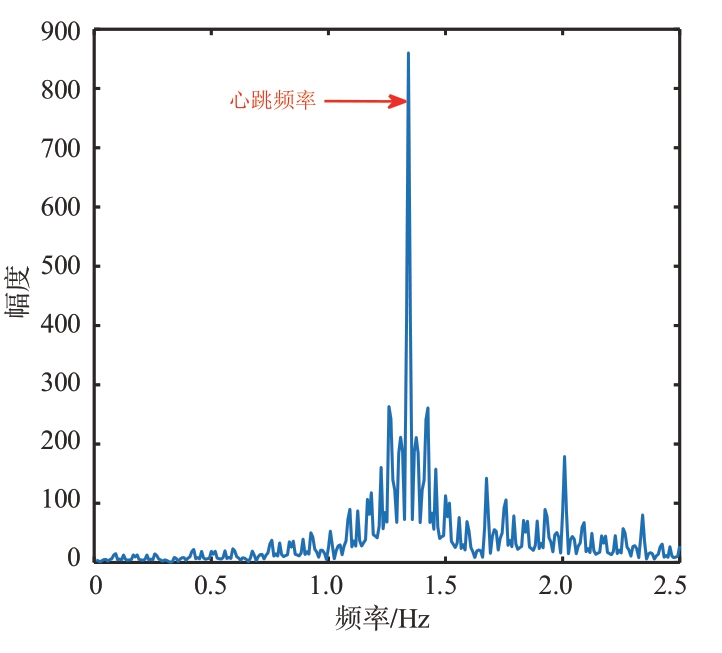
图18 SVD去噪效果图
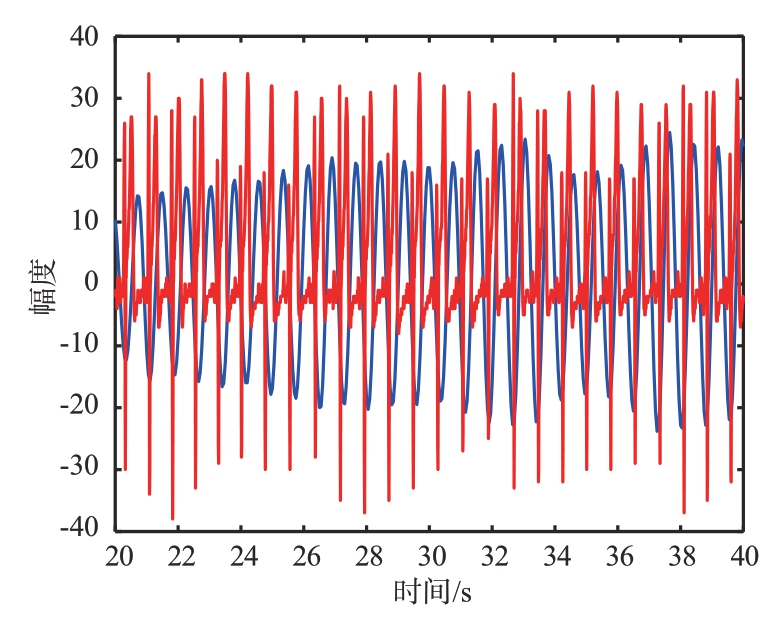
图19 心跳信号与参考信号对比图（20 s）
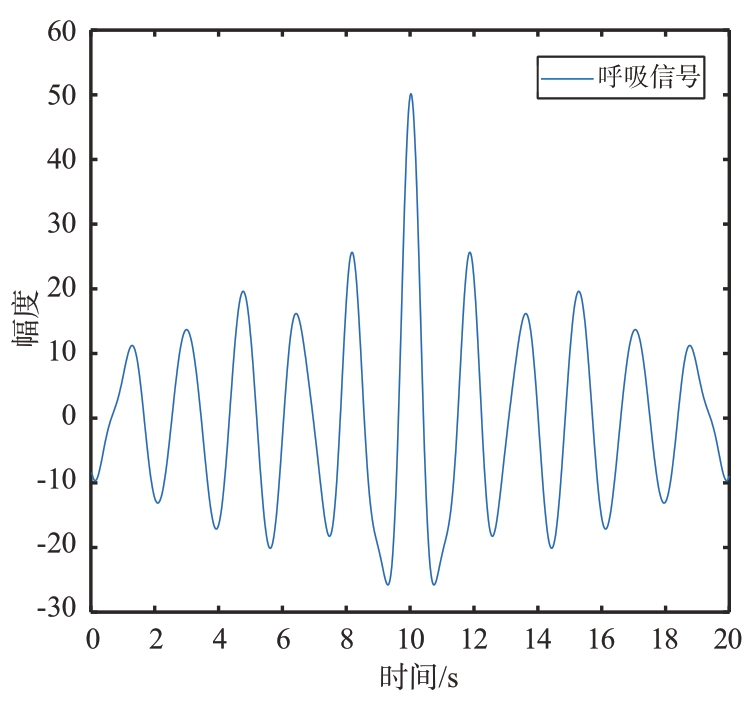
图20 呼吸信号波形图（20 s）
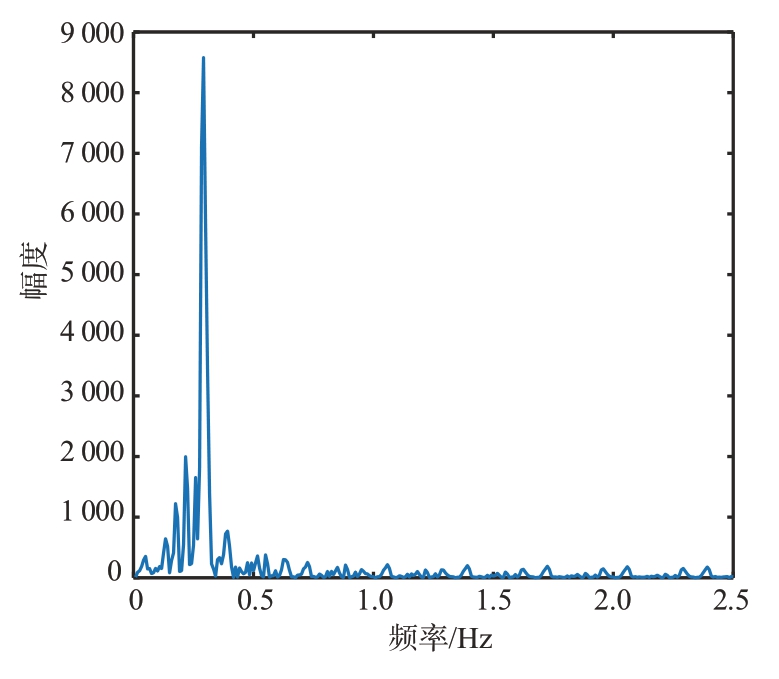
图21 呼吸信号频谱图
2.3 数据分析
为了评估不同算法的性能，本研究设计并重复执行了多组实验，分别应用FFT 频谱分析法、VMD 信号重构算法［10］、CEEMDAN-ICA 算法［14］以及本文提出的算法进行目标心率的估算，并将结果与参考设备测得的心率值进行对比，计算误差。鉴于呼吸导致的胸腔起伏幅度远大于心跳，不易区分各算法的优劣，因此本实验主要集中于分析目标的心率数据。
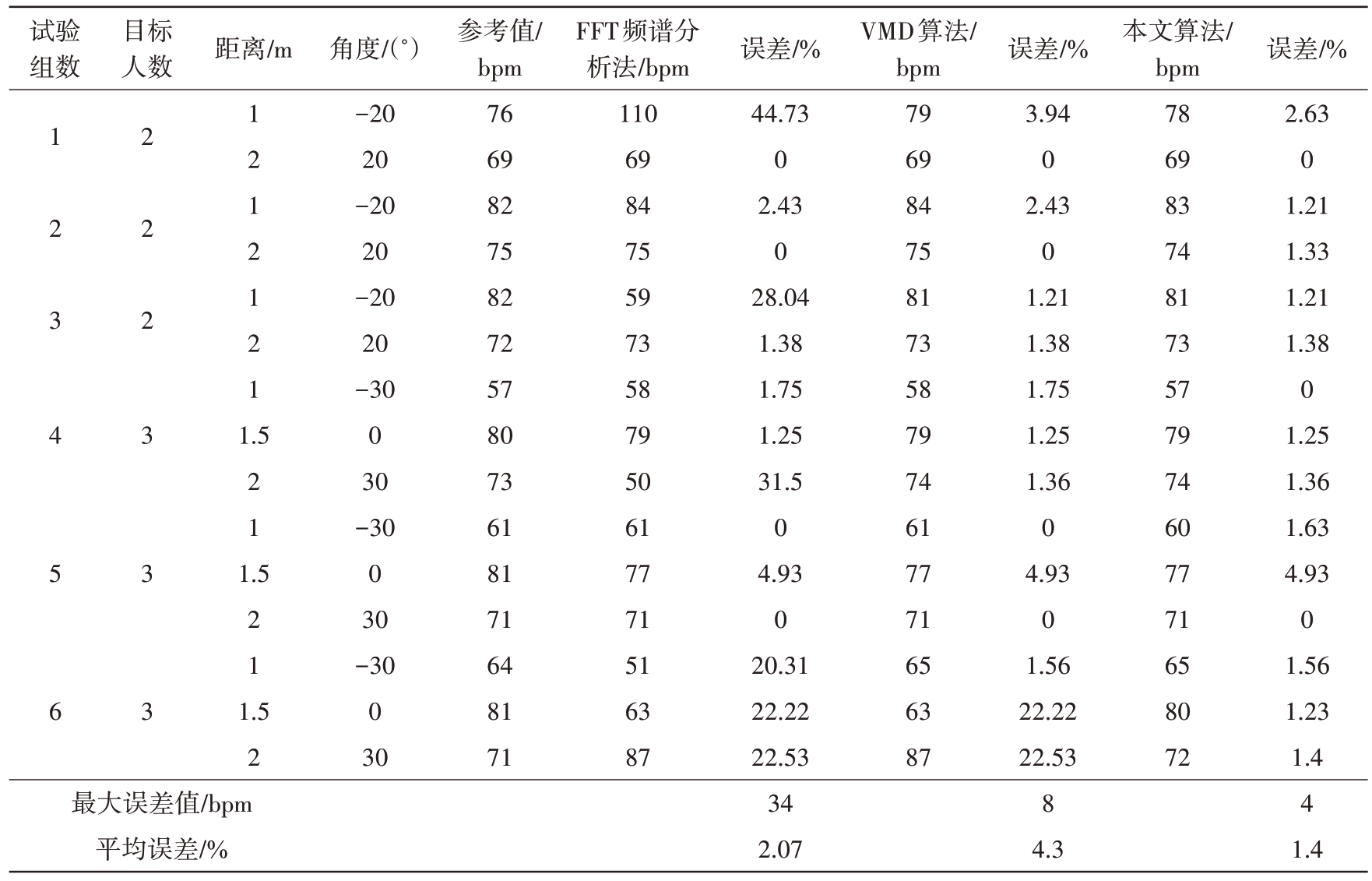
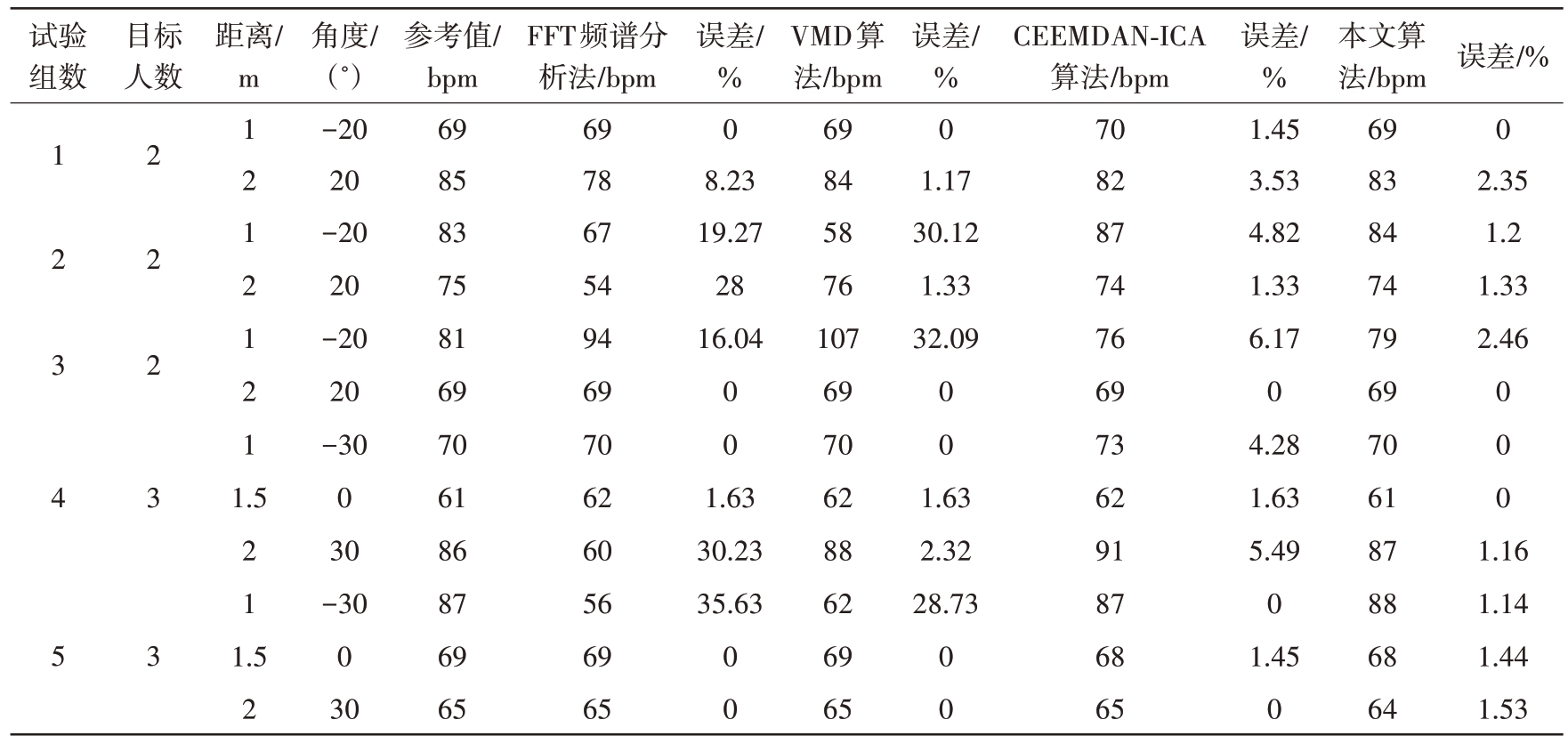
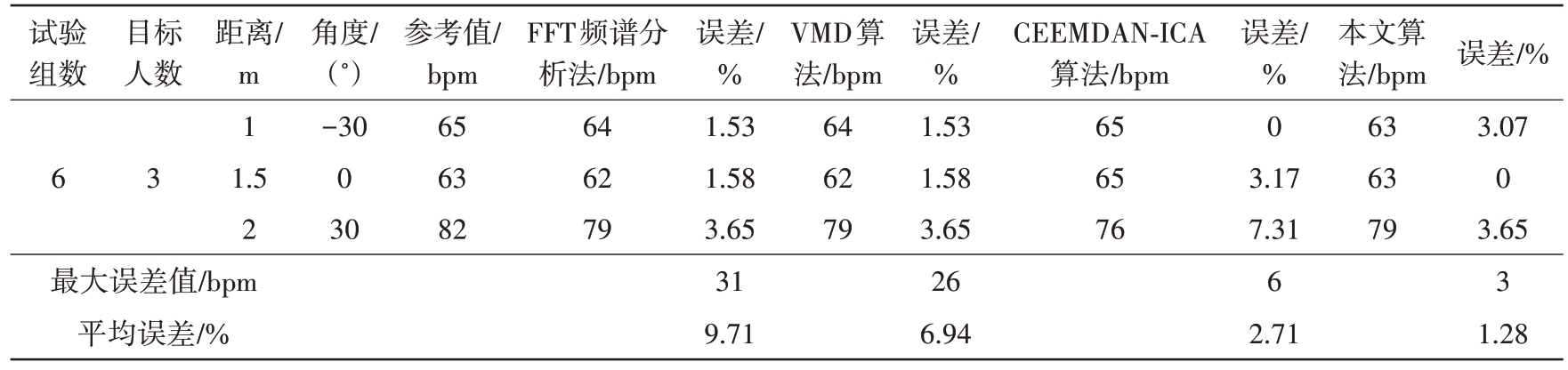
表2 是目标相距雷达不同距离情况下的多组实验数据统计，据表分析,在信号信噪比较高的情况下，3 种算法都能较为准确地估算出目标的心率；但在信号受干扰严重时，FFT 频谱分析法的心率估算准确率最低，易受杂波和噪声干扰而导致估算错误；其次是VMD信号重构算法，平均误差率相较于FFT 频谱分析法降低了7.77%，但仍受干扰影响较大；本文提出的算法准确率最高，相较于FFT 频谱分析法和VMD 信号重构算法分别降低了10.67%和2.9%。表3 是目标相距雷达同距离情况下的多组实验数据统计，本文算法相较于FFT频谱分析法、VMD 信号重构算法、CEEMDAN-ICA 算法分别降低了8.43%、5.66%和1.43%。由实验数据分析可知，本文算法在4种实验场景下均具有较高的准确率，验证了本文所提算法的有效性和普适性。
表2 不同距离目标场景下的多组实验数据统计（心率）
试验组数1 2 3 4 5 6最大误差值/bpm平均误差/%目标人数2 2 2 3 3 3距离/m 1 2 1 2 1 2 1 1.5 2 1 1.5 2 1 1.5 2角度/（°）-20 20-20 20-20 20-30 0 30-30 0 30-30 0 30参考值/bpm 76 69 82 75 82 72 57 80 73 61 81 71 64 81 71 FFT频谱分析法/bpm 110 69 84 75 59 73 58 79 50 61 77 71 51 63 87误差/%44.73 0 2.43 0 28.04 1.38 1.75 1.25 31.5 0 4.93 0 20.31 22.22 22.53 34 2.07 VMD算法/bpm 79 69 84 75 81 73 58 79 74 61 77 71 65 63 87误差/%3.94 0 2.43 0 1.21 1.38 1.75 1.25 1.36 0 4.93 0 1.56 22.22 22.53 8 4.3本文算法/bpm 78 69 83 74 81 73 57 79 74 60 77 71 65 80 72误差/%2.63 0 1.21 1.33 1.21 1.38 0 1.25 1.36 1.63 4.93 0 1.56 1.23 1.4 4 1.4
表3 相同距离目标场景下的多组实验数据统计（心率）
1 2 3 4 5 2 2 2 3 3 1 2 1 2 1 2 1 1.5 2 1 1.5 2-20 20-20 20-20 20-30 0 30-30 0 30 69 85 83 75 81 69 70 61 86 87 69 65 69 78 67 54 94 69 70 62 60 56 69 65 0 8.23 19.27 28 16.04 0 0 1.63 30.23 35.63 0 0 69 84 58 76 107 69 70 62 88 62 69 65 0 1.17 30.12 1.33 32.09 0 0 1.63 2.32 28.73 0 0 70 82 87 74 76 69 73 62 91 87 68 65 1.45 3.53 4.82 1.33 6.17 0 4.28 1.63 5.49 0 1.45 0 69 83 84 74 79 69 70 61 87 88 68 64 0 2.35 1.2 1.33 2.46 0 0 0 1.16 1.14 1.44 1.53试验组数目标人数距离/m角度/（°）参考值/bpm FFT频谱分析法/bpm误差/%VMD算法/bpm误差/%CEEMDAN-ICA算法/bpm误差/%本文算法/bpm 误差/%
续表
6最大误差值/bpm平均误差/%3 1 1.5 2-30 0 30 65 63 82 64 62 79 1.53 1.58 3.65 31 9.71 64 62 79 1.53 1.58 3.65 26 6.94 65 65 76 0 3.17 7.31 6 2.71 63 63 79 3.07 0 3.65 3 1.28试验组数目标人数距离/m角度/（°）参考值/bpm FFT频谱分析法/bpm误差/%VMD算法/bpm误差/%CEEMDAN-ICA算法/bpm误差/%本文算法/bpm 误差/%
2.4 抗干扰实验分析
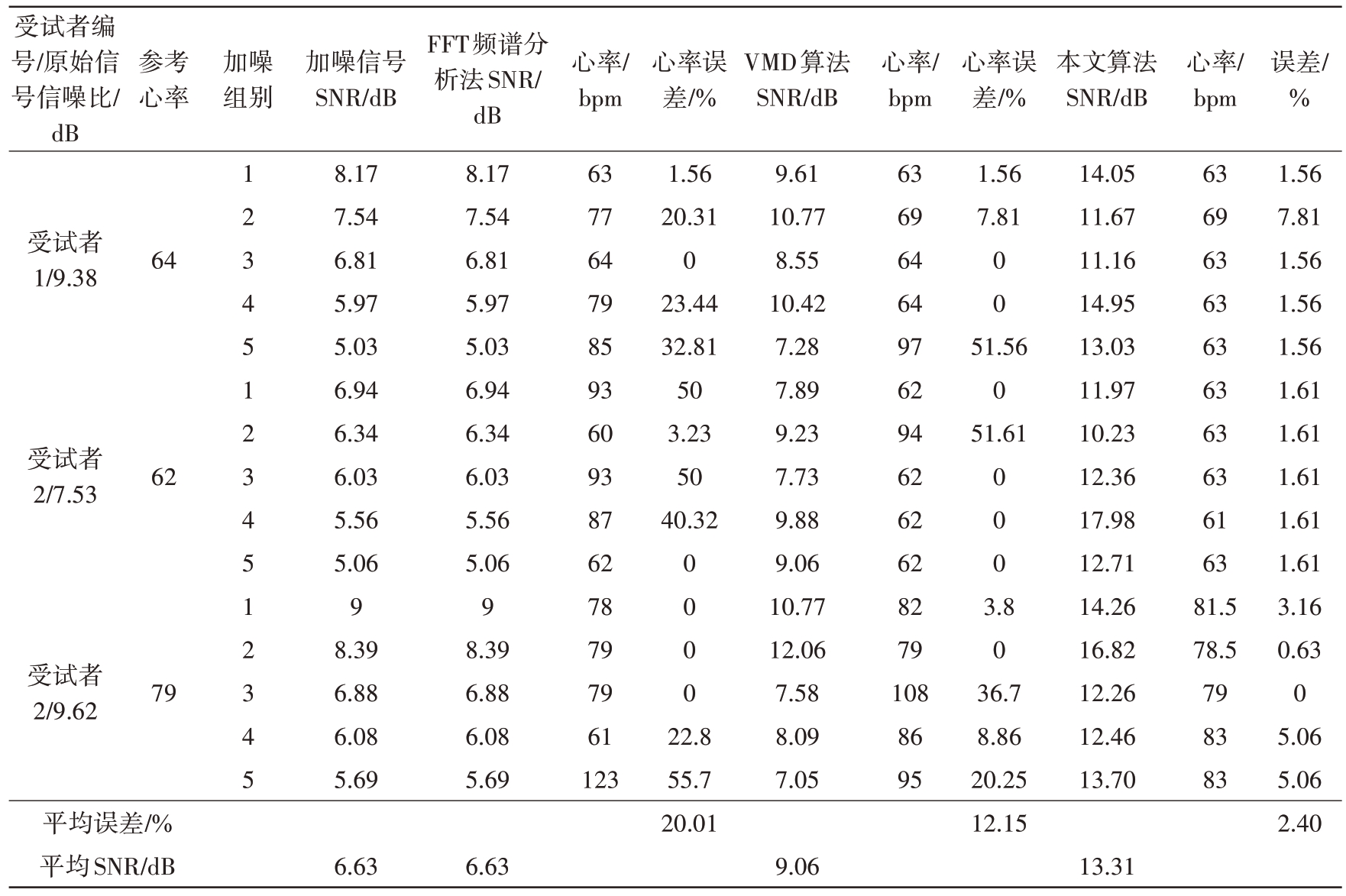
为了进一步验证本文算法的抗干扰性能，我们在上述测得的数据基础上添加了一定程度的人为噪声，以评估该算法在噪声环境下的鲁棒性。本次实验挑选了上述相同距离目标场景下的其中一组实验数据，对每位受试者的生命体征信号分别添加不同程度的噪声，共5 组，以心率误差和信号信噪比（SNR）为评估标准，检测不同算法在干扰情况中的鲁棒性。
表4记录了实验数据及计算得出的平均误差。从表中可以看出，加噪信号的SNR 相对于原始信号减少了1～4 dB 不等。其中，FFT 频谱分析法测得的平均心率误差为20.01%，信噪比无变化；VMD算法测得的平均心率误差为12.14%，信噪比增加了2.43 dB；本文算法测得的平均心率误差为2.4%，信噪比增加了6.68 dB，验证了本算法在抗干扰性能方面的优越性。
表4 算法鲁棒性试验
受试者编号/原始信号信噪比/dB受试者1/9.38受试者2/7.53受试者2/9.62平均误差/%平均SNR/dB参考心率64 62 79加噪组别1 2 3 4 5 1 2 3 4 5 1 2 3 4 5加噪信号SNR/dB 8.17 7.54 6.81 5.97 5.03 6.94 6.34 6.03 5.56 5.06 9 8.39 6.88 6.08 5.69 6.63 FFT频谱分析法SNR/dB 8.17 7.54 6.81 5.97 5.03 6.94 6.34 6.03 5.56 5.06 9 8.39 6.88 6.08 5.69 6.63心率/bpm 63 77 64 79 85 93 60 93 87 62 78 79 79 61 123心率误差/%1.56 20.31 0 23.44 32.81 50 3.23 50 40.32 0 0 0 0 22.8 55.7 20.01 VMD算法SNR/dB 9.61 10.77 8.55 10.42 7.28 7.89 9.23 7.73 9.88 9.06 10.77 12.06 7.58 8.09 7.05 9.06心率/bpm 63 69 64 64 97 62 94 62 62 62 82 79 108 86 95心率误差/%1.56 7.81 0 0 51.56 0 51.61 0 0 0 3.8 0 36.7 8.86 20.25 12.15本文算法SNR/dB 14.05 11.67 11.16 14.95 13.03 11.97 10.23 12.36 17.98 12.71 14.26 16.82 12.26 12.46 13.70 13.31心率/bpm 63 69 63 63 63 63 63 63 61 63 81.5 78.5 79 83 83误差/%1.56 7.81 1.56 1.56 1.56 1.61 1.61 1.61 1.61 1.61 3.16 0.63 0 5.06 5.06 2.40
2.5 工程应用边界条件分析
此外，本文针对实际工程应用进行了边界条件分析实验。在上述的实验条件下，利用本算法进行多目标生命体征检测的最小距离约为0.6 m，在此距离下目标之间的间隔角度最小约为40°，如图22 所示；最大约为130°，如图23 所示；最大距离约为4 m，在此距离下两个目标间的间隔角度最小约为20°，如图24 所示；最大间隔角度约为60°，如图25所示。
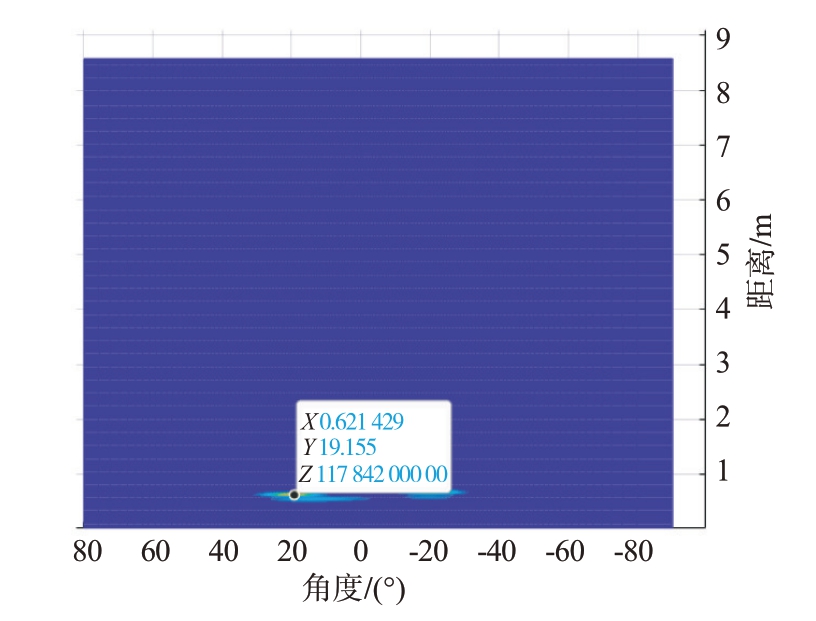
图22 最小距离-最小间隔角度阈值检测图
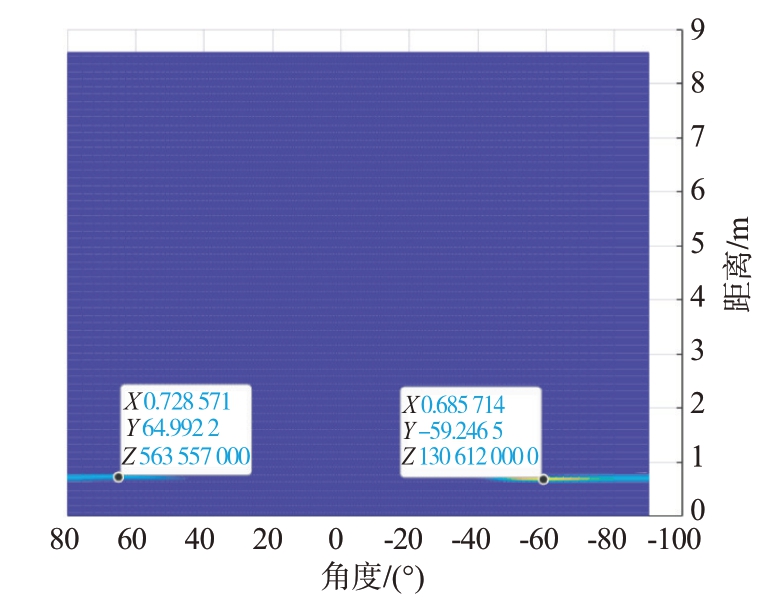
图23 最小距离-最大间隔角度阈值检测图
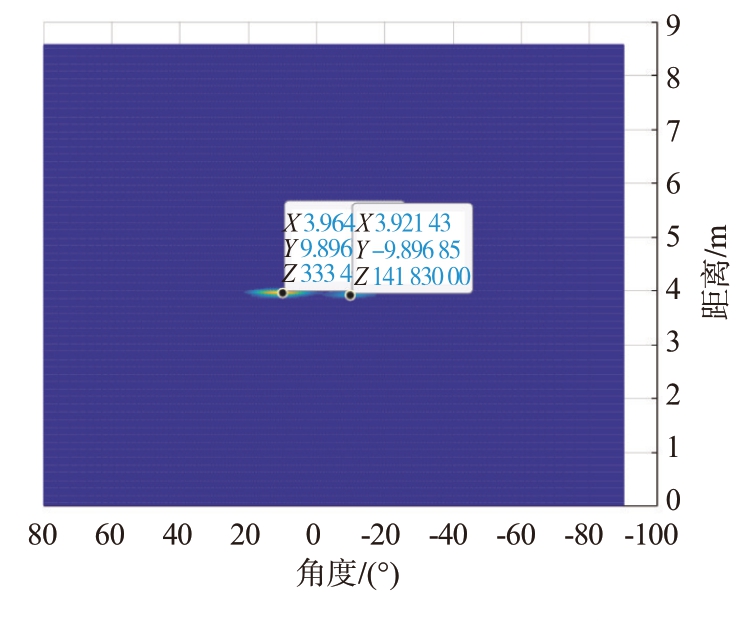
图24 最大距离-最小间隔角度阈值检测图
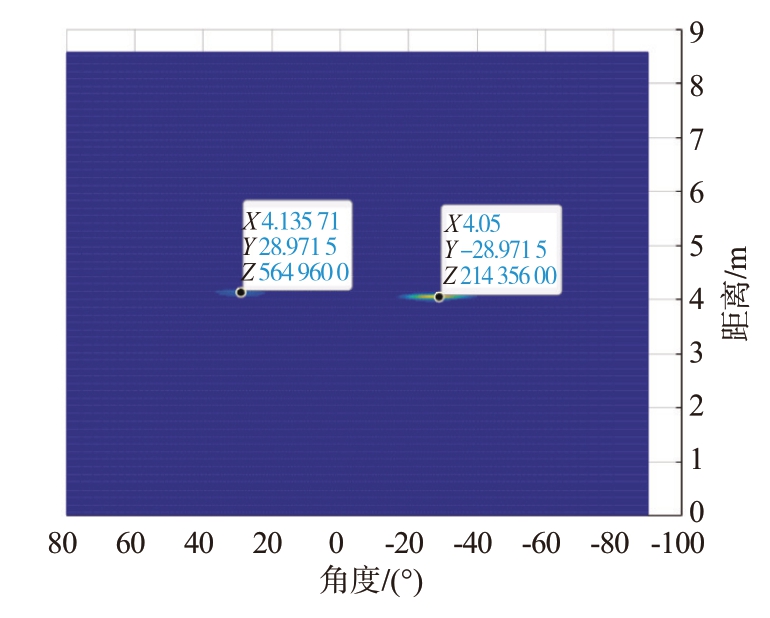
图25 最大距离-最大间隔角度阈值检测图
本次实验结果测得的最小距离和该距离下的最小间隔角度受限于人体目标的体积，因为人体目标是大体积目标，两目标间会有一定距离上的间隔，同理，最小距离下的最大间隔角度也是受限于人体目标体积，因为这种情况下人体一部分会超过雷达的探测角度，因此在用于单目标生命体征检测时，该距离能进一步减小。而雷达进行多目标生命体征检测的最大距离和该距离下的最大间隔角度则受限于雷达的硬件条件，包括天线的发射功率、接收天线的增益等；最大距离下的最小间隔角度受限于天线数量。因此要改善工程应用边界条件，可以增加雷达发射天线的发射功率、接收天线的接收增益、天线数量等措施。
3 结束语
在面对雷达多目标生命体征检测场景中存在的挑战，特别是多个目标位于相同距离和心跳信号容易受到干扰的问题时，本研究提出了一种新的基于调频连续波（FMCW）雷达的多目标生命体征检测算法。通过对实验数据的深入分析，论证了该算法的有效性与普适性。
本文算法采用距离-方位维FFT 与方差法的结合，成功消除了静态杂波和直流分量的干扰，实现了对同一距离以及不同距离上的多个目标的有效检测。此外，通过应用VMD 信号重构法并结合自相关方法与SVD 去噪，能够有效滤除噪声，提高了对目标生命体征信号的检测准确率，相比于传统的检测算法具备更高的准确率。
多个不同场景下的测试结果和鲁棒性实验进一步验证了本研究提出算法的可行性和准确性，此外还进行了工程应用边界条件分析，为技术落实到实际应用提供了一些指标和方向。通过这些实验验证，本研究解决了现有技术中存在的一些问题，为雷达多目标生命体征检测技术的发展提供了一项有效的技术方案。
［1］CHAVES C S, GESCHKE R H, SHARGORODSKYY M,et al. Multisensor Polarimetric MIMO Radar Network for Disaster Scenario Detection of Persons［J］.IEEE Microwave and Wireless Components Letters,2021,32（3）:238-240.
［2］ROHMAN B P A, RUDRAPPA M T, SHARGORODSKYY M, et al. Moving Human Respiration Sign Detection Using mm-Wave Radar via Motion Path Reconstruction［C］//2021 International Conference on Radar, Antenna, Microwave, Electronics and Telecommunications,Bandung,Indonesia:IEEE,2021:196-200.
［3］STOCKEL P, WALLRATH P, HERSCHEL R, et al. Detection and Monitoring of People in Collapsed Buildings Using a Rotating Radar on a UAV［J］. IEEE Trans on Radar Systems,2023,2:13-23.
［4］CHAVES C S, GESCHKE R H, SHARGORODSKYY M,et al. Polarimetric UAV-Deployed FMCW Radar for Buried People Detection in Rescue Scenarios［C］//2021 18th European Radar Conference, London, UK:IEEE, 2022:5-8.
［5］LAI Jun, LU Jingyun, GU Changzhan, et al. Non-Contact Vital Sign Monitoring of Cat Using Continuous-Wave Doppler Radar［C］//2022 International Conference on Microwave and Millimeter Wave Technology, Harbin, China:IEEE,2022:1-3.
［6］YANG Hanchun,LUO Yunlong,QI A,et al.FMCW-Radar-Based Vital-Sign Monitoring of Pet［C］//2021 13th International Symposium on Antennas, Propagation and EM Theory,Zhuhai,China:IEEE,2021:1-3.
［7］SCHWARZ C, ZAINAB H, DASGUPTA S, et al. Heartbeat Measurement with Millimeter Wave Radar in the Driving Environment［C］//2021 IEEE Radar Conference,Atlanta,GA,USA:IEEE,2021:1-6.
［8］DESERNO T M,WARNECKE J M,FLORMANN M,et al.Combining Vehicle BUS and Vital Sign Sensors for Continuous Health Monitoring During Driving: Concept and First Results［C］//2022 International Conference on Electrical,Computer, Communications and Mechatronics Engineering,Maldives:IEEE,2022:1-6.
［9］HU Wei, ZHAO Zhangyan, WANG Yunfeng, et al. Noncontact Accurate Measurement of Cardiopulmonary Activity Using a Compact Quadrature Doppler Radar Sensor［J］.IEEE Trans on Biomedical Engineering,2013,61（3）:725-735.
［10］XIA Zilang, WANG Xinhuai, WEI Hongbo, et al. Detection of Vital Signs Based on Variational Mode Decomposition Using FMCW Radar［C］//2021 International Conference on Microwave and Millimeter Wave Technology,Nanjing,China:IEEE,2021:1-3.
［11］杨路，雷雨霄，余翔.基于FMCW 雷达的人体生命体征信号预测算法［J］.雷达科学与技术，2024，22（1）：43-56.
［12］ZHAO Yanhua,SARK V,KRSTIC M,et al.Multi-Target Vital Signs Remote Monitoring Using mmWave FMCW Radar［C］//2021 IEEE Microwave Theory and Techniques in Wireless Communications, Riga, Latvia: IEEE,2021:290-295.
［13］ZHU Jiale, XU Dalong, XU Wenwen, et al. Multi-Target Vital Sign Detection Based on Capon Spatial Spectrum［C］//2022 International Conference on Microwave and Millimeter Wave Technology, Harbin, China: IEEE,2022:1-3.
［14］DONG Xichao, FENG Yun, CUI Chang, et al. CEEMDAN-ICA-Based Radar Monitoring of Adjacent Multi-Target Vital Signs［J］.Electronics,2023,12（12）:2732.