0 引 言
随着现代军事科技的发展,雷达已经成为重要的军事电子装备,其在目标探测与识别、重点区域成像、精确制导等方面发挥着重要作用[1]。因此,雷达信号参数如到达时间(Time of Arrival,TOA)、脉冲宽度(Pulse Width,PW)、载频(Radio Frequency,RF)与调制类型识别等在对雷达信号测量与分选方面具有重要的现实意义[2-5]。
雷达信号时域参数的测量如TOA 和PW 与检测方法有关,目前主流的信号检测算法有能量累积检测法[6]、自相关检测法[7]、小波变换法[8]和随机共振法[9]。自相关检测法对信噪比(Signal to Noise Ratio,SNR)要求低,易于工程实现,但时域参数测量的误差较大;小波变换法可以很好地进行信号检测,但是不适合对未知信号的检测;随机共振法可以很好地利用噪声,但是只适用于小频率信号的检测。而频域参数,如载频的测量,常使用快速傅里叶变换算法(Fast Fourier Transform,FFT)将信号变换到频域,测量频谱峰值的方式计算;但在非合作方式下,信号脉宽不同,FFT点数不固定,传统算法对大时宽带宽积信号计算时,资源消耗大、不便于工程实现。
常见的雷达信号主要包括单载频(Normal Signal,NS)、二相编码(Binary Phase Shift Keying,BPSK)、线性调频(Linear Frequency Modulation,LFM)等,而传统的雷达信号识别流程大都先需要进行FFT,将信号大致分为调相信号和调频信号[10],再进一步采用自相关等算法,确定NS 信号、BPSK 信号等具体类型[11]。这种识别方式的识别准确率较高,但运算量较大,在工程上又难以实现。
基于此,本文提出一种适用于低信噪比下,雷达信号参数与调制方式联合测量与识别的方法,并进行工程实现。该方法整体采用流水线形式设计,复杂度低、资源占用较少,并且可以联合信号参数测量和调制方式识别同时进行,有效提高信号处理的实时性,适用于数字信道化处理后多路的雷达信号参数测量与识别,具有一定的实用价值。
1 低信噪比下信号联合参数测量与识别方法
1.1 非相参累积检测算法
经过数字信道化处理,将输入实雷达信号转换成复信号,可以表示为
式中,A0 表示信号的幅值,t 为采样时间,φ(t)表示信号的相位。在FPGA 中,信号的相位和幅值可以采用CORDIC 算法计算得出[12]。CORDIC 算法的转换模式可将矢量由直角坐标旋转到极坐标,由经过旋转后的极坐标表示方式就可得该点信号的幅值A0和相位φ(t)。
信号检测是雷达信号参数测量和信号识别的前提,本系统采用非相参累积检测算法进行脉冲检测,即对经过CORDIC 算法计算出的信号幅值进行累积。记下信号检测过门限时间,即可得被侦察脉冲到达时间。
如图1 所示,将前端CORDIC 算法计算出的信号幅值送入采样窗口中并以1为步长滑动,每滑动一次对三组各16 个点的信号模值累加,即进行能量累积,并与门限进行对比,当第一组能量积累小于门限,第二组、第三组能量积累大于门限时,即可认为此时脉冲前沿已经到来。脉冲信号到达时间可由第二组中的某个点确定,具体方法见3.1节,此时将到达时间记为Ta。
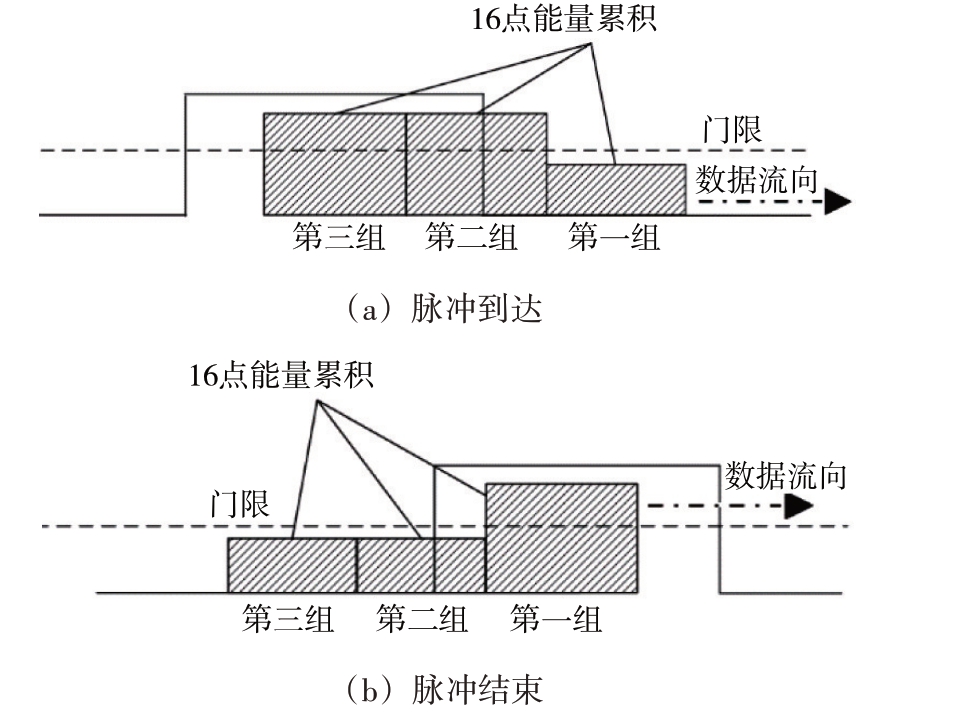
图1 非相参累积检测算法示意图
当第一组能量积累大于门限,第二组、第三组能量积累小于门限时,即可认为此时脉冲很大概率已经结束。脉冲信号结束时间也可由第二组中的某个点确认,记脉冲结束时间为Td。则雷达信号的脉冲宽度(PW)可表示为
1.2 联合载频测量与信号识别方法
线性调频信号和二相编码信号的频谱如图2所示。传统参数测量方法是通过傅里叶变换得到辐射源的载频参数,频域方法存在以下问题:BPSK信号的频谱比较分散,难以准确找到中心频率;另外对于调频类波形,需要对整个脉冲的信号进行傅里叶变换才能找到中心频率,而脉宽的不同使得傅里叶变换的点数不同,且大时宽带宽积信号的计算量非常大,在工程上实现困难。另外传统方法对辐射源参数测量后截取脉冲信号,然后进行分析,识别信号调制方式,需要进行顺序计算,增加了系统复杂度。因此针对传统方法存在的不足,本文提出一种联合载频测量与信号识别方法。
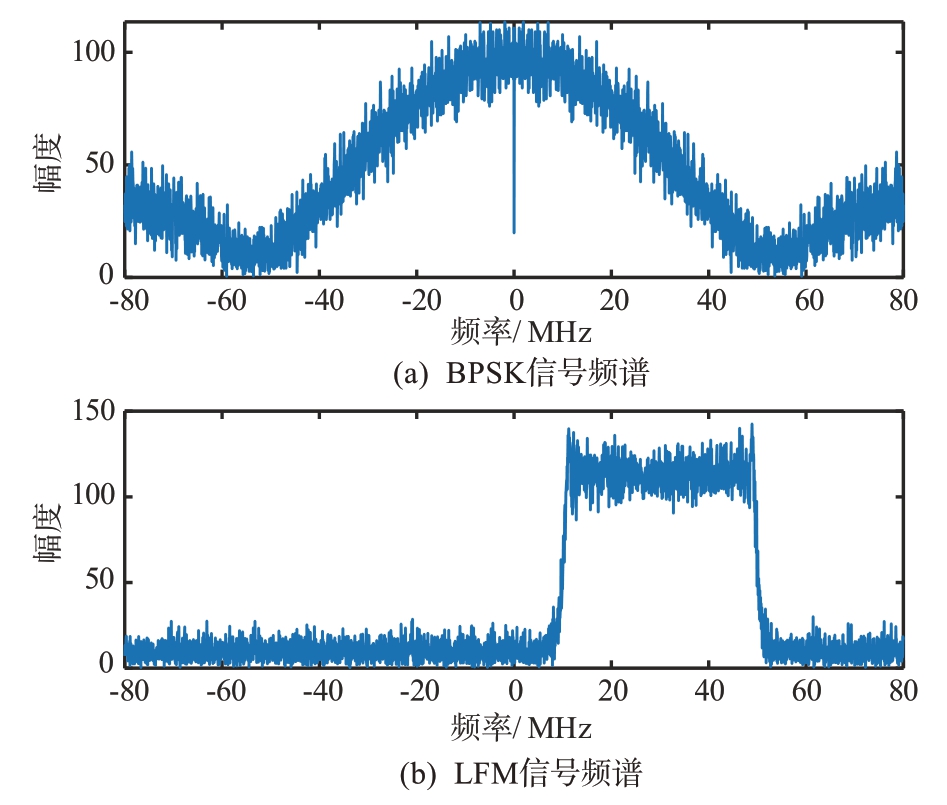
图2 BPSK信号与LFM信号频谱图
常见的雷达信号主要包括单载频信号、线性调频信号和二相编码信号等,其相位函数可统一表示为
式中,f0为载频,φ0为初始相位,Cd(t)为编码函数。当Cd(t)取0 或1 编码时,则该信号为二相编码信号[13];当Cd(t)只取0 时,该信号为单载频信号;当Cd(t) = k t2 时,该信号为线性调频信号,其中k 为调频斜率。
经数字采样后,信号的瞬时相位为
式中,n 为采样时刻序号,fs 为采样频率。雷达信号瞬时相位和瞬时频率的对应关系为
式中,θ(n)为瞬时相位,θ(n) - θ(n - 1)为一阶相位差。由于θ(n)相位周期性从-π 变化到π,所以θ(n) - θ(n - 1)区间为[-2π,2π],此时相位越过了2π 无模糊区间,出现相位模糊,需要对相位进行去模糊。为此根据相位序列的后向差分大小,添加一个解模糊序列C(n),可记为
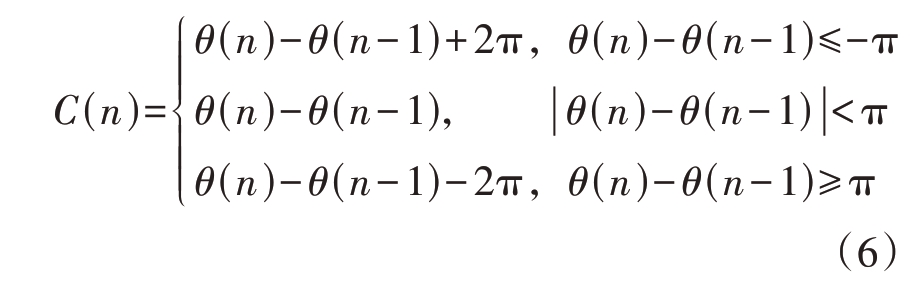
由式(4)和式(5)可知,线性调频信号的瞬时相位差为一条斜率为k的直线;单载频信号的瞬时相位差为一条水平的直线;二相编码的瞬时相位差在编码变化处存在π 的瞬时相位跳变。所以,可以通过不同信号的瞬时相位特征来识别信号和计算信号载频,这明显减小了工程实现难度。
而为了进一步抑制噪声导致的奇异值和二相编码信号的瞬时相位跳变对载频测量精度和信号识别准确度的影响,对瞬时相位差进行差分运算时,设置一个π 2的跳变阈值。当二阶差分大于阈值时,可抛去该点,同时,通过记录跳变点数来判断二相编码信号,而对于单载频信号和线性调频信号可以通过曲线斜率判断。
设解模糊后的瞬时相位差序列C 的拟合曲线为
式中,b0为常数。将计算得出的瞬时相位差和采样点数代入式(7),可得超定方程组:
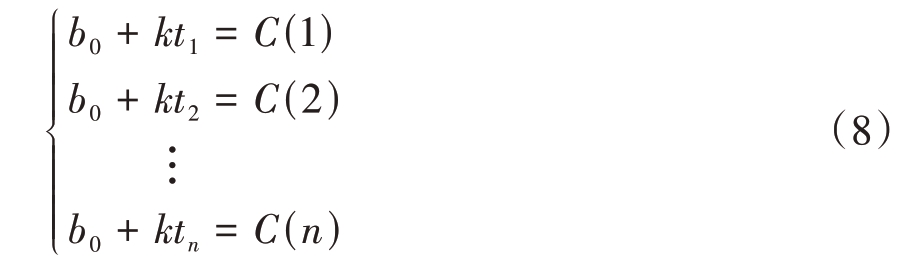
式中![]() 为采样时刻。
为采样时刻。
曲线拟合的最小二乘法可以看成求以上超定方程组的最小二乘解的问题。式(8)所示超定方程组的矩阵形式可表示为
式中:
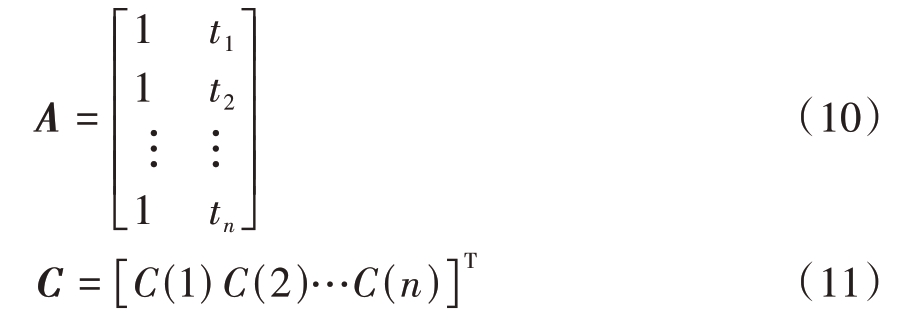
式中表示求转置运算。
因此,
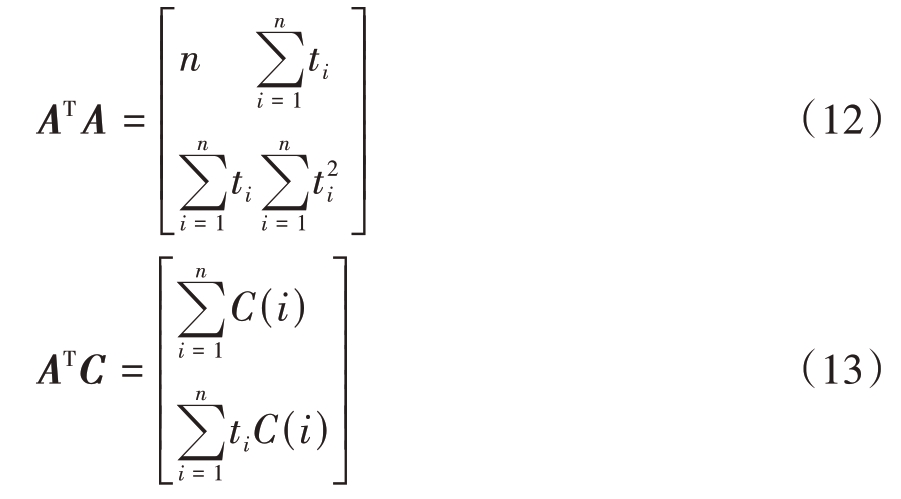
综上所述,法方程组为
基于最小二乘法,可解出瞬时相位差的斜率k为
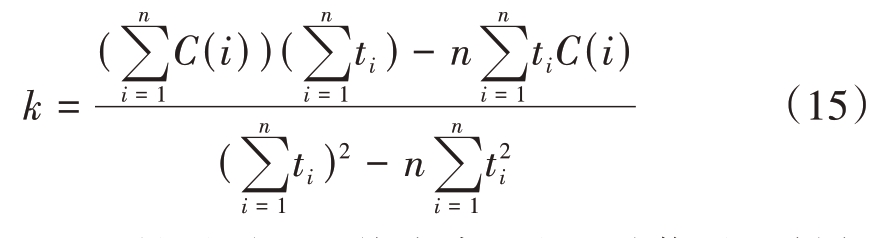
因此,针对雷达系统中常见的3种信号调制方式识别,本方法处理流程如图3所示。
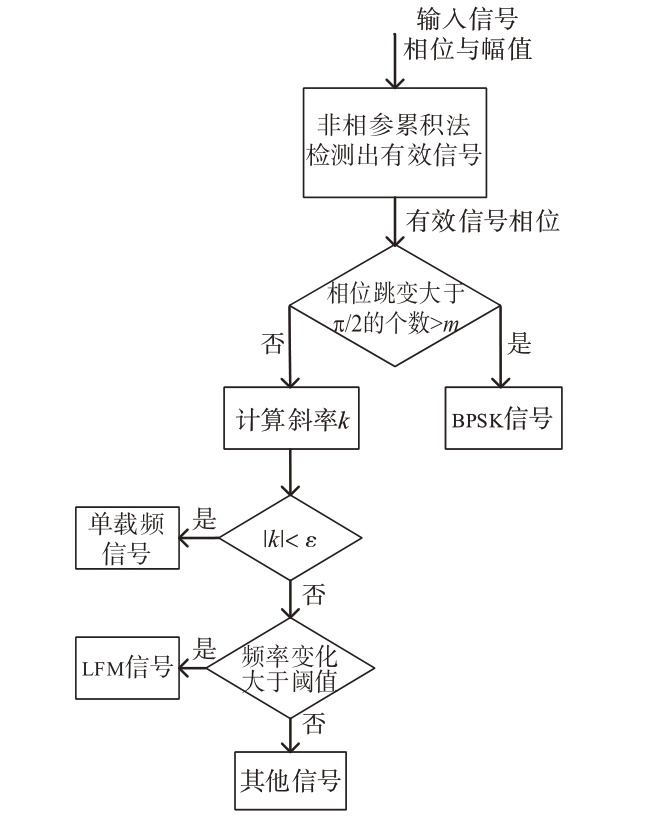
图3 信号调制类型识别流程图
其中,跳变个数m 的值与二相编码信号的编码方式和码元个数有关。当拟合曲线斜率k 的绝对值小于ε(ε 为很小的实常数)时,判断该信号为单载频信号;否则选取第一个点与最后一个点代入拟合曲线,得出瞬时频率并作差,计算频率变化范围,可设置一个频率变化阈值,当频率变化大于阈值时,即可判断为线性调频信号,否则为其他信号。
而载频可由均值法计算得出,如式(16)所示,其中fc 为信道化后的中心频率;fs为采样频率;m为抛去跳变点后的有效瞬时相位差分点数;C(i)为处理后的瞬时相位差分序列。

本方法复杂度低,可以很好地适用于非合作形式下的信号测量,并且便于工程实现;数据处理方式采用流水线形式,在参数测量的同时识别了信号类型,实时性好。
2 工程实现
2.1 算法实现架构
经天线和接收数字采样后,采用FPGA 实现信号联合参数测量与识别系统的框图如图4 所示。首先将经过数字信道化处理的辐射源信号利用CORDIC 算法计算出幅值和瞬时相位,将信号的幅值输入至非相参累积检测模块,检测出雷达信号后即可得到信号的到达时间,同时将有效信号的瞬时相位传输至后续模块计算瞬时相位差,再根据本文所提方法同时计算出信号的脉宽、载频和信号类型,实时性好。
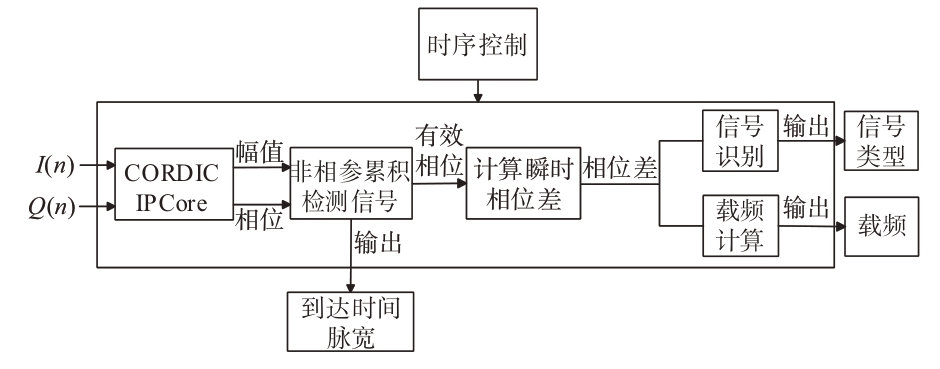
图4 FPGA系统架构
2.2 系统实现
如图5所示,本系统采用天线、高速大带宽采集与处理板板卡和上位机结构,大大降低处理难度、提升处理速率,满足后续信号参数测量的实时性要求。
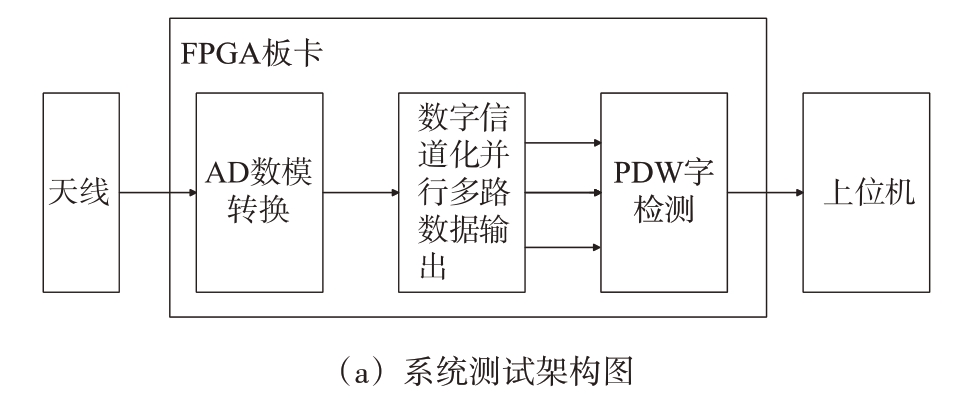

图5 系统测试架构与FPGA板卡
2.3 计算复杂度对比分析
设输入线性调频脉冲信号的有效脉宽为4 μs、脉冲周期为10 μs、中心频率为30 MHz、采样率为150 MHz,分别采用传统的50 点自相关检测算法[14]和本文的非相参累积检测算法对脉冲进行检测,忽略少量其他逻辑运算,两种方法计算复杂度对比分析结果如表1所示。
表1 两种信号检测算法计算复杂度对比

实数加法与乘法次数实数加法次数实数乘法次数50点自相关检测算法72 500 72 500本文非相参累积检测算法8 760 0
从表1可以看出,本文所提信号检测方法的计算量明显小于传统检测方法,本文采用的非相参累积检测算法只需进行加法运算且计算复杂度更低,在硬件实现中可节省运算资源,易于工程实现。
对频域参数(如载频等参数)测量,传统方法常采用FFT 变换,将信号变换到频域、测量频谱峰值的方式计算。但在被动侦察领域,目标为非合作目标,非合作方式下,信号脉宽不确定,FFT点数不固定,变长度的傅里叶变换在FPGA 等硬件上很难实现,只能不论信号长短采用固定较长点数的傅里叶变换,这种方法对窄脉宽信号存在较大资源浪费;对大时宽信号,很可能傅里叶变换的点数又不足,造成测量误差。传统算法对大时宽带宽积信号计算时,资源消耗大、不利于工程实现。
以传统的1 024 点傅里叶变换测载频法为例,与本文所提的瞬时相位差载频测量方法进行对比。设输入线性调频脉冲信号有效脉宽为4 μs、脉冲周期为10 μs、中心频率为30 MHz、采样率为150 MHz,分别采用传统的1 024 点FFT 测载频法和本文的瞬时相位差测载频法,忽略少量其他逻辑运算,两种方法的计算复杂度对比分析结果如表2所示。
表2 两种信号载频测量算法计算复杂度对比

实数加法与乘法次数实数加法次数实数乘法次数FFT测频算法30 720 20 480本文瞬时相位差测频算法22 181 3
从表2可以看出,本文所提载频测量方法的计算量明显小于传统FFT 变换测载频法,本文采用的瞬时相位差测载频算法计算复杂度低,避免了非合作目标信号脉宽不确定、FFT点数不固定造成的测量偏差和计算资源浪费,在硬件实现中可节省运算资源,易于工程实现。
3 仿真分析
3.1 非相参累积检测算法上升沿和下降沿位置仿真
设置中心频率为30 MHz、带宽为10 MHz、有效脉宽为4 μs、脉冲周期为10 μs 的LFM 信号,采样率为150 MHz。在不同信噪比下,选取3 组不同的上升沿和下降沿位置:位置1 为图1 中第二组采样窗口的第7 点;位置2 为第二组采样窗口的中间位置即第8点;位置3为第二组采样窗口的第9点。在不同信噪比下分别进行10 000 次蒙特卡洛实验,仿真结果如图6所示。
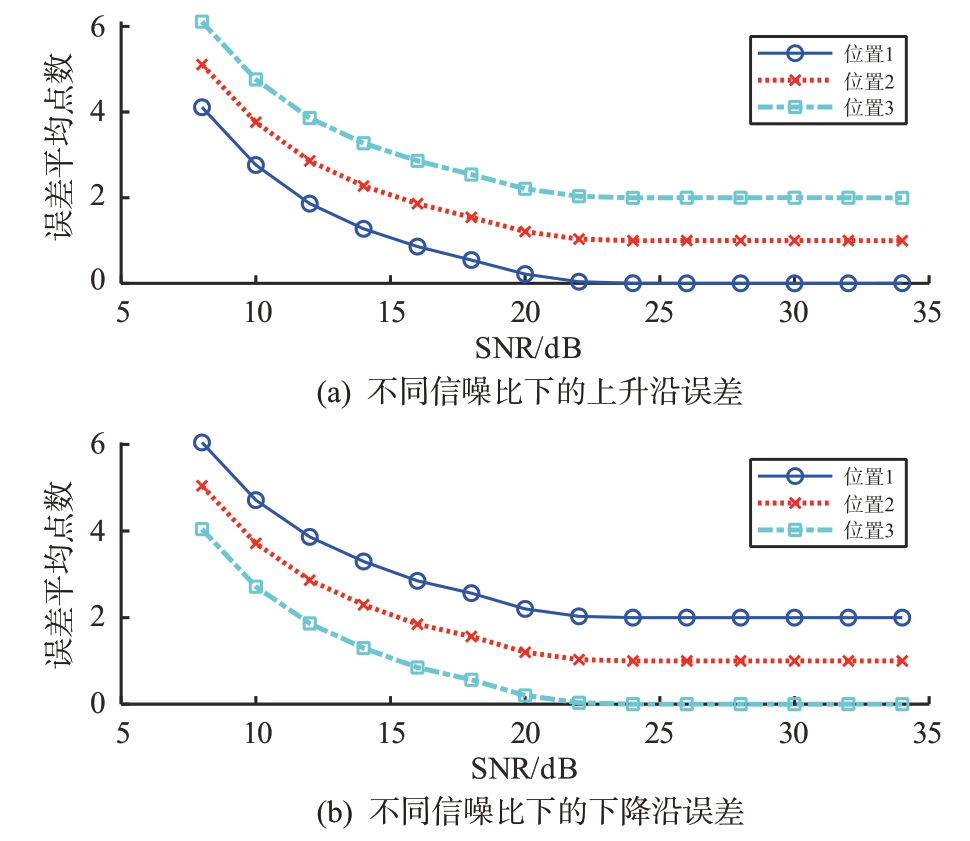
图6 不同信噪比下上升沿和下降沿误差
由图6 可知,上升沿选取在位置1 处,即第二组采样窗口的第7点时误差更小;下降沿选取在位置3,即第二组采样窗口的第9 点时更准确,此时,低信噪比下平均误差为4个点左右。
3.2 TOA与脉宽测量精度仿真
设输入信号为有效脉宽为4 μs、脉冲周期为10 μs、中心频率为30 MHz、带宽为10 MHz 的线性调频信号,采样率为150 MHz。在不同信噪比下分别进行10 000 次蒙特卡洛实验,自相关信号检测法和本系统采用的非相参累积检测算法测量出TOA 和PW 的均方根误差(Root Mean Squared Error,RMSE)如图7 所示。由图7 可以看出,与传统的自相关检测算法相比,非相参累积检测算法对TOA的检测精度更高;且PW 的检测精度在低信噪比下优于自相关检测算法。仿真结果表明本文所提方法具有更好的检测精度。
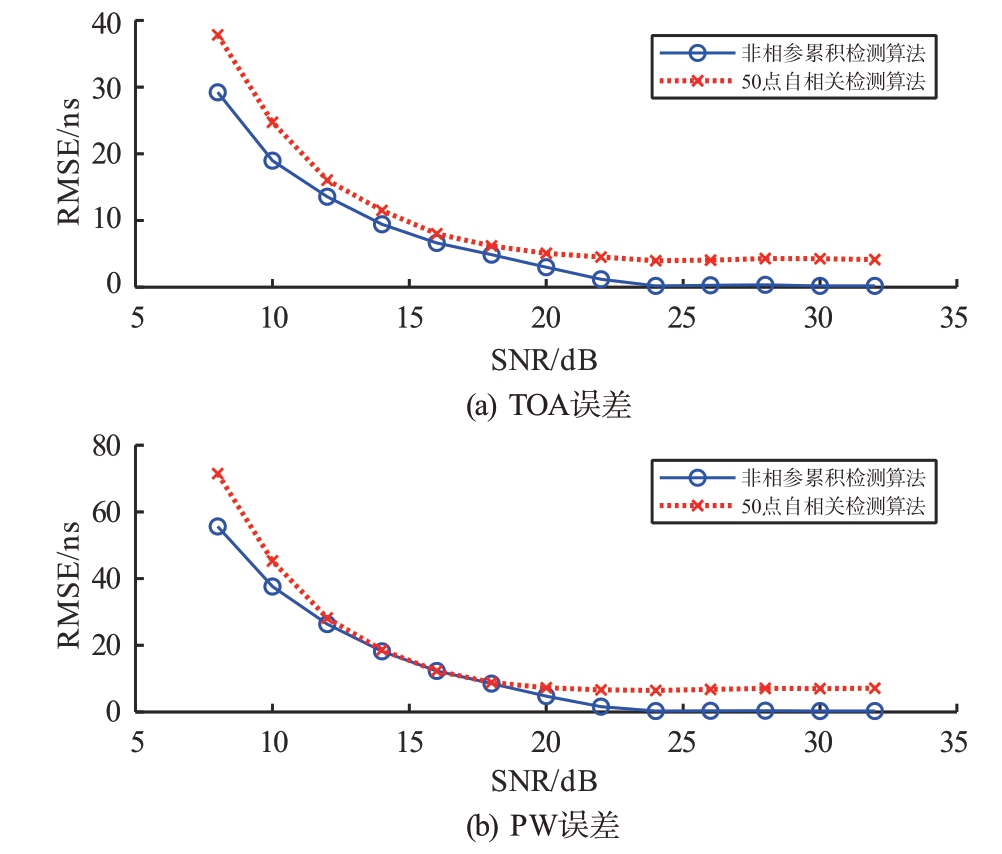
图7 两种算法的时域参数测量精度对比图
设输入信号分别为有效脉宽为4 μs、中心频率为30 MHz、带宽为30 MHz的线性调频信号;中心频率10 MHz 的二相编码信号,码元宽度为200 ns;以及中心频率为-30 MHz的单载频信号,采样率都为150 MHz。采用非相参累积检测算法,在不同信噪比下进行10 000 次蒙特卡洛实验,测量出的TOA 和PW 均方根误差如图8 所示。由图8 可知,针对不同频率、不同调制类型的信号,非相参累积检测算法测量出的TOA和PW精度基本相同。
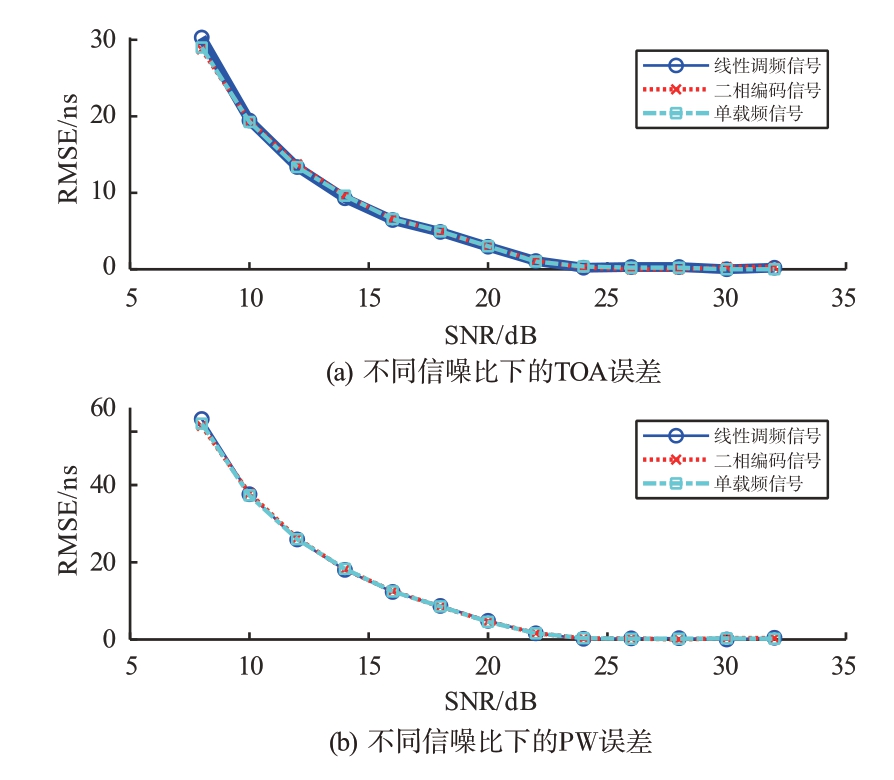
图8 不同调制类型信号的时域参数测量精度图
3.3 载频测量仿真
本文采用瞬时相位差计算载频,为减小低信噪比下的载频测量误差、提高信号识别准确度,需要采用1.2节中的方法对信号的瞬时相位差预处理。
设置有效脉宽为4 μs、脉冲周期为10 μs、中心频率为30 MHz、带宽为10 MHz 的线性调频信号;有效脉宽为4 μs、中心频率为-30 MHz的单载频信号;中心频率0 MHz 的二相编码信号,输入信噪比为10 dB。本文所提算法处理前与处理后的瞬时相位差如图9 所示。由图9 可知,经过处理后的二相编码信号的跳变相位值和单载频信号、线性调频信号的部分被噪声干扰后的异常值都被剔除;处理后,二相编码信号、单载频信号和线性调频信号的载频均可用均值法测出,有效提升了载频测量精度,降低了工程实现的难度。
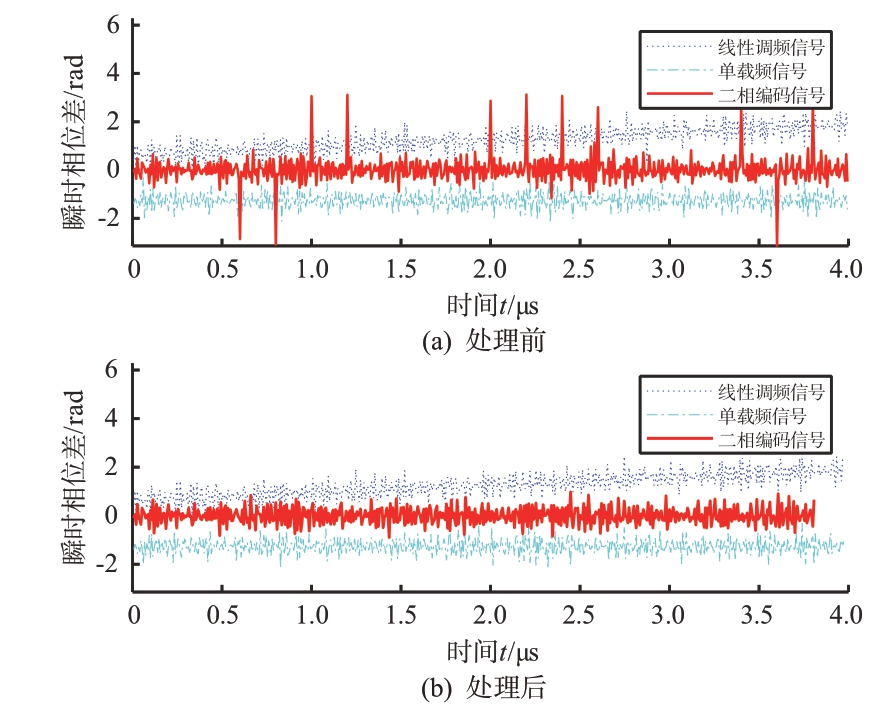
图9 载频测量预处理前后对比图
图10 给出了不同信噪比下的载频测量精度,蒙特卡洛实验次数为10 000。由图10 可知,在抛去噪声导致的奇异值和跳变点后的3 种信号的频率测量精度相差不大,因此本文方法针对不同信号具有较好的适应性。
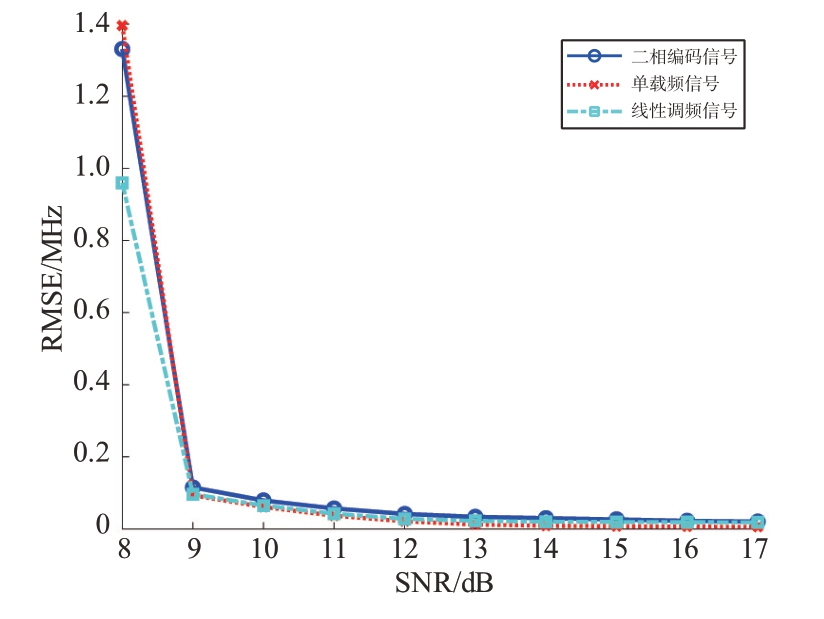
图10 各信号的载频测量精度
设输入有效脉宽为4 μs、脉冲周期为10 μs、中心频率为30 MHz 的线性调频信号,带宽分别为10、20 和30 MHz,采样率为150 MHz,在不同信噪比下分别进行10 000 次蒙特卡洛实验,载频测量精度如图11 所示。由图11 可以看出,针对不同带宽的线性调频信号,其频率测量精度基本一致,可知使用本方法对常见的辐射源信号进行载频测量均有较好的适应性。
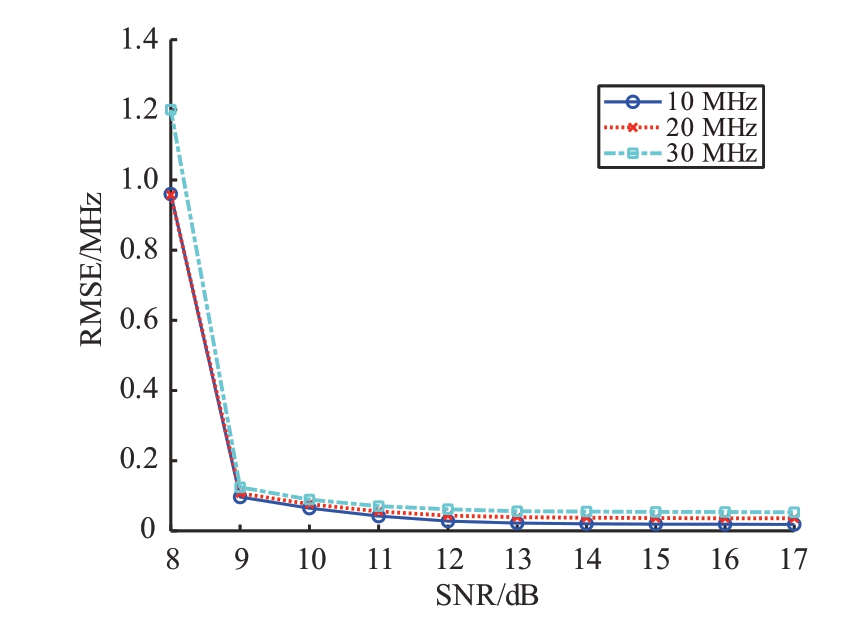
图11 不同带宽的LFM信号载频测量精度
3.4 识别概率仿真
设输入信号脉冲宽度为4 μs,采样率为150 MHz,随机设置中心频率为-50~50 MHz;线性调频信号带宽设置为10 MHz;二相编码信号码元宽度为200 ns。在不同信噪比下各进行1 000 次蒙特卡洛实验,信号识别的准确率如图12所示。
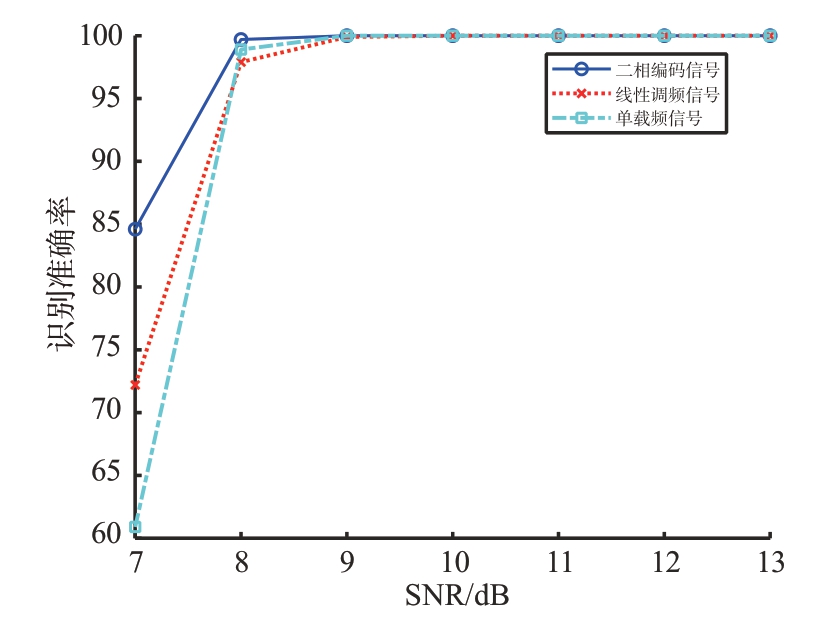
图12 信号识别准确率
由图12可知,采用本文所提识别方法,当信噪比大于8 dB 时,信号调制类型的识别准确率均在95%以上,而且所提识别方法易于实现、复杂度低、具有较高的工程应用价值。
3.5 实测结果分析
搭建信号发射系统,发射3 800 MHz 的单载频信号,脉冲宽度为20 μs,重复周期为50 μs,实测数据经数字信道化处理后,进行信号检测,检测结果如图13 所示。可以看出,系统检测到的脉冲参数与实际信号的脉冲基本吻合,验证了非相参累积检测算法的可行性。

图13 实测结果时域图
为统计本文所提算法性能,系统发射频率为800~5 600 MHz 的单载频信号,接收端实际接收信号的信噪比约为7 dB,每段频率脉冲个数为3 000,脉冲宽度分别为50 μs 和20 μs,脉冲重复周期为100 μs 和50 μs,并将处理结果导出至Matlab 中进行分析,载频、脉宽、重复周期测量的均方根误差如表3所示。可以看出本文所提方法对不同频率、不同脉宽和不同重复周期的信号,载频、脉宽和重复周期测量误差均较小,验证了所提方法的可行性。
表3 实测数据误差
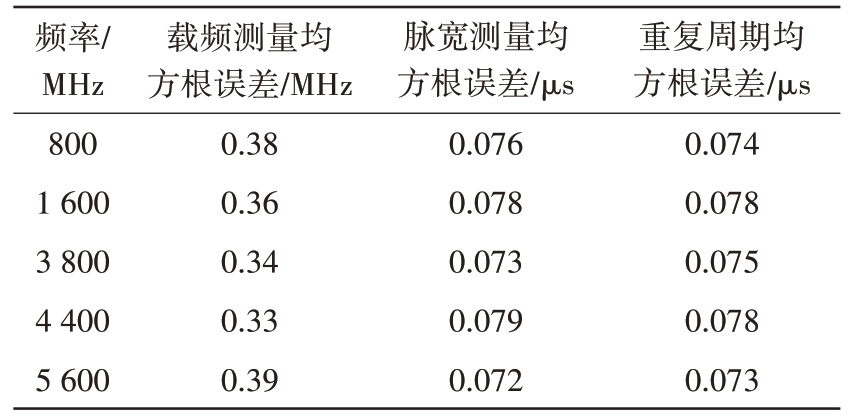
频率/MHz 800 1 600 3 800 4 400 5 600载频测量均方根误差/MHz 0.38 0.36 0.34 0.33 0.39脉宽测量均方根误差/μs 0.076 0.078 0.073 0.079 0.072重复周期均方根误差/μs 0.074 0.078 0.075 0.078 0.073
4 结束语
基于辐射源信号的瞬时相位差特征,本文提出一种适用于低信噪比下的非相参累积检测算法和信号联合参数测量与识别方法。非相参累积检测算法检测出信号并计算出信号的瞬时相位差,通过信号的瞬时相位差特征测量信号载频并联合进行信号识别。仿真和实测数据分析结果验证该方法测量误差较小、信号识别准确率较高、计算复杂度较低,在FPGA 实现的过程中资源占用较少,便于工程实现。硬件实现采用流水线方式,实时性好,具有一定的实用价值。
[1]韩啸.雷达辐射源开集识别关键技术研究[D].郑州:战略支援部队信息工程大学,2023.
[2]齐美彬,程佩琳,靳学明,等.基于密集连接卷积网络的雷达辐射源信号分选[J].雷达科学与技术,2022,20(6):635-642.
[3]石荣,杜宇,刘江.雷达信号脉内调制类型及PDW 表征的演变与发展[J].电子信息对抗技术,2020,35(1):1-6.
[4]刘松涛,赵帅,汪慧阳.雷达辐射源识别技术新进展[J].中国电子科学研究院学报,2022,17(6):523-533.
[5]张庆庆.雷达信号识别方法研究及硬件设计[D].西安:西安电子科技大学,2023.
[6]李文奎.雷达侦察检测系统技术研究[D].西安:西安电子科技大学,2018.
[7]夏开华,何彩霞,王巍,等.基于自相关检测的参数测量[J].数字技术与应用,2018,36(5):92-94.
[8]ZHEN Pan, ZHANG Bangning, CHEN Zhibo, et al. Spectrum Sensing Method Based on Wavelet Transform and Residual Network[J]. IEEE Wireless Communications Letters,2022,11(12):2517-2521.
[9]崔琳.基于随机共振理论的弱信号检测算法研究[D].长沙:国防科技大学,2021.
[10]LIAO Yilin, LI Haozhe, CAO Yizhi,et al. Fast Fourier Transform with Multihead Attention for Specific Emitter Identification[J]. IEEE Trans on Instrumentation and Measurement,2024,73:1-12.
[11]刘方建,李贺,陈云帆,等.基于雷达信号脉内调制识别的算法仿真与验证[J].青岛大学学报(工程技术版),2023,38(2):68-74.
[12]蚩建峰.雷达信号侦察处理系统研究[J].舰船电子对抗,2021,44(2):88-95.
[13]沙祥,刘永坚,崔国龙,等.用于高速目标检测的相位编码信号处理方法和性能研究[J].雷达科学与技术,2023,21(6):591-596.
[14]邹斯旻.宽带数字信道化侦察接收机的高效FPGA 实现研究[D].成都:电子科技大学,2011.