0 引 言
随着武器装备隐身技术不断演进,隐身技术已成为现代化联合作战体系中不可或缺的关键组成部分[1]。雷达散射截面(Radar Cross Section,RCS)作为衡量目标隐身性能的关键参数[2],其精确测量对于评估和提升武器装备性能具有重要意义。当前,RCS的定量获取主要依赖于理论预估和实际测量两种方法[3]。理论预估方法基于电磁散射理论,通过计算目标在雷达波照射下的散射强度来预测RCS 值[4]。这种方法主要适用于几何形状和材料较为简单的目标。在实际应用中,由于模型的精度、算法复杂度等的限制,理论预估方法的准确性往往受到很大的挑战。相比之下,实际测量方法在这方面更有优势。
随着测量技术的不断突破与精进,RCS测量技术已经步入了一个高度成熟的发展阶段。这一领域涵盖了多元化的测量方法,包括远场测量[5]、紧缩场测量[6]以及近场测量[7]等,它们共同构成了完整的测量体系。这一体系中,微波光子高分辨成像雷达技术尤为瞩目,它通过显著扩大信号带宽,实现了分辨率的显著提升,从而大幅增强了RCS测量的精确度[8]。此外,研究人员还精细地利用残余相位,进一步提升了距离分辨率的精确度,使得测量结果更加精准[9]。同时,聚类算法的引入为部件的RCS 测量带来了革命性的变化,使得测量过程更加精准可靠[10]。而针对高温环境的RCS 测量技术,则为特殊应用场景提供了强有力的技术支持[11]。这些技术均已臻于完善,其测量误差能够控制在1 dB 以下,展示了极高的精确性和可靠性。然而,科研工作者仍在不断探索与创新,致力于推动RCS 测量技术向更高的测试精度、更完善的功能特性迈进,以适应日益复杂且严苛的应用场景和测试需求。
面对弱散射目标测量中难以消除的背景杂波,以及对特定局部区域RCS 的精细化测量需求,新兴的成像测量方法作为一种解决方案被提出[12],它能够在一定程度上提升RCS 测量精度。RCS 成像测量方法的流程大致如下:首先使用成像算法对定标球进行二维SAR 成像,接着使用成像提取算法,获取定标球的二维谱域数据,然后利用同样的方法获得目标的二维谱域数据,最后进行反演获得目标的RCS[13]。其中,传统的成像提取算法多是以人工加窗提取算法为主[12]。该算法通过使用窗函数提取目标散射像获得目标的二维谱域数据。然而,在实际应用中,这种方法仍然面临着诸多挑战。由于目标散射像的形态各异,当采用规则窗函数来提取目标散射像时,不可避免地会掺杂进杂波干扰。特别是在干扰电平较高的环境下,这些杂波对目标RCS 测量精度的影响尤为显著,可能导致测量结果出现较大偏差。此外,人为因素在加窗过程中扮演着至关重要的角色。不同的研究人员在处理相同数据时,可能会基于个人经验和判断采用不同的加窗策略,这进一步加大了数据比较和交叉验证的难度,使得结果的可靠性和一致性难以保证。
为了解决以上问题,本文提出了一种基于全局自适应提取的目标RCS 成像测量算法。该算法不仅能提高RCS 的测量精度,而且在成像测量过程中的提取环节无需研究人员的介入,可以应用在自动化测量系统中,提高测量效率。
1 算法分析
1.1 SAR图像与目标RCS的关系
目标的雷达图像特征与其真实的物理散射特性(即RCS)存在着密切的关联。因此,通过合成孔径雷达(Synthetic Aperture Radar, SAR)图像,能够精确地获取目标的RCS 值。在获得雷达的二维SAR 图像后,可以通过成像提取的方法获得目标的散射像为
式中,γ0(x,y)为目标的空间反射率分布。
对式(1)进行二维傅里叶变换,可以获得目标的谱域数据:
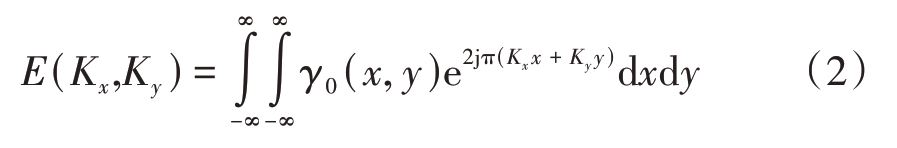
由于积分变量的不同,我们需要对E(Kx,Ky)进行插值,得到随f和θ变化的E( f,θ),插值公式为

同样的方法对RCS 为σ0 的定标体,可以得到金属球谱域数据E0( f,θ)。然后根据式(3)、式(4)最终得到被测目标的RCS[12]:
1.2 成像提取方法
1.2.1 传统提取算法
传统提取算法也被称为人工加窗提取算法。在得到SAR 图像后,可以根据已知的目标位置信息,以目标为中心对SAR 图像加窗,以滤除杂波对RCS 测量的影响。传统方法往往使用圆形窗函数对SAR 图像加窗,式(6)表示了以坐标原点为中心,半径为a的圆形窗。
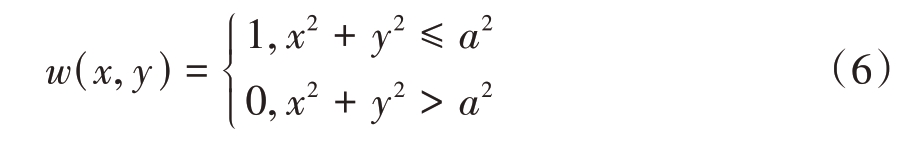
使用该窗函数对目标进行提取,得到新的散射像为
在处理定标球时重复这项操作,获得定标球的散射像。
由于传统提取算法提取时需要手动确定圆形窗的大小和位置,以保证尽量完整提取目标散射像。当目标散射像的形状不规则时,必然会面临一种抉择。如果窗口可以完整覆盖目标散射像,那么就必然引入杂波干扰。如果尽量避免杂波干扰,那么目标必然提取不完整。两种决策都会造成RCS测量精度的下降。
1.2.2 全局自适应提取算法
由于传统提取算法存在诸多问题,本文提出了一种基于全局自适应提取的RCS 成像测量算法。该算法基于最大类间方差准则自适应确定阈值,然后利用八连通准则剔除干扰,确定目标区域从而实现目标散射像的提取,进而实现目标RCS的测量。
1)基于最大类间方差准则的阈值选择
最大类间方差准则是一种基于图像灰度特性的自适应阈值选取方法,其核心目标是将图像有效地划分为前景区域与背景区域两个部分。该准则认为,在找到最优阈值点时,应当使得这两部分之间的区分度达到最大状态。而用来量化这种区分度的指标就是“最大类间方差”。类间方差的大小直接反映了图像中前景区域与背景区域间的显著性差异程度:类间方差值越高,意味着前景区域与背景区域的区分越鲜明;反之,如果出现前景区域被错误地划入背景区域,或者背景区域被错误地归为前景区域的情况,将会导致计算得出的类间方差值下降。因此,当所取阈值的分割使类间方差最大时,意味着错分概率最小[14]。
设T为前景与背景的分割阈值,前景点数占图像比例为w0,平均灰度为u0,背景点数占图像比例为w1,平均灰度为u1。图像的总平均灰度为u,前景和背景图像的方差为g,则有
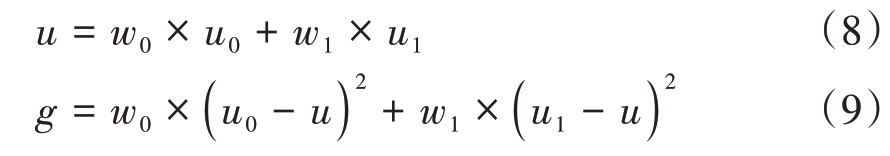
联立两式可得
或
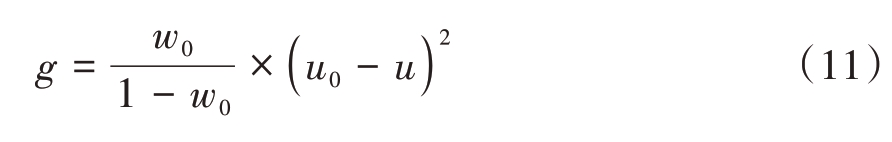
当方差g 最大时,此时前景和背景差异最大,此时的灰度T是最佳阈值。
2)基于八连通准则的目标划分方法
连通性(邻接性)是描述区域和边界的关键概念。它用于确定像素之间的关系,特别是哪些像素属于同一区域。在数字图像处理中,四连通和八连通概念是用来描述像素之间连通性的两种方式。四连通原理指出,如果一个像素位于二维图像网格中,那么它仅与紧邻的上、下、左、右四个像素点被视为连通,构建出一个类似棋盘格的正方形邻域结构。而八连通规则进一步扩展了这一概念,除了包括四连通中的四个相邻像素外,还把左上、右上、左下、右下这四个对角相邻的像素也纳入到连通的范畴内。换句话说,一个像素的邻域就构成了一个更大且形状接近正八边形的结构,如图1所示。
图1 八连通示意图
如图1 所示,如果q 和p 的像素值都是集合V的元素,并且q 在黄色区域,那么就说p 和q 是邻接的。八连通准则是指,如果两个像素点是临接的且满足同一条件,那么这两个点就归为一个物体。与四连通相比,八连通考虑了更多的像素连接关系,因此在某些情况下能够更好地描述图像的细节和结构。综上所述,使用全局自适应提取算法进行目标散射像提取的具体步骤如图2所示:获取到二维SAR 图像后,基于最大类间方差法计算全局阈值,用于分辨前景区域和背景区域,然后使用八连通准则提取感兴趣的目标从而达到自适应提取目标散射像的目的。
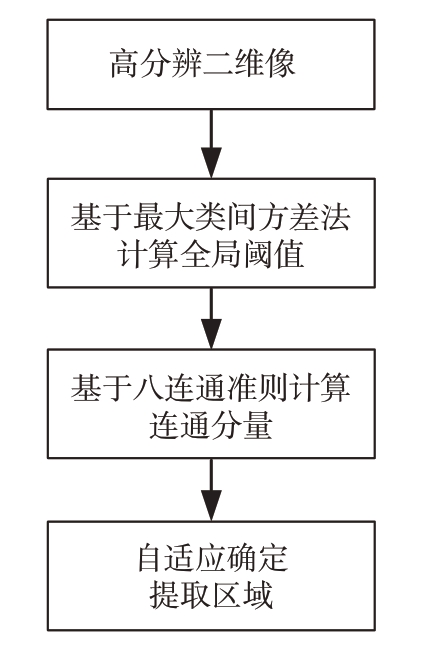
图2 全局自适应提取算法步骤
2 实验验证
2.1 算法有效性验证
人工加窗提取算法在提取目标散射像的时候往往需要按照经验选用不同大小的窗函数。为了探究不同大小的窗函数对RCS 测量的影响,设置了如下实验:目标为直径200 mm 的金属球,干扰为距离目标200 mm 的一个直径20 mm 的金属球,定标体为直径100 mm 的定标球。仿真模型如图3所示。

图3 两个金属球仿真模型示意图
图4为窗函数为0.062 m 的散射像提取结果图,图5 为不同窗函数下目标RCS 结果对比图,从图中可以观察到:
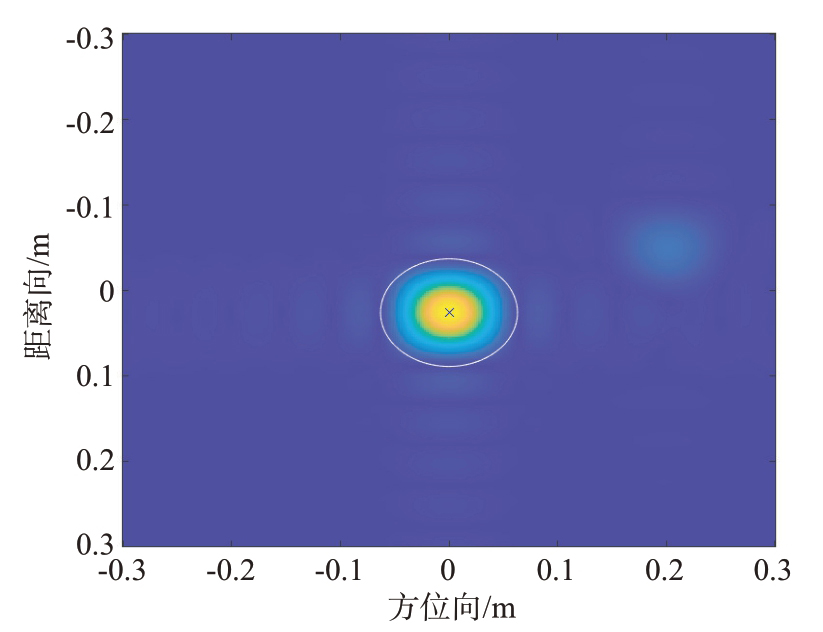
图4 窗函数为0.062 m的散射像提取结果
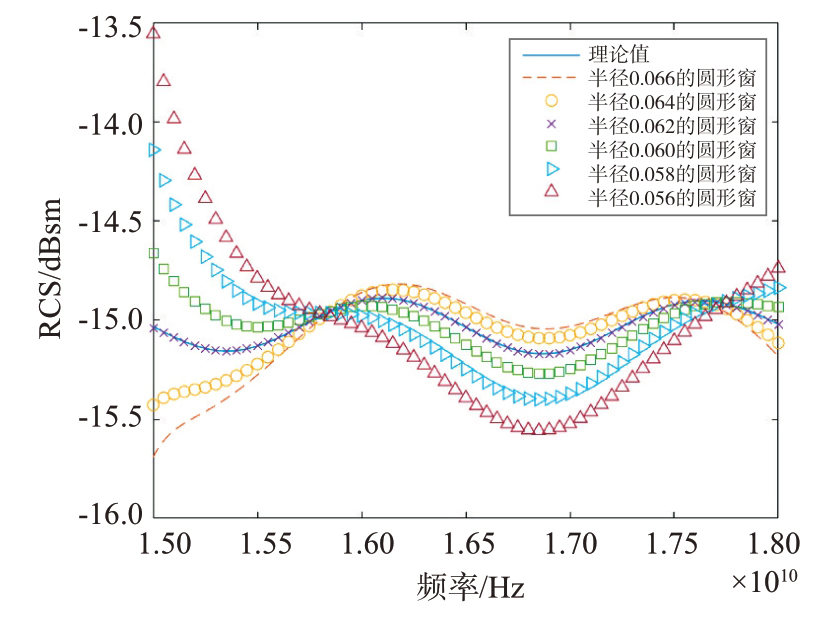
图5 不同大小窗函数下目标RCS结果对比
1)当窗函数大小适中(半径为0.062 m)时,由于目标散射像提取清晰,背景干扰得到了有效抑制,所以RCS测量精度较高。
2)随着窗函数大小的增大(半径超过0.062 m),由于目标散射像提取效果逐渐变差,杂波干扰对RCS测量的影响逐渐增大。
3)当窗函数大小变小(半径小于0.062 m)时,由于目标散射像提取不完全,导致RCS 测量精度下降。
综上可得,窗函数的细微差异都会引起RCS测量精度的变化。在实际测量时,由于目标RCS未知,所以很难确定哪一种窗函数得到的测量结果最为准确。
接下来,采用全局自适应提取算法对目标散射像进行提取。作为对比,人工加窗提取算法使用的是半径为0.062 m 的窗函数。图6为全局自适应提取算法的提取结果示意图。图7 和图8 分别为人工加窗提取算法和全局自适应提取算法下的目标RCS 结果图。为方便观察,给出方位向为0°、5°时的RCS提取结果,如图9和图10所示。
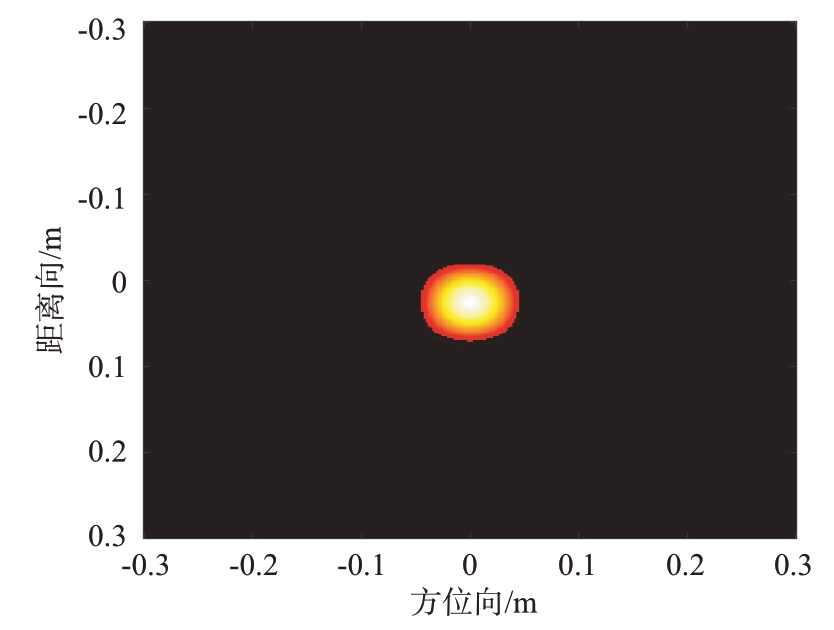
图6 全局自适应提取算法提取结果
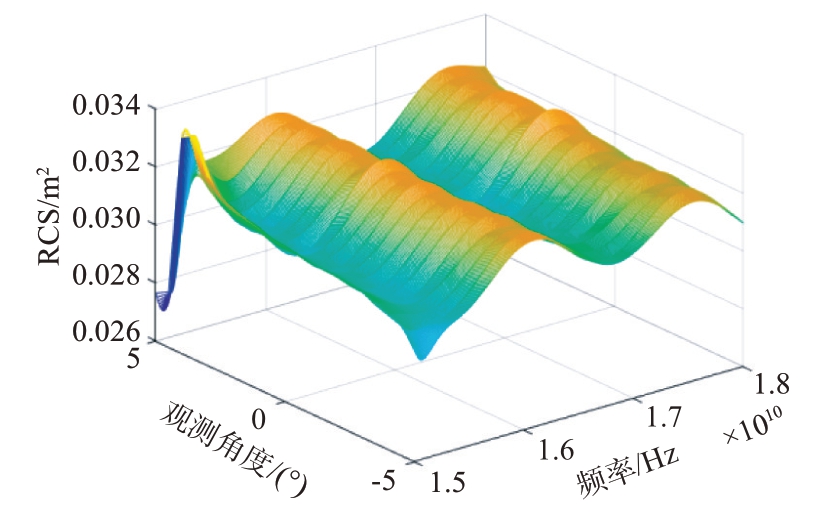
图7 人工加窗提取算法下目标RCS结果
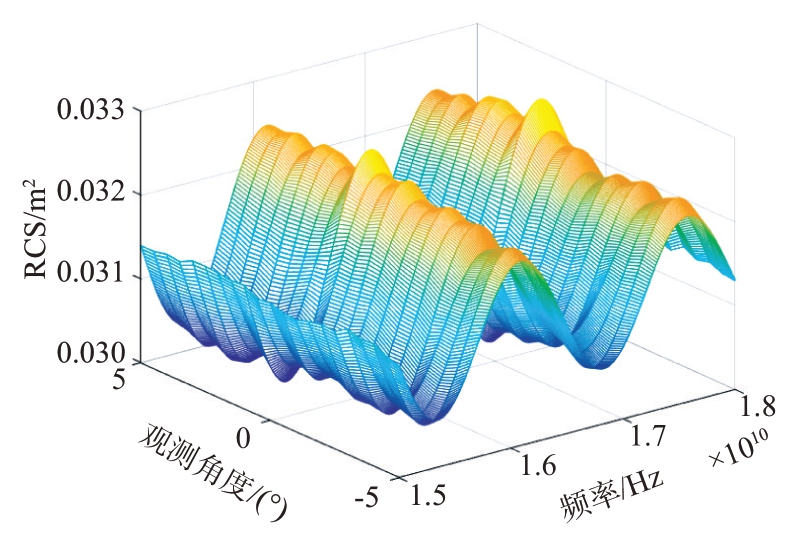
图8 全局自适应提取算法下目标RCS结果
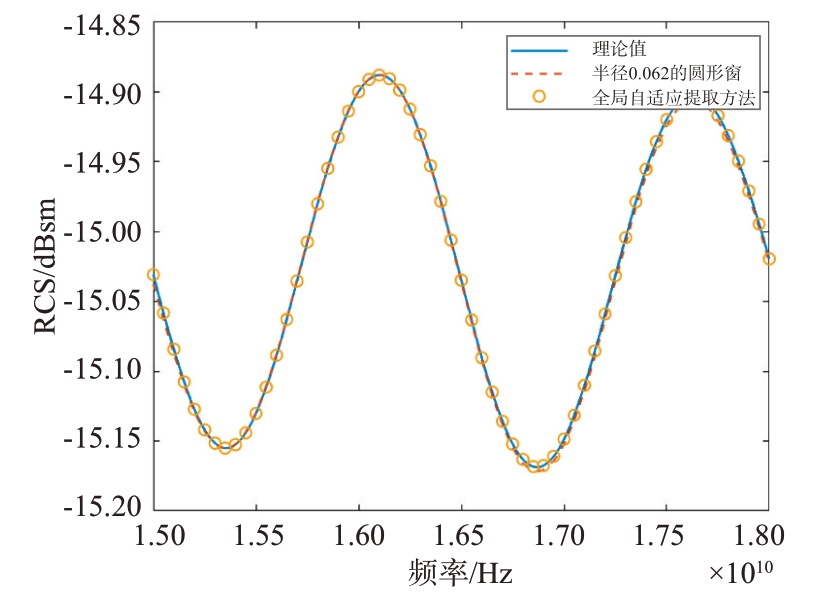
图9 方位向为0°时提取的RCS对比
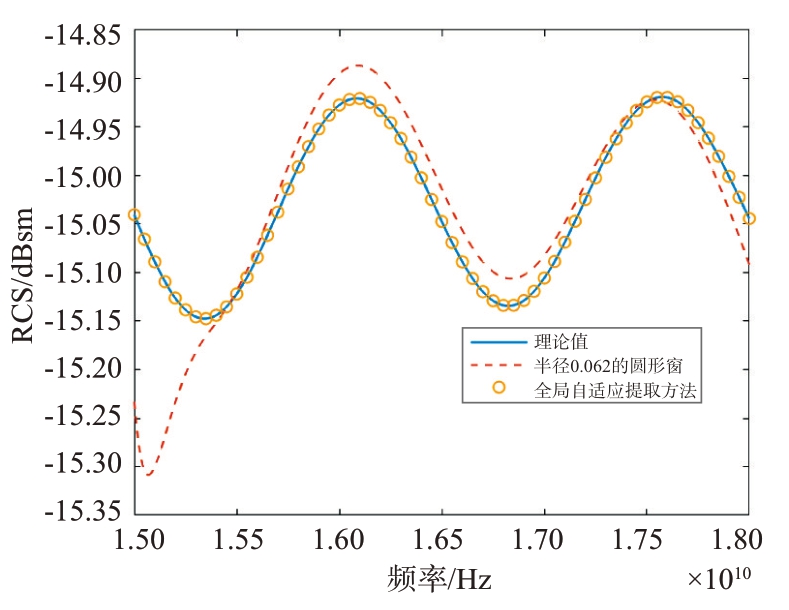
图10 方位向为5°时提取的RCS对比
从图7~10 可以看出,窗函数提取的RCS 数据在边缘处有明显的误差,而采用全局自适应处理算法则没有这个问题,原因在于使用窗函数在提取目标散射像时,由于窗函数大小固定,导致截取的图像断面参差不齐。而全局自适应算法因为是按照选取的阈值划分的目标范围,所以不存在这个问题,因而RCS测量精度更高。
2.2 不规则目标RCS测量分析
在目标RCS 测量中,大部分目标的散射像都不是一个规则的形状。为了探究这一因素的影响,设置了如下实验。目标是一个直径200 mm 的金属球,其球心处放置了一个边长200 mm 正方形金属板,仿真模型如图11所示。

图11 金属球和正方形板仿真模型示意图
图12为半径0.1 m 的人工加窗提取算法提取结果图,图13 为不同窗函数下目标RCS 的计算结果对比图,其中dBsm为分贝平方米。
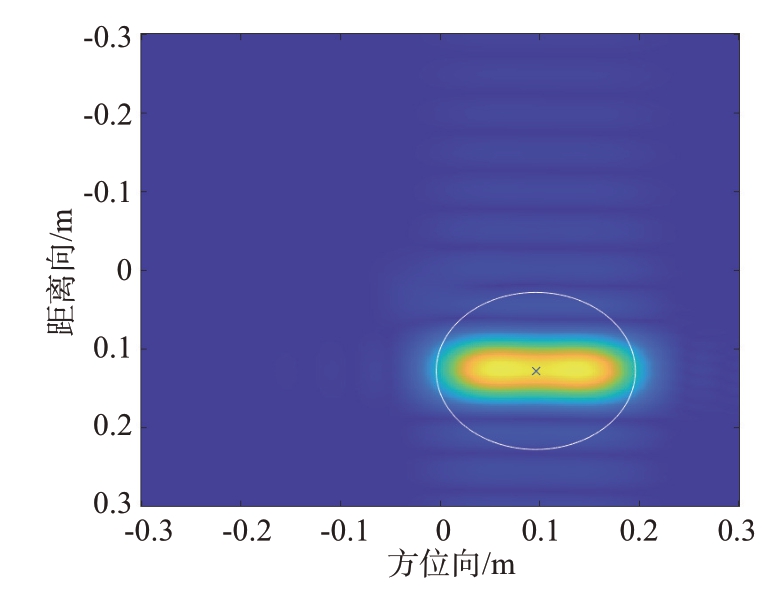
图12 人工加窗算法提取示意图
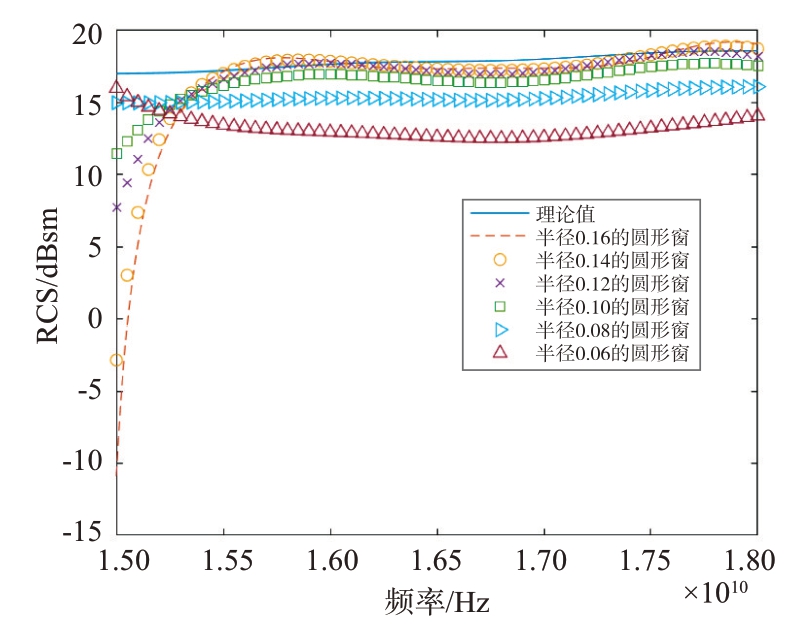
图13 不同大小窗函数下目标RCS结果对比
从图12 可以看出,目标散射像并不是一个规则的形状。根据图13 的RCS 测量结果,计算不同窗函数下目标RCS 测量精度(不同频率下真实值与测量值的绝对误差的均值),如表1 所示。通过表1可以得知,使用半径为0.12 m 的圆形窗提取计算得到的目标RCS测量误差比较小。
表1 不同窗函数下目标RCS测量精度
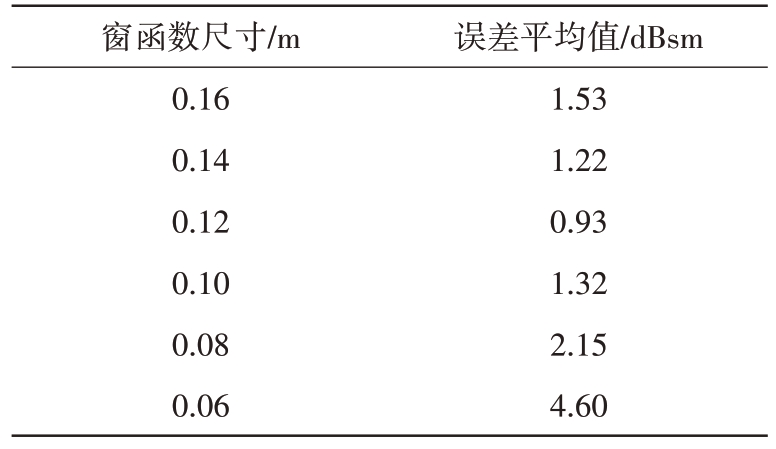
窗函数尺寸/m 0.16 0.14 0.12 0.10 0.08 0.06误差平均值/dBsm 1.53 1.22 0.93 1.32 2.15 4.60
图14 为全局自适应提取算法提取结果图,从图12 和图14 可以观察到,全局自适应提取算法能更精准地将目标散射像提取。而人工加窗提取的方法由于窗函数无法完全精确覆盖目标的所有散射区域。
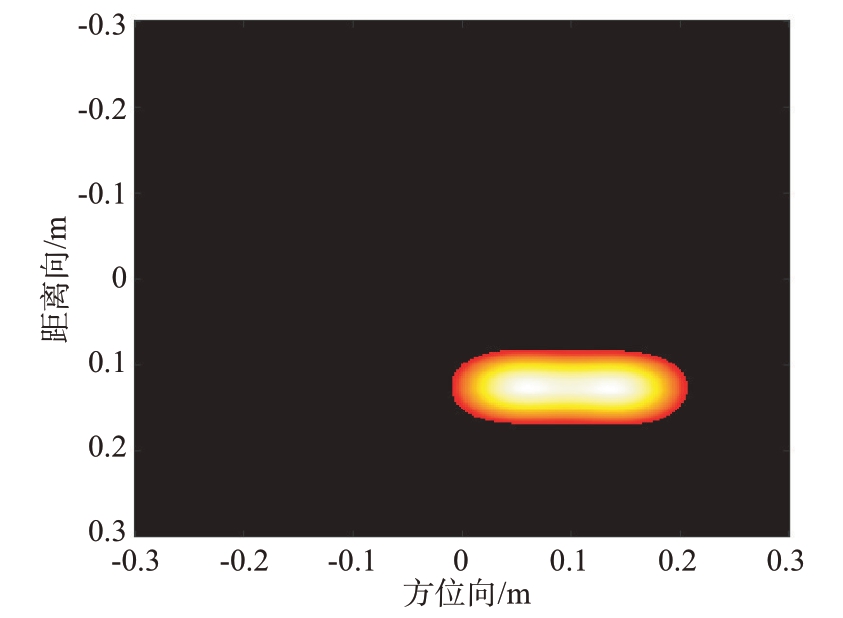
图14 全局自适应提取算法提取结果图
根据提取结果计算RCS 结果,如图15 和图16所示。可以看出,由于形状上的约束,人工加窗提取算法在提取目标散射像的过程引入的杂波和噪声更多,并且由于直接加窗截断,造成RCS 的误差依然存在。方位向为0°时目标的RCS 测量精度对比图如图17 所示,两种算法下目标RCS 测量误差如表2所示。通过分析图17和表2可得,相比于人工加窗提取算法,采用全局自适应提取算法测量得到的目标RCS精度更高。
表2 两种算法下目标RCS测量误差对比

成像提取算法人工加窗提取全局自适应提取误差平均值/dBsm 0.93 0.44
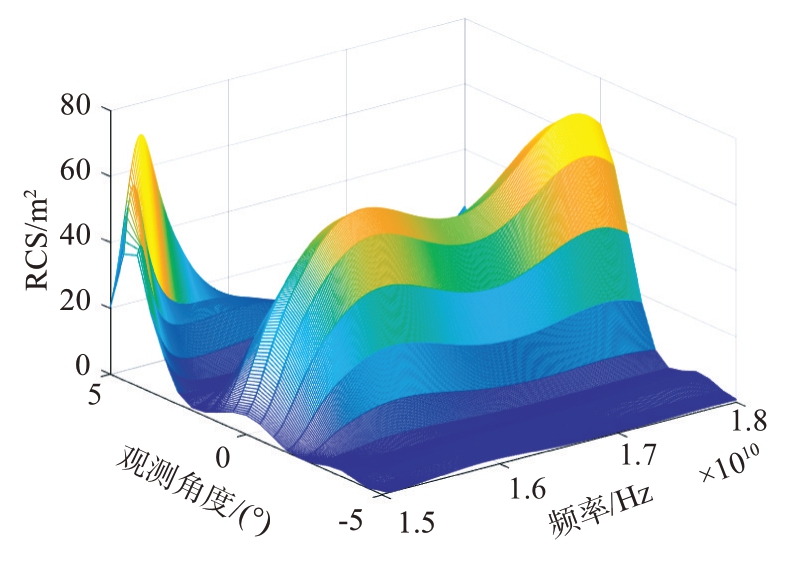
图15 人工加窗提取算法RCS提取结果
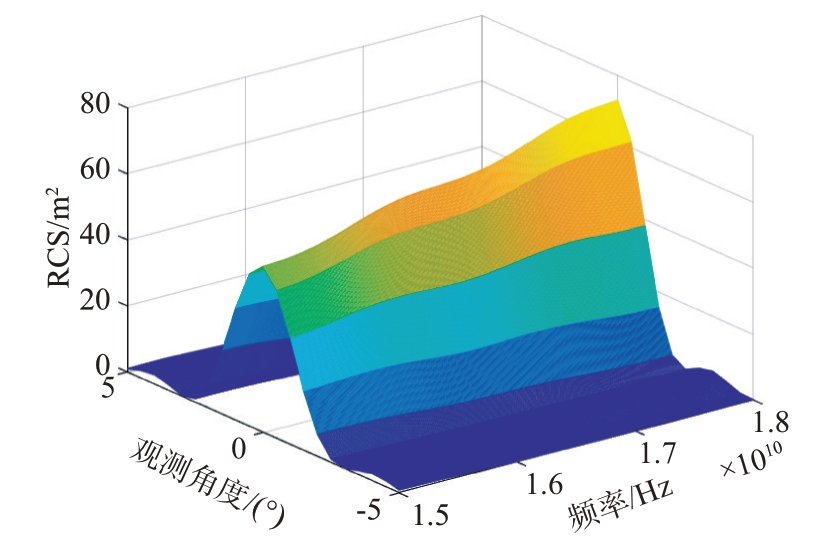
图16 全局自适应提取算法RCS提取结果
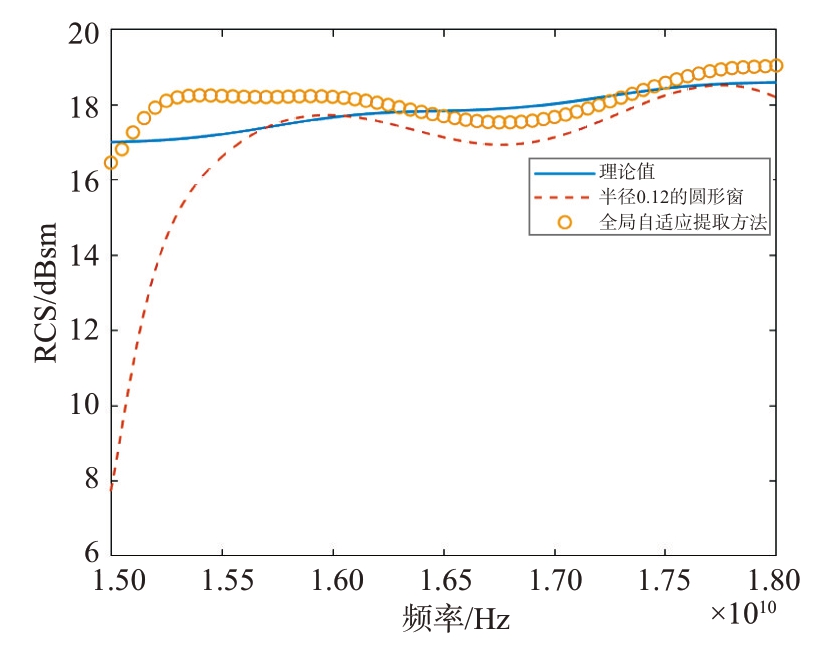
图17 方位向为0°时目标RCS测量精度对比
2.3 不同测量环境对目标RCS测量的影响
为验证不同测量环境对目标RCS 测量的影响,本文使用了暗室和室外场景作为不同测量环境对比算法的性能。
1)暗室下的实测实验
目标选为已知RCS 的直径150 mm 金属球,如图18所示,定标体采用150 mm 定标球。成像结果如图19所示。

图18 150 mm目标球
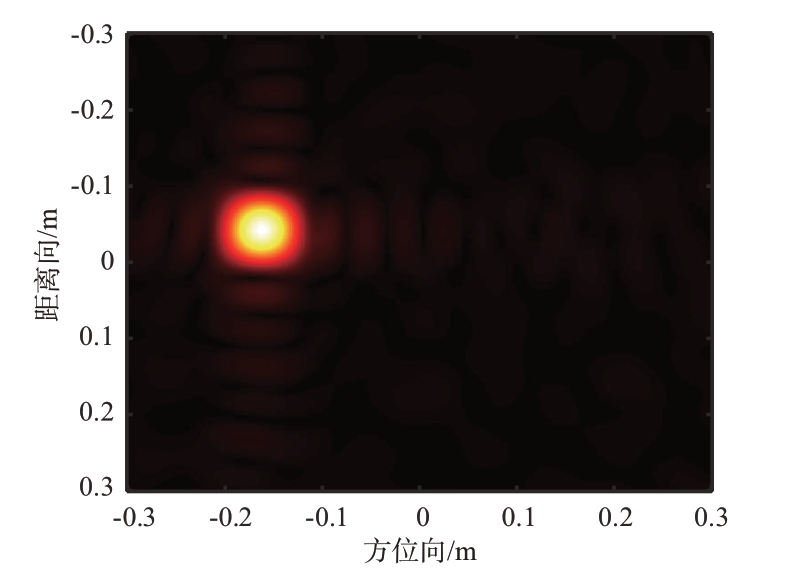
图19 模型成像结果图
下面依然采取不同大小的圆形窗,选取一个结果最好的圆形窗,不同窗函数提取的RCS 结果如图20所示。
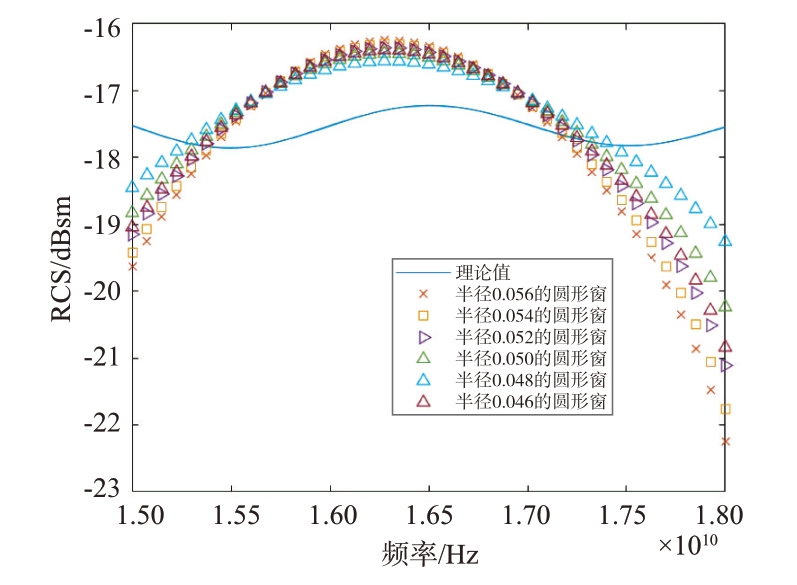
图20 不同大小窗函数提取的RCS对比
根据图20 的RCS 测量结果,计算不同窗函数下的提取精度如表3所示。
表3 不同窗函数下的目标RCS测量精度
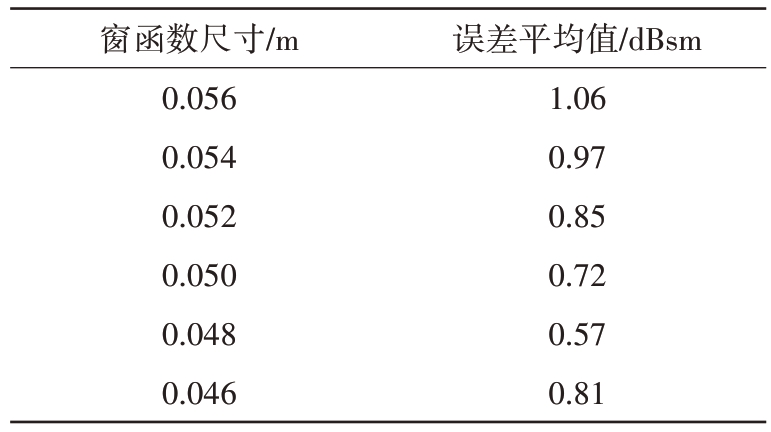
窗函数尺寸/m 0.056 0.054 0.052 0.050 0.048 0.046误差平均值/dBsm 1.06 0.97 0.85 0.72 0.57 0.81
结合表3测量数据的定量分析结果,可以清晰地看到,不同窗函数对于RCS 测量精度影响较大。选取的窗函数的细微差异都有可能带来较大的精度区别。换句话说,人工加窗提取算法具有测量的不稳定性,这无疑增加了数据比较和交叉验证的困难。
通过表3也可以看出,测量误差比较小的是半径为0.048 m 的圆形窗。接下来以这个圆形窗为例进行RCS的成像提取。
图21和图22是两种算法的目标提取结果,图23和图24 是根据提取结果计算得到的RCS,图25 是方位向为0°时目标RCS测量精度对比图。
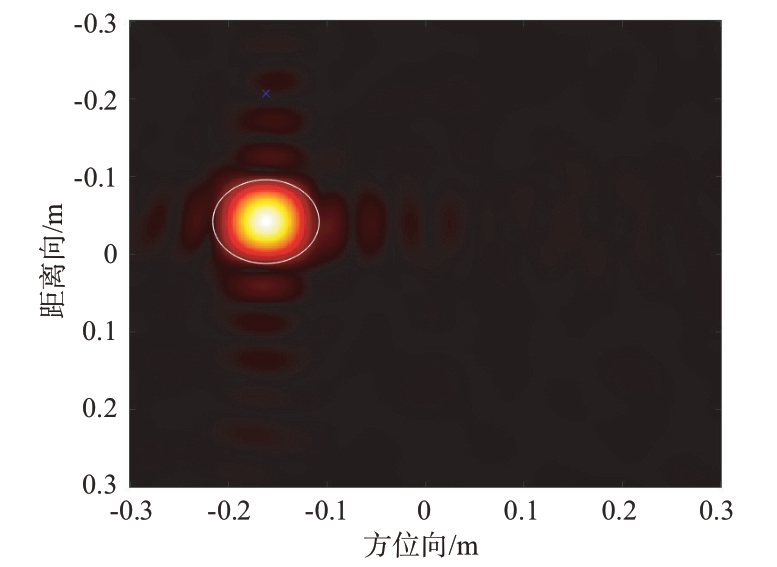
图21 半径0.048 m的窗函数提取图
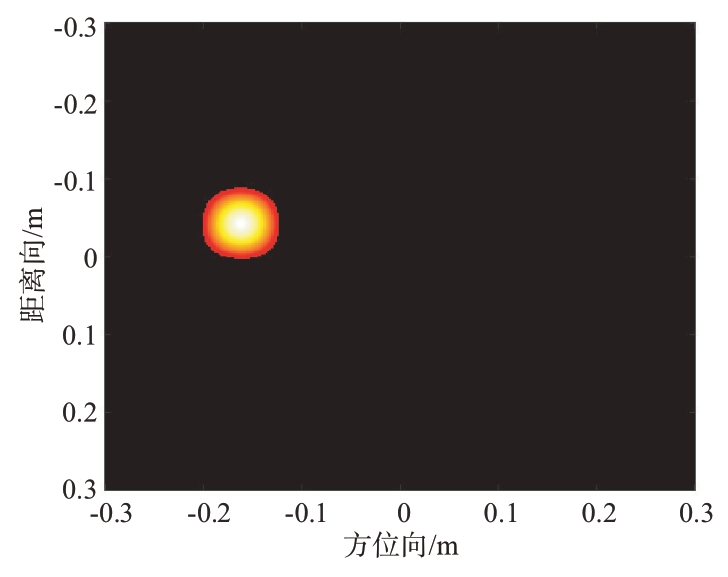
图22 全局自适应提取算法提取图

图23 人工加窗提取算法RCS提取结果
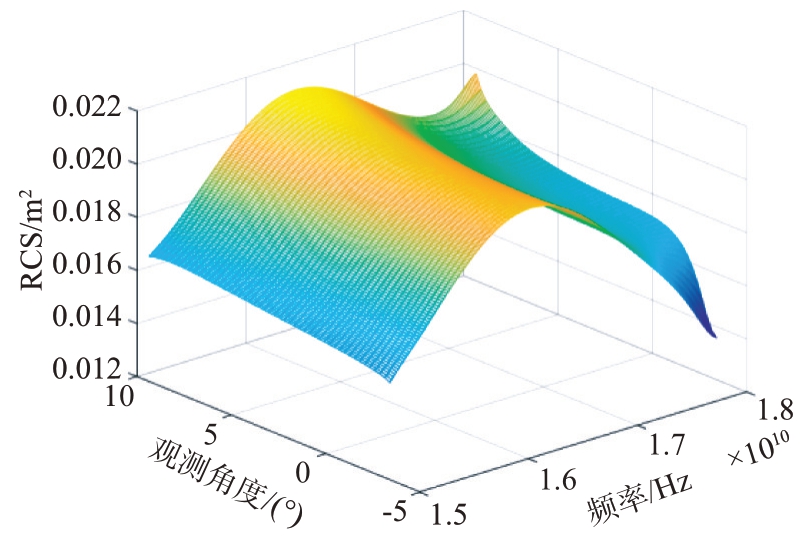
图24 全局自适应提取算法RCS提取结果
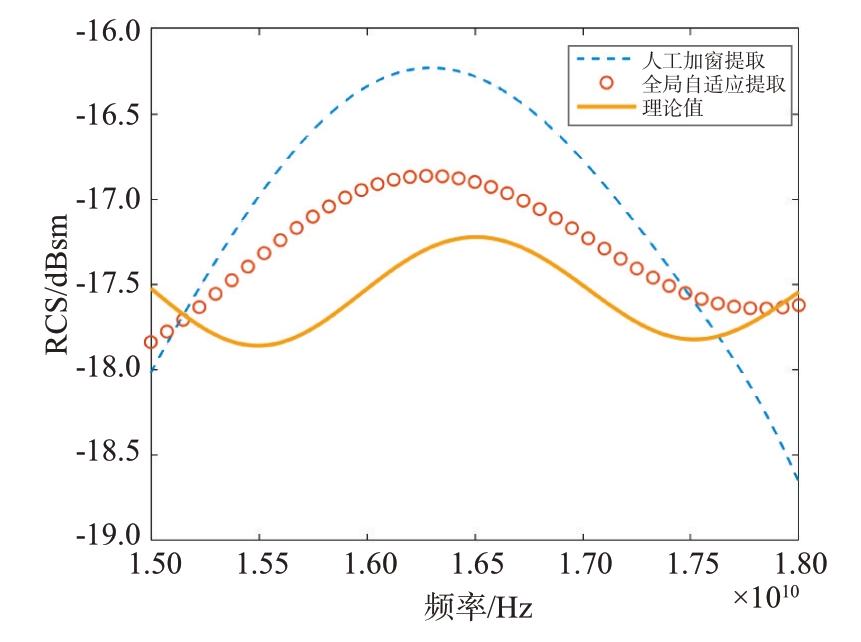
图25 方位向为0°时目标RCS测量精度对比
表4是两种算法下目标RCS测量误差对比,通过对图25 和表4 的定量分析,可以观察到对于这种简单的模型,如果恰好选择了最优的窗函数,两种算法的提取精度相差不大。但在测量目标RCS的时候,由于目标RCS 未知,无法通过遍历窗函数选取最优的窗函数进行测量。综上,全局自适应提取算法因无需窗函数的选择,所以性能更好。
表4 两种算法下目标RCS测量误差对比
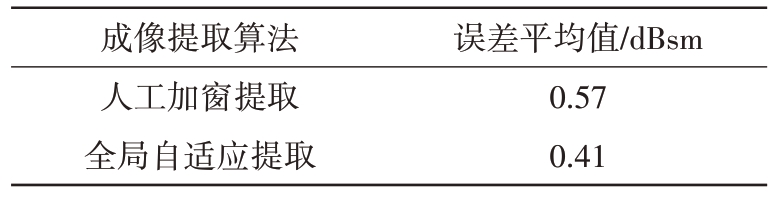
成像提取算法人工加窗提取全局自适应提取误差平均值/dBsm 0.57 0.41
2)室外场景下实测实验
室外测量场景如图26 所示,目标为200 mm 金属球放置在锥形支架上。

图26 室外测量场景
图27为采用人工加窗提取算法(窗函数半径为0.22 m)提取的目标散射像。从图27 可以观察到,目标球的散射像并不是一个规则的形状,传统的人工加窗提取方法提取的散射像(图27 中白色圆圈内的散射像)不仅包含了目标球的散射像,还有一部分杂波、背景噪声等所构成的散射像。这部分非目标的散射像会对后续的RCS 散射测量带来误差,造成测量精度的下降。与之相反的是,如图28 全局自适应提取算法提取的目标散射像所示,全局自适应提取算法可以更有效地避免杂波、背景噪声的干扰,更精准地提取到目标的散射像,从而保持较高的测量精度。
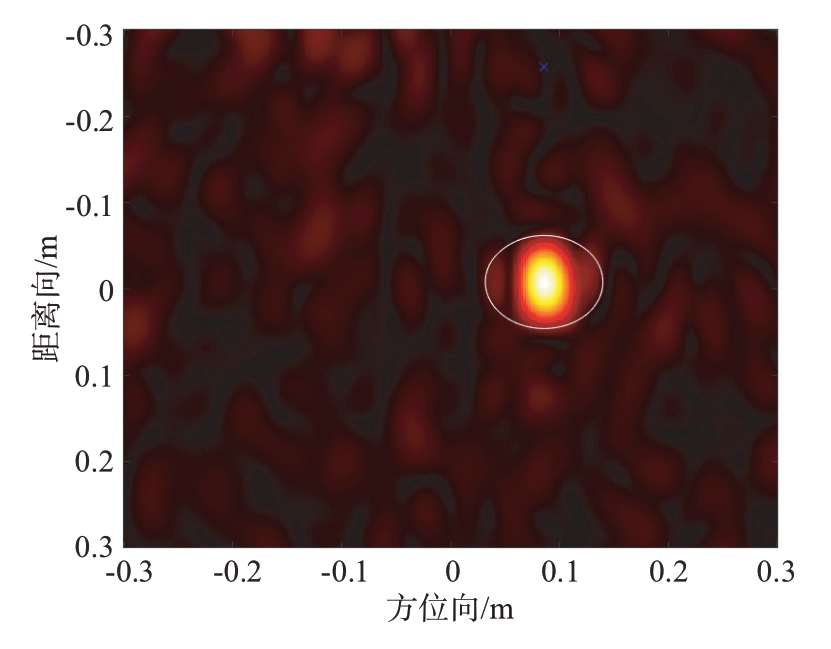
图27 半径0.22 m的窗函数提取示意图
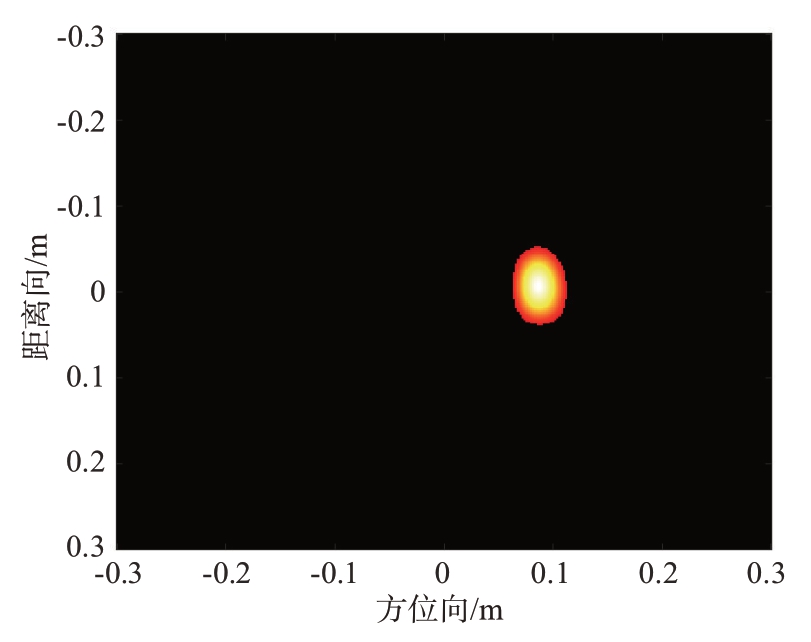
图28 全局自适应提取算法提取示意图
图29 和图30 分别为采用人工加窗提取算法和全局自适应提取算法计算得到的目标RCS 测量结果图。从图29 和图30 可以直观地看到,人工加窗提取算法在边缘处畸变依然存在,而全局自适应提取算法虽然也有一部分畸变,但对目标RCS测量精度影响较小。
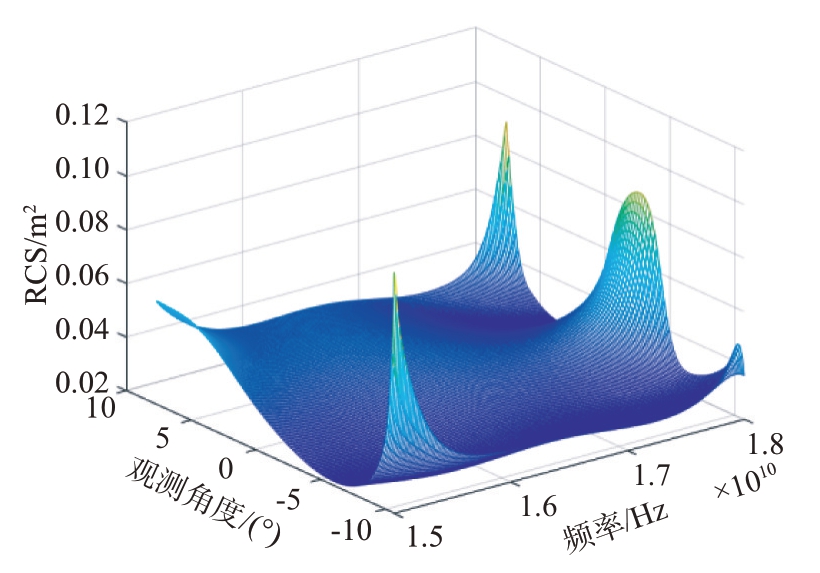
图29 人工加窗提取算法下目标RCS测量结果
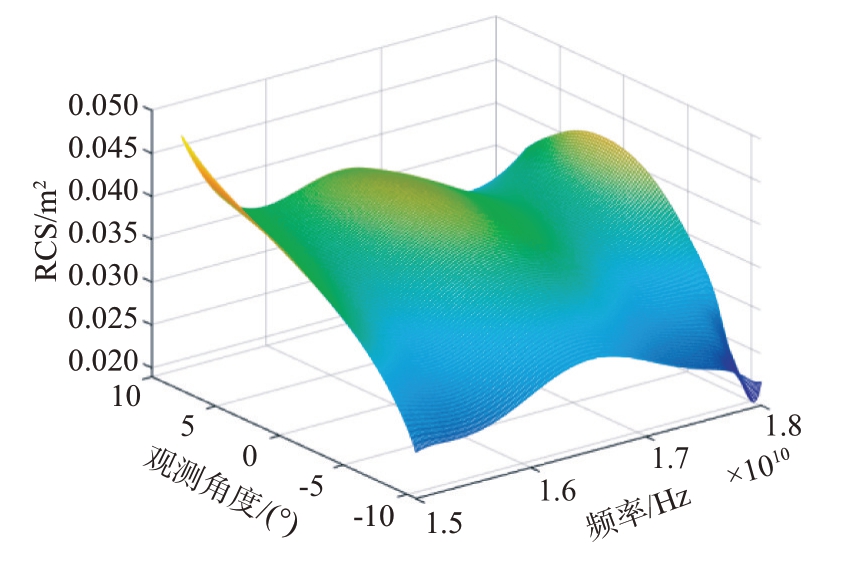
图30 全局自适应提取算法下目标RCS测量结果
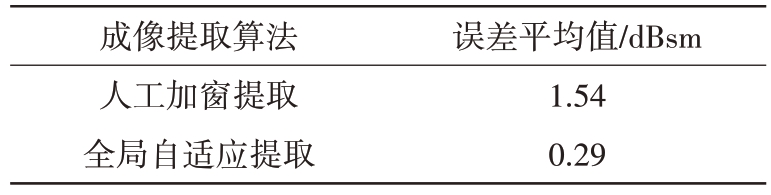
图31是方位向为0°时的目标RCS测量精度对比图,表5 是两种算法下目标RCS 测量误差对比表。通过图31 和表5 可以清晰看到,采用全局自适应提取算法得到的目标RCS 测量精度更高。由此可见,全局自适应提取算法在处理不规则的目标散射像时优势更为明显。原因在于,在复杂的室外场景下存在更多的干扰和噪声,因而精确地提取目标的散射像就能获得更高精度的RCS值。
表5 两种算法下目标RCS测量误差对比
成像提取算法人工加窗提取全局自适应提取误差平均值/dBsm 1.54 0.29
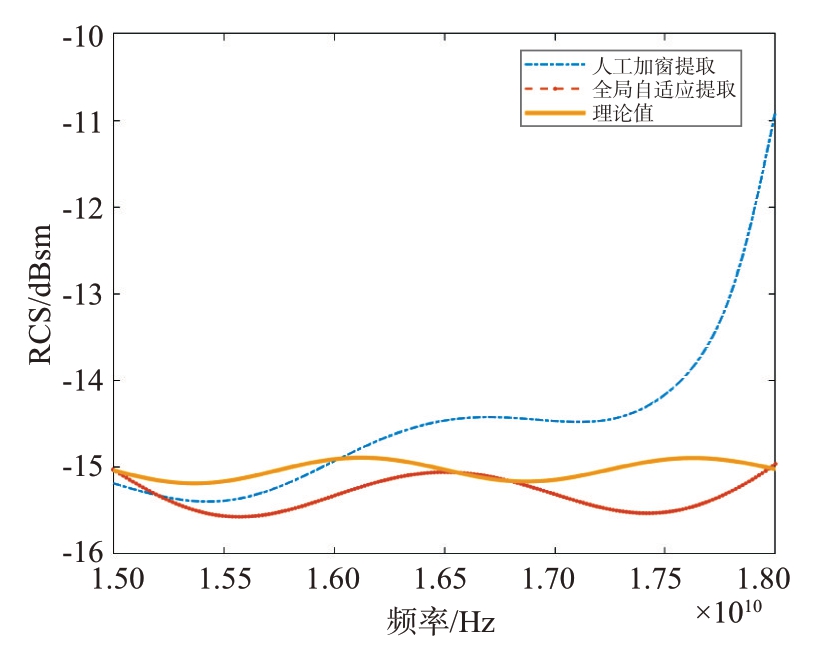
图31 方位向为0°时目标RCS测量精度对比
3 结束语
在RCS 成像测量方法中,目标散射像的提取是其必不可少的一环。然而,传统的人工加窗提取算法,RCS 的提取精度和选择的窗函数息息相关。不同的测量目标、不同的测量环境等都会影响到窗函数的选择,而且窗函数的细微变化会引起RCS 测量精度的大幅变化。针对以上问题,本文提出了基于全局自适应提取的目标RCS 成像测量算法,该算法能够根据不同的SAR 图像精准提取出目标的散射像,从而获得更高精度的测量结果。可以预见,该算法在RCS 测量领域将会有越来越多的应用。
[1]孙佳兴,姚慧婧.基于联合处理的复杂目标RCS估计方法[J].雷达科学与技术,2022,20(2):181-186.
[2]沈鑫.基于极化转换的RCS减缩技术的研究[D].成都:电子科技大学,2021.
[3]贾润强.基于雷达成像的目标RCS 测量方法研究[D].西安:西安电子科技大学,2022.
[4]何昊天,吴玲,卢发兴.基于高频算法的舰艇RCS 仿真与特性分析[J].舰船电子工程,2022,42(10):87-92.
[5]刘密歌,张麟兮,李南京.基于矢量网络分析仪的RCS测量系统及应用[J].电子测量与仪器学报,2007,21(1):82-85.
[6]马玉丰,李薇,胡鹏展,等.一种扩展紧缩场低频测试频率的时域测试方法[J].数字通信世界,2022(12):68-69.
[7]张金涛.X 波段电大尺寸目标RCS 近场测试[D].成都:电子科技大学,2022.
[8]MENG Chenkai, WANG Xiangchuan, MA Cang, et al.Fast and Multi-Band RCS Measurement Based on a Microwave Photonic Inverse Synthetic Aperture Radar[C]//2022 20th International Conference on Optical Communications and Networks,Shenzhen,China:IEEE,2022:1-3.
[9]刘依纯,朱莉,王斌.基于分辨率增强的亚毫米波RCS成像分析[J].微波学报,2023,39(S1):333-337.
[10]毕志超,张依轩,杨玉禾,等.基于ISAR 成像与改进聚类算法的部件RCS 测量方法[C]//2023 年全国天线年会论文集(下),哈尔滨:中国电子学会,2023:19-21.
[11]袁正阳.高温RCS 近场测试技术[D].成都:电子科技大学,2024.
[12]李南京,徐志浩,胡楚锋,等.基于成像提取的RCS精确测量方法研究[J].仪器仪表学报,2017,38(1):74-82.
[13]梁大伟.雷达目标RCS成像测量系统测控软件设计与开发[D].西安:西安电子科技大学,2022.
[14]OTSU N.A Threshold Selection Method from Gray-Level Histograms[J]. IEEE Trans on Systems, Man, and Cybernetics,1979,9(1):62-66.