0 引 言
合成孔径雷达(Synthetic Aperture Radar,SAR)是一种微波成像雷达,它通过雷达装载平台和目标间的相对运动,将雷达在不同位置处接收的回波信号进行相干处理获得二维图像,具有全天时、全天候的特点,在军事和民用领域得到了非常广泛的应用[1-4]。高速无人机及临近空间高速机动平台具有灵活多样的飞行轨迹,它的飞行速度快、实时性要求高,给SAR 成像系统实时成像处理带来了很大的困难[5-6],其工作时序设计也与机载、星载平台SAR等有较大的区别[7-8]。
在脉冲体制雷达系统设计中,脉冲重复频率(Pulse Repetition Frequency,PRF)是最重要参数之一,它的选取与雷达工作频率、飞行速度、天线波束、测绘带宽、视角等参数密切关联,不但影响雷达发射信号脉宽、平均功率以及处理数据率等参数的设计,还决定了观测距离和多普勒频率的模糊程度[9-11]。文献[12]针对SAR 成像过程中高度不断变化给PRF 设计带来的困难,提出了按高度变化分段调整PRF 的解决方法。文献[13]提出了一种基于穷举法的聚束SAR 成像的PRF 设计方法,但是存在PRF 下限值过大导致PRF 参数无法选取的问题。文献[14]通过场景点遍历的方式得到天线波束覆盖地面场景区域多普勒频率的最大值与最小值,进而计算出多普勒带宽和准确的PRF下限值。文献[15]以距离向分辨率为间隔,提出了基于等距离环的PRF 下限值计算方法,需要通过遍历距离环的方式计算最大多普勒带宽,该方法有效降低了PRF 下限值。由于上述两种方法均需遍历整个波束覆盖的地面场景区域,均存在PRF下限值计算量较大的问题,难以满足平台实时计算需求。另外文献[12-15]中方法均是在假定发射信号脉宽已知的前提下来推导关于PRF 的发射脉冲干扰、平台正下方回波干扰以及距离向无模糊等约束方程,由此设计出的PRF,与假定的脉宽以及峰值功率计算得到的平均发射功率可能无法满足SAR 成像作用距离需求。实际上,应先根据SAR 成像雷达方程计算出所需的平均发射功率,而平均发射功率等于峰值功率和工作占空比之积,相当于要先计算出工作占空比;在设计出合适的PRF 后,基于工作占空比与PRF、信号脉宽的关系式再确定信号脉宽。基于此,本文将信号脉宽表示为占空比与PRF 之比的形式,并将其代入发射脉冲干扰、平台正下方回波干扰以及距离向模糊限制等关于PRF 的约束方程,得到PRF 关于工作占空、回波近距以及回波远距的约束关系式;然后针对高速机动平台SAR 成像系统PRF 下限值较高的问题提出距离向分段SAR 成像处理情况下的PRF 设计方法。通过仿真实验验证了本文方法能更好地满足实际工程应用。
1 SAR图像信噪比
SAR 成像系统的一个重要参数是雷达图像信噪比,由雷达方程导出[16]:式中,Pav 为雷达平均发射功率,G 为天线收发增益,λ为发射信号波长,σ0为归一化后向散射系数,c 为光速,R 为作用距离,k 为玻耳兹曼常数,T 为接收机温度,BT 为发射信号带宽,Fn 为噪声系数,Ls为系统损耗,v为平台速度,θ 为波束入射角。平均发射功率Pav 可表示为Pav = Ptdt,其中Pt 为峰值发射功率,dt 为工作占空比,而占空比又取决于系统发射信号脉宽与PRF,即dt = τ × PRF,发射信号脉宽τ与PRF有着关联性,在进行SAR成像PRF设计时若先假定脉宽为固定值,再进行PRF 选择设计,得到的占空比不一定合理,此时须进行解耦,下文将τ = dt/PRF 代入发射脉冲干扰、平台正下方回波干扰以及距离模糊限制等约束方程进行PRF设计。
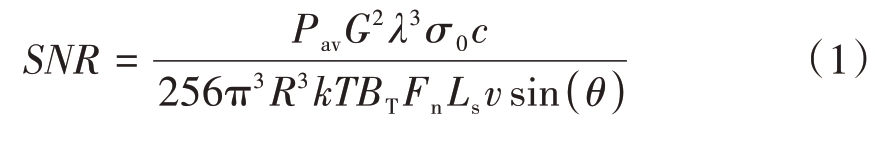
2 PRF设计原则
2.1 避开发射脉冲干扰
相控阵雷达通常采用收发共用天线,在天线发射脉冲时间窗口内,无法接收回波信号,PRF 的设计需使地物场景回波信号的返回时间窗口与发射脉冲时间窗口错开,同时要满足波束覆盖地面场景区域的近距与远距回波信号落在同一个脉冲重复周期接收窗口时间内,得到以下约束关系[12]:
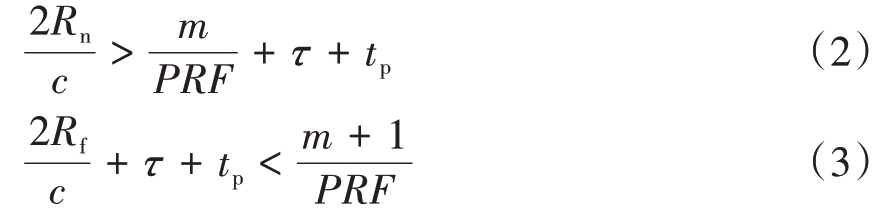
式中,Rn 和Rf 分别为天线波束覆盖地面场景区域近端和远端斜距,m 为距离模糊数,τ 为发射信号脉宽,tp 为发射与接收时序保护时间。根据第1 节分析将τ = dt/PRF 代入上述两个约束方程,经整理可得PRF关于占空比dt的约束关系式为
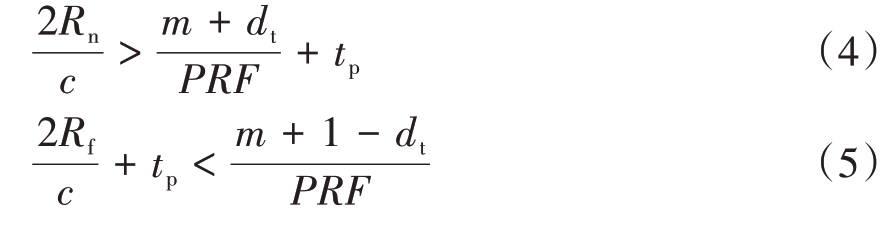
2.2 避开平台正下方回波干扰
平台正下方回波是雷达天线从平台下方接收到的旁瓣回波,其覆盖区域内的各散射点到雷达的时间差异比较小。平台正下方回波干扰距离假定为平台高度H,PRF 设计应使平台正下方回波落入发射脉冲时间窗口内,应满足以下约束关系式[11]:
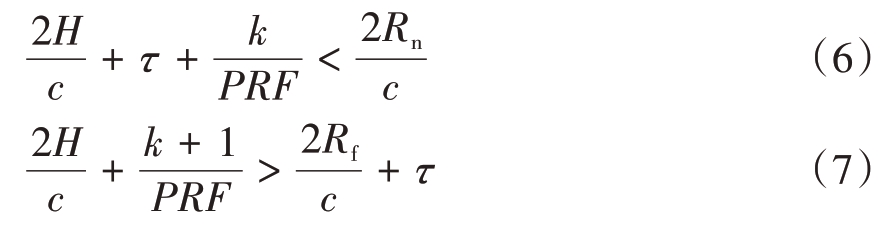
式中,k 为主瓣回波近距对应的距离模糊数与平台正下方旁瓣回波远距对应的距离模糊数之差。
将τ = dt/PRF 代入上述两个约束方程式,经整理可得PRF 关于占空比dt 的避开平台正下方旁瓣回波干扰的约束方程式为
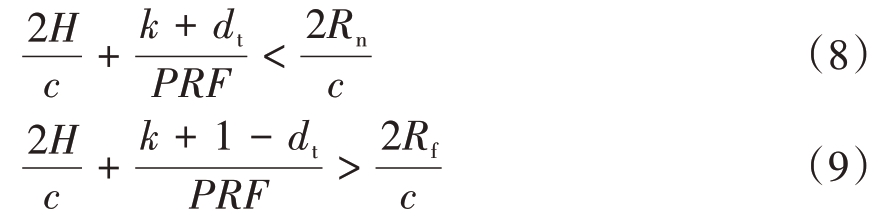
2.3 距离模糊限制
雷达天线波束照射地面时有一定的覆盖范围,覆盖地面场景区域的近距点Rn 和远距点Rf 对应的回波信号延时会有差异,PRF设计时需要考虑天线主瓣覆盖地面场景区域回波信号的时间宽度。设回波距离模糊数为m,近距Rn 和远距Rf 对应的回波延时分别为2Rn/c和2Rf/c,雷达发射与接收信号的时序关系如图1所示。

图1 雷达发射与接收信号时序
图1中,PRT是脉冲重复周期,发射脉冲1的回波信号在第m+1个PRT后被接收。PRF需满足
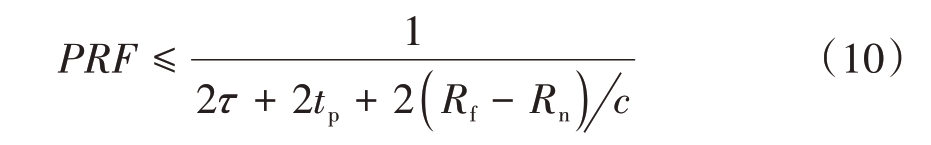
将τ = dt/PRF代入上式,经整理可得
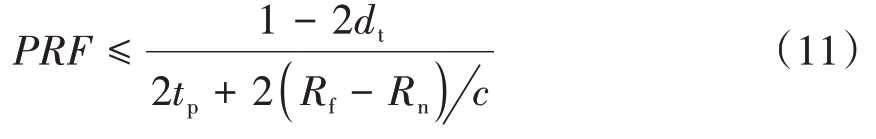
2.4 方位模糊限制
PRF相当于方位向回波信号的采样率,它的取值应大于方位向多普勒信号带宽的主要部分[15],即
式中,l 为方位向过采样率,一般取为1.1~1.4,B 为方位向多普勒带宽。
聚束SAR 成像模式的方位向多普勒带宽由瞬时多普勒带宽和多普勒中心频率的变化[15]两部分组成,如下式所示:
式中:![]() 为雷达天线波束覆盖地面场景区域内的瞬时多普勒带宽,ρm和ρn 分别表示波束覆盖地面场景区域内任意两点m 和n 对应的等效斜视角;
为雷达天线波束覆盖地面场景区域内的瞬时多普勒带宽,ρm和ρn 分别表示波束覆盖地面场景区域内任意两点m 和n 对应的等效斜视角;![]() 为多普勒中心频率变化范围,va 为方位向速度,ψ为速度矢量和斜距矢量的夹角,Ta 为方位向积累时间。
为多普勒中心频率变化范围,va 为方位向速度,ψ为速度矢量和斜距矢量的夹角,Ta 为方位向积累时间。
3 基于距离向分段的PRF设计和SAR成像处理
3.1 PRF设计
对于机动平台飞行速度快、SAR 成像作用距离远、雷达天线波束宽的情况,现有文献[12-15]中的PRF 设计方法根据方位模糊限制计算出的PRF下限值会出现大于距离模糊限制计算出的PRF 上限值的情况,这时无法选择合适的PRF 值。需设法降低PRF 下限值,这里将雷达回波信号沿距离向按子段进行划分,对每个子段分别进行SAR 成像处理,然后进行拼接得到完整的SAR 图像[17],这样只需考虑距离子段内的多普勒中心频率变化和瞬时多普勒带宽用于PRF 下限值计算,能够有效降低PRF 下限值,扩展PRF 可选择的区间。下面首先进行PRF下限值设计。
SAR 成像几何场景如图2 所示,O 为成像系坐标原点,P 为平台位置,天线波束覆盖地面场景区域近似为椭圆,椭圆长径和短径分别为天线方位与俯仰波束覆盖地面场景区域的方位向与距离向宽度的一半[15],即椭圆长径和短径为
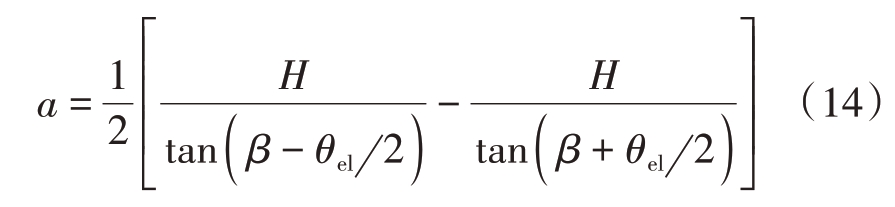
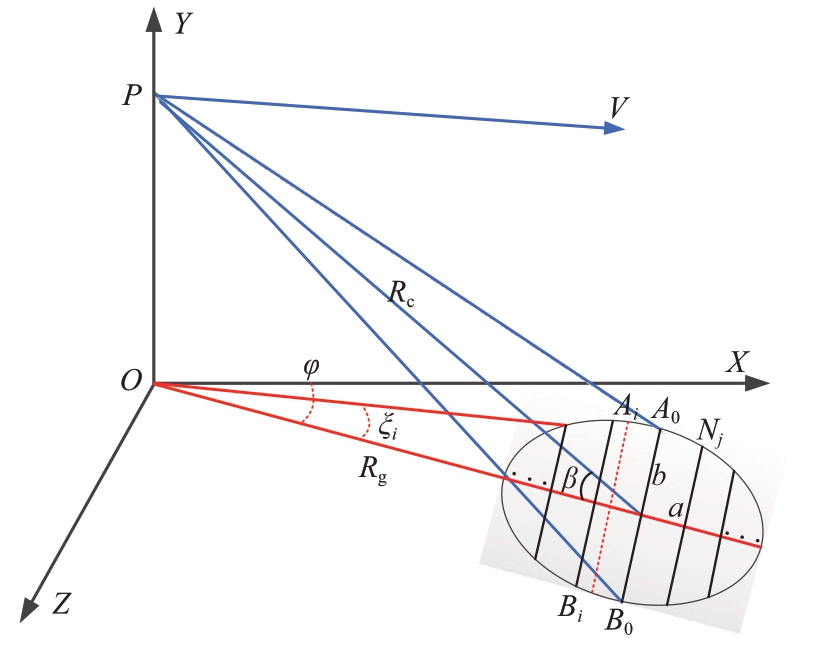
图2 前斜SAR成像几何模型
式中,H 为平台高度,θaz 和θel 分别为雷达天线方位与俯仰波束宽度,β 为天线波束擦地角。图中,前斜角φ 为天线波束指向矢量在地面上的投影与X轴的夹角,Rc为中心斜距,Rg为地距。
步骤1 以地面距离向分辨率为间隔,将天线波束覆盖地面椭圆区域分成等距离分辨率线,如图2所示,椭圆长径所在距离线对应的椭圆区域交点为Ai 和Bi,i = -M,…, - 1,0,1,…,M,其中A0 和B0为椭圆中心点所在距离线对应的交点。首先求出点A0 和B0 对应的多普勒频率差,椭圆中心点对应的地距为
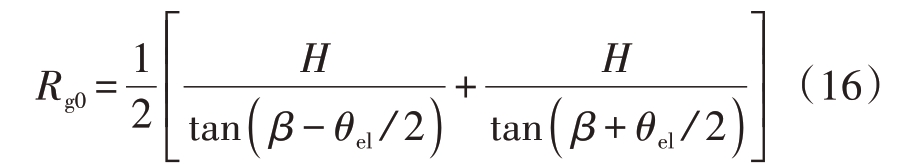
矢量![]() 与天线波束指向矢量在地面上投影之间的夹角为
与天线波束指向矢量在地面上投影之间的夹角为
令![]() 则点A0 与B0 的坐标可求解为
则点A0 与B0 的坐标可求解为
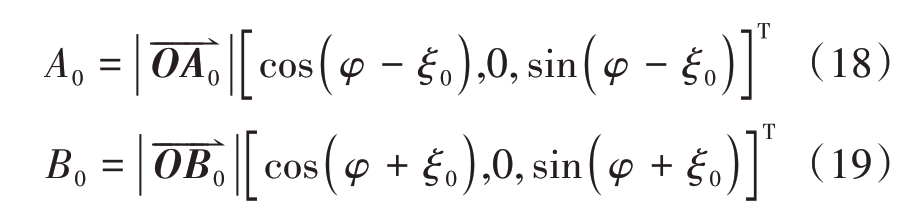
平台速度矢量与矢量![]() 的夹角分别为
的夹角分别为
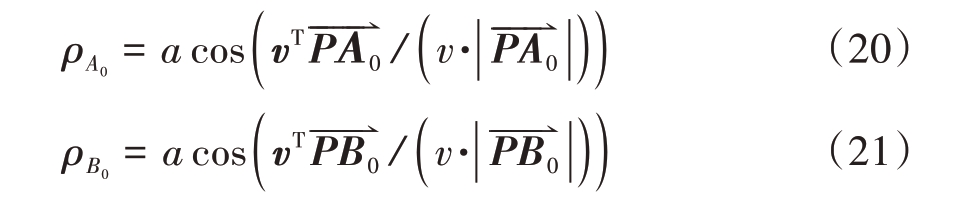
式中,v为平台速度矢量,上标T代表转置,| | 表示2-范数。
则椭圆中心点所在距离线所对应的多普勒带宽可以近似用下式求解:
步骤2 以椭圆中心点为起始点、地面距离向分辨率为步进间隔,令i = 0,以远距端为例,沿长径向椭圆远端方向计算交点(Ai + 1,Bi + 1)多普勒带宽Bdi + 1(计算方式同Bd 0)
将Bdi + 1 与Bdi 进行比较,若Bdi <Bdi + 1,令Bdi =Bdi + 1,i = i + 1,重新计算Bdi + 1,直到出现Bdi >Bdi + 1,则Bdi即为以距离分辨率为间隔对应的最大多普勒带宽。
步骤3 将天线波束覆盖地面椭圆区域沿距离向等间隔划分为2N 个距离子段,首先找到步骤2 得到的最大多普勒带宽对应距离线所在距离子段Nj,然后计算该距离段内最大多普勒带宽:
式中ρNj 为距离子段Nj 椭圆区域点对应的等效斜视角。
步骤4 将BdNj 代入式(13),可得到所有距离子段的最大方位向多普勒带宽B = Ba + BdNj,进而根据式(12)求得距离向子段的方位模糊限制约束的PRF下限值为
综上,可得PRF具体设计步骤如下:
1)根据式(11)确定距离模糊约束的PRF 上限值;
2)根据式(25)确定方位模糊约束的PRF 下限值;
3)根据发射脉冲干扰约束关系式(4)、(5)和平台正下方回波干扰关系式(8)、(9)绘制斑马图,其横坐标表示的脉冲重复频率的范围由PRF 的上限值和下限值确定;
4)根据斑马图以及雷达回波近距和远距的波束入射角选择相应的PRF 值,这里要遵循的一个原则是尽可能选择较低的PRF 值,以减少处理数据量。
3.2 SAR成像处理
基于距离向分段的SAR 成像处理流程主要包括距离向回波子段划分、子块成像、图像拼接和几何校正等步骤[17],如图3(a)所示;图3(b)给出了子块成像处理流程,分为距离压缩、距离走动补偿、距离弯曲补偿和方位压缩4 个步骤。距离向分段的好处是只需考虑每个子段内的最大多普勒带宽,降低系统PRF下限值。
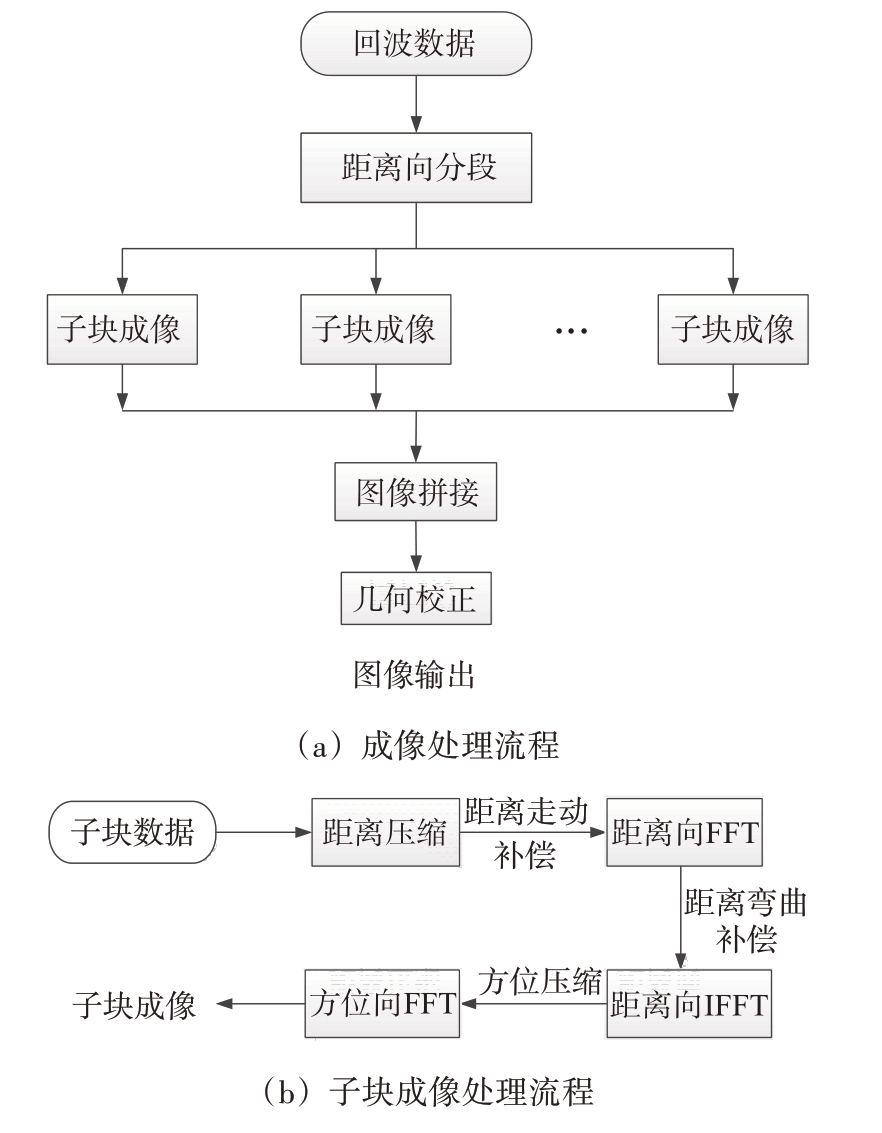
图3 距离分段SAR成像处理流程
4 仿真实验
设置仿真实验参数同文献[14]:雷达波长为0.015 m,平台高度为16 832 m,运动速度为1 724.2 m/s,天线方位和俯仰波束宽度分别为4°和5°,发射与接收保护时间为0.5 μs。设置作用距离为40 km对应的占空比为0.2,距离分段数为32。
首先分析本文所提基于距离分段的PRF 下限值,并将其与文献[14]中的基于天线波束覆盖地面场景区域遍历点的方式(简称“遍历法”)、文献[15]中的基于等距离环方法计算的PRF 下限值结果进行对比。图4 给出了3 种方法PRF 下限值和距离模糊约束PRF上限值随前斜角φ变化的结果。
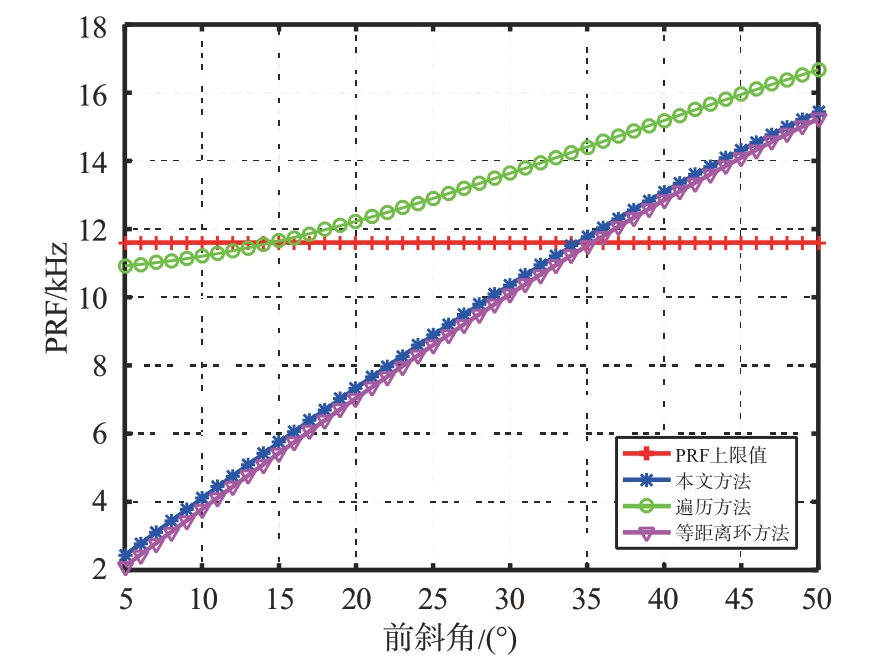
图4 3种方法PRF下限值随前斜角变化曲线
从图4可以看出,距离模糊限制PRF上限值为11.61 kHz;在前斜角φ=5°时,遍历法的PRF下限值达到10.92 kHz,很接近上限值;本文方法和中等距离环法的PRF 下限值比较接近,分别为2.43 kHz 和2.11 kHz;随着前斜角的变大,3种方法PRF下限值均快速增加,在前斜角为15°时,遍历法的PRF 下限值超过距离模糊限制的PRF 上限值,而本文方法和等距离环法的PRF 下限值分别在35°和36°时超出PRF上限值。
图5 给出了前斜角为20°时3 种方法PRF 下限值和距离模糊限制的PRF 上限值随平台运动速度v变化的曲线,可以看出,PRF上限值仍为11.61 kHz,3种方法PRF的下限值随着运动速度v的增加均快速增加,遍历法PRF下限值在运动速度为1 600 m/s时即超出上限值,本文方法和等距离环法PRF 下限值分别在运动速度分别为2 750 m/s 和2 850 m/s时超出PRF上限值。

图5 3种方法PRF下限值随运动速度变化曲线
在雷达天线俯仰向波束宽度增大或者中心斜距增加时,天线波束覆盖地面椭圆区域相应增加,会导致距离模糊约束PRF 上限值大幅下降。图6和图7 分别给出了PRF 上限值和3 种方法PRF 下限值随天线俯仰向波束宽度和中心斜距变化的曲线。可以看出,随着俯仰向波束宽度增大或者作用中心距离的增加,PRF 上限值迅速减小,遍历法PRF 下限值在俯仰波束宽度为5.4°和中心斜距为44 km 时超出PRF 上限值,而本文方法和等距离环法PRF 下限值均变化很小,分别保持在6 kHz 和5.75 kHz左右。

图6 3种方法PRF下限值随俯仰波束宽度变化曲线
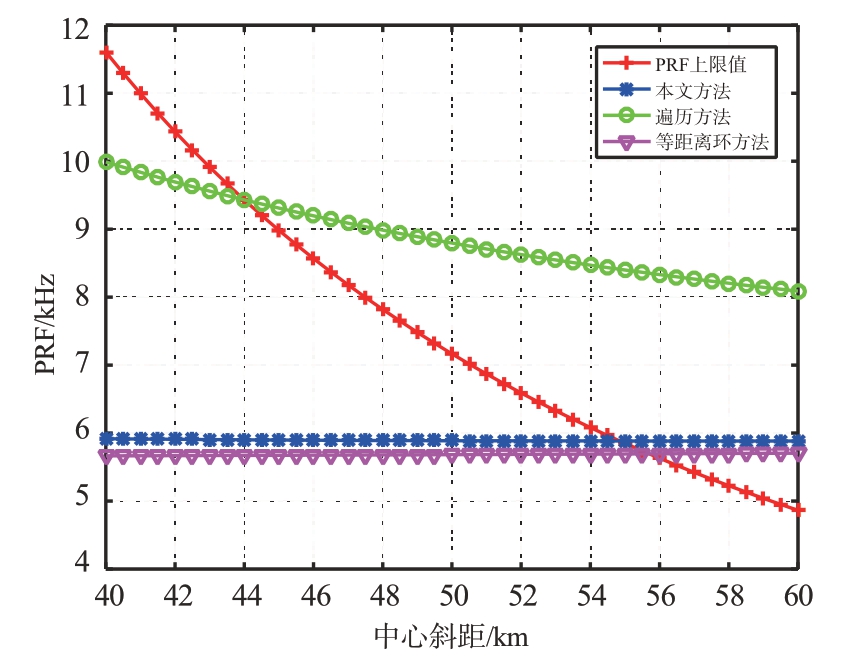
图7 3种方法PRF下限值随中心斜距变化曲线
从上述仿真结果可知,遍历法的PRF 下限值受前斜角、平台运动速度、天线波束宽度以及中心斜距等因素影响很大,比较容易超出距离模糊限制的PRF 上限值,从而导致无法选择有效的PRF值;与之相比,同等条件下本文方法与等距离环方法PRF 下限值比较相近,明显比遍历法小,能够适用于更大的前斜角、波束宽度以及更快的平台速度等较为复杂的成像场景。
接下来将本文方法计算PRF 下限值耗时与遍历法、等距离环法所用的计算耗时进行比较。文中计算耗时为在Matlab2017a 虚拟环境下进行1 000次仿真实验所用总时间除以总次数得到的平均值。表1给出了几种方法的计算耗时情况。
表1 计算耗时比较

算法文献[14]方法文献[15]方法本文方法耗时/ms 38.0 38.4 1.6
从表1可以看出,遍历法和等距离环法两种方法和等距离环法能够有效降低PRF 下限值,能适应更大的前斜角、运动速度、波束宽度和中心斜距,有效扩展了PRF 可选择的区间。方法耗时相当,均接近40 ms,而本文方法计算耗时仅为1.6 ms。这是因为:文献[14]遍历法首先通过遍历的方式得到波束覆盖地面椭圆区域内所有散射点等效斜视角余弦值的最大值和最小值,然后根据最大值与最小值之差求出多普勒中心偏移带宽,进而得到PRF 下限值;文献[15]等距离环法将椭圆区域以距离向分辨率为间隔划分为等距离环,通过遍历的方式求出所有距离环的最大多普勒带宽以得到PRF 下限值,两种方法均要通过遍历所有点以至于计算耗时长;而本文将椭圆区域划分为若干距离段,利用椭圆区域中间部分距离字段上点相对于边缘部分距离子段上点与平台运动速度矢量形成等效前斜角余弦值差异大、多普勒带宽也大的特点,以椭圆区域中间部分距离子段为起始,往椭圆区域两边缘递推比较相邻距离子段的多普勒带宽,当出现当前距离子段多普勒带宽大于远近两相邻距离段的多普勒带宽时,即取当前距离子段多普勒带宽参与PRF 下限值计算。由于椭圆区域中间部分距离子段上多普勒带宽相对边缘距离段大,实际上递推过程只需要计算较少的距离子段迭代就停止了。
为说明距离子段的多普勒带宽,将距离分段数设为64,对前斜角10°~50°情况下不同距离段的多普勒带宽进行计算,结果如图8所示。从图中可以看出,不同前斜角下距离分段多普勒带宽曲线呈现出中间部分距离子段多普勒带宽大、边缘部分距离子段多普勒带宽小的现象,只需递推迭代中间部分几个距离子段的多普勒带宽值,这样计算耗时就少很多。
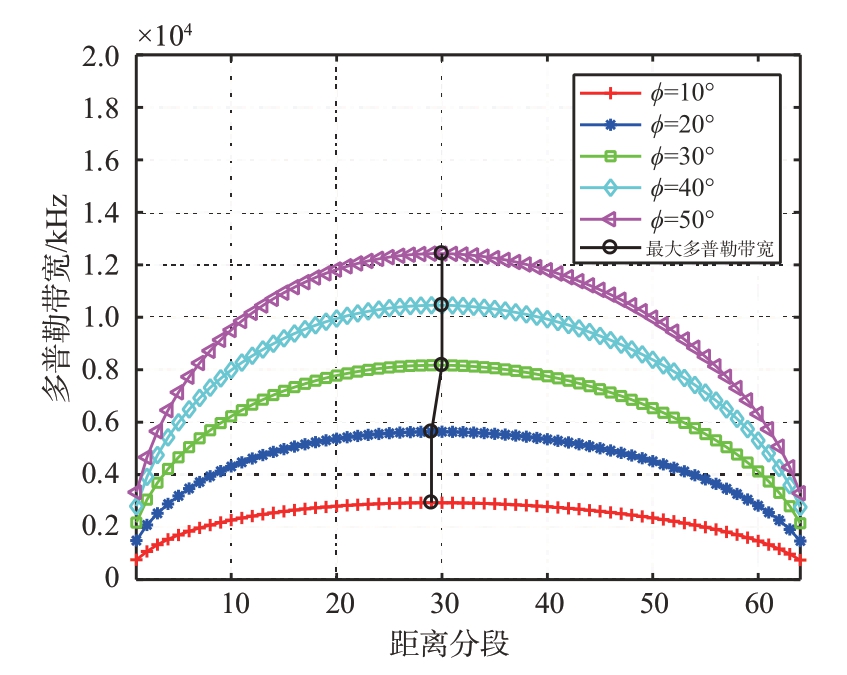
图8 距离子段多普勒带宽
最后对比本文方法与等距离环法的PRF 设计值,仿真实验参数设置同文献[15]中参数,根据式(11)计算的距离模糊限制的PRF上限值为6 963 Hz。图9给出了占空比为20%时的PRF斑马图(由于作用距离较远,雷达通常要工作在较高的占空比),在选择PRF 时需要避开发射脉冲干扰和平台正下方回波干扰,同时需要大于PRF 下限值,小于PRF上限值。图中空白区域为非干扰区,可将PRF 选择为设计为5 920 Hz,这时信号脉宽约为33.8 μs。而文献[14]在设定脉宽为10 μs的基础上得到PRF为5 500 Hz,对应占空比仅为5.5%,难以满足远距离SAR成像威力需求。
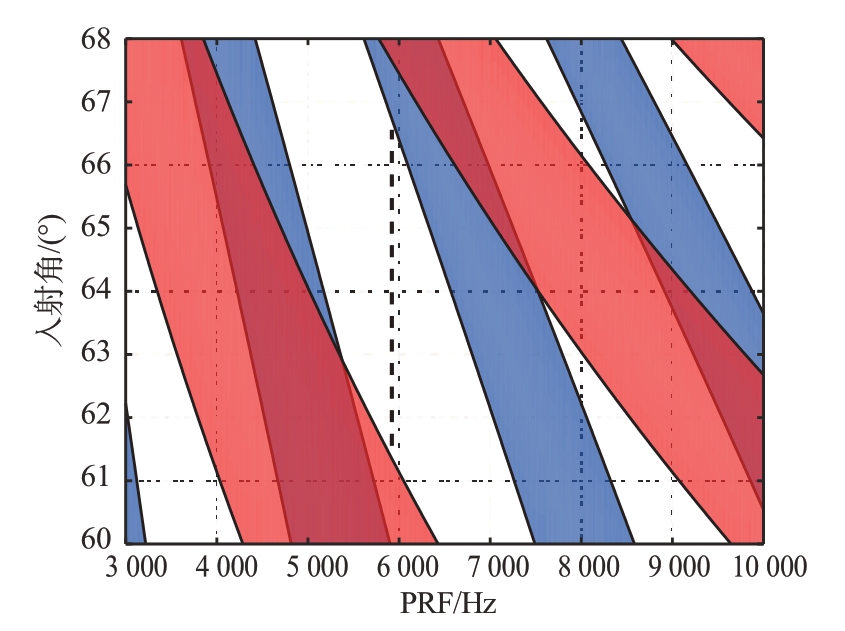
图9 PRF斑马图
对基于点阵目标的距离向分段回波进行SAR成像处理仿真,为便于说明将距离向回波划分为4段,子块图像拼接和校正后输出图像结果如图10(a)和(b)所示,可以看出图中每个距离子段内和校正后图像中的点目标均得到了很好的聚焦效果。
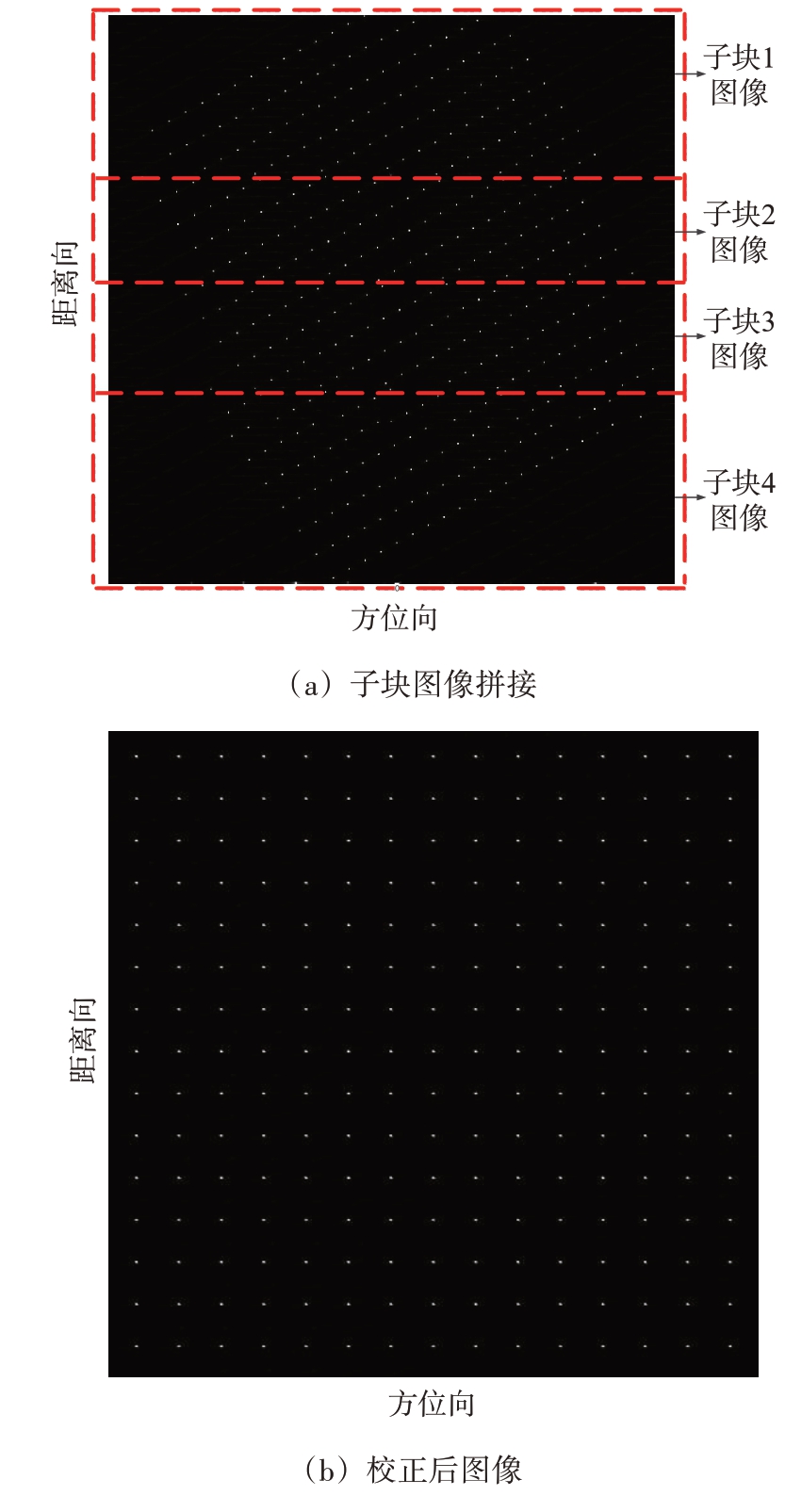
图10 距离向分段SAR成像处理结果
5 结束语
本文研究了高速机动平台SAR 成像PRF 设计方法。首先分析了雷达聚束SAR 成像发射脉冲干扰、平台正下方回波干扰以及距离向模糊限制等关联PRF 与占空比的约束方程式,然后针对高速、远距离聚束SAR 成像长径现有PRF 设计方法不适用的问题,提出了距离向分段处理情况下的方位模糊限制多普勒带宽计算方法,有效地扩展了PRF可选择的区间,能够适应更复杂的场景,设计出的PRF结果与相应的信号脉宽能更好地满足实际工程应用。通过仿真分析证实了所提方法的有效性和可行性。
[1]金秋,王雨晗,杨果,等.高速平台SAR脉内多普勒效应误差分析和校正[J].雷达科学与技术,2023,21(3):237-246.
[2]张丽丽,蔡健楠,刘雨轩,等.用于SAR图像舰船目标检测的MAF-Net和CS损失[J].雷达科学与技术,2024,22(1):14-20.
[3]王岩飞,李和平,韩松.天线阵列编码合成孔径成像[J].雷达学报,2023,12(1):1-12.
[4]姚佰栋,盛磊,孙光才,等.大椭圆轨道SAR系统设计及关键技术研究[J].雷达科学与技术,2020,18(4):373-380.
[5]郭媛,索志勇,王婷婷,等.弹载SAR系统参数优化设计方法[J].系统工程与电子技术,2020,42(7):1478-1483.
[6]郭媛.弹载平台单/双基SAR 系统设计及成像处理技术[D].西安:西安电子科技大学,2022.
[7]LI Yachao, DENG Huan, QUAN Yinghui, et al. Sequence Design for High Squint Spotlight SAR Imaging on Manoeuvring Descending Trajectory[J].IET Radar,Sonar&Navigation,2017,11(2):219-225.
[8]杜林鹏.毫米波制导雷达成像系统参数设计及方法研究[D].西安:西安电子科技大学,2021.
[9]陈粤,禹卫东.星载SAR 方位多通道TOPS 成像模式参数设计[J].雷达科学与技术,2022,20(2):142-149.
[10]王志.低轨星载多模式SAR系统设计与成像处理技术[D].西安:西安电子科技大学,2021.
[11]周鹏,赵家兴,吕伟强,等.星载SAR 系统参数设计过程自动化方法研究[J].雷达科学与技术,2023,21(4):440-446.
[12]郑陶冶,俞根苗.弹载SAR脉冲重复频率设计研究[J].雷达科学与技术,2010,8(3):217-222.
[13]谢华英,卢再奇,周剑雄,等.弹载平台聚束SAR 成像脉冲重复频率设计[J].系统工程与电子技术,2010,32(11):2294-2298.
[14]邓欢,李亚超,全英汇,等.弹载下降段大前斜聚束SAR 成像时序设计[J].系统工程与电子技术,2016,38(5):1032-1038.
[15]党彦锋,梁毅,张罡,等.机动平台俯冲大斜视SAR 脉冲重复频率设计[J].系统工程与电子技术,2020,42(3):575-581.
[16]CUMMING I G, WONG F H. Digital Processing of Synthetic Aperture Radar Data Algorithms and Implementation[M].USA:Artech House,2005.
[17]耿旭朴,董纯柱,殷红成.一种分段处理的大斜视SAR成像算法[J].微波学报,2012,28(S2):455-458.