0 引 言
基于连续波雷达的生命体征检测技术由于其非接触特性被广泛用于医疗健康领域[1],例如睡眠监测、呼吸异常检测、睡眠呼吸暂停检测、婴儿检测等[2],在近十几年中获得了很大的关注[3-5]。现有的大部分工作都只聚焦于检测单个目标的生命体征信号。在实际的检测场景中,比如在病房、卧室乃至于灾后搜救等场景,通常需要雷达能够同时检测多个目标的生命体征信号。但是当多个相邻目标位于同一距离、同一波束时,现有的大部分雷达系统受限于雷达体制或者分辨率,无法分离出检测场景中多个目标的生命体征信号。
现有的多目标生命体征检测方法主要可分为两种。第一种为基于空间分布距离门的解决方案,位于不同距离受试者的生命体征信号可通过提取各自所在距离门数据,实现多目标的生命体征检测。目前涉及到的雷达系统包括线性调频连续波[6]、步进频率连续波[7]、超宽带[8]等。但是该方案无法分离同一距离上的多个受试者。
另一种为基于空间分布波束的解决方案,利用不同角度指向的波束分离同一距离上多个受试者的生命体征信号。具体来说,工作可进一步分为基于机械扫描的解决方案、基于频扫天线的解决方案以及基于相控阵天线的解决方案。对于基于机械扫描的解决方案[9],波束的扫描是通过雷达天线的机械转动实现的。因此,受限于转台的变角速度,无法同时获得多个目标的生命体征信号。对于基于频扫天线的解决方案[10],通过改变发射信号的频率可实现波束的前后扫描。但是,波束角度与特定信号频率的关联降低了频谱效率。对于基于相控阵的解决方案[11],利用硬件改变每个射频通道的相位以实现波束的扫描。但是上述方案受制于体制或者分辨率,无法实现相邻目标的生命体征信号。
为了解决这一问题,本文提出了一种基于自适应波束形成的算法,来实现同一距离上相邻目标的生命体征信号检测。根据估计出的目标信息,分别生成相应数量的不同受试者角度指向的波束;我们这里采用的是基于线性约束最小方差(Linear Constraint Minimal Variance,LCMV)准则和最小均方误差准则(Minimum Mean Square Error,MMSE)的自适应波束形成,其可在干扰目标所在角度处生成零陷实现相邻目标的生命体征检测。为了验证所提算法的性能,设置了两个受试者肩并肩的检测实验,结果表明所设计系统的有效性以及算法的优越性。
1 基本原理
1.1 基于雷达的生命体征检测原理
图1 描述了基于雷达的生命体征检测原理示意图,从图中可以看出当雷达发射的电磁波达到受试者的胸腔时,受试者的生命体征信号将会以相位的形式调制到发射波形中,接收机接收到这个受调制的回波信号后,进行相位解调后即可获得受试者的生命体征信号。
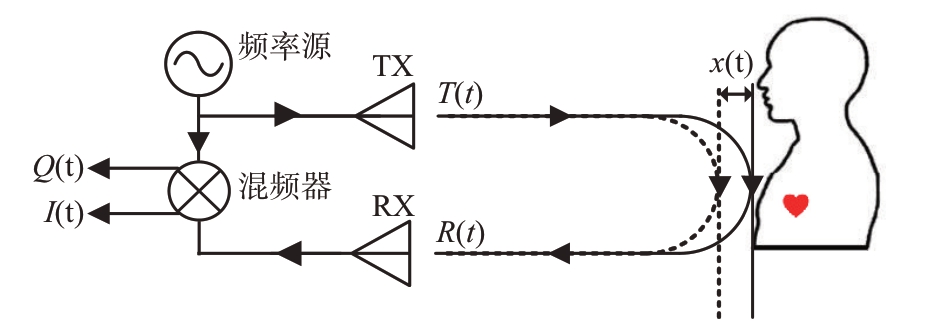
图1 基于雷达的生命体征检测原理示意图
单频CW雷达的发射波形为
式中,AT 为发射信号的幅度,f0 为载波频率,φ 为随机初相。
接收信号和发射信号相比有一个时间延时τ:
式中,r0 为雷达与受试者之间的距离,x( )t 为由呼吸和心跳引起的胸腔位移。
雷达回波信号可以表示为
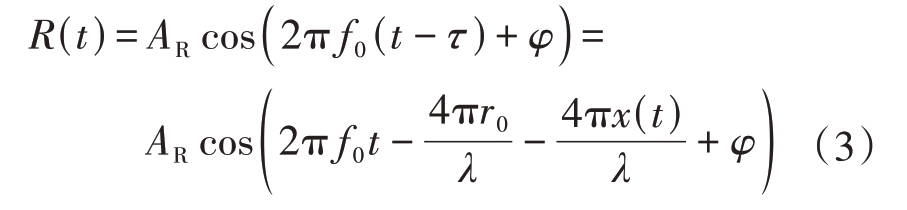
式中,AR为回波信号的幅度。
通过正交混频器后,可获得基带信号,其复表达式为
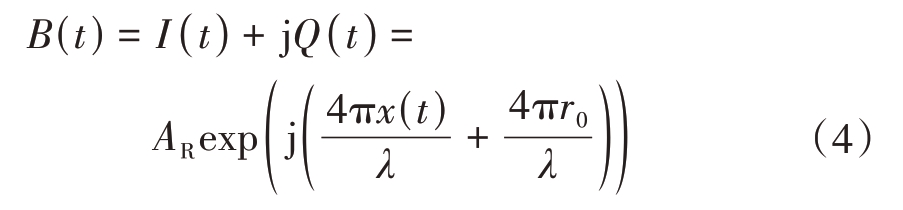
根据上式可知,受试者的生命体征信号是调制在基带信号的相位中的。因此只需对基带信号进行相位解调,就可以获得基带信号的生命体征信号。
最常见的相位解调方法就是反正切解调算法,可以表示为
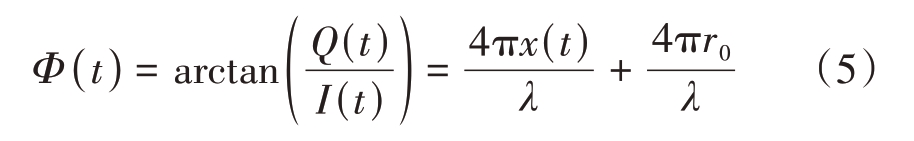
1.2 基于波束形成的多目标生命体征检测原理
1.2.1 阵列信号数学模型
为了仿真考察各算法的性能,需对阵列天线进行数学建模,论文中为了简化分析,如无特意注明,天线单元均为各项同性,且为均匀线阵,具体如图2所示。
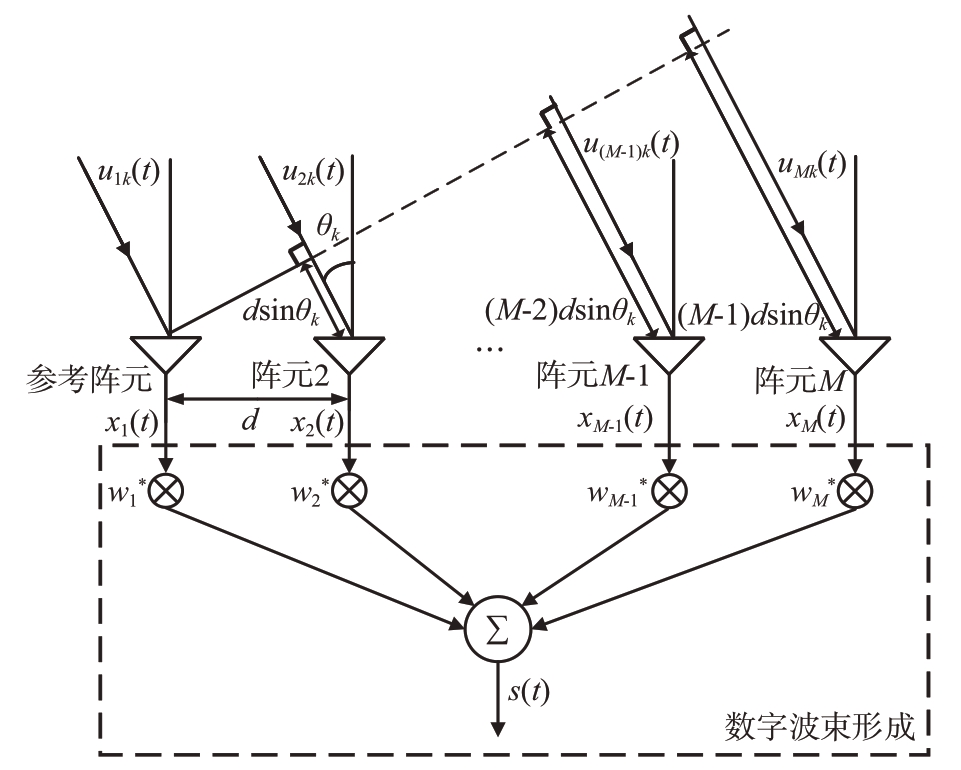
图2 数字波束形成示意图
假设空间中有K 个远场目标,其入射角为![]() 接收天线个数为M,那么第k 个目标入射到第m个接收天线的信号可表示为
接收天线个数为M,那么第k 个目标入射到第m个接收天线的信号可表示为
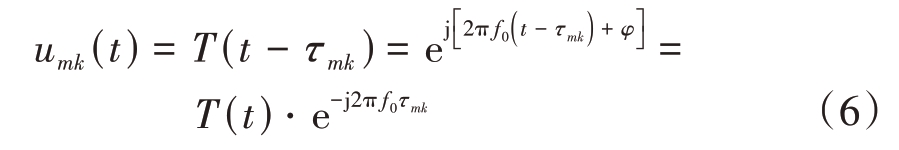
式中,m ∈[1,M],k ∈[1,K],τmk 为第k 个目标入射到第m个接收天线的信号与发射信号的时延。
为了方便后面的分析,我们将u1k(t)作为参考,则上式可变形为
由于阵列天线是等间距排列的,因此两个相邻天线阵元的时延差可以表示为
将式(8)代入式(7)中,可得到
每个接收天线接收到的信号可以表示为
阵列接收数据的向量形式如下:
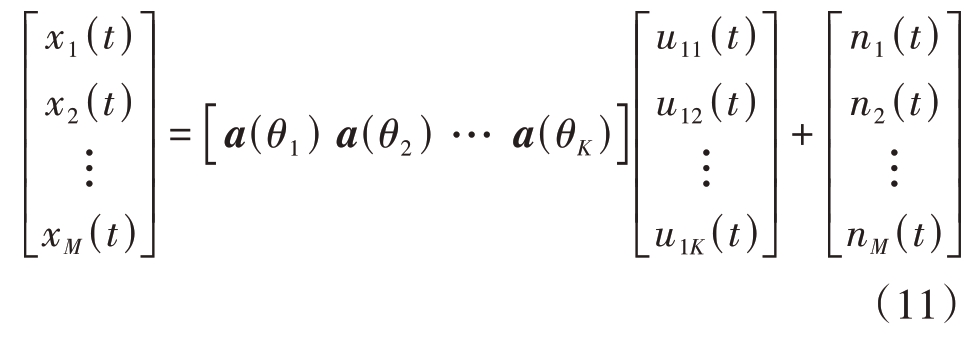
为了简化处理,将式(11)转换成矩阵相乘形式:
式中,N(t)为N × 1 噪声信号的矢量形式,U(t)为N × 1入射信号的矢量形式,A为阵列流形矩阵,可表示为
式中,a(θk)为第k 个目标的导向矢量,具体可表示为
对阵列天线来说,接收到的数据包括期望信号、干扰信号,数字波束形成的目的是为了增强特定方向的信号,消除或抑制其他方向的干扰信号和噪声。数字波束形成是以导向矢量作为加权矢量对空域进行滤波,控制主瓣波束的指向[11-12]。
数字波束形成具体实现过程为M 个天线阵元接收信号的加权相加,数字波束形成的最终输出信号可以表示为
式中,![]() 为数字波束形成的加权向量,(·)*表示共轭,(·)H表示共轭转置。
为数字波束形成的加权向量,(·)*表示共轭,(·)H表示共轭转置。
经过波束形成处理后,阵列信号的输出功率表示为![]()
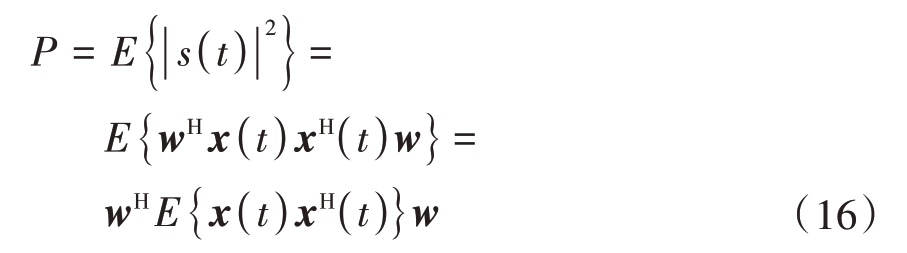
式中,![]() 表示数学期望,为协方差矩阵,其可分解为
表示数学期望,为协方差矩阵,其可分解为
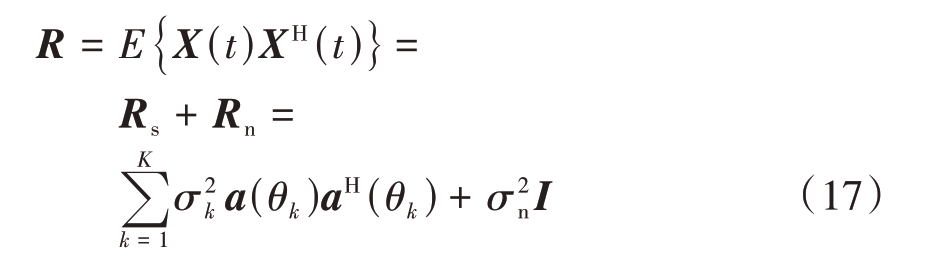
式中,![]() 为第k 个入射目标的信号功率,
为第k 个入射目标的信号功率,![]() 为阵列天线的噪声功率,
为阵列天线的噪声功率,![]()
在实际应用中,协方差矩阵可由下式估计得到:
式中,N为采样得到的数据长度。
1.2.2 基于LCMV的自适应波束形成
自适应波束形成算法基于指定的优化准则生成对应的最优权值,在不影响期望信号的前提下,使得干扰目标所在角度生成零陷。
LCMV 准则是在保证波束形成输出能量最小的条件下,对存在干扰的角度上进行抑制,因此其问题模型可表示为

式中,C 为约束矩阵,f 为约束响应矢量。为保证期望信号的能量不受衰减,同时在干扰所在角度进行抑制,因此C和f可以表示为
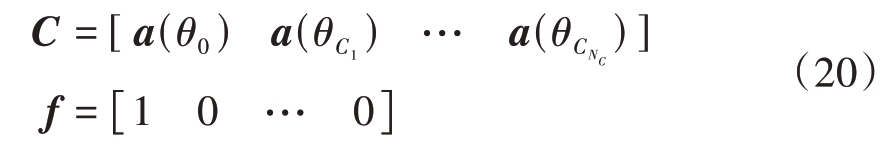
通过利用拉格朗日乘子法,构造代价函数,可求得LCMV准则的最优权值:
1.2.3 基于MMSE的自适应波束形成
MMSE准则是在已知参考信号特性的条件下,通过优化权值使得阵列的输出与参考信号的误差最小。
假设阵列的信号为![]()
![]() 为参考信号,其数学表达式为
为参考信号,其数学表达式为
式中,fr为期望获得受试者的呼吸信号频率。
数字波束形成的输出信号![]() 也即估计值
也即估计值![]() 为
为
误差可表示为
MMSE准则的性能函数为
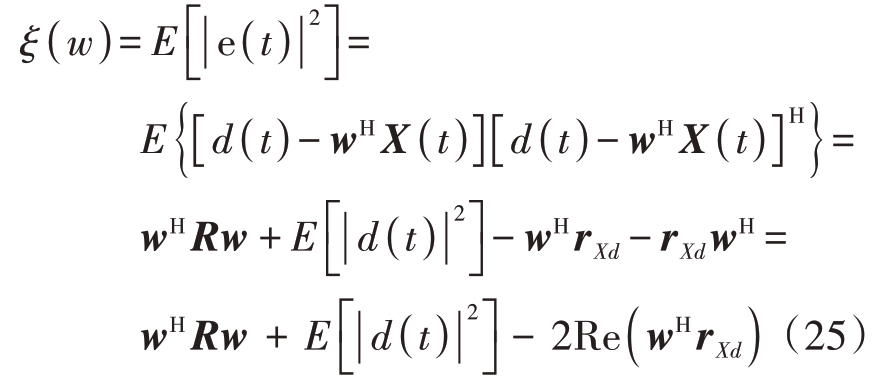
式中,R 为阵列数据的协方差矩阵,rXd =![]() 为阵列数据与期望信号的互相关向量。
为阵列数据与期望信号的互相关向量。
为求得MMSE 准则下的最优权值,对上式进行求导,使其为零,可得到
MMSE的最优权矢量为
2 相邻目标的生命体征检测原理
雷达通过测量由呼吸和心跳引起的胸腔起伏,实现非接触式的生命体征检测。由于人体胸腔不是一个点目标,当两个受试者位置相邻时,其中一个受试者的部分区域位于另一个受试者的主瓣范围内,可能会导致相邻目标的生命体征信号无法完全分离。
图3给出了相邻目标的经典波束形成方向图。两个相邻的受试者距离雷达2 m,受试者A位于0°,受试者B位于-15°,受试者胸腔的宽度约为50 cm,因此单个受试者胸腔的角度范围为±7°。如图所示当生成对准受试者B的波束时,受试者A胸腔的左半部分位于该波束的主瓣内,其最大的增益达到-4.8 dB,导致不能完全抑制受试者A 的生命体征信号,影响最终的分离结果。

图3 相邻目标的经典波束形成方向图
为了实现相邻目标的生命体征检测,我们利用自适应波束形成在另一个受试者的胸腔角度范围内生成零陷,最大程度抑制干扰受试者胸腔范围内的信号。图4 给出了相邻目标的自适应波束形成的波束方向图。从图中可以看出,利用自适应波束形成可在受试者A 胸腔的角度范围内生成一个置零区间,受试者B 胸腔中心位置处的增益为-1.56 dB,受试者A 胸腔范围内最大的增益由-4.8 dB 降为-14.6 dB,最大程度地抑制了受试者A 胸腔范围内的信号,实现相邻目标的生命体征信号的分离。
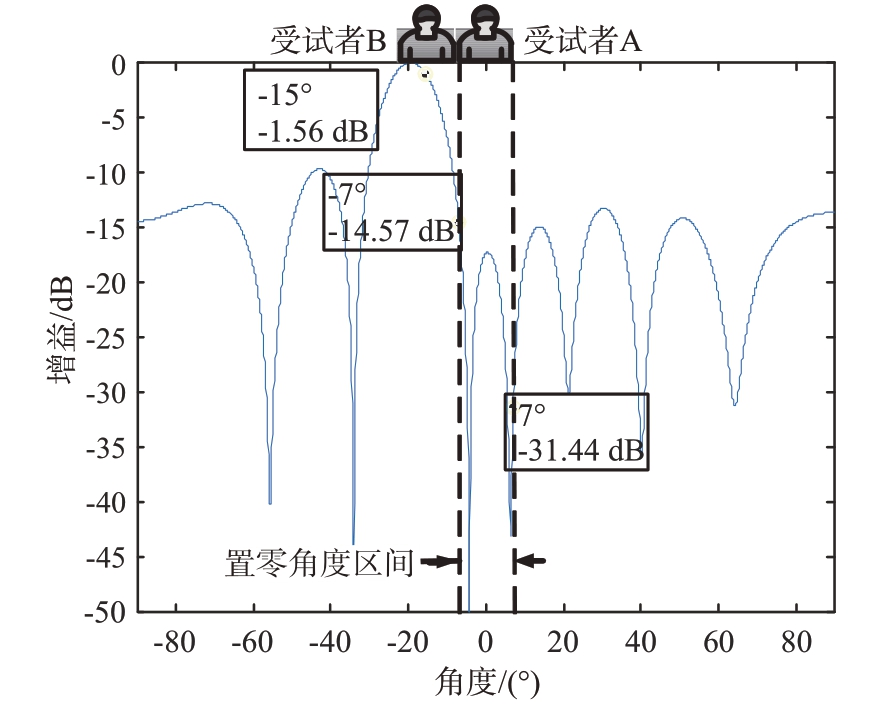
图4 相邻目标的自适应波束形成方向图
3 系统设计
3.1 硬件设计
图5 给出了单发多收雷达系统的实物图。信号源生成5.8 GHz 的射频信号后通过一分二功分器,一端接到发射天线作为发射,另一端接到一个放大器,经放大后通过一个一分八的功分器作为8个接收通道混频器的本征信号。雷达有8 个接收天线,相邻天线阵元的间距为2.5 cm,其对应的8个接收通道包含低噪放、带通滤波器、二级放大器、镜像抑制混频器以及基带放大器。在采样模块中,利用了两块AD7606 采样板实现8 路IQ 信号的同步采样。相应的时序控制以及数据传输是通过Altera Cyclone IV 这块FPGA实现的。


图5 单发多收雷达系统的实物图
3.2 软件设计
在得到8个基带信号后,首先进行射频信道幅相校正,对8个基带信号之间的相位和幅度差进行校正。根据校正后的信号,对于LCMV自适应波束形成,利用DOA 估计算法得到目标的数量和角度,输入到LCMV 自适应波束形成模块;对于MMSE 自适应波束形成,将估计出的呼吸频率输入到MMSE自适应波束形成模块。最后,通过ADBF,生成指向受试者所在角度的波束,同时该波束在干扰对象的角度处为零陷。具体的算法框图如图6所示。
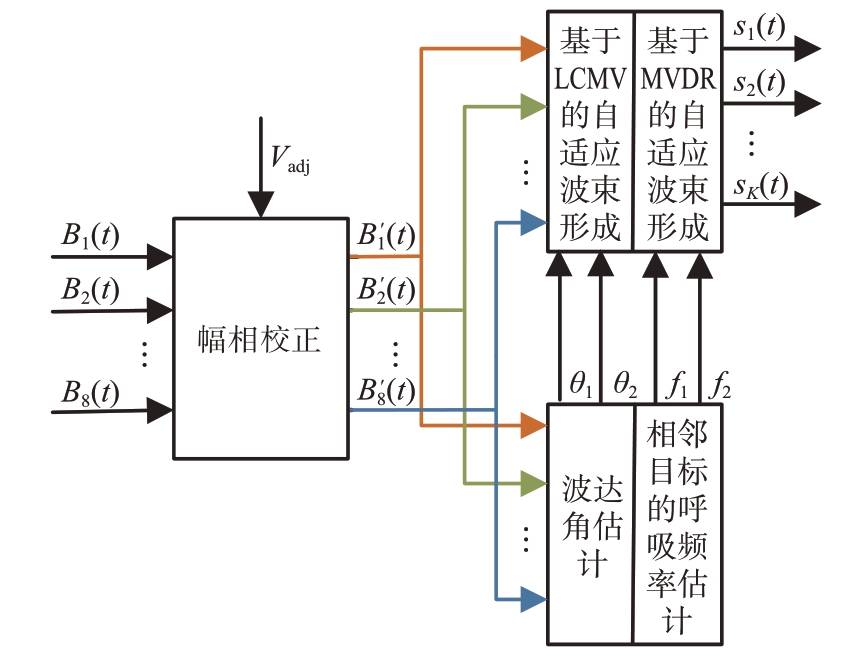
图6 基于LCMV和MMSE的相邻目标生命体征检测信号处理框图
4 多目标生命体征检测实验
本节利用3种方法来评估所提出方案的性能。在所有实验中,要求受试者佩戴压电式呼吸带(HKH-11C)作为参考信号,以验证本文所提算法的分离结果。2名男性志愿者,年龄分别为27岁和25岁,体重分别为83 kg和65 kg,身高分别为1.72 m和1.72 m,两个受试者肩并肩坐着,距离雷达2 m。第一个实验利用的传统波束形成算法,第二个和第三个实验利用的是自适应波束形成算法。
4.1 基于CBF的相邻目标生命体征检测实验
两个受试者肩并肩地坐着,距离雷达2 m,两者之间的角度差约为-15°,具体的实验场景如图7(a)和(b)所示。

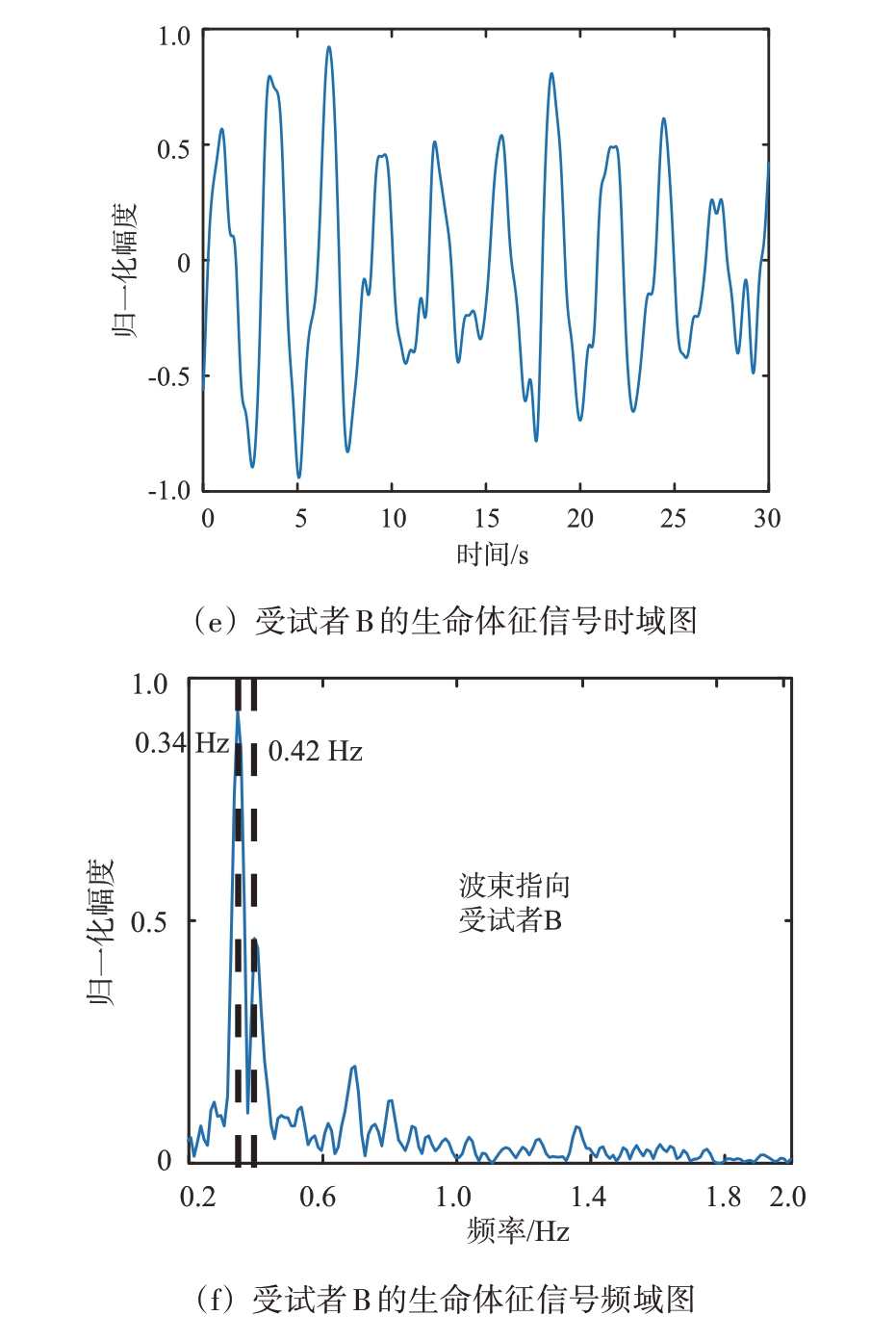
图7 基于经典波束形成的相邻目标生命体征检测实验结果
图7(c)~(f)为利用经典波束形成的分离结果。图7(c)和(d)是波束指向受试者A的分离结果,图7(e)和(f)是波束指向受试者B 的分离结果。受试者A 的呼吸频率是0.42 Hz,受试者B 的呼吸频率是0.34 Hz。从右边两个频谱图可以看出,波束指向受试者A 的时候,由于信干比不够,频谱图中患有受试者B 的呼吸信号频率分量。当波束指向受试者B的时候,其频谱图中也存在受试者A的呼吸频率分量。因此,经典波束形成算法不能完全分离出两个受试者的生命体征信号。
4.2 基于LCMV的相邻目标生命体征检测实验
图8是利用基于LCMV 自适应波束形成的分离结果。图8(a)是波达角估计的结果,两个受试者的估计来波方向分别为-0.5°和-14.5°。图8(b)是自适应波束形成的波束图,从图中可以看出,生成的两个波束均在另一目标所在角度区间生成零陷,与预期设想一致。图8(c)~(f)是两个相邻受试者的分离结果,其中蓝色实线为呼吸带的分离结果,红色实线为雷达的分离结果。两名受试者的呼吸频率分别为0.42 Hz 和0.34 Hz,与参考信号一致,从时域波形上看雷达检测到的呼吸信号与参考信号有很高的吻合度。由此可以得出结论,利用基于LCMV 的自适应波束形成算法后能够实现相邻目标的生命体征信号。
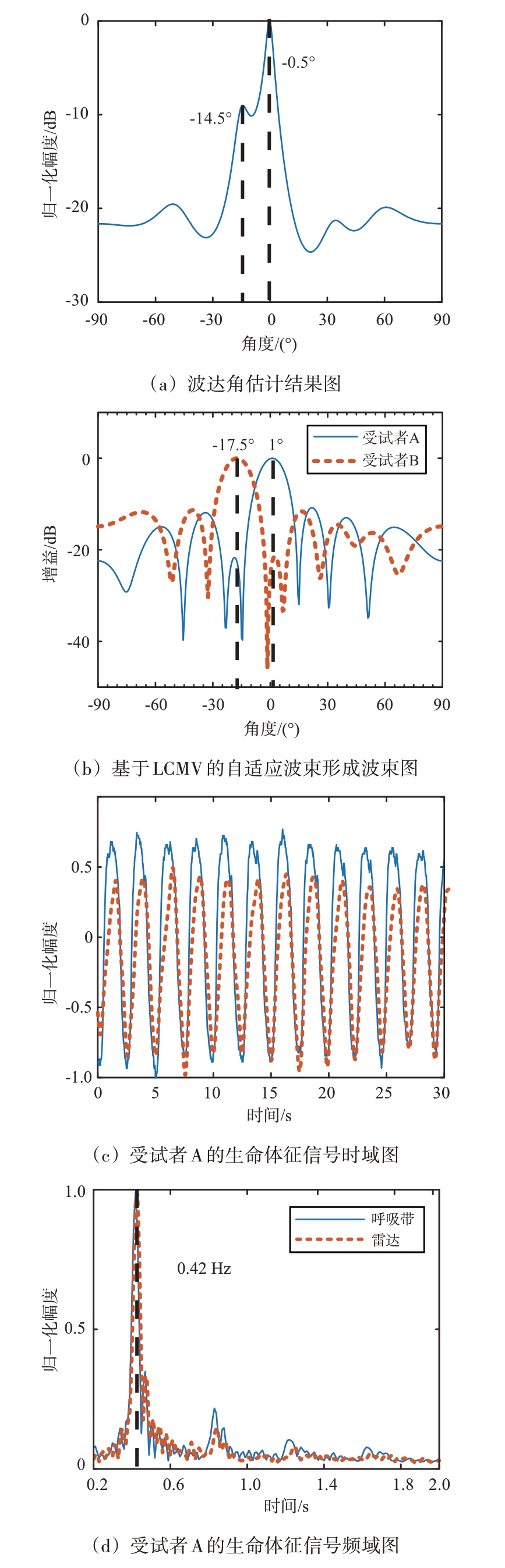
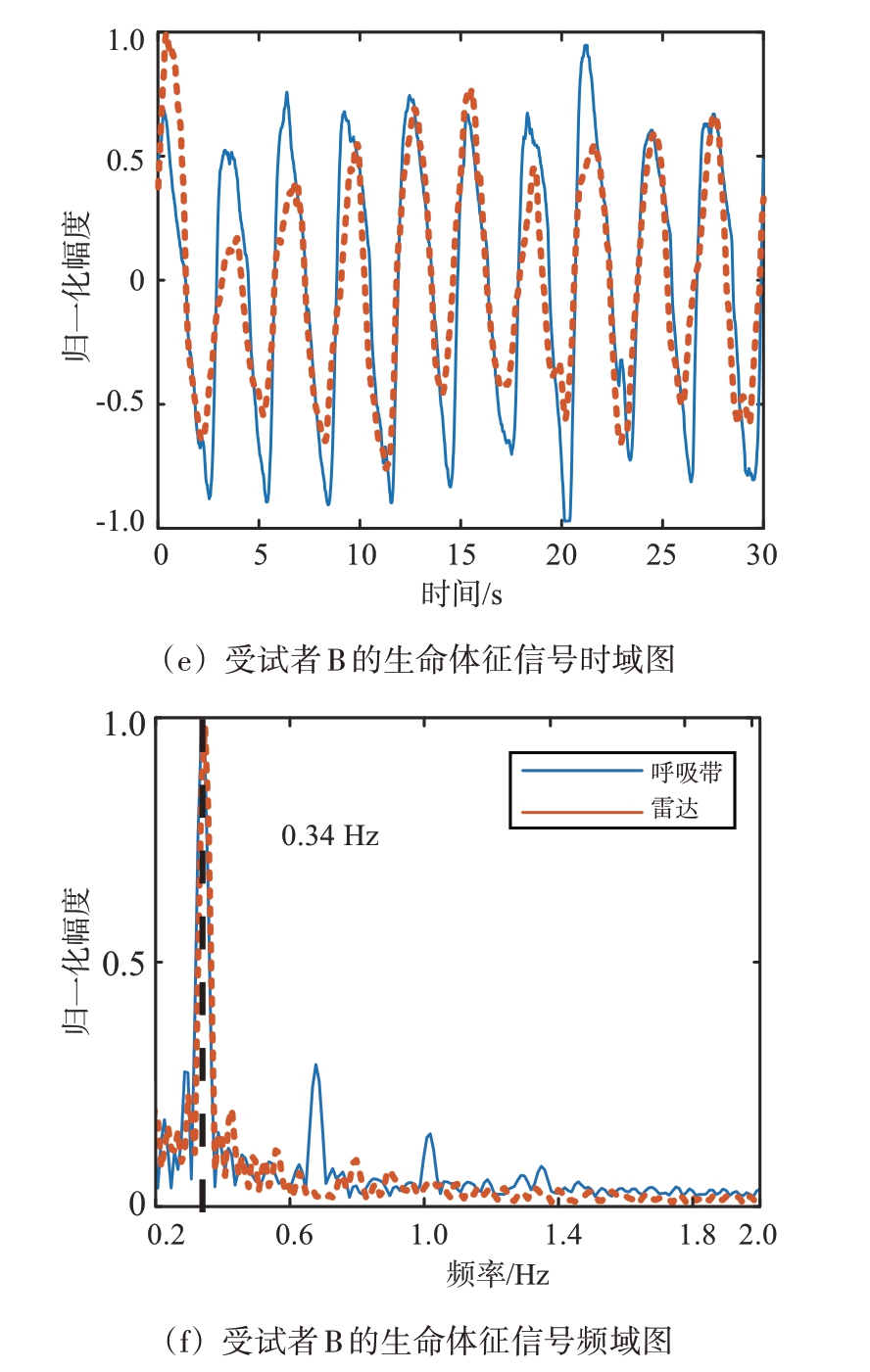
图8 基于LCMV自适应波束形成的相邻目标生命体征检测实验结果
4.3 基于MMSE的相邻目标生命体征检测实验
图9为基于MMSE 自适应波束形成的波束图。从图中可以看出生成的两个波束分别指向-16°和-3°,与实际相符合,同时均在另一受试者所在角度处生成零陷,实现信干比的提升。
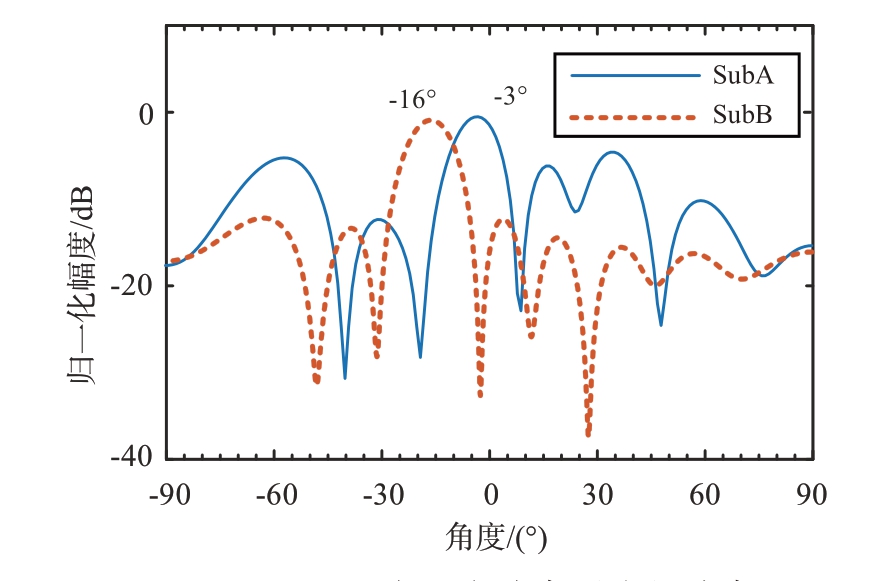
图9 基于MMSE自适应波束形成的波束图
图10 为基于MMSE 自适应波束形成的相邻目标的生命体征检测结果。与传统波束形成算法相比,利用MMSE 自适应波束形成后,能够进一步抑制干扰目标的信号能量,实现相邻目标的生命体征信号分离。
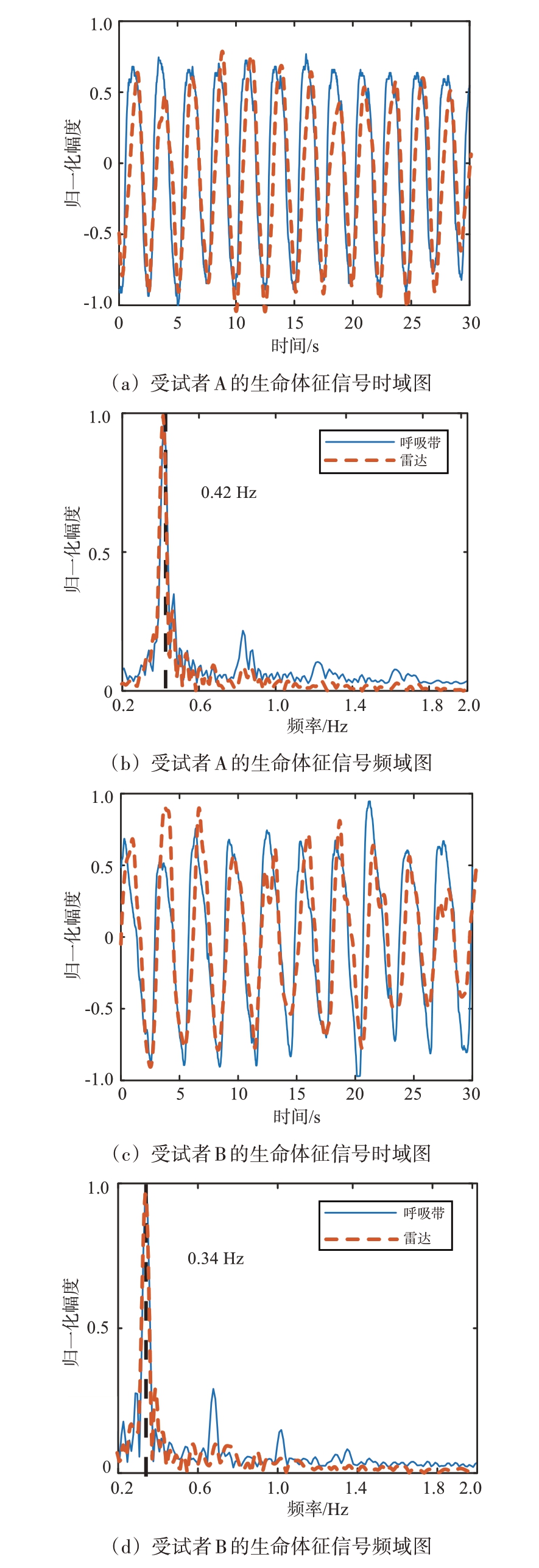
图10 基于MMSE自适应波束形成的相邻目标的生命体征检测实验结果
5 讨 论
从图11 可以看出,对于受试者B 来说,基于MMSE 的算法比基于LCMV 的算法能够更好地抑制0.42 Hz的信号。基于MMSE 算法干扰抑制的效果要优于基于LCMV 算法。基于MMSE 算法需要先估计受试者的呼吸信号频率,以此来形成参考信号,因此如果说两个受试者的呼吸频率一致,该方法就无法工作。基于LCMV 算法只需估计出受试者的角度,即可形成自适应波束,实现相邻目标的生命体征信号。因此在实际应用中,基于LCMV算法具有更好的适应性。
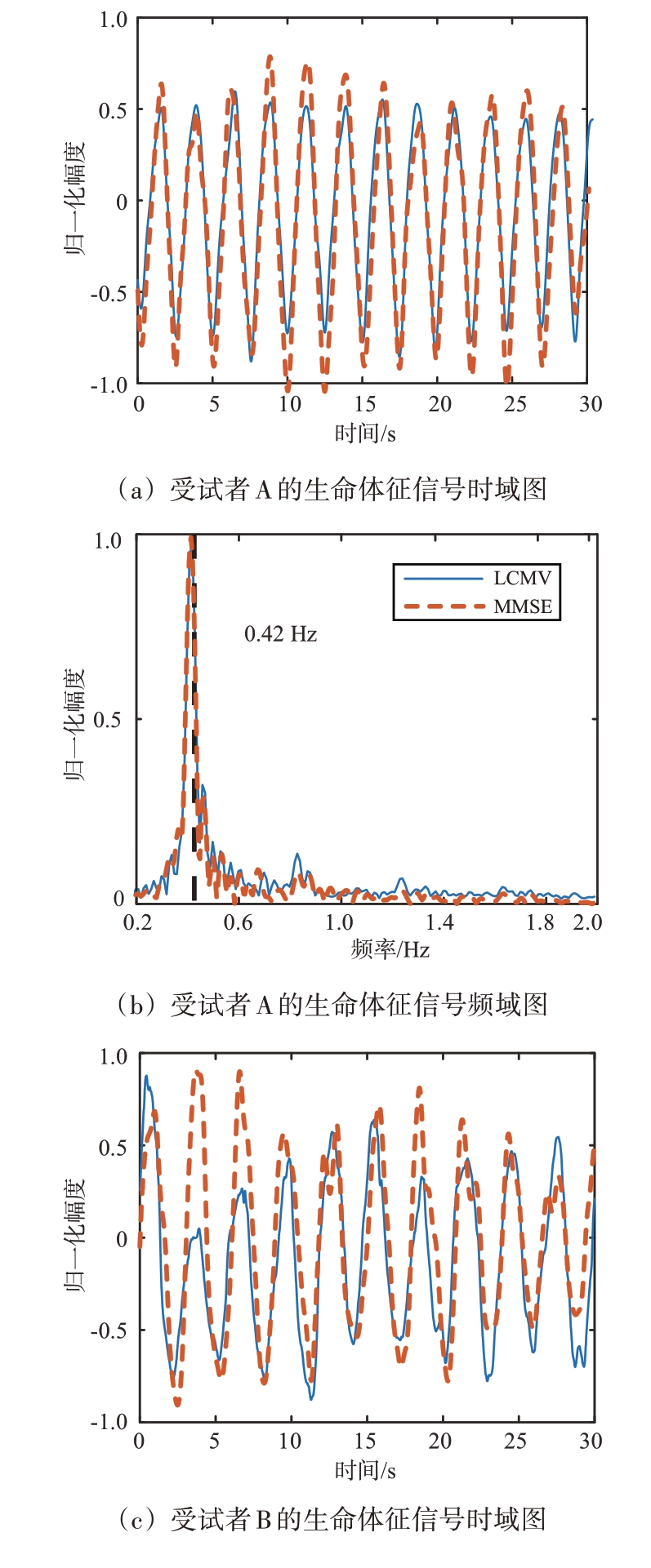
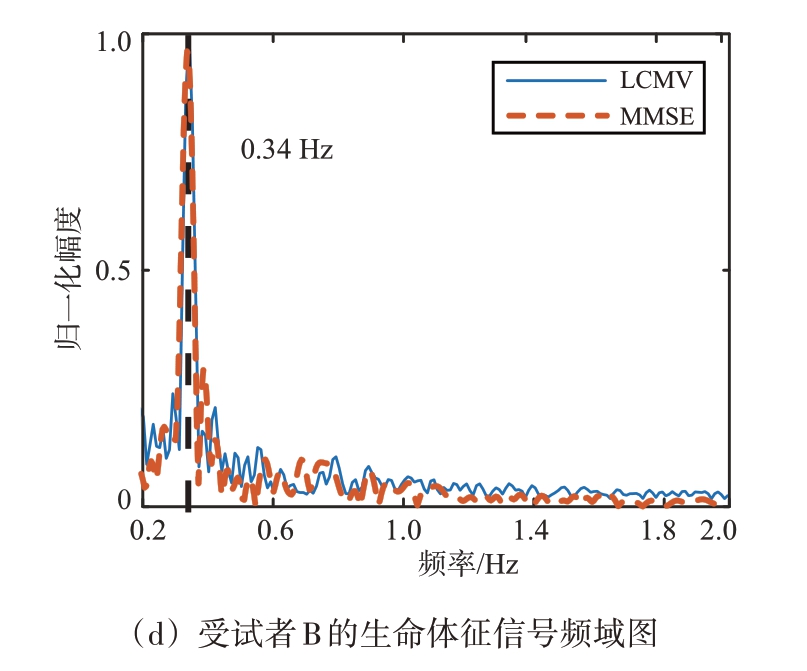
图11 基于MMSE和LCMV自适应波束形成的相邻目标的生命体征检测结果对比
6 结束语
针对相邻目标的生命体征检测,本文利用基于LCMV 和MMSE 的自适应波束形成算法,生成指向受试者波束的同时,在另一干扰受试者所在角度处生成零陷,进一步提高信干比,实现信号的分离。实验结果表明,基于LCMV 和MMSE 算法均能实现相邻目标的生命体征信号,并且基于MMSE算法的性能优于基于LCMV 算法,但是基于MMSE算法对于具有相同呼吸频率的信号无法分离,基于LCMV 算法无此限制。因此在实际应用中LCMV算法具有更好的适应性。
[1]LI Changzhi,YU Xiaogang,LEE C M,et al.High-Sensitivity Software-Configurable 5.8-GHz Radar Sensor Receiver Chip in 0.13-μm CMOS for Noncontact Vital Sign Detection[J]. IEEE Trans on Microwave Theory and Techniques,2010,58(5):1410-1419.
[2]HONG Hong, ZHANG Li, ZHAO Heng, et al. Microwave Sensing and Sleep: Noncontact Sleep-Monitoring Technology With Microwave Biomedical Radar[J]. IEEE Microwave Magazine,2019,20(8):18-29.
[3]LEE H, KIM B H, PARK J K, et al. A Novel Vital-Sign Sensing Algorithm for Multiple Subjects Based on 24-GHz FMCW Doppler Radar[J]. Remote Sensing, 2019, 11(10):1237.
[4]NOSRATI M, SHAHSAVARI S, LEE S, et al. A Concurrent Dual-Beam Phased-Array Doppler Radar Using MIMO Beamforming Techniques for Short-Range Vital-Signs Monitoring[J]. IEEE Trans on Antennas and Propagation,2019,67(4):2390-2404.
[5]杨路,雷雨霄,余翔.基于FMCW 雷达的人体生命体征信号预测算法[J].雷达科学与技术,2024,22(1):43-56.
[6]WANG Fukang, JUAN P H, CHIAN D M, et al. Multiple Range and Vital Sign Detection Based on Single-Conversion Self-Injection-Locked Hybrid Mode Radar with a Novel Frequency Estimation Algorithm[J]. IEEE Trans on Microwave Theory and Techniques,2020,68(5):1908-1920.
[7]NAHAR S, PHAN T, QUAIYUM F, et al. An Electromagnetic Model of Human Vital Signs Detection and Its Experimental Validation[J].IEEE Journal on Emerging and Selected Topics in Circuits and Systems,2018,8(2):338-349.
[8]WANG Yazhou, LIU Quanhua, FATHY A E. CW and Pulse-Doppler Radar Processing Based on FPGA for Human Sensing Applications[J]. IEEE Trans on Geoscience and Remote Sensing,2013,51(5):3097-3107.
[9]ISLAM S M M, BORIC-LUBECKE O, LUBEKCE V M.Concurrent Respiration Monitoring of Multiple Subjects by Phase-Comparison Monopulse Radar Using Independent Component Analysis(ICA)with JADE Algorithm and Direction of Arrival(DOA)[J]. IEEE Access, 2020,8:73558-73569.
[10]YUAN Yichao, LU Chunchi, CHEN A Y K, et al. Multi-Target Concurrent Vital Sign and Location Detection Using Metamaterial - Integrated Self - Injection - Locked Quadrature Radar Sensor[J]. IEEE Trans on Microwave Theory and Techniques,2019,67(12):5429-5437.
[11]毛晓军.高性能阵列天线稳健自适应波束形成技术研究[D].哈尔滨:哈尔滨工程大学,2017.
[12]苏保伟.阵列数字波束形成技术研究[D].长沙:国防科学技术大学,2006.