0 引 言
激光雷达[1]能够快速获取被测物体表面形状的点集,精确地呈现出被测物体表面形状,是一种高效的数据获取方式,因此被应用于很多领域[2],如三维物体重建、无人驾驶及激光测绘等。在三维重建领域中,三维网格重建是基于已有的二维数据或者三维数据,恢复模型本身三维结构的过程[3]。对于三维离散点的三角网构建算法,可以分为直接法和间接法两大类[4],常见的直接法包括雕刻法[5-6]、区域增长法[7]、距离函数法及表面生长法等。间接法主要是指映射法,该方法将局部的邻近点投影到切平面上进行二维三角化,然后将这些局部的三角网拼接成整体的三维表面模型[8]。在Yoo的距离场合最小二乘投影(Least Square Projection,LSP)算法[9-10]中直接在点云上处理,没有任何的显式或隐式的构网过程,效率可以大大提高,但是在一些密集的点云或者距离过远的点云之间容易形成误差,导致构网不准确,容易形成表面空洞以及法向量不一致等;Junior 等人[11]提出的三维空间中表示物体表面的无组织点云进行表面重建的多分辨率方法,该方法使用一组网格算子和简单规则进行选择性网格细化;Ivrissimtzis 等人[12]提出的通过网格细化从光探测和测距激光雷达点云生成三角形网格的增量算法,该算法直接从激光雷达输出中生成三角形网格,这种方法适用于计算受限的系统,如飞行器、移动机器人和智能手机等特定场景;基于Kohonen 的自组织映射(Self-Organizing Map,SOM),这种方法只能解决高程数据和开放拓扑网格的问题,而不能解决闭合曲面的重建问题,在局部点云还会有错误的几何形状网格,而且构网效率非常耗时;利用Ivrissimtzis 提出的生长细胞结构算法进行表面重建[12-13]和Lin 等人[14]提出的点云重构三角形网格曲面的算法以及Yuan 等人[15]提出的SSRNet(Scalable 3D Surface Reconstruction Network)表面重建算法,这些算法虽然能够产生非常好的结果,但主要缺点是算法复杂度高,比大多数算法慢;Poisson(泊松)算法[16]是非常流行的基于采样点的三维表面重建算法,它是由HuguesHoppe提出的,泊松表面重建算法是通过隐式曲面的重建来解决表面重建问题,泊松算法使用八叉树先对点云进行去噪及降采样处理,算法计算复杂度较高,对于非均匀采样或非光滑表面等情况,效果可能不理想;在Ge 等人[17]的算法中使用Delaunay 三角网格法[18-19]获取物体的3D 表面模型。Delaunay 三角网格法分为局部方法和全局方法[20-21],局部方法[22]的优点是计算速度比较快,容易实现,缺点是缺乏整体质量的把控,是一种启发式方法,全局方法[23]的优点是网格的全局质量容易把控,缺点也显而易见,强烈地依赖参数化方法,稳定高质量的实现会比较困难;Luo 等人[24]在Delaunay 三角剖分基础上提出DeepDT(Deep Delaunay Triangulation)网络架构,优点是不需要可见性信息,并输出精确的网格,然而,Deep-DT 暂时无法使用相同的策略来处理过大的输入;Sugiura 等人[25]是从图像中将三维表面重建为三角形网格的方法,该方法只能获得稀疏的3D 点云,然而直接从稀疏的3D 点云重建的3D 表面往往缺乏对象细节。
上述点云构网算法可以对多种仪器获取的点云进行处理,通用性较强,但是都需要对点云进行去噪、降采样、法向量提取等预处理,构网算法复杂度较高、速度慢。为了快速获得三维重建效果,其实,可以充分利用雷达采集过程中扫描轮廓(单线激光雷达在X-Y 水平方向旋转扫描360°后形成的一条轮廓数据)、方位角(X-Y 水平方向上360°旋转扫描范围内扫描点之间的角度差)等的点云初始信息,实现无需特征识别直接构网。因此本文提出的基于点云初始信息的单线激光雷达旋转扫描快速空间构网方法,在激光雷达旋转扫描的情况下,充分利用雷达采集过程中的初始信息,根据轮廓顺序以及方位角实现无需特征识别直接构网,该方法可以保证所有的三角面中点与点之间的连接关系,从而确保了构网的精度,同时这种基于方位角信息的单线激光雷达旋转扫描快速构网可以获得较高的构网速度。
1 激光雷达旋转扫描装置
1.1 激光雷达旋转扫描装置的组成
扫描装置包含旋转云台模块、雷达模块及软件模块,如图1 所示。旋转云台模块由底座、控制板、步进电机及云台组成;雷达模块由雷达电机、发射器及接收器组成;软件模块由数据处理、数据建模、数据分析组成。
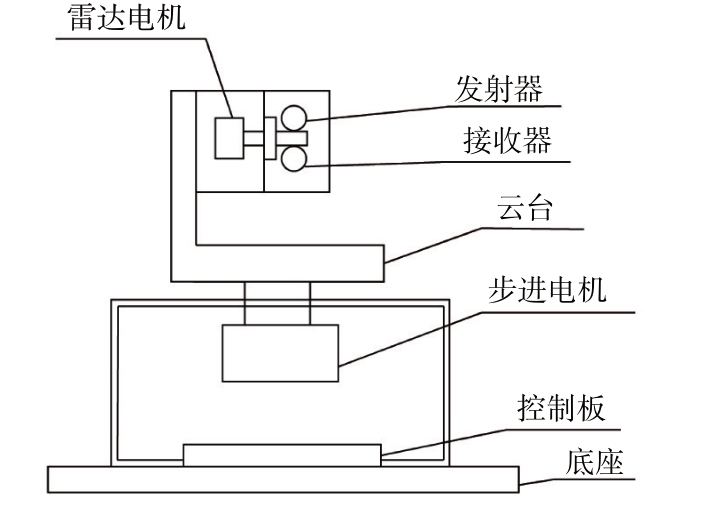
图1 激光雷达装置
1.2 激光雷达安装误差修正方法
本文利用人工立体标靶进行雷达误差修正,标定物固定不动,将激光雷达旋转扫描装置上电,归零后激光雷达初始位置对标定物扫描后得到初始轮廓,控制云台将激光雷达旋转180°后对标定物扫描后得到的轮廓进行比较,两条轮廓之间的距离就是雷达X方向上的平移参数,如图2(a)所示。
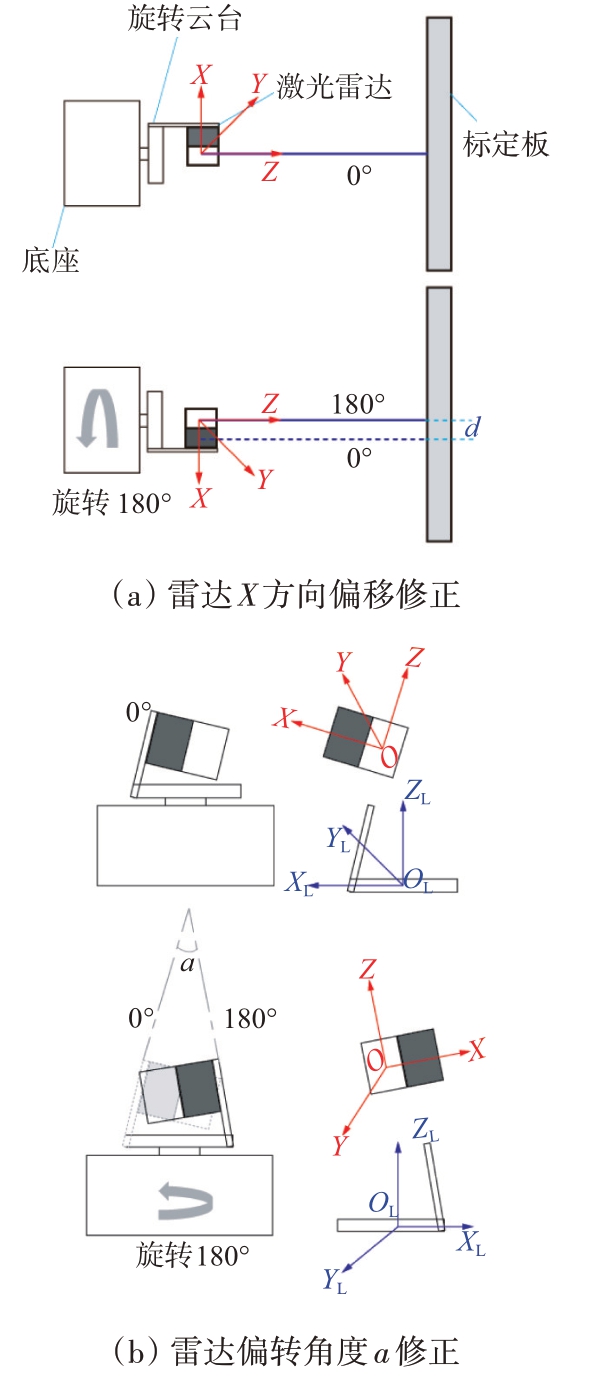
图2 雷达误差修正
云台转轴与激光雷达组合系统如图2(b)所示;将激光雷达固定在云台转轴上,通过步进电机带动云台转轴水平旋转,改变激光雷达扫描方向。激光雷达的坐标系为O-XYZ,随着转轴的转动,坐标系O-XYZ 会随之发生旋转,导致激光雷达采集的每一帧点云不处于同一坐标系中,所以需要将每帧点云都投影至云台转轴坐标系OL-XLYLZL中,由于安装误差的存在,导致激光雷达坐标系没有与云台转轴坐标系对齐,在0°位置时雷达的坐标轴与云台的坐标轴有偏差,通过转轴标定获取旋转矩阵R1;由于激光雷达中心与转轴中心的距离已知,可以得到每帧点云所处的坐标系O-XYZ 与云台转轴坐标系OL-XLYLZL之间的平移向量[0 Δy Δz]T。其次,通过电机的转轴旋转180°得到点云所处的雷达坐标系O-XYZ 与云台转轴坐标系OL-XLYLZL之间的旋转矩阵R2,因此

式中,xL、yL、zL和x'L、y'L、z'L分别为雷达坐标系在初始状态0°和旋转180°后在云台坐标系中的3 个单位向量。
根据旋转矩阵的性质,R中的每一行(或列)向量都表示了坐标系之间绕某一轴旋转的角度。因此,可以从R 中提取出旋转角度a,其中trace(R)表示旋转矩阵R的迹,即对角线元素之和。
通过上式可以从两个旋转矩阵R1和R2中得出雷达坐标系与云台坐标系之间需要修正的偏转角度a。
2 基于方位角信息的轮廓构网方法
基于方位角信息的轮廓构网利用激光雷达采集后的原始点云数据,激光雷达在旋转扫描过程中持续接收雷达数据包,当雷达数据包够一圈后解析为一条扫描轮廓,根据获取的数据包解析时间顺序将每一圈轮廓进行排序,生成一个二维轮廓集合C={C1,C2,C3,…,Ci},(i=1,2,3,…,300),每条轮廓上含有每个点的方位角θ、俯仰角φ 以及距离r,根据方位角对轮廓集合C上的点云进行排序,如图3(a)所示;最终每个轮廓上的点在空间中的位置关系在极坐标系中表示如下:
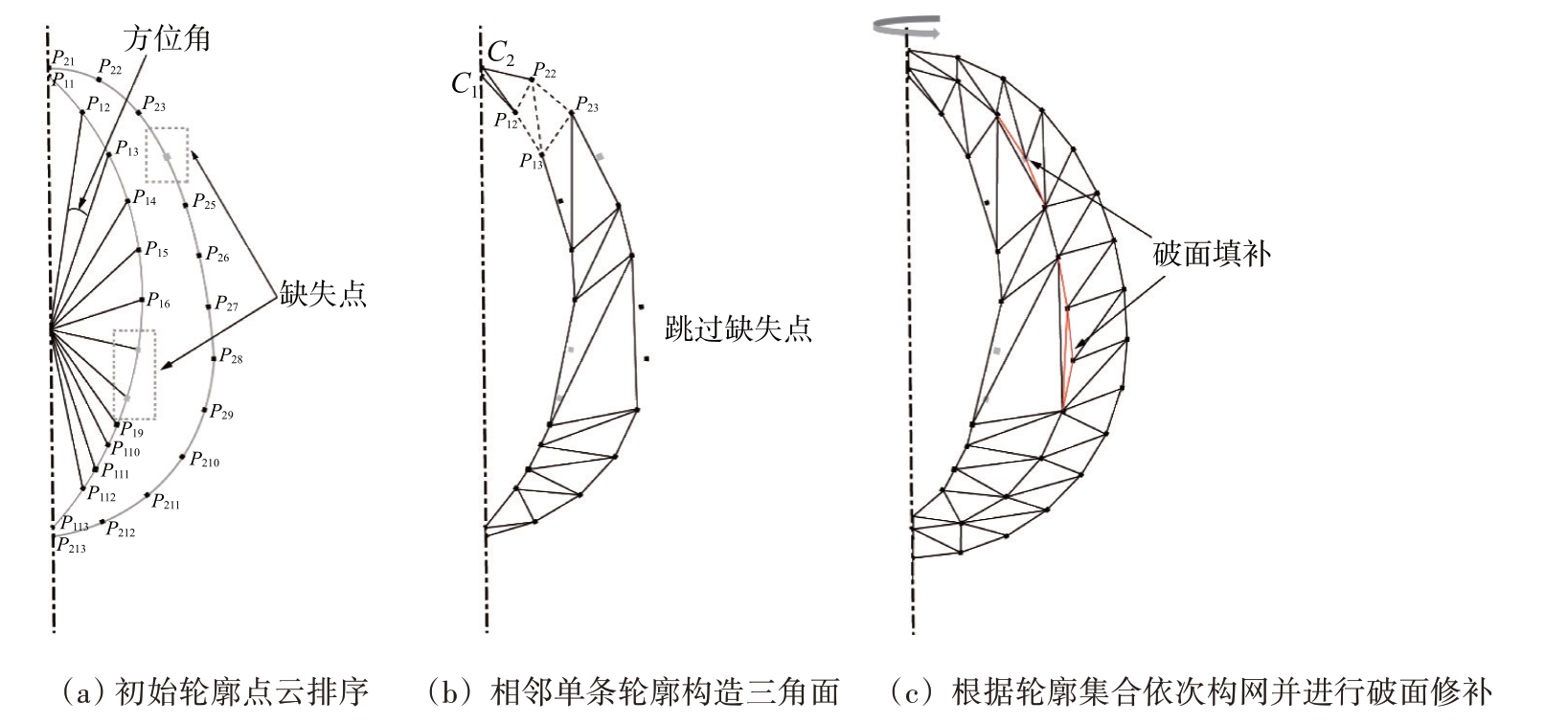
图3 基于方位角信息的轮廓构网过程
公式中Pij是集合Ci中第j 个点的位置;rij是点Pij到原点的距离;θij是点Pij相对于X 轴的方位角;φij是Pij的俯仰角。按照轮廓顺序选取Ci和Ci+1,当i=0 时,选取为C0和C1轮廓,i 依次递增2,Ci和Ci+1上的点按照方位角顺序依次取Ci 轮廓上的Pij,Pi(j+1)和Ci+1轮廓上的P(i+1)j,P(i+1)(j+1)进行构网,Pij是集合Ci中第j 个点的位置。如图3(b)所示,根据当前轮廓C1和索引P11,获取相邻轮廓C2中同一方位角的顶点索引P21。将当前轮廓顶点P11与该轮廓下一个点P12与相邻轮廓的顶点P21构成一个三角网格T{P11,P12,P21},紧接着相邻轮廓的顶点P21与该轮廓第二个点P22再与轮廓C1的第二个点P12构成三角网格T{P21,P22,P12},循环获取下一个三角形的3个顶点索引,直到C1和C2轮廓上所有的点都参与构网,按此方法构网最终得到三角网格集合为
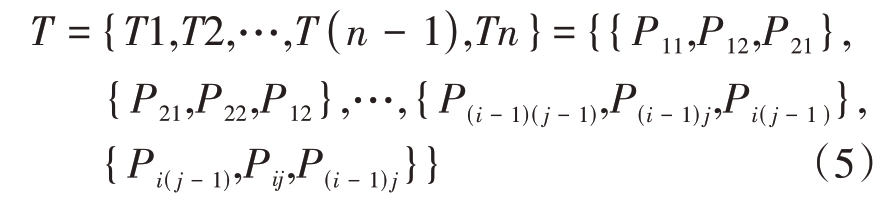
其中,i=j=1,2,3,…,n。但是在扫描过程中,某一方位角上的轮廓可能会丢失点,从而形成一个空的数据,因此针对这种情况,把缺失点的该方位上相邻轮廓不参与构网,跳过该顺序点;如图3(c)所示,C1 轮廓点云集合为C1={P11,P12,P13,P14,P15,P16,P19},P17、P18两点缺失,因此,将所有缺失的点按照顺序添加到一个新的空点列表中为后续破面修补使用;C2轮廓点云集合为C2={P21,P22,P23,P24,P25,P26,P27,P28,P29},取一个K 值,表示C1与C2的交集,方程式为K=C1∩C2,得到结果为K={P1,P2,P3,P4,P5,P6,P9},将C1与C2的交集集合K 参加构网,跳过了P27、P28两点。取Ci+1 轮廓P(i+1)j、P(i+1)(j+1)和Ci+2 轮廓P(i+2)j、P(i+2)(j+1)按照方位角顺序依次进行构网,例如:在C1轮廓与C2轮廓构网时跳过了P27、P28两点,在C3轮廓与C2轮廓构网时就会形成破面,因此对空点造成的破面进行修补,通过线性插值的方式从两边的点中估算缺失点的位置并对其补全。
设P(θ)为方位角θ 对应的点,其方位角在0°到360°范围内,0.25°为雷达角分辨率,每个点的索引j与其方位角θ的关系为
假设Pi1点的坐标是Pi1(x1,y1,z1),Pi3点的坐标是Pi3(x3,y3,z3),则缺失点Pi2修补的方程式为
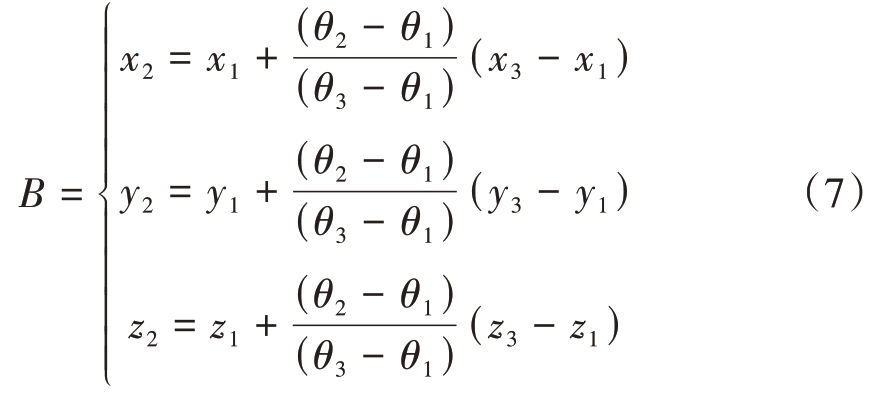
根据修补方程将两条轮廓缺失的点进行连接填充,根据空点列表顺序,将顺序相邻的点分割为一个新列表,形成n 个列表,将每个列表的首点与该点相邻的上一个点,尾点与该点相邻的下一个点添加到列表中,将每个列表的点按照顺序依次相连接,然后再将每个列表的所有点与最后一个点相连接进行破面修补。然后将轮廓列表依次进行拼接构网,形成最终三角网,最终得到的三角网格集合为
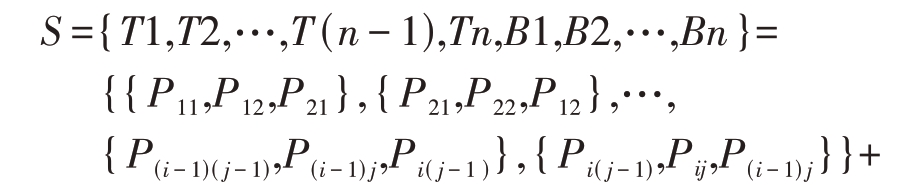
基于方位角信息的轮廓构网过程中可以有效避免三角形交叉,减少三维重建过程中三角形的重叠错误和破面错误。图4 为基于方位角信息的轮廓构网方法的流程图,算法1为基于方位角信息的轮廓构网伪代码。
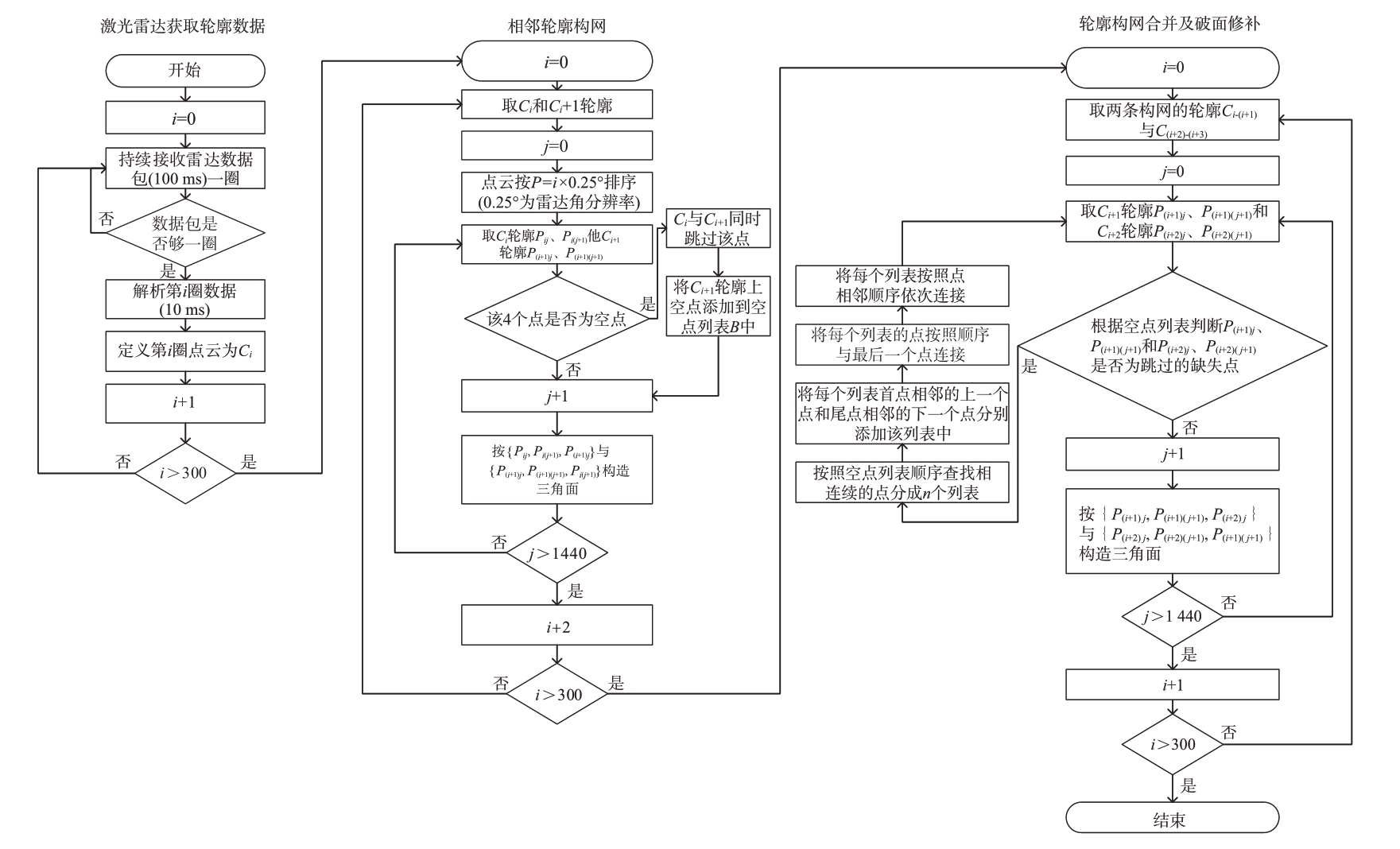
图4 基于方位角信息的轮廓构网方法处理流程
算法1 基于方位角信息的轮廓构网
输入:输入轮廓集合C
输出:输出最终轮廓构网结果S


3 分析与讨论
本文以程序运行环境是IntelI 4. CoreI i7-9750H CPU@2.60 GHz,8 GB 运行内存的Windows操作系统为实验平台,基于方位角信息的轮廓构网方法由C#软件编写,利用VTK 图形应用函数库显示激光雷达采集的点云,如图5 所示;采集点云数据时使用氪见KR SN50 激光雷达来获取点云数据;实验条件使用激光雷达对不同大小空间旋转扫描得到点云数据保存用于实验。设定角度阈值为180°,单线激光雷达扫描圈数为300圈。实验仪器具体参数如表1所示。
表1 实验仪器概述
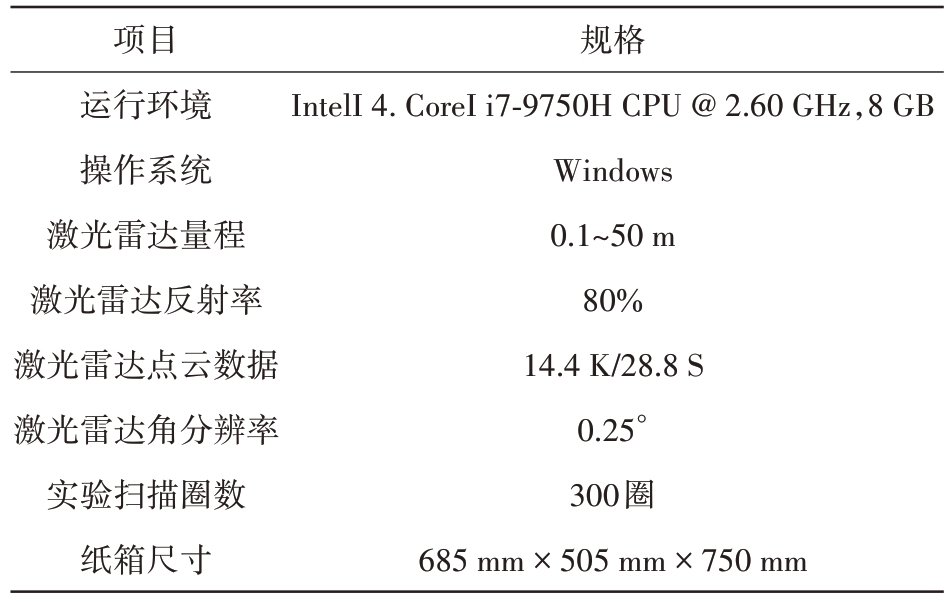
项目运行环境操作系统激光雷达量程激光雷达反射率激光雷达点云数据激光雷达角分辨率实验扫描圈数纸箱尺寸规格IntelI 4.CoreI i7-9750H CPU@2.60 GHz,8 GB Windows 0.1~50 m 80%14.4 K/28.8 S 0.25°300圈685 mm×505 mm×750 mm
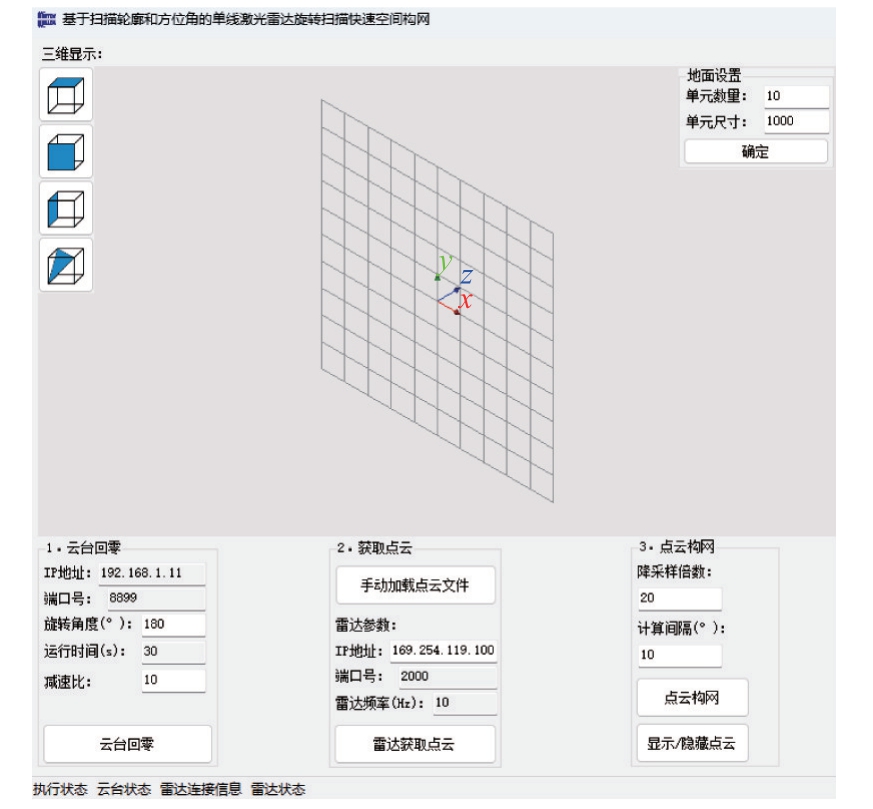
图5 VTK图形应用函数显示界面示意
3.1 雷达误差修正及点云精度验证
本文选用纸箱验证人工立体标靶方法对激光雷达的标定效果,激光雷达放在纸箱正下方,如图6(a)所示;纸箱与激光雷达位置如图6(b)所示,其位置较为均匀离散地分布于激光雷达的测量距离(1~50 m)、方位角(±180°)的量程范围内;利用C#软件驱动激光雷达旋转扫描,在扫描完成后由VTK 图形应用函数库显示如图6(c)所示的纸箱点云,在红色框内可以看到纸箱上表面的一条边出现了变形,由于激光雷达坐标系没有与云台转轴坐标系对齐,在旋转一圈后,激光雷达实际是以一定的偏斜角度旋转,因此造成这种结果。利用人工立体标靶对激光雷达进行误差修正后,重复上述步骤后显示的点云如图6(d)所示;在相同位置的红色框内可以看到在经过误差校准后的激光雷达装置把激光雷达坐标系与云台转轴坐标系对齐后在旋转一圈所得到的点云消除了因角度偏差使纸箱变形现象,修正后的纸箱点云更加接近真实纸箱形状,在图7 中,对修正后的激光雷达装置进行了精度验证,从图中红色方框所选结果来看,在Cloud Compare 软件中导入CAD 纸箱和修正后的dat格式的点云纸箱,经过粗配准以及ICP(Iterative Closest Point)精配准以后点云均匀地分布在纸箱误差范围内,有效地验证了误差经过修正后达到了理想的精度,补偿了误差对以后实验结果的影响。

图6 激光雷达误差修正示意
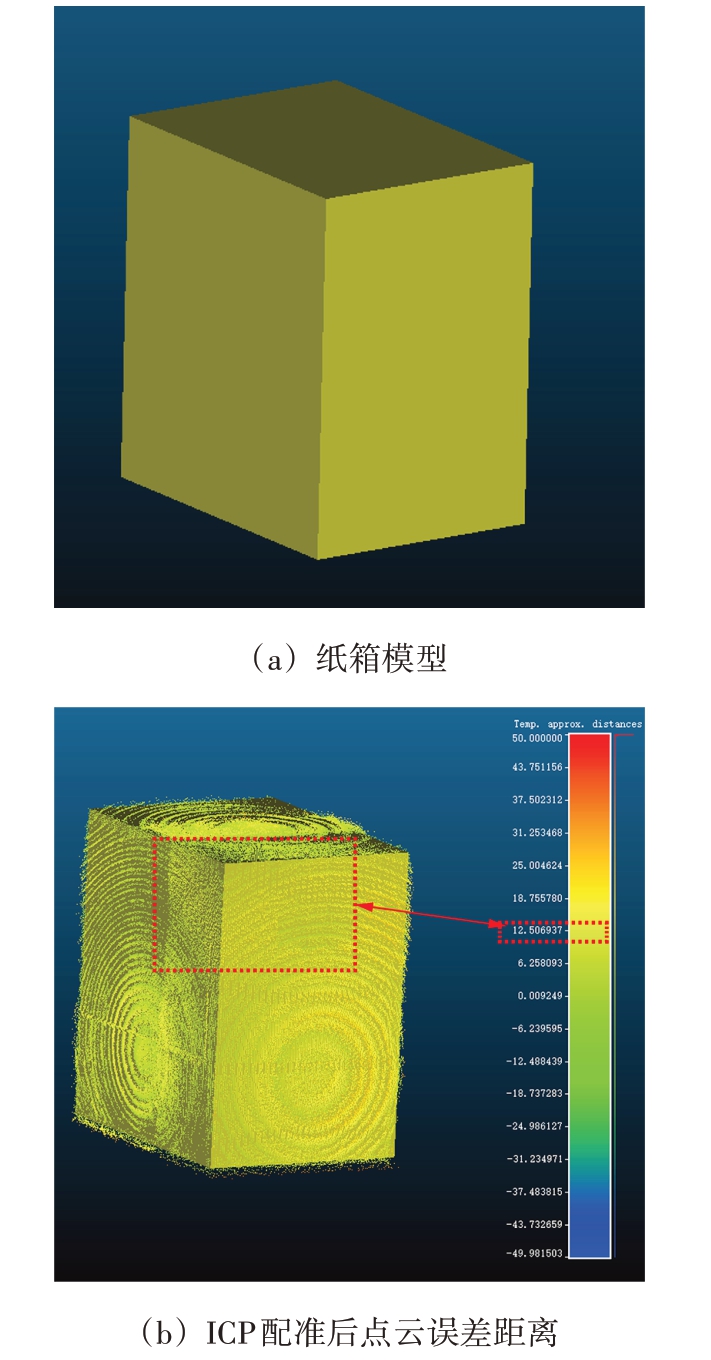
图7 误差修补示意(Cloud Compare软件)
3.2 基于方位角信息的轮廓构网过程验证
激光雷达扫描装置误差修正后,对轮廓构网过程以及在构网过程中出现的破面修补进行验证,如图8(a)所示,首先随机生成了两条轮廓,在每条轮廓上的45°方位角上按照0.25°生成了180个点,在任意方位角度上随机缺失点来模拟激光雷达扫描时某方位角缺点现象,然后将单条轮廓按照方位角顺序对轮廓上的点云进行排序,另一条轮廓重复上述步骤;根据方位角顺序获取两条轮廓中第一条轮廓当前顶点的索引以及该轮廓下一个点的索引作为当前三角网格上两个顶点,然后获取第二条轮廓同一方位角该点的索引作为第三个顶点,3 个顶点构建一个三角网格,如果某个方位角角度有空点,两条轮廓同时跳过该点,将该点的下一个点代替该点进行构网,循环获取下一个三角网格的3个顶点,遍历两条轮廓全部点云参与构网得到的结果如图8(b)所示;再增加一条同样的随机缺失点的轮廓,按照上述步骤进行轮廓间构网,如图8(c)所示;将三条轮廓所有的三角网格填充为三角面,但是在构网过程中第二条和第三条轮廓构网时因跳过缺失点,在填充为三角面时就会形成破面,也叫表面空洞,如图8(d)所示;因此针对破面现象,通过线性插值的方式补齐这些缺失的点,并且参与该点与相邻上下两点构网,从而得到最终理想的结果如图8(e)所示。
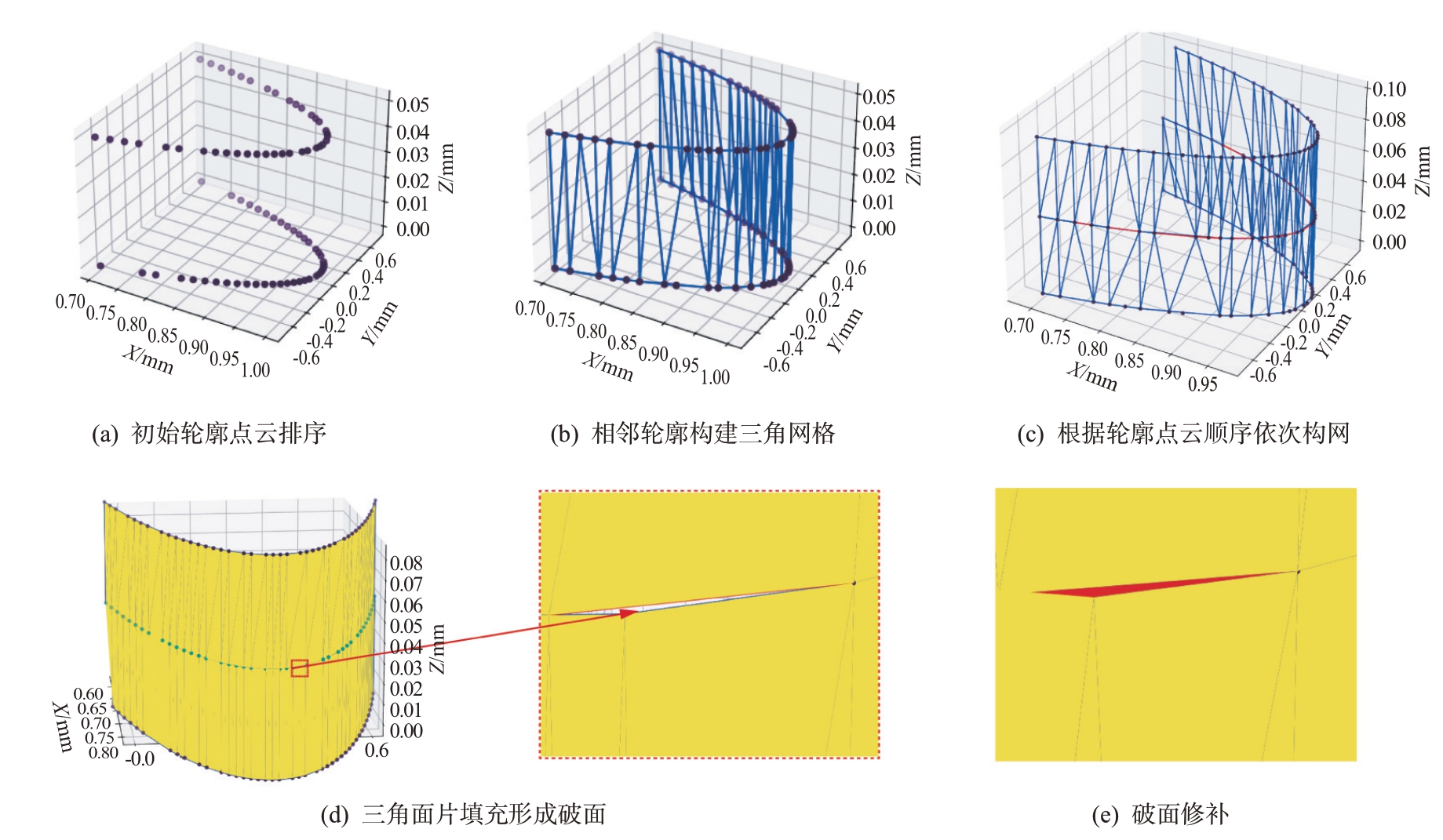
图8 轮廓构网过程示意
3.3 不同空间下的轮廓构网实验
本实验在不同大小的空间中进行构网测试,实验环境分别为纸箱、房间、走廊来模拟道路空洞、车厢、隧道,并将采集到的点云数据进行构网处理,验证该方法在这些特定的空间场景下构网的精度与速度,详细描述激光雷达旋转扫描构网的实验设计及过程、数据采集对比和结果分析。在采集过程中,确保激光雷达的位置保持固定,以便获得准确的结果。对研究对象的各处长度尺寸进行人工多次测量,测量的各处尺寸分别取平均值,方便与本方法所得结果进行比较。
3.3.1 小空间轮廓构网实验
经过标定后的激光雷达旋转扫描纸箱形成点云数据,将点云数据加载到Cloud Compare 软件上用泊松算法进行构网对比本方法构网。图9(a)为实际纸箱,图9(b)为经过法向量以及降采样后的纸箱点云,图9(d)为激光雷达采集后未经过任何处理的原始点云,图9(c)和图9(e)分别为泊松构网以及轮廓构网的结果图。泊松算法在构网时先计算所有点的法向量,再用八叉树进行降采样,降采样完成后进行构网重建;本方法在构网时将相邻轮廓上的点云按方位角顺序依次构网,得到三角构网的模型,很好地显示了每个点的连接关系,纸箱内壁长宽高测量结果如表2 所示。实验长度为经过数据处理构网后,根据软件测量工具分别测出构网后纸箱的长宽高距离,纸箱内壁尺寸为人工多次测量取平均值。根据图9 与表2 结果进行比较,可以看出构网精度比泊松算法高。在速度方面,泊松算法先计算法向量然后降采样最后再进行构网,算法流程复杂度高,构网时间在22.88 s,而本方法是直接在初始点云上进行处理,构网时间在3.69 s,构网速度显著提升。
表2 纸箱长宽高及耗时
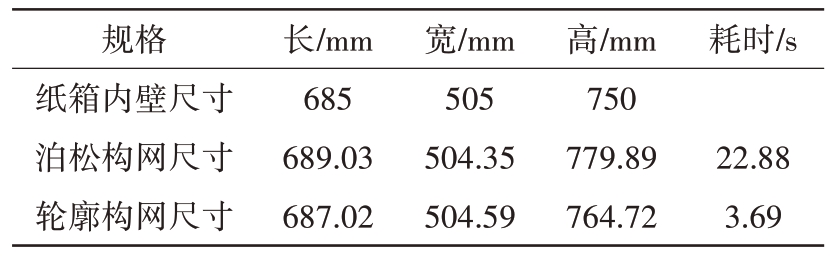
规格纸箱内壁尺寸泊松构网尺寸轮廓构网尺寸长/mm 685 689.03 687.02宽/mm 505 504.35 504.59高/mm 750 779.89 764.72耗时/s 22.88 3.69
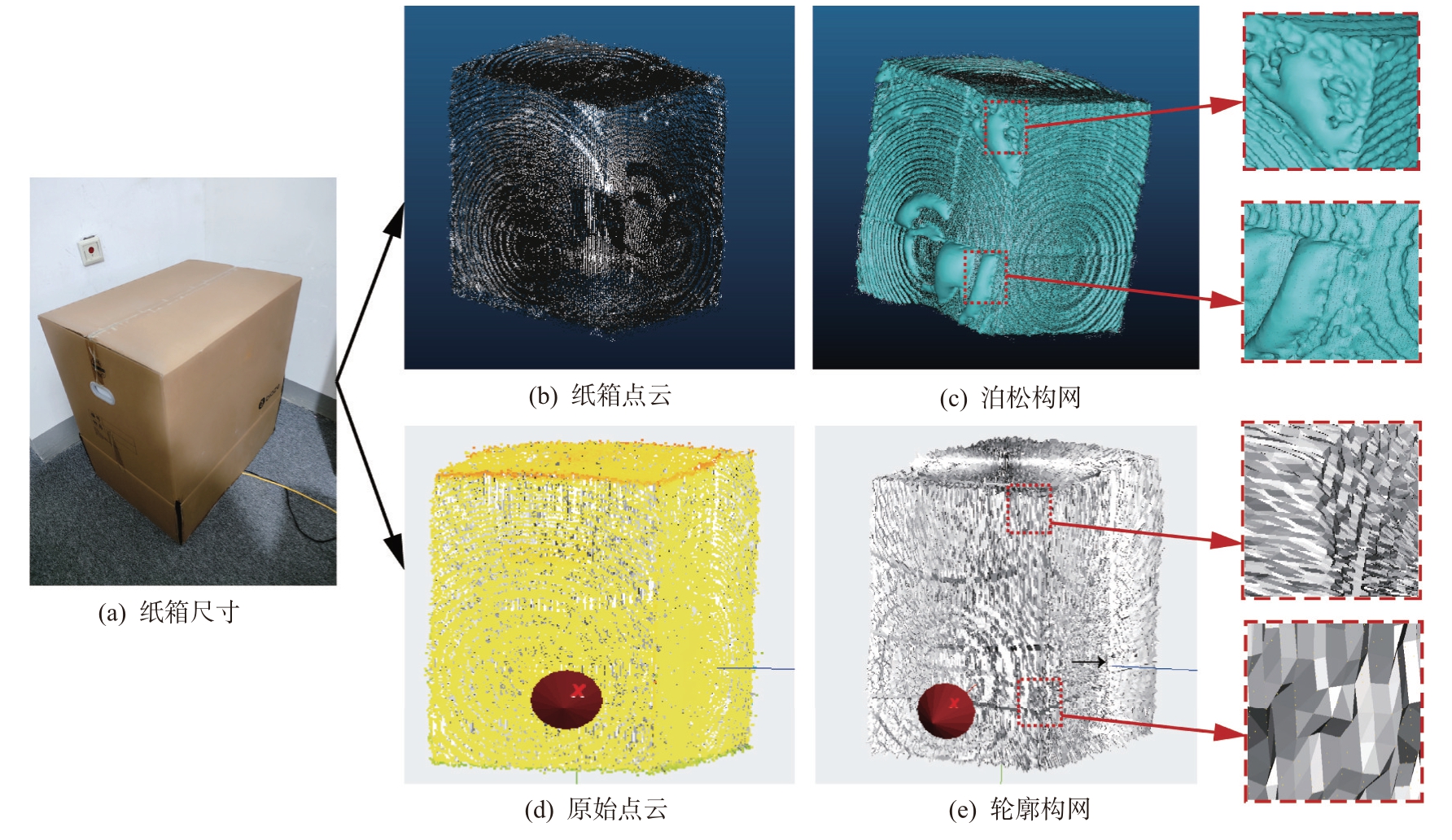
图9 泊松构网与轮廓构网对比
实验结果如图10 和表3 表明,纸箱长度、宽度和高度的最大尺寸为690.25、508.76和766.41 mm,纸箱的长度、宽度和高度的最小尺寸为680.52、502.38 和753.03 mm,纸箱的长度、宽度、高度极差范围在9.73、6.38 和13.38 mm,长度的平均相对误差为2.72 mm,宽度的平均相对误差为1.88 mm,高度的平均相对误差为9.06 mm。模型高度的预测精度略低于长度和宽度的预测精度;该模型预测其长度、宽度和高度的平均相对误差小于10 mm。
表3 纸箱实验结果分析 mm
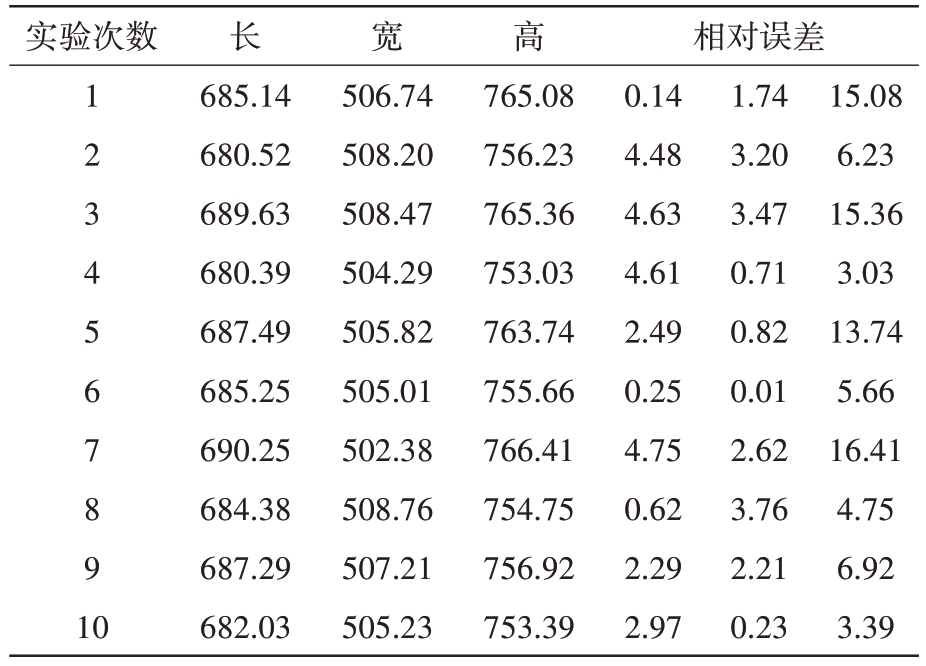
实验次数1 2 3 4 5 6 7 8 9 10长685.14 680.52 689.63 680.39 687.49 685.25 690.25 684.38 687.29 682.03宽506.74 508.20 508.47 504.29 505.82 505.01 502.38 508.76 507.21 505.23高765.08 756.23 765.36 753.03 763.74 755.66 766.41 754.75 756.92 753.39相对误差0.14 4.48 4.63 4.61 2.49 0.25 4.75 0.62 2.29 2.97 1.74 3.20 3.47 0.71 0.82 0.01 2.62 3.76 2.21 0.23 15.08 6.23 15.36 3.03 13.74 5.66 16.41 4.75 6.92 3.39
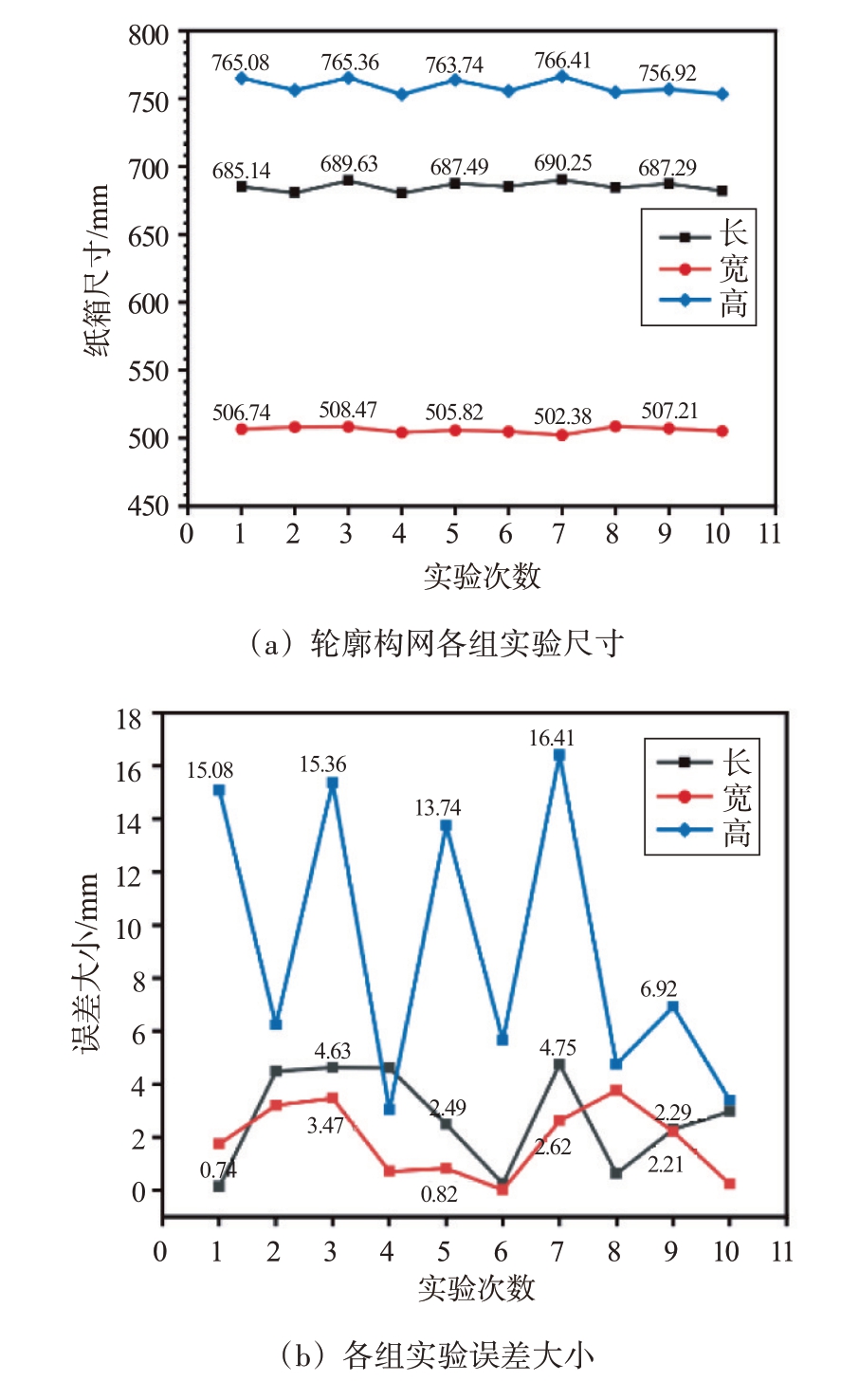
图10 纸箱轮廓构网尺寸及误差变化曲线
3.3.2 大空间轮廓构网实验
在房间构网实验中,图11(a)为实际房间环境,图11(b)为经过法向量以及降采样后的房间点云,图11(d)为激光雷达采集后未经过任何处理的原始点云,图11(c)和图11(e)分别为泊松构网以及轮廓构网的结果图。随着空间的增大,单线激光雷达旋转扫描得到的三维点云数据分布会变得离散,泊松构网及轮廓构网时间都会随之增加。在精度方面,泊松构网在空间增大后出现了凹坑变形,这是由于泊松算法在经过降采样时,把一部分点云去除后出现了变形,而本方法并没有对点云数据进行处理,因此精度并没有降低,构网效果与本实验所用的方法相比,轮廓构网效果比泊松构网效果更加还原空间物体形状,构网结果对比如图11 所示,房间长宽高测量结果如表4 所示,其中,实际长度为在实验场景中用测量工具实际测量得到的数值,实验长度为经过数据处理构网后,根据软件测量工具分别测出构网后房间的长宽高。在构网速度上泊松构网使用时间为97.70 s,而轮廓构网使用时间为5.37 s,可以看出泊松构网随着点云数据的增大,构网速度也呈现几何倍数增加,而轮廓构网随着点云数据增大,构网速度并不会像泊松构网几何倍数的增加。
表4 房间长宽高及耗时
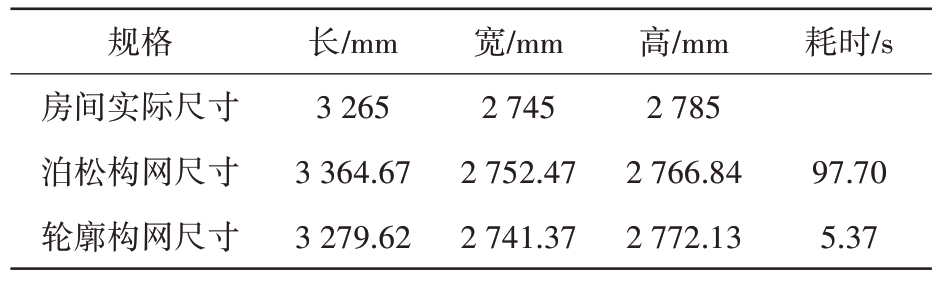
规格房间实际尺寸泊松构网尺寸轮廓构网尺寸长/mm 3 265 3 364.67 3 279.62宽/mm 2 745 2 752.47 2 741.37高/mm 2 785 2 766.84 2 772.13耗时/s 97.70 5.37
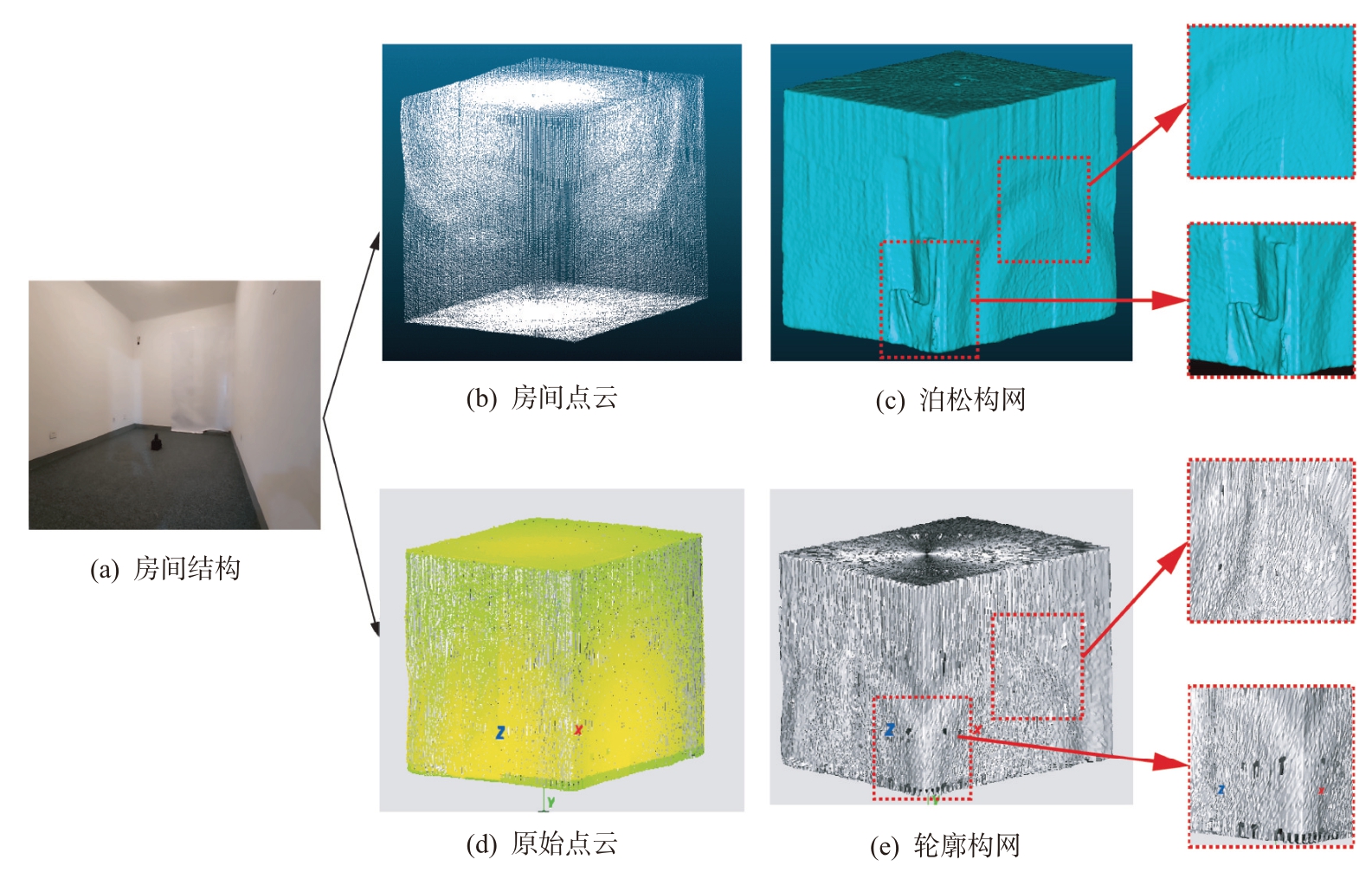
图11 房间构网效果对比
如表5 所示,实验结果表明,长度的平均相对误差为4.67 mm,宽度的平均相对误差为5.81 mm,高度的平均相对偏差为4.41 mm。模型宽度的预测精度略低于长度和高度的预测精度;该模型预测其长度、宽度和高度的平均相对误差小于10 mm。综合纸箱和房间的实验结果,平均相对误差都在10 mm内,充分验证了该方法的准确性和稳定性。
表5 房间实验结果分析 mm
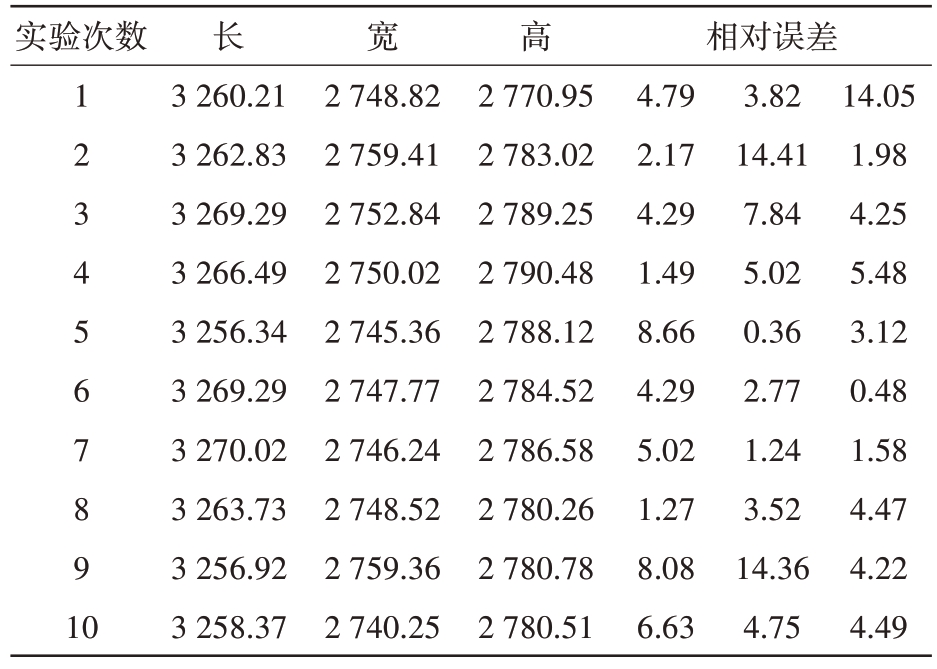
实验次数1 2 3 4 5 6 7 8 9 10长3 260.21 3 262.83 3 269.29 3 266.49 3 256.34 3 269.29 3 270.02 3 263.73 3 256.92 3 258.37宽2 748.82 2 759.41 2 752.84 2 750.02 2 745.36 2 747.77 2 746.24 2 748.52 2 759.36 2 740.25高2 770.95 2 783.02 2 789.25 2 790.48 2 788.12 2 784.52 2 786.58 2 780.26 2 780.78 2 780.51相对误差4.79 2.17 4.29 1.49 8.66 4.29 5.02 1.27 8.08 6.63 3.82 14.41 7.84 5.02 0.36 2.77 1.24 3.52 14.36 4.75 14.05 1.98 4.25 5.48 3.12 0.48 1.58 4.47 4.22 4.49
如图12(a)为经过法向量以及降采样后的泊松构网结果图,图12(b)为走廊轮廓构网结果图。对比走廊实验的精度和速度,因为扫描半径的增加,在扫描时随着扫描半径的增加点云就会变得稀疏,两点之间就会相距很远,泊松构网对距离过远的点云之间很容易形成误差,导致构网不准确,就会出现变形;在速度方面,泊松构网时出现好几次计算机死机现象,轮廓构网没有产生这种情况。

图12 走廊构网效果对比
经过上述实验验证,在已知方位角和轮廓信息条件下,本研究提出的构网方法在网格生成的精确度和效率上均超过了传统的泊松算法。特别是对于远距离且点云稀疏的区域,该方法依旧能维持良好的构网表现。表6 展示的平均误差结果更是加强了这一结论,显示出误差的SD 指标值在52%至74%之间得到了显著改善。这些数据进一步印证了本文方法在特定情形下相较于传统方法具有更好的实用性和有效性。因而,本研究的基于方位角信息的轮廓构网方法在特定应用场景下展现出更为突出的优势。
表6 算法在不同环境下的误差对比结果分析
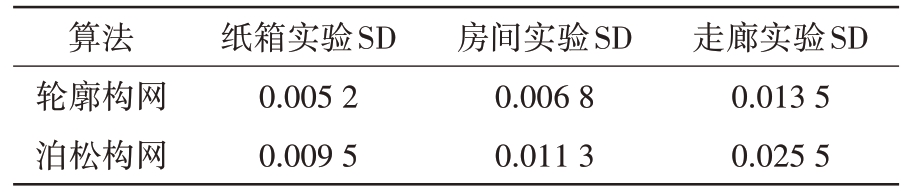
算法轮廓构网泊松构网纸箱实验SD 0.005 2 0.009 5房间实验SD 0.006 8 0.011 3走廊实验SD 0.013 5 0.025 5
4 结束语
本文设计了激光雷达旋转扫描装置,并且对激光雷达的安装误差进行修正,在此基础上提出了一种基于轮廓和方位角的单线激光雷达旋转扫描快速空间构网方法,该方法利用单线激光雷达旋转扫描形成的轮廓信息以及轮廓中每个点的方位角信息,按照相邻轮廓构网,然后进行了纸箱、房间、走廊等不同场景的实验。实验结果进一步证明了在已知轮廓和方位角信息的前提下,可以快速有效地对空间信息进行三维重建,提高了构网速度和鲁棒性,特别适用于某些特定的应用场景。
[1]秦庆国,许录平,孙学荣,等.基于激光雷达的多帧联合目标跟踪系统[J].雷达科学与技术,2022,20(1):98-108.
[2]晋良念,王燃.毫米波FMCW MIMO 雷达三维点云成像方法[J].雷达科学与技术,2022,20(5):497-506.
[3]钟雷声,夏辉,陈佳林.基于双目视觉和单线激光雷达的三维场景重建系统和算法[J].测绘通报,2024(5):48-52.
[4]李薇,楚慧娟.基于机载LiDAR 点云的电力线提取和三维重建方法[J].测绘与空间地理信息,2024,47(1):219-221.
[5]TURNER E, ZAKHOR A. Watertight Planar Surface Meshing of Indoor Point-Clouds with Voxel Carving[C]//2013 International Conference on 3D Vision-3DV 2013,Seattle,WA,USA:IEEE,2013:41-48.
[6]孙凌宇,秦红亮,师瑞卓,等.基于激光雷达的移动剖面式三维形貌重建方法研究[J].应用激光,2023,43(10):136-147.
[7]WANG Wen,SU Tianyun,LIU Haixing,et al.Surface Reconstruction from Unoriented Point Clouds by a New Triangle Selection Strategy[J].Computers& Graphics,2019,84:144-159.
[8]丁志文,邢艳秋,尹伯卿,等.融合无人机和地基激光雷达点云数据估测单木结构参数[J].森林工程,2024,40(1):142-151.
[9]YOO D J. Rapid Surface Reconstruction from a Point Cloud Using the Least-Squares Projection[J].International Journal of Precision Engineering and Manufacturing,2010,11:273-283.
[10]LAI Rongjie, LIANG Jiang, ZHAO Hongkai,et al. A Local Mesh Method for Solving PDEs on Point Clouds[J].Inverse Problems and Imaging,2013,7(3):737-755.
[11]JUNIOR A M B, NETO A D D, DE MELO J D, et al. An Adaptive Learning Approach for 3-D Surface Reconstruction from Point Clouds[J]. IEEE Trans on Neural Networks,2008,19(6):1130-1140.
[12]IVRISSIMTZIS I V, JEONG W K, SEIDEL H P. Using Growing Cell Structures for Surface Reconstruction[C]//2003 Shape Modeling International, Seoul, Korea(South):IEEE,2003:78-86.
[13]JUNIOR A M B, NETO A D D, DE MELO J D. Surface Reconstruction Using Neural Networks and Adaptive Geometry Meshes[C]//2004 IEEE International Joint Conference on Neural Networks,Budapest, Hungary:IEEE,2004:803-807.
[14]LIN Hongwei, TAI Chiewlan, WANG Guojin. A Mesh Reconstruction Algorithm Driven by an Intrinsic Property of a Point Cloud[J]. Computer-Aided Design, 2004,36(1):1-9.
[15]YUAN Ganzhangqin, FU Qiancheng, MI Zhenxing, et al.SSRNet:Scalable 3D Surface Reconstruction Network[J].IEEE Trans on Visualization and Computer Graphics,2023,29(12):4906-4919.
[16]XIAO Dong, SHI Zuoqiang, LI Siyu, et al. Point Normal Orientation and Surface Reconstruction by Incorporating Isovalue Constraints to Poisson Equation[J]. Computer Aided Geometric Design,2023,103:102195.
[17]GE Yunfeng, TANG Huiming, XIA Ding, et al. Automated Measurements of Discontinuity Geometric Properties from a 3D-Point Cloud Based on a Modified Region Growing Algorithm[J]. Engineering Geology, 2018, 242:44-54.
[18]LI Xiaojun, ZUO Yulong, ZHUANG Xiaoying,et al. Estimation of Fracture Trace Length Distributions Using Probability Weighted Moments and L-Moments[J].Engineering Geology,2014,168:69-85.
[19]GUIDOTTI V, ALONSO R, BRAVO M, et al. Delfin++:A Delaunay Based Algorithm for Finding 3D Polyhedral Voids in Galaxy Surveys[J]. Astronomy and Computing,2023,44:100713.
[20]LIU Songlin,WANG Liang,JIANG Yongdong,et al.Random Pore-Network Development Methodology Based on Voronoi and Delaunay Tessellations for Residual Coal Under Axial Stress[J].Fuel,2023,353:129267.
[21]AURENHAMMER F, KLEIN R, LEE D T. Voronoi Diagrams and Delaunay Triangulations[M].UK:Chapman and Hall/CRC,2017.
[22]GONG Wenyong,LIU Yongjin,TANG Kai,et al.Approximate Delaunay Mesh Reconstruction and Quality Estimation from Point Samples[J]. Journal of Computational and Applied Mathematics,2015,274:23-34.
[23]THAYYIL S B, YADAV S K, POLTHIER K, et al. Local Delaunay-Based High Fidelity Surface Reconstruction from 3D Point Sets[J]. Computer Aided Geometric Design,2021,86:101973.
[24]LUO Yimin, MI Zhenxing, TAO Wenbing. DeepDT:Learning Geometry from Delaunay Triangulation for Surface Reconstruction[C]//Proceedings of the AAAI Conference on Artificial Intelligence,[S.l.]:[s.n.],2021:2277-2285.
[25]SUGIURA T, TORII A, OKUTOMI M. 3D Surface Reconstruction from Point-and-Line Cloud[C]//2015 International Conference on 3D Vision, Lyon, France: IEEE,2015:264-272.