0 引 言
目标跟踪(Object/Target Tracking)是一项利用(单个或多个)传感器的观测数据来实时估计预测目标的位置、速度和加速度等动态信息的技术,广泛应用于海空侦察告警、防空反导和战场监视等军事领域与无人驾驶、机器人导航、交通监控等民用领域[1-2]。相比于单目标跟踪,多目标跟踪需要同时估计并分辨多个目标的实时状态信息,面临传感器数据中杂波虚警、数据缺损、目标漏检、不同目标数据难以分辨以及多传感器之间“异构、异质、异步”等复杂挑战[3-4]。经典的多目标跟踪解决思路即通过数据关联将多目标跟踪问题分解成单目标跟踪问题:假若不同目标、杂波、干扰源之间的数据能够完美分辨,即量测与目标之间的数据关联[5-6]能够完美解决,多目标跟踪问题就简化为了多个单目标跟踪问题的简单叠加,随之迎刃而解;若不同传感器之间的目标航迹关联等完美关联,则多传感器融合问题也能够迎刃而解。而这在绝大多数的多目标跟踪场景中难以做到,数据关联总是面临各类挑战,特别是在复杂对抗环境中,目标机动性能的提升、量测噪声的加大、数据丢包与杂波漏检的加剧以及日益增强的对抗干扰与诱骗战术等都使得数据关联面临巨大挑战,因此,数据关联性能直接决定了目标跟踪的精度、实时性和鲁棒性。
近年来,涌现了以随机集(Random Finite Set,RFS)滤波[1,7]为代表的多目标跟踪方法,弱化了对显式数据关联方法的依赖,通过多目标联合后验密度的估计实现多目标状态估计,取得了领域内广泛关注。代表性的RFS 滤波器包括概率假设密度滤波器[8]、多伯努利滤波器[9-10]以及广义标签多伯努利滤波器[11-12]等。有学者认为RFS 滤波摆脱了对数据关联技术的需求,实则不然:首先,RFS滤波器本身是将数据关联以概率的形式嵌入滤波器的迭代更新计算中,只是不需要“先关联、再滤波”的传统求解思路,滤波器更新时仍需要考虑量测和航迹的全部可能的概率关联,且在航迹输出时(无论是否采用标签)需要在时间序列上关联不同时刻状态估计[11-12];再者,无论是单传感器的航迹输出还是多传感器的滤波器融合[10,13],仍需要不同传感器目标航迹之间进行空间上关联匹配。因此,无论在传统的基于显式数据关联的多目标跟踪器(本文研究重点)、基于RFS框架和隐式数据关联的多目标跟踪器还是多传感器融合多目标跟踪器设计,数据关联都是关键技术,这是由物理现实中数据来源不确定性所导致的客观问题,无法避免。
1 数据关联
数据关联是经典雷达目标跟踪算法框架的一个核心环节,如图1所示,也是图像融合处理、地理大数据分析、多源信息融合等多学科研究领域的一项共用基础技术,即使在多目标跟踪研究领域,数据关联不限于量测与目标状态之间的关联,也包括一般的数据(包括量测与量测,航迹与航迹,状态与状态,目标与目标等)之间的关联。本文重点围绕多目标跟踪应用,为清楚起见,主要以量测与目标状态之间的关联为主,重在梳理清楚多目标跟踪应用中数据关联问题基本内容和主要解决思路,系统阐述和对比这些典型算法及其扩展方法的基本原理、各自适用条件和优缺点。首次将经典基于解析求解的数据关联分为确定性关联和概率性关联:前者采用“硬分配”策略,通过直接匹配量测数据与特定目标,建立唯一的最佳关联;概率性关联则采用“软分配”策略,通过概率模型来处理每个量测可能关联的所有目标,建立多对多的概率关联结果。确定性关联计算效率高,在环境简单、量测和目标之间的关系明确时效果较好,然而在目标密集或量测噪声大的场景易于出现关联错误。相比之下,概率性关联能够更加全面地处理量测数据的不确定性和目标之间的相互影响,可以更好地应对似然模糊的数据。不同于这两类解析求解的关联方法,针对更加丰富特征的数据(尤其是视觉数据),近年来也相继出现了一些基于学习优化的数据关联算法,这类算法往往不以特定模型下的解析最优关联为目标,而重在通过优化逼近或者对样本数据的深度学习,实现数据关联与目标检测跟踪识别、场景态势感知等一体化。
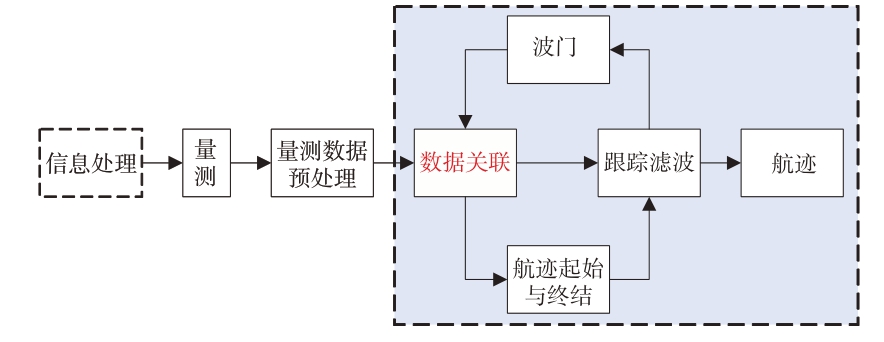
图1 经典的雷达目标跟踪框架
本文回顾的经典数据关联方法,包括确定性关联算法和概率性关联算法,如图2所示。确定性关联算法包括最近邻数据关联(Nearest Neighbor Data Association, NNDA)算法[14-15]、全局最近邻(Global Nearest Neighbor, GNN)算法[16]、多假设跟踪(Multiple Hypothesis Tracking, MHT)算法[17-18]等;概率性关联算法包括概率数据关联(Probability Data Association, PDA)算法[19]、联合概率数据关联(Joint PDA, JPDA)算法[20-22]、概率多假设跟踪(Probabilistic MHT, PMHT)算法[23]等。简单而言,确定性关联与概率关联算法主要区别在于前者的量测和目标之间的关联只存在一种假设(关联结果只包含可能性最高一种情况,舍弃其他小概率可能性),而后者存在多重假设(综合考虑多种甚至全部可能性,分别给予不同的置信度)。以下详细阐述各类方法的基本原理和主要的扩展改进思路。
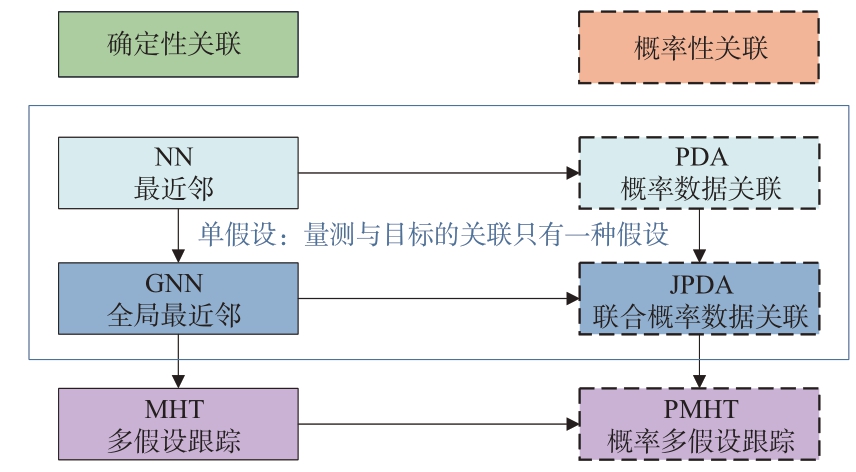
图2 确定性关联与概率性关联方法对应关系
2 确定性关联
确定性关联通常应用于需要精确匹配数据的场景中,其通过“硬分配”策略,即直接将量测数据与特定的目标进行匹配,通常依赖于优化固定的距离指标(如欧几里得距离)来寻找量测与目标之间的最佳匹配。这种方式确保在数据关联过程中,每个量测值只能关联到一个最适合的目标,确保关联的唯一性和精确性。令Aij 表示量测j 和目标i之间的关系,P表示关联事件的概率,那么对于确定性关联算法来说,有

2.1 最近邻数据关联算法
2.1.1 基本原理
最近邻数据关联(NNDA)算法最早由Singer等人[14-15]于1971 年提出,其核心原理是在某一时刻的所有量测中,只将距离跟踪目标预测位置最近的量测认定为与跟踪目标相关的真实量测。
定义目标i(i= 1,2,…,n),量测yj(j= 1,2,…,mk),最近邻数据关联示意图如图3 所示。目标i 在k 时刻状态预测位置位于跟踪门的中心,k 时刻落入跟踪门的量测为y1( k ),y2( k )和y3( k ),距离预测状态最近的量测将被优先选择。传感器接收到的量测被跟踪门划分为两部分:可能来自目标的量测和不可能来自目标的量测。跟踪门中心对应于目标的预测位置,大小由接收正确量测的概率确定,跟踪门能够滤除大部分杂波,因此跟踪门的大小和形状(常见的包括椭圆、矩形、环形和扇形)直接影响了关联过程的速度与跟踪的性能[24]。
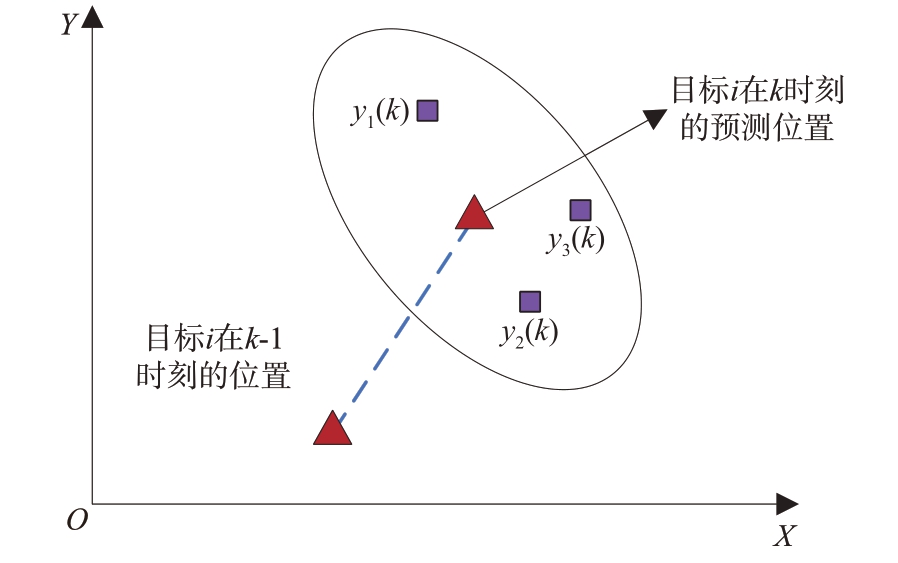
图3 最近邻数据关联示意图
定义量测yi( k )的统计距离为马氏距离(Mahalanobis Distance)d2( yi( k )):
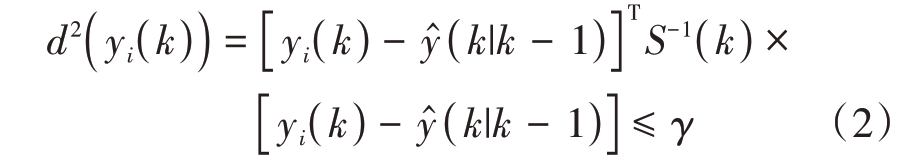
式中![]() 为k 时刻跟踪门中心(预测量测),S为新息协方差,γ为椭圆跟踪门阈值。
为k 时刻跟踪门中心(预测量测),S为新息协方差,γ为椭圆跟踪门阈值。
NNDA 的基本含义是确定地选择位于跟踪门内距离跟踪目标预测位置最近的唯一量测,以此作为与跟踪目标的关联对象,其他量测被视为虚警或来自其他目标。
2.1.2 算法改进
针对NNDA 算法只依据位置的相近程度进行关联,导致关联正确率较低的问题,王晓君等[25]使用马氏距离衡量量测与目标间的相关性和不确定性,但需要准确估计协方差矩阵。Li等[26]在最近邻算法中引入自适应阈值和权重因子,有效解决了多同源回波点关联问题并降低了错误关联率,但其阈值和权重需要动态调整。李可欣等[27]提出了一种抗干扰性强的角度NNDA 方法,用于解决多源传感器数据关联在密集区域性能不佳和易受杂波干扰的问题,显著提高了关联精度和抗干扰能力,但在数据量较小时无法确保初始关联准确性。Li 等[28]设计了近邻与最近邻(Near and Nearest Neighbor,NNN)关联方法,将一些虽不是最近邻但是很近邻的数据关联可能纳入考虑范畴,从而扩充关联的可能性,该方法也有概率性关联的属性。表1为NNDA算法改进方案表。
表1 NNDA算法改进方案

文献王晓君[25]Li[26]李可欣[27]Li[28]算法要点马氏距离度量相关性和不确定性加入自适应关联阈值和权重因子抗干扰的角度NNDA方法近邻与最近邻(NNN)优点提高正确率,处理关联的不确定性解决点关联问题降低错误关联率关联精度提高抗干扰能力增强增加考虑一些非最近邻但是非常近邻的关联缺点需要准确估计协方差矩阵需要动态调整阈值和权重数据量小时初始关联准确性较低需要设计合理的近邻阈值
2.2 全局最近邻数据关联算法
2.2.1 基本原理
最近邻关联的局限性在于它可能违背一一对应原则,即可能多个目标最近的量测都是同一量测,这就意味着一个量测可能与多个目标同时相关联,如图4 所示,目标1 和2 的最近邻量测都是y2(k)。
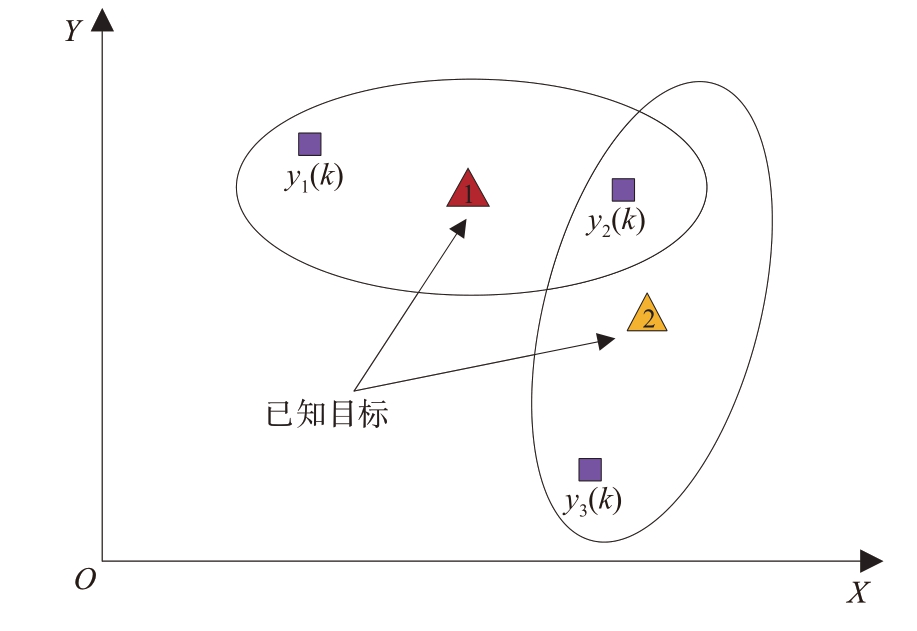
图4 最近邻数据关联异常场景
为了克服上述局限性,全局最近邻(GNN)算法被提出,它在全局范围内寻找最佳的关联匹配,从而避免局部的最优,如图4场景可能的GNN关联结果是:目标1 与y1(k)关联、目标2 与y2(k)关联。相比NNDA 仅寻求单个量测与预测关联对的最大相似度,GNN旨在寻找所有量测与预测关联对的相似度总和的最大值。GNN算法流程如图5所示。
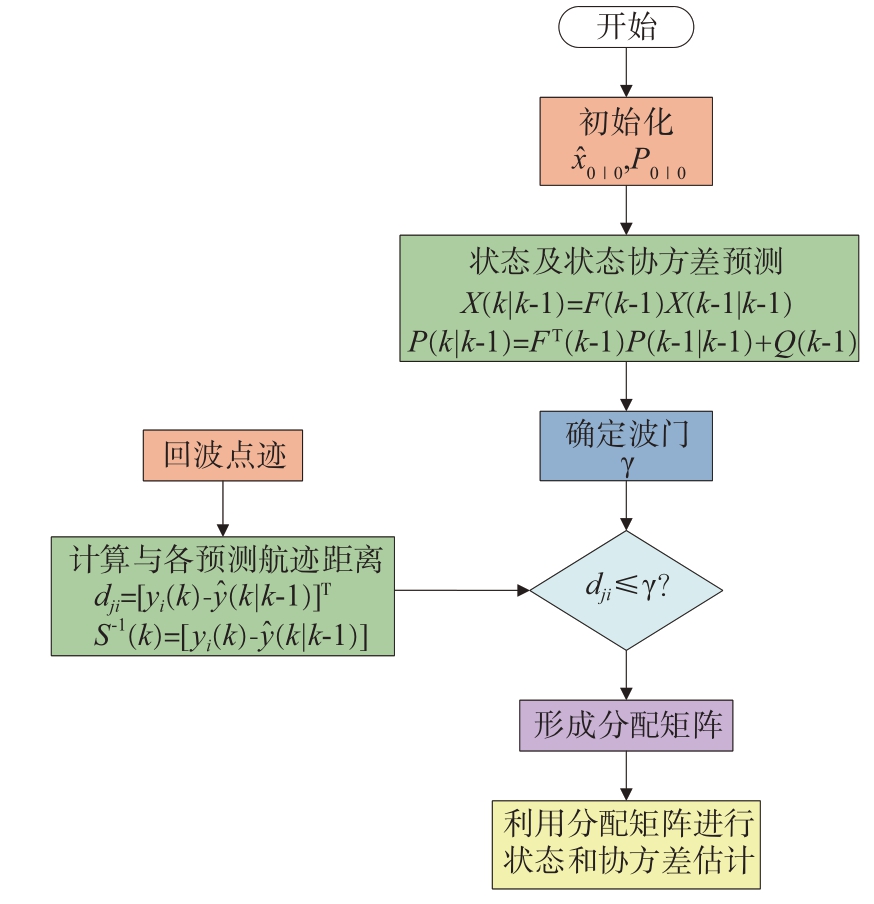
图5 全局最近邻算法流程图
对量测集合{yj( k ),j = 1,2,…,mk }和状态预测集合![]() 中每个可能的关联对计算相似度,采用如欧几里得距离、马氏距离和负对数似然等度量,即可建立代价矩阵C =
中每个可能的关联对计算相似度,采用如欧几里得距离、马氏距离和负对数似然等度量,即可建立代价矩阵C =![]() 和关联矩阵
和关联矩阵![]() 则全局最近邻算法目标函数可表述为
则全局最近邻算法目标函数可表述为![]()
定义为第j个量测和第i个状态预测之间的广义统计距离,dji 表示第j 个量测和第i个状态预测之间的马氏距离,![]() 为新息协方差的对数,关联矩阵
为新息协方差的对数,关联矩阵![]() 满足约束:
满足约束:
此时GNN 将关联问题转换为一个线性分配问题,可以采用如匈牙利算法[29]、拍卖算法[30]和Murty算法[31]来求解最优关联矩阵,从而获得量测集合与状态预测集合之间的最优关联。然而分析可知,NNDA 和GNN 在进行相似度计算时通常假设量测数据准确无误,而当量测数据出现偏差时,可能导致量测数据未落入目标跟踪门,从而引发错误的关联。
2.2.2 算法改进
多项研究通过不同策略来增强GNN 算法的性能,Allodi 等[32]通过多维结构的分类器和匈牙利算法优化异构传感器数据的关联。王宁等[33]使用关联代价与模糊隶属度二次滤除误关联。刘全仲等[34]通过可能性聚类优化关联矩阵的生成,以减少错误关联。Riahi等[35]定义了一个综合多种特征的亲和力函数,并计算目标与量测之间的联合亲和分数来构造成本矩阵。Wu 等[36]通过零均值高斯函数计算位置相似度,指数函数评估尺度相似度。同时在系统设计及统计方法方面,Piao等[37]通过引入两层数据关联架构和替代传统贝叶斯滤波器的MedianFlow 跟踪器,简化了计算过程并提高了系统运行速度。Shi 等[38]通过引入特征向量和统计距离计算减少传感器偏差影响,Li 等[39]则通过加权距离的GNN 算法提高了关联正确率。表2为GNN算法改进方案。
表2 GNN算法改进方案

文献Allodi[32]王宁[33]刘全仲[34]Riahi[35]Wu[36]Piao[37]Shi[38]Li[39]算法要点多维结构分类器和匈牙利算法优化关联代价与模糊隶属度滤除误关联可能性聚类优化关联矩阵多特征亲和力函数,构造成本矩阵零均值高斯函数和指数函数相似度两层关联架构和MedianFlow跟踪器特征向量和统计距离减少传感器偏差加权距离的GNN算法提高关联正确率优点提高异构数据关联效率减少误关联,提高关联准确性减少错误关联提高多特征数据的关联性精确评估相似度,提高关联准确性简化计算过程,提高系统运行速度减少偏差影响,提高数据处理稳定性提高关联正确率缺点对分类器的选择和设计要求高模糊逻辑参数需要精心选择需要合适的参数设置复杂度高,需要多种数据源对噪声和异常值的处理需要加强可能在复杂场景下准确性降低需要准确的统计模型和特征向量加权策略和网络结构需要优化
进一步的研究表明,结合先进的机器学习技术和优化算法可以更有效地处理数据关联问题,实现对成本矩阵的优化,详细阐述参见4.1节。
2.3 多假设跟踪算法
多假设跟踪(MHT)算法由Reid首先提出[18-19],该算法引入了关联假设的概念,涉及对结果空间进行3 个连续的细化步骤:编号、配置和分配。MHT 算法的核心组成部分包括假设树的形成、假设的生成以及各个假设的概率计算。这些步骤共同构成了算法的基础,使其能够维护和传播代表从测量到跟踪关联的多个假设。MHT 中提出的假设与JPDA 中联合事件概念在本质上是相似的。然而,它们之间存在主要的两个区别:首先,MHT在处理每个回波时不仅考虑了虚警的可能性,还考虑了新目标出现的可能性;其次,MHT 认为k 时刻的假设为k - 1 时刻的某个假设与当前数据集关联的结果,从而实现时间序列上的关联和状态估计的连续性。
自MHT 算法提出以来,其多种变体和扩展已经被发展和检验。例如,假设可以生成并关注特定的方面,如特征、测量或轨迹。MHT最广泛应用的两种变体是面向假设的MHT(Hypothesis-Oriented MHT, HOMHT)和面向航迹的MHT(Track-Oriented MHT, TOMHT)[17],后者又有两个分支,为基于树形的TOMHT[40-41]和基于非树形的TOMHT[42-43]。
2.3.1 面向假设的多假设跟踪
HOMHT 方法基于最小均方误差-最大后验概率(MMSE-MAP)策略,区别于TOMHT,它使用假设树来展现量测与目标之间的关联。在假设树中,每个节点代表一个潜在目标,节点间的连线则表示量测与这些目标之间的潜在关系。每个量测可以被视为以下三种情况之一:①已有航迹的延续量测;②一个新目标的初次探测;③一个虚警。
在HOMHT 中,每个扫描周期内均需对所有关联假设进行维护和更新,并根据新的量测在下一个周期内调整或剪枝假设。HOMHT 算法流程如图6所示,首先包括对落入跟踪门的量测构建分配矩阵,依据关联矩阵生成航迹假设,并计算假设概率,继而保留高概率的假设并修剪低概率的假设。最后,筛选的假设会更新到航迹中,生成并上报航迹。
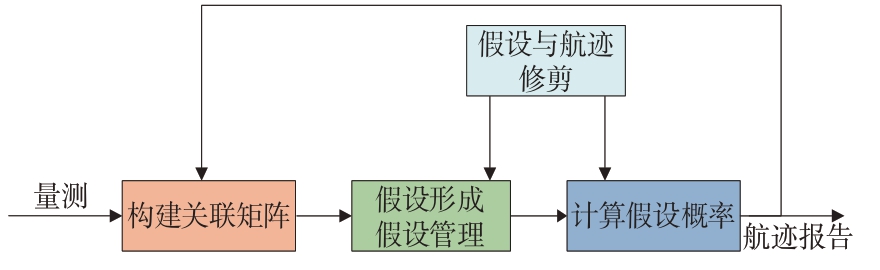
图6 HOMHT算法流程图
HOMHT 的核心问题是形成假设树,如图7 描述了一个HOMHT 算法场景,包含2 个已知目标和3 个量测的关联场景。k 时刻时量测y1(k) 落入目标1 跟踪门,量测y3( k )落入目标2 的跟踪门,y2( k)同时落入目标1和目标2的跟踪门。
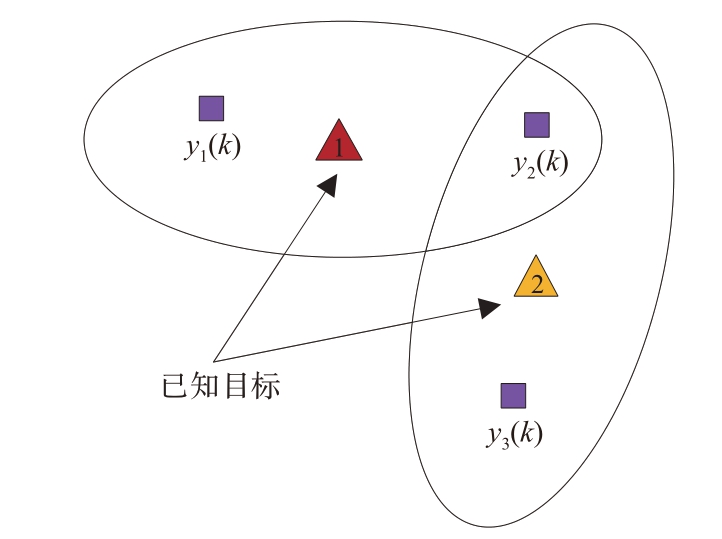
图7 HOMHT算法场景
图8 给出了与图7 算法场景相对应的假设树。对于量测y1(k) ,由于其只落入目标1 跟踪门内,可以将其关联至目标1,而y1(k) 也存在是新生目标或者虚警的概率。量测y2(k) 同时落入目标1 和目标2 跟踪门内,于是当量测y1(k) 与目标1、新生目标或虚警目标关联时,可将量测y2(k) 与目标1、目标2、新生目标或虚警目标关联;而在量测y1( k )与目标1 关联时,量测y2( k )只能与目标2、新生目标或虚警目标关联。而量测y3( k )的假设建立类似量测y2( k )。图8 中从假设树顶部到叶的目标序列可形成一个假设。
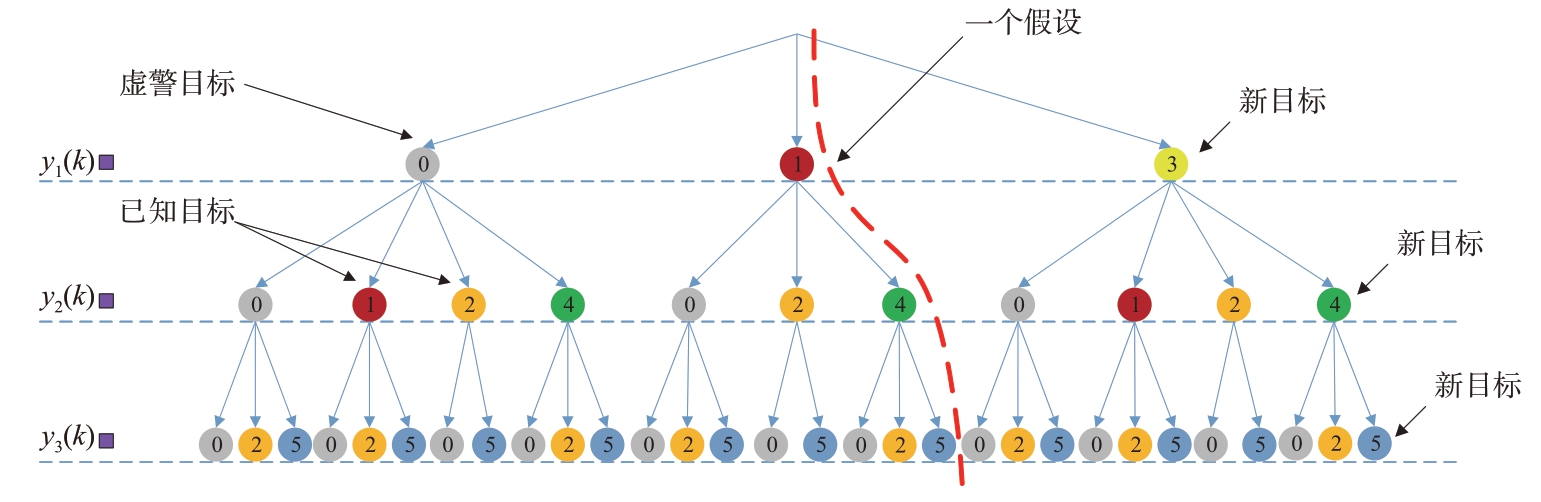
图8 HOMHT假设树
以下详述HOMHT 假设概率计算。令![]() 表示k + 1 时刻下的假设集Ωk + 1 中的第l个假设。这个假设可以被视为由时刻k 的某个假设
表示k + 1 时刻下的假设集Ωk + 1 中的第l个假设。这个假设可以被视为由时刻k 的某个假设![]() 与量测分配事件yh 组合而成,即
与量测分配事件yh 组合而成,即![]() ,令Yk 表示从初始到时刻k 的所有量测数据集合。根据贝叶斯定理,
,令Yk 表示从初始到时刻k 的所有量测数据集合。根据贝叶斯定理,![]() 的后验概率表示为
的后验概率表示为
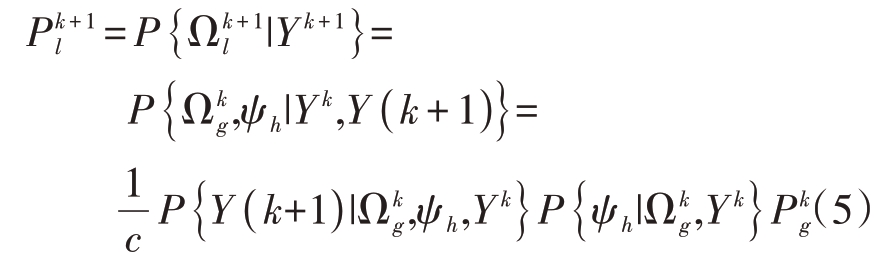
这里,c 是归一化常数,Y( k )为时刻k 的量测数据,![]() 是给定所有量测Yk 后假设
是给定所有量测Yk 后假设![]() 的概率。在量测区域内,假设新生目标出现和虚警的概率密度为均匀分布,已存在目标的量测为高斯分布。于是,条件概率
的概率。在量测区域内,假设新生目标出现和虚警的概率密度为均匀分布,已存在目标的量测为高斯分布。于是,条件概率![]() 可以写作
可以写作
式中![]() 是时刻k + 1的第j个量测,ij表示目标和第j 个量测相关联,τj = 1 表示第j 个量测与航迹成功匹配
是时刻k + 1的第j个量测,ij表示目标和第j 个量测相关联,τj = 1 表示第j 个量测与航迹成功匹配![]() 表示高斯分布的概率密度函数。
表示高斯分布的概率密度函数。
设mk 为时刻k 的总量测数目,量测在分配事件ψh 中源于虚警、新生目标及已有目标的数目分别记为NFT( h )、NNT( h )和NDT( h ),并满足NFT + NDT +NNT = mk。假设已存在的目标数目为二项分布,新生目标和虚警的数目为泊松分布。量测分配事件ψh的条件概率为
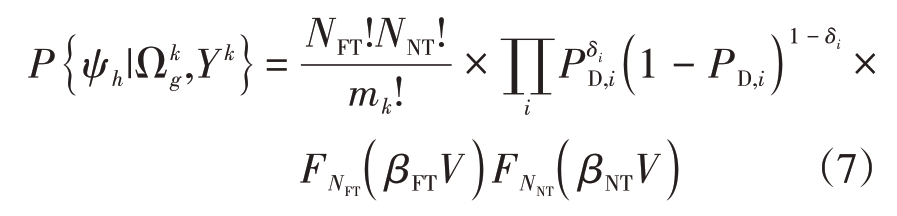
这里,δi 为目标检测器,δi = 1 时表示假设![]() 中第i个目标被检测到,PD,i 为检测到第i 个目标的概率,βNT 和βFT 分别表示新目标和虚警的空间密度,
中第i个目标被检测到,PD,i 为检测到第i 个目标的概率,βNT 和βFT 分别表示新目标和虚警的空间密度,![]() 表示量测区域内出现NNT个新目标和NFT 个虚警的概率。则可得到假设
表示量测区域内出现NNT个新目标和NFT 个虚警的概率。则可得到假设![]() 的概率为
的概率为
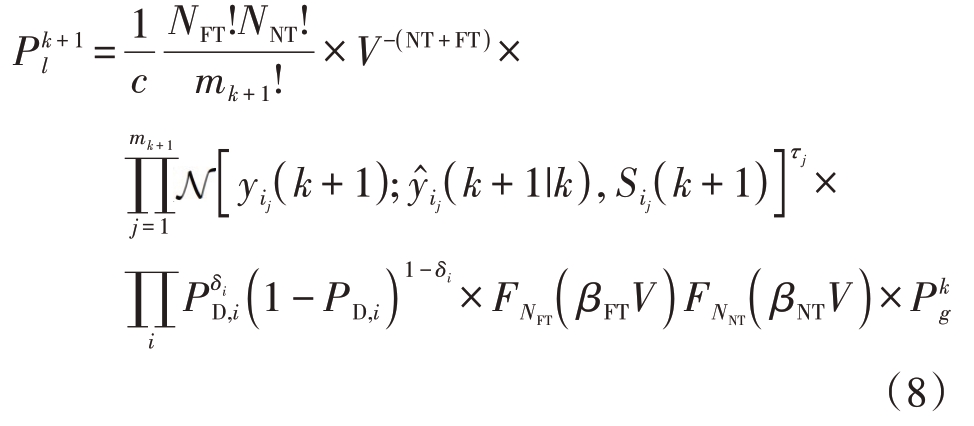
通过调整式(8)的具体参数,可求得相应的假设概率。递推其他时刻的假设概率后,假设生成和概率计算即告完成,接着可以进行状态估计,并在假设约简步骤中输出结果。
2.3.2 面向航迹的多假设跟踪
TOMHT 方法基于最小均方误差-最大似然(MMSE-ML)策略,假设一个量测可能来自航迹的延续、新生目标或虚假目标,并通过为每个目标建立一个目标树来描述量测和目标之间的可能关联关系。通过计算每种关联方式的概率,选择具有最高概率的关联作为最终决策,有效传递每个扫描周期中可能存在的航迹信息。图9 展示了TOMHT 算法流程:首先对已有航迹Kalman 预测,然后进行数据关联,并对形成的航迹进行删除和确认,接着在剩余的航迹中生成假设、删除假设并进行全局概率计算,最后基于全局概率对全局航迹删除。
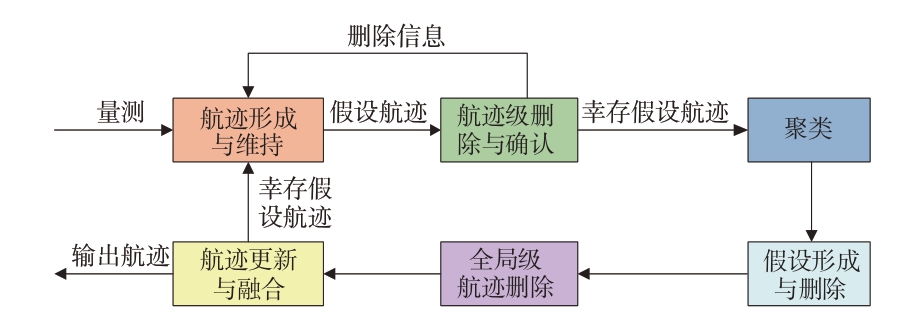
图9 TOMHT算法流程图
图10 描述了一个TOMHT 算法的场景,包含2个已知目标和2个量测的关联场景。k时刻时量测y1( k )落入目标1 跟踪门内,量测y2( k )落入目标2跟踪门内;k + 1 时刻时量测y1(k + 1) 同时落入目标1 与目标2 跟踪门内。图11 展示了针对图10 给出的关联场景所建立的TOMHT 算法目标树。目标树的顶端表示目标的初始出现,每个目标树含有多个航迹假设,分别对应该目标的不同可能轨迹。树上从根节点到叶节点的每一条路径都描述了该目标的量测历史。全局假设是通过从不同目标树中选择航迹假设组合而成的,并且每个目标树中只能最多选取一个航迹假设。在k时刻时,只有量测y1( k )能够和目标1 关联,量测y2( k )和目标2 关联;目标1 和目标2 可能未被检测到,此时目标不和任何量测关联y0( k );此外,量测y1( k )和y2( k)也可能作为新生目标3和目标4。在k + 1时刻时,量测y1(k + 1) 能同时与目标1 和目标2 关联;目标1、2、3、4 也可能未被检测到,即不与任何量测关联y0(k + 1) ;同时,量测y1(k + 1) 也可能作为新生目标5。
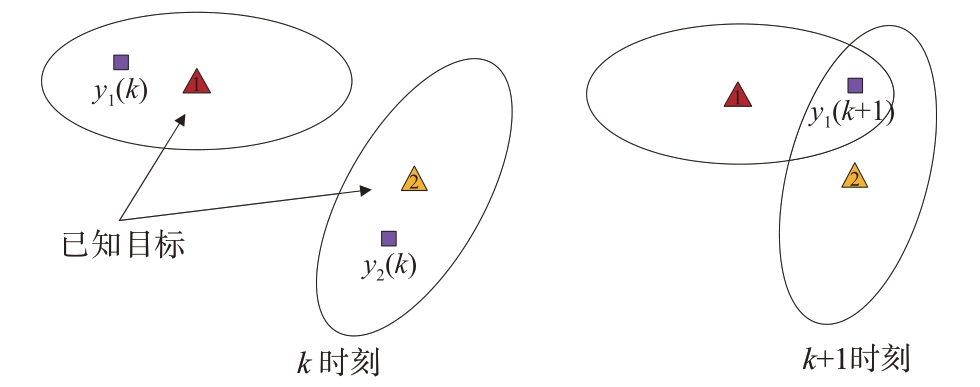
图10 TOMHT算法场景
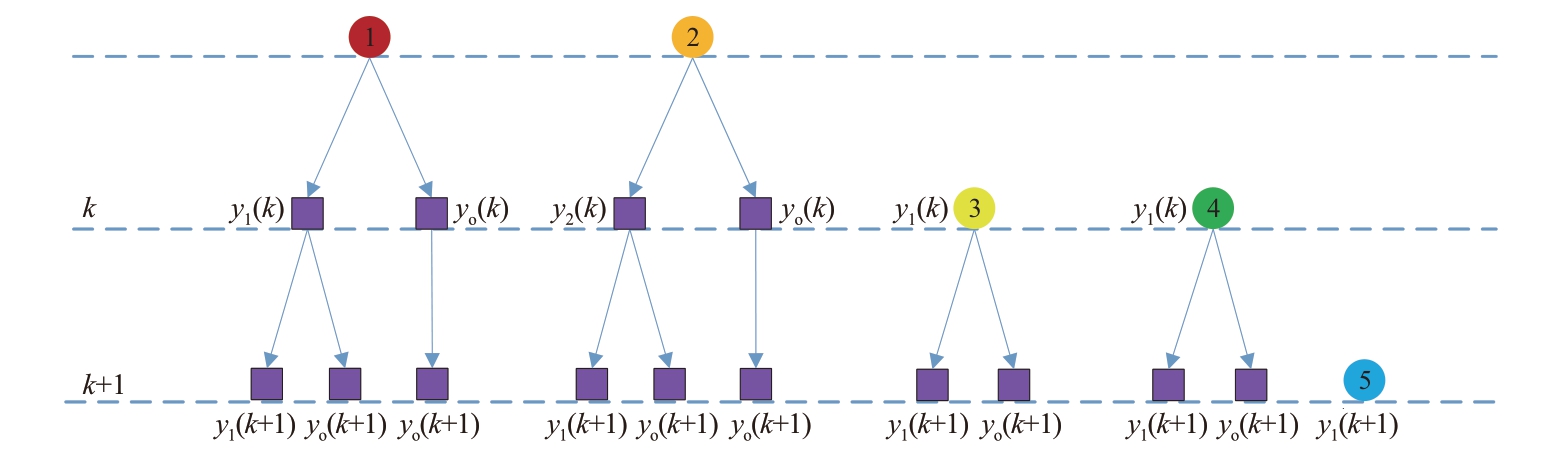
图11 TOMHT目标树
1) 航迹形成与维持
TOMHT 算法首先接收并评估新的量测数据,根据这些量测与现有航迹的关系来决定航迹的处理。通过计算新量测的新息及其协方差,采用概率统计方法评估量测能否作为候选回波。当量测数据满足概率门限测试时,将其用于扩展现有航迹或初始化新的航迹。此过程包括在当前目标树上生成新的分支,并为每个假设航迹(分支)赋予一个确认概率,此概率反映该航迹为真实目标航迹可能性。随着时间推移,算法中的假设航迹的数量会呈指数增长。为了减少计算复杂度,必须有效管理这些假设航迹,并及时剔除虚假航迹。
2) 航迹确认与航迹删除
经过航迹形成步骤后,需对每个假设航迹进行评估。通常,假设的后验概率可以通过将其对数形式递推分解为航迹概率的似然值来计算,即航迹得分。设![]() 为从1 到k 时刻所有量测Yk 条件下假设
为从1 到k 时刻所有量测Yk 条件下假设![]() 的概率,设
的概率,设![]() 在k + 1 时刻的某个子假设为
在k + 1 时刻的某个子假设为![]() 则假设后验概率的对数形式可以表示为
则假设后验概率的对数形式可以表示为
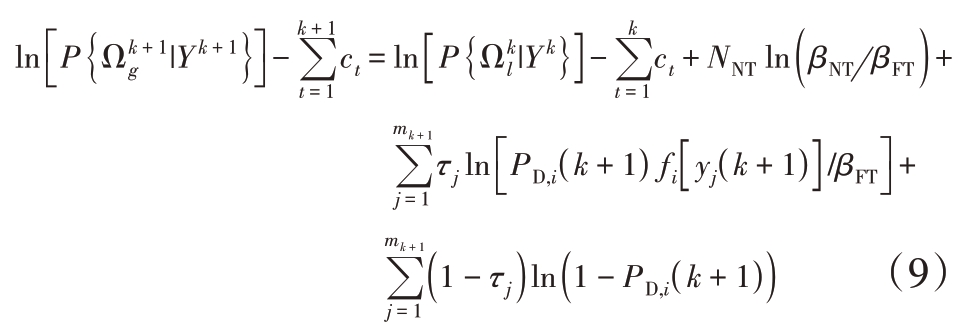
式中:ct为第t扫描中与假设无关的常数;PD,i(k + 1)表示目标在k + 1 时刻被传感器检测到且量测落入跟踪门的概率;fi[yj(k + 1) ]表示在量测为yj(k + 1) 目标关联量测yj(k + 1) 的概率密度函数(Probability Density Function, PDF)。式(9)等式左侧为![]() 的假设得分,假设的得分由目标的不同情况贡献:新生目标的贡献为ln(βNT/βFT);目标i未关联任何量测时的贡献为1 - PD,i(k + 1);而当目标i关联量测yj(k + 1) 时,产生的贡献为ln[PD,i(k + 1)×fi[yj(k + 1) ]/βFT ]。
的假设得分,假设的得分由目标的不同情况贡献:新生目标的贡献为ln(βNT/βFT);目标i未关联任何量测时的贡献为1 - PD,i(k + 1);而当目标i关联量测yj(k + 1) 时,产生的贡献为ln[PD,i(k + 1)×fi[yj(k + 1) ]/βFT ]。
目标i在k扫描的得分sk可定义为
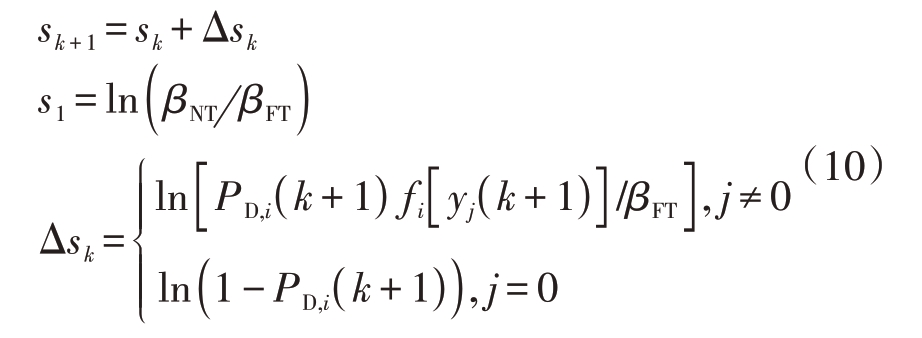
3) 聚类
在TOMHT 算法中,聚类步骤旨在将假设航迹按共享的量测信息分为若干独立子集(簇),以降低计算复杂度并提高效率。具体步骤包括:
① 建立航迹相容性矩阵:通过判断航迹之间是否共享量测来确定它们是否相容。
② 执行图论聚类:将假设航迹视为图的顶点,共享量测为边,通过聚类将顶点划分为极大连通子集。
③ 独立处理每个簇:在每个簇中独立进行假设生成、全局级航迹删减和更新等操作。
4) 全局假设形成与删除
在TOMHT 中,航迹得分反映了量测与运动模型匹配的程度,并不考虑其他航迹的影响。而全局假设考虑所有可能的量测来源。全局假设形成与删除适合并行处理,具体步骤如下:① 生成正得分航迹的优先全局假设;② 从负得分航迹中生成独立集;③ 合并这些集合,形成最终全局假设,为跟踪决策提供支持。
最优假设由得分最高的假设组成,代表最可能的数据关联方案。为处理高目标密度和虚警情况,TOMHT 可采用图论中的最大权独立集(Maximum Weight Independent Set, MWIS)问题,通过贪心随机自适应搜索程序(Greedy Randomized Adaptive Search Procedure, GRASP)等启发式方法进行求解。
TOMHT算法的假设数目可能随扫描次数指数增长,导致组合爆炸现象。N-Scan 剪枝能够限制假设树深度,继而完成对假设数量的控制。其通过在当前扫描k 找出最优假设,然后回溯到k - N时刻,删除非最优假设中的所有航迹分支。以N =2 为例,从最优解点开始,回溯到k - 2 时刻,所有具有根节点但未包含在最优假设航迹中的分支将被移除。图12 展示了N-Scan 剪枝方法的示意图,其中节点2、3、5 代表出现在最优假设中的航迹节点,称为最优节点。
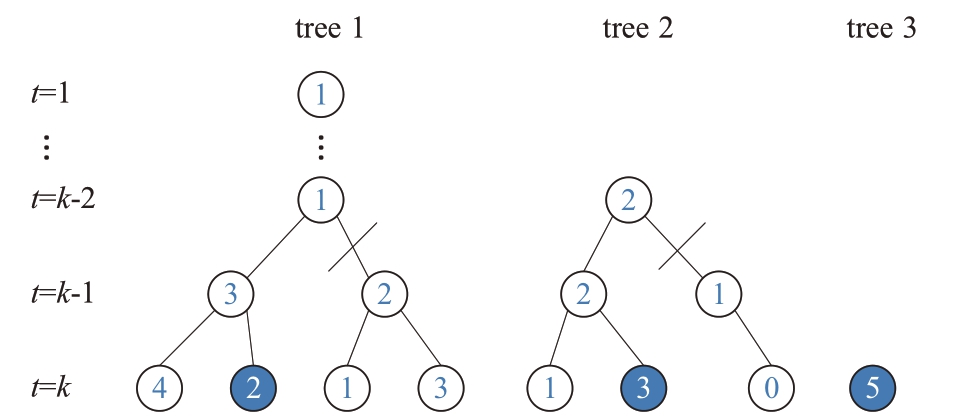
图12 N-Scan剪枝方法示意图
全局的假设删除是在N-Scan 剪枝后,对剩余的假设航迹进一步筛选。根据公式(11),通过计算假设航迹的后验概率进行筛除:
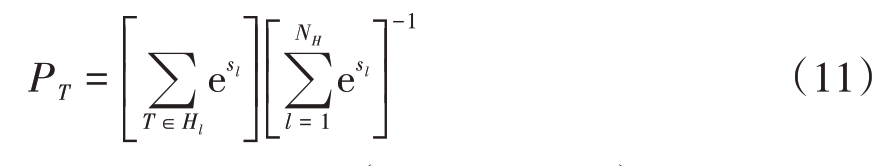
式中,e为自然对数,Hl(l = 1,2,…,NH) 为全局假设,其对应得分为sl。全局的航迹删除分两步进行:
① 通过设定的概率门限,移除后验概率小于设定概率门限的假设航迹;
② 删除航迹树中后验概率较低的航迹,确保每个树中假设航迹数不超过规定最大值。
2.3.3 算法改进
MHT 主要面临的问题是计算效率低和复杂度高,因此,针对MHT的改进方案通常集中在提升其计算效率和降低复杂度上。Kojima 等[44]讨论了面向轨迹的多假设跟踪方法,主要关注如何在密集环境中提高多目标跟踪的效率和准确性。通过生成假设来简化目标轨迹的提取过程。Thomaidis等[45]则采用滑动窗口和修改过的假设管理方案,以减少假设数量并提高数据关联的计算效率。Kosuge 等[46]提出了改进的TOMHT 算法,专门针对机动目标跟踪问题,通过推迟决策以接收更多的测量数据。
He等[47]结合了禁忌搜索和吉布斯抽样来设计算法,而Sheng 等[48]提出了一种新颖的迭代MWIS算法,引入多项式时间近似算法以提高效率。
刘建锋[49]提出了一种m-最优假设N 扫描多假设跟踪方法,使用特定的假设生成策略并通过滑窗来生成最优的可行假设。Xing 等[50]提出了一种利用GNN 指导的多假设跟踪方法,通过GNN 的结果来指导轨迹分支的形成,改进数据关联。表3为MHT算法改进方案。
表3 MHT算法改进方案

Kojima[44]Thomaidis[45]Kosuge[46]He[47]面向轨迹的MHT滑动窗口和修改过的假设管理改进TOMHT算法针对机动目标结合禁忌搜索和吉布斯抽样提高效率准确性简化轨迹提取减少假设数量,提高计算效率推迟决策接收测量针对机动目标提高MHT方法的计算效率非密集环境不如其他方法灵活窗口大小和假设管理选择敏感推迟决策可能导致实时性降低调整禁忌搜索吉布斯抽样的参数文献算法要点优点缺点
续表

Sheng[48]刘建锋[49]Xing[50]迭代MWIS多项式时间近似算法m-最优假设N-Scan下MHT GNN指导的多假设跟踪方法提高效率,优化多假设跟踪平衡性能和效率生成最优假设GNN结果指导轨迹分支形成近似算法在某些情况下牺牲精度生成策略和滑窗大小需要设计延时决策且依赖GNN的准确性文献算法要点优点缺点
3 概率性关联
概率性关联采用一种更为灵活的“软分配”策略。在这种方法中,每个量测不是简单地与一个特定目标匹配,而是通过概率模型来评估与多个目标的关联概率。这种方式允许每个量测根据概率权重与多个目标关联,从而处理量测数据的不确定性和模糊性。同时,对于概率性关联算法来说,量测j 和目标i 之间的关联事件的概率在0 到1之间,表示量测j 和目标i 之间往往非排他性唯一匹配,而是以概率形式存在,且满足:
这显然有别于确定性关联。
3.1 概率数据关联算法
3.1.1 基本原理
不同于NNDA,PDA 只要量测落入关联波门,就将其视为可能来自于真实目标,不过各量测属于目标的概率并不相同,该算法的关键在于如何利用波门内的量测来计算各自的概率加权系数,并利用这些系数对航迹状态进行更新。图13 为PDA算法流程图。
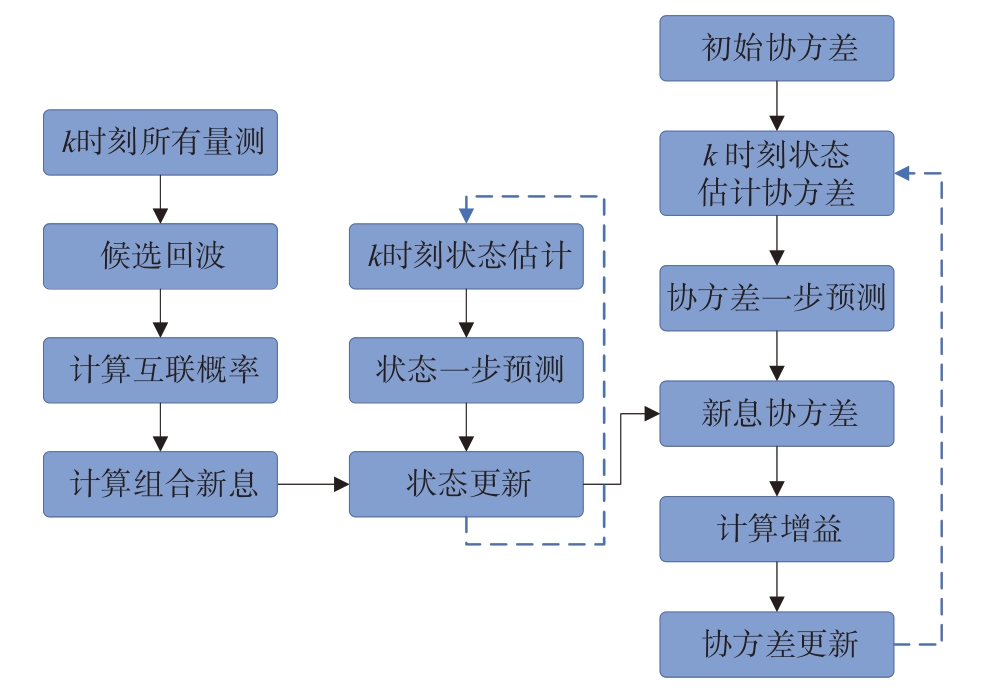
图13 PDA算法流程图
在k 时刻,跟踪门内有mk 个量测数据Y( k )=![]() 针对目标与量测的匹配问题,定义以下事件:
针对目标与量测的匹配问题,定义以下事件:
1) θ0( k )表示k时刻没有量测与目标相匹配。
2) θj( k )表示yj( k )是k时刻与目标匹配的量测。
用概率βj( k )表示yj( k )正确关联的后验概率,![]() 目标状态的估计值为
目标状态的估计值为
式中![]()
![]() 表示相应的新息。当j = 0 时
表示相应的新息。当j = 0 时![]()
![]()
状态预测和自相关矩阵分别为
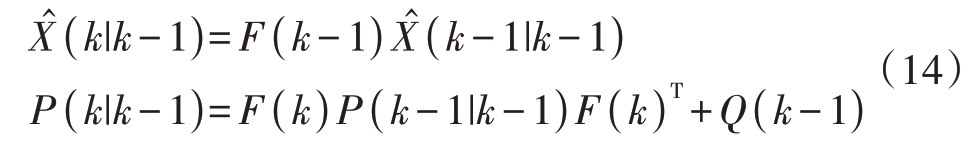
定义卡尔曼增益为K(k) ,则状态滤波方程为
式中![]() 表示组合新息,协方差矩阵方程为
表示组合新息,协方差矩阵方程为
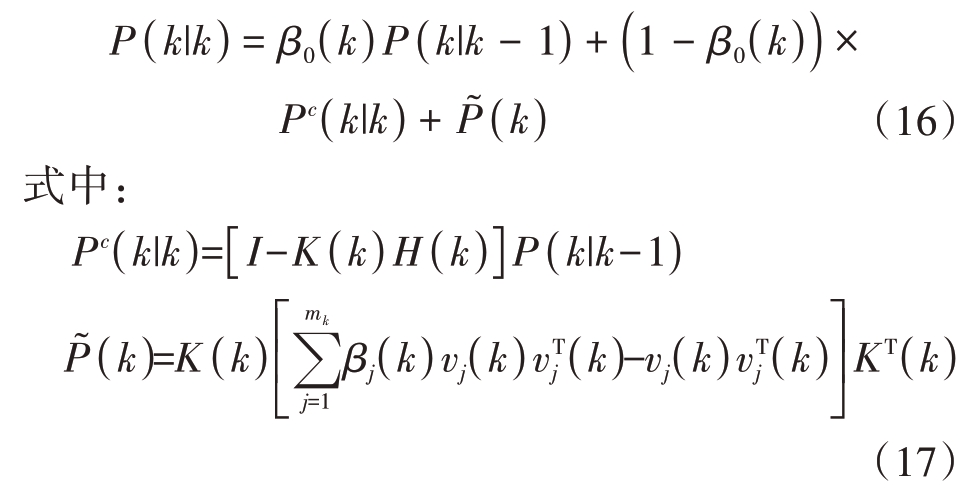
假设杂波的数量是参数为λVk 的泊松分布,Vk为跟踪门体积,λ 表示杂波密度。跟踪门内量测概率为
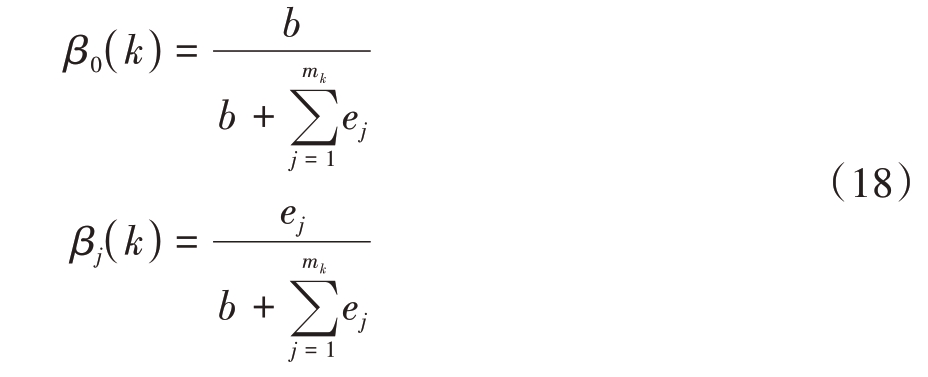
式中,
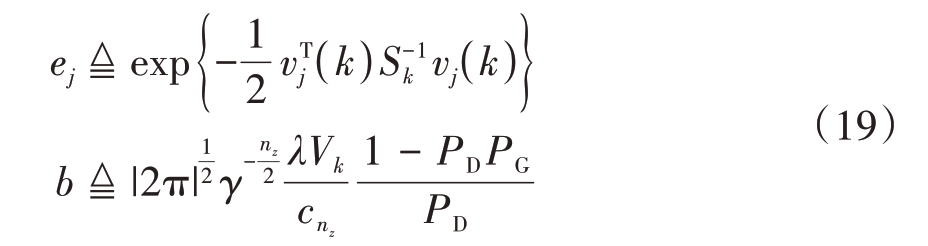
式中,nz 表示yi( k )的维数,PD 为检测概率,PG 表示真实量测落入跟踪门的概率。当杂波数量为均匀分布或扩散先验分布时,将式(19)中λVk 改为mk即可。
图14 为PDA 算法场景图。其中k 时刻落入目标跟踪门内的量测有y1( k )、y2( k )和y3( k )。通过对y1( k )、y2( k )和y3( k )的量测计算关联概率β1( k )、β2( k )和β3( k ),得到加权量测用于更新目标状态估计。
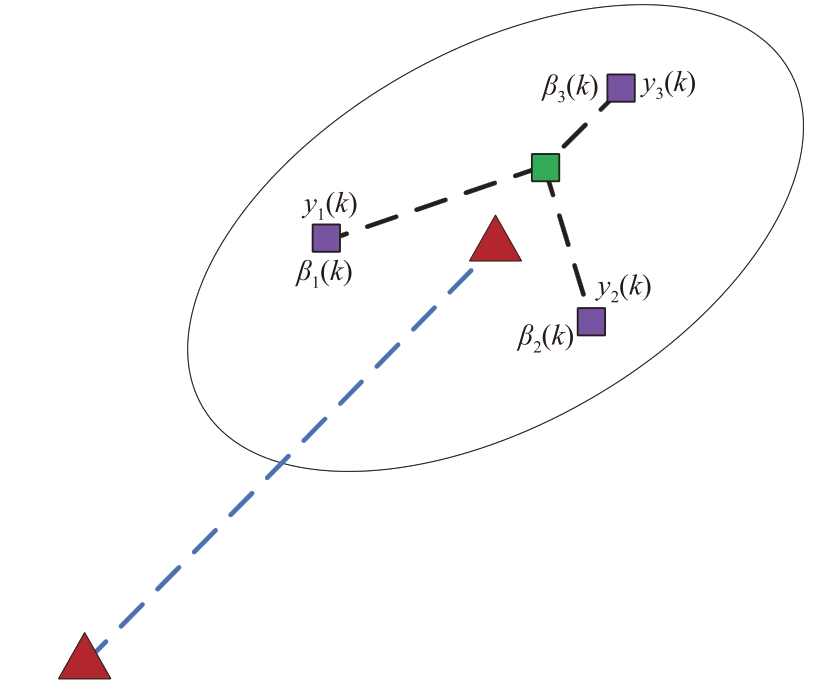
图14 PDA算法场景
3.1.2 算法改进
为了应对现有PDA 技术中遇到的挑战,如处理复杂性高、对环境噪声敏感和在动态条件下性能下降的问题,许多改进方案被提出以解决PDA算法的局限性。其中最为知名的当属Musichi 等人提出的集成概率数据关联滤波器(Integrated PDA Filter, IPDAF)[51],通过定义航迹存在概率,将航迹起始和消亡集成到数据关联问题中。而在技术与优化方面,Ni 等[52]利用粗糙集理论提出了基于粗糙集的概率数据关联(Rough Set-based PDA,RS-PDA)算法,有效减少了数据关联的复杂性和时间消耗,提升了跟踪结果的准确性。此外,Memon等[53]利用双向滤波器技术改进概率数据关联(Modified Smoothing Integrated PDA, MSIPDA),在杂波环境中显著提升目标状态估计的准确性和假目标识别性能。
在算法框架与理论方面,恽鹏等[54]基于变分贝叶斯方法改进概率数据关联算法(Variational Bayesian PDA, VB-PDA),采用多项分布模型提升状态估计的实时性和准确性。Petersen 等[55]提出了适用于李群的IPDAF,有效处理了在李群上定义的目标运动和测量问题,保持了轨迹的完整性和精确性。表4为PDA算法改进方案。
表4 PDA算法改进方案

文献Musichi [51]Ni[52]Memon[53]恽鹏[54]Petersen[55]算法要点集成PDA:IPDAF基于粗糙集JPDA (RS-PDA)双向滤波器改进JPDA (MSIPDA)变分贝叶斯的JPDA (VB-PDA)适用于李群的IPDAF优点解决航迹起始等问题,计算效率高复杂度降低,提升效率和准确性估计准确性和假目标识别性提高提升状态估计的实时性和准确性保持轨迹完整性和精确性缺点对粗糙集参数选择敏感算法实现复杂需要合理选择多项分布模型对李群的理解和应用要求高
3.2 联合概率数据关联算法
3.2.1 基本原理
对于多目标跟踪,如果各个目标的跟踪门不存在交叉重合的情况,可以直接使用PDA 算法对关联问题进行处理。然而当目标的跟踪门出现交叉重合的情况时,PDA 算法不再适合。JPDA 算法解决了PDA 算法在处理多目标情况时的局限性,它综合考虑了所有落入跟踪波门内的量测,并认为公共量测可能来源于多个不同的目标。为此,JPDA算法专为应对杂波环境下的多目标跟踪而设计。图15为JPDA算法流程图。
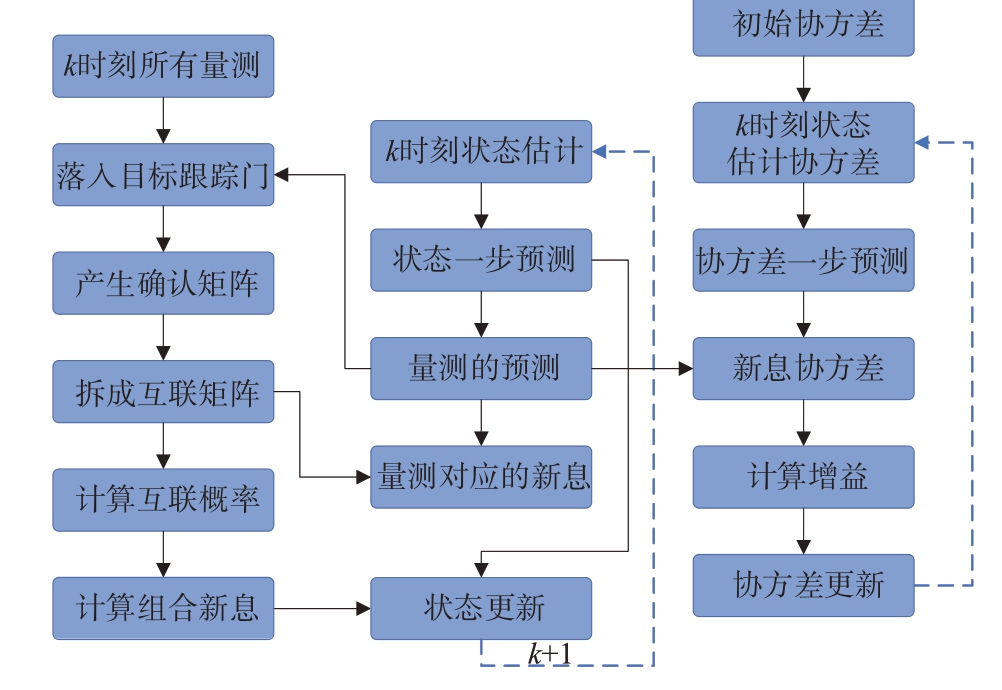
图15 JPDA算法流程图
JPDA 通过定义确认矩阵,描述跟踪门交叉区域中的目标及其候选量测之间的关联关系。确认矩阵表示为
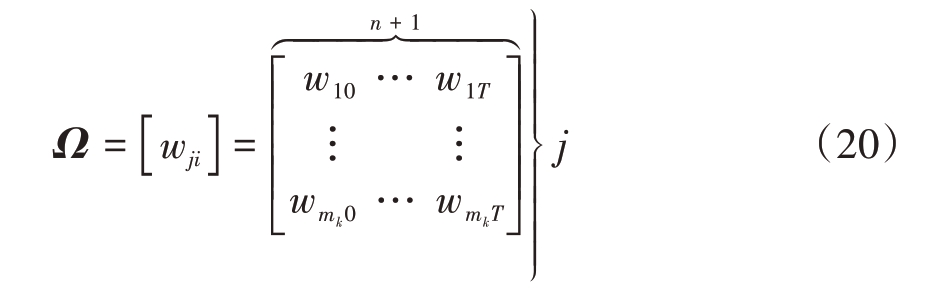
式中:i 为目标编号,i = 0,1,…,n,i = 0 表示杂波或虚警; j为量测序列编号, j = 1,2,…,mk;wji = 1表示第j个量测点迹落入目标i的跟踪门内,wji = 0表示第j 个量测点迹未落入目标i 的跟踪门内。所有候选回波均可能来自杂波或虚警,则有wj0 = 1, j =1,2,…,mk。
在得到确认矩阵之后,进一步枚举可能的目标或杂波与候选量测的关联情况,并用互联矩阵表示。这种关联情况定义为互联事件,定义ϑr( k)为第r 个互联事件。定义![]() 为每个互联事件r中候选量测和目标i的对应关系。基于下面两个假设来确定互联事件:
为每个互联事件r中候选量测和目标i的对应关系。基于下面两个假设来确定互联事件:
① 对于任一量测,其只能源于确认矩阵内的一个目标或虚警,即
② 对于任一目标,其最多只能产生一个量测,即
式中,量测互联指示τj[ϑr( k )]表示ϑr( k )是否存在与量测j 相关联的目标;目标检测指示δi[ϑr( k )]表示ϑr( k )中是否存在与目标i 相匹配的量测。第j个候选量测和目标i的概率,即互联概率为
式中,nk为互联事件的总数。k时刻互联事件ϑr( k)的后验概率:
式中,c为归一化常数。同时有
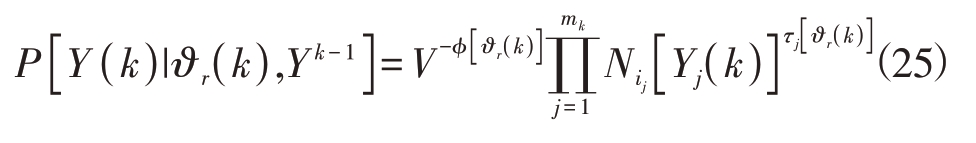
ϕ[ϑr( k )]为互联事件ϑr( k )中虚假观测的个数,
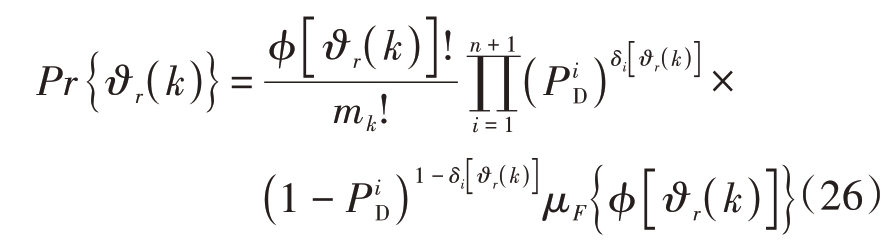
μF{ϕ[ϑr( k )]}为虚假量测概率质量函数,![]() 为目标i 的检测概率。带入式(27)和式(28)即可求出互联事件ϑr( k )的后验概率。具体形式如下:
为目标i 的检测概率。带入式(27)和式(28)即可求出互联事件ϑr( k )的后验概率。具体形式如下:
对于参数模型,其后验概率为
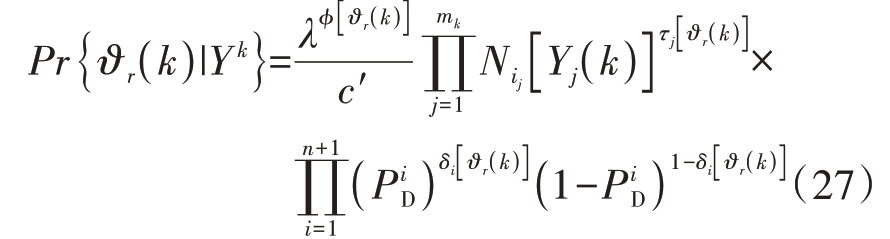
对于非参数模型,其后验概率为

式中,c′和c″为归一化常数。与概率数据关联算法类似,求出关联概率之后,即可对目标状态及协方差矩阵进行加权更新。
图16 为JPDA 算法场景图。k 时刻落入目标1跟踪门内的量测为y1( k ),落入目标2 跟踪门内的量测为y3( k ),y2( k )同时落入目标1 和目标2 的跟踪门内。通过对量测y1( k )和y3( k )分别计算关联概率β11( k )、β32( k ),以及对量测y2( k )计算关联概率β21( k )和β22( k ),然后根据每个量测的关联概率对每个目标的状态以及协方差矩阵进行更新。
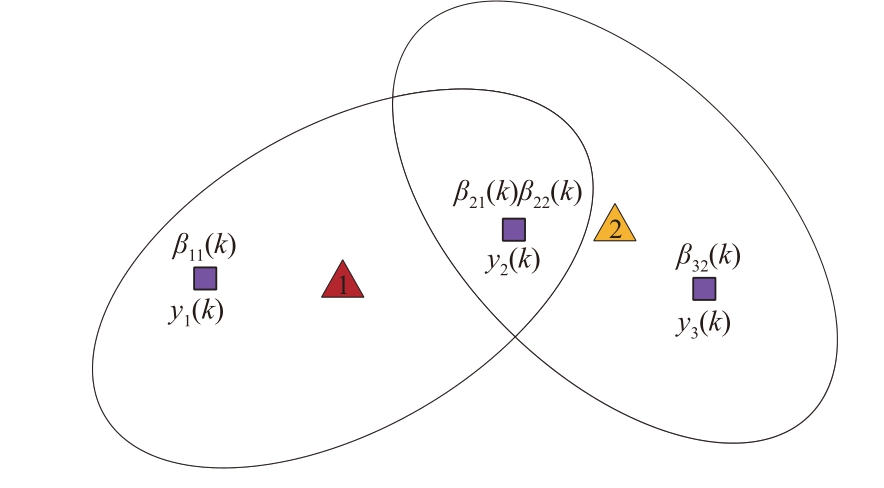
图16 JPDA算法场景图
JPDA算法是PDA算法的演进版本,不同于PDA算法,JPDA能够处理跟踪门交叉重叠情况,评估各个量测与目标的从属关系。如果目标的跟踪门不重叠,多目标关联问题简化为若干单目标问题。但当跟踪门重叠目标增多时,产生的互联事件数目指数增长,导致计算复杂度增加,限制了其工程应用。值得说明的是,早在1970-1972 年间,苏联科学家Achkasov[56]就基于随机流(Stochastic Flows)理论推导出了JPDA 的原型,远早于目前文献中广为人知的1983年Fortmann 和Bar-Shalom 等人的工作[20],详细的文献对比分析可参考文献[57]。
3.2.2 算法改进
JPDA 算法在处理大规模目标跟踪时,常会遇到计算复杂度高和实时性要求严格的问题。因此,研究人员一直在探索更高效、更精确的算法改进方案,以提高JPDA 的性能和实用性。其中一种经典有效的做法是可以单独对没有共同门限内量测的目标进行计算,对不同的量测和门限进行分组处理,即簇(Cluster)JPDA。以下介绍了一系列针对JPDA 的最新研究进展,涵盖了计算效率提升、跟踪精度和鲁棒性的改进,以及特定环境下的适应性提高等方面。
在计算效率和复杂度方面,Rezatofighi 等[58]通过将JPDA 的分配得分计算转化为一系列整数线性规划(Integer Linear Programming, ILP)问题,并采用m-best 算法来近似联合得分。刘昀晓等[59]结合NN 算法与JPDA,提出k近邻联合概率数据关联算法,降低联合事件数量,提高数据关联的效率。Lee 等[60]提出了基于马尔可夫链的联合积分概率数据关联(Markov Chain JIPDA, MCJIPDA)算法,通过生成目标群的马尔可夫链来近似多目标数据关联概率,显著降低了计算复杂度。Qu 等[61]提出基于强化学习的JPDA (Reinforcement Learning-based JPDA, RL-JPDA),通过动态调整策略参数,结合目标运动特性和量测分布,提高JPDA 的准确性。盛涛等[62]引入公共量测影响因子修正关联概率,从而解决密集杂波环境下组合爆炸的问题。
在精度与鲁棒性方面,Zhang 等[63]提出结合遮挡置信指示器和基于样本的JPDAF(Sample-based JPDA Filter, SJPDAF)方法,改善复杂反射和遮挡环境中的状态估计。Liang等[64]提出多目标跟踪滤波器柯西-施瓦茨集JPDA (Cauchy-Schwarz Set JPDA, CSSJPDA),通过优化后验高斯混合密度提高跟踪精度。Habtemariam 等[65]提出多检测JPDAF(Multiple Detection JPDA Filter, MD-JPDAF),采用量测到目标的多对一关联策略,提高状态估计精度。毕文豪等[66]提出在杂波环境下基于最大熵模糊聚类的联合概率数据关联算法(Maximum Entropy Fuzzy Clustering-based JPDA, MEFC-JPDA),通过调整量测修正因子和最大熵模糊聚类来优化关联概率矩阵,有效改善JPDA精度与实时性。
进一步在环境与特定情况适应性上,Zhou等[67]提出融合方向信息的神经联合概率数据关联(Neural JPDA, NJPDA)方法,高斯加权方法修正测量的似然函数,将目标运动的方向信息与距离信息进行融合,以计算数据关联概率。Kropfreiter 等[68]提出分布式多传感器联合概率数据关联(Integrated Probabilistic Data Association, IPDA)滤波器,从而解决去中心化传感网络中的多目标跟踪问题,通过近似关联分布的边际分布以简化计算过程。He等[69]通过利用随机Gibbs 抽样,通过事件发生来近似边缘关联概率,完成在传感器网络中适用的多目标跟踪JPDA算法。表5为JPDA算法改进方案。
表5 JPDA算法改进方案

文献Rezatofighi[58]刘昀晓[59]Lee[60]Qu[61]盛涛[62]Zhang[63]Liang[64]Habtemariam[65]毕文豪[66]Zhou[67]Kropfreiter[68]He[69]算法要点JPDA分配转化为ILP、m-best近似k近邻JPDA结合NN算法基于马尔可夫链的MCJIPDA算法基于强化学习的JPDA (RL-JPDA)公共量测影响因子修正关联概率结合遮挡置信指示器的SJPDAF CSSJPDA优化后验高斯混合密度MD-JPDAF采用多对一关联策略最大熵模糊聚类优化关联矩阵融合方向信息的NJPDA分布式多传感器IPDA滤波器随机Gibbs抽样的JPDA算法优点提高计算效率近似处理分配降低联合事件数量,提高效率显著降低计算复杂度动态调整策略参数,提高准确性解决密集杂波环境下的问题改善复杂反射和遮挡环境中的状态估计提高跟踪精度提高状态估计精度JPDA精度与实时性有效改善目标运动方向与距离信息融合去中心化传感网络中多目标跟踪适用传感器网络中的多目标跟踪缺点牺牲一些精确度对k的选择敏感近似误差强化学习训练需要大量数据对参数选择敏感需要有效的样本生成方法需要精确的后验概率模型在某些情况下可能引入误差需要调整的参数较多需要有效的方向信息提取需要合理的网络协同机制需要合理的抽样和事件处理
3.3 概率多假设跟踪算法
3.3.1 基本原理
在上述的确定性关联算法中,如GNN 算法和MHT 算法,每个量测与目标一一对应的假设虽然在某些情况下可以简化问题的处理,但也会导致算法在处理大规模数据时的计算量急剧增长。而PMHT 算法修正了这种假设,如图17 所示,传统的关联算法如PDA、MHT 等算法的假设中,每个量测只能和一个目标关联。而PMHT 算法允许一个目标产生多个量测数据,同时每个量测数据只能来源于一个目标,其核心在于将量测与目标的关联过程视为独立的概率事件,从而得到在极大似然条件下的最优跟踪。
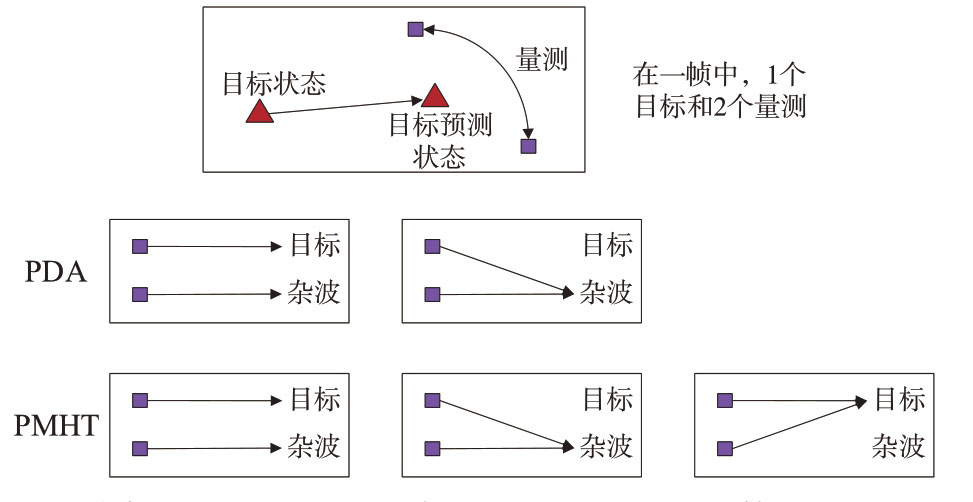
图17 传统跟踪算法和PMHT量测模型的区别
PMHT 算法是一种基于期望最大化(EM)方法的多目标跟踪批处理算法。通过EM 算法的迭代计算,PMHT 可以得到目标状态的最大后验(或似然)估计。这种方法摒弃了传统的门控跟踪思想,采用更为优化的算法框架,因此被视为是一种最优化算法。在PMHT中,目标与测量之间的关联是独立的,其计算复杂度随目标数量线性增加。
EM算法的基本思想包含两个步骤:
1) 期望步骤(E-step):基于当前参数估计值,计算对隐变量的条件期望。
2) 最大化步骤(M-step):更新参数,以最大化似然函数的期望值。
通过这种方式,EM 算法可以在缺少完整数据的情况下有效地求解最大似然估计(MLE)或最大后验估计(MAP)。
定义X 表示需要求最大后验估计的随机变量集合,Y 表示可观测的随机变量集合即量测,K 表示不可观测的随机变量集合。EM 算法的目的是在无法直接观测K的情况下,通过迭代优化的方式估计X的最大后验,其可表示为
由于完备数据集( Y, K )未知,无法直接进行MAP估计求解。定义对数似然函数:
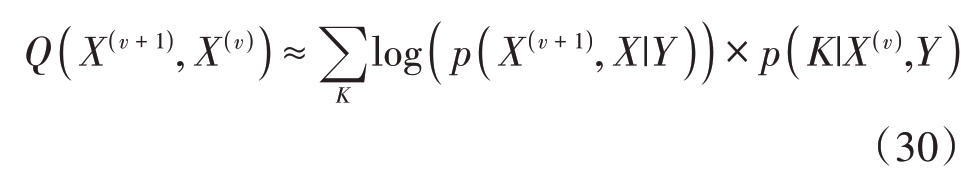
式中,v 表示迭代次数。通过多次迭代得到最大化的Q,从而求解X 的后验期望,第v + 1 次迭代的后验期望为
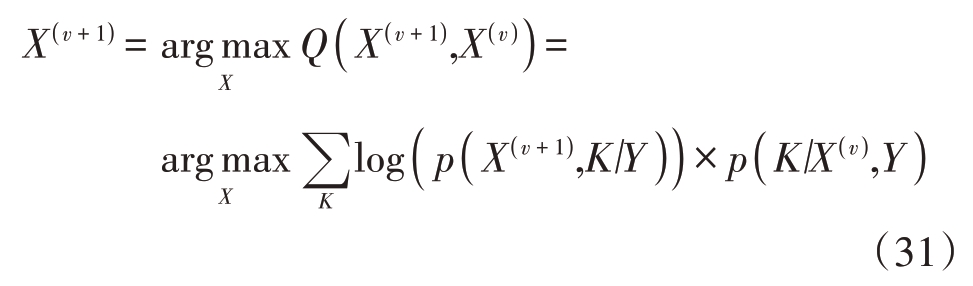
概率密度函数p(X(v + 1), K|Y )表示联合K 的后验概率,由条件概率公式得
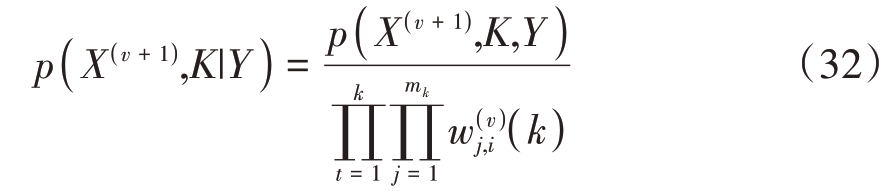
式中,t表示时间,mk表示k时刻的量测数量,![]() 表示第j个量测来源于目标i的概率:
表示第j个量测来源于目标i的概率:
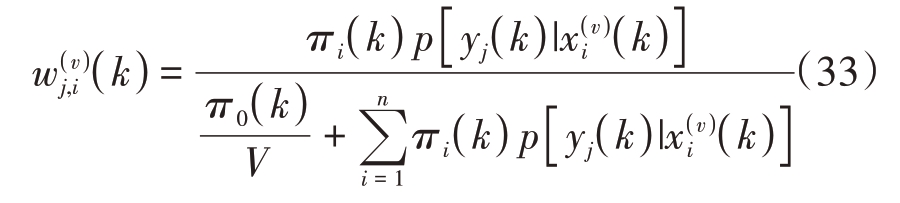
式中,V 表示量测空间,πi( k )表示k 时刻量测来源于目标i 的先验概率,PMHT 同时需要计算目标的综合量测![]() 和协方差
和协方差![]() :
:
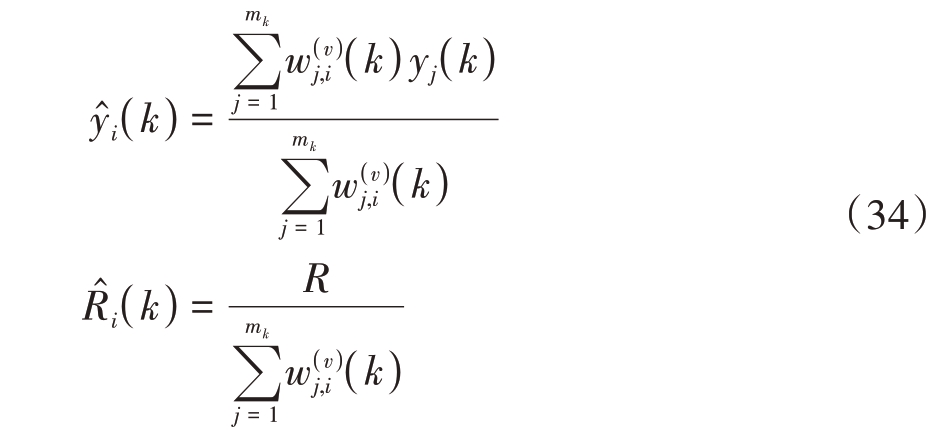
之后再通过Kalman滤波器即可完成对目标的跟踪。
3.3.2 算法改进
标准的概率多假设跟踪(PMHT)算法在多目标跟踪领域广泛应用,其核心优势在于能够处理多目标和杂波环境下的数据关联问题。然而,这种算法在处理复杂杂波场景和干扰情况下存在局限性,尤其是当实际量测可能来源于非目标干扰时,这会导致跟踪航迹的丢失。此外,PMHT 算法对初始值的依赖性强,初始值设置偏差过大会显著降低跟踪性能。
为应对这些挑战,学术界提出了多种改进方案。Rago等[70]引入Homothetic PMHT 算法,其假设每个目标有多个量测模型,通过将同均值不同量测噪声的多量测模型引入PMHT 算法来提高航迹的稳定性。而Homothetic PMHT 的引入同时激发了许多PMHT 的改进,如Multi-Frame PMHT[71]、Spirograph PMHT[72]和自适应Homothetic PMHT[73]等。李晓花等[74]结合确定性退火技术与HPMHT算法提出DA-HPMHT 算法,通过借鉴退火过程减小了对初值的敏感。
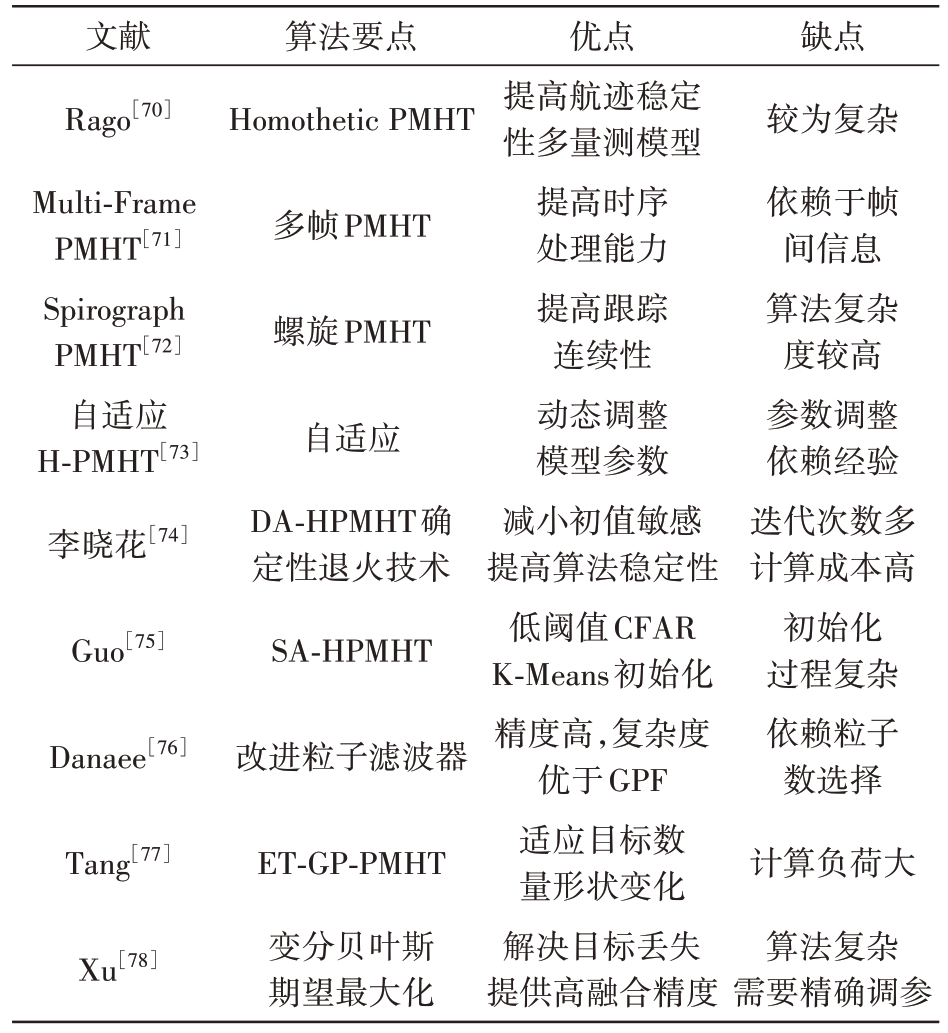
进一步的研究中,Guo等[75]提出了一种状态增强直方图概率多假设跟踪(SA-HPMHT)算法,利用低阈值恒虚警率(Constant False Alarm Rate, CFAR)检测器和K-Means来初始化轨迹,通过状态增强和M/N 逻辑技术改进目标跟踪的精度。Danaee 等[76]提出了一种改进的Gibbs粒子滤波器(Modified Gibbs Particle Filter, MGPF)用于PMHT 算法中的数据关联,其在估计精度及计算复杂度上均优于传统Gibbs粒子滤波器(Gibbs Particle Filter, GPF)。Tang等[77]针对杂波漏检问题,提出一种扩展目标高斯过程PMHT,该方法通过动态泊松测量率来适应目标数量和形状的变化,有效地跟踪点目标和扩展目标。Xu等[78]采用变分贝叶斯期望最大化(Variational Bayesian Expectation Maximization, VBEM)算法,提出了变分概率多假设跟踪(Variational PMHT,VPMHT),能有效解决目标轨迹丢失的问题。表6为PMHT算法改进方案。
表6 PMHT算法改进方案
文献Rago[70]Multi-Frame PMHT[71]Spirograph PMHT[72]自适应H-PMHT[73]李晓花[74]Guo[75]Danaee[76]Tang[77]Xu[78]算法要点Homothetic PMHT多帧PMHT螺旋PMHT自适应DA-HPMHT确定性退火技术SA-HPMHT改进粒子滤波器ET-GP-PMHT变分贝叶斯期望最大化优点提高航迹稳定性多量测模型提高时序处理能力提高跟踪连续性动态调整模型参数减小初值敏感提高算法稳定性低阈值CFAR K-Means初始化精度高,复杂度优于GPF适应目标数量形状变化解决目标丢失提供高融合精度缺点较为复杂依赖于帧间信息算法复杂度较高参数调整依赖经验迭代次数多计算成本高初始化过程复杂依赖粒子数选择计算负荷大算法复杂需要精确调参
4 基于优化学习的关联方法
基于上述经典的点集数据关联方法来看,数据关联本质上是一个优化问题,除了通过解析的方法求得确定性最优解或概率性最优解之外,还可以设计一些优化学习算法求解,从而弱化对于问题模型和统计学先验信息(如虚警率、漏检率、噪声方差等)的依赖,并可以挖掘数据(特别是视觉)深层次的关联关系[79]。这类算法往往不以特定模型下的解析最优关联为目标,而重在通过关联优化逼近或者对样本数据的深度学习,且关联任务往往与目标的检测识别等结合,更能有效应对数据之间存在重叠和不明确的相关性等。一种最典型的应用场景是通过分布式多传感器信息关联融合,实现对目标信息和态势更精准、更稳健、更高效的把握和推理,扩大感知范围、提升感知精度、增强感知可靠性。针对该类问题,一类有效的关联方法是聚类(Clustering),可以有效应对未知杂波率、虚警率等甚至未知数目目标,相比传统的关联方法提高了算法的普适性和鲁棒性,可参见笔者在多传感器多目标跟踪研究方向的一些聚类算法初探[80-83]及所给出的相关参考文献。本文对于这类偏启发式聚类算法的数据关联研究不做过多介绍,以下重点介绍在视觉数据领域基于优化学习的数据关联方法研究进展。总而言之,这方面的研究繁杂众多,本节仅做一些初探分析;已有部分综述研究可参见文献[5]和文献[6]等,其对数据关联方法的关注略显不足。
4.1 视觉数据关联难点
相比于雷达目标信息,视觉传感器的视觉图像往往包含更为丰富的目标特征和属性信息如目标的颜色、纹理和形状,可为目标识别跟踪提供更丰富的信息,但同时也为数据关联处理带来更多挑战。如图18 所示,视觉多目标跟踪的一般框架包括4个主要步骤:目标检测、特征提取和预测、相似度计算和数据关联[84]。目标检测阶段利用深度学习方法如Faster Regions CNN[85]、YOLO[86]等或者传统信号处理技术来识别发现所有感兴趣的目标。特征提取和预测涉及利用算法提取每个目标的外观、形状、运动及其他传感器特征,常通过卷积神经网络[87](CNN)等从图像中提取具有区分度的特征,颜色直方图、局部二值模式以及方向梯度直方图等传统方法也广泛应用于特征提取,基于这些特征和目标的动力学模型来预测目标在未来帧中的状态(跟踪器的预测步),相似度计算使用如余弦相似度或欧氏距离等方法来衡量不同目标之间的相似性[88]。数据关联步骤将根据相似度计算的结果,将当前帧的量测与之前帧的跟踪目标进行匹配,以维持每个目标并跟踪其运动轨迹[6]。
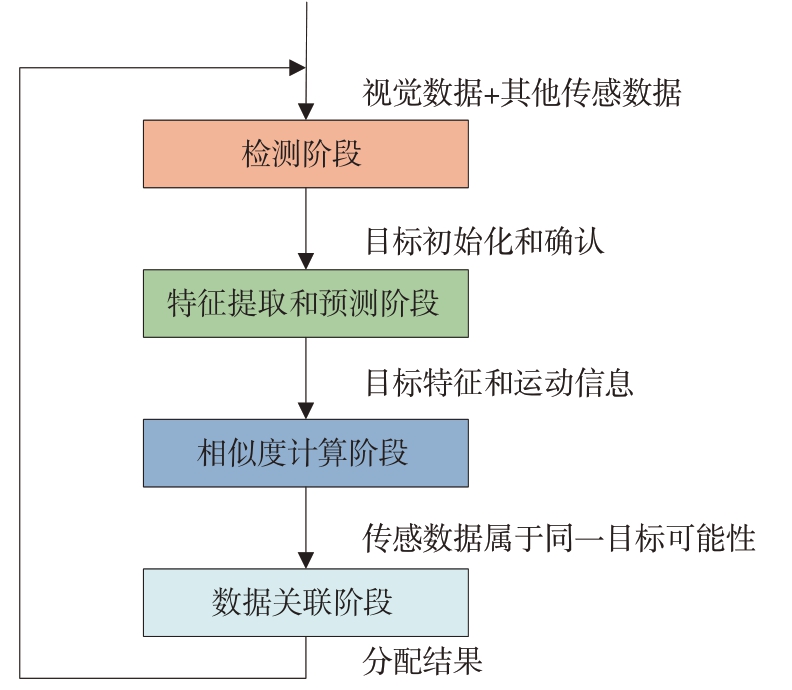
图18 视觉多目标跟踪的一般框架
面向视觉跟踪的数据关联的特殊性主要表现在与目标外观检测、特征提取与跟踪任务的紧密结合上[89-91],面临如下挑战:1) 目标遮挡与交互;2) 弱小目标难检测;3) 目标外观相似性(目标形变、光照变化);4) 目标身份确认和维持;5) 轨迹起始与终止等[92]。另外,为提高数据关联准确性,视觉跟踪引入了多模态数据融合技术。通过结合不同传感器(如红外、光学摄像头等)的异构数据,可增加信息维度,增强了目标检测和数据关联的正确性和鲁棒性,提升了跟踪的精度。这方面的研究方心未艾,且仍有不少难题待解决。
4.2 特征学习数据关联方法
在深度学习出现之前,数据特征学习方法主要包括判别模型和度量学习两种。Li 等[93]结合了RankBoost 和AdaBoost 提出一种新的数据驱动学习方法HybridBoost,通过组合多个弱学习器形成强学习器,并通过离线训练学习正确的关联。Bae等[94]使用增量线性判别分析(Incremental Linear Discriminant Analysis, ILDA)来改善基于外观的模型在线学习,ILDA 在识别精度和计算效率上优于传统Boosting。Kuo 等[95]采用层次分解方法,并结合在线应用AdaBoost 和匈牙利算法来学习成本矩阵。结构化支持向量机[96-97]通过结构化SVM 方法来学习复杂图形模型中的关联成本,虽然这些方法通常限于线性成本函数,但提供了一种系统化处理数据关联问题的有效工具。而其他度量学习研究[98-100],在多目标跟踪中学习外观亲和模型的特征向量间距离,优化识别过程中的关联成本,使得同一轨迹片段内的特征向量间距离较小,而不同轨迹片段间距离较大。
针对模糊逻辑及决策,Zhang等[101]基于Takagi-Sugeno 直觉模糊模型的多目标数据关联算法,通过构建模型和相似度比较提高关联精度。
在概率和统计方法上,Jeon 等[102]基于贝叶斯混合高斯过程的数据关联方法,通过期望最大化(EM)算法提高数据关联的精度,Lan 等[103]利用信念传播和平均场近似处理目标运动状态估计与目标可见性状态决策的耦合问题,以有效解决目标跟踪问题。
在优化及分类方法上,He 等[104]利用学习图匹配的方法,将数据关联转变为图匹配问题,通过连续二次规划和KKT 条件实现端到端的关联。刘伟强等[105]提出主动雷达信息与被动侦察信息融合的数据关联方法,成功提高了态势感知效率并消除欺骗干扰和假目标。Bu 等[106]通过统一的贝叶斯框架,将联合数据关联和偏差补偿问题转换为传统的数据关联和滤波问题,这一方法无需在数据关联和偏差估计之间进行迭代优化,其中数据关联采用了拍卖算法。
在神经网络中,目标与量测的关联问题可分为多个分类的子问题,如图19 表示其匹配过程。输入包括S 和Y( k ),分别表示目标i 的4 个历史状态以及当前时刻k 的所有量测。网络为每个目标预测量测分配,输出匹配向量w,表示目标与量测的匹配概率,未检测到的目标关联到虚拟量测,如图中紫色目标示例。Meneses 等[107]通过反向传播算法训练的多层感知器(Multilayer Perceptron, MLP)神经网络,实时计算关联成本,实现关联置信度学习。Liu 等[108]研究了基于长短期记忆网络(Long Short-Term Memory Network, LSTM) 的模型,近似解决NP-Hard(Non-deterministic Polynomial-time Hard)数据关联问题。Lee等[109]提出使用深度神经网络来解决线性和问题(Linear Sum Assignment Problem, LSAP),但仅适用于分配问题受到1-1 约束的情况。其他网络同时也被用于解决数据关联问题,如Sun 等[110]使用的深度亲和网络(Deep Affinity Network,DAN),通过使用真实的关联矩阵作为监督来训练,预测最优的线性分配。Xu 等[111]提出深度匈牙利网络(Deep Hungarian Network,DHN),在量测和目标之间的成本矩阵中预测最优线性分配。Zhang 等[112]利用JPDA-LSTM 网络来预测目标的运动参数,通过RNN 建立一个目标存在概率模型来评估跟踪的质量,采用网络实现JPDA功能。李文娜等[113]提出了一种基于Transformer网络的数据关联算法,求解多个目标与多个量测之间的匹配问题。Chu 等[114]通过特征关联矩阵网络(Feature Affinity Matrix Network)直接预测MDAP(Multi-Dimensional Assignment Problem)的分配张量,使用滑动窗口构建假设轨迹集,由亲和网络输出MDAP 的亲和张量。然后通过一个可微分的行/列张量归一化层直接输出分配。总的来说,鉴于视觉信息的丰富性和复杂性,在设计更深层次的数据关联方法以及将数据关联与目标特征的提取识别与态势分析结合方面仍有很多未解难题。表7为基于学习与网络的关联跟踪方法。
表7 基于学习与网络的关联跟踪方法

文献Li[93]Bae[94]Kuo[95]Structured SVM[96-97]Metric learning[98-100]Zhang[101]Jeon[102]Lan[103]He[104]刘伟强[105]Bu[106]Meneses[107]Liu[108]Lee[109]Sun[110]Xu[111]Zhang[112]李文娜[113]Chu[114]算法要点HybridBoost ILDA层次分解方法构化SVM学习图模型关联成本学习外观亲和模型特征向量距离Takagi-Sugeno模型关联贝叶斯混合高斯过程的关联信念传播和平均场近似状态关联任务转化为图匹配主动雷达与被动侦察融合关联联合数据关联和偏差补偿反向传播算法训练MLP计算关联成本LSTM解决NP-Hard问题神经网络解决LSAP关联矩阵训练预测最优分配预测最优线性分配JPDA-LSTM预测运动参数Transformer关联网络输出张量归一化输出分配优点增强模型整体性能和准确性识别精度和计算效率提高适用于动态变化数据适用学习图形模型关联成本优化了识别中的关联成本提高关联精度模型灵活通过EM算法提高精度解决目标跟踪问题端到端关联连续二次规划提高态势感知效率能够数据关联同时补偿系统时间偏差实时计算关联成本,提高性能能处理长期依赖问题高效专注于分配问题准确学习数据间关联性效率和准确性提高适用于时间序列预测高效处理长距离依赖提高复杂场景和动态环境适应性缺点需要较多计算资源和时间非线性数据效果下降依赖特定场景下成本矩阵设定处理非线性关系时效果不佳依赖距离度量选择和参数设置计算复杂度较高对初始化敏感需要合理的近似方法复杂度高大量训练数据复杂度高特征提取难算法复杂度高需要充分训练网络以适应各种情况参数多易过拟合仅适用于1-1约束的情况大量数据训练耗时依赖数据质量和前处理需要大量数据计算资源消耗大计算资源增加
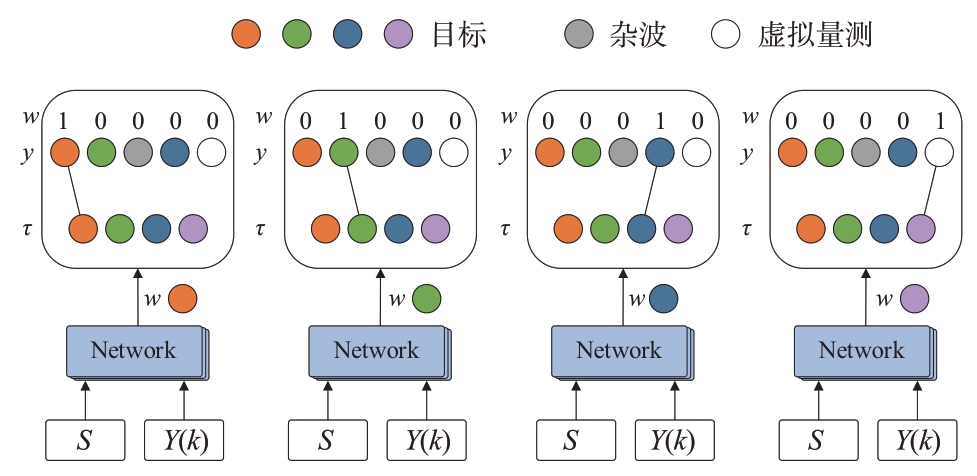
图19 神经网络下目标与量测匹配关联示意图
5 结束语
本文围绕多目标跟踪应用,梳理了数据关联问题基本内容和主要解决思路,将数据关联问题分为确定性关联、概率性关联以及基于优化学习的关联,系统阐述和对比了一些典型算法及其扩展方法的基本原理、各自适用条件、优缺点和相互关联性。伴随基础算力、智能算法以及各类应用需求的不断发展,各领域中对目标跟踪与数据关联的要求也不断提高。与此同时,面对复杂对抗场景下统计模型未知的杂波、虚警、干扰和复杂的目标交互等挑战,数据关联与信息融合处理研究仍有很多亟待解决的难题,多传感器多目标同时跟踪能力仍是多源信息融合领域的技术瓶颈。
传感与通信技术、信息获取与处理技术、人工智能与计算机技术的快速发展为多目标跟踪与数据关联的发展注入新的动力,未来目标跟踪与数据关联将在理论框架、模型、算法实现与技术系统等各个层面持续不断突破。以笔者敝见,以下2个研究方向值得关注:
1) 海量数据关联网络化
① 分布式数据关联:结合分布式系统需求,开发分布式算法实时关联融合、处理分析传感器收集的数据,以减少延迟并提高系统的可扩展性和健壮性。
② 高维深层关联融合:有效整合不同领域和来源的“异构、异质、异步”数据,挖掘数据更高维度更深层次的信息,从而提升关联的精确度和系统的通用性。
③ 隐私保护与深度学习:如探索如何在确保数据隐私和安全的基础上,利用复杂的神经网络模型来提高关联的准确性和适应复杂环境海量的能力。
2) 数据关联与信息处理的联合优化
① 联合学习策略:通过多任务联合优化和学习框架,整合目标检测跟踪、态势感知和数据关联步骤。增强系统对动态环境的适应性,实现任务模块一体化系统设计。
② 增强反馈机制:引入实时反馈与在线自评估机制,实现在线动态调整关联策略,预测并适应目标行为的突变,自适应调整阈值或更新特征提取算法,以优化整体性能。
③ 模型数据双驱动:结合统计模型的突出可解释性和数据学习的自适应性和鲁棒性,基于实际数据关联任务特殊性,最大化结合模型和数据两方面优势。
[1] VO B, MALLICK M, BAR-SHALOM Y, et al. Multitarget Tracking[J]. Wiley Encyclopedia of Electrical and Electronics Engineering, 2015(9):1-15.
[2] JAVADI S H, FARINA A. Radar Networks: A Review of Features and Challenges[J]. Information Fusion, 2020,61:48-55.
[3] 李天成,范红旗,孙树栋.粒子滤波理论、方法及其在多目标跟踪中的应用[J].自动化学报,2015,41(12):1981-2002.
[4] 何友,修建娟,刘瑜,等.雷达数据处理及应用[M].4版.北京:电子工业出版社,2022.
[5] RAKAI L, SONG H, SUN S, et al. Data Association in Multiple Object Tracking: A Survey of Recent Techniques[J]. Expert Systems with Applications, 2022, 192:116300.
[6] 龚轩,乐孜纯,王慧,等.多目标跟踪中的数据关联技术综述[J].计算机科学,2020,47(10):136-144.
[7] MAHLER R P S. Advances in Statistical Multisource-Multitarget Information Fusion[M]. Boston: Artech House,2014.
[8] MAHLER R P S. Multitarget Bayes Filtering via First-Order Multitarget Moments[J]. IEEE Trans on Aerospace and Electronic systems, 2003, 39(4):1152-1178.
[9] VO B N, VO B T, CANTONI A. The Cardinality Balanced Multitarget Multi-Bernoulli Filter and its Implementations[J].IEEE Trans on Signal Processing, 2009, 57(2):409-423.
[10] LI Tiancheng, WANG Xiaoxu, LIANG Yan, et al. On Arithmetic Average Fusion and its Application for Distributed Multi-Bernoulli Multitarget Tracking[J]. IEEE Trans on Signal Processing, 2020, 68:2883-2896.
[11] VO B T, VO B N. Labeled Random Finite Sets and Multi-Object Conjugate Priors [J]. IEEE Trans on Signal Processing, 2013, 61(13):3460-3475.
[12] VO B N, VO B T. A Multi-Scan Labeled Random Finite Set Model for Multi-Object State Estimation [J]. IEEE Trans on Signal Processing, 2019, 67(19):4948-4963.
[13] LI Tiancheng. Arithmetic Average Density Fusion-Part II: Unified Derivation for Unlabeled and Labeled RFS Fusion[J].IEEE Trans on Aerospace and Electronic Systems, 2024, 60(3):3255-3268.
[14] SINGER R, SEA R. New Results in Optimizing Surveillance System Tracking and Data Correlation Performance in Dense Multitarget Environments[J]. IEEE Trans on Automatic Control, 1973, 18(6):571-582.
[15] SONG T L, LEE D G, RYU J. A Probabilistic Nearest Neighbor Filter Algorithm for Tracking in a Clutter Environment[J]. Signal Processing, 2005, 85(10):2044-2053.
[16] FUKUNAGA K, FLICK T E. An Optimal Global Nearest Neighbor Metric[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 1984, 6(3):314-318.
[17] BLACKMAN S S. Multiple Hypothesis Tracking for Multiple Target Tracking[J]. IEEE Aerospace and Electronic Systems Magazine, 2004, 19(1):5-18.
[18] REID D. An Algorithm for Tracking Multiple Targets[J].IEEE Trans on Automatic Control, 1979, 24(6):843-854.
[19] BAR-SHALOM Y, TSE E. Tracking in a Cluttered Environment with Probabilistic Data Association[J]. Automatica, 1975, 11(5):451-460.
[20] FORTMANN T, BAR-SHALOM Y, SCHEFFE M. Sonar Tracking of Multiple Targets Using Joint Probabilistic Data Association[J]. IEEE Journal of Oceanic Engineering, 1983, 8(3):173-184.
[21] COLEGROVE S B, DAVIS A W, AYLIFFE J K. Track Initiation and Nearest Neighbours Incorporated Into Probabilistic Data Association[J]. Journal of Electrical and Electronics Engineers, Australia, 1986, 6(3):191-198.
[22] CHANG K C,BAR-SHALOM Y. Joint Probabilistic Data Association for Multitarget Tracking with Possibly Unresolved Measurements and Maneuvers[J]. IEEE Trans on Automatic Control, 1984, 29(7):585-594.
[23] STREIT R L, LUGINBUHL T E. Maximum Likelihood Method for Probabilistic Multihypothesis Tracking[C]//Signal and Data Processing of Small Targets, Orlando,FL, USA: SPIE, 1994:394-405.
[24] 潘泉.多源信息融合理论及应用[M].北京:清华大学出版社,2013.
[25] 王晓君,裴福俊,刘红云.一种改进马氏距离的最近邻数据关联算法[J].导航定位学报,2015,3(4):50-56.
[26] LI Yuan, PAN Dinghai, ZHANG Mengmeng, et al. Novel Nearest-Neighbor Data Association Algorithm with an Adaptive Threshold[C]// 2022 3rd International Conference on Big Data, Artificial Intelligence and Internet of Things Engineering, Xi’an China: IEEE, 2022:669-673.
[27] 李可欣,郭健,王宇君,等.基于SAR 和AIS 的角度最近邻数据关联方法[J].地球信息科学学报,2023,25(1):131-141.
[28] LI Tiancheng, CORCHADO J M, SUN S, et al. Multi-EAP: Extended EAP for Multi-Estimate Extraction for SMC-PHD Filter[J]. Chinese Journal of Aeronautics,2017, 30(1):368-379.
[29] KUHN H W. The Hungarian Method for the Assignment Problem[J]. Naval Research Logistics Quarterly, 1955, 2(1-2):83-97.
[30] BERTSEKAS D P. An Auction Algorithm for Shortest Paths[J]. SIAM Journal on Optimization, 1991, 1(4):425-447.
[31] MURTY K G. Letter to the Editor —An Algorithm for Ranking all the Assignments in Order of Increasing Cost[J]. Operations Research, 1968, 16(3):682-687.
[32] ALLODI M, BROGGI A, GIAQUINTO D, et al. Machine Learning in Tracking Associations with Stereo Vision and Lidar Observations for an Autonomous Vehicle[C]//2016 IEEE Intelligent Vehicles Symposium, Gotenburg,Sweden: IEEE, 2016:648-653.
[33] 王宁,李立刚,戴永寿,等.一种改进全局最近邻关联的无人船双雷达目标跟踪算法[J].舰船科学技术,2022,44(22):58-62.
[34] 刘全仲,李良群.基于带约束可能性聚类的多目标跟踪新算法[J].火力与指挥控制,2023,48(6):14-18.
[35] RIAHI D, BILODEAU G A. Multiple Object Tracking Based on Sparse Generative Appearance Modeling[C]//2015 IEEE International Conference on Image Processing, Quebec City Canada: IEEE, 2015:4017-4021.
[36] WU Huiling, LI Weihai. Robust Online Multi-Object Tracking Based on KCF Trackers and Reassignment[C]// 2016 IEEE Global Conference on Signal and Information Processing, Washington, D.C. ,USA:IEEE, 2016:124-128.
[37] PIAO Songlin, SUTJARITVORAKUL T, BERNS K. Compact Data Association in Multiple Object Tracking: Pedestrian Tracking on Mobile Vehicle as Case Study[J].IFAC Symposium on Intelligent Autonomous Vehicles,2016, 49(15):175-180.
[38] SHI Mengzhao, LING Qiang, YU Zhaohua, et al. Association Using Modified Global Nearest Neighbor in the Presence of Bias[C]//Proceedings of the 32nd Chinese Control Conference, Xi′an, China:IEEE, 2013:4688-4691.
[39] LI Kaishuo, CHEN Xiaozhong, XU Tao, et al. Research on Monitoring Technology Based on the Fusion of 4D Millimeter Wave Radar and Machine Vision[C]// Proceedings of International Conference on Image, Vision and Intelligent Systems 2023, Singapore: Springer Nature, 2024:379-388.
[40] KURIEN T. Issues in the Design of Practical Multitarget Tracking Algorithms[J]. Multitarget-Multisensor Tracking: Advanced Applications, 1990:43-84.
[41] SVENSSON D. Target Tracking in Complex Scenarios[D]. Sweden: Chalmers Tekniska Hogskola, 2010.
[42] SATHYAN T, SINHA A, KIRUBARAJAN T, et al. MDABased Data Association with Prior Track Information for Passive Multitarget Tracking[J]. IEEE Trans on Aerospace and Electronic Systems, 2011, 47(1):539-556.
[43] THARMARASA R, SUTHARSAN S, KIRUBARAJAN T, et al. Multiframe Assignment Tracker for MSTWG Data[C]// 2009 12th International Conference on Information Fusion, Seattle, WA, USA: IEEE, 2009:1837-1844.
[44] KOJIMA M, KAMEDA H, TSUJIMICHI S, et al. A Study of Target Tracking Using Track-Oriented Multiple Hypothesis Tracking[C]// Proceedings of the 37th SICE Annual Conference, Chiba, Japan: IEEE, 1998:933-938.
[45] THOMAIDIS G, TSOGAS M, LYTRIVIS P, et al. Multiple Hypothesis Tracking for Data Association in Vehicular Networks[J]. Information Fusion, 2013, 14(4):374-383.
[46] KOSUGE Y, KOJIMA M, TSUJIMICHI S. Multiple Manoeuvre Model Track-Oriented MHT (Multiple Hypothesis Tracking)[C]// Proceedings of the 38th SICE Annual Conference, Morioka Japan: IEEE, 1999:1129-1134.
[47] HE Shaoming, SHIN H S, TSOURDOS A. Track-Oriented Multiple Hypothesis Tracking Based on Tabu Search and Gibbs Sampling[J]. IEEE Sensors Journal, 2018, 18(1):328-339.
[48] SHENG Hao, CHEN Jiahui, ZHANG Yang, et al. Iterative Multiple Hypothesis Tracking with Tracklet-Level Association[J]. IEEE Trans on Circuits and Systems for Video Technology, 2019, 29(12):3660-3672.
[49] 刘建锋.面向量测的m-最优N 扫描多假设跟踪方法[J].计算机应用研究,2021,38(1):282-286.
[50] XING Wenge, XIE Dingbao, WANG Jin. GNN-Guided Track Branch Formation for Multiple Hypothesis Tracking[C]// 2022 4th International Conference on Communications, Information System and Computer Engineering, Shenzhen, China:IEEE, 2022:57-60.
[51] MUSICHI D, EVANS R, STANKOVIC S. Integrated Probabilistic Data Association [J]. IEEE Trans on Automatic Control, 1994, 39(6):1237-1241.
[52] NI Longqiang, GAO Shesheng, FENG Pengcheng, et al.Rough Sets Probabilistic Data Association Algorithm and its Application in Multi-Target Tracking[J]. Defence Technology, 2013, 9(4):208-216.
[53] MEMON S A, SONG T L, MEMON K H, et al. Modified Smoothing Data Association for Target Tracking in Clutter[J]. Expert Systems with Applications, 2020, 141:112969.
[54] 恽鹏,吴盘龙,李星秀,等.变分贝叶斯概率数据关联算法[J].自动化学报,2022,48(10):2486-2495.
[55] PETERSEN M E, BEARD R W. The Integrated Probabilistic Data Association Filter Adapted to Lie Groups[J].IEEE Trans on Aerospace and Electronic Systems, 2023,59(3):2266-2285.
[56] ACHKASOV Y S. Finding Trajectories by a Posteriori Analysis of Flows[J]. Engineering Cybernetics, 1971, 9(5):919-926.
[57] O’ROURKE S M. Closing the Ivory Validation Gates: a Historical Analysis of Achkasov’s Data Association Filters[C]// 2023 26th International Conference on Information Fusion, Charleston, SC, USA:IEEE, 2023:1-8.
[58] REZATOFIGHI S H, MILAN A, ZHANG Zhen, et al.Joint Probabilistic Data Association Revisited[C]// 2015 IEEE International Conference on Computer Vision, Santiago, Chile:IEEE, 2015:3047-3055.
[59] 刘昀晓,王东峰,曹林,等.基于车辆数据的k 近邻联合概率数据关联算法[J].电讯技术,2020,60(4):448-454.
[60] LEE E, ZHANG Qiang, SONG T. Markov Chain Realization of Joint Integrated Probabilistic Data Association[J]. Sensors, 2017, 17(12):2865.
[61] QU Chengzhi, ZHANG Yan, ZHANG Xin, et al. Reinforcement Learning-Based Data Association for Multiple Target Tracking in Clutter[J]. Sensors, 2020, 20(22):6595.
[62] 盛涛,夏海宝,杨永建,等.密集杂波环境下的简化JPDA多目标跟踪算法[J].信号处理,2020,36(8):1280-1287.
[63] ZHANG Tinghao,TANG Chiwei. Multiple-Target Tracking on Mixed Images with Reflections and Occlusions[J]. Journal of Visual Communication and Image Representation, 2018, 52:45-57.
[64] LIANG Shuang, ZHU Yun, GONG Maoguo, et al. Cauchy-Schwarz Divergence-Based Set Joint Probabilistic Data Association Filter for Tracking Multiple Objects in Cluttered Environment[J]. IEEE Trans on Geoscience and Remote Sensing, 2024, 62:1-15.
[65] HABTEMARIAM B, THARMARASA R, THAYAPARAN T, et al. A Multiple-Detection Joint Probabilistic Data Association Filter[J]. IEEE Journal of Selected Topics in Signal Processing, 2013, 7(3):461-471.
[66] 毕文豪,周杰,张安,等.杂波环境下基于最大熵模糊聚类的JPDA 算法[J].系统工程与电子技术,2023,45(7):1920-1927.
[67] ZHOU Yulong, FANG Dan, LI Jianchao, et al. Research on Multi-Target Data Association of the Infrared Fish-Eye Warning System[J]. Heliyon, 2023, 9(12):e22628.
[68] KROPFREITER T, MEYER F, HLAWATSCH F. A Distributed Joint Integrated Probabilistic Data Association(JIPDA) Filter with Soft Object Association[C]//2024 IEEE International Conference on Acoustics, Speech and Signal Processing, Seoul Korea(South): IEEE, 2024:12906-12910.
[69] HE Shaomin, SHIN H S, TSOURDOS A. Distributed Multiple Model Joint Probabilistic Data Association with Gibbs Sampling-Aided Implementation[J]. Information Fusion, 2020, 64:20-31.
[70] RAGO C, WILLETT P, STREIT R. A Comparison of the JPDAF and PMHT Tracking Algorithms[C]// 1995 International Conference on Acoustics, Speech, and Signal Processing, Detroit, MI, USA:IEEE, 1995:3571-3574.
[71] WILLETT P K, RUAN Y, STREIT R L. PMHT for Maneuvering Targets[C]// Conference on Signal and Data Processing of Small Targets, Orlando, FL ,USA:SPIE,1998:416-427.
[72] WILLETT P, RUAN Y, STREIT R. PMHT: Problems and Some Solutions[J]. IEEE Trans on Aerospace and Electronic Systems, 2002, 38(3):738-754.
[73] JEONG H,PARK J. An EM-Based Adaptive Multiple Target Tracking Filter[J]. International Journal of Adaptive Control and Signal Processing, 2002, 16(1):1-23.
[74] 李晓花,李亚安,陈晓,等.密集杂波环境下确定性退火DA-HPMHT 跟踪算法[J].西北工业大学学报,2015,33(3):432-437.
[75] GUO Yunfei, TENG Kai, SHI Liwei. SA-HPMHT for Maritime Dim Targets Tracking with Sensor Location Uncertainty[J]. IEEE Sensors Journal, 2023, 23(5):5134-5145.
[76] DANAEE M R,BEHNIA F. Modified Gibbs Sampler Procedure for Bearing-Only Multitarget Tracking[J]. International Review on Modelling and Simulations, 2012, 5(4):1532-1540.
[77] TANG X, LI M, THARMARASA R, et al. Seamless Tracking of Apparent Point and Extended Targets Using Gaussian Process PMHT[J]. IEEE Trans on Signal Processing, 2019, 67(18):4825-4838.
[78] XU Shuoyan, SHIN H S, TSOURDOS A. Variational Probabilistic Multi-Hypothesis Tracking[J]. arXiv, 2021.https://doi.org/10.48550/arXiv.2110.11954.
[79] EMAMI P, PARDALOS P M, ELEFTERIADOU L, et al.Machine Learning Methods for Data Association in Multi-Object Tracking[J]. ACM Computing Surveys , 2020, 53(4):1-34.
[80] LI Tiancheng, CORCHADO J M, SUN Shudong, et al.Clustering for Filtering: Multi-Object Detection and Estimation Using Multiple/Massive Sensors[J]. Information Sciences, 2017, 388:172-190.
[81] LI Tiancheng, PRIETO F, CORCHADO J M. Multi-Source Homogeneous Data Clustering for Multi-Target Detection from Cluttered Background with Misdetection[J]. Applied Soft Computing, 2017, 60:436-446.
[82] LI Tiancheng, PRIETO F, CORCHADO J M. A Robust Multi-Sensor PHD Filter Based on Multi-Sensor Measurement Clustering[J]. IEEE Communications Letters,2018, 22(10):2064-2067.
[83] LI Tiancheng, SONG Yan, FAN Hongqi. From Target Tracking to Targeting Track: A Data-Driven yet Analytical Approach to Joint Target Detection and Tracking[J].Signal Processing, 2023, 205:108883.
[84] 程稳,陈忠碧,李庆庆,等.时空特征对齐的多目标跟踪算法[J].光电工程,2023,50(6):68-81.
[85] GIRSHICK R. Fast R-CNN[C]// 2015 IEEE International Conference on Computer Vision, Santiago, Chile: IEEE,2015:1440-1448.
[86] TERVEN J, CORDOVA-ESPARZA D. A Comprehensive Review of YOLO Architectures in Computer Vision:From YOLOv1 to YOLOv8 and YOLO-NAS[J]. Machine Learning and Knowledge Extraction, 2023, 5(4):1680-1716.
[87] JOGIN M, MADHULIKA M S, DIVYA G D, et al. Feature Extraction Using Convolution Neural Networks(CNN) and Deep Learning[C]// 2018 3rd IEEE International Conference on Recent Trends in Electronics, Information & Communication Technology, Bangalore, India:IEEE, 2018:2319-2323.
[88] 张重生,陈杰,李岐龙,等.深度对比学习综述[J].自动化学报,2023,49(1):15-39.
[89] 孔庆群,吴福朝,樊彬.基于深度学习的图像匹配:方法、应用与挑战[J].计算机学报,2024,47(7):1485-1520.
[90] 李玺,查宇飞,张天柱,等.深度学习的目标跟踪算法综述[J].中国图象图形学报,2019,24(12):2057-2080.
[91] 周雪,梁超,何均洋,等.一体化多目标跟踪算法研究综述[J].电子科技大学学报,2022,51(5):728-736.
[92] LUO W, XING J, MILAN A, et al. Multiple Object Tracking: a Literature Review[J].Artificial Intelligence, 2021,293:103448.
[93] LI Yuan, HUANG Chang, NEVATIA R. Learning to Associate: Hybridboosted Multi-Target Tracker for Crowded Scene[C]// 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA:IEEE,2009:2953-2960.
[94] BAE S H,YOON K J. Robust Online Multi-Object Tracking Based on Tracklet Confidence and Online Discriminative Appearance Learning[C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus ,OH, USA:IEEE, 2014:1218-1225.
[95] KUO Chenghao, HUANG Chang, NEVATIA R. Multi-Target Tracking by On-Line Learned Discriminative Appearance Models[C]// 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA: IEEE, 2010:685-692.
[96] CHOI W. Near-Online Multi-Target Tracking with Aggregated Local Flow Descriptor[C]//2015 IEEE International Conference on Computer Vision, Santiago, Chile:IEEE,2015:3029-3037.
[97] WANG Shaofei, FOWLKES C C. Learning Optimal Parameters for Multi-Target Tracking with Contextual Interactions[J]. International Journal of Computer Vision,2017, 122(3):484-501.
[98] WANG Bing, WANG Gang, CHAN K L, et al. Tracklet Association by Online Target-Specific Metric Learning and Coherent Dynamics Estimation[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2016, 39(3):589-602.
[99] WANG Bing, WANG Gang, CHAN K L, et al. Tracklet Association with Online Target-Specific Metric Learning[C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus ,OH, USA:IEEE, 2014:1234-1241.
[100]WANG Xiaoyu, HUA Gang, HAN T X. Discriminative Tracking by Metric Learning[C]// 11th European Conference on Computer Vision, Heraklion Crete Greece:Springer Berlin Heidelberg, 2010:200-214.
[101] ZHANG Chuyun, LI Liangqun, HUANG Shuai. Multiple Target Data-Association Algorithm Based on Takagi-Sugeno Intuitionistic Fuzzy Model[J]. Neurocomputing, 2023, 536:114-124.
[102] JEON Y, HWANG G. Bayesian Mixture of Gaussian Processes for Data Association Problem[J]. Pattern Recognition, 2022, 127:108592.
[103] LAN Hua, MA Jirong, WANG Zengfu, et al. A Message Passing Approach for Multiple Maneuvering Target Tracking[J]. Signal Processing, 2020, 174:107621.
[104] HE Jiawei, HUANG Zehao, WANG Naiyan, et al.Learnable Graph Matching: a Practical Paradigm for Data Association[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2024, 46(7):4880-4895.
[105] 刘伟强,陈莉,黄子纯,等.基于主被动复合导引头的干扰态势构建[J].雷达科学与技术,2024,22(2):187-198.
[106] BU Shizhe, ZHOU Gongjian. Joint Data Association,Spatiotemporal Bias Compensation and Fusion for Multisensor Multitarget Tracking[J]. IEEE Trans on Signal Processing, 2023, 71:1509-1523.
[107] MENESES M, MATOS L, PRADO B, et al. Learning to Associate Detections for Real-Time Multiple Object Tracking[J]. arXiv, 2020.https://doi.org/10.48550/arXiv.2007.06041.
[108] LIU Huajun, ZHANG Hui, MERTZ C. DeepDA: LSTMBased Deep Data Association Network for Multi-Targets Tracking in Clutter[C]//2019 22th International Conference on Information Fusion, Ottawa, ON, Canada:IEEE, 2019:1-8.
[109] LEE Mengyuan, XIONG Yuanhao, YU Guanding, et al.Deep Neural Networks for Linear Sum Assignment Problems[J]. IEEE Wireless Communications Letters,2018, 7(6):962-965.
[110] SUN Shijie, AKHTAR N, SONG Huansheng, et al.Deep Affinity Network for Multiple Object Tracking[J].IEEE Trans on Pattern Analysis and Machine Intelligence, 2019, 43(1):104-119.
[111] XU Yihong, BAN Yutong, ALAMEDA-PINEDA X, et al. DeepMOT: a Differentiable Framework for Training Multiple Object Trackers[J]. arXiv, 2019. https://doi.org/10.48550/arXiv.1906.06618.
[112] ZHANG Hui, LIU Huajun, WANG Cailing. Learning to Multi-Target Tracking in Dense Clutter Environment with JPDA-Recurrent Neural Networks[J]. Journal of Physics: Conference Series, 2019, 1207:012011.
[113] 李文娜,张顺生,王文钦.基于Transformer 网络的机载雷达多目标跟踪方法[J].雷达学报,2022,11(3):469-478.
[114] CHU Peng, LING Haibin. Famnet: Joint Learning of Feature, Affinity and Multi-Dimensional Assignment for Online Multiple Object Tracking[C]// Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul Korea (South): IEEE, 2019:6172-6181.