0 引 言
无源定位是一种不主动向目标发射电磁波,而是依赖于接收到的信号来估算目标位置的技术,由于其具有定位精度高、隐蔽性强、能耗低和不占用频谱资源等优点［1］,已广泛应用于雷达、声呐、无线传感器网络以及通信系统等领域［2-4］。无源定位通常包含两个步骤,首先从接收信号中提取相应的观测量,包括信号传播时延（Time Delay,TD）、到达时间差（Time Difference of Arrival, TDOA）、到达角（Angle of Arrival, AOA）等。随后利用这些观测量求解非线性/非凸性定位问题,从而估计目标位置。当目标和观测站之间存在相互运动时,也可以联合频率信息进一步提升目标位置估计精度。
无源定位主要可以分为非合作目标定位和合作目标定位两大类,这些定位问题中观测方程与未知参数之间存在高度非线性关系,直接对最大似然问题搜索求解会带来较高的计算复杂度,且搜索也容易陷入局部最优解,为此,国内外学者提出了多种算法以提升定位精度。非合作目标主要应用于敌方目标侦察定位,由于难以精准获取信号发射时间,现有研究主要是通过采用TDOA 等观测量进行定位。文献［5］通过泰勒级数展开法进行迭代求解,但是该算法的定位性能严重依赖于良好的初始值,若初始值选取不恰当,该算法可能无法保证收敛。为了克服这个问题,文献［6］阐述了经典的两步加权最小二乘（Two Stage Weighted Least Square, TSWLS）算法,该算法通过引入额外变量,利用连续加权最小二乘技术（Weighted Least Square, WLS）给出目标参数估计值,同时在适度的高斯测量误差下可达到克拉美罗下界（Cramer-Rao Lower Bound, CRLB）［7］。随后,文献［8-9］将该算法拓展至存在站址误差下的无源定位场景,并且详细分析了忽略观测站误差对定位性能的影响,分别提出基于加权最小二乘以及校准目标辅助的闭式算法。近些年,研究学者分别从利用修正极坐标系定位［10］、信号传播速度未知场景定位［11］等方面进一步完善非合作目标定位体系,对于精确感知敌方目标具有重要意义。合作目标定位主要应用于民用和商业领域,例如基站、无人机等合作式目标往往随机布置［9］,己方系统在使用时无法精确已知它们的位置坐标（即使有GPS 等定位设备,但是它们的位置依旧不够精确）,必须设计相应算法对它们精确定位,才能为后续例如城市环境探测、资源部署等任务［12］提升准确位置信息。此外,在水下定位场景中对己方航行器进行定位也可能会涉及合作式目标定位范畴,准确的航行器位置同样可以提升水下定位任务质量［13］。因而,合作目标定位对于民用商业等领域具有重要作用。合作目标通常会携带有发射信号时刻信息,因此合作目标定位通常采用信号传播时延这一观测量进行定位。其中,文献［14］借鉴了TSWLS 方法,通过引入额外变量构建矩阵方程进行求解。文献［15］则基于TSWLS思路构建了约束问题,随后利用半定松弛技术进行求解,近些年研究学者分别从考虑减小定位偏差［16］、缓解时钟同步误差［17］等角度出发,提出针对性的改进算法,进一步提升基于时延的合作目标定位精度。本文主要聚焦于合作式目标定位。
尽管上述定位算法在适当的测量误差、站址误差或时钟同步误差下均可实现CRLB 性能,但上述算法均需要求目标与观测站之间为视距（Line of Sight, LOS）传播路径,在实际存在密集建筑的城市环境中该模型可能难以适用。例如,在城市环境中对低空无人机等合作目标进行定位感知时,城市中的密集建筑群可能难以保证LOS 场景定位,若继续采用现有LOS 定位方法可能会导致定位性能大幅下降,甚至对城市通信与交通安全等方面产生影响。尽管已有学者对非视距（Non Line of Sight, NLOS）场景开展了一系列研究［18-20］,但NLOS 模型会引入较大的额外误差,且NLOS 定位算法通常需要利用优化算法,计算效率偏低。因此,研究如何将遮挡场景转化为视距模型,利用闭式算法求解目标位置具有重要意义。
本文通过引入中继收发器,构造间接传播路径尽可能避免产生遮挡问题,同时考虑中继和观测站位置存在随机误差,提出一种单站合作目标定位闭式算法。从本质上讲,中继收发器桥接未知目标和观测站,它们只负责放大并转发接收到的信号［21-22］,且收发器是非专用低成本设备,例如无人机、飞机等现有设备［23-25］。所提算法首先引入单一校准目标,利用校准目标-中继-观测站所得额外观测量修正中继与观测站的位置,随后,基于修正的位置参数连续使用WLS 算法给出目标位置估计值。理论分析表明了所提算法可实现CRLB性能,仿真实验进一步验证了算法的有效性。
1 定位模型
如图1所示,本文考虑在三维场景中利用由Nt个中继和单一观测站所构成的定位系统对静止合作目标进行定位。未知目标和观测站的真实位置向量分别记为
每个中继的真实位置向量记作
其中,i =1,2,…,Nt。
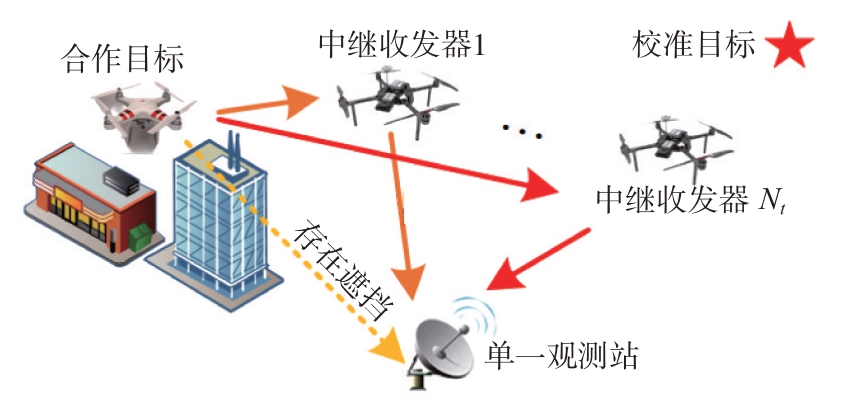
图1 定位场景示意图
在实际应用场景中,由于中继和观测站的真实位置常常受到随机误差的影响而难以精确获取,因此令
为可利用的位置参数,其中Δti和Δs为位置的随机误差。可以得到可利用的位置参数的向量形式：
式中,
分别表示真实的位置参数向量和可利用的位置参数向量,Δβ =[ΔtT, ΔsT]T =
为服从均值为零的高斯分布的误差向量,将其协方差矩阵记为E[ΔβTΔβ]= Qβ。
由于合作式目标定位发射信号通常携带有信号发射时刻信息,或通过控制中心也可得到发射时间戳信息［15］,因此观测站可提取得到信号经过目标-中继收发器i-观测站这一路径的传播时间,其真实值可表示为
式中,
为目标与第i 个中继的真实距离,
为中继与观测站的真实距离,
为信号传播距离。此外,c 为无线电信号在自由空间的传播速度（该值已知为c = 3 × 108 m/s）。由于时延与距离可以通过线性关系转换得到［14-16］,为了阐述方便,下文以距离为例进行分析。
考虑实际中存在观测误差的影响,式（2）中实际的距离观测量可建模为
式中,Δni 为测量误差项。将全部测量值表示为向量形式,有
式中，
分别为关于未知目标的测量向量及其真实值。Δn =
为服从高斯零均值分布的误差向量,其协方差矩阵记作Qr。
为了缓解中继和观测站位置误差导致的性能下降问题,借鉴文献［9］校准传感器位置误差的思路,引入单一校准目标对中继和观测站进行参数修正,校准目标的位置记作c =(xc, yc, zc)T,与未知目标观测量建模过程类似,校准目标-中继i-观测站这一信号传播路径时延乘以对应的传播速度可得真实距离为
式中,
分别表示中继与校准目标和观测站的真实距离。式（5）的观测版本可建模为
其中,Δni,c 为测量误差。将全部的测量值表示为向量形式,有
式中,
为关于校准目标的测量向量及其真实值。测量误差向量Δnc =[Δn1,c,Δn2,c,…,ΔnNt,c]T 服从零均值高斯分布,其协方差矩阵为
需要强调的是本文在观测量建模的过程中并未考虑中继产生的延迟,这主要是由于以下两方面原因：1）当中继选用配备有高效放大转发装置（例如智能反射面）的无人机、商用飞机等设备时,由于中继转发和放大信号的时间相比于信号传播的总时间较小,即引起的距离变化相较信号传播距离较小,为了简化定位模型可忽略中继产生的延迟时间［26］；2）即使该延迟无法忽略,由于中继是由己方配置得到,因此其放大转发所消耗的时间延迟理论上是可计算的,剔除这些时延后,仍可以得到到达时间（Time of Arrival, TOA）观测模型。
2 CRLB性能分析
前节给出本文的定位场景以及定位模型,本节利用第1节所述定位模型,给出了目标位置估计方差下界,即CRLB 表达式,作为后续算法性能评估的标准,并分析引入校准目标对于定位性能的提升。
记未知向量φ =[uoT, βoT]T,根据估计理论［7］可知,基于已有高斯模型观测向量β、r以及rc 下未知量φ的CRLB为
式中,各矩阵的表达式为
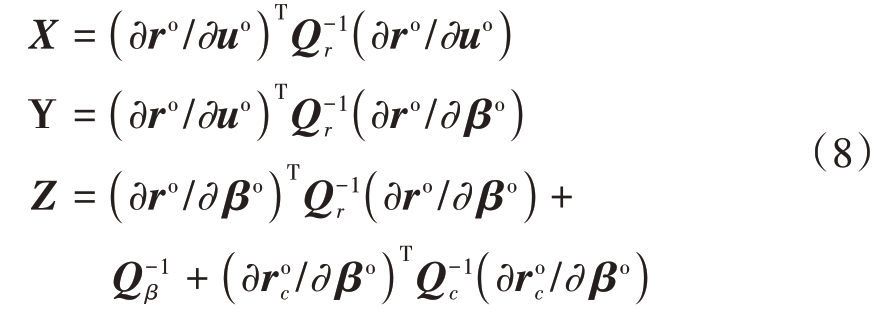
式中,各项偏导的表达式为
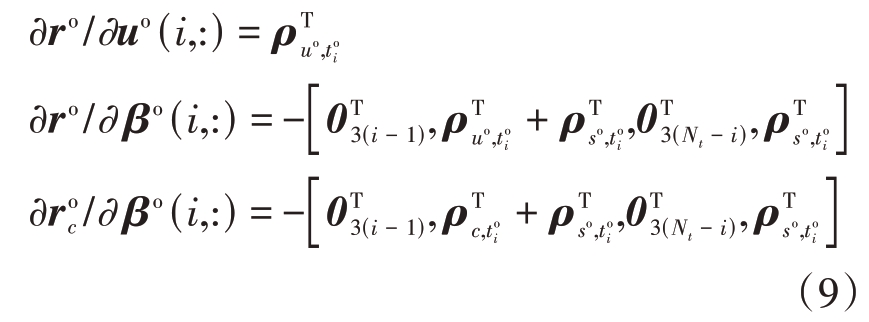
式中,ρa,b的表达式为ρa,b =(a - b)/||a - b||,下同。
利用分块矩阵求逆理论知识,目标位置的CRLB表达式可改写为
当未引入校准目标时,目标位置CRLB 的表达式与式（10）具有相同的形式,如下：
式中
定义表达式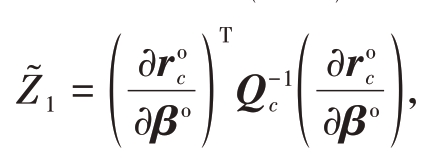
将该表达式代入式（10）中,并且利用矩阵求逆引理可得
对矩阵Qc 应用乔列斯基分解有
那么P表达式为
式中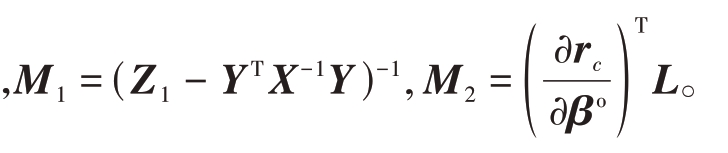
式（12）给出在引入校准目标与未引入校准目标两种情况下目标位置估计的CRLB 表达式关系,由于
无法保证列满秩,那么式（12）中X-1YPYTX-1 项必定为半正定矩阵,因此,引入校准目标后,至少不会降低目标位置估计性能。
3 所提三步加权最小二乘算法
第2节通过理论分析给出了所提模型的CRLB解析表达,本节进一步设计定位算法,以期实现CRLB 性能。所提算法可分为3 个步骤：第一步利用由校准目标所得额外观测量对观测站、中继收发器位置参数进行校准。第二步基于改进后的位置参数,利用未知目标-中继-观测站传播路径的观测向量,引入额外变量并构建伪线性矩阵方程,给出目标位置粗略估计值,最后一步利用额外变量与未知向量的关系进一步提升目标估计精度。
3.1 观测站与中继位置修正
文献［8-9］已充分讨论并证明了直接利用存在随机误差的位置信息会引起定位性能较大幅度的下降,因此必须先修正这些位置信息。本部分借鉴了文献［9］利用单一校准目标对传感器位置修正的思想,利用由校准目标所得观测向量修正中继以及观测站位置。
将
在可利用的中继收发器和观测站处进行线性泰勒级数展开可得
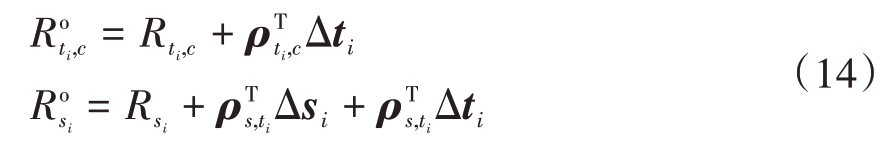
式中,Rti,c = ||c - ti||,Rsi = ||ti - s||为实际得到的中继与校准目标和观测站的距离。将式（14）带入式（5）中,经过适当的整理可得如下表达式：
将式（15）利用矩阵形式表示有
式中
由于Δβ 和Δαc 均服从高斯分布,因此根据贝叶斯高斯-马尔可夫定理［7,9］,可得Δβ 的线性最小均方误差估计解为
因此,修正后的中继收发器和观测站位置可表示为
式中
最后需要说明的一点是3.1 节仅利用单一校准目标即可实现中继与观测站的位置修正,这主要是因为：1） 待修正的M 个中继收发器及1 个观测站位置元素个数共为3(M + 1),单一校准目标可获得M 个TOA 观测信息；另外,存在位置误差的中继收发器和观测站已知（元素个数为3(M + 1)）,因此,先验信息元素个数为4M + 3,大于未知元素个数,即通过单一校准目标可实现位置修正。2） 位置修正借鉴了文献［9］中利用单一校准目标修正传感器位置误差的思路。这里构建的等式方程（16）完全符合贝叶斯高斯-马尔可夫模型［7,9］,且最终仿真实验也可表明该修正方法的有效性。本文选择单一校准目标的原因在于节约成本,多校准目标理论上同样可以提升定位性能,这可作为后续聚焦的研究方向。综上所述,无论是从理论还是仿真实验,本文利用单一校准目标实现位置修正是合理的。
3.2 目标位置粗略解
3.1节已通过关于校准目标的观测量实现了中继以及观测站位置的修正,本节进一步利用这些修正后的参数给出目标位置的粗略解,具体步骤如下。
将
对两边进行平方并将
带入后得到
将
在修正后的中继与观测站处进行泰勒级数线性展开可得
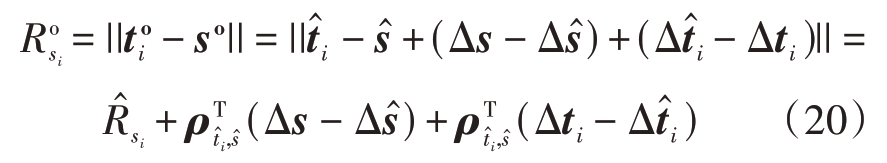
式中,
将式（2）、（18）以及式（20）带入式（19）中有
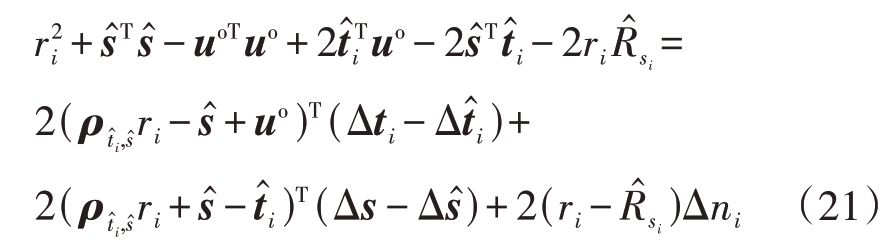
将式（21）所有方程写为矩阵形式有
式中
为未知变量,
此外,误差向量ε1可表示为
式中,误差系数矩阵B1和D1分别由下式计算得到：
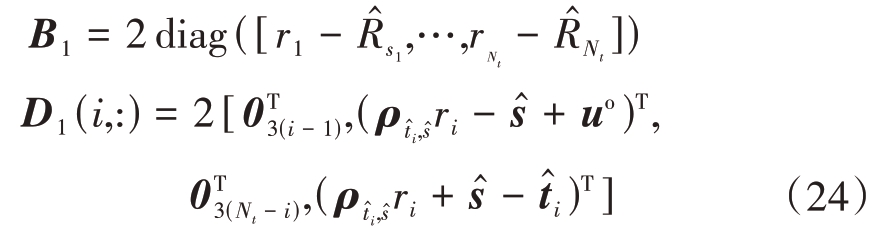
通过加权最小二乘可得式（22）的估计解为
式中
为目标位置的粗略估计值,
为额外变量估计值,加权矩阵W1为
此外
估计误差可表示为
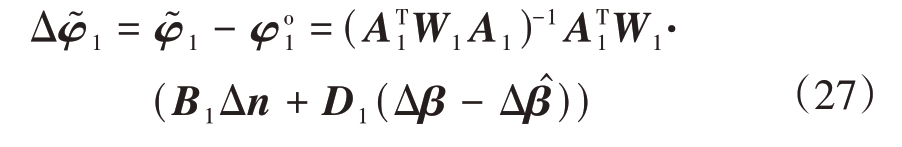
当位置误差估计向量Δβ - Δβ̂和测量误差向量Δn足够小时,忽略二阶及以上误差项有E(Δφ͂ 1)≈0,即第二步近似为无偏估计,则其协方差矩阵为
3.3 目标位置最终解
3.2 节在构造伪线性方程的过程中,认为目标位置和额外变量是相互独立的,但实际上它们并不独立,因此本节需要进一步利用目标位置与额外变量的非线性关系,构建新的矩阵方程,进一步提升估计精度。
构造未知变量
利用估计误差表达式
有
将式（29）写为矩阵形式有
式中,观测向量b2、观测矩阵A2以及误差向量ε2分别为
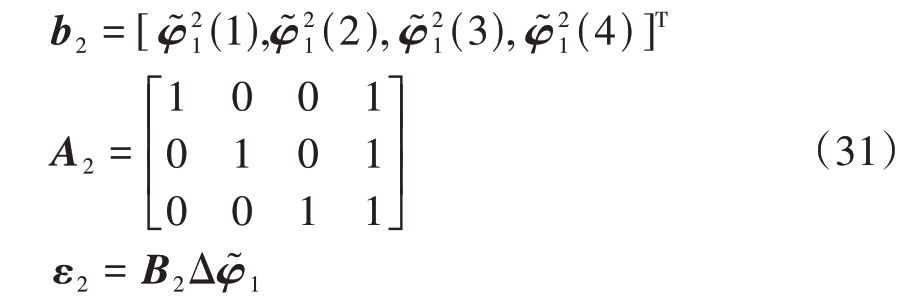
式中,B2 = diag([2uT,1])。再次利用加权最小二乘技术可得式（30）的解为
式中,加权矩阵
因此,未知目标最终位置的估计值为
需要强调的是计算加权矩阵W1需要未知目标的真值。为了解决这个问题,我们首先令W1 = Q-1r ,并通过式（25）获得未知目标的初始估计值。然后,利用初始值更新W1 并给出目标位置的粗略解,接着利用该解生成A2、W2 和b2,通过式（32）给出目标位置最终的估计值。
4 算法性能分析
本节首先证明了第3 节所提算法在测量误差较小的时候近似无偏估计,随后进一步给出理论分析证明了所提算法在测量误差较小时可实现第2节所述CRLB,具体分析如下。
首先,目标位置估计值的估计误差和φ͂ 2 的估计误差可分别表示为
将式（34）第一个等式带入第二个等式中,仅保留线性误差项可得最终估计误差表达式为
式中, 
可将目标位置估计误差Δu改写为
当测量误差和位置误差较小时,忽略二阶误差项有E(Δu) ≈0,即所提算法近似为无偏估计,那么其协方差矩阵可写为
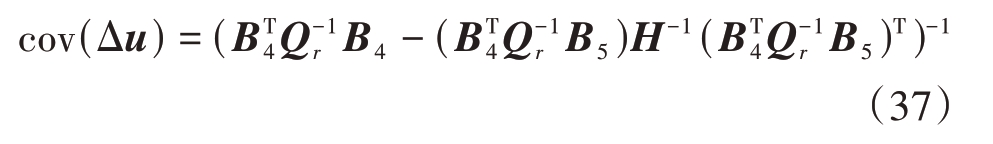
式中
因此CRLB表达式（10）可改写为
不难发现,式（37）和（38）具有相同的矩阵形式,当测量误差和位置误差较小时,通过矩阵运算操作可得
即当测量误差与位置误差较小时,有cov(Δu) ≈CRLB(uo),所提算法可实现CRLB。
5 仿真实验
本节通过仿真实验进一步证明上述理论分析的正确性,同时评估所提算法的定位性能。对比算法包括不进行第一步位置校准的本文所提算法、泰勒级数展开算法［5］,另外,仿真实验对文献［22］所提中继辅助的合作目标定位方法进行了适当调整,以符合本文多中继单站定位场景。同时,这些算法所对应的CRLB 性能也在仿真实验中给出。为了描述简洁,上述这些算法在仿真实验中分别简写为所提算法、所提算法（无校准目标）、文献［6］算法、文献［22］算法、所提算法CRLB,以及无校准目标算法CRLB。另外,未知目标-中继-观测站和校准目标-中继-观测站的距离测量误差协方差矩阵分别建模为
其中
分别为未知目标和校准目标的距离测量误差方差。此外,中继与观测站的位置参数是通过将零均值的高斯随机误差添加到对应真实值后而生成的,位置误差的协方差矩阵设置为
其中
表示中继和观测站位置的误差方差。观测站的真实位置为so =[450,450,300]T m,校准目标的真实位置为c =[1 450,1 550,1 600]T m。仿真平台为搭载MATLAB2020a的笔记本电脑（CPU为Intel Core i5）。
仿真场景主要分为3个,前两个场景分别考虑位置误差方差
和测量误差方差
对近场/远场目标定位性能的影响,近场和远场未知目标的三维位置坐标分别由［-800,800］ m×［-800,800］ m×［-800,800］ m和［-3 000,3 000］ m×［-3 000,3 000］m×［-3 000,3 000］ m 的立方体均匀分布产生,中继的真实位置如表1 所示。第三个仿真场景则考虑中继数量对定位性能的影响,未知目标和中继的三维位置均由［-500,500］ m×［-500,500］ m×［-500,500］ m随机产生。所有仿真实验中
统一设置为0.001 m2,且泰勒级数算法［6］选取目标真实位置作为迭代初始值,通过均方根误差（Root Mean Square Error, RMSE）来对不同算法的精度进行评估,其定义式如下：
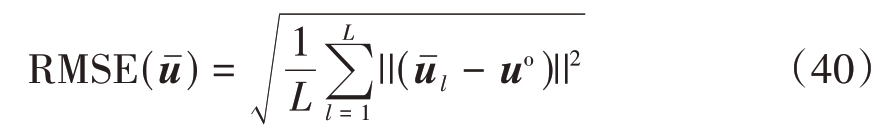
表1 中继的真实位置 m
中继收发器序号1 2 3 4 5 xo i 130-200 150 200 250 yo i-200 300-300 120 300 zo i 80 100 200 140 200
式中
表示第l次的位置估计结果,L = 5 000为蒙特卡洛仿真实验的次数。
5.1 定位性能随位置误差方差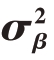
的变化情况
本节考虑所提算法定位性能随位置误差方差
变化的情况,测量误差方差
设置为
图2 中绘制了不同算法在随机近场和远场目标情况下的定位性能。根据图2（a）可得,相比本文算法未引入校准目标以及文献［22］中基于半定松弛的算法,引入校准目标的所提算法显然具有更低的近场目标位置估计RMSE,这主要归因于第一步利用校准目标所获取的额外信息对观测站与中继进行了位置校准,从而为后续两步提供了相对准确的位置参数,这与第2节理论分析保持一致。
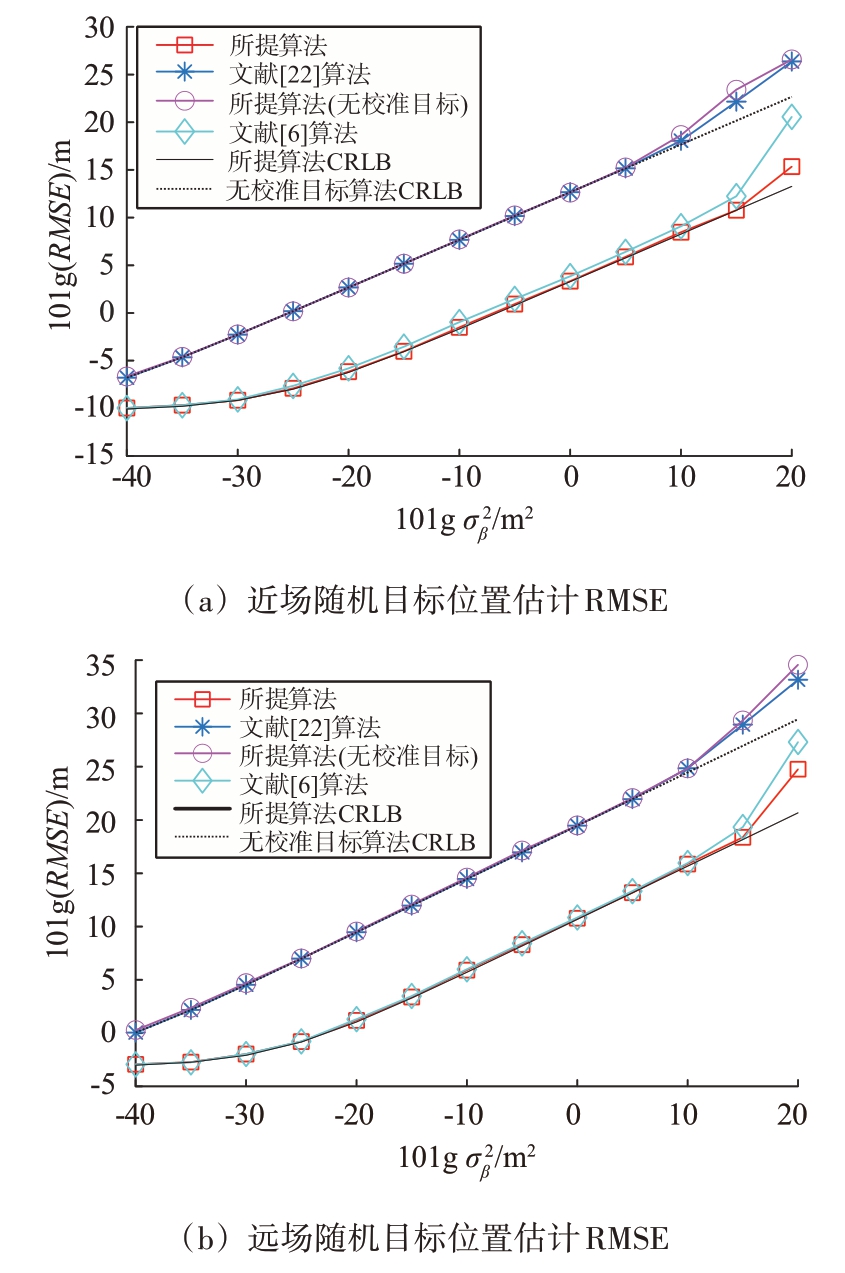
图2 不同算法定位性能随传感器位置误差的变化情况
另外,当位置误差方差
不超过10 m2时,所提算法和文献［6］算法都十分接近CRLB 性能,当
大于10 m2 时,文献［6］算法开始逐渐偏离CRLB,并且随着
的继续增加,该算法产生了阈值效应［9］,这可能是由于最小值附近的误差表面不规则,使得文献［6］基于梯度的算法对位置误差非常敏感。相比较而言,本文所提算法在
大于101.5 m2时才开始偏离CRLB,并且在相同位置误差下本文所提算法偏离程度更小,具有更低的RMSE。需要注意的是,文献［6］算法在小位置误差条件下之所以有如此好的性能,主要是因为初值选取了目标位置的真实值,但该值在实际中往往难以获得。随着位置误差的继续增大,文献［6］算法开始遭受到阈值效应［8］,这可能是因为基于梯度的泰勒展开算法对误差比较敏感所导致。
图2（b）中绘制了不同算法在随机远场目标情况下的定位性能,仿真结果再次表明引入校准目标对中继与观测站位置进行校准的重要性,这也为工程应用提供了一定的理论支撑。此外,所提算法与文献［6］算法在适度的位置误差方差下同样能够实现CRLB 性能。当位置误差方程
超过101.5 m2时,所提算法与文献［6］算法同时开始偏离CRLB性能,但本文所提算法偏离程度相对较小。
5.2 定位性能与测量误差方差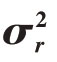
的变化情况
本节评估了所提算法的定位性能随测量误差方差
的变化情况,位置误差方差
设置为10 m2,实验结果在图3中给出。根据仿真结果可知,所提算法比本文所提无校准目标算法以及基于半定松弛的算法［22］具有更低的目标位置估计RMSE（尤其是当测量误差较小时）,再次证明了引入校准目标的重要性。比较有趣的现象是随着
的逐渐增大,无校准目标的定位性能开始逐渐逼近所提算法,该现象在现有定位相关研究［24-25］中也经常出现,这主要是因为位置误差固定时,较大的测量误差占据了定位性能的主导定位,中继与观测站位置校准对于定位性能的提升性能较弱。所提算法在整个测量误差范围内都十分逼近CRLB 性能,且位置参数估计RMSE 略低于文献［6］算法,表明了所提算法对测量误差同样具有良好的鲁棒性。
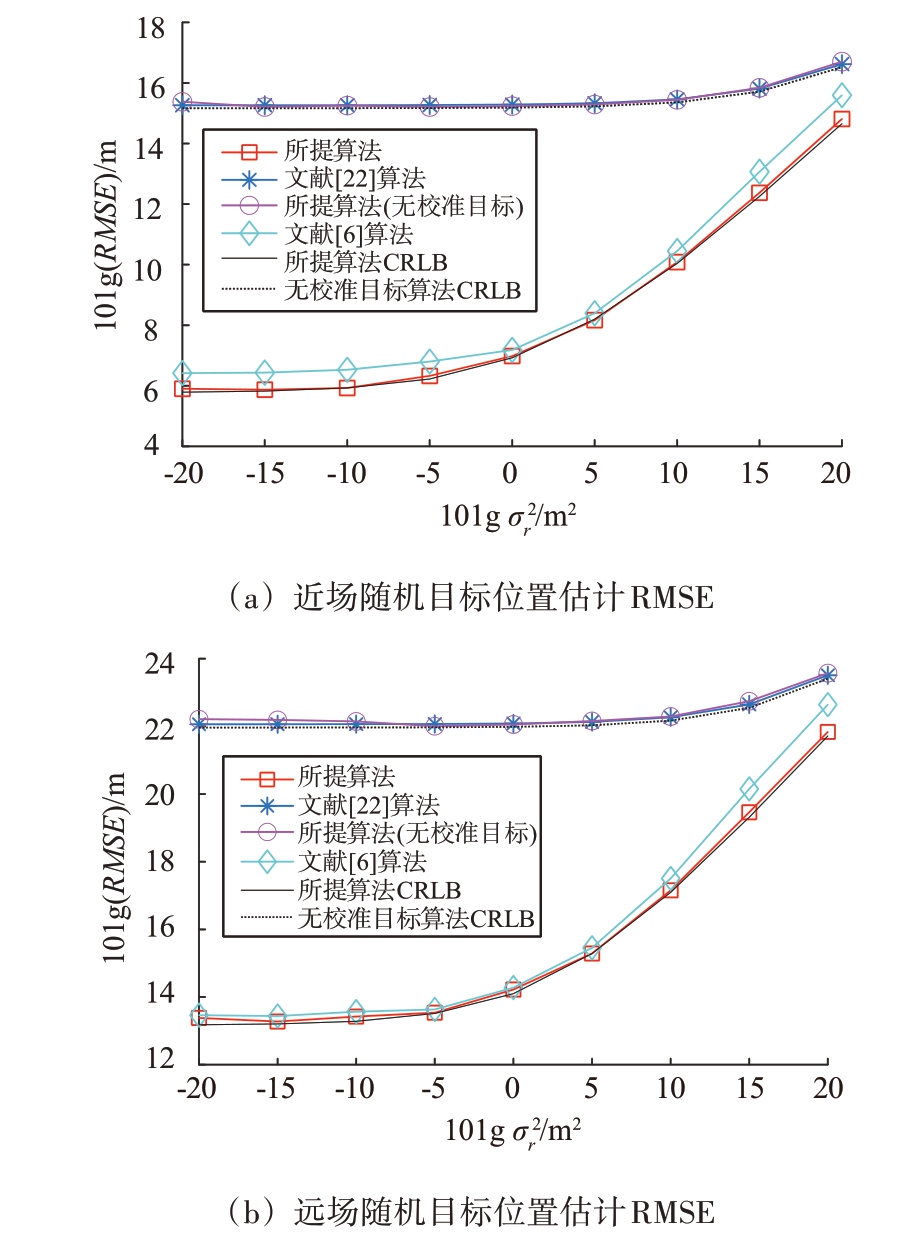
图3 不同算法定位性能随测量误差的变化情况
5.3 定位性能与中继数量的关系
本节给出所提算法的定位性能随中继数量变化的情况,位置误差和测量误差方差均设置为10 m2。实验结果在图4 中给出。仿真结果再次印证了引入校准目标进行位置修正对定位性能的贡献,且仿真实验还表明中继数量增多也会提升定位性能,文献［6］算法良好的定位性能主要是由于选取了真实位置参数作为初始值,但在实际中该算法得到较好的初始值相对困难,且该算法需要多次迭代保证定位精度。从工程应用的角度考虑,采用集群无人机等现有设备充当中继收发器在节省成本的同时,还能显著提升定位性能,因此所提算法对目标定位的工程应用具有较强的指导意义。
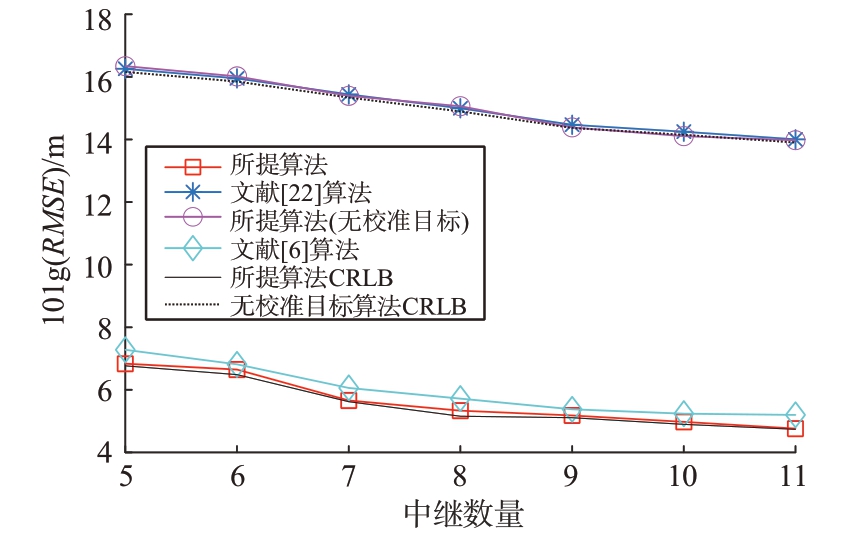
图4 不同中继数量下的定位精度
最后,表2给出了不同算法的平均执行时间对比情况。不进行第一步中继与观测站位置校准的本文所提算法在定位性能方面与文献［22］算法相对接近,但是根据表2 所给算法执行时间,无校准目标算法计算效率较高。另外,所提算法耗时略高于无校准目标算法,主要是由于所提算法包含利用校准目标修正位置参数的步骤。
表2 不同算法平均执行时间
算法所提算法所提算法（无校准目标）文献［22］算法文献［6］算法平均执行时间/ms 2.61 2.52 1 211.13 434.24
6 结束语
本文针对现有无源定位算法应用于密集城市环境遮挡场景的局限性,开展基于中继收发器的单站目标定位算法研究,通过构造中继与观测站之间的间接传播路径,有效规避了遮挡问题,并提出一种闭式算法确定未知目标位置。该算法首先引入校准目标对中继与观测站的位置进行修正,随后连续构建两个伪线性定位问题分别给出目标位置的粗略解和最终解。理论分析表明所提算法在适度的误差条件下可达到CRLB,仿真实验进一步验证了理论分析,同时表明所提算法具有一定的工程应用价值。此外,本文工作仍存在不足之处,未涉及引入中继后的混合视距及非视距定位以及非合作目标定位问题等,未来研究将主要聚焦于这些工作开展深入分析。
［1］ 赵研,陶海红,畅鑫,等.基于差分模型的近场无源定位算法［J］.雷达科学与技术,2023,21（4）:405-410.
［2］ 孙霆,董春曦.传感器参数误差下的运动目标TDOA/FDOA无源定位算法［J］.航空学报,2020,41（2）:262-271.
［3］ 范超,王鼎,杨宾,等.信号传播速度未知下水下多基地声呐定位算法［J］.兵工学报,2022,43（3）:637-652.
［4］ ZHAO Yue, LI Zan, CHENG Nan, et al. Covert Localization in Wireless Networks: Feasibility and Performance Analysis［J］. IEEE Trans on Wireless Communications,2020, 19（10）:6549-6563.
［5］ FOY W H. Position-Location Solutions by Taylor-Series Estimation［J］. IEEE Trans on Aerospace and Electronic Systems, 1976, 12（2）:187-194.
［6］ HO K C, XU Wenwei. An Accurate Algebraic Solution for Moving Source Location Using TDOA and FDOA Measurements［J］. IEEE Trans on Signal Processing, 2004, 52（9）:2453-2463.
［7］ KAY S M. Fundamentals of Statistical Signal Processing［M］. USA:Prentice Hall, 1993.
［8］ HO K C, LU Xiaoning, KOVAVISARUCH L. Source Localization Using TDOA and FDOA Measurements in the Presence of Receiver Location Errors: Analysis and Solution［J］. IEEE Trans on Signal Processing, 2007, 55（2）:684-696.
［9］ HO K C, YANG Le. On the Use of a Calibration Emitter for Source Localization in the Presence of Sensor Position Uncertainty ［J］. IEEE Trans on Signal Processing, 2008,56（12）:5758-5772.
［10］ 孙奕髦,徐屹淮,唐北川,等.近远场统一定位模型：基于子空间的方法与局限性分析［J］.电子学报,2023,51（8）:2134-2143.
［11］ SUN Yimao, HO K C, YANG Yanbing, et al. An Asymptotically Optimal Estimator for Source Location and Propagation Speed by TDOA［J］. IEEE Signal Processing Letters, 2023, 30:1037-1041.
［12］ WANG Wei, WANG Gang, HO K C, et al. Robust TDOA Localization Based on Maximum Correntropy Criterion with Variable Center［J］. Signal Processing, 2023, 205:1-9.
［13］ 贾天一,高婧洁,申晓红,等.声速不确定条件下的运动水下航行器自定位［J］.系统工程与电子技术,2022,44（9）:2699-2706.
［14］ LI Jingzhou, HO K C, GUO Fucheng, et al. Improving the Projection Method for TOA Source Localization in the Presence of Sensor Position Errors［C］//2014 IEEE 8th Sensor Array and Multichannel Signal Processing Workshop, A Coruna, Spain:IEEE, 2014:1-4.
［15］ SHI Jiong, WANG Gang, JIN Liping. Moving Source Localization Using TOA and FOA Measurements with Imperfect Synchronization［J］. Signal Processing, 2021, 186:1-15.
［16］ ZHANG Ziqiang, WANG Ding, YANG Bin, et al. Weighted Multidimensional Scaling Localization Method with Bias Reduction Based on TOA［J］. IEEE Sensors Journal, 2023, 23（17）:19803-19814.
［17］ 王鼎,尹洁昕,郑娜娥,等.收发未精确同步条件下非相关多运动辐射源TOAs/FOAs 协同定位方法［J］.电子学报,2024,52（2）:550-563.
［18］ YUAN Bingbing, HE Ruisi, AI Bo, et al. UAV-Assisted Localization Based on Joint TOA-RSS NLOS Identification［J］. IEEE Communication Letters, 2024, 28（1）:63-67.
［19］ CHEN Haotian, WANG Gang, ANSARI N. Improved Robust TOA-Based Localization via NLOS Balancing Parameter Estimation［J］. IEEE Trans on Vehicular Technology, 2019, 68（6）:6177-6181.
［20］ BAYAT S, AMIRI R. Advances in UAV-Assisted Localization: Joint Source and UAV Parameter Estimation［J］.IEEE Sensors Journal, 2023, 72（11）:14268-14278.
［21］ HO K C. Localization Through Transceivers in Unknown Constant Velocity Trajectories［J］. IEEE Trans on Signal Processing, 2022, 70:3011-3028.
［22］ PEI Jian, WANG Gang, HO K C, et al. Moving Transceivers Aided Localization of a Far-Field Object［J］. IEEE Trans on Mobile Computing, 2024, 23（12）:12795-12810.
［23］ 郑纪彬,杨志伟,杨洋,等.集群无人机载雷达阵列波束合成［J］.雷达科学与技术,2023,21（1）:24-34.
［24］ SUN Ting, WANG Wei. Joint Moving Target and Antenna Localization for Distributed MIMO Radar with a Calibration Object［J］. IEEE Trans on Vehicular Technology, 2023, 72（10）:13781-13786.
［25］ SUN Ting, YU Zehua. Moving Target Localization in Distributed MIMO Radar Systems with Sensor Position Errors in the Presence of a Calibration Object［J］. Digital Signal Processing, 2022, 131:1-16.
［26］ JIA Tianyi, WANG Haiyan, WANG Gang, et al. Localization Using Time-Delay and Doppler Shift by Moving Monostatic Sensors［J］. IEEE Trans on Aerospace and Electronic Systems, 2022,58（3）:2560-2567.