0 引 言
频控阵(Frequency Diverse Array,FDA)通过在阵列中的相邻阵元之间引入微小的频率偏移,可以产生距离-角度域相关的、时变的波束图。因此,FDA 天线有望在未来得到广泛的应用,特别是在现代雷达和通信系统中[1-3]。
FDA 产生的“S”形波束图在不同距离和角度下都会出现极大值,导致了距离-角度域的耦合现象[4],这阻碍了单点波束图的产生。因此,多种基于频偏调整的点状波束综合与优化方法被提出[5-7]。然而,这些关于FDA 的研究都是基于常规的线性阵列的,其扫描角度有限,无法实现360°全向扫描。因此,环形阵列[8]的概念被引入到频控阵中,但是现有的环形FDA 结构本质为圆形的面阵[9-10],而非本文研究的环形阵列。此外考虑到在实际应用中,理想环形条件过于苛刻,阵列物理构造较为复杂,波束合成仿真过程中模型无法完全捕捉实际环境中的复杂条件,例如天线制造中的公差、阵列几何布局的微小偏差等[11],很难确保其机械结构的精度与一致性,这会影响雷达的探测精度与灵敏度[12]。与常规的线性FDA 相比,环形FDA 雷达可以针对不同的波束聚焦角度激活对应的子阵列来产生距离-角度域相关的波束,进而实现多个方向的精准波束聚焦,即多波束FDA。在点对点通信的场景中,如何在形成多波束的同时避免某个位置处的信号被接收或截获,即如何有效抑制特定距离-角度处的能量,并保持目标的精确聚焦至关重要。当下已经有许多学者将各种波束优化算法[13-14]与FDA 相结合,探索它们在FDA波束优化中的应用[15-19]。
针对理想环形阵列结构在制造和工程应用中难以实现的问题,本文提出通过组合多个线性阵列来近似实现环形阵列的改进方法。但是环形阵列由于其弧形结构,能够提供较好的全向覆盖性能的同时,也会导致波束畸变。因此本文引入了一种相位补偿技术,通过调整每个阵元的激励相位来校正由弧形结构引起的波束畸变,从而改善阵列的指向性和波束形成效果。同时提出了将多载波信号与线性约束最小方差法(LCMV)相结合引入到环形频控阵的波束优化中。通过多载波信号扩展LCMV的约束矩阵维度,并利用改进的距离-角度域二维LCMV波束形成方法,在所需目标的位置形成零陷,抑制信号生成。但是由于FDA 的方向图不仅是距离-角度域相关的,也是时变的,为解决这一问题,文献[20-21]特别研究了FDA 在自由空间传播条件下的阵列因子,并基于频率-相位关系和时间-距离关系,对FDA 信号模型进行了重新构建。基于环形FDA 的多波束多零陷波束优化方法,使其能够在给定的空间位置上更好地聚焦目标信号,并有效抑制特定距离角度域内的旁瓣电平。最后,通过一组实例仿真验证了多波束环形频控阵零陷形成方法的有效性。
1 阵列模型
改进的环形频控阵列模型采用多个线性阵列的组合来近似理想的环形阵列,其三维结构模型如图1所示。整个系统包含阵列天线基座(黑色部分)、线性阵列单元(红色部分)和信号处理单元(绿色部分)3个部分。
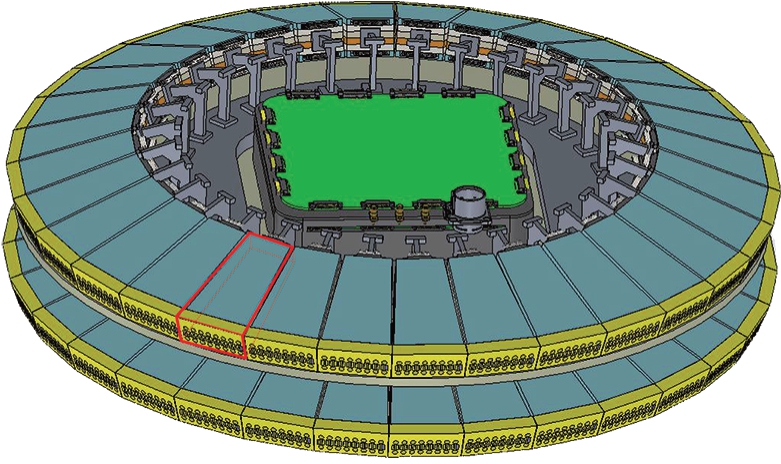
图1 改进的环形频控阵列模型
为了便于分析,将图1 的三维模型简化为图2的二维平面图形。假设一个环形频控阵由Nside 个线性阵列单元(灰色部分)组成,每一个线性阵列单元所占角度为ϕE,包含Nele 个各向同性天线,其辐射口面朝向外侧且以相同角度间隔均匀分布,相邻阵元之间的角度间隔为Δϕ(蓝色部分),总计Ntotal个阵元。若以角度θ为0时的方向作为参考方向并标记阵元索引编号为0时,其余的阵元依次从0 到Ntotal - 1 编号。为了使波束聚焦到目标点(r,θ)处,激活以第nref个阵元为中心的NA个阵元形成一个弧形的子阵列(红色部分),所占的孔径角为ϕ。其中θ 为波束聚焦方向与参考方向的夹角,r 为波束聚焦距离到阵元之间的距离。当需要照射多个目标时,同时激活不同方位的子阵列即可。
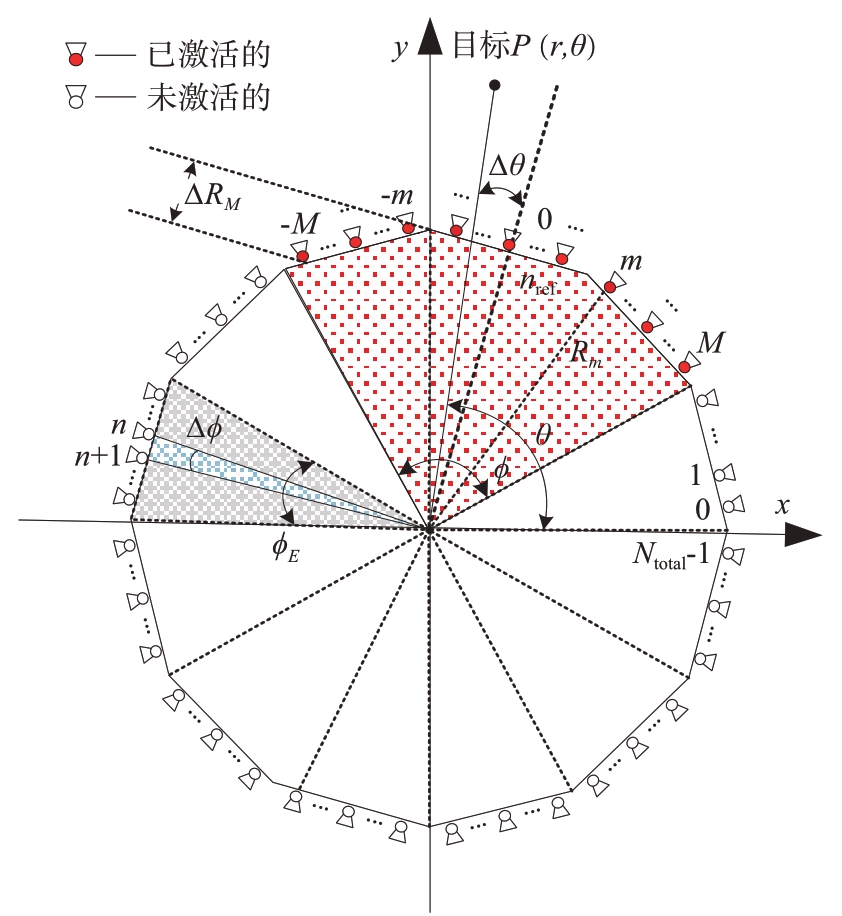
图2 改进的环形频控阵列二维平面图
以发射单个波束为例,为了使波束聚焦到目标点(r,θ)处,设置参考阵元索引编号nref,nref 所对应的阵元作为每个发射子阵列的参考阵元位置,可以根据波束聚焦角度来确定:
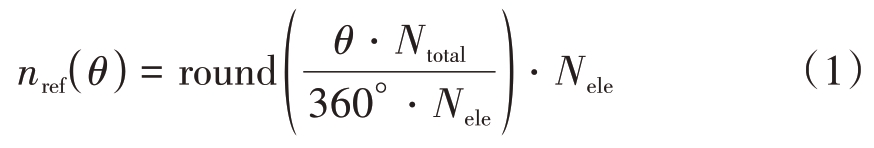
式中round(⋅)表示四舍五入运算,为了确保每一个发射子阵列的参考阵元为子阵列的中心,这一步骤的计算是必不可少的。为了便于分析,对发射子阵列中的阵元进行重新编号。将索引编号nref对应的阵元作为参考阵元重新编号为0,当激活的子阵列阵元个数为NA = 2M + 1 时,子阵列对应的编号为-M,…,-m,…0,…, m,…,M,如图2所示。
在环形频控阵的发射阵列中,由于阵元排列在曲线上,使阵元与目标之间的相位关系在空间传播过程中发生变化,导致各阵元的信号相位无法保持一致,从而引起波束畸变。这种畸变会降低波束聚焦精度,因此根据每个阵元在子阵列中的位置,计算其与中心参考阵元的垂直相对距离ΔRm,并据此确定各阵元的相位补偿量φm 是必要的,如图2 所示。其中垂直相对距离ΔRm 可以表示为
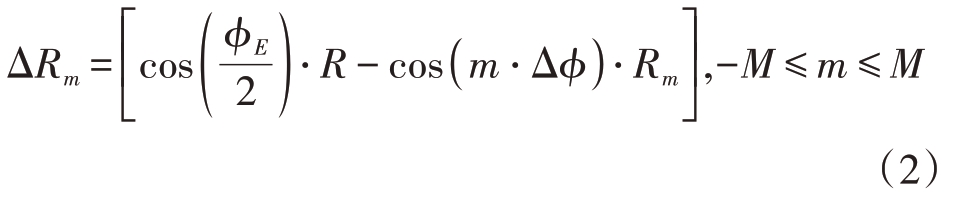
式中R 为该阵列的外接圆半径,Rm 为子阵列中各个阵元到圆心的距离。通过计算每个阵元的垂直相对距离ΔRm,可以确定相应的相位补偿φm,第m个阵元的相位补偿可以表示为
将计算得到的相位补偿应用到子阵列中每个阵元的发射信号上,可以补偿由于阵列曲率引起的相位变化,有效避免由阵列结构引起的波束畸变问题。
2 信号模型
当线性频控阵的阵元间距为d 时,在角度θ 下的波程差可以表示为Δrm = md sin θ,但是在环形频控阵中,由于其独特的环形结构,导致其波程差不仅与θ有关,还与Rm和Δϕ有关:

考虑到一个发射子阵列包含NA = 2M + 1 个发射阵元,Nc + 1 个载波,提出的多波束零陷方案如图3 所示。若被观测目标在任意位置处满足远场近似条件,则在距离-角度位置P(r,θ)处对应的发射方向图可以表示为
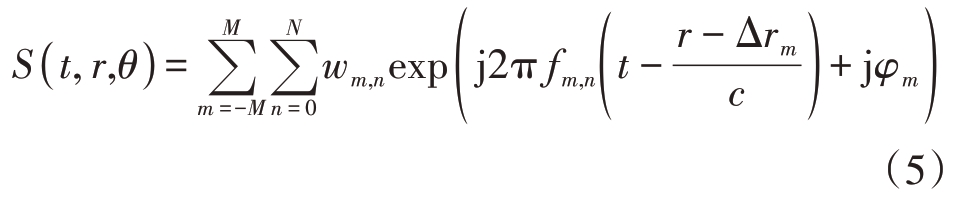

图3 信号处理流程
式中c为光速,t为时间变量,wm,n为第m 个阵元第n个信号的权值。
考虑到频控阵波束方向图的时变特性,结合文献[20]中提出的修正的时间依赖频率偏置解决方案,当中心阵元的载波频率f0 = fc 时,第m 个阵元的第n个载波的频率fm, n可以表示为

式中Δfm 和Δfn 分别为阵元频率偏置与载波频率偏置,r0 为波束期望距离。fc ≫Δfm + Δfn,分别可以表示为Δfm = lg( ||m + 1) ⋅cos(2πm/1.3) ⋅Δf 和Δfn = lg(n + 1) ⋅Δf。
将式(3)和式(5)代入式(4)中可以得到在空间P点处的导向矢量AF:
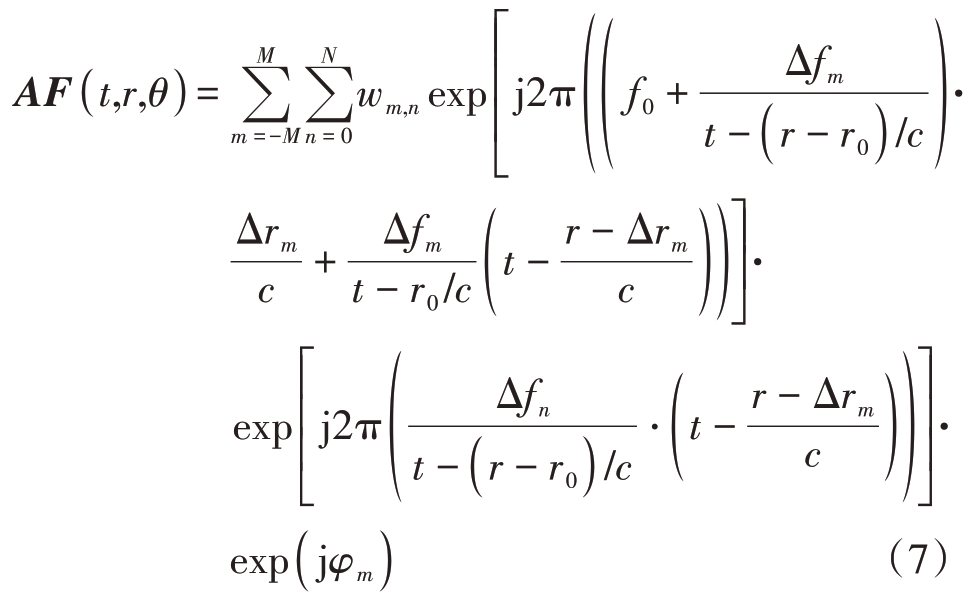
根据式(6)可知,空间中目标点处的导向矢量的维度为(2M + 1) ×(N + 1),与常规的频控阵相比,扩大了导向矢量的维度。在进行波束形成时,通过对每一个导向矢量都设置相对应的权值矢量,可以对波束进行更精准的优化。本文采取改进的LCMV 波束形成器以适用于多频载波环形频控阵列的距离角度域二维零陷生成,可以表示为
式中![]() 为约束矩阵
为约束矩阵![]() 为对应的约束响应向量,
为对应的约束响应向量,![]() 为所需的最优权矢量,其中(2M + 1)为激活的阵元数目,(P +J)为P 个期望目标和J 个抑制目标,N 为多载波数量,n = 0,1,…,N。假设期望距离-角度为(rp,θp),抑制距离-角度为(rj,θj),为了降低J 个方位的旁瓣电平,在距离-角度(rj,θj)处形成零陷,同时避免因为导向矢量误差的存在,使零陷位置没有准确地对准所需抑制区域的真实方向,通过在干扰位置处设置多个零点,从而达到零陷展宽,增加波束形成器对零陷的位置误差的稳健性。设置距离域和角度域分别需要的零陷宽度为2Δθ和2Δr,则约束矩阵为
为所需的最优权矢量,其中(2M + 1)为激活的阵元数目,(P +J)为P 个期望目标和J 个抑制目标,N 为多载波数量,n = 0,1,…,N。假设期望距离-角度为(rp,θp),抑制距离-角度为(rj,θj),为了降低J 个方位的旁瓣电平,在距离-角度(rj,θj)处形成零陷,同时避免因为导向矢量误差的存在,使零陷位置没有准确地对准所需抑制区域的真实方向,通过在干扰位置处设置多个零点,从而达到零陷展宽,增加波束形成器对零陷的位置误差的稳健性。设置距离域和角度域分别需要的零陷宽度为2Δθ和2Δr,则约束矩阵为

约束矩阵和约束相应向量可以分别表示为

式中Rn 为条件极值问题信号的自相关矩阵,可以表示为
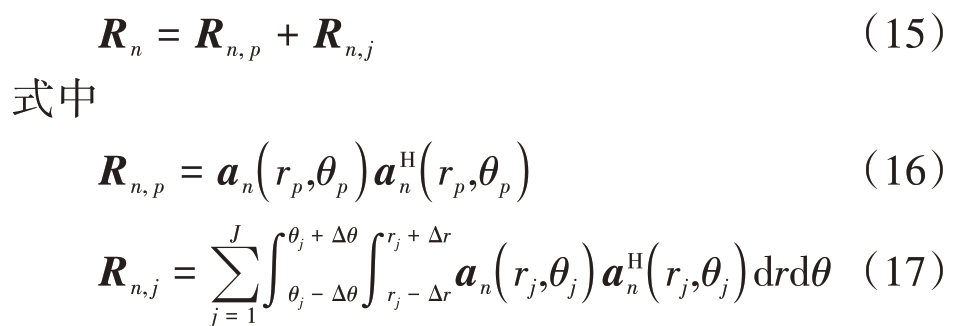
基于多载波LCMV的零陷展宽算法的最优权矢量为
3 仿真验证分析
本节主要通过数值仿真验证环形频控阵可以在360°全向形成多个波束,并且在特定位置处形成宽零陷。仿真分析中所涉及的环形阵列的基本参数如下:阵列外接圆半径R = 0.64 m,阵元频率偏置Δfm = 30 kHz,载波频率偏置Δfn = 1 kHz,线性阵列单元个数Nside = 29 个,每个线性阵列单元包含Nele = 5 个阵元,共计145 个阵元。在波束聚焦过程中,每个目标激活的子阵列由5个线性阵列单元组成,总计25 个阵元被激活。为了验证多波束环形频控阵零陷形成方法的有效性,分别对单波束零陷和多波束零陷两种场景进行分析。
3.1 单波束零陷
相较于常规的线性阵列,环形阵列最大的优势在于激活子阵列的灵活性。当目标角度偏移量θ大于整数倍个线性阵列单元所占的角度ϕE时,可以重新计算参考发射阵元编号nref来激活对应的子阵列。即将360°范围内较大的目标角度偏移量θ减小到ϕE 内,可以有效避免大角度偏移量下的波束主瓣展宽问题。同时对每一个发射信号进行相位补偿,解决了环形阵列波束形成时存在的畸变问题。当波束聚焦点(rd1,θd1)=(40 km, 90°)时,环形频控阵未经过相位补偿的波束图如图4(a)所示,波束无法正确聚焦在所需位置。经过相位补偿后的波束图如图4(b)所示,波束正确聚焦在所需位置,并且在360°的全向范围内有且仅有一个聚焦波束。若要在特定位置区域(rj1,θj1)=(38 km,270°)处抑制旁瓣电平,经过优化后的波束图如图4(c)所示。为了更清晰地展示,图5给出了对应的波束剖面图,可见对于单波束单零陷的情况下,该方法可以形成-110 dB 的零陷深度。若增加一个旁瓣抑制区域(rj2,θj2)=(35 km,63°),经过优化后的波束图如图4(d)所示。与图4(b)对比可以看出,在已知的两个特定区域J1和J2内,均形成了零陷。为了更清晰地展示其零陷性能,给出了两个抑制区域的波束剖面图,如图6所示。两个区域位置处均能形成-80 dB以上的零陷深度。
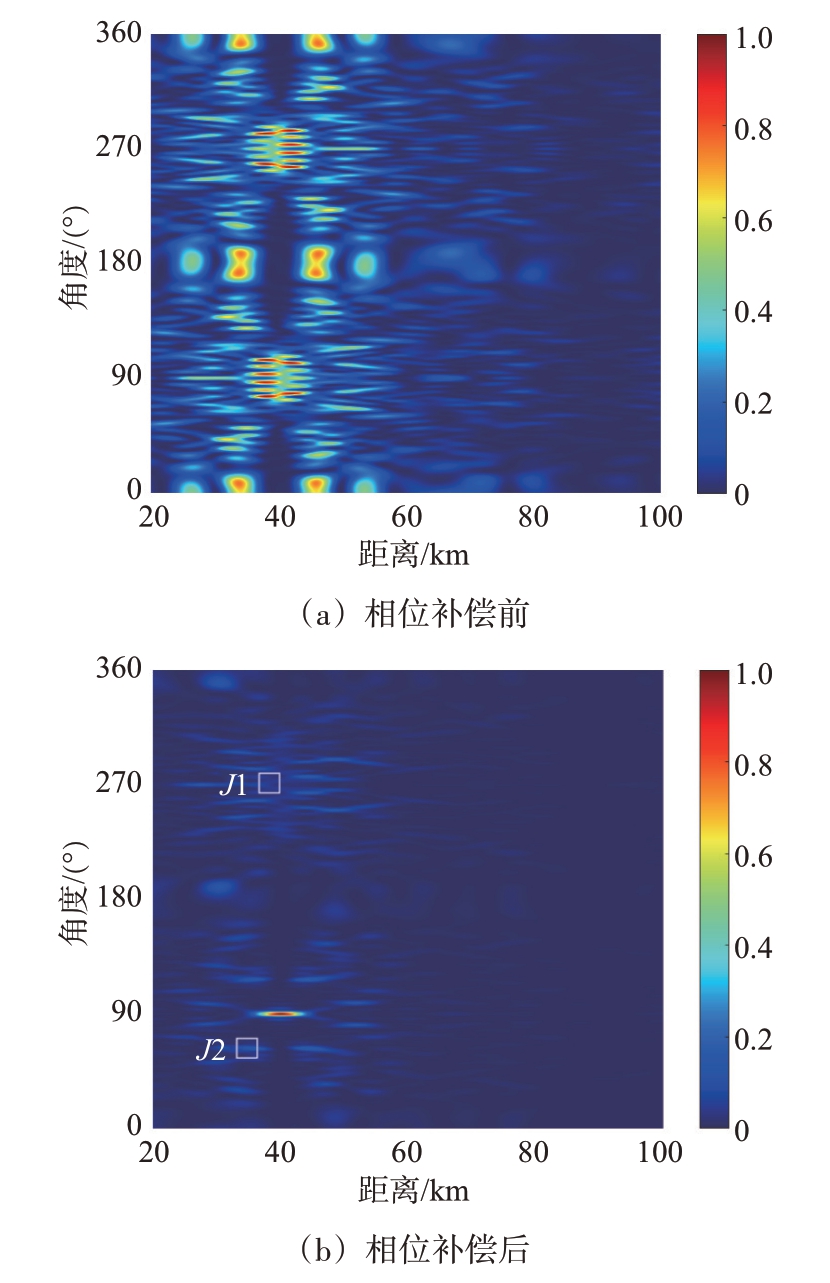
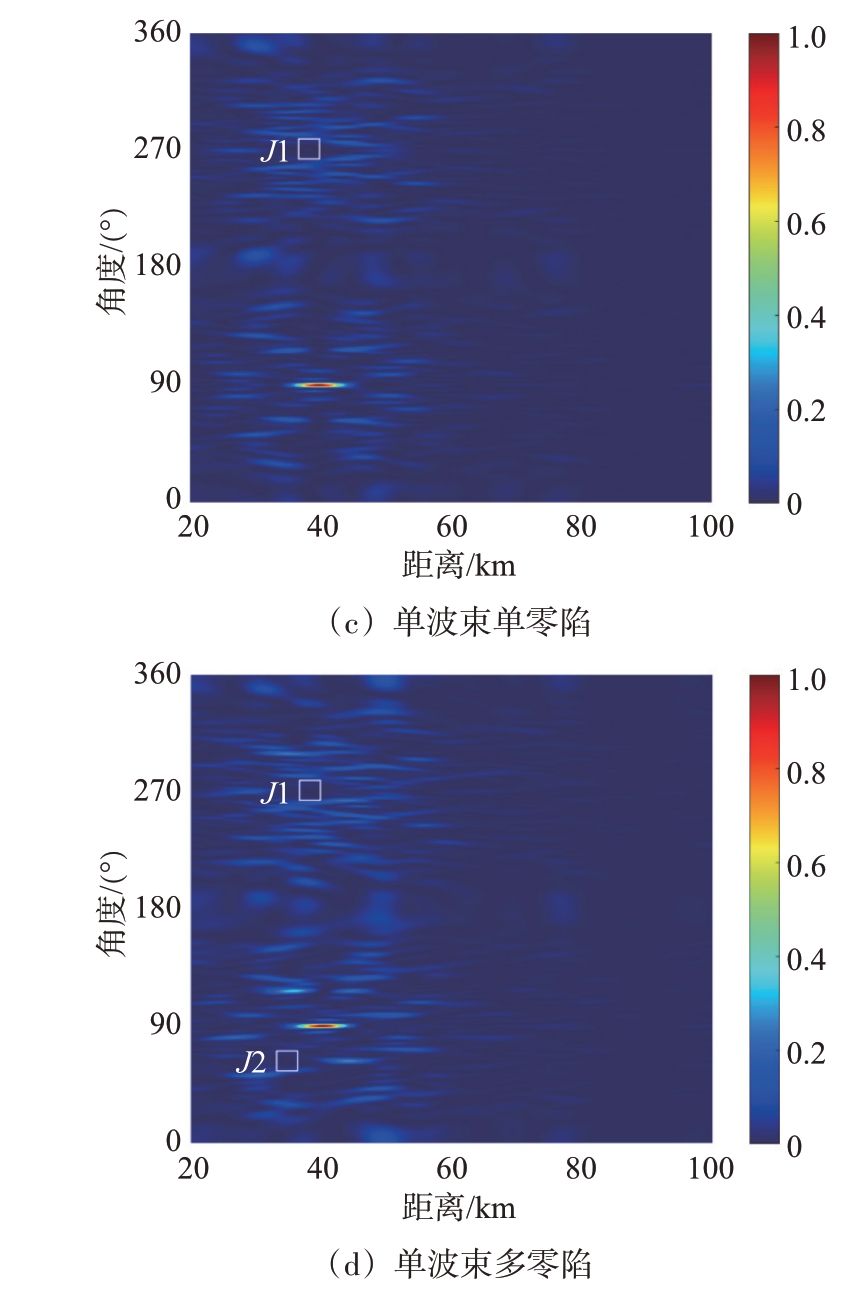
图4 单波束环形频控阵波束图
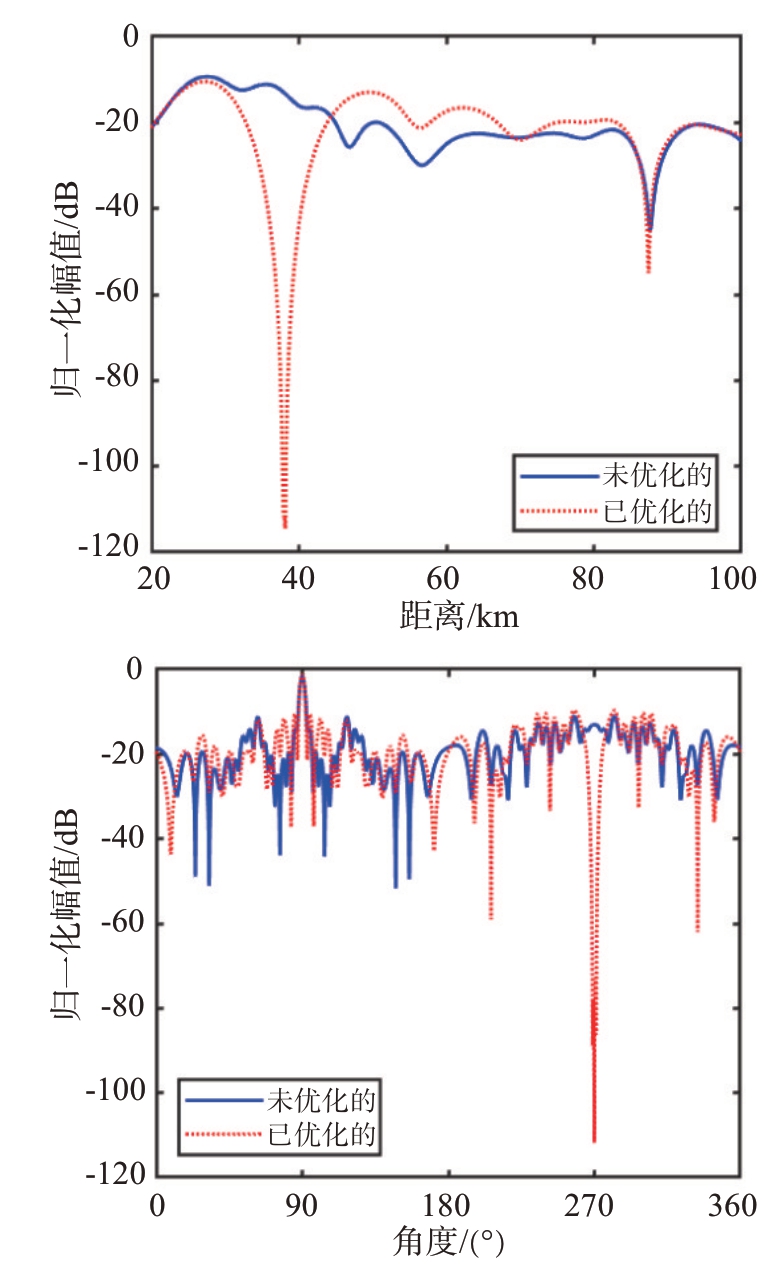
图5 单波束单零陷J1处的剖面图对比
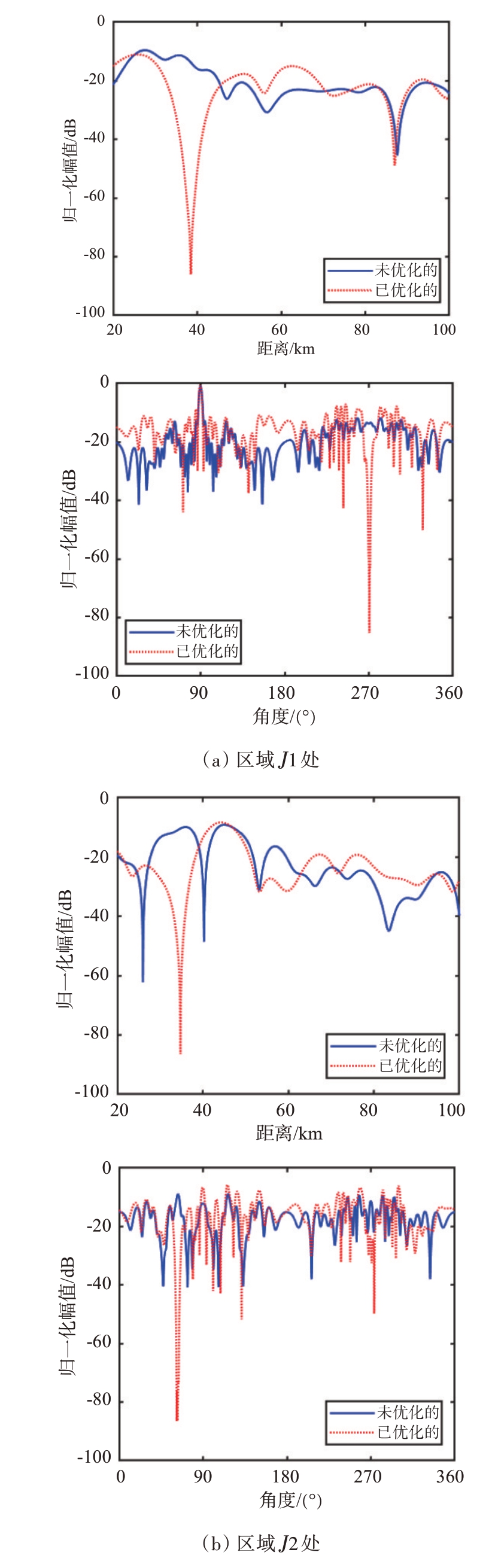
图6 单波束多零陷剖面图对比
3.2 多波束零陷
环形阵列具有多波束合成的能力,当波束聚焦点为(rp1,θd1)=(40 km, 90°),(rp2,θd2)=(60 km,270°)和(rp3,θd3)=(80 km,180°)时,环形阵列未经相位补偿的多波束图如图7(a)所示,波束发生严重畸变,无法在所需位置处形成波束聚焦点。经过相位补偿后的多波束图如图7(b)所示,波束已经可以正确地指向目标所在区域,说明了相位补偿方案的有效性。当已知旁瓣抑制区域(rj1,θj1)=(38 km, 271°),(rj2,θj2)=(70 km,80°)以及(rj3,θj3)=(70 km,279°)时,针对单零陷进行验证,抑制区域为J3,经过优化后的单零陷波束图如图7(c)所示,可以观察到抑制区域的归一化幅值明显降低,抑制区域的波束剖面图如图8 所示,可以达到-80 dB 的零陷深度。针对多零陷进行验证,抑制区域为J1,J2 和J3,优化后的波束图如图7(d)所示,其可以在形成多波束的情况下在多个已知区域形成零陷。为了更清晰地展示其零陷性能,给出了3 个区域J1,J2 和J3 处的波束剖面图,3 个区域位置处均能形成-80 dB以上的零陷深度,如图9所示。需要说明的是,由于区域J2与J3到阵列的距离相同,仅角度不同,因此其角度域剖面图是一致的。经验证,所提出多波束环形频控阵可以在360°内形成多个波束且在干扰区域形成零陷,对于提高通信的安全性或防止干扰方面是有意义的。
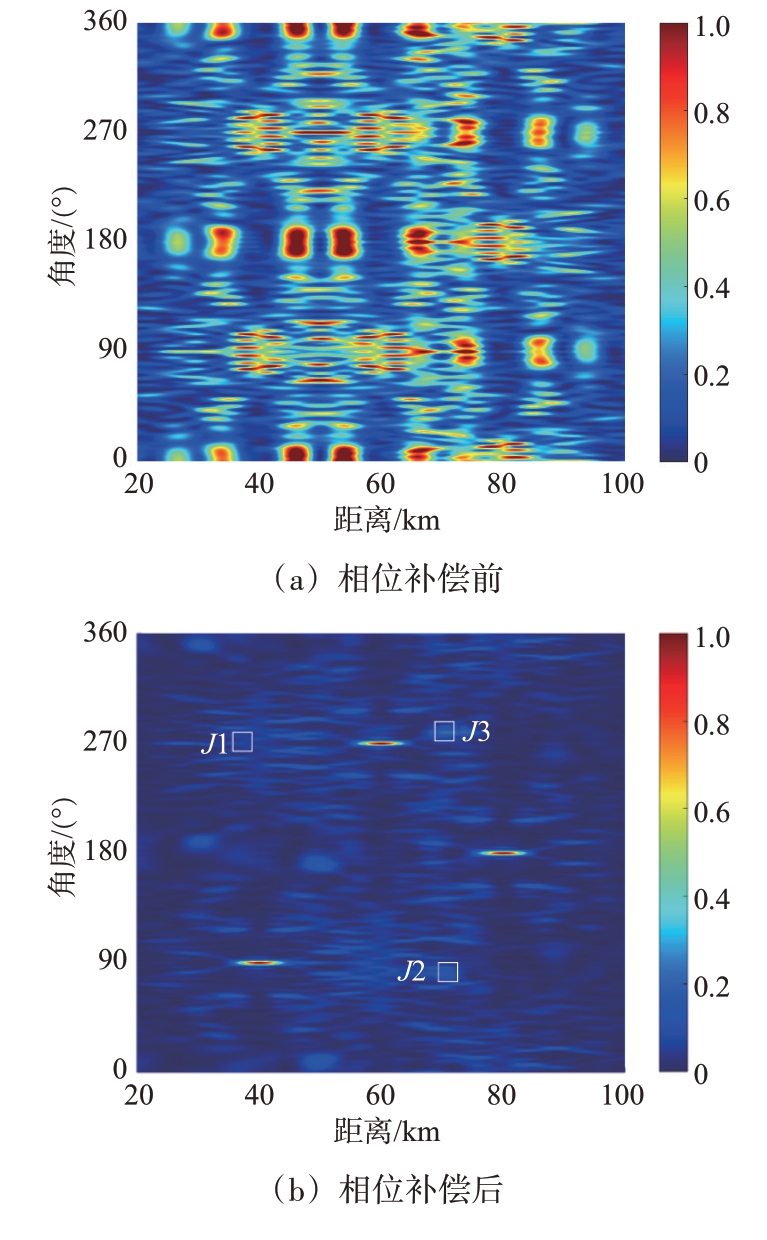
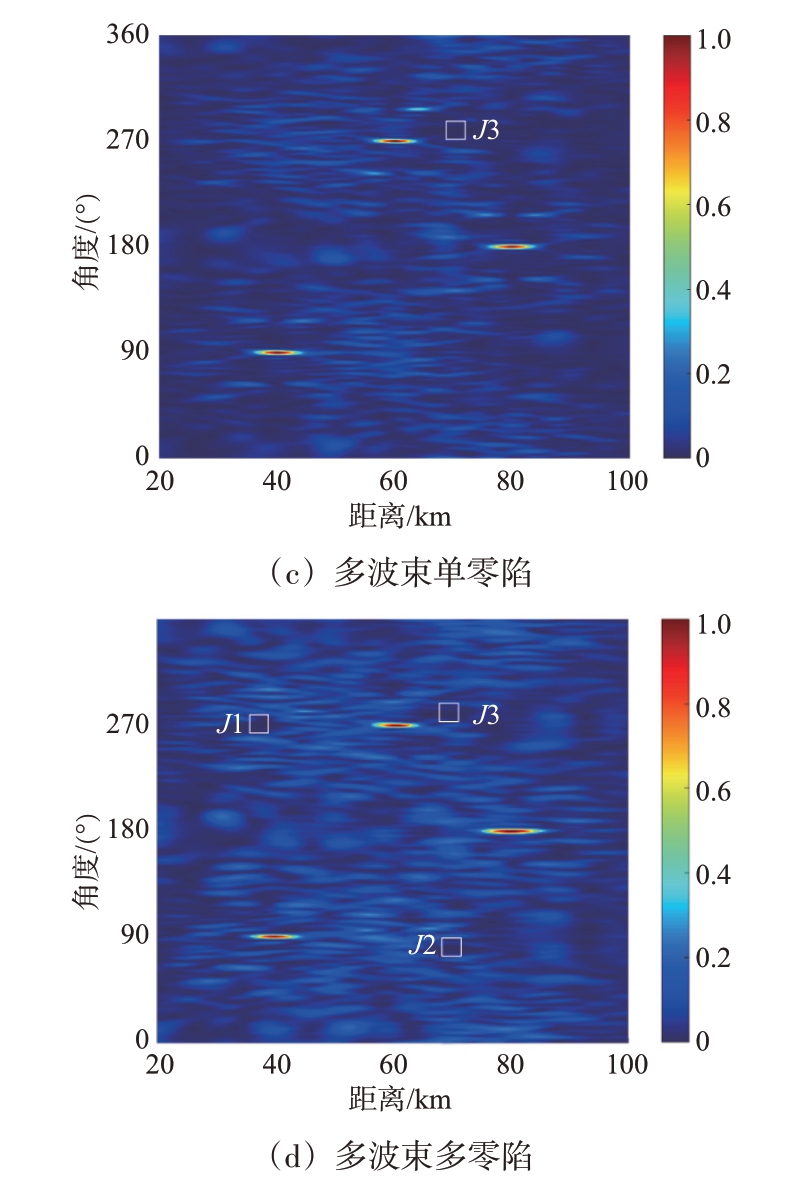
图7 多波束环形频控阵波束图
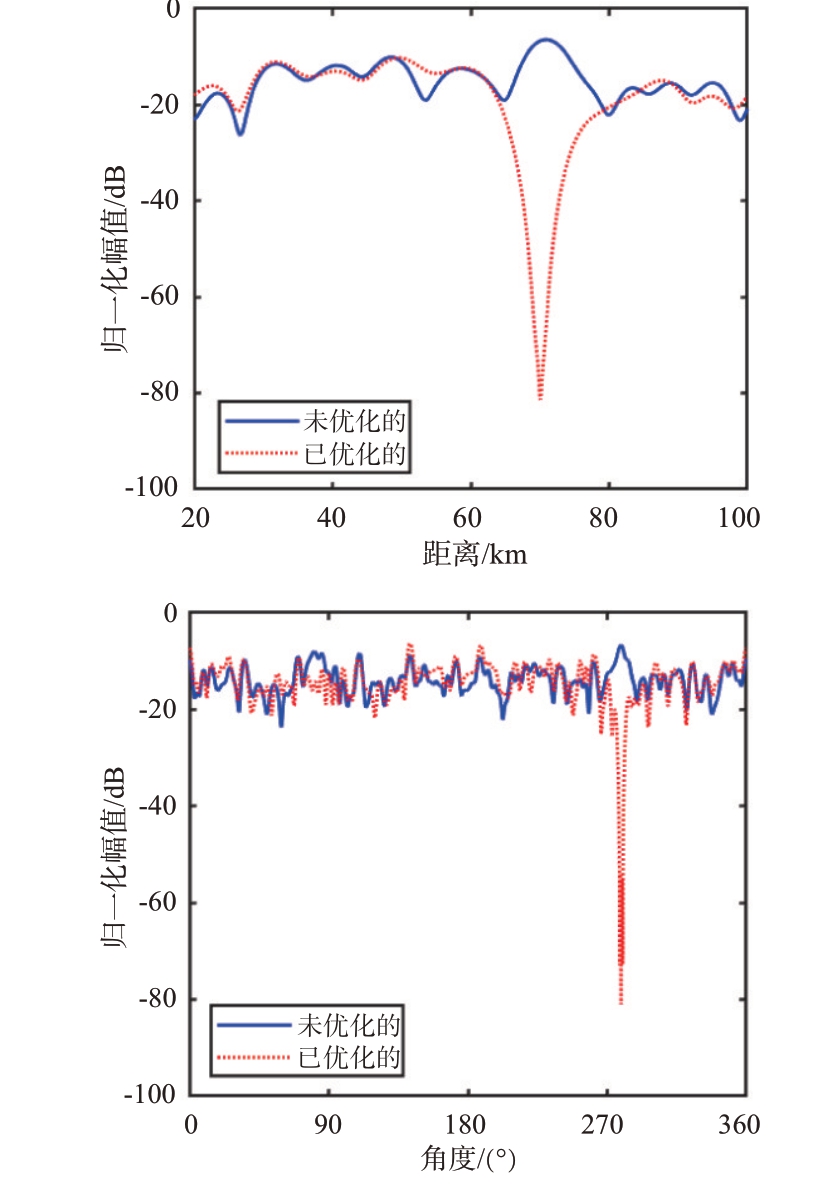
图8 多波束单零陷J3处的剖面图对比
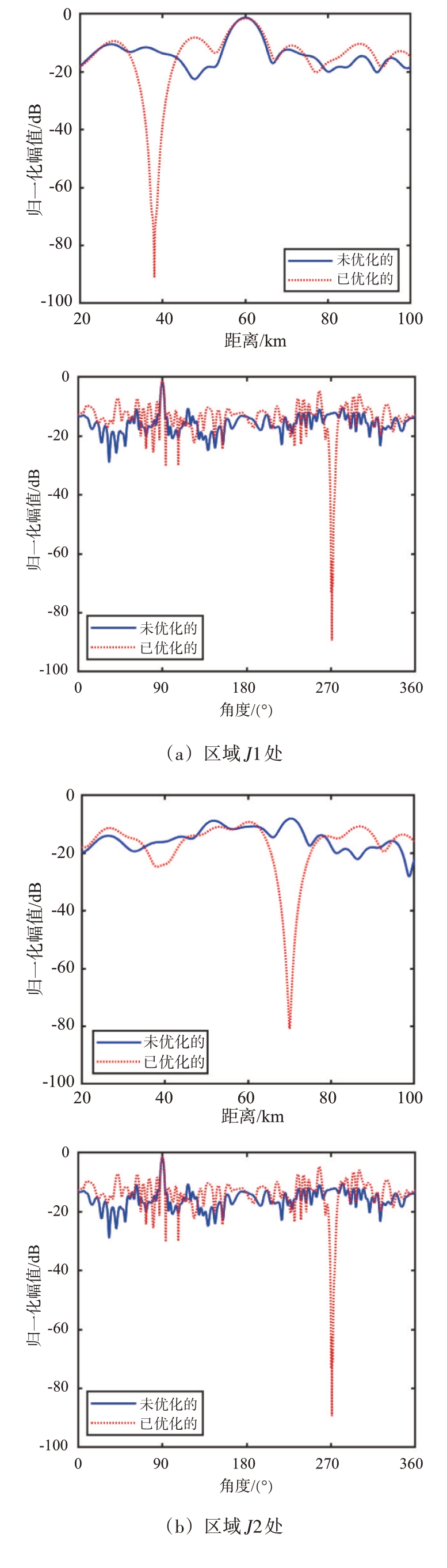
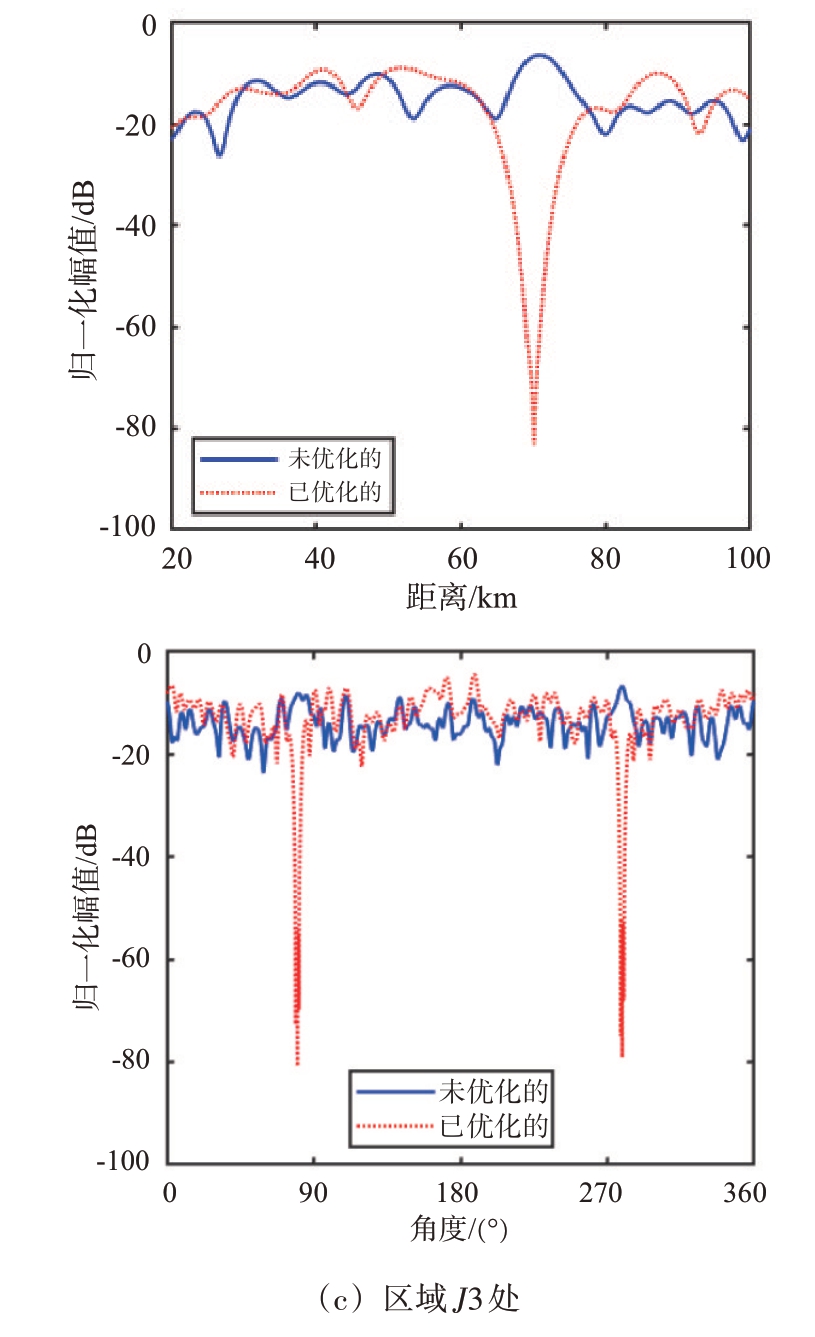
图9 多波束多零陷剖面图对比
4 结束语
本文提出了一种多波束环形频控阵零陷形成方法,首先通过将多个线性阵列组合来近似实现环形阵列结构,解决了理想环形阵列在物理实现上的困难。并利用相位补偿方案校正了环形阵列存在的波束畸变问题,可以实现在360°全向范围内形成多个可聚焦的波束。同时针对点对点通信过程中方向图优化和零陷控制问题,提出了多频载波信号与LCMV 相结合的零陷形成方法。将多频载波信号与二维LCMV相结合,在多波束条件的多个特定目标区域成功形成了零陷。仿真结果验证了本文所提方法的有效性,为复杂通信环境中的方向图优化和抗干扰能力提升提供了新的技术路径。
[1] 王文钦,陈慧,郑植,等.频控阵雷达技术及其应用研究进展[J].雷达学报,2018,7(2):153-166.
[2] 许京伟,朱圣棋,廖桂生,等.频率分集阵雷达技术探讨[J].雷达学报,2018,7(2):167-182.
[3] XU Yanhong, SHI Xiaowei, XU Jingwei, et al. Range-Angle-Dependent Beamforming of Pulsed Frequency Diverse Array[J]. IEEE Trans on Antennas and Propagation,2015, 63(7):3262-3267.
[4] AHMAD Zeeshan, CHEN Meng, BAO Shudi. Beampattern Analysis of Frequency Diverse Array Radar: A Review[J]. EURASIP Journal on Wireless Communications and Networking, 2021(1):189.
[5] XU Wei, ZHANG Lihua, BI Hui, et al. FDA Beampattern Synthesis with Both Nonuniform Frequency Offset and Array Spacing[J]. IEEE Antennas and Wireless Propagation Letters, 2021, 20(12):2354-2358.
[6] XIONG Jie, WANG Wenqin, SHAO Huaizong, et al. Frequency Diverse Array Transmit Beampattern Optimization with Genetic Algorithm[J]. IEEE Antennas and Wireless Propagation Letters, 2017, 16:469-472.
[7] LIAO Yi, TANG Hu, CHEN Xiaolong, et al. Frequency Diverse Array Beampattern Synthesis with Taylor Windowed Frequency Offsets[J]. IEEE Antennas and Wireless Propagation Letters, 2020, 19(11):1901-1905.
[8] XU Wei, DENG Zhuo, HUANG Pingping, et al. Beampattern Synthesis and Optimization for Frequency Diverse Arc Array Based on the Virtual Element[J]. Electronics,2023, 12(10):2231.
[9] SAEED S, QURESHI I M, KHAN W, et al. An Investigation into Uniform Circular Frequency Diverse Array(UCFDA) Radars[J]. Remote Sensing Letters, 2015, 6(9):707-714.
[10] RASTGARKISOMI S, MOHSENI ARMAKI S H,RASHIDI A J, et al. A Circular Planar Frequency Diverse Array for Monostatic Radar Applications[J]. Remote Sensing Letters, 2019, 10(9):835-843.
[11] 唐虎,曾光辉,廖轶,等.基于区间算法的频控阵阵元位置误差分析[J].系统工程与电子技术,2023,45(1):15-24.
[12] LIAO Yi, TANG Hu, LUO Zhibang, et al. Analysis of Frequency Offset Errors Through Interval Arithmetic in Frequency Diverse Arrays[J]. IEEE Trans on Aerospace and Electronic Systems, 2023, 59(3):3424-3431.
[13] WEN Hao, GU Pengfei, HE Zi, et al. Optimal Function-Based Frequency Offset Design Based on Polynomial Fitting for Frequency Diverse Array Beampattern Synthesis[J]. IEEE Antennas and Wireless Propagation Letters,2024, 23(1):149-153.
[14] VAIDYANATHAN P P. A Note on the Unit-Circle-Zeros Property of the MVDR Beamformer[J]. IEEE Signal Processing Letters, 2024, 31:171-175.
[15] 巩朋成,吴云韬.基于ADMM 改进的低截获FDA-MIMO雷达发射波束设计[J].通信学报,2022,43(4):133-142.
[16] CHENG Jie, WANG Wenqin, HOU Yudian, et al. Multipath Jamming Suppression and Target Detection Based on FDA Radar[J]. Journal of Signal Processing, 2022, 38(1):28-34.
[17] SHAO Xiaolang, HU Taiyang, ZHANG Jinyu, et al. Synthesis of Frequency Diverse Array with Large Null Depths via a Hybrid Optimization Approach of Mayfly Algorithm and Convex Programming[J]. IET Signal Processing, 2022, 16(9):1085-1093.
[18] 严济鸿,王顺祥,居宇欢,等.一种频控阵鉴别距离欺骗目标方法的优化[J].雷达科学与技术,2023,21(2):215-221.
[19] 张晶,王博,孟国祥,等.频控阵雷达对雷达侦察测向的欺骗机理研究[J].航空兵器,2024,31(1):71-76.
[20] CHEN Kejin, YANG Shiwen, CHEN Yikai, et al. Accurate Models of Time-Invariant Beampatterns for Frequency Diverse Arrays[J]. IEEE Trans on Antennas and Propagation, 2019, 67(5):3022-3029.
[21] LIAO Yi, ZENG Guanghui, LUO Zhibang, et al. Time-Variance Analysis for Frequency-Diverse Array Beampatterns[J]. IEEE Trans on Antennas and Propagation,2023, 71(8):6558-6567.