0 引 言
雷达伺服转台是雷达的重要组成部分,为雷达实现跟踪目标和定位测量等功能时提供精确动力转向和支撑作用,其控制精密程度会直接影响到雷达最终观测结果。在转台传动机构运行时,齿轮啮合位置接触齿面受力的同时,非接触齿面之间的齿隙会在转台加减速变换瞬间带来一定滞后性,使得整个传动机构的输入与输出之间的线性度降低,并且随着转台传动机构的磨损,齿隙也会增大,这就会给雷达系统带来更多的非线性位置误差,因此,如何有效地消除齿隙带来的传动误差成为业内一直关注和研究的问题。
针对传动机构齿隙的消除,现阶段多采用双电机或多电机消隙驱动的方式,文献［1］论述通过加入偏置力矩实现双电机消隙的原理,实现消除齿隙的非线性影响。文献［2］进一步对双电机消隙模型的偏置力矩进行了探索,通过对4种偏置力矩施加形式进行分析和对比,论述了不同消隙控制过程对消隙效果的影响。然而所有的偏置力矩控制过程的处理只是对偏置电流输出过程的一种优化体现,并没有将实际传动机构运行状态与偏置电流范围进行匹配和关联,依据经验统一设定的偏置电流范围显然无法使得不同设备都能达到最佳的消隙效果。
随着人工智能和机器学习的发展,深度卷积神经网络（DCNN）是近年来深度学习领域快速发展的一个方向,具有较大的网络层数,因其优越的深层特征提取能力逐渐被推广用于检测识别机械设备的状态中,文献［3］提出的基于CWT-DCNN 模型可实现船用齿轮箱故障,文献［4］将ResNet 网络与常规深度卷积网络进行对比证明其高精度和有效性,文献［5］提出通过短时傅里叶变换提取桥臂电压信号中的故障特征进而结合深度置信网络实现故障类型的检测与定位,文献［6］提出利用智能提升小波核的可解释网络LW-Net 进行机械特征提取和故障诊断,文献［7］提出利用轴承加速度信号等物理特性指导设计CNN 参数规格,使得网络分析更加精确,文献［8］提出的ResNet-SVM 模型的特征提取器对故障的诊断实验准确率可超过99.9%。多种研究和应用结果表明,深度学习在评估设备状态层面有着较为优越的性能,因此本文基于某型雷达伺服转台系统,提出一种基于DCNN的雷达伺服转台消隙策略,能够利用雷达伺服转台传动机构的振动信号评估出当前齿隙磨损状态,进而准确指导消隙策略的控制参数,以达到最佳消隙效果,提高雷达伺服转台精度和可靠性。
1 齿隙与双电机消隙
1.1 齿轮传动误差分析
两个齿轮相互啮合时工作齿面相互接触,在其非工作齿面间所形成的间隙称之为齿隙。齿隙作为伺服传动机构设计中的重要考虑部分,受到机构制造、安装过程以及后期转台运行磨损等多重影响,最终会体现到机构的末级传动误差上,也就是我们常说的伺服机械精度。
末级传动误差的计算：转台主齿轮齿距累计公差为Fpd,小齿轮齿距累积公差为Fpx,末级齿轮副齿距累积误差为Fp=Fpd+Fpx,所以半径为rd的末级齿轮副齿距累积误差造成的传动误差角度φ为
传动误差的存在会导致伺服转台在加减速换向过程以及低速爬行过程中产生振荡,从而影响到整个转台的控制精度。
1.2 双电机消隙策略设计
雷达伺服转台采用双电机驱动的结构形式,通过双电机消隙来达到精密跟踪功能。双电机消隙具体是将两个电机通过减速机带动小齿轮与转台大齿轮啮合,并按双电机消隙动态偏置力矩曲线进行驱动,任意时刻至少有一个电机会对主齿轮施加不为0 的转矩,在此转矩的作用下,消除转台大齿轮的运动间隙。
双电机驱动结构形式完全相同,如图1所示由伺服电机、减速机、小齿轮和安装板组成,其中小齿轮与回转支承外齿啮合齿隙通过调整安装板位置来调节,一般单侧末级传动链齿隙控制在0.3～0.5 mm之间可认为是正常无磨损状态。
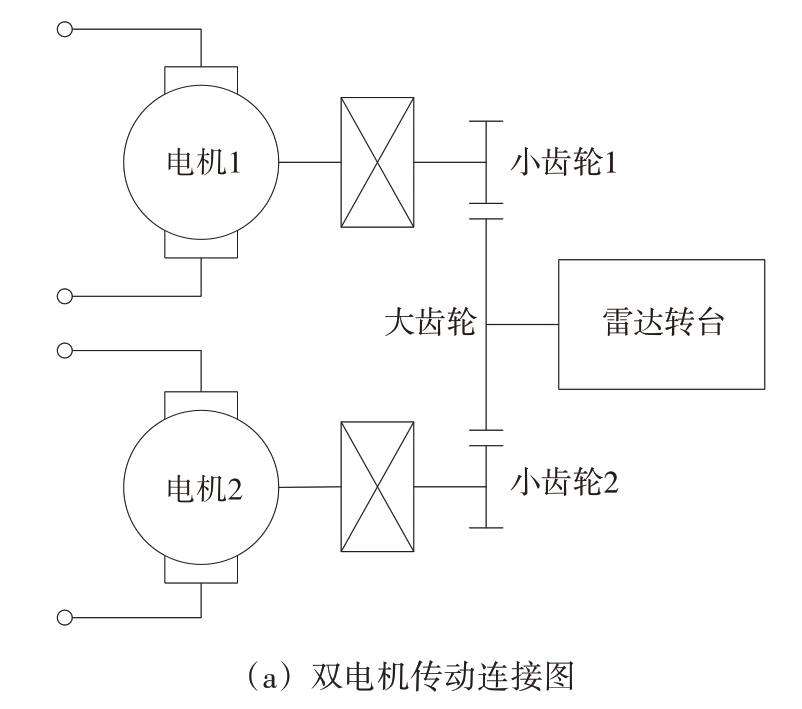
图1 双电机消隙转台示意图
对于实际伺服转台系统,齿隙大小和双电机消隙偏置力矩大小紧密相关,而双电机偏置力矩与控制偏置电流关系如图2 所示。大量的设备实践过程发现,若偏置电流过小,齿轮齿廓接触强度被削弱,从而双电机消隙效果变差,系统精度降低。若偏置电流过大,齿轮齿廓接触强度加大不仅消耗系统能量还会加剧齿隙啮合处的磨损,加快伺服转台系统动态特性衰减的过程。因此根据齿隙大小和磨损状况匹配相合适的消隙偏置电流,将对伺服转台系统的可靠性提升有着至关重要的作用。
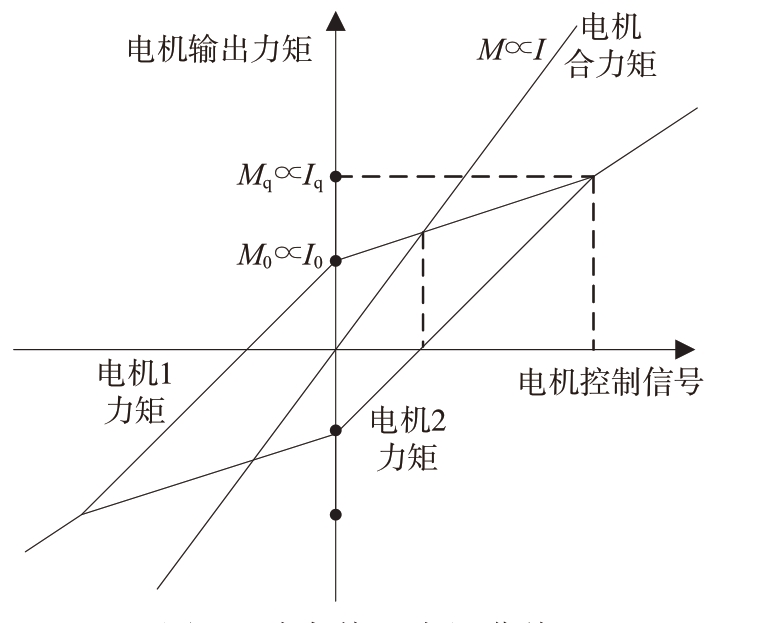
图2 动态偏置力矩曲线
2 时频特征深度卷积网络
精密雷达伺服转台传动机构出现齿隙磨损表现形式为雷达机械跟踪精度降低,其特征包含在转台动态运行过程的振动信号中,而振动信号的时域分析仅能有限地观察到振幅变化,对于需要做到机构磨损程度的判断来说远不够。时频图能反映信号所有频率成分随时间的变化关系,二维图像包含信息量更大,更适合作为深度学习训练输入的样本,而深度卷积神经网络相比于传统网络,其更深的层级结构能够学习到更加复杂的特征表示,从而极大增加了分析判定结果的准确性。
2.1 连续小波变换
目前较为常用的将时域信号转变为时频信号的方法有短时傅里叶变换（STFT）和连续小波变换（CWT）两种,文献［9-10］分别采用了STFT 和CWT 两种方式对机械振动信号进行时域频域特征的提取,其中STFT 较早被用于处理非线性信号时频特征提取,但由于其窗口函数长度固定,导致了STFT 变换对信号中高低频的差异区分较差,而小波变换通过可变的尺度因子,实现了窗长的变化,尺度因子与窗长的乘积为乘积常数,可以很好地保证取得时域与频域之间的平衡,表现出优越的自适应及多分辨率特性。因此本文采用CWT对伺服转台传动机构振动信号进行时频处理。其理论如下：
选取基本小波ψ(t),且ψ(t) ∈L2(R),得到小波基系数为
式中a为尺度参数,b为位置参数,且a,b ∈R,a > 0。从而对任意信号f(t) ∈L2(R),其CWT表达式为
代入式（2）得到信号f(t)的CWT表达式为
式中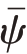
为小波函数ψ 复共轭。本文分别选用Morlet 小波和Bump 小波函数作为CWT 的小波基函数,两种均为CWT 获取信号时频表示的方法中较为常用的小波基,具有振荡衰减特征,可较好拟合突变信号从而能够良好地匹配伺服转台动态过程的振动信号,Morlet小波函数定义为
式中ω0 为中心频率参数,t 为时间。典型Bump 小波函数定义为
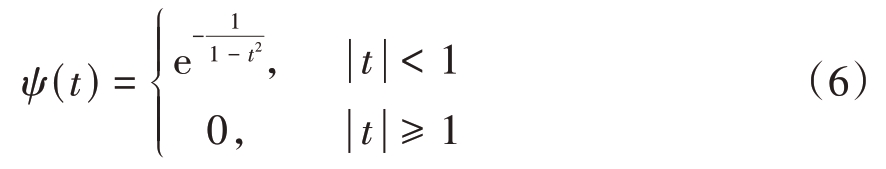
时间t 在区间（-1,1）内是光滑的,且区间外为0,具有良好局部性和光滑性。
2.2 深度卷积神经网络
深度卷积神经网络（DCNN）因其具有较大的网络层数,可以“深度”进行卷积和池化逐层提取输入图像特征,极大提高了模型分类效果。本文模型采用深度残差网络ResNet50 模型作为参考设计训练和识别模型,ResNet50 模型结构如图3 所示。
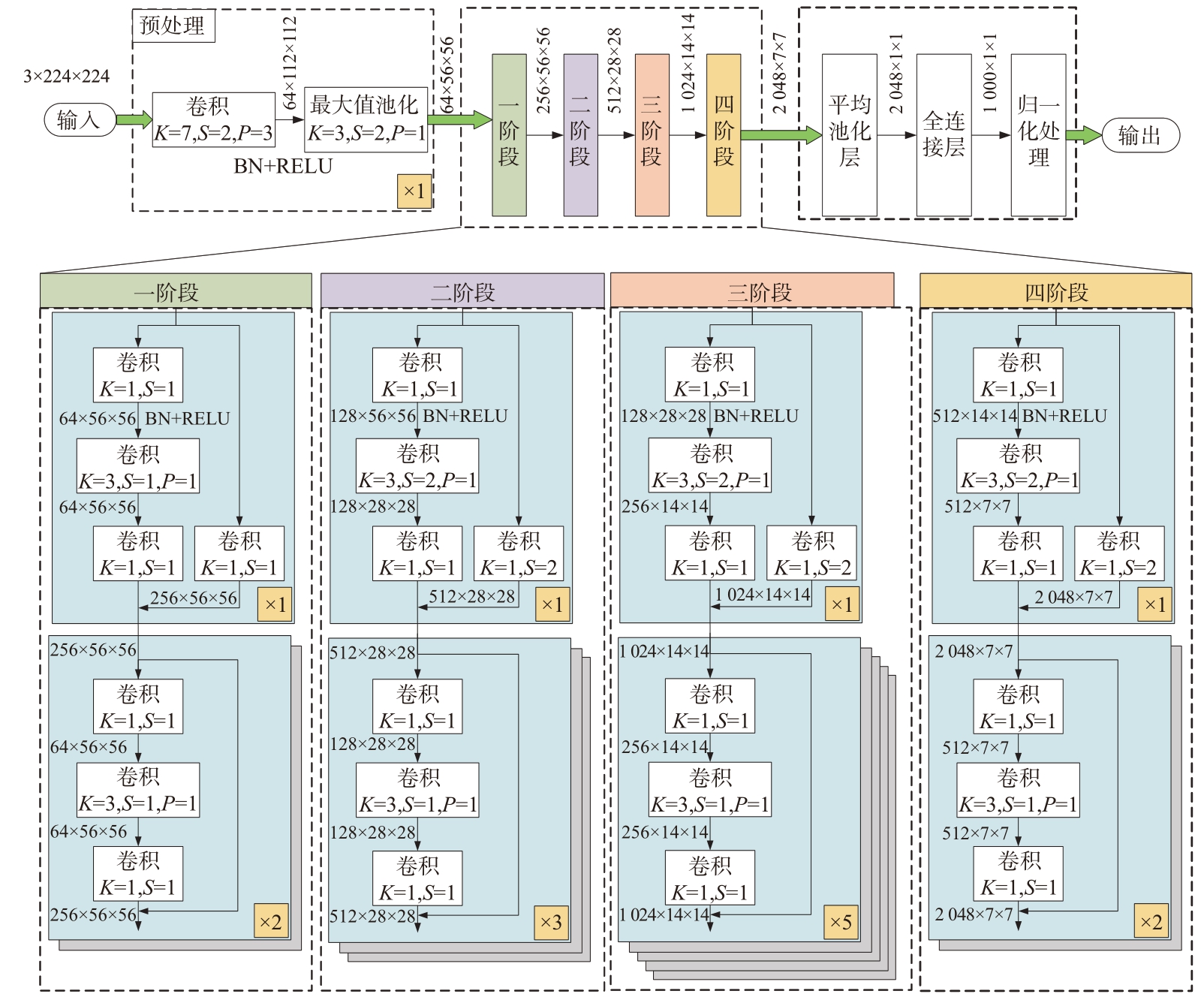
图3 深度残差网络模型架构
在输入层输入RGB 三通道尺寸为224×224 像素图像后,经过预处理的单独卷积运算后依次再经历4 组阶段运算,最终通过平均池化层、全连接层和回归分类得到输出。其中4 组阶段均为一个加入下采样的残差块和数个相同残差块构成,图中虚线框右下角数字表示相同残差块数量,K为卷积核尺寸,S为步长,P为填充像素。残差块通过卷积层进行残差学习,ResNet50 通过残差块来进行特征传递,可有效解决梯度消失和梯度爆炸的问题,相比传统网络结构,残差块提供了更直接的路径传递梯度,使得网络更容易训练和收敛。
3 测试与验证
为使整个采样训练结果能够准确反映转台齿隙真实状况,对消隙策略提出有效修正指导,试验将振动传感器安装在雷达伺服转台内与消隙电机啮合的传动齿轴心同轴方向,通过调整传动齿安装板位置改变齿隙大小,从而模拟不同磨损程度的齿隙。采集4 组不同齿隙下转台低速爬行振动信号,通过对信号的去噪、分段等步骤处理将其分成多个一定长度的小段信号,再对这些小段信号分别进行时频变换,利用得到的4组时频图数据集对DCNN模型进行训练,再用训练好的模型对不同齿隙下的转台低速爬行振动信号进行识别分类,根据磨损程度的判定结果对应的调节消隙策略,最后对比位置环稳态误差进行效果验证,整个试验流程如图4所示。
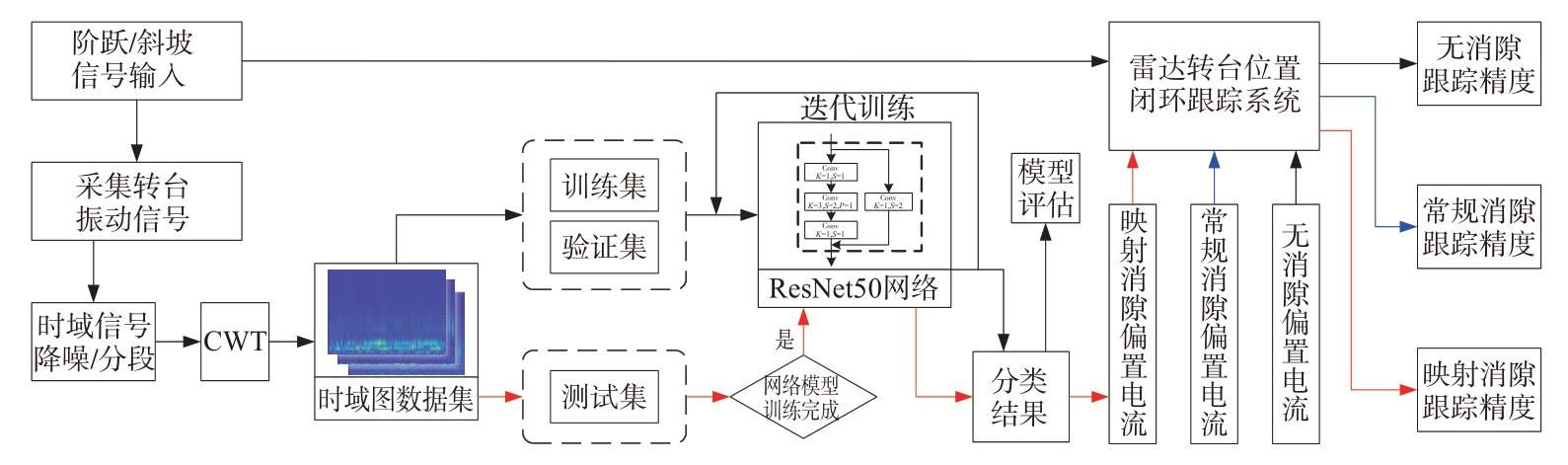
图4 训练、测试与对比验证流程图
3.1 数据采集与处理
考虑到消隙控制主要体现在加减速换向过程中,该过程大多会出现在定位指向位置闭环扰动以及低速爬行克服摩擦力矩转动的过程中,因此本试验设定雷达伺服转台按照位置闭环输入0.1°阶跃信号以及斜率为0.1°/s 斜坡信号进行定位指向和低速爬行测试,以此提高模型泛化能力和鲁棒性。如表1 所示将伺服转台传动机构按齿隙大小与磨损程度对应分为4组,采集时长均为10 min,得到4个测量点位振动量的时域信号。
表1 振动时域信号数据分组
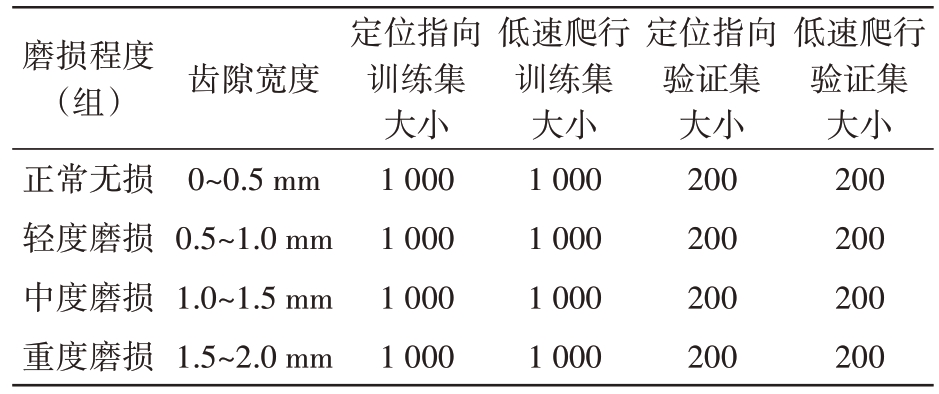
磨损程度（组）正常无损轻度磨损中度磨损重度磨损齿隙宽度0～0.5 mm 0.5～1.0 mm 1.0～1.5 mm 1.5～2.0 mm定位指向训练集大小1 000 1 000 1 000 1 000低速爬行训练集大小1 000 1 000 1 000 1 000定位指向验证集大小200 200 200 200低速爬行验证集大小200 200 200 200
考虑到声音振动等随机振动带来的影响,又对每组时域信号进行小波变换阈值去噪预处理,减少后期网络学习计算负担并提高模型性能。具体流程如图5所示,原始信号和噪声信号在小波分解后通过计算通用阈值进行软阈值和硬阈值去噪,重构后可再次得到4组时域信号。
图5 小波阈值降噪步骤
最后将每组600 s 的重构时域信号按0.5 s 间隔截取成1 200 段,其中1 000 段作为之后的训练集,200段作为之后的验证集。
3.2 时频图生成
本试验通过CWT 方式分别对每组2 400 段时域信号进行处理。具体为先将分段信号通过一个图基窗口,避免截断产生的跳变带来吉布斯效应污染信号频谱,再对分段信号CWT处理,分别采用Morlet小波和Bump小波作为小波基。分组时域信号和对应某分段时频图如图6所示。
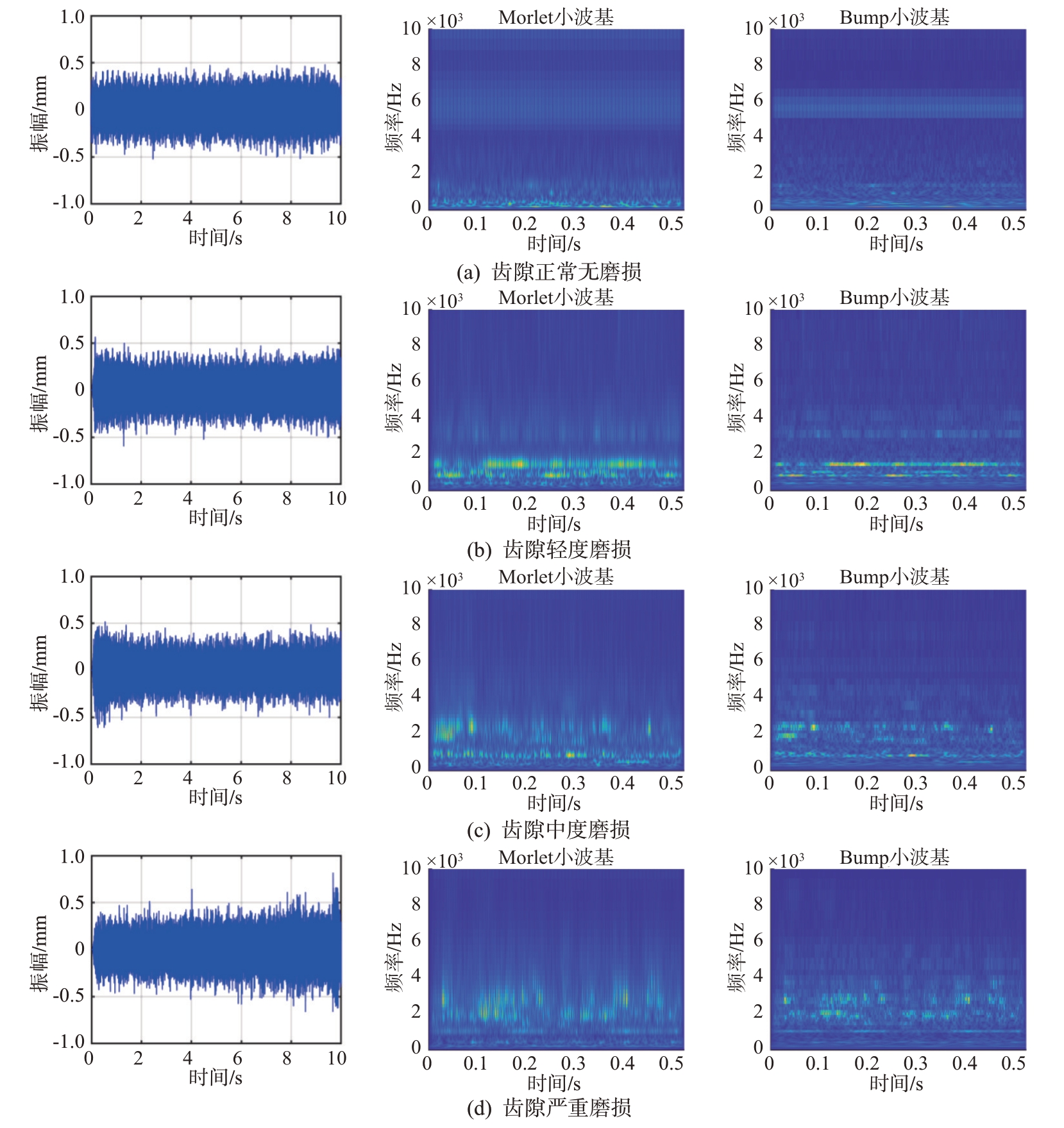
图6 不同磨损情况下振动信号时域图和时频图
由图6（a）的时频图可以看出,当齿隙状态良好时（处于消隙效果较好或者无磨损状态下）,驱动器载波频率6 kHz 能隐约体现出来。由图6（b）可知齿隙轻度磨损时低频段能量较为明显,但随着齿隙加大,从中度磨损程度到严重磨损程度,图6（c）和图6（d）表现为时频图高频段逐渐明显。
3.3 识别与消隙策略更新
3.3.1 模型训练
如表1 所示,将通过Morlet 连续小波变换得到的4 组共4 800 张时频图按5:1 比例分为训练集和验证集,经过迭代训练后,得到训练好的CWTDCNN 模型可以对振动时域信号进行识别分析,得出分类信息映射到消隙控制策略的偏置电流占比,改变偏置电流及对应的拐点电流值,通过同样的位置闭环控制模式后,比较实测角度误差大小情况,验证本文方法的有效性。
在使用DCNN 模型训练时,设定ResNet50 网络的最小批量数据（batch size）为64,初始学习率（initial learn rate）为常数0.01,最大迭代次数（epoch）为300,测试验证设定迭代次数为50,最终得到训练好的模型。训练主要阶段数据记录如表2所示,从表中可看出随着迭代次数增加,小批量损失和验证损失均为下降趋势,基本当进行200次迭代后模型趋于稳定,最终300次迭代后模型准确率达到99.17%。
表2 训练过程记录
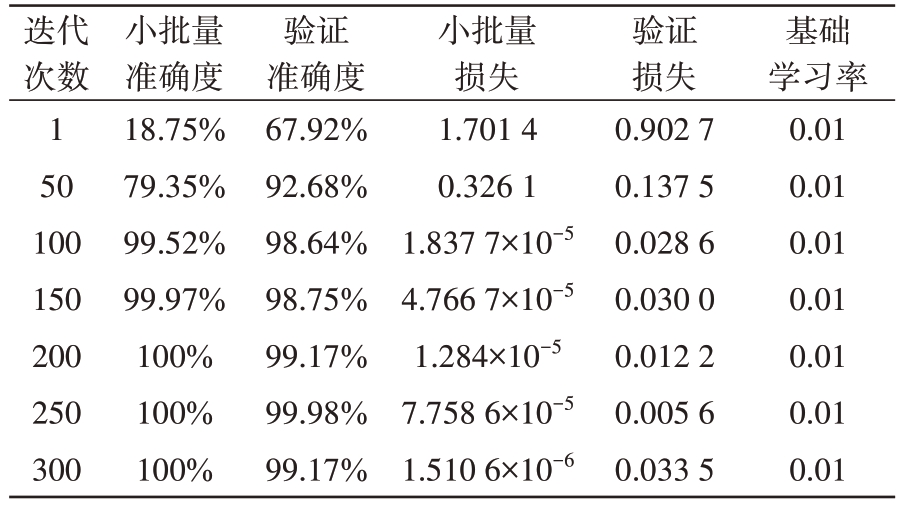
迭代次数1 50 100 150 200 250 300小批量准确度18.75%79.35%99.52%99.97%100%100%100%验证准确度67.92%92.68%98.64%98.75%99.17%99.98%99.17%小批量损失1.701 4 0.326 1 1.837 7×10-5 4.766 7×10-5 1.284×10-5 7.758 6×10-5 1.510 6×10-6验证损失0.902 7 0.137 5 0.028 6 0.030 0 0.012 2 0.005 6 0.033 5基础学习率0.01 0.01 0.01 0.01 0.01 0.01 0.01
为了验证方法的有效性,同样的处理过程再通过Bump 连续小波变换进行一遍,最后将模型分类结果分别进行混淆矩阵分析,并对模型归一化处理的SoftMax 层激活值做t-SNE 分析可实现数据集聚类的可视化,如图7所示。图中不同磨损程度聚类效果较好,虽然中度磨损出现极少的聚类错误,但错误聚类介于轻度磨损和重度磨损之间,没有出现跳跃式跨类混淆,如图7（b）所示。因此对于之后的偏置电流映射环节,可以确保高准确性分类映射到合适偏置电流的同时,能够避免正常齿隙匹配偏置电流过大导致消隙效果过强,从而加剧传动齿磨损,或者重度磨损齿隙匹配过小偏置电流导致消隙效果变弱,位置闭环精度降低的情况。
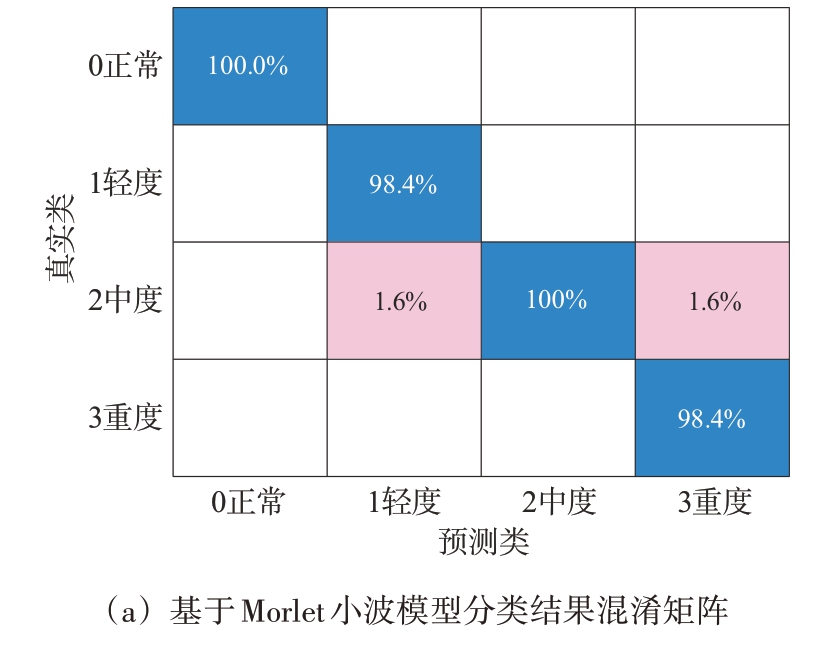
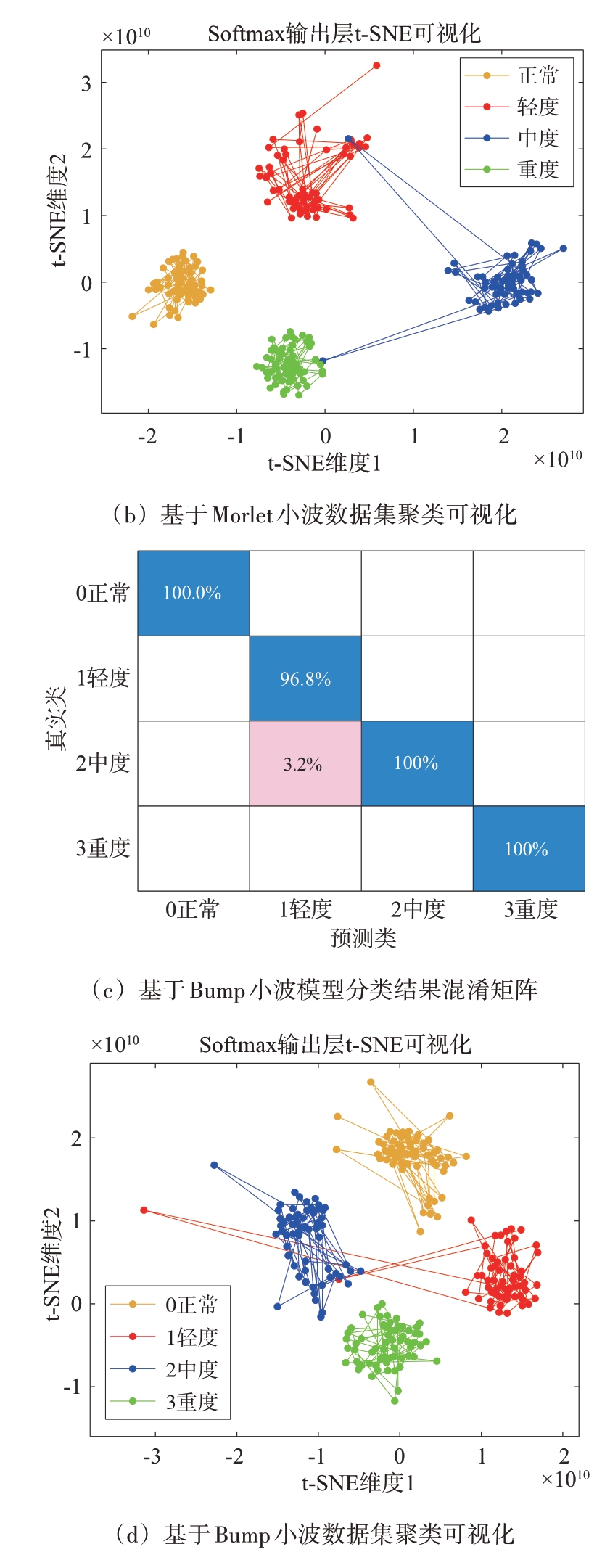
图7 DCNN模型识别效果分析
通过图7（a）和图7（c）对比可知,用Bump 小波替换Morlet 小波生成的时频图数据集对最终深度卷积神经网络的分类效果相近,验证了本文方法的有效性。
3.3.2 映射消隙效果对比
模型训练好后,再次对4组试验雷达伺服转台进行位置闭环输入0.1°阶跃信号以及位置环0.1°/s斜坡信号输入试验,得到处理后的时频图作为测试组,再根据表3的分类映射消隙关系修改偏置电流以及拐点电流大小,拐点电流设定为偏置电流大小的2 倍,表中占比即偏置电流占额定电流比例,该比例结合Morlet 小波时频图训练的DCNN 模型的归一化分类概率向量进行设定,即预测结果标签i 按磨损程度加深对应5%、10%、15%、20%的4个偏置电流占比分级xi,再乘以SoftMax层输出值Pi,求和得到映射偏置电流占比期望：
表3 齿隙宽度分组与消隙策略跟踪测试结果
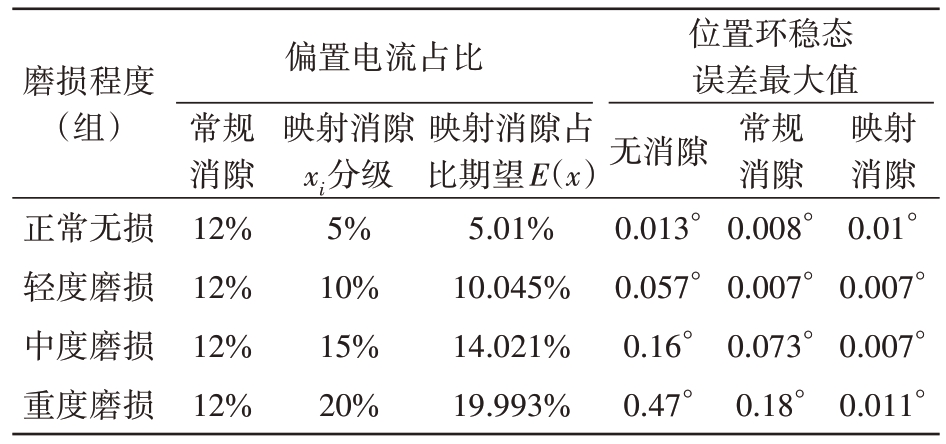
磨损程度（组）正常无损轻度磨损中度磨损重度磨损偏置电流占比常规消隙12%12%12%12%映射消隙xi分级5%10%15%20%映射消隙占比期望E（x）5.01%10.045%14.021%19.993%位置环稳态误差最大值无消隙0.013°0.057°0.16°0.47°常规消隙0.008°0.007°0.073°0.18°映射消隙0.01°0.007°0.007°0.011°
此方法使得系统偏置电流连续自适应控制,映射结果更加合理。例如图8 所示为测试集中随机选取的一张中度磨损时频图测试DCNN 模型归一化输出概率向量结果P1为0%、P2为99.1%、P3为0.9%、P4为0%,根据式（7）计算可得此时映射消隙偏置电流占比为10.045%。
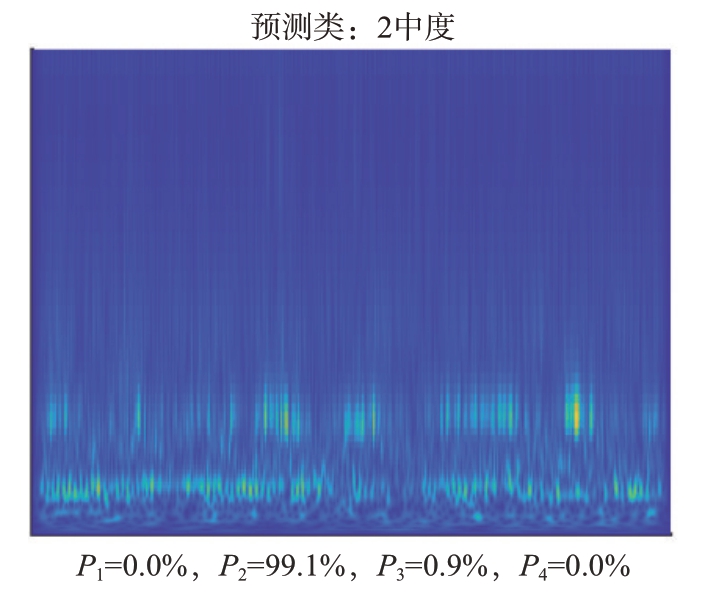
图8 测试归一化输出
按上述方法分别测试记录加入映射消隙控制下位置环跟踪进入稳态后误差最大值。
重复试验步骤,记录未加消隙控制和常规消隙控制两种情况下的位置环跟踪稳态误差,对比验证新消隙策略效果。
图9（a）为中度磨损试验组在无消隙、常规消隙和映射消隙三种消隙控制策略下的位置环误差随时间变化情况,该试验组可以较为明显地看出设备中度磨损时常规消隙的效果已经有所减弱,而映射消隙由于偏置电流是随着识别到磨损程度映射变化的,因而仍然能很好地保持位置环精度。图9（b）反映出常规消隙效果会随着设备磨损程度逐渐加深而减弱,从而无法保持高精度跟踪,而映射消隙鲁棒性较好,误差波动很小。同时证明了随着齿隙宽度变化利用训练好的DCNN模型进行识别和不断调整消隙偏置电流策略的有效性。
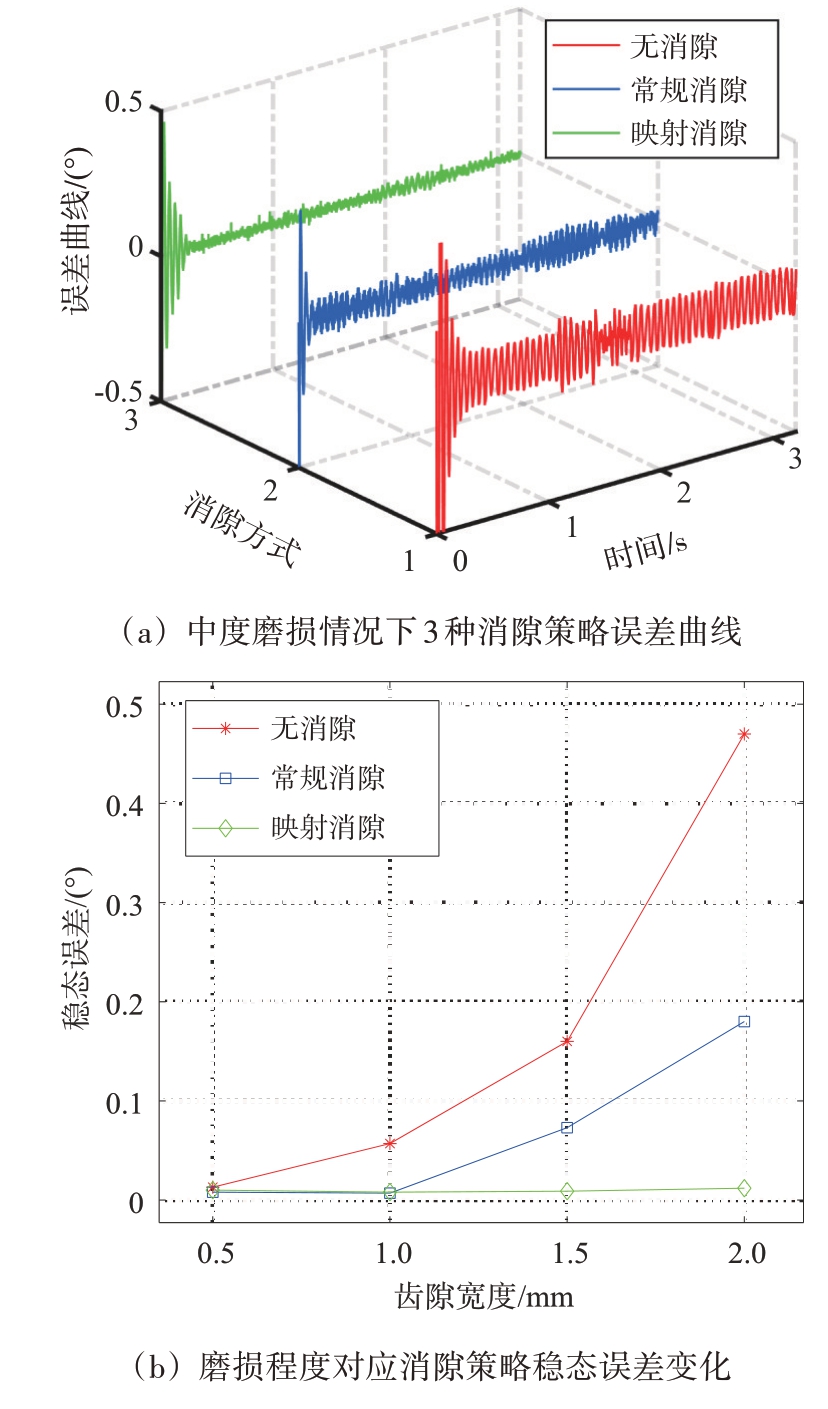
图9 不同消隙策略对应磨损程度下的跟踪误差对比
4 结束语
本文对精密雷达伺服转台的消隙策略进行研究,传统双电机或多电机消隙策略是依据经验设定偏置电流有效范围,这种方式对于工况较好的新设备浪费功率的同时还加剧了磨损,而对老旧传动机构磨损设备则会表现出消隙效果不足、精度下降等问题。对此本文提出了基于深度卷积神经网络的雷达伺服转台消隙策略,可以对转台传动机构振动信号的时频图提取特征,深层数的训练学习确保了模型的分类效果,最后通过实验验证训练好的模型能够准确对传动机构齿隙进行识别分类,以分类映射消隙的方式动态匹配以适合的偏置电流从而保证雷达伺服转台的机械跟踪精度,对提升雷达装备系统运行的可靠性、降低雷达伺服转台的维护成本有着重要意义。
［1］ 汤辉,吴影生.双电机驱动精密二维测试转台伺服系统设计与实现［J］.电子机械工程,2009,25（5）:38-40.
［2］ 刘增辉.大惯量随动系统双电机同步消隙控制方法研究［D］.杭州：浙江大学,2019.
［3］ 杜世一.基于CWT-DCNN 的船用齿轮箱在线状态监测研究［D］.哈尔滨：哈尔滨工业大学,2022.
［4］ 卓奕弘,熊敬伟,潘继飞,等.基于多尺度注意力机制ResNet 的雷达工作模式识别［J］.雷达科学与技术,2024,22（2）:170-179.
［5］ 朱琴跃,于逸尘,占岩文,等.基于短时傅里叶变换和深度网络的模块化多电平换流器子模块IGBT 开路故障诊断［J］.电工技术学报,2024,39（12）:3840-3854.
［6］ YUAN Jing,CAO Shuwei,REN Gangxing,et al.LW-Net:An Interpretable Network with Smart Lifting Wavelet Kernel for Mechanical Feature Extraction and Fault Diagnosis［J］.Neural Computing and Applications,2022,34（18）:15661-15672.
［7］ RUAN Diwang,WANG Jin,YAN Jianping,et al.CNN Parameter Design Based on Fault Signal Analysis and Its Application in Bearing Fault Diagnosis［J］.Advanced Engineering Informatics,2023,55:101877.
［8］ ZHANG Xiancheng,PAN Xin,ZENG Hao,et al.Intelligent Diagnosis Method for Typical Co-Frequency Vibration Faults of Rotating Machinery Based on SAE and Ensembled ResNet-SVM［J］.Chinese Journal of Mechanical Engineering,2024,37（1）:1-16.
［9］ PENG Binsen,XIA Hong,LV Xinzhi,et al.An Intelligent Fault Diagnosis Method for Rotating Machinery Based on Data Fusion and Deep Residual Neural Network［J］.Applied Intelligence, 2021, 52（3）:3051-3065.
［10］ GU Jun,PENG Yuxing,LU Hao,et al.A Novel Fault Diagnosis Method of Rotating Machinery via VMD, CWT and Improved CNN［J］. Measurement, 2022, 200:111635.