0 引 言
雷达信号识别[1]是电子战中电子侦察的重要步骤,战场电磁环境逐渐复杂化,新型体制雷达信号得到了各方广泛的青睐,其中低截获概率(Low Probability of Intercept,LPI)雷达信号由于其很难被拦截接收机检测到的特点在众多信号中脱颖而出。随着深度学习的横向发展,所涉及的领域也越来越多,在低截获雷达信号识别领域,低截获概率雷达信号在低信噪比时识别准确率低且很多研究人员所采用的模型是单通道的神经网络,其需要大量的数据集做支撑,才能够训练出比较好的网络模型。由于低截获雷达信号的难以捕捉性,能够获得的数据量往往并不充足,这大大增加了样本数量不足且低信噪比时的低截获概率雷达信号的识别难度。
王海英等[2]分析了几种典型LPI 雷达信号的脉内特征,梳理了LPI雷达信号调制识别及参数估计的传统和主流方法,并说明其原理、优缺点和研究现状。苏丹宁等[3]在文中表示在小样本条件下,由于样本数量不足等问题,深度学习模型识别准确率和稳定性大大下降。为改善样本不足条件下LPI 雷达信号识别准确率低的问题,不同的学者所采用的办法也是大相径庭。如石涵宇等[4]提出了一种基于分数阶频谱四阶原点矩的识别方法,且具有较好的识别效果,但存在计算复杂度大的问题;Xiao 等[5]提出了一种新的短时傅里叶变换(Short-Time Fourier Transform,STFT)和k-means 时频转换方法,该方法在信噪比为-8 dB 时识别准确率在90%以上;Huang 等[6]提出了一种多重自相关联合决策模型,得到了表征同一信号的多个时频图像(Time-Frequency Image, TFI);于濛等[7]提出一种稀缺样本条件下基于迁移学习的雷达信号识别及其优化算法,该方法在识别稀缺样本目标时训练时长短,识别精度高;庞伊琼等[8]针对小样本问题设计了一种由CNN和LSTM组成的并行网路,引入了信号类内与类间距离的联合损失函数;为了改善常规调制信号分选准确率低的问题,王华华等[9]提出了三网联合算法,即利用GAN 降噪、CNN和LSTM 来识别和分选,此方法使得整体分选率提升了2%~7%;文献[10]提出了一种基于Choi-Williams 分布和多重同步压缩变换(MSST)的双通道卷积神经网络模型实现对雷达信号的识别;Ni等[11]提出了一种基于傅里叶的同步压缩变换(FSST)与多分辨率融合的方法,在SNR=-8 dB 时,识别准确率达到了85.2%;Yao 等[12]试图利用深层卷积生成对抗网络(Deep Convolutional GAN, DCGAN)生成多类别和高质量的雷达信号TFI,但导致非常冗余的网络结构且增加计算成本。
齐美彬等[13]提出一种基于密集连接卷积网络(Densely Connected Convolutional Networks, Dense-Net)的雷达辐射源信号分选算法;徐帅等[14]提出了一种原型网络(Prototypical Networks, P-Net)的雷达信号识别算法,将视频信息映射到样本空间,最终在-2 dB 时识别率可达90%以上;文献[15]阐述提出了基于多重同步压缩(MSST)时频变换及方向梯度直方图(HOG)特征提取的雷达辐射源信号识别算法,在-8 dB 时,9种典型的雷达信号识别率达到了90%;于浩洋等[16]对DCGAN 模型进行了改进得到了SDCGAN,利用其生成逼近真实分布的样本,混合数据,构造新数据集,提高了小样本条件下雷达信号的识别精度;针对样本数据难获取、捕捉样本类别不全面等样本不足的小样本学习识别准确率不高的困境,提出基于数据增强的小样本辐射源个体识别方法。王艺卉等[17]针对样本数据难获取、捕捉样本类别不全面等样本不足的小样本学习识别准确率不高的困境,提出基于数据增强的小样本辐射源个体识别方法。Jiang等[18]提出了一种改进的元学习用于深度学习时间序列预测模型选择的元学习框架;谢智东等[19]设计了包含层归一化的深度卷积生成对抗网络(LDCGAN),与普通深度卷积生成对抗网络相比,其生成数据映射至高维空间后特征更加明显。
综上所述,就小样本条件下且低信噪比时LPI雷达信号识别率的问题而言,大体分为两种解决思路,一部分学者通过利用生成对抗网络及其分支网络对时频图像进行近似逼真生成,以实现数据的扩增来提高卷积神经网络的识别精度;另一种则是利用数字图像处理技术对时频图像进行处理,使LPI 雷达信号识别准确率得到一定的提升。上述办法都存在一定的缺陷,如做数据生成可能造成其与真实数据存在较大的差异,而数字图像处理技术是对时频图像进行降噪,则会对原始信号的时频特征进行滤除,最终获得的信息会有极大损失。因此,本文提出了一种崭新的解决思路,即将同一含噪的LPI 雷达信号分别经历局部最大化同步压缩变换(Local Maximum Synchrosqueezing Transform, LMSST)与平滑伪维格纳维尔变换(Smoothed Pseudo Wigner - Ville Distribution, SPWVD)。为防止时频图像特征信息的丢失,不对时频图像做任何图像去噪,而是利用循环对抗生成网络对双通道的输入数据进行简单扩充,其生成的数据更加逼近真实图像,进而通过一种双通道的网络模型,分别对LMSST 与SPWVD 时频图像进行特征提取,将提取到的特征进行早特征融合,最终送入Softmax分类器进行识别分选。
1 数据集介绍
1.1 LPI雷达信号参数
本文共针对12 种调制类型的LPI 雷达信号(BPSK、Costas、Frank、LFM、P1-P4、T1-T4)进行识别分选。为了贴近更加真实的电磁环境,本文首先利用MATLAB 2020b仿真出I路和Q路时域信号的数据信息,按照正交调制的原理合成更为真实的复信号,其信号参数是在一定范围内随机波动,具体的参数见表1。向复信号中加入随机的高斯白噪声,为了模拟小样本条件,在-10~6 dB 下每间隔2 dB、单种信号单个信噪比仅生成180 个LPI 雷达信号(共计19 440 个数据),训练集和测试集按照2∶1的比例进行划分。表1中的fs=50 MHz,[fs /8,fs/4]指其范围内的随机数。
表1 LPI雷达信号的参数

信号类型LFM Costas BPSK Frank,P1,P2 P3,P4 T1,T2 T3,T4仿真参数载波频率f0带宽B基准频率fmin跳频数L载波频率f0巴克码长度LC相位码周期CPP载波频率f0步进频率数M相位码周期CPP载波频率f0子码数Nc相位码周期CPP载波频率f0段数m载波频率f0带宽B参数范围[fs/8, fs/4][fs/12, fs/8][fs/5, fs/4][6,10][fs/8, fs/4]{7,11,13}[6,10][fs/8, fs/4][6,10][2,5][fs/8, fs/4]{36,49,64,81,100}[2,5][fs/8, fs/4][4,6][fs/8, fs/4][fs/12, fs/8]
1.2 信号的时频分析
信号处理主要方法分为时域、频域和时频域,时域信号特征值太多不利于识别分选,频域分析则是将时域信号通过傅里叶变换转换成频谱从而对其进行识别分选,频域分析擅长对平稳信号进行分析,但是面对非平稳信号已然不再适用。对于非平稳信号,时频分析是对其进行分析的一种主流方法,它通过聚焦信号的能量特征,将一维的时间序列转换成二维的时频图像,能够清晰地表达出时间和频率的特征。
1.2.1 局部最大同步压缩变换
短时傅里叶变换是常见的时频分析方法之一。但STFT 拥有很明显的缺点,即需要找寻合适的窗函数的长度且能量聚集性低。其无法准确反映出频率信息和时域分辨率且在低信噪比时容易受到噪声的干扰从而导致特征被淹没。针对此问题提出了LMSST,它属于STFT 的后处理过程,相较经典的时频分析方法,LMSST 可以生成能量更集中的时频表示,并且允许信号重建。LMSST 通过对频率方向上各分量瞬时频率附近的时频系数集进行积分,即可重构各单分量成分,因此获得更高能量聚集的时频图像。其具体演化过程如下:
假设时域信号为f(t),首先对信号进行STFT,可以得到时频谱G(t, ω)为
式中,t为时间序,u为时间变量,ω为角频率,g(u-t)为可滑动的时间窗函数。![]() 是频率为ω0的谐波信号。将式(1)进行泰勒级数展开:
是频率为ω0的谐波信号。将式(1)进行泰勒级数展开:
式中,Ak(t)为顺时振幅![]() 代表g(u-t)的傅里叶变换,然后定义一个新的频率重排算子ωm(t, ω),其中ω[ω-∆,ω+∆],具体表达式如下:
代表g(u-t)的傅里叶变换,然后定义一个新的频率重排算子ωm(t, ω),其中ω[ω-∆,ω+∆],具体表达式如下:
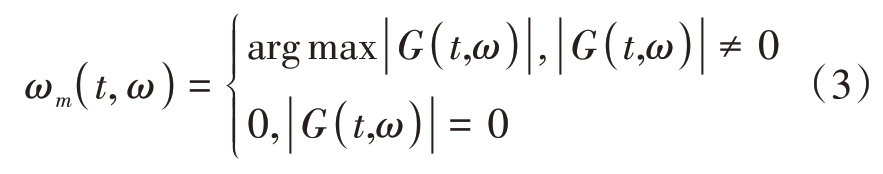
组成多分量信号的任意两个分量瞬时频率满足条件ωk+1(t)-ωk(t)>2∆时,这两个分量即可被很好地分离。考虑窗函数的短时Fourier 变换在ω=0 时取最大值,即ĝ(ω) ≤ĝ(0)。对于t∈ℝ, k∈{1,…, K},
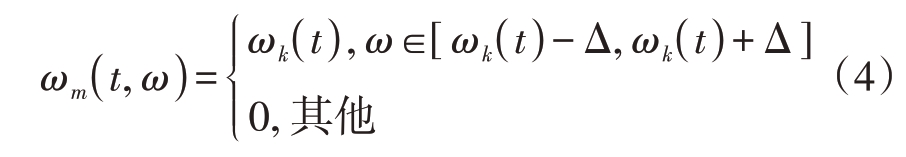
对短时Fourier 变换后的时频谱图进行局部最大化同步压缩变换(LMSST),其表达式如下:
信噪比为-2 dB 下12 种LPI 雷达信号经过同步提取变换得到的时频图像如图1所示。
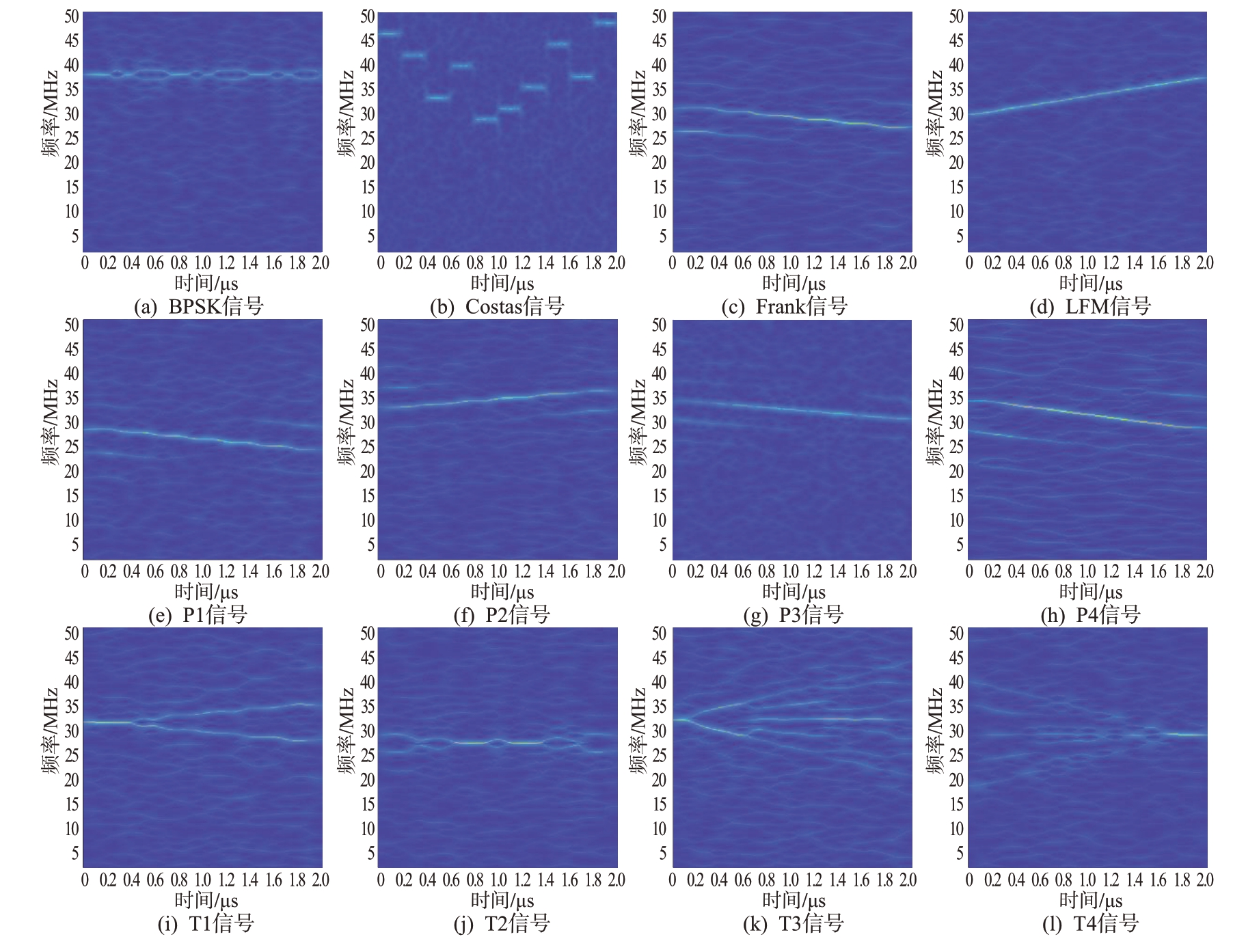
图1 LMSST时频变换图像
如图1 所示,水平方向代表时间信息,竖直方向代表频率信息,能够很清晰地看出频率随时间变化的趋势,并且还能看出LPI雷达信号的能量具有很强的聚焦性,这在很大程度上提高了特征分析的能力。
1.2.2 平滑伪维格纳分布
维格纳(Wigner-Ville Distribution,WVD)时频分析方法在用于多个信号分量时,会产生交叉项的干扰,随着大量噪声的污染,会严重影响接收到的LPI 雷达信号,这里采用的SPWVD 在其基础上进行加窗和参数优化的操作,其对WVD 带来的交叉干扰项进行了有效缓解。其具体的计算过程如下:
对WVD 进行时域加窗可以得到PWVD 时频变换的数学表达式:
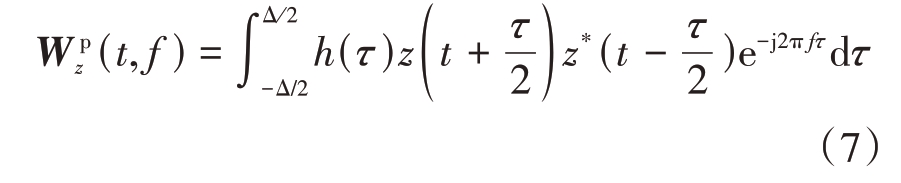
式中,h(τ)表示时域上的窗函数,对PWVD 在频域上再次加窗,并且进行继续平滑移动,就可以得到SPWVD时频变换,其表达式如下:
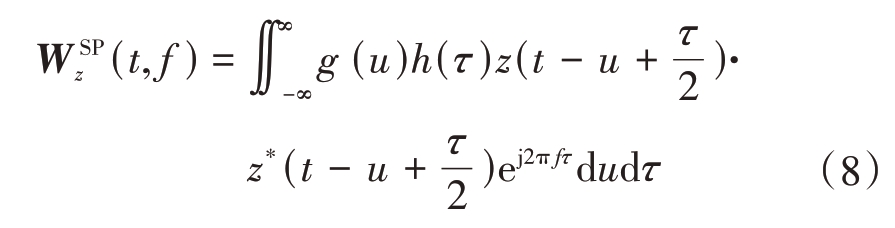
g(u)表示频域上的窗函数,对频域进行滤波,因而对交叉项的抑制效果更佳了。
12 种低截获概率雷达信号在信噪比为-2 dB时的SPWVD时频图像如图2所示,不同种类的LPI雷达信号的时频特征在-2 dB 的信噪比下具有较大差异,并且能够非常直观地获得低截获概率雷达信号能量的分布。随着信噪比的降低,信号的特征变得模糊,时频图像的特征也容易混淆。

图2 SPWVD时频变换图像
2 网络结构
2.1 小样本条件下LPI雷达信号识别流程
根据表1 中LPI 雷达信号的随机参数,利用MATLAB 2020b 生成I 路和Q 路信息,向信号中加入固定信噪比(信号与噪声的功率之比)的高斯白噪声,利用信号频谱仪进行数据采集,即可获得小样本数量的LPI 雷达信号。分别对采集到的信号进行LMSST 和SPWVD 以获得时频特征图像。本文利用循环对抗生成网络对两种时频图像分别扩充,扩充数据为原数据的1/6。为了更好地适应网络结构,采用双三次插值法对TFI进行时频图像剪切。其计算精度高,处理后的图像损失最少。双三次插值算法具体计算过程如下:
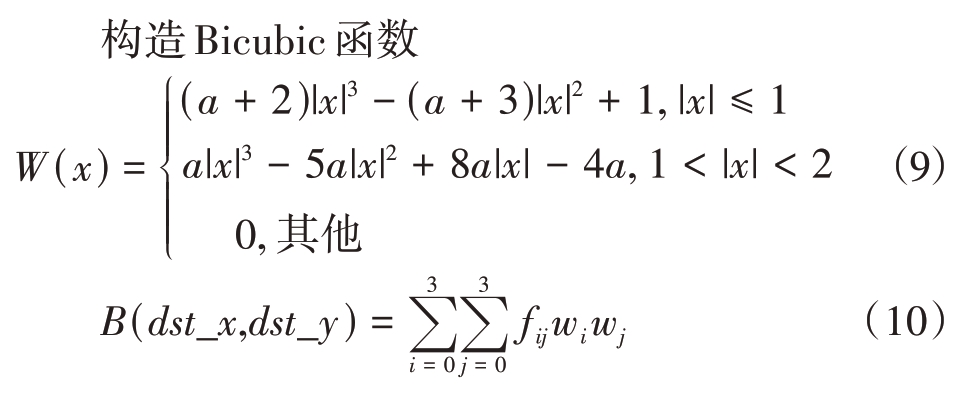
设置a=-0.5,这是一个经验值,旨在平衡平滑性和细节保留,过大过小会导致图像信息模糊。fij表示原图中aij的像素值,wi、wj分别表示该点在对应方向的权重,B(·)为插值结果。
最终获得本文所用的数据集,且2/3 用于训练,1/3 用于测试。将其送入所设计的双通道神经网络进行特征提取,并且在提取完特征之后进行早特征融合,最后送入Softmax 分类器进行识别和分选。具体的识别流程如图3所示。
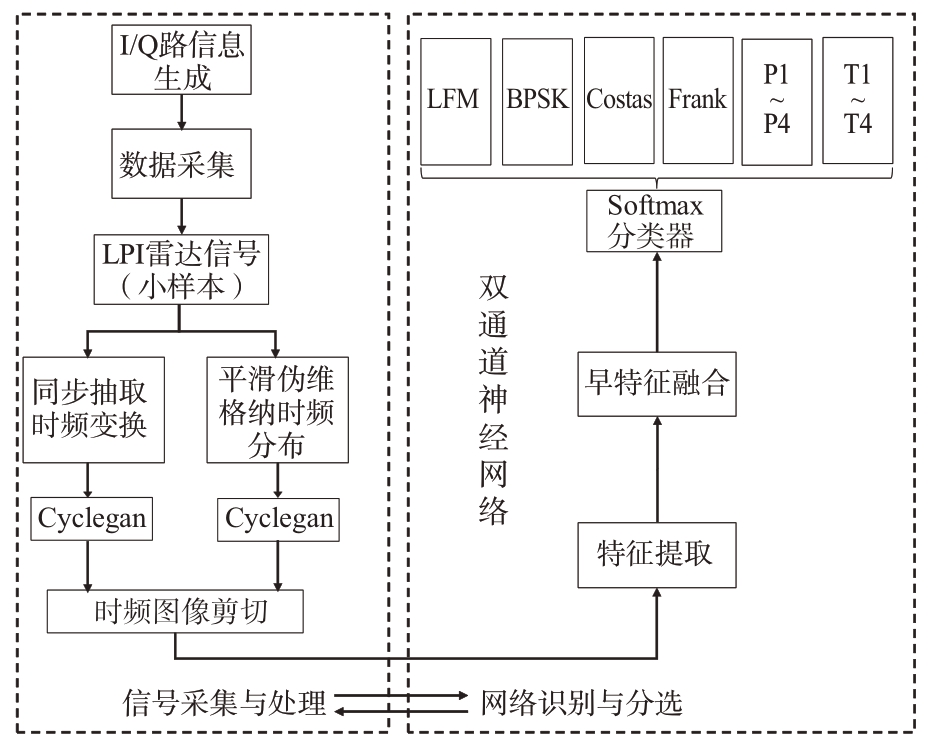
图3 小样本信号识别流程图
2.2 循环对抗生成网络架构
为解决样本数目不足的问题,本文利用循环对抗生成网络(Cyclegan)对数据实现扩充,分别对LMSST 和SPWVD 的TFI 进行数据扩增,将不同SNR 下同种LPI 雷达信号的TFI 作为Train A 和Train B 的输入,其内部的TFI不需一一对应。经过Cyclegan 循环训练,最终实现同种信号在两种SNR下的风格迁移。
如图4 所示,此模型拥有两个生成器和判别器,GA2B的功能为实现Train A到Train B的TFI风格迁移,GB2A则是Train B 到Train A 的生成。具体而言,Train A 中的TFI 通过GA2B生成Fake B,再通过GB2A重构回Train A 输入的原图像Cyc A;Train B 中的TFI 同理。Da和Db负责对生成A 和B 图像的判别,其判别结果用于模型参数的自动优化。只需首次训练好模型,再加载训练好的权重即可实现不同SNR、不同LPI雷达信号TFI的生成;将生成的不同SNR、不同信号的TFI 放入分选训练集中相对应的类别,进而利用所设计的双通道网络进行识别及分选。
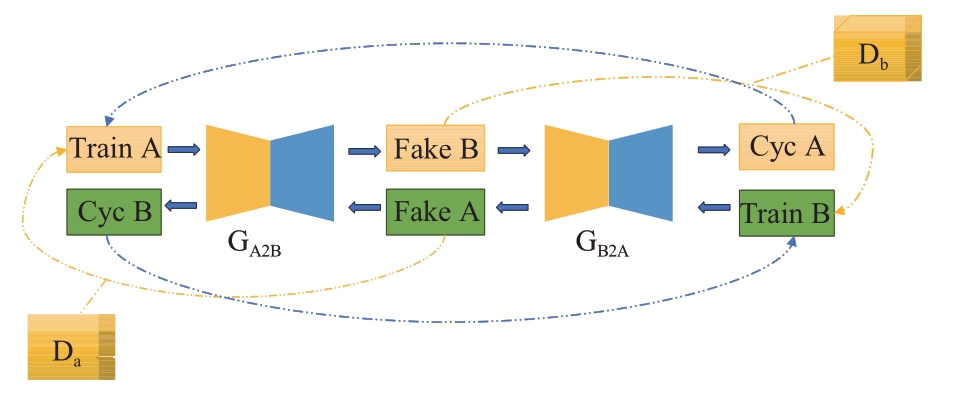
图4 Cyclegan原理图
2.2.1 生成器与判别器模型
在所有类型生成对抗网络中,生成器和判别器的网络结构在整个训练过程中起着至关重要的作用,其决定了网络生成图像质量。本文使用实例归一化(Instance Normalization, IN)对图像进行归一化操作。相较于批量归一化(Batch Normalization, BN),IN针对每个通道和每个空间维度进行计算即可产生更高像素的图像。
Cyclegan 的生成器与判别器的结构示意图见图5。进入生成器时,经过一个二维反射填充层,其利用输入边界的镜像来填充输入张量;填充后的张量依次进入Conv 层、IN2d 层和Relu 激活函数,迭代三次,输入通道由3 变为256;为了获得更多的有效信息,在此加入9 个残差模块提取信息;信息提取完成后,送入转置卷积模块,将特征图的空间维度进行放大,从而实现图像的上采样,这样的操作有助于增加图像的细节和清晰度,从而使生成的图像更加逼真和可信;最终在经过一个镜像填充层、卷积层和Tanh激活函数,将图像的像素值归化到[-1,1]区间内。判别器则是先用Conv 层将3 维的张量转变到64 维,这里不再采用Relu 激活函数而是采用LeakyRelu 激活函数,其作用为帮助提高模型的性能和训练稳定性,同样迭代三次张量维度转变为512 维;最终张量转变为1 维向量,此时输入的特征图进行自适应的平均池化操作,将特征图的大小调整为固定的尺寸,使得网络具有尺度不变性,从而更好地实现图像的分类任务。
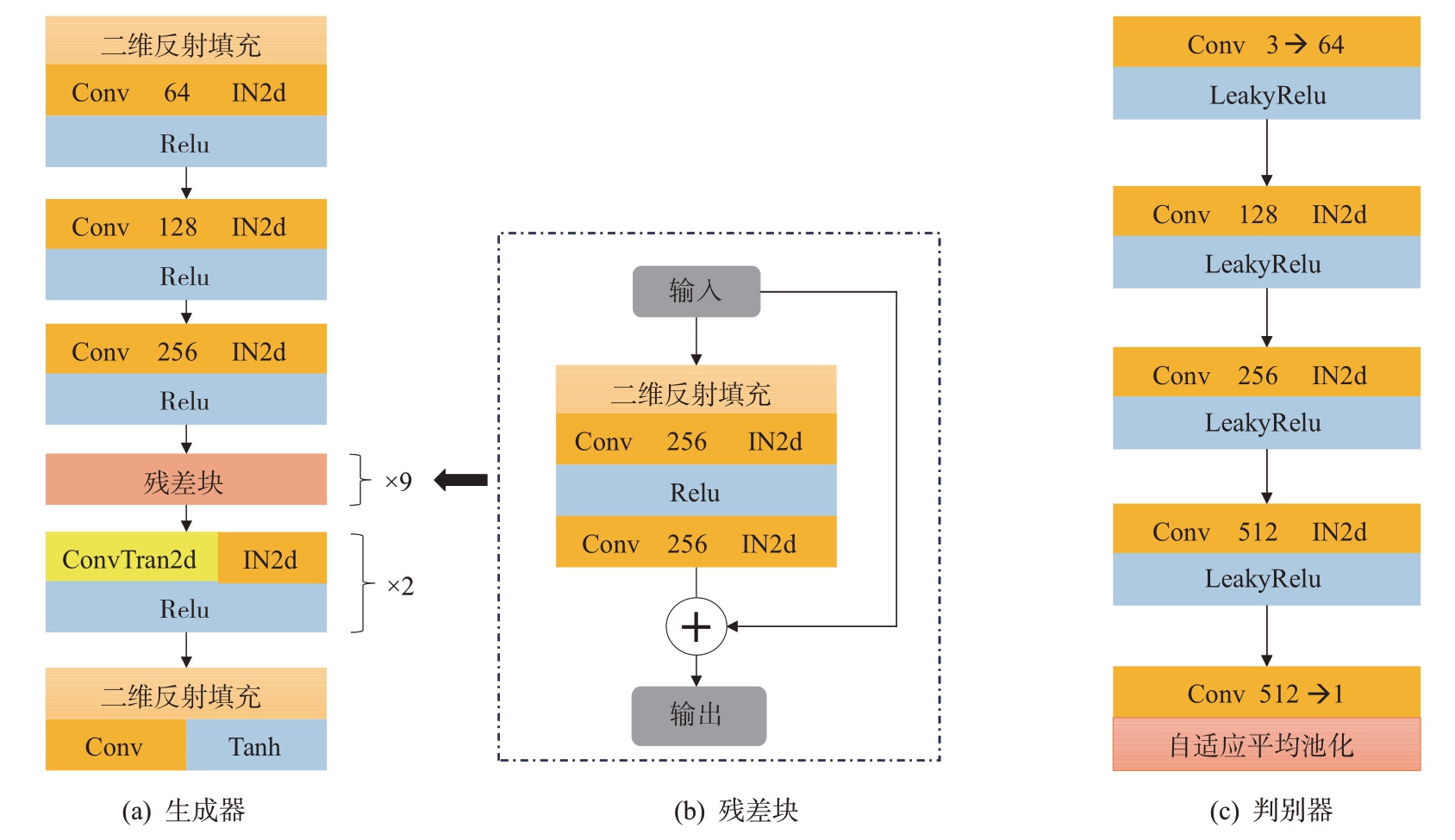
图5 生成器、残差块和判别器的结构示意图
2.2.2 损失函数
损失函数在网络中能够指导网络参数向最优结果进行调参。在此将A、B 中的数据分别记作X和Y,则损失主要由A 到B 之间互相转换构成的损失和循环一致性损失三部分构成,其具体数学表达式如下:
生成器GA2B与判别器DB部分:
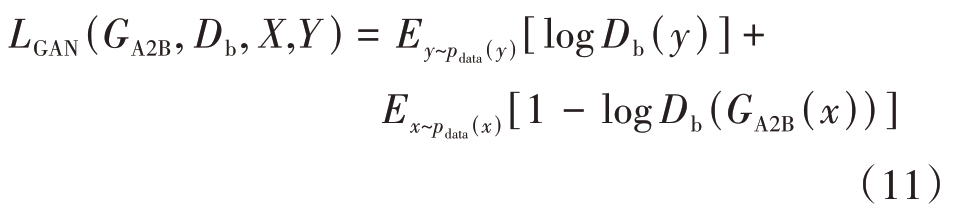
生成器GB2A与判别器DA部分:
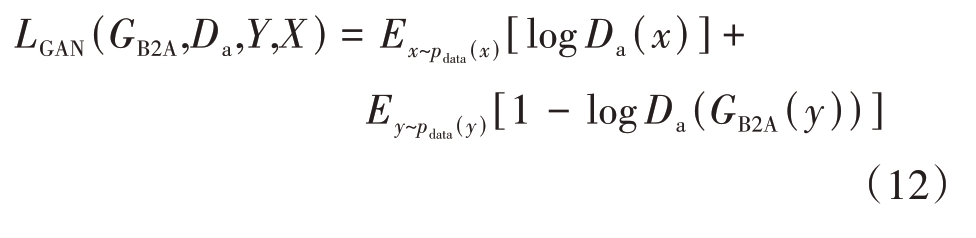
循环一致性损失部分:
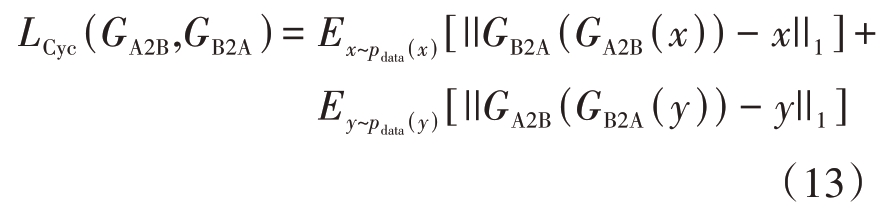
总损失函数:
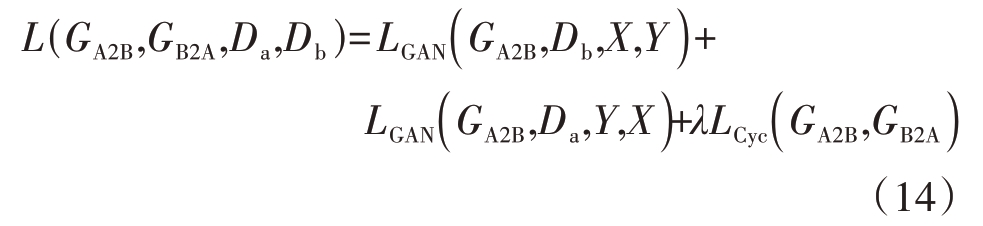
其中![]() 表示矩阵1-范数,即所有矩阵的列向量中元素绝对值之和最大的那个值。
表示矩阵1-范数,即所有矩阵的列向量中元素绝对值之和最大的那个值。
2.3 双通道神经网络结构
由于单通道卷积神经网络对小样本数据集的适应性能差及识别准确率低,在此提出了一种双通道的网络模型,该模型以LPI 雷达信号经过LMSST 和SPWVD 时频变换后的时频图像作为输入,分别送入特定的通道经过卷积模块进行特征提取。再对提取的特征进行早融合,即先融合多层的特征,等到特征完全融合后,对Softmax进行重点训练识别分选任务。所提出的双通道神经网络模型框架如图6所示。
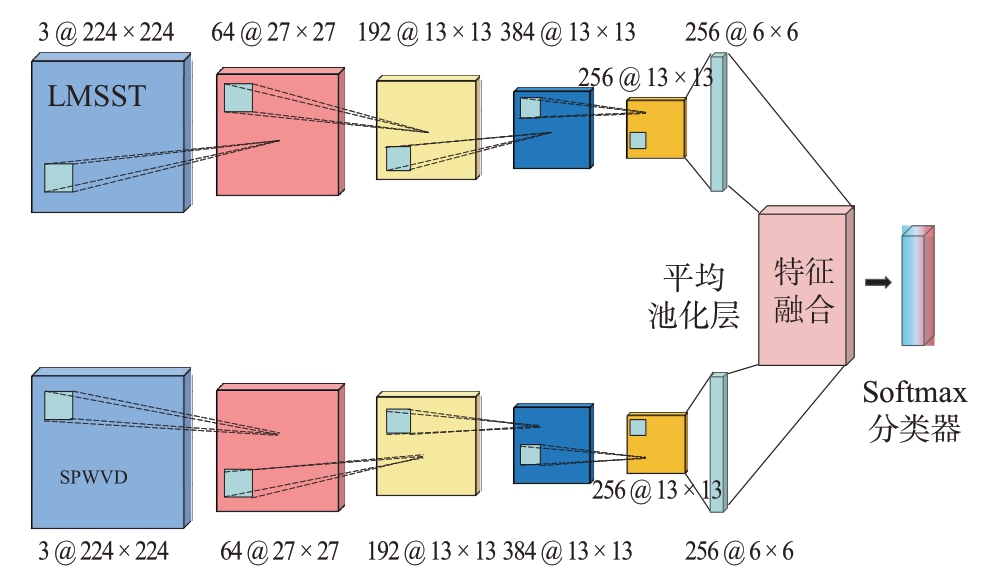
图6 双通道网络结构模型
将预处理后的LMSST 时频图像和SPWVD 时频图像通过双三次插值法将图像归整为3×224×224 的大小,然后分别送入各自的网络通道进行特征提取,特征提取层首先经过两次卷积模块1,即包含卷积层、Relu 激活函数、最大池化操作,且在第一个卷积模块1中,为了增加网络的感受视野采用大卷积核的方式。随后进行两次卷积模块2,其包含卷积层和激活函数。在进行一次卷积模块1得到最终提取到的特征矩阵,利用二维自适应平均池化函数输出指定尺寸的特征。为了使特征向量包含更多的有效信息,将两个通道提取到的特征进行融合,采用add(·)函数和早融合方式,即在提取到的特征进行完全融合后,再进行LPI雷达信号的识别分选。为了防止网络的过拟合,在Softmax 层加入了两个Dropout(·)函数,且神经元随机失活的概率设置为0.3,最终得到各个信噪比下的识别结果。特征提取模块的主要网络层及其参数见表2。
表2 特征提取模块主要参数
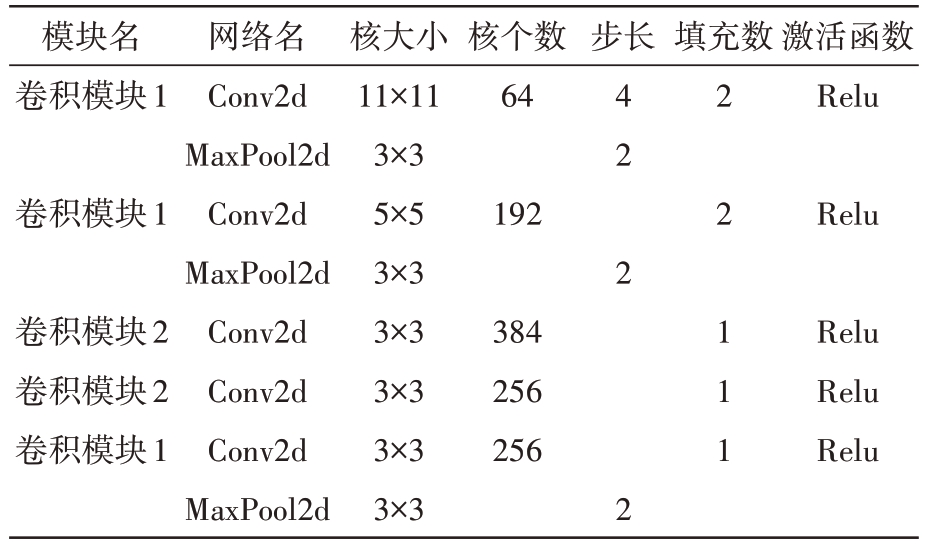
模块名卷积模块1卷积模块1卷积模块2卷积模块2卷积模块1网络名Conv2d MaxPool2d Conv2d MaxPool2d Conv2d Conv2d Conv2d MaxPool2d核大小11×11 3×3 5×5 3×3 3×3 3×3 3×3 3×3核个数64 192 384 256 256步长填充数4 2 2 2 2 2 1 1 1激活函数Relu Relu Relu Relu Relu
本文的实验环境见表3。
表3 实验环境

配置处理器及内存操作系统显卡语言框架运算平台型号Intel(R) Xeon(R) W-2265 CPU@ 3.50GHz Win 10 NVIDIA Quadro RTX 4000 Python Pytorch CUDA参数64G内存64 位8G 3.8.18 1.12.1 11.3
3 实验论证与分析
在电子对抗战中,LPI 雷达信号的接收和发出都会受到大量噪声源的干扰,在此采用信噪比的方式向LPI 雷达信号中加入固定信噪比的高斯白噪声去模拟低信噪比环境。此外,由于低截获概率雷达信号的低截获特性,可以获取到的样本数量往往不足,为了更加贴切其特性,在小样本的条件下进行实验。为了验证所提方法的有效性,本节将双通道特征融合模型与SET 和SPWVD 单通道的神经网络的识别精度进行对比,并且对不同信噪比下的12种低截获概率雷达信号的识别准确率进行了分析,所采用的Batch_size=32,Epoch=40,损失函数为SGD,初始的学习速率为0.001 且在每8 轮训练之后学习速率变为原来的0.1 倍,具体分析过程如下。
3.1 识别准确率分析
在样本充足时,低信噪比下的低截获概率雷达信号识别准确率较高,我们则是在此基础上考虑了样本难以获取的条件,故对小样本条件下的低信噪比时低截获概率雷达信号进行识别分选,难度比起拥有充足的样本时更加困难。LMSST 单通道和SPWVD 单通道与本文的双通道网络模型的整体识别精度如图7所示,在SNR=-10 dB 时,本文所提议的双通道模型的识别率比LMSST 通道的高7%且比SPWVD 通道的高6%;单通道的识别精度不足80%,而本文所提双通道模型则达到了83%,且在每个信噪比时双通道的识别准确率都超过了单通道的方法。如图8所示,小样本条件下在-10 dB 的信噪比时,LFM、P2 和T2 雷达信号的识别精度达到了85%,并且随着信噪比的增大,其准确率达到了100%;在-8 dB 时,Costas、LFM、P2、T1、T2、T3、T4共计7种LPI雷达信号的识别准确率达到95%以上。
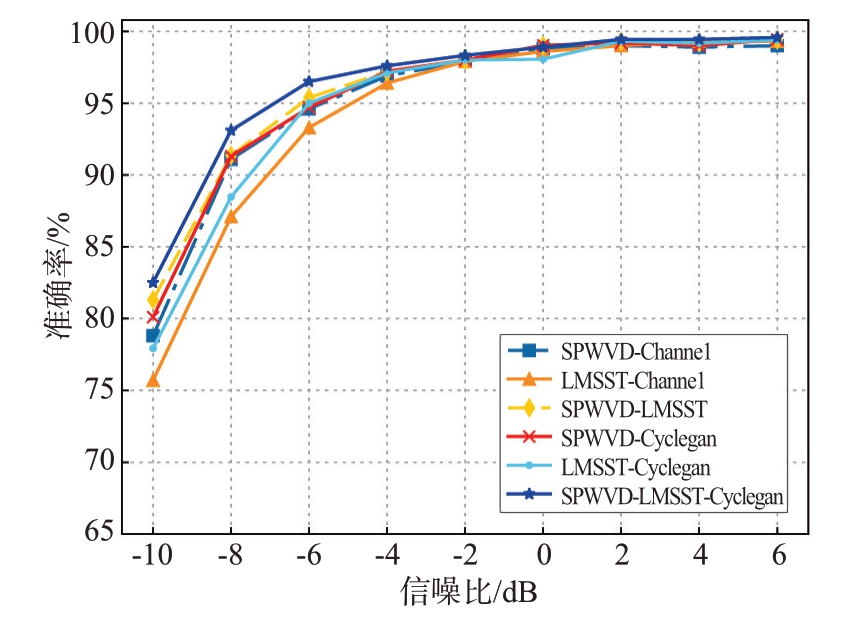
图7 12种LPI雷达信号的整体识别精度
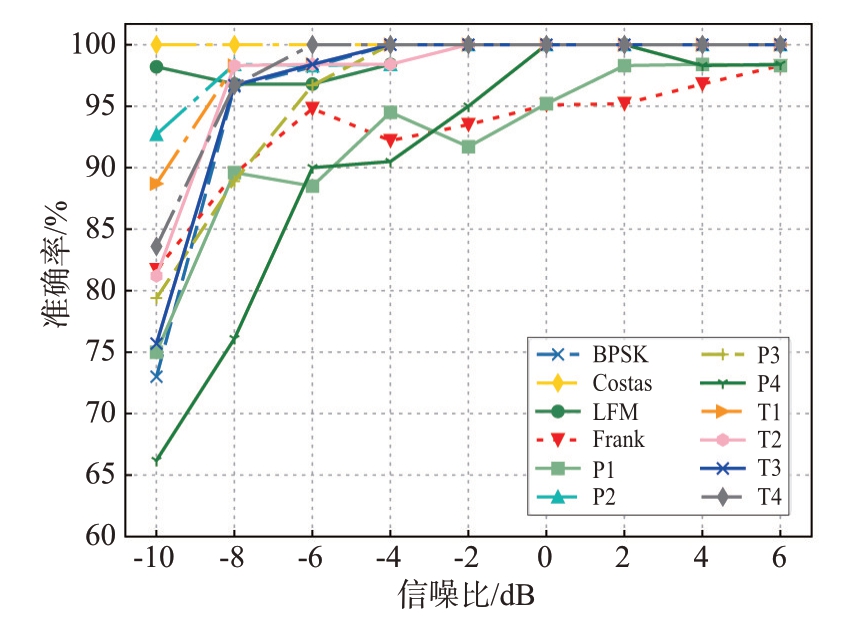
图8 12种LPI雷达信号识别准确率
3.2 混淆矩阵
为进一步验证本文所提方案的有效性,分别在单种信号单一信噪比下选取60张图像作为验证集,12种LPI雷达信号被精确识别的混淆矩阵如图9所示。
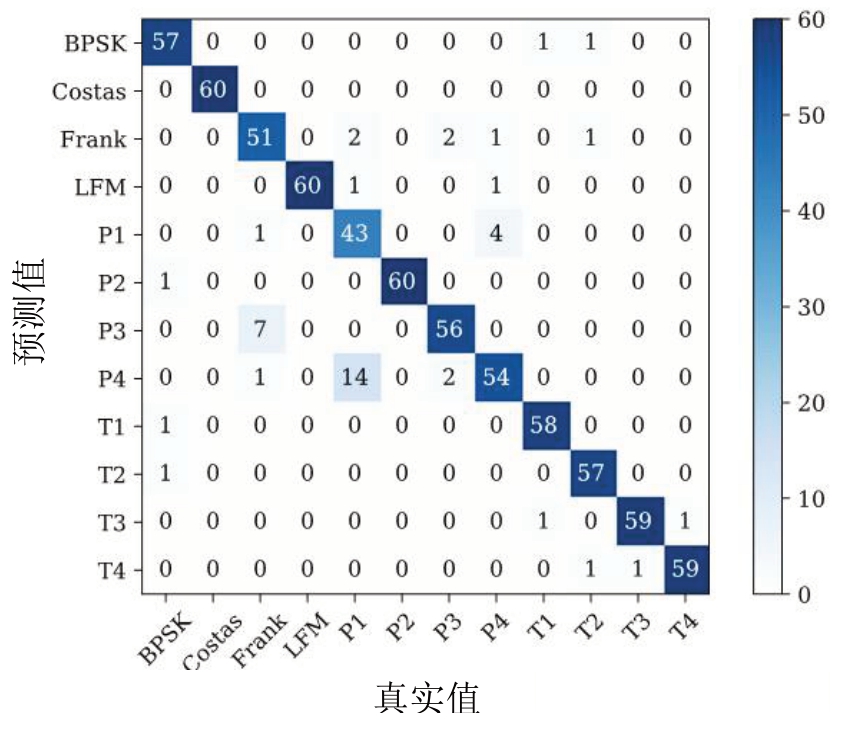
图9 -8 dB时12种LPI雷达信号的混淆矩阵
如图9 所示,除P1 之外,其他信号的识别准确率都达到了85%,LFM、BPSK、Costas、P2、T1~T4 信号识别精度在95%以上。P3 信号中11.6%被错误识别成Frank 信号,P1 和P4 信号互相识别错误,其中P1 信号中23.3%被识别成P4 信号,P4 信号中有6%被错误地识别成了P1 信号。产生错误识别的原因主要是因为P1 和P4 的时频图像相似性很高且可获取的有效的数据量不足,所以这两个信号很容易混淆。在低信噪比时相位跳转比较相似,Frank信号有11.6%被误认为BPSK信号。此外,在低信噪比时,其时间信息和频率特征都被噪声淹没,给识别带来了巨大的困难,也降低了识别精度。
3.3 鲁棒性验证
为了进一步验证在小样本条件下所提双通道融合网络的鲁棒性能,不同于以往减少数据集数量的方式,而是在小样本条件下采用不同信噪比交叉验证的方法进行研究论证。
鲁棒性能实验结果见表4,同一模型在测试集的信噪比提升时识别率也跟着提升,且当测试信噪比大于-8 时,模型对12 种LPI 雷达信号的识别精度始终在90%及以上,在不同信噪比时,模型的鲁棒性能较好。
表4 鲁棒性实验结果
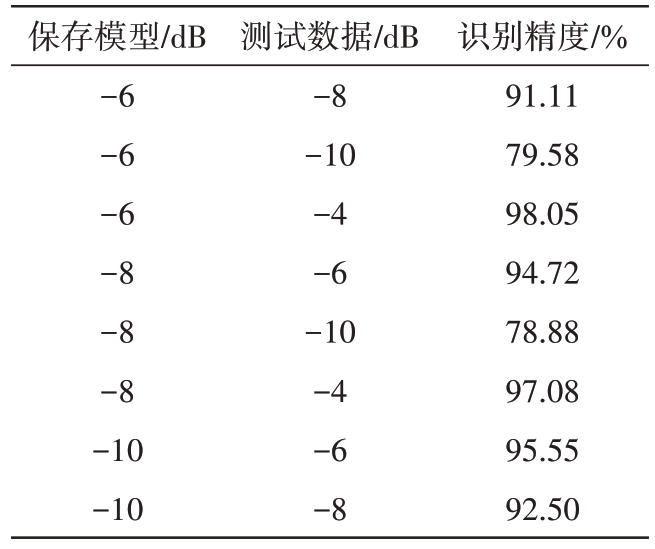
保存模型/dB-6-6-6-8-8-8-10-10测试数据/dB-8-10-4-6-10-4-6-8识别精度/%91.11 79.58 98.05 94.72 78.88 97.08 95.55 92.50
4 结束语
本文提出了在小样本条件下基于双通道神经网络的LPI 雷达信号识别方法。即利用双通道神经网络将局部最大化同步压缩变换和平滑伪维格纳时频分布的时频图像特征进行了早特征融合。研究结果表明:在小样本条件下,信噪比为-10 dB时该方法相对于单通道网络识别准确率提升了6%~7%,在-8 dB 的信噪比下的识别准确率可达93.1%。在样本数量不足时此研究方法能够有效地识别TFI的细微特征;同时为解决现代电子战中LPI 雷达信号分选准确率低的问题提供了一套有效的方案。经过鲁棒性实验,该网络模型还具有良好的鲁棒性能,为后面的学者对于小样本条件下LPI雷达信号识别技术的研究提供了理论基础。
[1] 聂千祁,沙明辉,朱应申.基于改进残差神经网络的雷达信号识别方法[J].系统工程与电子技术,2024,46(10):3356-3364.
[2] 王海英,张群英,成文海,等.LPI 雷达信号调制识别及参数估计研究进展[J].系统工程与电子技术,2024,46(6):1908-1924.
[3] 苏丹宁,曹桂涛,王燕楠,等.小样本雷达辐射源识别的深度学习方法综述[J].计算机科学,2022,49(7):226-235.
[4] 石涵宇,司伟建,夏新凡.低信噪比下典型雷达信号调制类型识别[J].制导与引信,2023,44(4):9-16.
[5] XIAO Zhiling, YAN Zhenya. Radar Emitter Identification Based on Novel Time-Frequency Spectrum and Convolutional Neural Network [J]. IEEE Communications Letters,2021, 25(8):2634-2638.
[6] HUANG Zhi, MA Zhiyuan, HUANG Gaoming. Radar Waveform Recognition Based on Multiple Autocorrelation Images [J]. IEEE Access, 2019, 7:98653-98668.
[7] 于濛,杜天有.一种稀缺样本条件下的雷达信号识别方法[J].现代导航,2022,13(4):303-309.
[8] 庞伊琼,许华,蒋磊,等.基于元学习的小样本调制识别算法[J].空军工程大学学报,2022,23(5):77-82.
[9] 王华华,张睿哲,黄永洪.基于生成式对抗网络和多模态注意力机制的扩频与常规调制信号识别方法[J]. 电子与信息学报,2024,16(4):1212-1221.
[10] 全大英,陈赟,唐泽雨,等.基于双通道卷积神经网络的雷达信号识别[J].上海交通大学学报,2022,56(7):877-885.
[11] NI Xue, WANG Huali, MENG Fan, et al. LPI Radar Waveform Recognition Based on Multi-Resolution Deep Feature Fusion [J]. IEEE Access, 2021, 9:26138-26146.
[12] YAO Xin, SHI Xiaoran, LI Yaxin, et al. GMT-WGAN:An Adversarial Sample Expansion Method for Ground Moving Targets Classification[J]. Remote Sensing, 2022,14(1):123.
[13] 齐美彬,程佩琳,靳学明,等.基于密集连接卷积网络的雷达辐射源信号分选[J].雷达科学与技术,2022,20(6):635-642.
[14] 徐帅,刘鲁涛.P-Net 框架下的小样本雷达信号识别算法[J].哈尔滨工程大学学报,2022,43(5):739-744.
[15] 全大英,唐泽雨,陈赟,等.基于MSST 及HOG 特征提取的雷达辐射源信号识别[J].北京航空航天大学学报,2023,49(3):538-547.
[16] 于浩洋,尹良,李书芳,等.生成对抗网络小样本雷达调制信号识别算法[J].西安电子科技大学学报,2021,48(6):96-104.
[17] 王艺卉,闫文君,段可欣,等.基于数据增强的小样本辐射源个体识别方法[J].雷达科学与技术,2024,22(1):104-110.
[18] JIANG Wentao, LING Liwen, ZHANG Dabin, et al. A Time Series Forecasting Model Selection Framework Using CNN and Data Augmentation for Small Sample Data[J].Neural Processing Letters, 2023, 55(5):5783-5810.
[19] 谢智东,谭信,袁昕旺,等.基于生成对抗数据增强支持向量机的小样本信号调制识别算法[J].电子与信息学报,2023,45(6):2071-2080.