0 引 言
由于阵列天线的方向图可通过调整阵元加权的幅度和相位进行灵活调控,因此阵列波束形成问题一直是学术和工程研究中的热点。在优化阵元加权时,可对加权系数施加恒模约束,仅通过调整阵元的相位加权实现对阵列发射方向图的调控,这就是唯相位波束形成（Phase-Only Beamforming, POB）的核心概念［1-2］。POB 的优势首先在于能够充分利用阵列发射功率。其次,由于POB 仅需要移相器就能实现对阵列发射波束的调控,因此阵列的硬件复杂度有所下降。目前,对POB 技术的研究主要集中在恒模约束导致的非凸问题的求解中,较为成功的方法包括二阶锥优化（Second Order Cone Programming, SOCP）［3-4］、半正定松弛规划（Semidefinite Relaxation, SDR）［5-6］、交替方向乘子法（Alternating Direction Method of Multipliers,ADMM）［7］以及新提出的基于黎曼流型的共轭梯度迭代方法（Riemannian Manifold Optimization-based Conjugate Gradient, RMOCG）［8-9］等。
目前在阵列波束形成的研究中,我们希望生成的主瓣增益较高,旁瓣增益较低,从而实现期望信号的无失真接收和非期望方向的杂波抑制。然而在发射波束形成角度,具有高增益的主瓣意味着对方干扰/侦察设备能够轻松感知我方雷达的信息,这就会降低我方雷达的生存性。若要降低对方干扰/侦察设备对雷达波束主瓣的感知度,需要在主瓣区域内生成发射零陷,单纯的空域波束形成方法在处理这类问题时会造成波束主瓣的畸变［10］,虽然可使用阻塞矩阵方法在隔离主瓣干扰后进行自适应波束形成［11］,但是当目标和零陷的空域角度较近时,目标信号同样会被抑制。目前,由于空域-极化域波束形成方法能够充分利用干扰和目标信号的空域和极化域差异,这类方法在解决主瓣干扰问题中的潜力得到了重视,近年来有学者相继提出了基于主辅阵的联合域波束形成技术、基于混合极化系统单脉冲系统的主瓣干扰抑制技术和基于零陷解耦的极化阵列多点源干扰抑制技术［12-14］等。这些方法的问题在于仍然立足于阵列雷达接收波束的调控,缺乏对发射波束形成问题的探讨。在另一方面,低旁瓣的发射波束虽然能够降低旁瓣区域的发射功率,但是现有方法大多讨论空域-频域或者空域-时域波束形成问题,无法根据实际需求调控发射波束的极化参数［15-16］。综上所述,目前基于接收角度提出的阵列波束形成方法已难以应对更加复杂的战场电磁环境,亟需提出阵列发射波束形成新方法,以提高我方雷达的反侦察性能。
为了充分利用阵列发射功率,提高阵列雷达系统的反侦察性能,本文提出了一种基于凸优化理论的双极化阵列发射波束唯相位形成方法。本方法在传统的唯相位恒模约束的基础上增加了极化约束,即优化水平和垂直阵列在特定空域角度上的幅度和相位,生成具有特定极化状态的高增益主瓣波束和极化域-空域旁瓣零陷,从而在有效降低了波束在干扰区域的发射功率的同时,主瓣畸变较小。本方法在维持波束主瓣优良性能的同时提高了阵列雷达的生存性。在求解中,本文将功率约束进行泰勒展开从而将非凸优化问题转化为凸问题,并且对约束区域的波束相位进行迭代修正,确保形成的波束极化状态满足约束。仿真结果验证了本文提出方法的正确性。
1 双极化阵列的唯相位发射波束形成准则
1.1 信号模型
唯相位发射陈列示意图如图1所示。
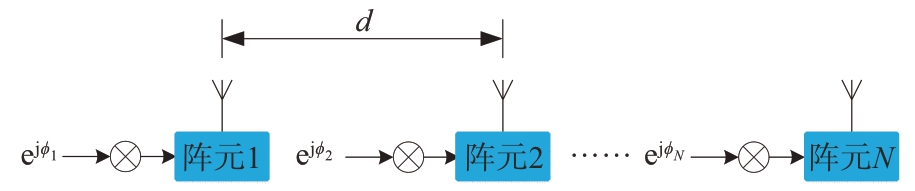
图1 唯相位发射阵列示意图
根据图1,一个N 维线阵的阵列导向矢量可写为
式中,rn( n = 1,…,N )为第n 个阵元位置,θ 为信号发射角度。若设波束指向角为θ0,侦察机角度为θi( i = 1,2,…,I ),则阵列发射信号为
式中,s0 表示发射信号波形,si 为第i 个干扰信号波形,n为高斯白噪声。根据式（2）,发射信号的协方差矩阵可写为RX = xxH。
由于希望发射阵列在保持特定角度和发射功率的同时,降低侦察机对应角度的信号功率,并且还要考虑阵列加权的唯相位约束,结合经典的Capon 波束形成方法,可得到基本的唯相位波束形成准则:
式中,(⋅)H 为共轭转置运算符,‖ ⋅‖表示取Frobenius范数,w 表示阵元加权向量,θ0 为波束主瓣指向角度。考虑恒模约束后,该向量可写为
式中,ϕi( i = 1,2,…,N )表示每个阵元的加权相位值,[ ⋅]T为转置运算符。
1.2 双极化阵列的唯相位约束准则
双极化唯相位发射阵列示意图如图2所示。
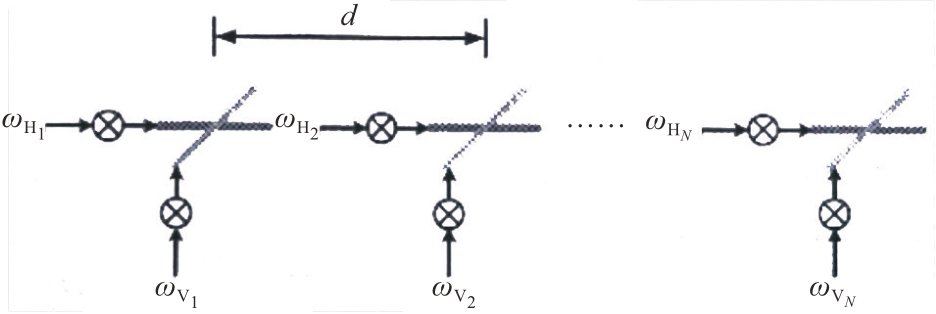
图2 双极化唯相位发射阵列
对图2所示的双极化阵列,水平（Horizontal,H）和垂直（Vertical, V）极化阵元的加权系数可写为［12］
式中,CH 和CV 为转换矩阵,具体表达式为:CH =[ I 0 ]N × 2N,CV =[ 0 I ]N × 2N。其 中,I 为N 阶 单 位矩阵。
为了在极化域有效抑制发射能量,通常期望阵列发射波束主瓣的极化状态和对方侦察天线的极化状态相互正交。侦察天线的极化状态p 可用Jones矢量描述:
式中,参数γ和δ为描述电磁波极化状态的Jones参数,其定义域为
那么阵列发射波束主瓣的极化状态可写为p⊥,二者间的关系为p ⊥p⊥。为了使得该关系成立,需调控波束主瓣极化比r⊥满足如下关系:
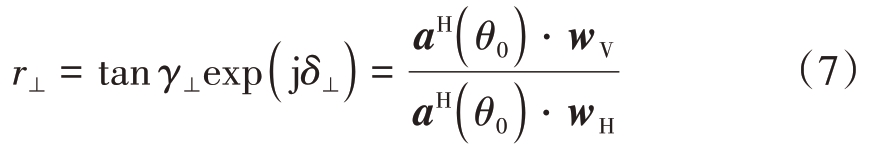
式中,Jones 矢量参数(γ ⊥, δ⊥)描述了波束主瓣极化状态,有p⊥=[ cos γ⊥ sin γ⊥exp( jδ⊥)]T成立。综合式（6）和式（7）,并结合式（3）,可得到双极化阵列的发射波束形成准则:
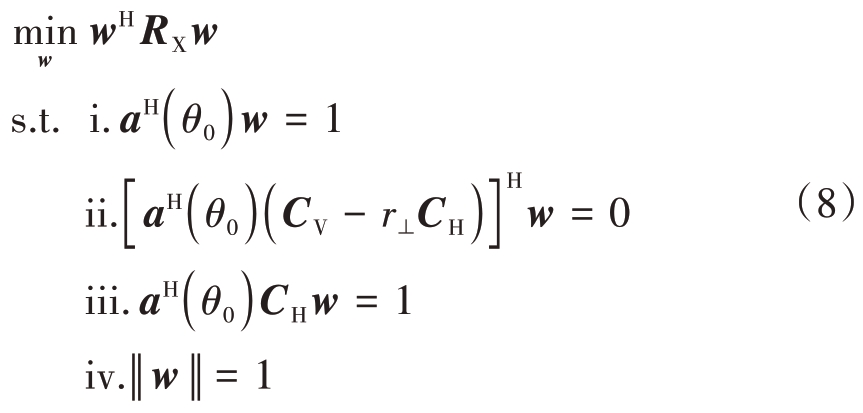
优化式（8）中的各约束条件意义为:
i. 在对阵列加权后,阵列发射信号无失真；
ii. 在波束指向角度生成满足极化比条件约束的发射波束；
iii. H阵列在波束指向有无失真响应；
iv. 唯相恒模约束。
1.3 非凸优化问题的松弛求解
和经典唯相位问题一样,优化式（8）也是非凸问题,若使用遗传算法或模拟退火算法等启发式方法求解,无法保证算法收敛性或者得到全局最优解。为此可考虑将该模型中的功率约束准则在相位空间进行泰勒展开,将其转化为凸优化问题以实现近似求解［3-4］。
功率约束目标函数可写为
考虑将调整阵列单元加权相位的过程视为加权系数的相位扰动,该过程为
在该扰动较小时,存在w →ejΔw。此时波束优化的目标函数和约束函数可以用相位矢量的泰勒一阶展开近似,相位扰动系数Δ为
将相位扰动ejΔw进行泰勒展开后有
将式（12）代入式（9）后,功率函数可写为
在上式中有
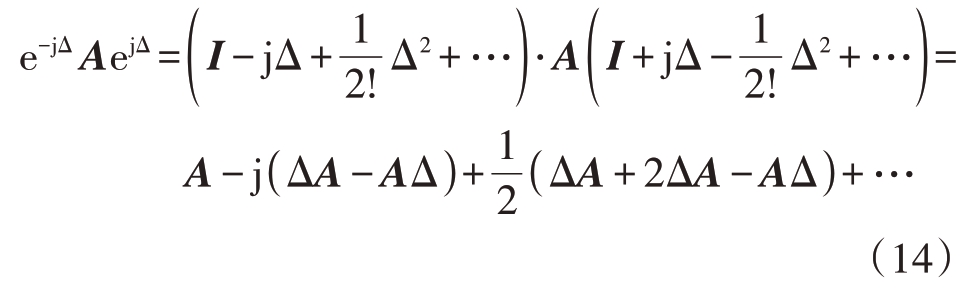
这里可将式（14）代入式（13）,省略高次项后有
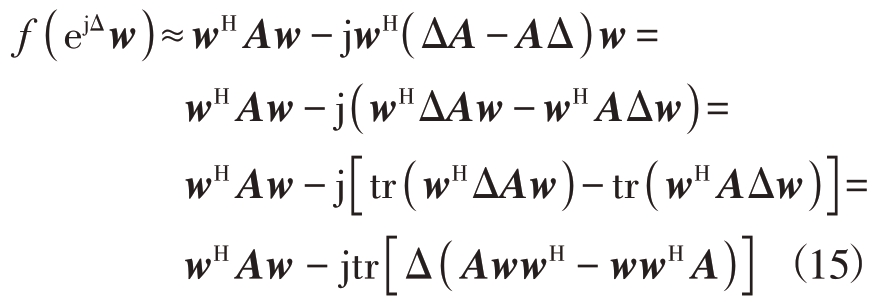
式（15）中的矩阵AwwH - wwH A 为反Hermitian 阵,每个矩阵元素均为虚数。可设函数:
式中,diag(⋅)表示取矩阵对角线元素,Im(⋅)表示取复数虚部。
此时式（15）简化为
式中,相位扰动向量δ =[ δ1 δ2 … δN]T。
将优化式（8）中的约束条件i 进行泰勒展开,得到近似优化模型为
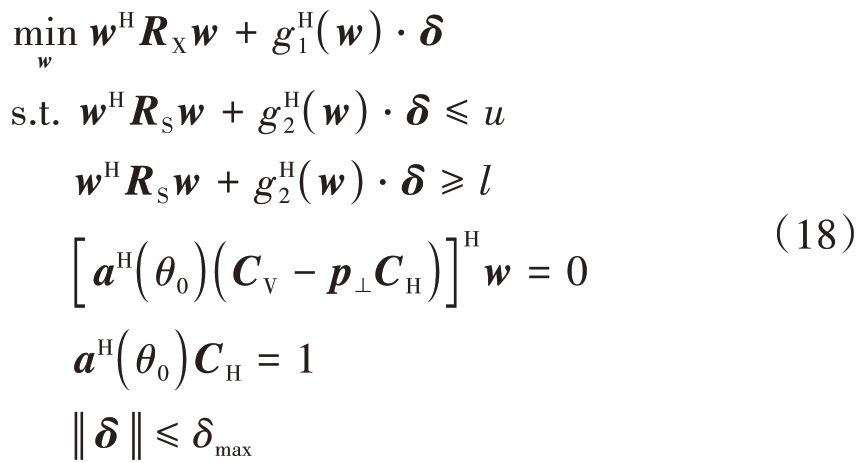
在式（18）中,u 和l 分别表示约束的上下界,δmax 表示相位扰动最大范围,这些参数均为正实数。此 外,RS = a( θ0 )aH( θ0 ),g1 = g( w )|RX 和g2 =g( w )|RS 分别为发射信号功率的上界和下界函数。将原问题中的约束和目标函数进行泰勒展开后,优化模型式（18）是一个凸优化问题,本文中选择使用迭代二阶锥规划方法（Iterative Second Order Cone Programming, ISOCP）求解,该流程为:
①选择初始加权相位
,其中
,这里有联合域导向矢量s( θ0 )= p⊥⊗a( θ0 ),⊗为Kronecker 积。
则需根据主瓣极化比需求生成,需满足主瓣极化比约束:
本文中约束门限κ = 0.004。
②根 据 式（16）计 算g1( w )和g2( w ),其 中g1( w )= Im[ diag(R XwwH - wwHRX )],g2( w )=Im [ diag（RSwwH - wwHRS）]。
③ 根据式（11）和式（18）计算δ。
④ 更新唯相位加权系数wk + 1 = ejΔ ⋅wk。
⑤ 持续迭代,直到迭代后的wHRXw +
输出小于门限值t,本文中取t = 0.02。此时得到的加权系数w已经满足极化比幅度约束。
⑥ 调整根据阵列加权w 生成的波束指向处极化比相位。为了保持极化比幅度约束,这里对波束指向角度±0.5°左右处的极化比相位进行松弛,
即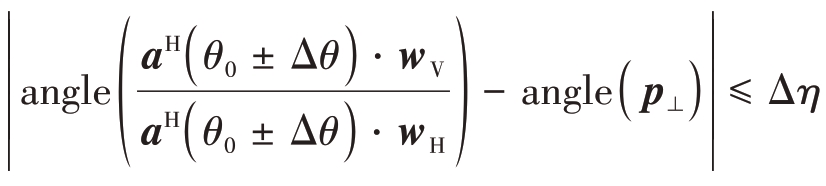
,这里的Δθ = 0.5°,松弛相位Δη < 4°；调整后的加权系数为wmix =[ wH wV ⋅exp( jδmix)]T,这里的δmix 为相位修正值。在执行本步骤时,可将H 阵列在波束指向处的增益设置为1,因此H 阵迭代的初始加权系数可设置为全1矢量；而V 阵的增益需要根据主瓣极化比约束进行调整,因此在选择V 阵的迭代初始加权系数时需要对其相位进行初选,首先需满足极化比幅度约束。在生成V 阵迭代初始加权系数时,可以在一定相位调整范围内随机选择不同阵元的初始加权相位,这里的初始加权相位服从均匀分布。最后根据主瓣极化比选择得到合适的迭代初始加权系数后即可进行二阶锥优化求解。
⑦ 重复过程②到⑥,直到波束指向处的极化比幅相误差和联合域零陷误差达到最小。
2 数值仿真
本节通过和传统联合域线性约束最小方差（Linearly Constrained Minimum Variance,LCMV）方法进行对比验证本文所提方法的有效性。
2.1 仿真设置
首先设置一个由17个阵元组成的双极化均匀线阵,阵元间距为半波长,快拍数为1 024,该场景如图3所示。天线主瓣指向为5°,设置发射信号的信噪比为10 dB,主瓣极化参数为γ⊥= 10°, δ⊥= 90°。场景中旁瓣干扰参数列在表1 中。这里将本文方法与基于LCMV 准则的极化域-空域波束形成方法进行对比［17］,得到图4中的结果。
表1 仿真参数设置
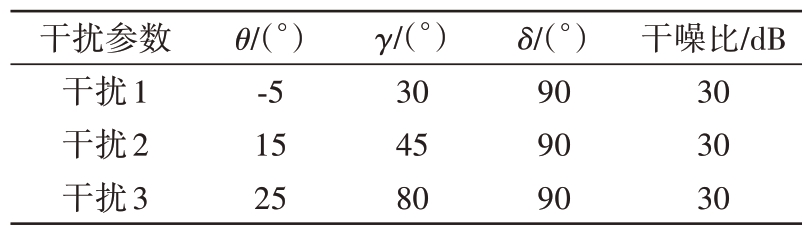
干扰参数干扰1干扰2干扰3 θ/（°）-5 15 25 γ/（°）30 45 80 δ/（°）90 90 90干噪比/dB 30 30 30
图3 仿真场景示意图
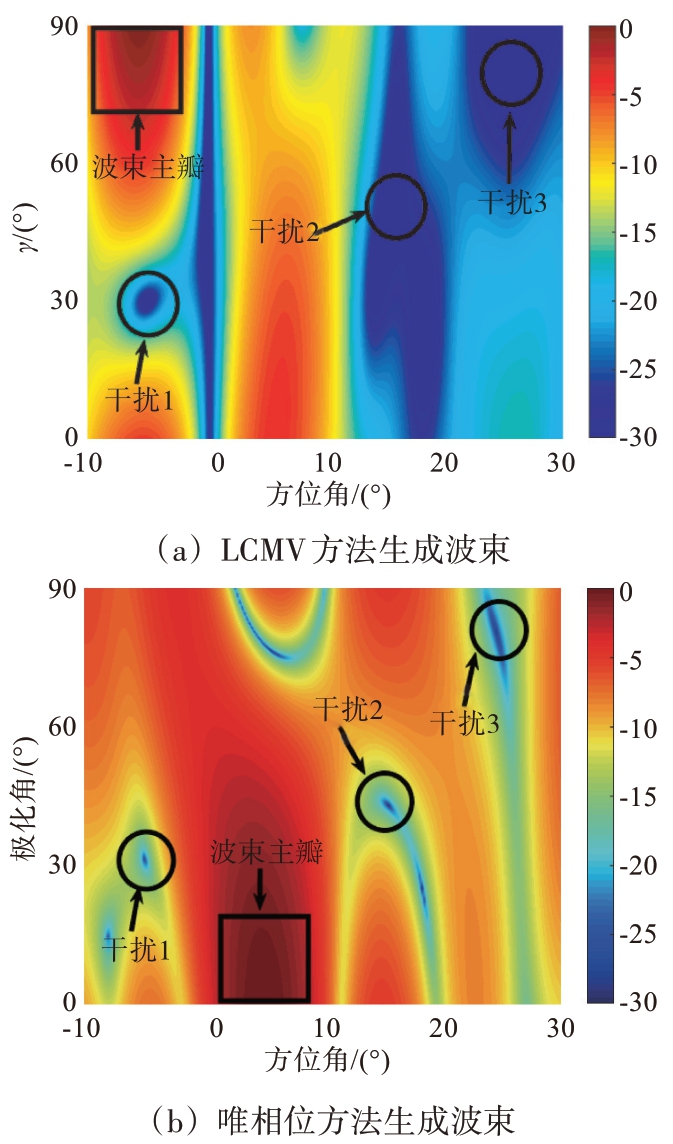
图4 两种方法生成波束对比
2.2 仿真结果
比较图4中两种方法形成的波束可知,LCMV方法形成波束的主瓣方位角度在-5°左右,对应的极化γ角在85°附近。而使用唯相位方法生成的波束主瓣方位角度在5°左右,对应的极化γ 角在10°附近。在设定的主瓣区域内,LCMV 方法的增益为-4.5 dB,而唯相位方法生成波束的主瓣增益在-0.15 dB 左右。这说明传统方法生成波束的主瓣畸变严重,不适合作为阵列雷达的发射波束。
这里将图4（b）中3 个抗干扰零陷中心位置列在表2中。进一步地,可以对比唯相位方法生成的H 阵和V 阵波束以及主瓣波束Jones 矢量参数( γ,η ),如图5所示。通过图5（a）可知,唯相位方法生成的波束主瓣指向角为5.075°,在该角度上生成的主瓣波束γ 参数为12.09°,η 参数为90.78°,考虑到在求解中对波束指向角度进行了一定的松弛,该结果在可控误差范围内。综上所述,通过本文方法能够生成较为稳健的发射零陷的同时调控主瓣波束的极化状态。
表2 唯相位方法生成的波束零陷中心位置
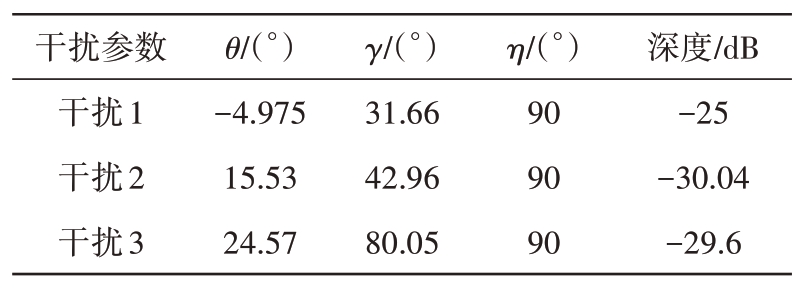
干扰参数干扰1干扰2干扰3 θ/（°）-4.975 15.53 24.57 γ/（°）31.66 42.96 80.05 η/（°）90 90 90深度/dB-25-30.04-29.6
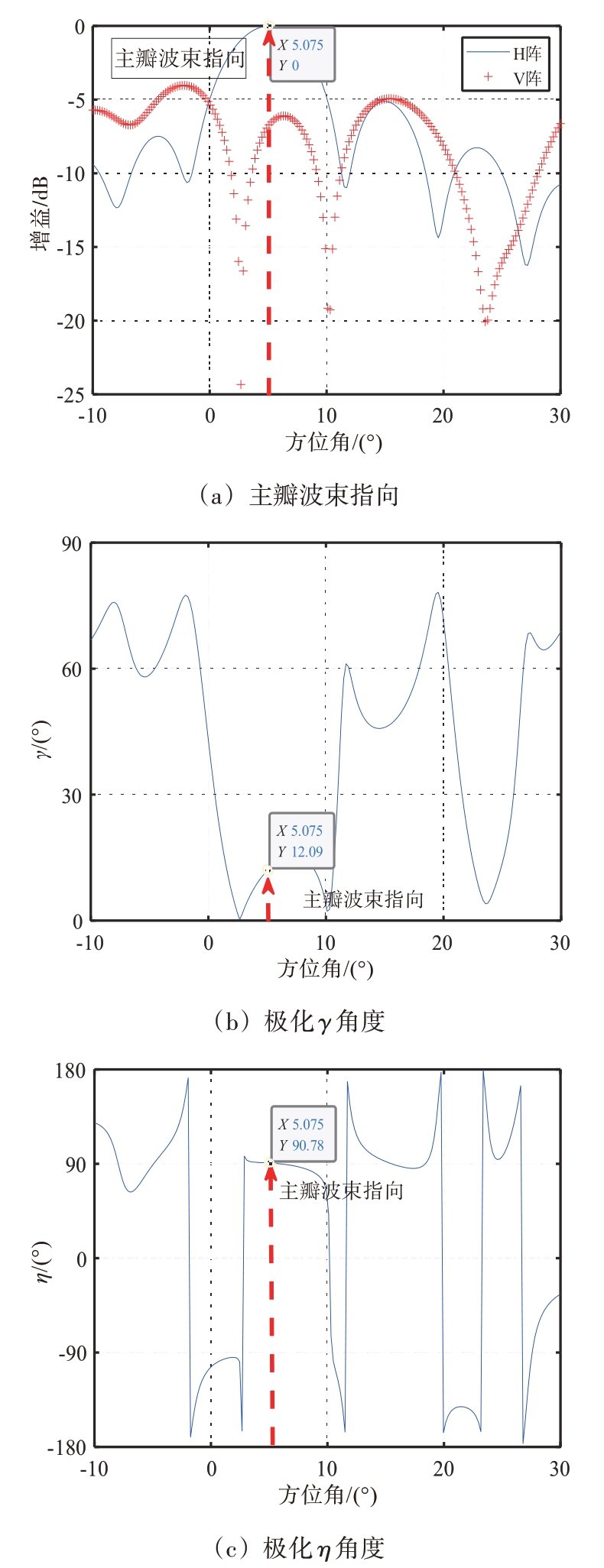
图5 唯相位方法生成波束主瓣的Jones矢量参数
3 结束语
本文在传统的唯相位波束形成方法中加入了双极化阵列的幅相约束,在调控生成具有特定极化状态的发射波束高增益主瓣的同时生成旁瓣零陷,在降低干扰区域发射功率的同时使得波束主瓣的畸变较小。为了保证主瓣波束极化状态的稳健性,本文方法对约束区域的波束相位进行了松弛迭代修正,确保生成的波束主瓣极化参数误差可控。该方法在降低阵列硬件复杂度的同时能够降低对方侦察机的接收功率,从而提高阵列雷达发射波束的反侦抗扰性能。本文的仿真结果说明该方法生成的主瓣波束极化状态比传统的极化域-空域波束形成方法更加可控,主瓣增益损失低,发射波束性能更加优良。
［1］ LU Chengjun, MENG Ziqiang, SHAN Jiaolong. A Novel Phase-Only Pattern Nulling Algorithm, IET International Radar Conference［C］//IET International Radar Conference, Chongqing, China:IET, 2023:502-505.
［2］ LEE Y. Adaptive Beamforming with Continuous/Discrete Phase Shifters via Convex Relaxation［J］. IEEE Open Journal of Antennas and Propagation, 2022, 3:557-567.
［3］ 路成军,盛卫星,韩玉兵,等.基于迭代二阶锥的唯相位波束形成［J］.电子与信息学报,2014,36（2）:266-270.
［4］ 吴凯,苏涛,李强.迭代优化最小化唯相位波束形成［J］.电子与信息学报,2017,39（3）:662-669.
［5］ KAJENSKI P J. Phase-Only Antenna Pattern Notching via a Semidefinite Programming Relaxation［J］. IEEE Trans on Antennas & Propagation, 2012, 60（5）:2562-2565.
［6］ LEE Y. Adaptive Interference Suppression of Phase-only Thinned Arrays via Convex Optimization［J］. IEEE Trans on Antennas and Propagation, 2020, 68（6）:4583-4592.
［7］ WEN Cai, HUANG Yan, PENG Jinye, et al.Reconfigurable Sparse Array Synthesis with Phase-Only Control via Consensus-ADMM-Based Sparse Optimization［J］. IEEE Trans on Vehicular Technology, 2021, 70（7）:6647-6661.
［8］ CONG Yang, HU Jinfeng, ZHONG Kai, et al. The Phase-Only Null Beamforming Synthesis via Manifold Optimization［C］//IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia:IEEE, 2022:799-802.
［9］ ZHONG Kai, HU Jinfeng, CONG Yang, et al. RMOCG: A Riemannian Manifold Optimization Based on Conjugate Gradient Method for Phase-Only Beamforming Synthesis［J］. IEEE Antennas and Wireless Propagation Letters,2022, 21（8）:1625-1629.
［10］ LIU Fulai, YANG Jinwei, YU Qiuying, et al. Wideband Adaptive Beamforming via Multiscale Channel Attention Convolutional Neural Network［J］. IEEE Sensors Journal, 2024, 24（18）:29323-29330.
［11］ 胡海涛,张剑云.基于阻塞滤波器的抗主瓣干扰方法［J］.雷达科学与技术,2020,18（1）:82-86.
［12］ 任博,施龙飞,王国玉.基于环境扰动模型的干扰抑制极化滤波器性能研究［J］.电子学报,2016,44（3）:527-534.
［13］ MA Jiazhi, SHI Longfei, LI Yongzhen, et al. Angle Estimation of Extended Targets in Main-Lobe Interference with Polarization Filtering［J］. IEEE Trans on Aerospace and Electronic Systems, 2017, 53（1）:169-189.
［14］ LU Yawei, MA Jiazhi, SHI Longfei,et al. Multiple Interferences Suppression with Space-Polarization Null-Decoupling for Polarimetric Array［J］. Journal of Systems Engineering and Electronics, 2021, 32（1）: 44-52.
［15］ LIAO Yi, TANG Hu, WANG Wenqin, et al. A Low Sidelobe Deceptive Jamming Suppression Beamforming Method with a Frequency Diverse Array［J］. IEEE Trans on Antennas and Propagation, 2022, 70（6）: 4884-4889.
［16］ CHEN Qiaoyu, ZHANG Jindong, LUO Dengyue, et al. Low-Sidelobe Single-Sideband Time-Modulated Phased Array Using Stepped Waveforms with Different Amplitudes［J］. IEEE Trans on Antennas and Propagation, 2023, 71（12）: 9643-9654.
［17］ 徐振海,王雪松,肖顺平,等.极化敏感阵列滤波性能分析:完全极化情形［J］.电子学报,2004,32（8）:1310-1313.