0 引 言
数字射频存储（Digital Radio Frequency Memory,DRFM）技术的应用催生了多种新型有源干扰,典型的间歇采样转发干扰相较于传统的压制干扰或欺骗干扰,响应速度更快,可对截获的雷达信号快速精准地复制并转发,形成的干扰信号与真实目标回波高度相关,在单一变换域难以区分,严重影响雷达的作战效能。针对间歇采样转发干扰对抗问题,国内外对此已有不少的研究,典型的有通过信号处理实现干扰对抗以及波形设计结合信号处理手段实现干扰对抗。基于回波信号中间歇采样转发干扰收发分时的特点,文献［1］首先对去斜处理后回波信号进行时频分析,利用干扰信号的不连续特征,提供了两种构造带通滤波器的方法实现干扰抑制。文献［2］利用干扰与目标的能量函数差异,通过提取未受干扰的回波数据,构建压缩感知模型重构目标信号进而实现干扰对抗。文献［3］在脉压时频图上辨识干扰,进而确定目标以及干扰所在距离单元,最终构造时频滤波器实现目标提取以及干扰抑制。文献［4］利用干扰与目标在统计域中的差异,构造频移滤波器抑制掉ISRJ形成的虚假目标。文献［5］对回波信号采用不同阶次的分数阶相关处理,进而改变干扰形成的假目标分布位置,最后利用相参处理实现干扰对抗。文献［6］基于图像分割类算法对受干扰的脉冲进行识别与剔除。文献［7］对回波信号在匹配滤波过程中添加“差分窗”,利用差分域上的特征差异来实现干扰抑制,具有较好的工程适用性。文献［8］在全极化雷达体制下,设计了一种非匹配滤波器,以脉冲压缩后信号最小旁瓣能量输出和干扰最小积分能量输出为出发点,基于罚函数的思想和帕累托参数的组合加权构造目标函数,可实现对干扰的有效抑制。文献［9］以信噪比损失为约束,基于梯度的非线性规划求解器和拉格朗日乘子法交替用于优化序列和构造滤波器,具有良好的干扰抑制性能。文献［10］利用间歇采样转发干扰形成的假目标在距离多普勒处理后大部分会被白化的特性,基于重构的假目标距离多普勒谱设计了抑制矩阵来抑制干扰。上述方法直接通过信号处理实现干扰抑制,雷达处于被动接收的状态,难以掌握战场主动权。为了提升雷达的主动对抗能力,大量学者从波形设计的角度出发,设计雷达的发射波形增加干扰与目标的正交性［11］。文献［12］设计了一种脉冲正交的相频编码信号,在信号处理中分别对每个子信号进行匹配滤波处理,进而实现干扰抑制。文献［13］设计了一种稀疏多普勒敏感波形,利用所设计波形的稀疏多普勒特性,显露出干扰的主假目标,在干扰参数准确已知的条件下,可以实现干扰抑制。文献［14］提出了一种基于完全互补码波形设计的抗间歇采样转发干扰方法,利用干扰时域不连续的特点,结合子脉冲掩护的思想实现干扰对抗。文献［15］在同时全极化的雷达体制下,对正交发射波形以及接收滤波器联合设计实现干扰抑制。文献［16］从波形设计和时频分析的角度出发,提出了一种基于短时分数阶傅里叶变换（Short-Time Fractional Fourier Transform, STFrFT）的主瓣ISRJ 抑制方法,基于所设计的脉内捷变波形,实现干扰抑制。文献［17］通过对相位编码波形以及非匹配滤波器的联合优化实现干扰抑制。文献［18］根据干扰信号的不连续采样特征设计了互补脉冲信号,该信号可在被干扰机截获后,保证信号强度在干扰脉冲信号的间隔内,使得干扰信号获得较低的脉冲压缩增益。现有的间歇采样转发干扰的波形设计有相位编码波形设计、稀疏多普勒敏感波形设计等,通过波形设计联合失配滤波实现干扰抑制,但是在基于变换域的脉内捷变波形优化设计方面研究较少。间歇采样转发干扰对抗常用的变换域有时域、频域、时频域、分数阶傅里叶域等,不同变换域可提供的特征不同,但由于间歇采样转发干扰与目标的强相关性,在单一变换域下难以区分干扰与目标。
本文针对在单一变换域难以区分间歇采样转发干扰与目标的问题,以提升雷达主动干扰对抗的能力为目的,提出了一种基于时频重叠度的脉内捷变波形设计与干扰对抗算法。首先,以干扰与目标的时频重叠度为目标函数,通过优化子脉冲个数以及编码序列,降低干扰对目标的时频重叠区域。进一步地,通过边缘检测算法实现对干扰区域的识别,并构造时频滤波器实现干扰抑制,所提算法可实现在干扰识别与抑制的同时,尽可能减小信号损失。
1 脉内捷变波形优化设计方法
1.1 信号模型
设脉内捷变波形的子脉冲个数为K,子脉冲脉宽为Tsub,子脉冲带宽为Bsub,信号带宽为B,信号脉冲宽度Tp = KTsub,信号瞬时带宽B = KBsub,则第k个基带子脉冲信号可以表示为
式中:t 表示快时间；γ = Bsub/ Tsub 表示子脉冲的调频斜率； fk表示第n个脉冲的第k个子脉冲的频率；
表示脉内频率编码序列,ck ∈{1 ,2,…,K },k = 1,2,…,K。雷 达 发 射 信 号 表示为
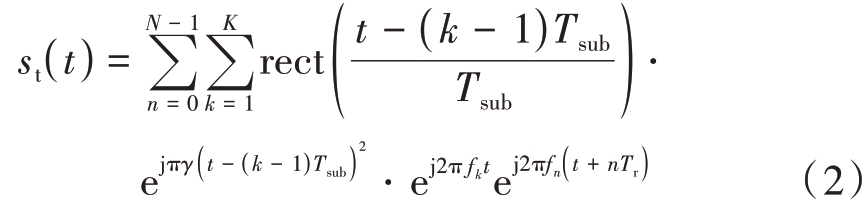
式中,N 为一个相参处理间隔内的发射脉冲个数,Tr为脉冲重复周期。
采用脉内捷变波形的目标回波信号表示为
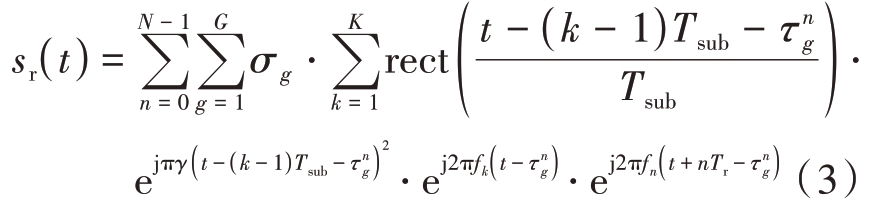
式中, fn 为第n 个发射脉冲载频,G 为场景中的点目标个数
表示第g 个目标对应的时延,σg 表示第g个目标的散射系数。
改变子脉冲个数K 以及相应的频率编码序列αK =[ c1 … ck … cK ],ck ∈{1 ,2,…,K },对干扰与目标的时频重叠区域会产生不同的影响。如图1所示,以自卫干扰为例,设置间歇采样直接转发干扰参数为采样时长2 μs,采样周期4 μs,图中蓝色区域表示目标回波信号,绿色区域表示干扰回波信号,而红色区域则表示重叠部分,对比采用脉内捷变波形以及LFM 的时频图,LFM 波形下间歇采样转发干扰与目标间隔较近,而采用脉内捷变波形增加了目标与干扰的区分度,有效减小了干扰与目标的重叠区域。
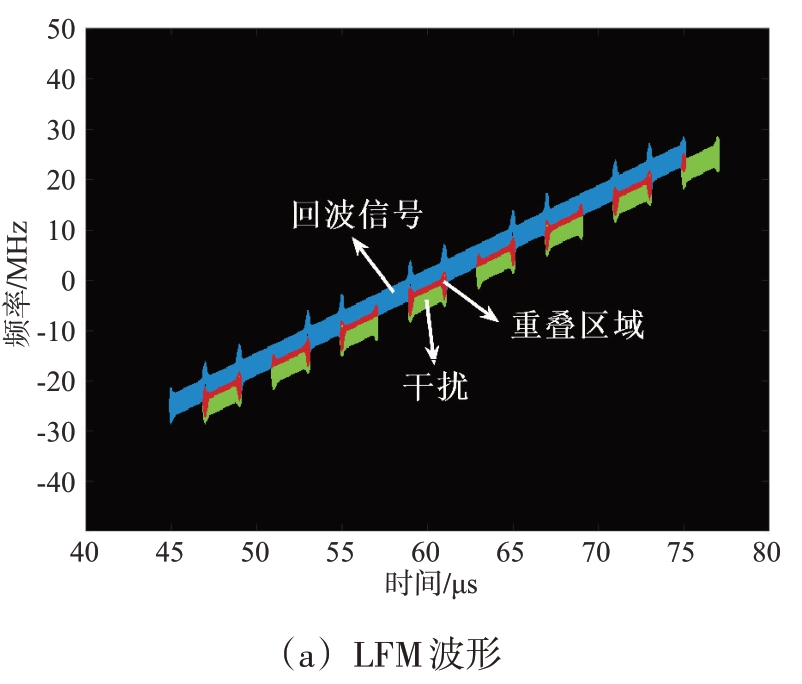
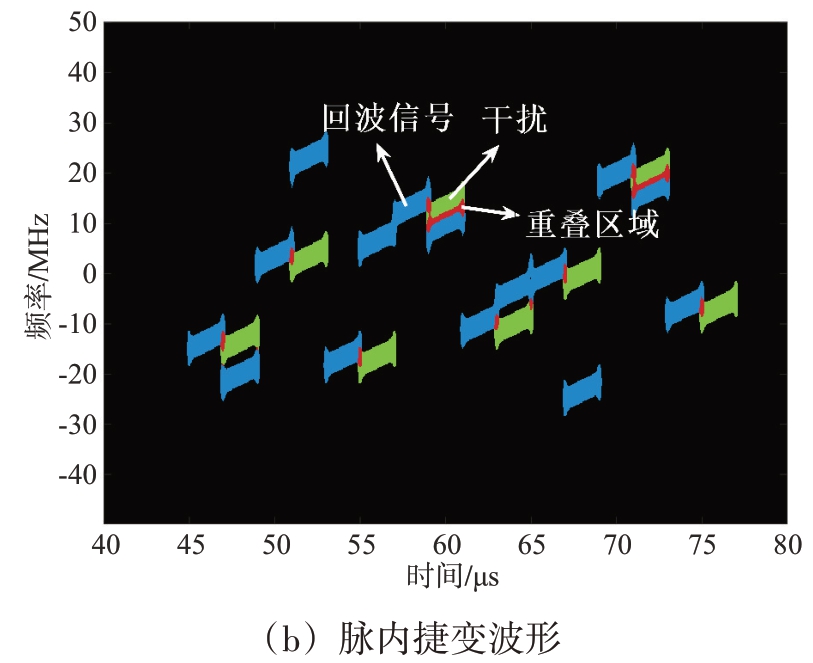
图1 不同波形的时频图
1.2 基于贪婪算法的脉内捷变波形设计
基于干扰认知信息θj 以及干扰信号J(t)与脉内捷变波形sr(t)。假设场景中的干扰个数为D,
表示第d 个间歇采样转发干扰；定义子脉冲的个数为K,对应的脉内编码序列为αK =[ c1 … ck … cK ],ck ∈{1 ,2,…,K }。θj 为干扰感知参数,包括干扰机个数,干扰采样时长以及转发次数。sr(t)与脉内捷变波形的编码序列有关,将其表示为sr(t ; αK ),干扰信号与干扰的参数以及脉内捷变波形有关,记为J(t ; αK, θj )；对两者分别进行短时傅里叶变换,如式（4）和式（5）所示,ω 表示窗函数,t′为窗函数的中心。
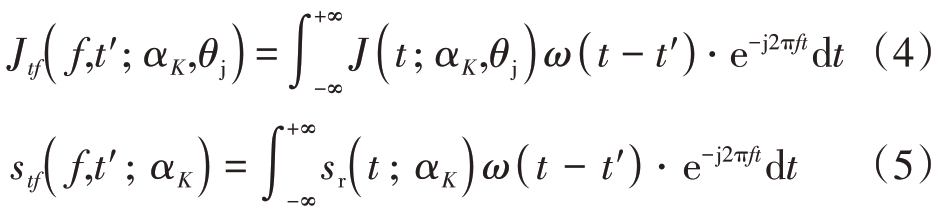
进一步对干扰与目标的时频数据离散化处理。定义目标的时频矩阵为Λs( αK ),其中Λs( αK)的第p 行q 列元素为Λs(p ,q; αK )=
为频率维度大小,Q 为时间维度大小,1 ≤p ≤P,
分别表示离散化后的时间以及频率。定义干扰时频矩阵为Λj( αK,θj ),其中Λj( αK,θj )中的第p行q列元素为
为了便于计算干扰与目标的重叠区域,对目标时频矩阵Λs( αK )二值化后得到的矩阵为
,对干扰时频矩阵Λj( αK,θj )二值化后得到的矩阵为
͂为常数,‖· ‖表示对元素求模值。
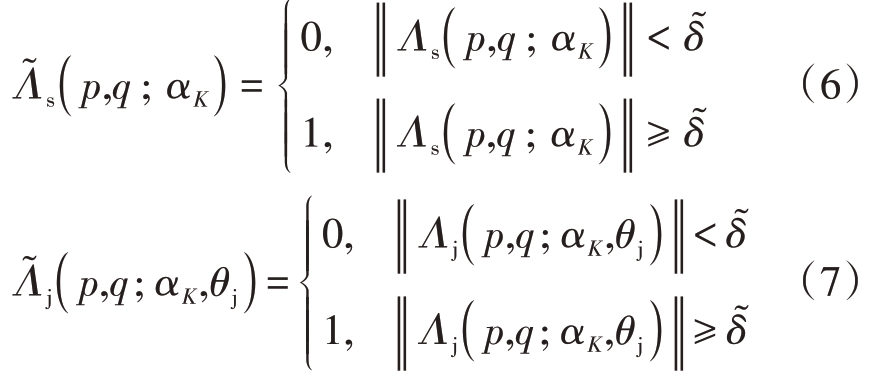
干扰信号与目标信号经过短时傅里叶变换后为离散的时频数据组成的时频矩阵,二值化后
定义ΘK 为子脉冲个数为K 时,对应的频率编码序列的解集,子脉冲个数K 不同时,相应的解集ΘK 不同。将二值化后的干扰矩阵
与目标矩阵
对应相乘后进行累加,得到干扰对目标的重叠度σK( αK,θj )的定义如下:
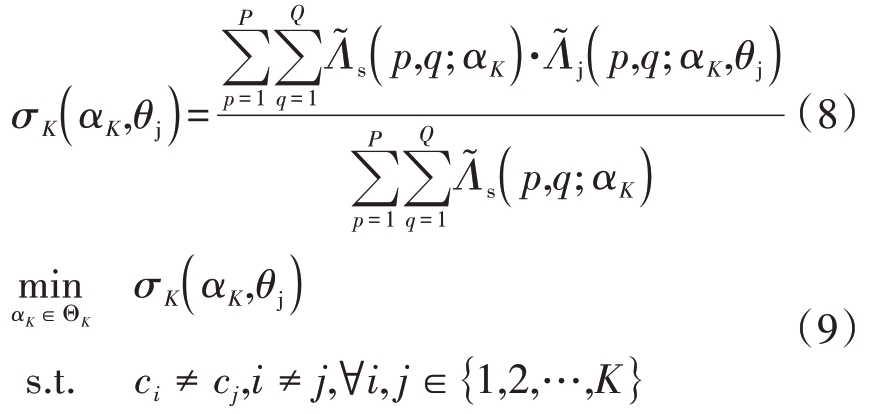
不同的子脉冲个数对应的脉内编码序列不同,即ΘK 不同。令子脉冲个数为Kz,约束子脉冲个数的变化范围
之后固定子脉冲个数优化脉内编码序列,子脉冲个数为Kz时,对应的编码序列数量为Kz!。因此,编码序列的解集大小为
基于式（9）,采用贪婪算法对子脉冲个数以及频率编码序列的求解步骤如下:
步骤1: 初始化当前的子脉冲个数为Kz,对每个子脉冲编号,对第k 个子脉冲的编号为k,k ∈{1 ,2,…,Kz },初始化脉内编码序列为顺序步进1～Kz,即LFM 波形,代入式（9）得到一个初始重叠度σz0。
步骤2: 按照编号顺序对每个子脉冲的编码进行优化,优化编号为k 的子脉冲的编码时,其余的Kz - 1个子脉冲的编码保持不变。首先对编号为1的子脉冲编码进行优化,该子脉冲编码的解集为
通过搜索整个解空间,得到使目标函数最优的编码β1 ∈η1。之后对编号为2 的子脉冲编码进行优化,更新解空间为
,搜索解空间得到目标函数最优时对应的β2 ∈η2,以此类推,直到编号为Kz - 1的子脉冲。
步骤3: 对编号为Kz 的子脉冲编码不需要再进行优化,该子脉冲编码的解集ηKz 中仅包含一个元素。至此,得到子脉冲个数为Kz的编码序列最终解
以及相应的目标函数值
步骤4: 判断子脉冲个数Kz 是否到达右边界,如未达到右边界,则Kz = Kz + 1,并返回步骤1 求解更新子脉冲个数后的编码序列,如达到右边界,则迭代结束。寻找不同子脉冲个数Kz 得到的最终解
,目标函数最小的
对应的
为优化后的编码序列最终解,对应的长度为子脉冲个数。
2 基于时频滤波的干扰抑制算法
基于优化后的脉内捷变波形,可通过对时频图滤波实现干扰抑制。具体的干扰抑制步骤如下:
步骤1: 对回波信号S( t )进行短时傅里叶变换,得到回波信号的时频矩阵Λr ∈ℂP × Q,对取模值得到实数矩阵
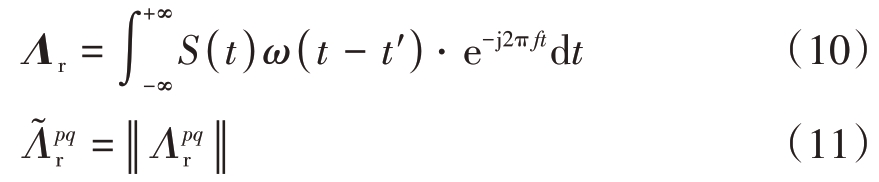
式中
表示
中的第p 行q 列元素
表示Λr中的第p行q列元素。
步骤2: 利用图像分割算法对矩阵
求得分类值ο1。寻找矩阵
中大于ο1 的元素,并记录元素的位置记为
形成时频滤波器Η,将
与滤波器相乘,得到抑制干扰主峰后的
,如式（13）所示。
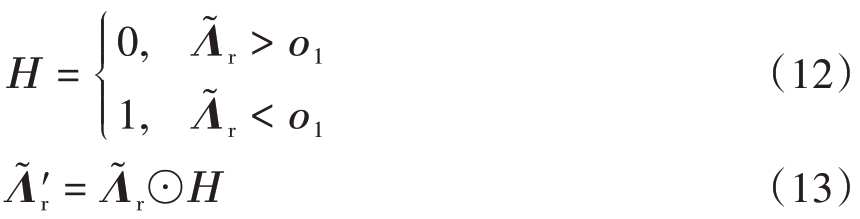
步骤3: 利用Sobel 边缘检测［18］方法对
进行处理,并对检测到的边缘位置进行提取,得到
中干扰主峰的所有边缘区域位置,ϕi=[ ϑi1 … ϑil … ϑiL ],i ∈[ 1, I ], l ∈[ 1, L ], I 为主峰区域的个数,ϑil 为第i个区域的第l 个位置索引,L 为主峰区域的位置索引个数,不同主峰区域的位置索引个数有所不同。为了对边缘区域的点进行处理,以κ为半径取边缘附近的点,令近邻区域为ψ。
步骤4: 基于矩阵
以主峰边缘的近邻区域
的均值
区域的点进行判决,记录大于
的区域为
式中,mean(· ) 为均值函数。
步骤5: 基于
以及
得到干扰抑制的时频滤波器
,对回波时频矩阵Λr ∈ℂP × Q滤波,得到干扰抑制后的时频矩阵
式中,⊙表示哈达玛积。
步骤6: 利用逆短时傅里叶变换对干扰抑制后的时频矩阵
反变换,得到干扰抑制后的时域信号
式中,ISTFT(· ) 表示逆短时傅里叶变换。
以两个间歇采样转发干扰场景为例,设置间歇采样转发干扰参数分别为采样时长1.5 μs,采样周期4.5 μs,以及采样时长2 μs,采样周期4 μs。如图2所示,采用优化后的脉内捷变波形,得到的时域回波信号时域图以及时频图如图2（a）和（b）所示,利用边缘检测算法得到的主瓣区域如图2（c）所示,干扰抑制后的时频图如图2（d）所示。
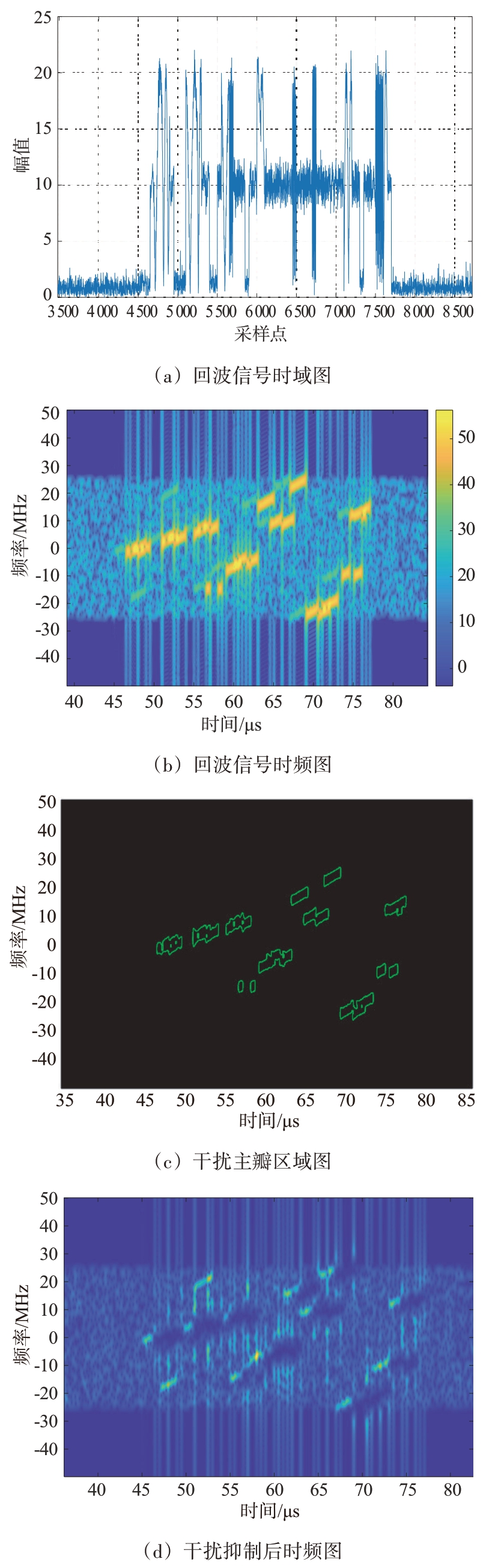
图2 干扰抑制部分结果图
干扰抑制流程图如图3所示。
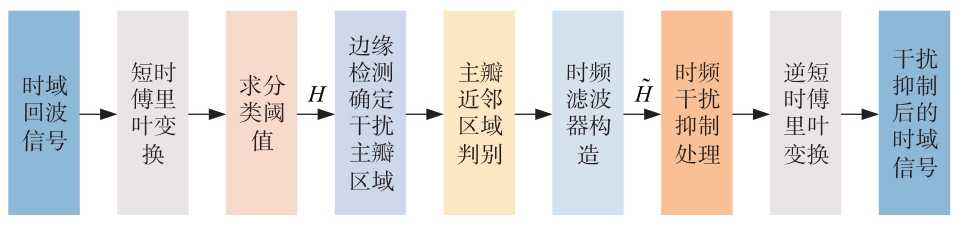
图3 干扰抑制流程图
图4为采用所提算法实现干扰识别与抑制后提取的一列频率维数据,可以看出所提算法可以较好地识别与抑制干扰。
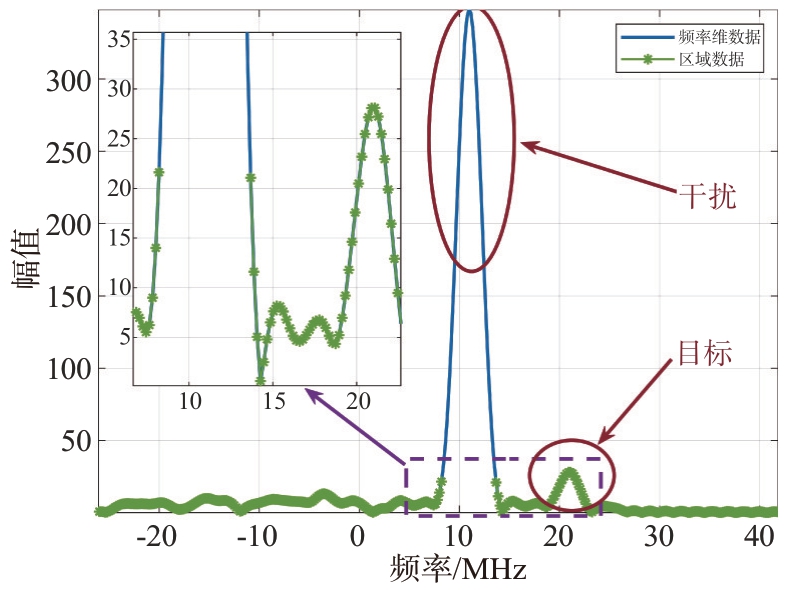
图4 频率维数据
3 仿真实验与实测数据处理
通过仿真验证以及实测数据处理在单个以及多个间歇采样转发干扰场景下,所提波形设计以及干扰对抗算法的有效性。利用信干比改善因子（Signal to Jamming Ratio Improvement Factor, SJRIF）［20］以及脉冲压缩后的信号损失作为评价指标,SJRIF的定义如下:
式中,SJRin 和SJRout分别表示干扰抑制前后信号的信号与干扰的功率之比。
脉冲压缩后信号损失的计算方式为
式中,A0 表示干扰抑制前的脉冲压缩信号幅值,A1表示干扰抑制后的脉冲压缩信号幅值。
实验一
仿真单个间歇采样重复转发干扰场景,仿真参数如表1和表2所示。
表1 雷达波形和目标参数
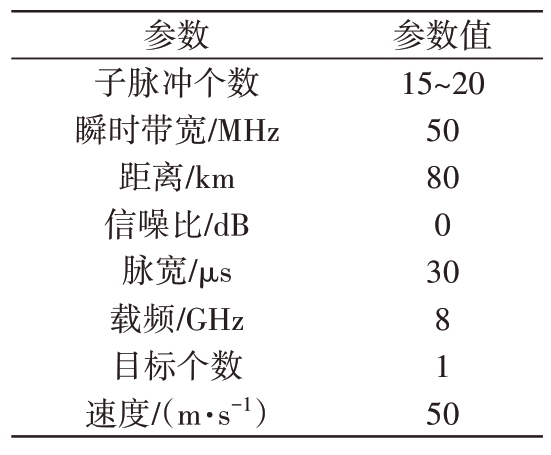
参数子脉冲个数瞬时带宽/MHz距离/km信噪比/dB脉宽/μs载频/GHz目标个数速度/（m·s-1）参数值15～20 50 80 0 30 815 0
表2 间歇采样转发干扰参数
参数采样时长/μs转发次数采样周期/μs干信比/dB参数值1.5 2 4.5 20
基于干扰认知信息对子脉冲个数以及编码序列进行优化,如图5所示。图5（a）为子脉冲个数为15 时,干扰对目标的时频重叠度由23%降低至7%,图5（b）为子脉冲个数为20 时,干扰对目标的时频重叠度由22%降低到4%,选择子脉冲个数为20时的编码序列作为发射波形。
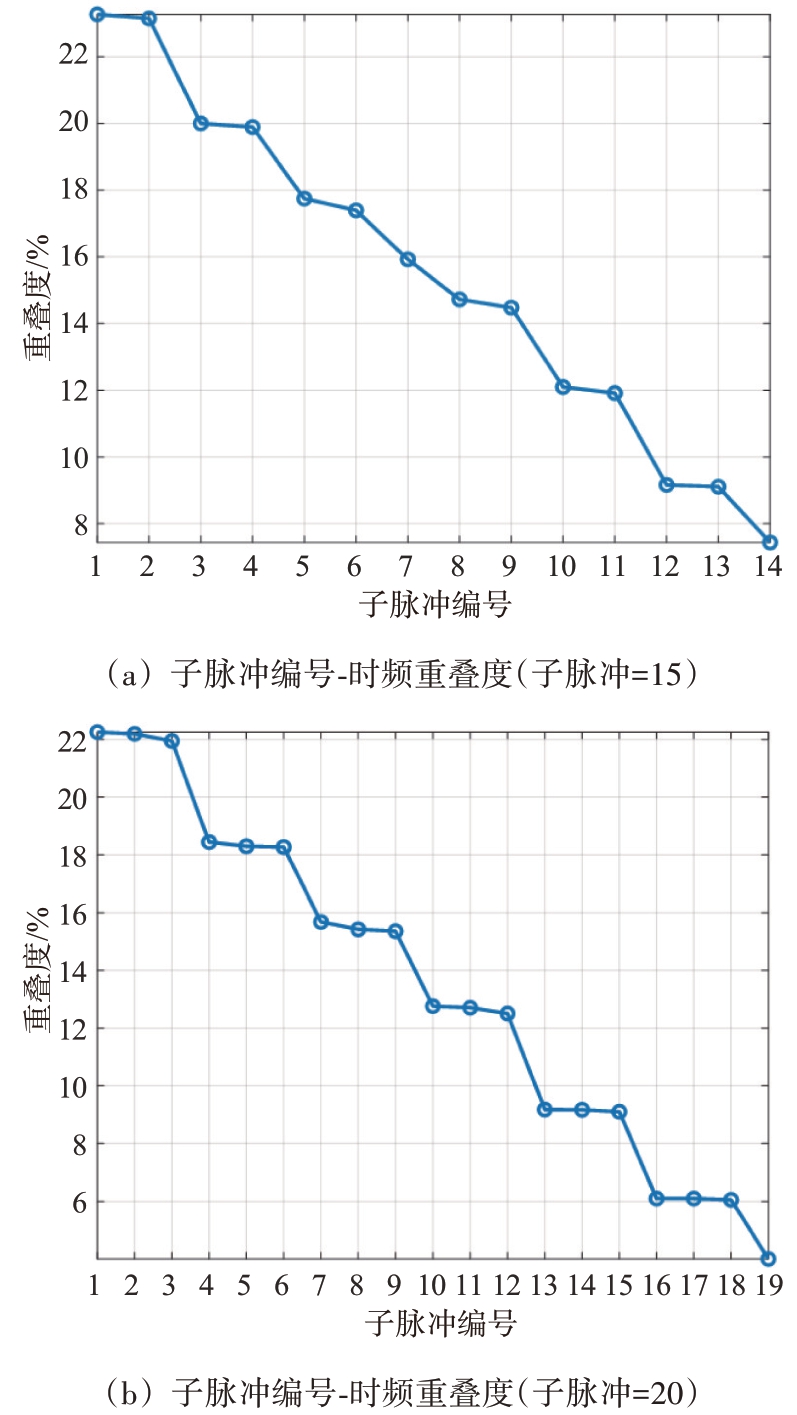
图5 回波时频图以及干扰与目标的时频重叠度优化图
基于优化后的脉内捷变波形,采用所提的干扰抑制算法实现干扰抑制。图6（a）为干扰抑制后的时频图；图6（b）为干扰抑制前的脉冲压缩结果,对于单个间歇采样重复转发干扰而言,干扰信号脉冲压缩后形成两个主假目标；图6（c）为采用优化前后波形的干扰抑制结果,基于优化的脉内捷变波形,时频滤波之后目标的损失较小,此时SJRIF=37.5 dB；未优化波形为子脉冲个数为15 的随机脉内捷变波形,对未优化波形时频滤波处理后的信号损失高于优化后波形。
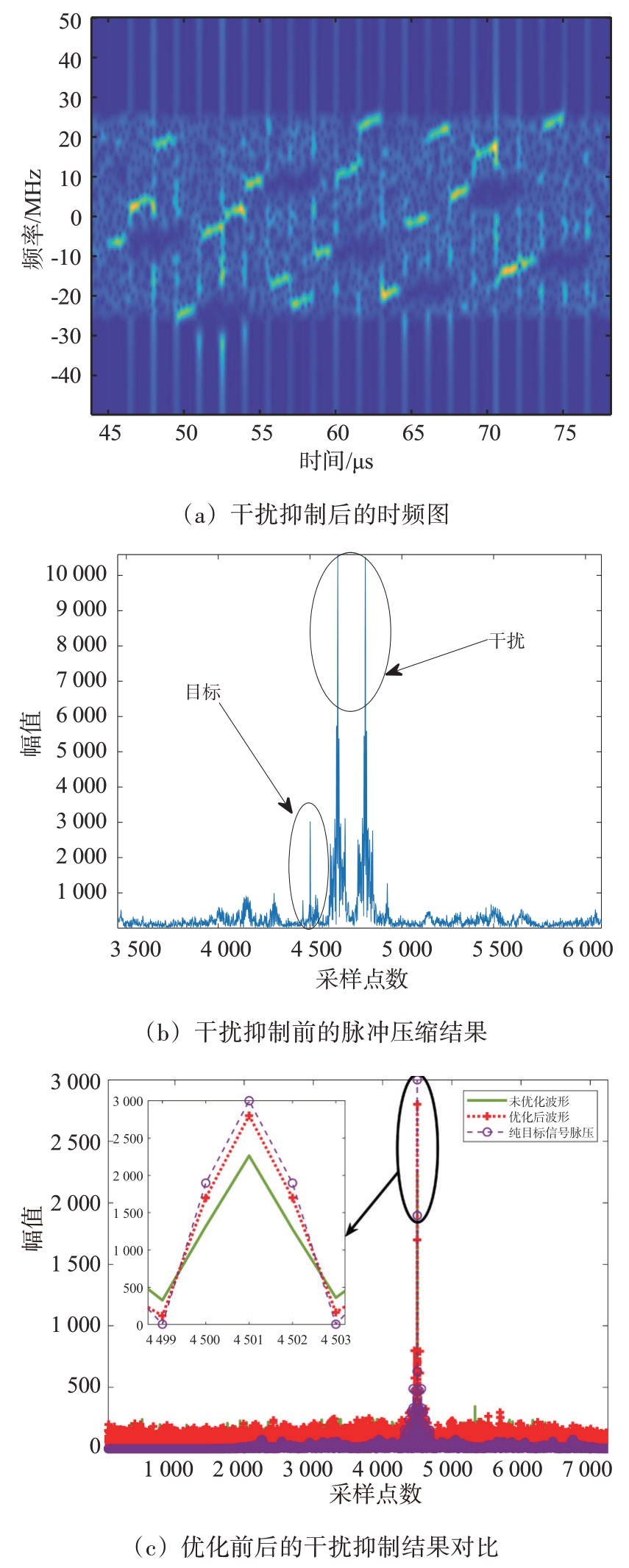
图6 干扰抑制前后结果对比
实验二
在两个间歇采样转发干扰场景下,仿真采用的干扰参数如表3所示。
表3 间歇采样转发干扰参数
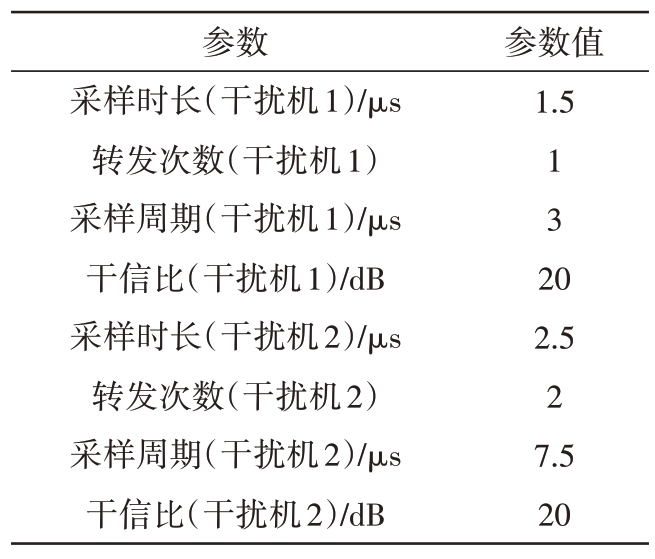
参数采样时长（干扰机1）/μs转发次数（干扰机1）采样周期（干扰机1）/μs干信比（干扰机1）/dB采样时长（干扰机2）/μs转发次数（干扰机2）采样周期（干扰机2）/μs干信比（干扰机2）/dB参数值1.5 13 2 0 2.5 2 7.5 20
图7（a）为子脉冲个数为15 时,干扰对目标的时频重叠度由34%降低至12%,图7（b）为子脉冲个数为20 时,干扰对目标的时频重叠度由34%降低到5.7%,选择子脉冲个数为20 时的编码序列作为发射波形。
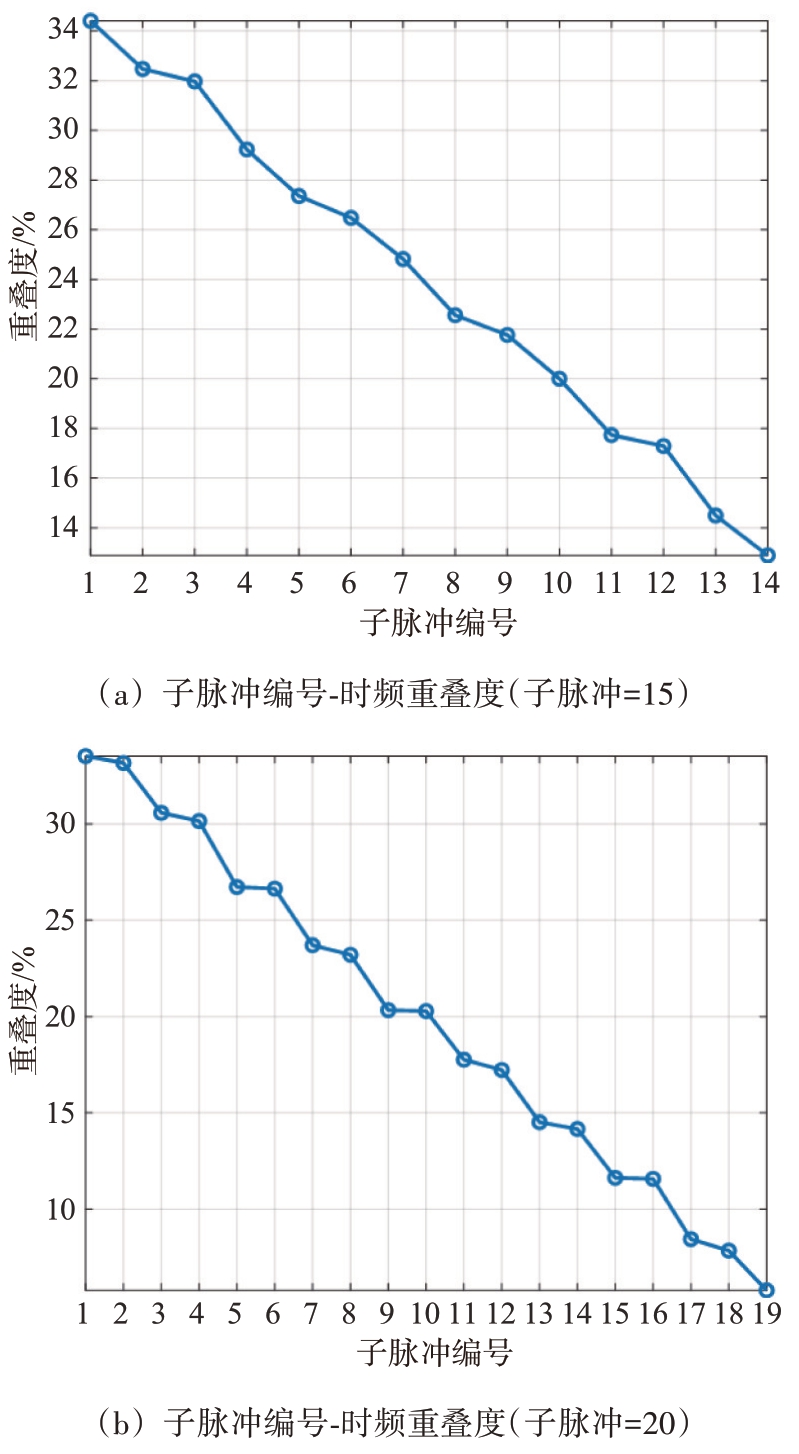
图7 回波时频图以及干扰与目标的时频重叠度优化图
图8（a）为干扰抑制后的时频图；图8（b）为干扰抑制前的脉冲压缩结果,在多干扰场景下,干扰形成的假目标幅值大于单个干扰形成的假目标幅值；图8（c）为采用优化前后波形的干扰抑制结果,基于优化后的脉内捷变波形,SJRIF=34.4 dB,干扰抑制效果较好；未优化波形为子脉冲个数为15 的随机脉内捷变波形,对未优化波形时频滤波处理后的信号损失高于优化后波形,进一步说明了波形优化的有效性。
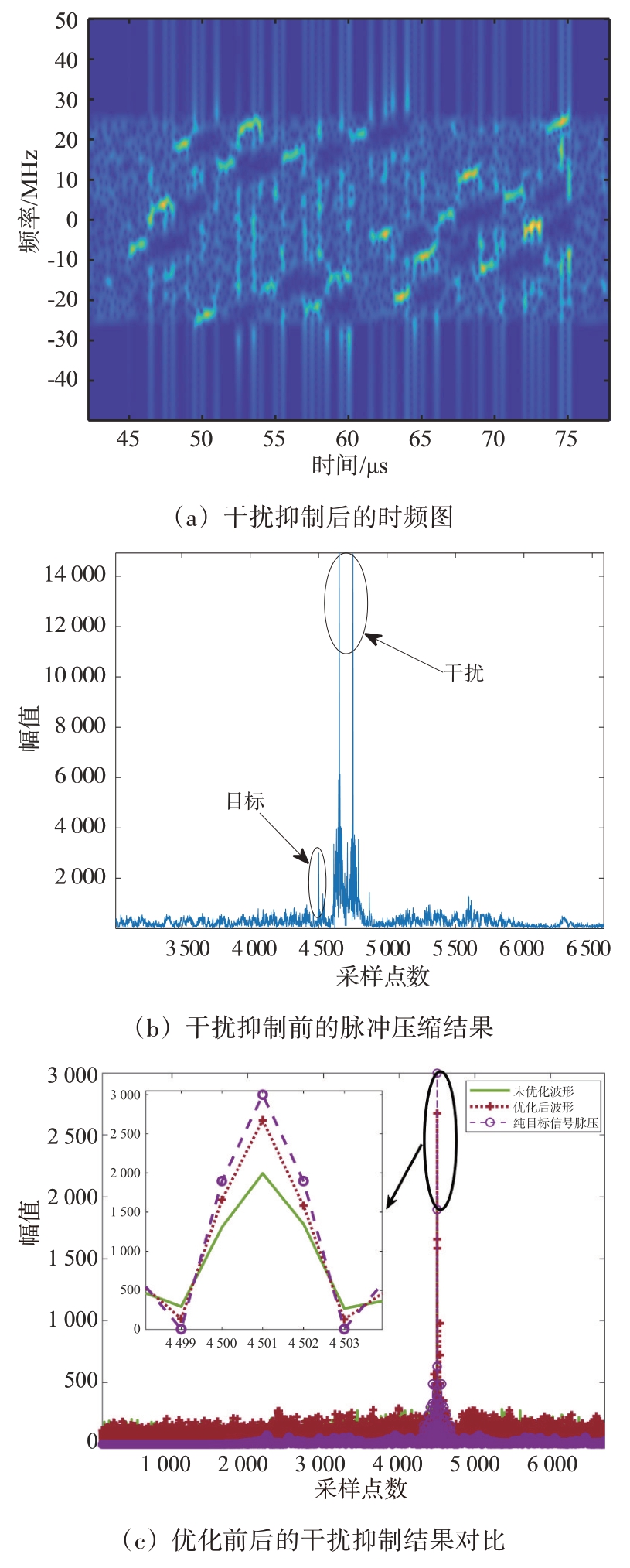
图8 干扰抑制前后结果对比
实测数据处理
为了进一步验证波形设计以及干扰抑制算法的有效性,采用所提算法进行实测数据处理。场景参数如表4所示。
表4 场景参数
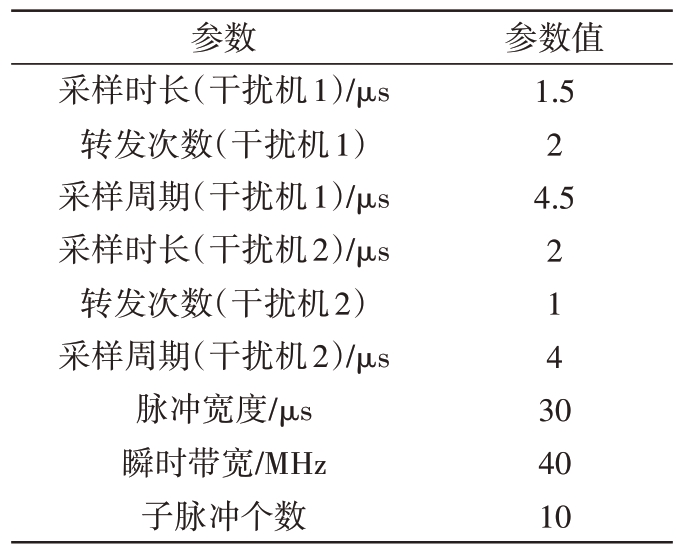
参数采样时长（干扰机1）/μs转发次数（干扰机1）采样周期（干扰机1）/μs采样时长（干扰机2）/μs转发次数（干扰机2）采样周期（干扰机2）/μs脉冲宽度/μs瞬时带宽/MHz子脉冲个数参数值1.5 2 4.5 2143 0 40 10
图9（a）为回波信号的时域波形（优化波形）；图9（b）为回波信号的时频图（优化波形）；图9（c）为回波信号的时域波形（随机波形）；图9（d）为回波信号的时频图（随机波形）,可以看出采用优化波形以及随机波形,干扰与目标的时域重叠基本一致；图9（e）为干扰抑制前后的结果对比,采用优化后波形的目标信号损失较小,相较于未优化波形的干扰抑制结果,目标损失减少了2 dB。
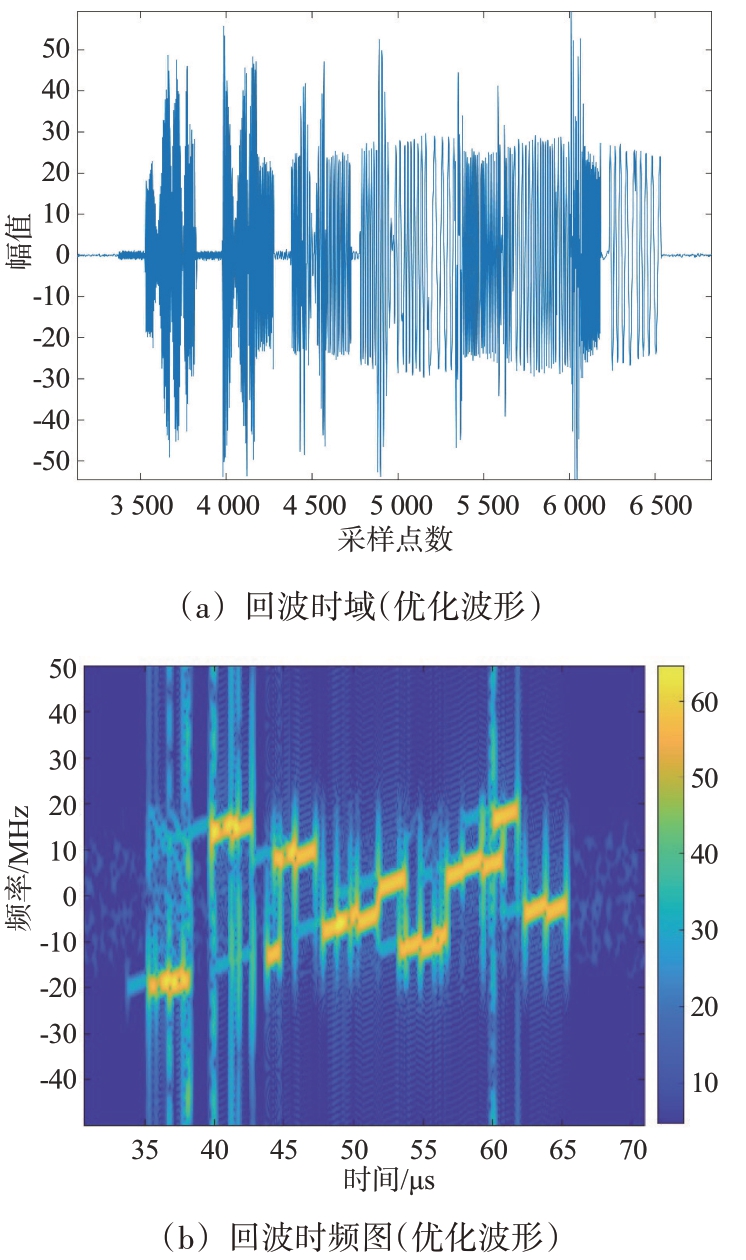
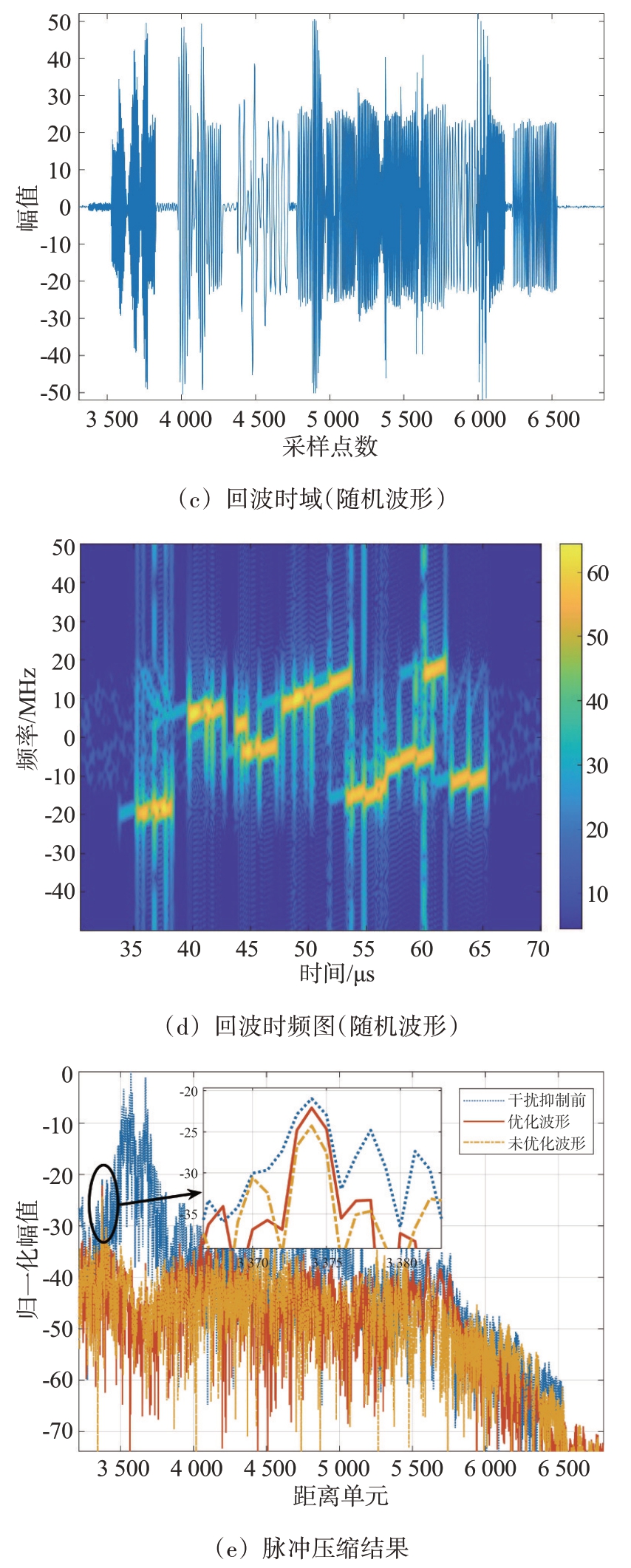
图9 干扰抑制前后结果对比
4 性能分析
分析随着干信比变化条件下SJRIF 以及脉冲压缩后信号损失的变换趋势,对比优化前后波形、随机编码波形（子脉冲个数与优化后的脉内捷变波形子脉冲个数一致）干扰抑制处理以及文献［3］提出的脉冲压缩后提取目标的干扰抑制算法（脉压后干扰抑制）；分析在不同采样延时以及干扰参数估计误差的条件下所提算法的性能,设置蒙特卡洛实验次数为100次。
1） 在单个间歇采样重复转发干扰场景下,干扰参数如表2所示。图10（a）为SJRIF 的变化趋势,优化后波形的SJRIF 最优且较稳定,可以达到36 dB 以上；图10（b）为脉冲压缩后的信号损失随着干信比增加的变化趋势,优化后波形具备干扰与目标重叠区域低的优势,因此脉冲压缩后的信号损失较小,而随机波形以及优化前波形干扰与目标的时频重叠度较高,在干扰抑制时存在较多信号损失。
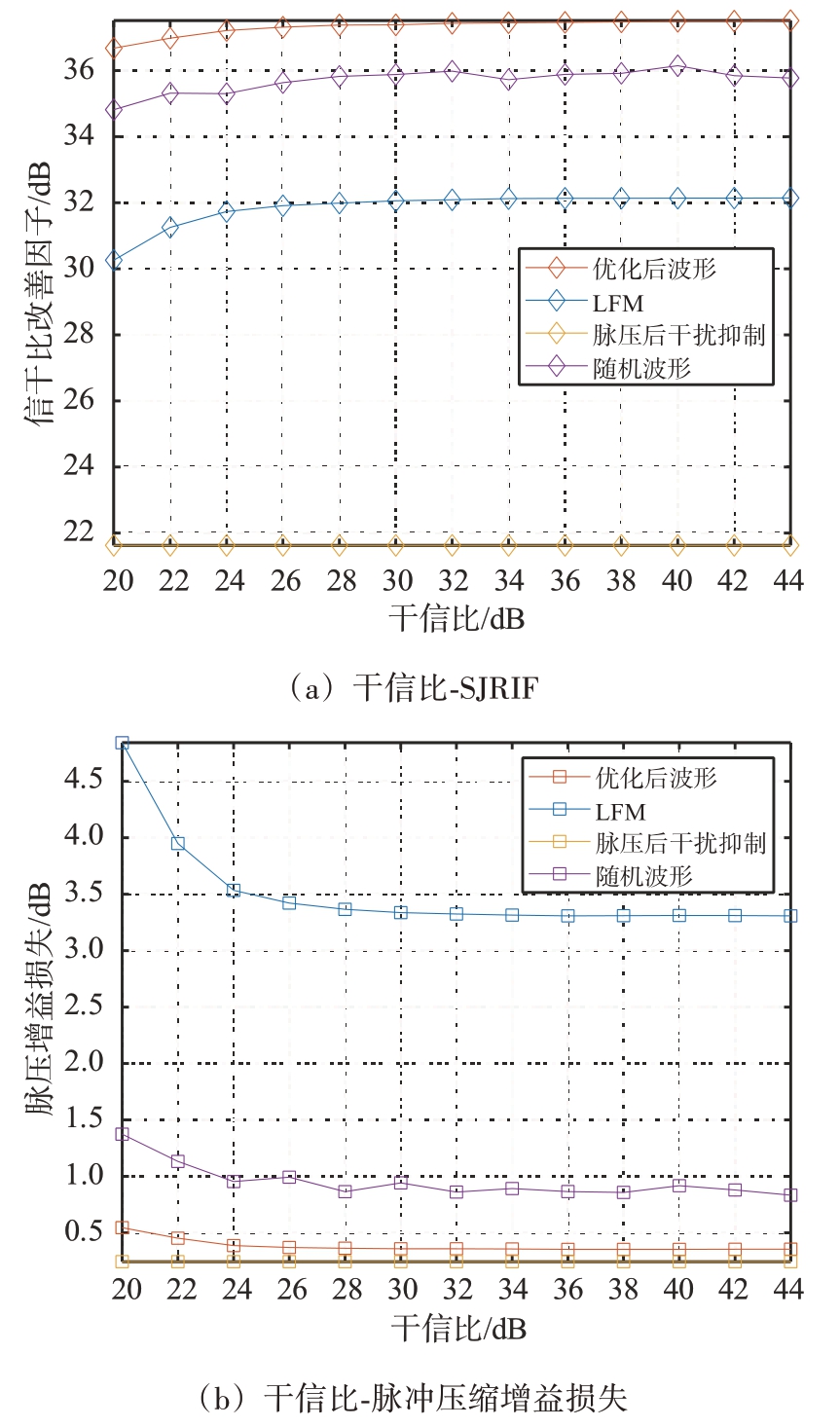
图10 间歇采样重复转发干扰（实验二场景）
2） 分析在间歇采样直接转发干扰以及间歇采样重复转发干扰场景下,当干扰机为非同步采样即存在不同采样延时时,SJRIF 以及脉冲压缩后信号损失的变化趋势。
如图11所示,ISDJ为间歇采样直接转发干扰,ISRJ 为间歇采样重复转发干扰,图11（a）为SJRIF随着采样延时的变化趋势,图11（b）为脉冲压缩后信号损失随着采样延时的变化趋势,可以看出在单个干扰场景下,基于优化后的波形,采用本节所提的干扰抑制算法后,干扰抑制性能以及信号损失受到采样延时的影响不大,算法性能较稳定。
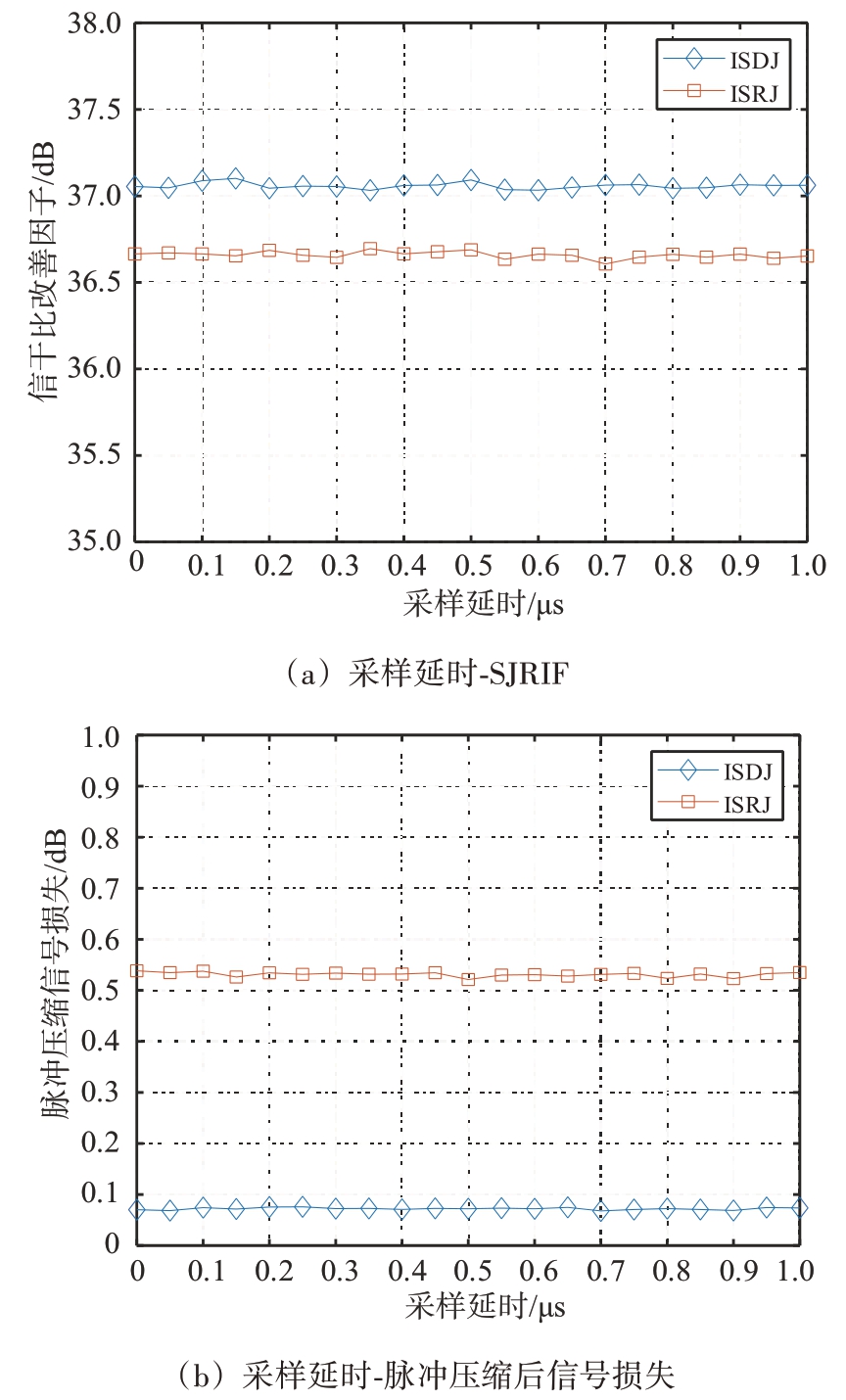
图11 采样延时性能分析
3） 分析在间歇采样直接转发干扰以及间歇采样重复转发干扰场景下,当干扰切片时长的估计存在误差时所提的干扰抑制算法性能,干扰误差变换范围在[ -0.5,0.5 ]变化。
图12（a）为SJRIF 随着估计误差的变化趋势；图12（b）为信号损失随着估计误差的变化趋势。在单个干扰场景下,脉冲压缩后的信号损失逐渐减小,这是因为对干扰的估计误差小于0 时,此时的真实采样时长小于估计的采样时长,真实干扰与目标的重叠度增大,在进行干扰抑制处理后的信号损失较多。随着真实干扰的采样时长逐渐增加,干扰与目标的重叠程度相较于采样时长短的干扰更小,因此干扰抑制处理后的信号损失也较小。图12（a）中SJRIF 在一定范围内抖动,干扰估计误差在-20%～20%之间时,SJRIF 的抖动不超过±5 dB。
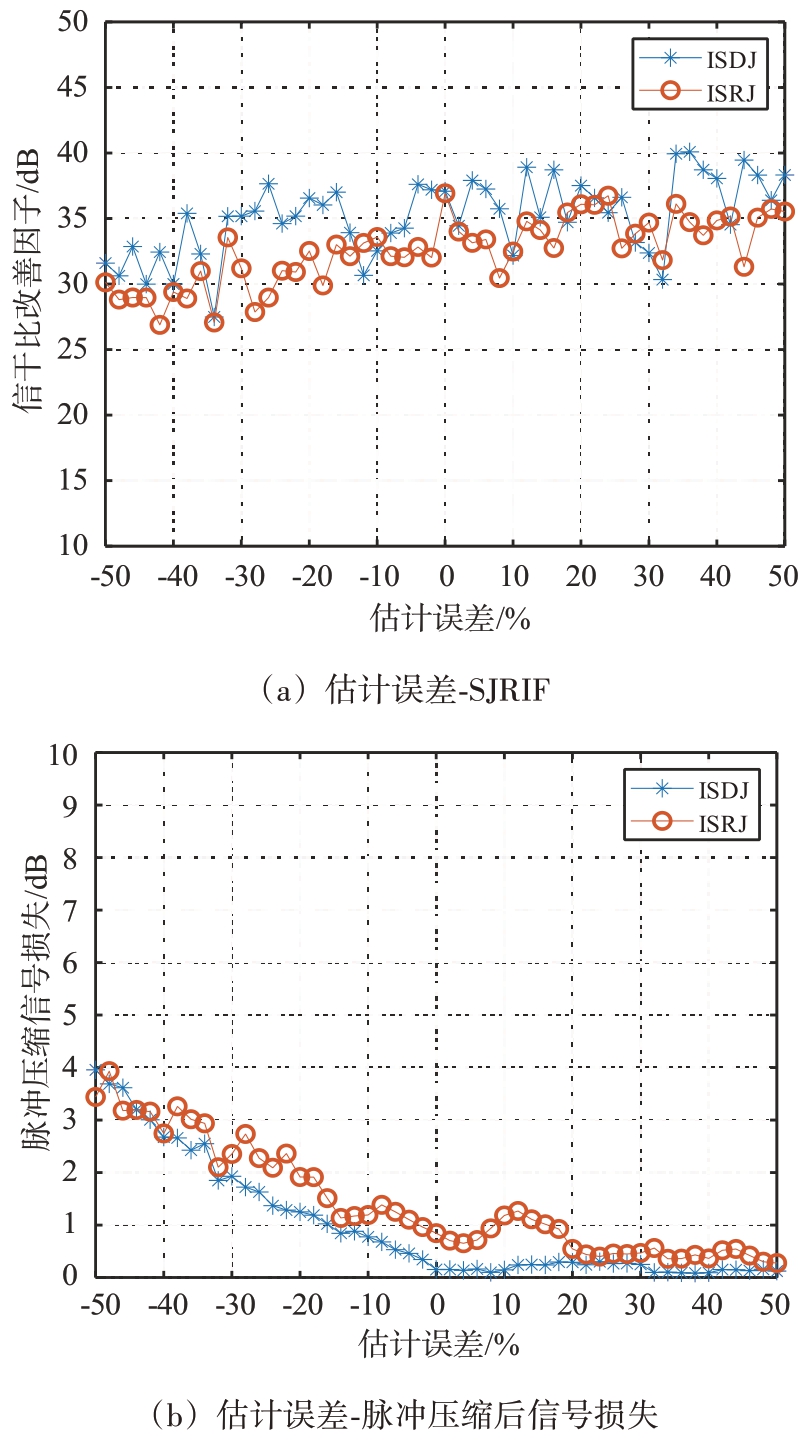
图12 估计误差性能分析
5 结束语
本文提出了一种基于时频重叠度的脉内捷变波形设计与干扰对抗算法,基于干扰认知信息,构建了干扰与目标时频重叠区域的目标函数,利用贪婪算法对子脉冲个数以及脉内编码序列进行优化,降低干扰对目标的时频重叠度。基于优化后波形,将回波信号变换到时频域,基于边缘检测算法对干扰进行识别与抑制。仿真结果表明,所提的算法可以实现对单个以及多个间歇采样转发干扰实现有效抑制,且对干扰参数的敏感性较弱,相较于基于时频滑窗的干扰抑制算法,本文所提算法受到非同步采样以及干扰估计误差的影响较小,且在多干扰场景下也具有较好的对抗效果。
［1］ GONG Shixian, WEI Xizhang, LI Xiang. ECCM Scheme Against Interrupted Sampling Repeater Jammer Based on Time-Frequency Analysis［J］. Journal of Systems Engineering and Electronics, 2014,25（6）:996-1003.
［2］ 原慧,王春阳,安磊,等.基于压缩感知信号重构的间歇采样转发干扰对抗方法［J］.系统工程与电子技术,2018,40（4）:717-725.
［3］ 周超,刘泉华,胡程.间歇采样转发式干扰的时频域辨识与抑制［J］.雷达学报,2019,8（1）:100-106.
［4］ LI Feng, HAN Xue, LI Yang, et al. Interrupted-Sampling Repeater Jamming （ISRJ） Suppression Based on Cyclostationarity［C］//IET International Radar Conference, Online:IET, 2020:793-797.
［5］ 张亮,程正宇,李德栋,等.基于分数阶相关的间歇采样转发干扰抑制算法［J］.电光与控制,2021,28（10）:26-30.
［6］ 董淑仙,全英汇,沙明辉,等.捷变频雷达联合脉内频率编码抗间歇采样干扰［J］.系统工程与电子技术,2022,44（11）:3371-3379.
［7］ 盖季妤,姜维,张凯翔,等.基于差分特征的间歇采样转发干扰辨识与抑制方法［J］.雷达学报,2023,12（1）:186-196.
［8］ 王栗沅,何华锋,韩晓斐,等.全极化雷达抗间歇采样转发式干扰的非匹配滤波方法［J］.雷达科学与技术,2023,21（6）:661-669.
［9］ WANG Fulai, LI Nanjun, PANG Chen, et al. Complementary Sequences and Receiving Filters Design for Suppressing Interrupted Sampling Repeater Jamming［J］. IEEE Geoscience and Remote Sensing Letters, 2022, 19:1-5.
［10］ ZHANG Yang, YU Lei, WEI Yinsheng. Interrupted Sampling Repeater Jamming Countermeasure Technology Based on Random Interpulse Frequency Coding LFM Signal［J］. Digital Signal Processing, 2022（11）:103755.
［11］ WANG Bingqie, GAO Yuliang. ADC Design Techniques in DRFM System Based on EMC［C］// 2002 3rd International Symposium on Electromagnetic Compatibility,Beijing, China:IEEE, 2002:787-790.
［12］ REN Zhifeng, JIANG Miao, ZHANG Lei. Orthogonal Phase-Frequency Coded Signal in a Pulse Against Interrupted Sampling Repeater Jamming［J］. The Journal of Engineering, 2019（21）:7573-7576.
［13］ 周畅,汤子跃,朱振波,等.抗间歇采样转发干扰的波形设计方法［J］.电子与信息学报,2018,40（9）:2198-2205.
［14］ 余涛,周正春,杜小勇,等.一种基于完全互补码波形设计的抗间歇式采样转发干扰方法［J］.电子与信息学报,2023,45（11）:3896-3905.
［15］ 王福来,庞晨,黄大通,等.一种同时全极化雷达发射波形和接收滤波器联合设计的抗间歇采样转发干扰方法［J］.中国科学:信息科学,2022,52（7）:1333-1348.
［16］ 李晋杰,曹运合,张钰林,等.基于STFrFT 的间歇采样转发干扰抑制［J］.系统工程与电子技术,2024,46（10）:3312-3324.
［17］ 周凯,李德鑫,粟毅,等.基于雷达发射波形和非匹配滤波联合设计的间歇采样转发干扰抑制方法［J］.电子与信息学报,2021,43（7）:1939-1946.
［18］ SHI Zhaopeng, WANG Wantian, WU Hao, et al. A New Pulse Modulated LFM Waveform Design Method for Suppressing Interrupted Sampling Repeater Jamming［C］//2023 IEEE 23rd International Conference on Communication Technology, Wuxi, China:IEEE, 2023:336-340.
［19］ 刘逢丁,曹杰,王营博,等.激光雷达距离像的实时边缘检测［J］.光学技术,2021,47（4）:404-409.
［20］ 刘智星.捷变雷达抗干扰及相参处理技术研究［D］.西安:西安电子科技大学,2022.