0 引 言
由于良好的全天时、全天候工作能力,毫米波雷达已经在智能驾驶领域扮演着越来越重要的角色[1-2]。毫米波调频连续波(Frequency Modulated Continuous Wave, FMCW)雷达片上系统(System on Chip, SoC)芯片技术的进步,降低了雷达设计成本和难度,推动了毫米波雷达在汽车上的大规模部署。但大量毫米波FMCW 雷达在临近区域工作,使得雷达系统间相互干扰风险急剧攀升,严重影响车辆的行驶安全。因此,在先进驾驶辅助系统和智能驾驶汽车市场不断增长的背景下,有效减轻雷达间的相互干扰对提高汽车雷达工作能力至关重要。
汽车雷达的干扰抑制是车载毫米波FMCW 雷达研究的热点问题之一。特别地,由于只需在现有雷达系统上,通过改变信号处理流程即可实现干扰抑制,基于信号处理的干扰抑制方法备受青睐[3]。基于信号处理的干扰抑制方法可以分为两大类:传统信号处理方法和基于深度学习的方法。深度学习方法最近被用于FMCW 雷达的干扰抑制[4-6]。但这些方法通常需要在各种情况下获得大量数据集进行训练,复杂度高。所以本文重点关注的是第一大类传统信号处理方法。
通常,传统的信号处理方法通过不同域(即空间、时间、时频、频率等)的滤波或信号分离实现干扰抑制问题。对于多输入多输出(Multiple Input Multiple Output, MIMO)体制的毫米波雷达系统而言,可以通过波束形成进行干扰零陷实现空域干扰抑制[7-9]。然而,当目标信号和干扰信号的方向相同或相近时,由于分辨率有限,目标信号也有可能被抑制掉。
针对空域干扰抑制的不足,文献[10]在时域上对接收信号的扰动部分进行迫零(Zeroing),实现了干扰功率的衰减,但这也丢失了与干扰重叠的部分有用的信号。文献[11]则采用小波分解降噪法去除干扰。由于小波变换的分解特性,可以很好地保留未受干扰成分中的有用信号。此外,文献[12]提出了一种基于经验模态分解的迭代方法,将FMCW 雷达回波信号在时域内分解为一系列经验模态。文献[11-12]所提方法的性能会随着采样信号中受干扰样本的增加而下降。另外,文献[13]介绍了一种基于自回归模型的信号重建技术,该方法能够外推干扰部分的有用信号,比迫零方法能够检测到更多的目标。但当干扰持续时间较长时,该方法的重建质量会下降。为了克服重建质量下降问题,文献[14]提出了稀疏低秩Hankel 矩阵分解法,该方法通过构建Hankel 矩阵,并使用鲁棒主成分分析算法将目标信号提取出来,从而达到干扰抑制的目的。但是该算法迭代次数多,运行时间较长。
相对于时域,时频域可以呈现目标与干扰之间更多的差异。文献[15]在干扰背景下对接收信号进行时频分析,定位出干扰时间跨度区域,进而恢复出目标回波。同样在时频域中,文献[16]则介绍了一种基于恒虚警(Constant False-Alarm Rate, CFAR)的干扰抑制方法。该方法通过CFAR检测器定位出干扰,然后分别通过归零、幅度校正和基于Burg 的外推法进行信号重建。实验结果表明,基于时频分析的干扰抑制方法优于时域方法,但其所需的计算成本较高。
毫米波FMCW 雷达间的相互干扰在时域呈现类似脉冲特性[10],经过距离FFT 之后,它将抬升噪底,即干扰信号将散布于整个频谱。基于干扰与目标信号在频域特征上的差异,文献[17]设计了最小均方自适应噪声对消器(Adaptive Noise Canceller based on Least Mean Square,ANC-LMS),以降低干扰的影响。尽管该方法的计算效率很高,但其LMS 步长为固定值,无法同时满足收敛速度和收敛精度的要求。
针对ANC-LMS 算法对FMCW 雷达相互干扰抑制能力的不足,本文基于双曲正切函数框架,设计了一种新的代价函数来获取最优滤波器权系数,提高了算法对干扰的抑制能力。此外,本文通过使用归一化误差的Logistic 函数来自动更新步长,算法在迭代初期采用较大步长,加快收敛速度;而在收敛后,使用较小的步长,以提升收敛精度,最终改善算法稳态性能。仿真与实测实验表明,与ANC-LMS等其他干扰抑制方法相比,提出的VSHTLMS算法在提高信干比等性能方面有着更优的表现。
1 提出算法
FMCW 雷达相互间的干扰,在混频与低通滤波之后,泄露到通带内的干扰在时域呈现脉冲噪声特性[10]。本节在介绍时域脉冲类干扰产生机理及其频域抑制模型的基础上,针对传统LMS 算法的缺点,提出Logistic 变步长双曲正切最小均方算法 —— VSHTLMS,并给出其完整的流程。
1.1 脉冲干扰信号的产生
在道路场景中,当至少有两辆装配毫米波FMCW 雷达的车辆对向行驶时,就会发生相互干扰。根据干扰雷达与被干扰雷达使用的波形是否不同,一般可以将干扰分为两类,一是交叉干扰,这是最常见的情况,二是鬼影干扰,其发生的概率较小[18]。所以本文的重点是处理第一类干扰,其时频图如图1所示。
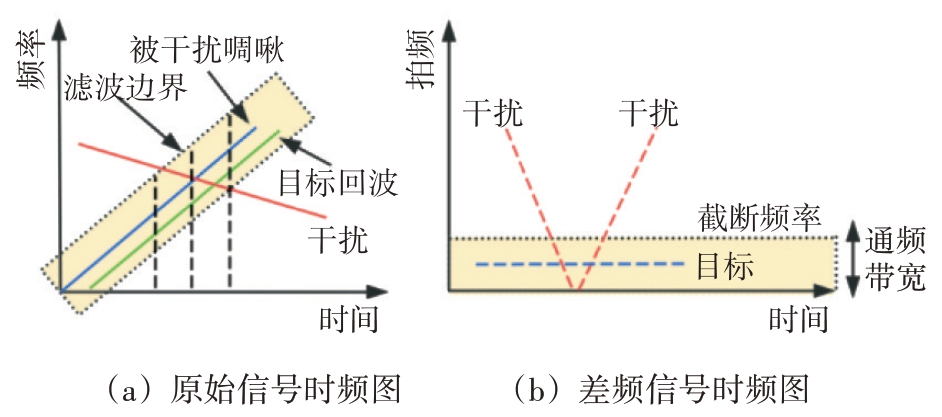
图1 脉冲干扰信号的时频图
在交叉干扰情况下,带外干扰的拍频被低通滤波器截断,而其余的干扰泄漏到低通滤波器的通带中。由于干扰覆盖了整个通频带宽,相应地在时域表现出类似脉冲的特点。当干扰源位于目标FMCW 雷达附近时,干扰雷达信号的接收电平远高于来自目标的反射信号。强的脉冲干扰在距离FFT 之后,将大幅抬升噪底,从而会导致目标漏检。
1.2 干扰抑制模型
对于交叉干扰,当干扰雷达的啁啾频率高于被干扰雷达时,在频率的负半部分产生干扰,如图2所示。反之,将出现正半部分干扰。另一方面,由于真实目标回波总是发射啁啾的延时版本,因此拍频总是在频率的正半部分。借助目标拍频信号和干扰信号在频谱上的上述特性,可以设计相应的交叉干扰抑制方法。例如文献[17]用负半频率的干扰作为参考,使用LMS 算法消除了正半频率的干扰。
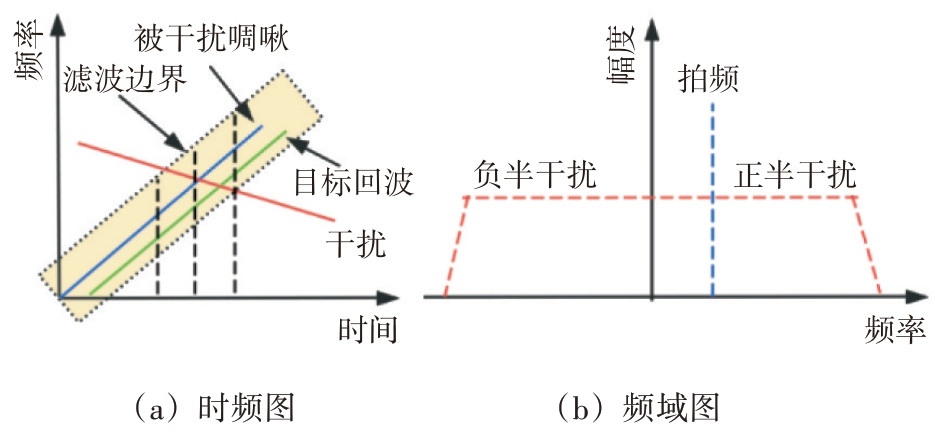
图2 两种不同FMCW汽车雷达之间的干扰信号特征分析
自适应干扰抑制系统框图如图3所示,e 表示由真实目标回波引起的拍频,ε 表示干扰抑制后的目标频谱,ip 和in 分别表示FFT 正半段和负半段的干扰,它们是共轭对称的。
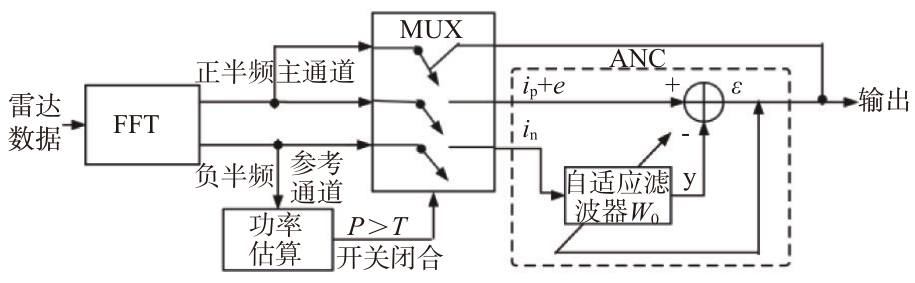
图3 采用自适应噪声对消器的干扰抑制框架图
雷达回波数据经过距离FFT 后,当估计的功率大于某个阈值T 时,激活自适应噪声对消器(Adaptive Noise Canceller,ANC)。同时利用误差信号的平均值来更新步长。否则,ANC 将被绕过以节省计算资源。
1.3 双曲正切最小均方算法
如图3所示,LMS 算法中误差的计算公式表示为
式中,y(k)为滤波器的输出,其计算公式为
式中,wk为长度为L × 1 的权向量,H 为共轭转置,fk =[ in(k), in(k - 1), …, in(k - L + 1)]H。滤 波 器长度L 根据实际情况来选择,较长的L 值可以提供更好的频率选择性和抗干扰能力,但会影响近距离干扰抑制能力。
对非高斯噪声,传统LMS 算法的性能将退化[19]。为提高LMS 算法对脉冲干扰抑制的稳健性,本文借助双曲正切函数,定义一个新的代价函数:
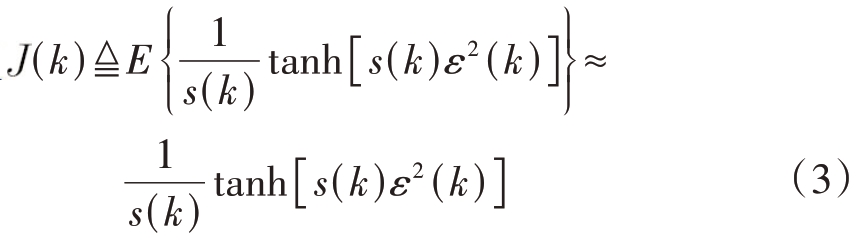
式中,E(·)表示数学期望,双曲正切函数表达式为
s(k)为归一化误差,用来进一步抑制脉冲干扰的影响,其更新公式如下[20]:
式中,c(k)为误差累积值,u(k)为误差累积值的平均值,它们的计算公式如下:
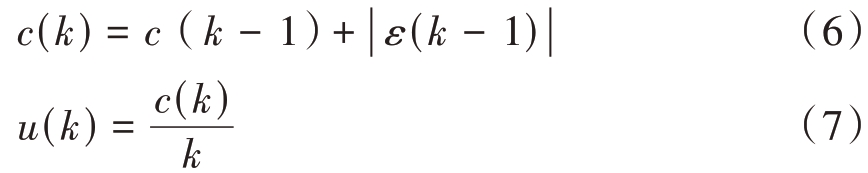
注意到s(k)也利用了双曲正切函数的非线性,而且它包含了误差累积值的平均值,因此能够缓解瞬时误差的影响,提高算法对脉冲干扰的稳健性。
由于s(k)的取值与误差的当前值ε(k)无关,在当前时刻可以将其视为已知量,因此式(3)中的代价函数关于滤波器权向量wk 的导数可以表示为
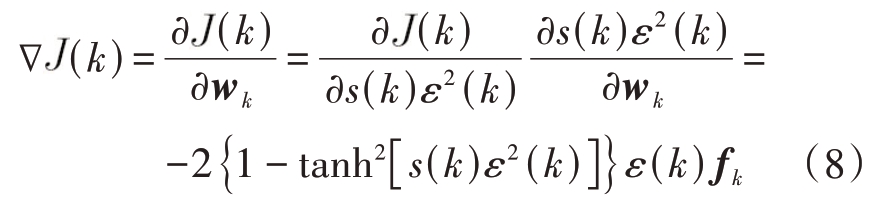
于是,当采用最速下降法时,权值的更新公式可表示为
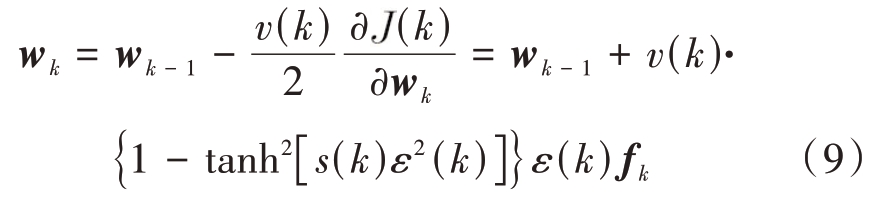
式中,v(k)为变步长函数,将在下一小节给出。
1.4 Logistic变步长算法
传统LMS 算法步长采用固定值,无法同时满足收敛速度和收敛精度的要求。使用大步长可以提高收敛速度,但无法获得较小的稳态误差;小步长可以获得较小的稳态误差,但是收敛速度慢[20]。针对上述问题,本文提出一种基于Logistic 函数的变步长LMS 算法。通过利用Logistic 函数构建步长与误差归一化值之间的非线性关系,使得算法在迭代初期获得较大步长,加快收敛速度;而在收敛后,使用较小的步长,以提升收敛精度,最终改善算法稳态性能。
Logistic函数的一般形式为
在式(10)基础上,本文使用归一化误差的Logistic函数,并增加一个常数来控制步长变化的快慢,即
式中,q是一个常量,取值范围在(0,1)之间。
最后,基于变步长的双曲正切最小均方自适应降噪算法的完整流程如表1所示。
表1 提出的VSHTLMS算法
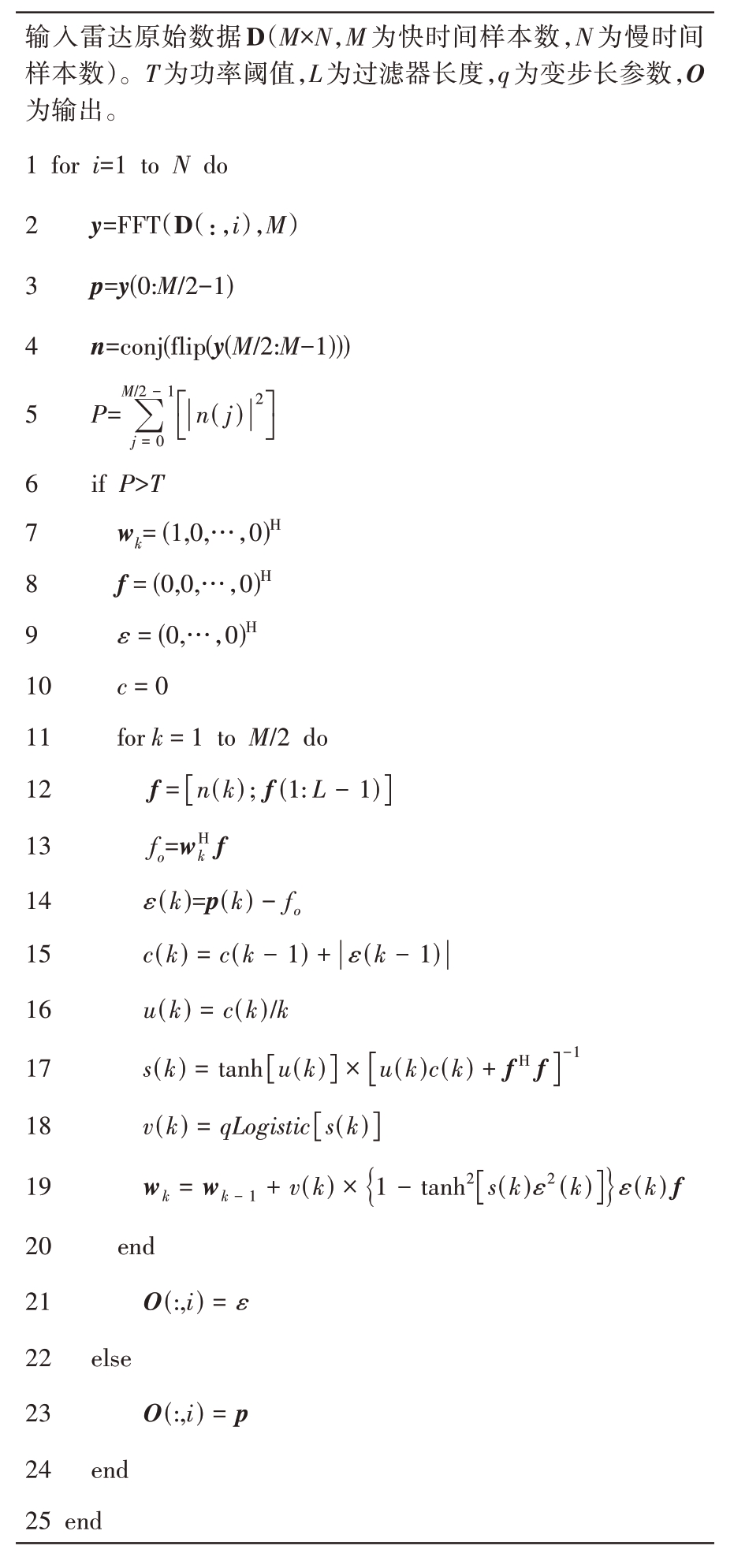
输入雷达原始数据D(M×N,M 为快时间样本数,N 为慢时间样本数)。T为功率阈值,L为过滤器长度,q为变步长参数,O为输出。1 for i=1 to N do 2 y=FFT(D(:,i),M)3 p=y(0:M/2-1)4 n=conj(flip(y(M/2:M-1)))5 P=∑j = 0 M/2 - 1■■|n(j)|■■2 6 if P>T 7 wk= (1,0,…,0)H 8 f = (0,0,…,0)H 9 ε = (0,…,0)H 10 c = 0 11 for k = 1 to M/2 do 12 f = [ ]n(k); f(1: L - 1)13 fo=wHk f 14 ε(k)=p(k) - fo 15 c(k) = c(k - 1) + ||ε(k - 1)16 u(k) = c(k)/k 17 s(k) = tanh[ ]u(k) ×[ ]u(k)c(k) + fH f-1 18 v(k) = qLogistic[ ]s(k)19 wk = wk - 1 + v(k) ×{ }1 - tanh2[ ]s(k)ε2(k) ε(k)f 20 end 21 O(:,i) = ε 22 else 23 O(:,i) = p 24 end 25 end
2 数值仿真
为了验证误差归一化值s(k)对抗干扰性能的影响,本节首先分析代价函数中嵌入s(k)前后的性能进行分析,随后再将提出的VSHTLMS 算法与Zeroing、ANC-LMS方法进行了比较。
2.1 性能指标
为了便于在不同的干扰抑制(Interference Mitigation, IM)方法之间进行比较,本文选取典型的含有20 个参考单元和6 个保护单元的恒定虚警率窗口来计算SIR 用以评估频域的干扰抑制性能[17]。SIR定义为

式中,Ftarget 和Fnoise-floor 分别为目标所在的正半频谱幅度值以及目标旁边的噪声基底幅度值。通常SIR越高,说明抑制干扰的性能越好。
2.2 目标仿真
以典型的汽车雷达参数进行数值仿真,如表2所示。在仿真场景中,目标1,2分别在50 m,105 m处;未进行干扰抑制之前目标1的SIR为8.345 3 dB,目标2的SIR为8.579 dB。
表2 FMCW 雷达仿真系统参数
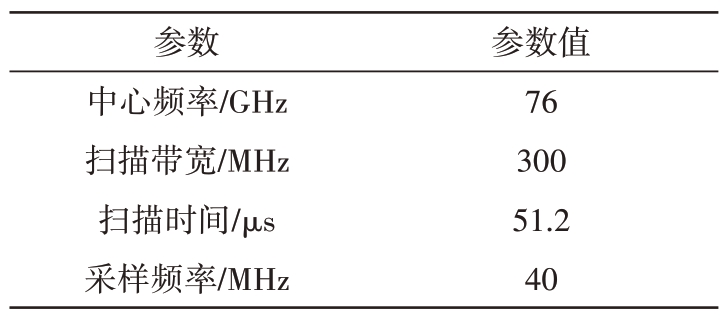
参数中心频率/GHz扫描带宽/MHz扫描时间/μs采样频率/MHz参数值76 300 51.2 40
首先将接收到的雷达数据分为正负频谱,然后分别送入到主通道以及参考通道,干扰阈值T设置为0.5,滤波器长度L 设为8,变步长参数q 为4×10-4。
为了验证本文所提出的新代价函数的有效性,下面分析代价函数中嵌入s(k)前后的性能差异,如图4所示。
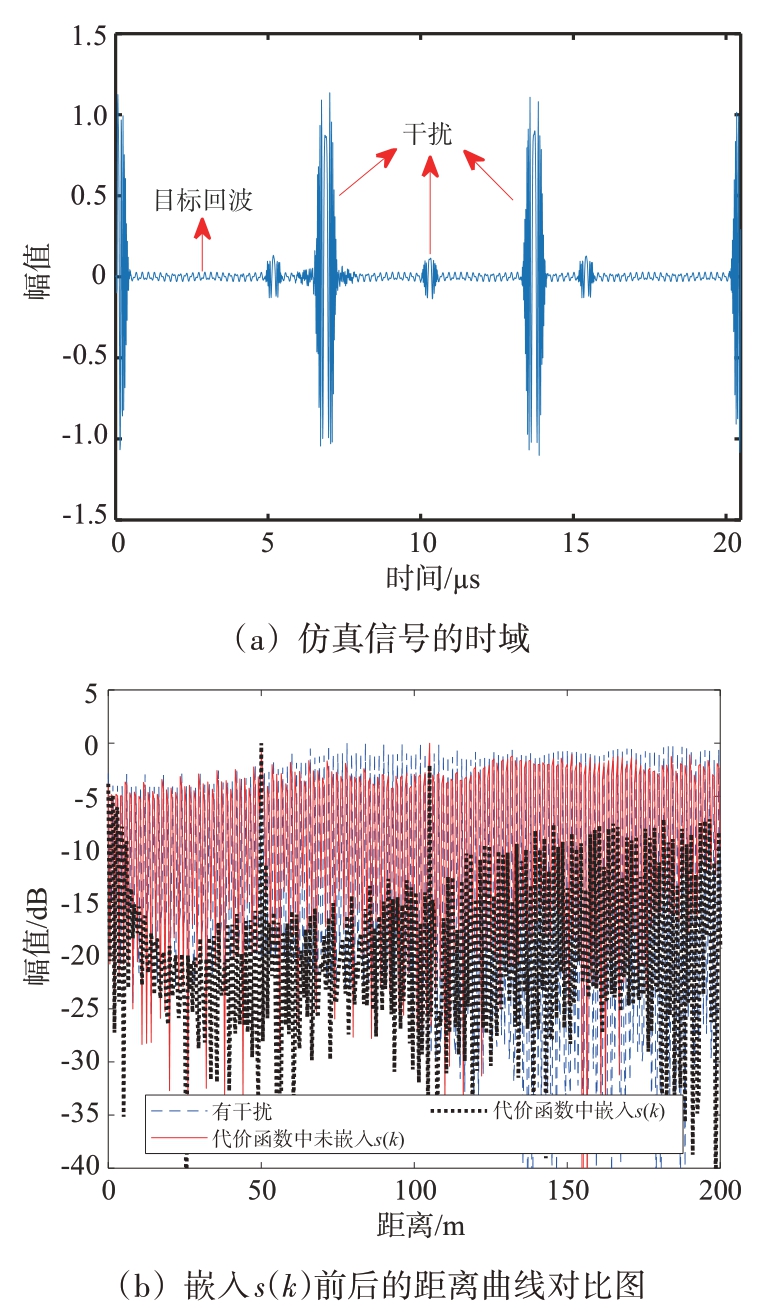
图4 仿真信号时域和距离曲线图
对图4(a)的干扰进行抑制,从图4(b)中很明显可以看出,在双曲正切代价函数中嵌入s(k)后,可以很好地抑制脉冲干扰,降低目标旁瓣。当嵌入s(k)到代价函数之后,目标1 和目标2 的SIR 比未嵌入s(k),分别提高15.277 1 dB 和11.660 9 dB。由此表明本文所设计的新代价函数,可以进一步抑制脉冲干扰的影响,提高算法对脉冲干扰的稳健性。
另外,为了更好地验证所提出算法的有效性,下面将本文提出的VSHTLMS算法与Zeroing、ANCLMS 方法进行了比较。对于ANC-LMS 方法,固定步长参数设为150,干扰阈值和滤波器长度均与VSHTLMS算法相同。处理效果如图5所示。
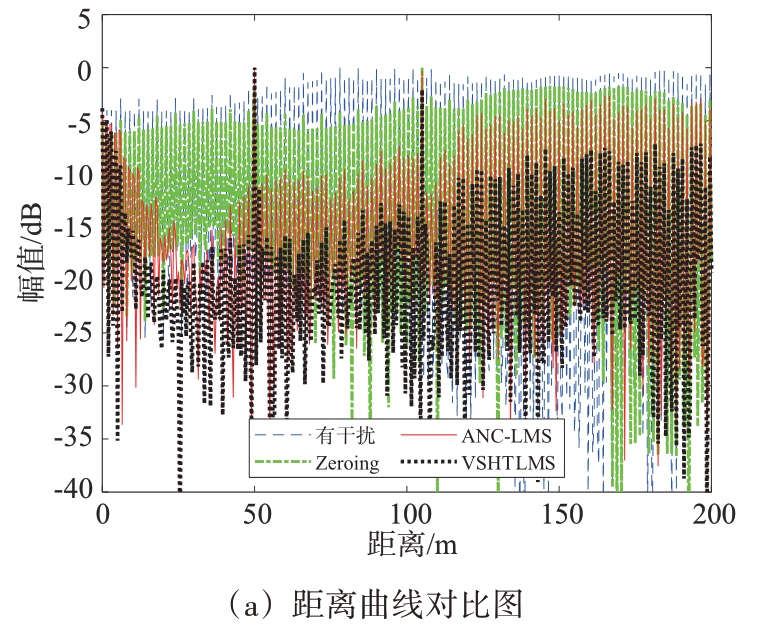
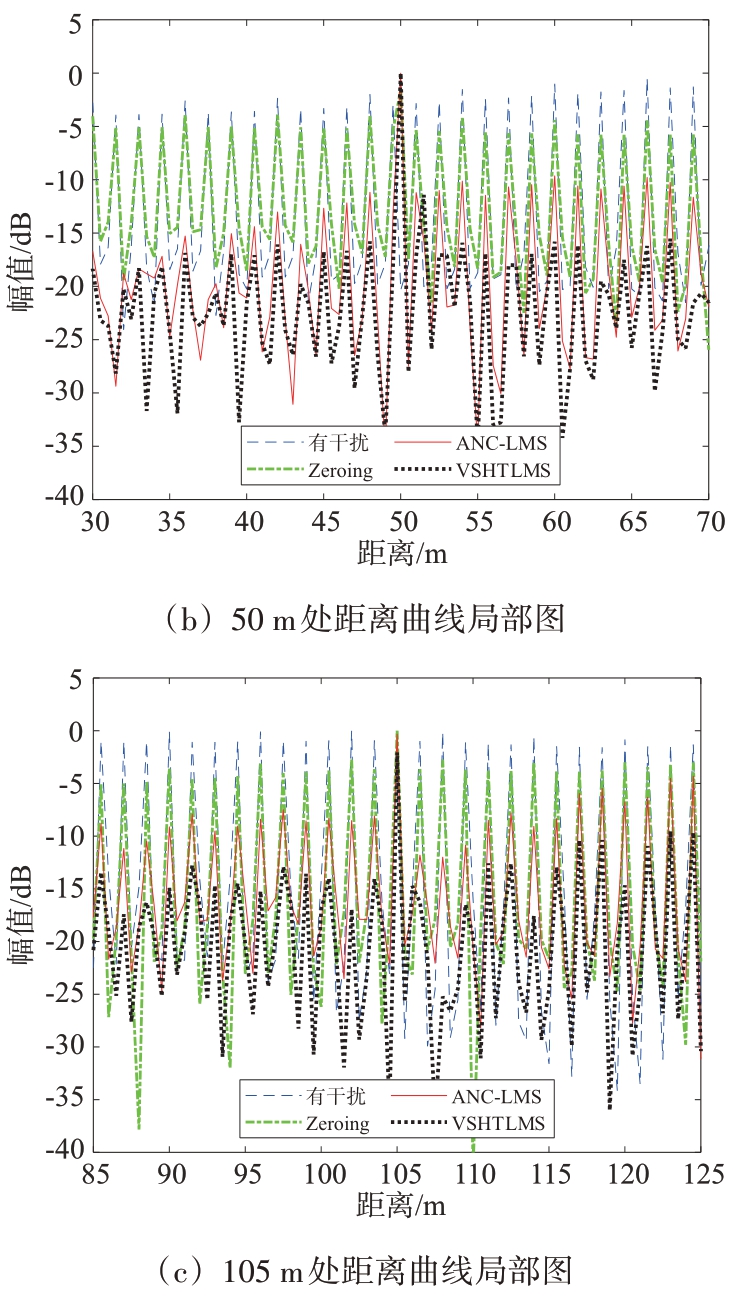
图5 距离曲线对比图
对图4(a)的干扰进行抑制后,得到图5(a)、(b)、(c)中目标的距离曲线。与IM 前相比,所提出的算法比Zeroing、ANC-LMS 更好地降低了目标的本底噪声。此外,Zeroing 在进行IM 后目标1 和目标2的SIR分别减少了0.979 03 dB、0.168 67 dB,这是因为有用信号与干扰重叠的部分也被归零,从而造成了目标SIR的损失。ANC-LMS在进行IM后,目标1的SIR为15.860 6 dB,目标2的SIR为13.233 dB,较IM 前分别提高了7.515 3 dB 和4.654 dB。而VSHTLMS 结果中目标1 和目标2 的SIR 分别为19.844 2 dB,16.995 5 dB,较IM 前分别提高了11.498 9 dB 和8.416 5 dB。如表3所示,以SIR 为衡量指标,VSHTLMS 方法比ANC-LMS、Zeroing 实现了更优的IM性能。
表3 目标SIR变化
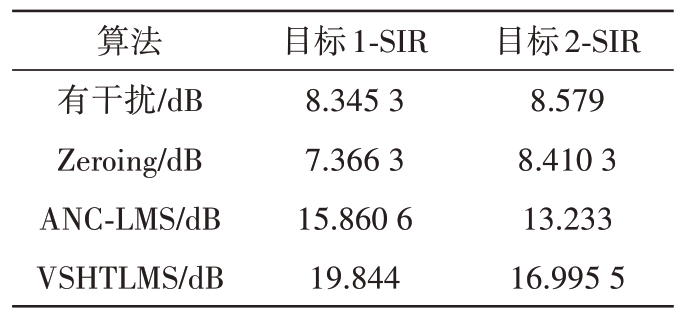
算法有干扰/dB Zeroing/dB ANC-LMS/dB VSHTLMS/dB目标1-SIR 8.345 3 7.366 3 15.860 6 19.844目标2-SIR 8.579 8.410 3 13.233 16.995 5
3 实测试验
本节采用公开数据集,以验证提出的VSHTLMS 算法在实测数据中依然具有良好的表现。实测数据来源于文献[17],实验场景如图6所示。车辆在14~15 m 来回行驶,充当移动目标。干扰雷达放置在被干扰雷达前面,距离为2 m。实验设置的雷达配置如表4所示。
表4 雷达实验配置
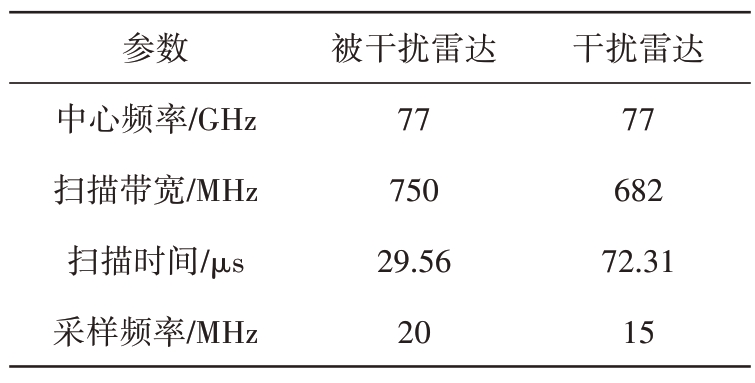
参数中心频率/GHz扫描带宽/MHz扫描时间/μs采样频率/MHz被干扰雷达77 750 29.56 20干扰雷达77 682 72.31 15

图6 真实场景
在此实验中,计算得到在有干扰情况下目标的SIR 为0.404 2 dB。此外,设置ANC-LMS 的固定步长为80,VSHTLMS 变步长参数为8×10-2,其余的参数均与仿真实验相同。IM前后如图7所示。
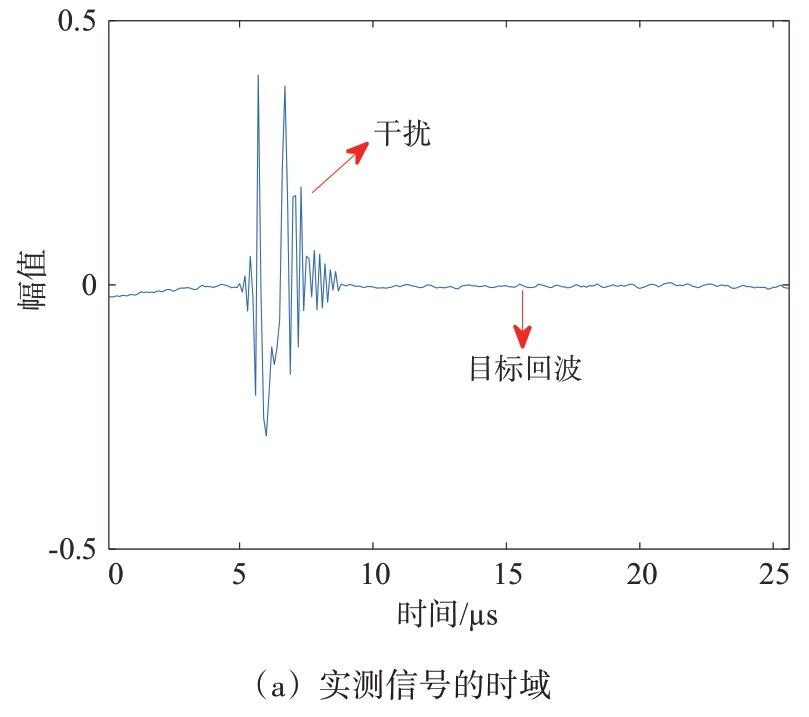
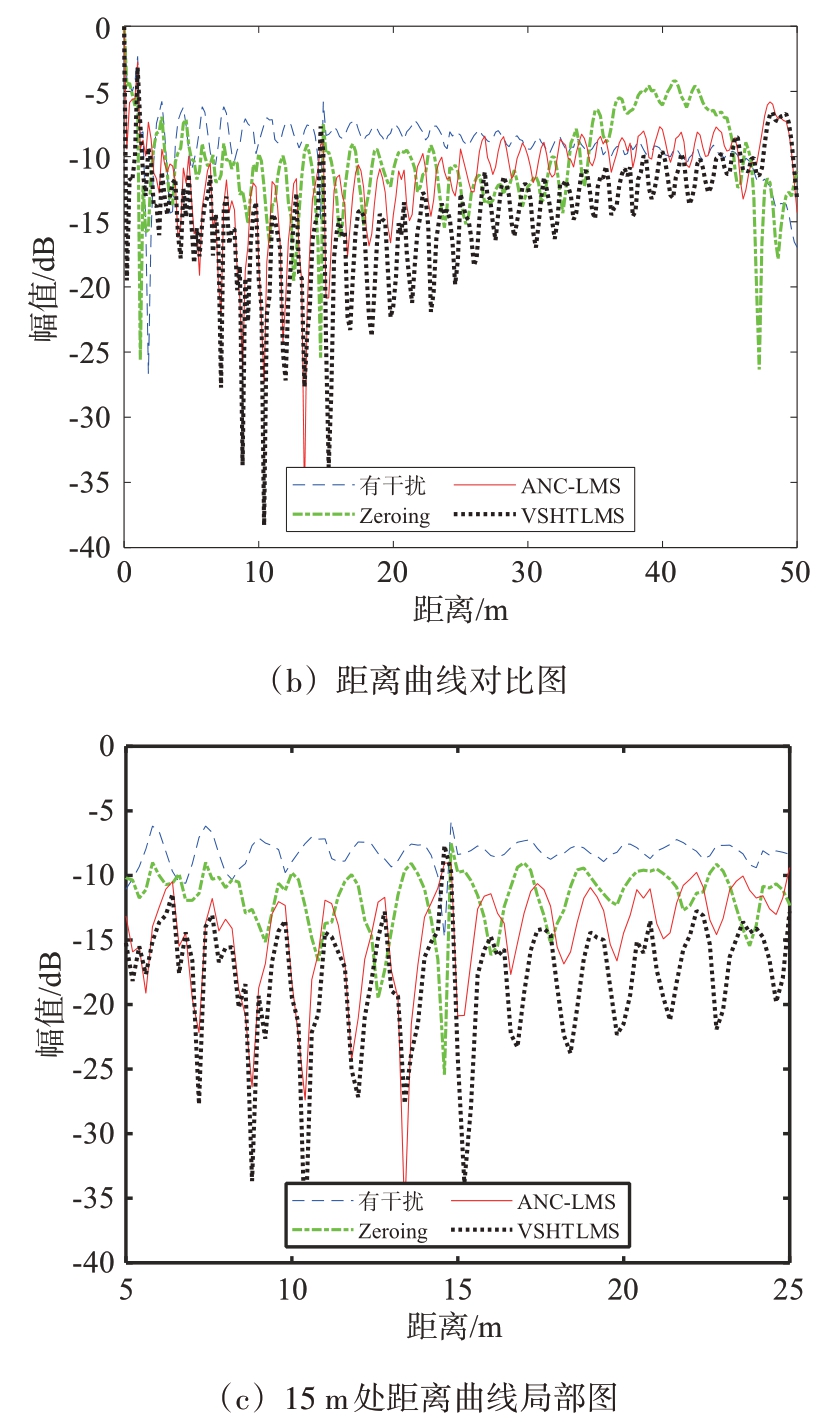
图7 实测信号时域和距离曲线图
对图7(a)的干扰进行抑制后,得到图7(b)、(c)中目标的距离曲线。与IM 前相比,较Zeroing、ANC-LMS,提出的算法更好地降低了噪底。此外,Zeroing在目标15 m处的SIR为-13.840 9 dB,损失了目标的SIR。而ANC-LMS 较IM 前目标SIR 提高了4.88 dB 。VSHTLMS在目标15 m处的SIR为10.191 8 dB,比IM 前提高了9.787 6 dB,如表5所示。因此,就距离曲线的旁瓣、SIR 而言,基于变步长双曲正切LMS 的方法比Zeroing、ANC-LMS 实现了最佳的IM性能。
表5 目标SIR变化
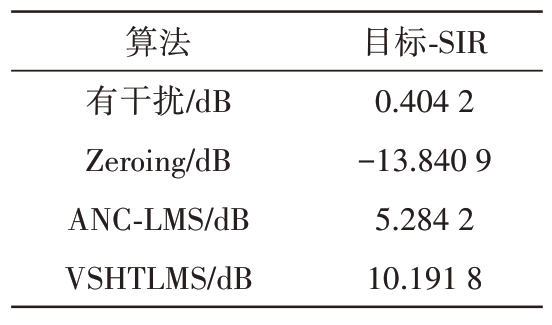
算法有干扰/dB Zeroing/dB ANC-LMS/dB VSHTLMS/dB目标-SIR 0.404 2-13.840 9 5.284 2 10.191 8
此外,本文对距离FFT 数据进行多普勒-FFT处理,得到的距离-多普勒图如图8所示。
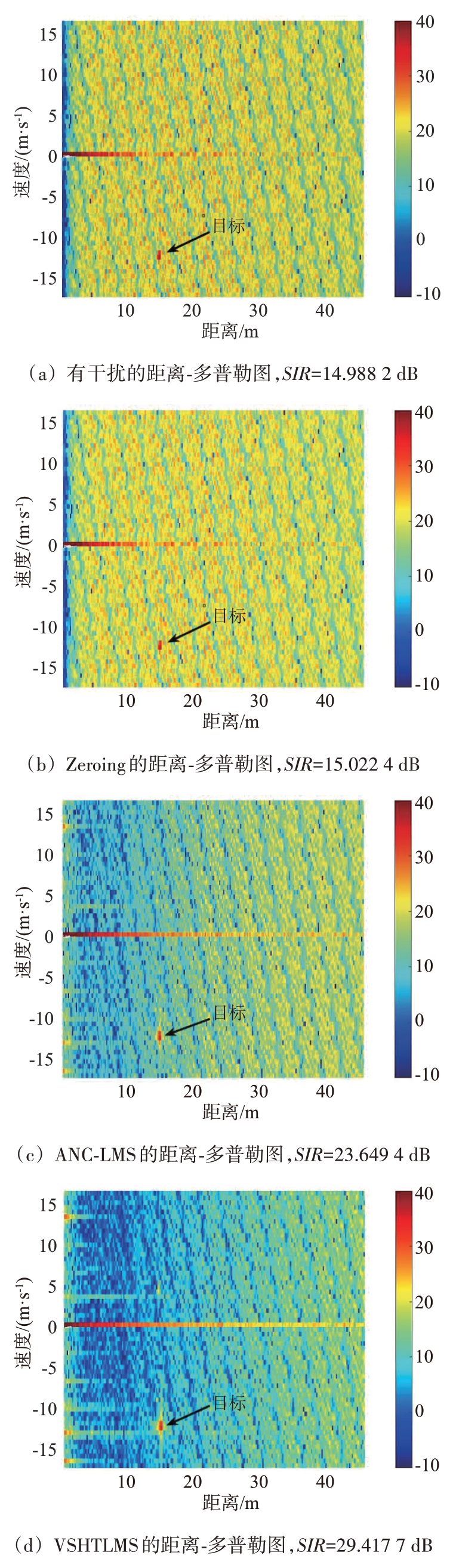
图8 距离-多普勒对比图
作为对比,图8(a)显示了干扰雷达开启时目标的距离-多普勒图,图中明显可见,15 m 处的目标基本被噪声淹没。图8(b)显示了Zeroing的距离-多普勒图,由于该算法在进行迫零时损失了目标的相位信息,因此其并没有消除相位干扰。图8(d)显示了VSHTLMS的距离-多普勒图,与图8(c)ANCLMS 方法相比,VSHTLMS 比ANC-LMS 的目标SIR多增加了5.768 3 dB,更好地抑制了干扰。
4 结束语
本文利用毫米波FMCW 雷达相互间干扰具有类似脉冲噪声特性,提出了一种变步长的双曲正切最小均方自适应干扰抑制算法。对于脉冲干扰,传统的自适应 LMS 算法的性能较差,无法更好地应对干扰雷达所引起的噪底抬升问题。而本文通过在双曲正切最小均方算法的代价函数中引入归一化误差,实现了对脉冲干扰的有效抑制。仿真与实测数据均证实了提出的VSHTLMS 能够改善SIR,进而降低FMCW 雷达相互干扰对后续信号处理和参数估计的影响。
[1] 黄壮,夏伟杰,余思伟,等.基于扩频的汽车雷达后向散射通信系统研究[J].雷达科学与技术,2020,18(3):247-253.
[2] 段宗明,刘明,吴博文,等.应用于智能驾驶的77 GHz毫米波汽车雷达收发机芯片[J].雷达科学与技术,2021,19(2):130-136.
[3] WANG Yunxuan, HUANG Yan, WEN Cai, et al. Mutual Interference Mitigation for Automotive FMCW Radar with Time and Frequency Domain Decomposition[J]. IEEE Trans on Microwave Theory and Techniques, 2023, 71(11):5028-5044.
[4] ROCK J, TOTH M, MEISSNER P, et al. Deep Interference Mitigation and Denoising of Real-World FMCW Radar Signals[C]//Proceedings of the 2020 IEEE International Radar Conference, Washington, DC, USA: IEEE, 2020:624-629.
[5] 文豪,高勇.自注意双路径RNN 用于汽车雷达干扰抑制[J].雷达科学与技术,2022,20(6):678-687.
[6] WANG Jianping, LI Runlong, HE Yuan, et al. Prior-Guided Deep Interference Mitigation for FMCW Radars[J]. IEEE Trans on Geoscience and Remote Sensing, 2022, 60:1-16.
[7] BECHTER J, RAMEEZ M, WALDSCHMIDT C. Analytical and Experimental Investigations on Mitigation of Interference in a DBF MIMO Radar[J].IEEE Trans on Microwave Theory and Techniques, 2017, 65(5):1727-1734.
[8] ARTYUKHIN I, ERMOLAEV V, FLAKSMAN A, et al.Development of Effective Anti-Interference Primary Signal Processing for mmWave Automotive Radar[C]//Proceedings of the 2019 International Conference on Engineering and Telecommunication, Dolgoprudny, Russia:IEEE, 2019:1-5.
[9] RAMEEZ M, DAHL M, PETTERSSON M I. Adaptive Digital Beamforming for Interference Suppression in Automotive FMCW Radars[C]//Proceedings of the 2018 IEEE Radar Conference, Oklahoma, OK, USA: IEEE, 2018:252-256.
[10] NOZAWA T, MAKINO Y, TAKAYA N, et al. An Anti-Collision Automotive FMCW Radar Using Time-Domain Interference Detection and Suppression[C]//Proceedings of the 2017 International Conference on Radar Systems,Belfast,UK: IET, 2017:1-5.
[11] LEE S, LEE J Y, KIM S C. Mutual Interference Suppression Using Wavelet Denoising in Automotive FMCW Radar Systems[J]. IEEE Trans on Intelligent Transportation Systems, 2019, 22(2): 887-897.
[12] WU Jiayan, YANG Siyuan, LU Wei, et al. Iterative Modified Threshold Method Based on EMD for Interference Suppression in FMCW Radars[J]. IET Radar, Sonar &Navigation, 2020, 14(8):1219-1228.
[13] RAMEEZ M, DAHL M, PETTERSSON M I. Autoregressive Model-Based Signal Reconstruction for Automotive Radar Interference Mitigation[J]. IEEE Sensors Journal,2020, 21(5):6575-6586.
[14] WANG Jianping, DING Min, YAROVOY A. Interference Mitigation for FMCW Radar with Sparse and Low-Rank Hankel Matrix Decomposition[J]. IEEE Trans on Signal Processing, 2022, 70:822-834.
[15] NEEMAT S, KRASNOV O, YAROVOY A. An Interference Mitigation Technique for FMCW Radar Using Beat-Frequencies Interpolation in the STFT Domain[J]. IEEE Trans on Microwave Theory and Techniques, 2018, 67(3):1207-1220.
[16] WANG Jianping. CFAR-Based Interference Mitigation for FMCW Automotive Radar Systems[J]. IEEE Trans on Intelligent Transportation Systems,2022, 23(8): 12229-12238.
[17] JIN Feng, CAO Siyang. Automotive Radar Interference Mitigation Using Adaptive Noise Canceller[J]. IEEE Trans on Vehicular Technology, 2019, 68(4):3747-3754.
[18] BROOKER G M. Mutual Interference of Millimeter-Wave Radar Systems[J]. IEEE Trans on Electromagnetic Compatibility, 2007, 49(1):170-181.
[19] 王彪,李涵琼,高世杰,等.一种变步长最小平均p 范数自适应滤波算法[J].电子与信息学报,2022,44(2):661-667.
[20] 赵雪松.LMS 自适应滤波算法性能研究[D].哈尔滨:哈尔滨理工大学,2022.