0 引 言
线性调频(Linear Frequency Modulation, LFM)信号作为现代雷达中应用最广泛的信号,在多辐射源脉冲交错背景下对来自不同辐射源的LFM 信号分别进行提取并准确估计参数,是雷达对抗侦察的重要任务,也是实施电子攻击和电子防护的基础和前提[1-2]。
为实时获取战场电子情报和态势的支援侦察需要在距离对方辐射源较远的位置或在旁瓣信号内完成,在这种情况下,由于信噪比较低且脉冲内部存在起伏,雷达对抗接收机截获到的往往不是完整的脉冲,在输出脉冲参数时产生脉冲分裂的现象。同时,接收机所处的电磁环境呈现脉冲密度高、信号样式复杂的特点[3-4],接收机会同时截获到包含目标雷达在内的多辐射源信号。因此在实际对抗侦察场景中,接收机截获到的通常是一个多辐射源脉冲交错、交叠、分裂的复杂脉冲流,严重影响目标雷达信号的分选和参数准确测量,甚至影响后续电子战任务的实施。
现有的雷达辐射源信号分选方法主要分为基于脉内调制特征、基于脉间调制特征和基于机器学习的分选三大类[5-6]。其中,基于脉内调制特征的时频分析法、模糊函数法等通过在时频域提取信号脉内特征来完成分选,但这些方法抗噪性较差,无法适应低信噪比的复杂电磁环境[7-8]。基于脉间调制特征的分选方法中最具代表性的序列差值直方图法(Sequential Difference Histogram, SDIF)、PRI 变换法等是通过在交叠脉冲流中提取潜在的脉冲重复周期(Pulse Repetitive Interval, PRI)进行分选[9-11],但这些方法在信号密集、形式复杂的现代雷达战场环境中难以完全实现脉冲流的去交错[12-14]。基于机器学习的分选主要应用在处理序列数据中具有优势的循环神经网络(Recurrent Neural Networks, RNN)、长短时记忆网络(Long Short-Term Memory, LSTM)和卷积神经网络(Convolutional Neural Networks, CNN)等从样本数据中挖掘规律并据此对未知数据进行预测[15-17],但这类方法在训练样本获取和算法实时性上仍面临较多挑战[18]。整体来看,现有的分选算法普遍基于脉冲信号完整侦收和高信噪比的理想假设,在多辐射源脉冲交错、分裂严重的条件下难以达到理想的效果。
针对雷达对抗侦察场景中多辐射源脉冲交错、交叠、分裂条件下LFM 信号参数准确测量的需求和现有辐射源信号分选方法的不足,本文提出了一种LFM 信号两阶段提取与参数估计的方法:首先对接收机截获到的原始脉冲流进行分类,得到所有LFM 信号脉冲组成的序列;其次将不同辐射源的LFM信号脉冲分别提取到脉冲子序列中;最后在每个子序列中估计对应原始信号的参数信息。
1 信号模型
受雷达平台的限制和低截获概率的要求,雷达辐射的脉冲峰值功率无法无限制地拉高,而为了增大探测距离,一般用相对较低的峰值功率与较大的脉宽实现辐射能量增大,对于大脉宽与距离方向的高分辨矛盾,接收端通常采用脉冲压缩的方式进行处理。现代脉冲压缩雷达广泛采用的调制信号是线性调频(LFM)信号,其数学表达式如式(1)所示。
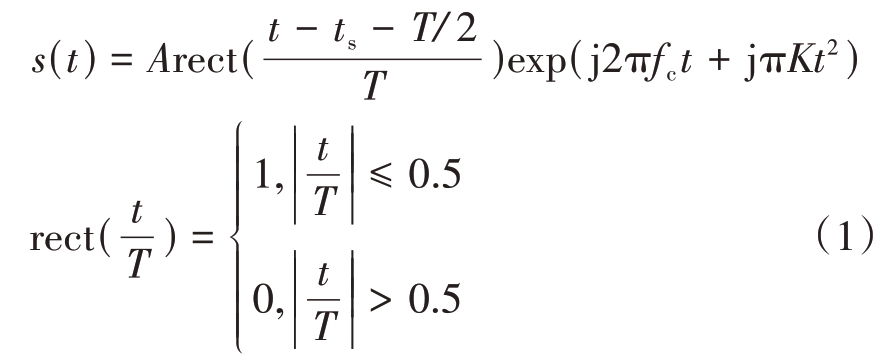
式中,rect(⋅)为单位矩形窗函数,A为信号幅度,ts为脉冲到达时间,T 为脉冲宽度, fc 为载波频率,B 为带宽,K =B T为调频斜率。
T为调频斜率。
现有的雷达对抗侦察技术路线主要以截获到的雷达脉冲描述字(Pulse Descriptive Word, PDW)为基础进行数据处理,以准确估计信号的脉宽、带宽、重复周期等参数[19]。通常,PDW由脉冲到达时间(Time of Arrival, TOA)、 载 频 (Radio Frequency, RF)、脉冲宽度(Pulse Width, PW)、脉冲幅度(Pulse Amplitude, PA) 和到达方向(Direction of Arrival, DOA)5个参数组成。在这种信号处理流程下,PDW 的完整性与可分辨性是准确侦察的关键。
在支援侦察场景中,由于远距离接收或旁瓣侦察等原因,接收机截获到的雷达信号PDW 通常不完整,主要表现为脉冲分裂。具体而言,一是为尽远尽早侦察,截获到的旁瓣信号功率较低;二是为尽全尽广侦察,对抗接收机频段宽开,大功率的猝发信号压制低功率的大脉宽LFM 信号。对处于检测门限附近的LFM 信号,完整的脉冲如图1(a)所示,受噪声和传播路径等环境影响,大脉宽通常分裂为随机的不规则小脉宽,其模型可描述为式(2)所示的形式。
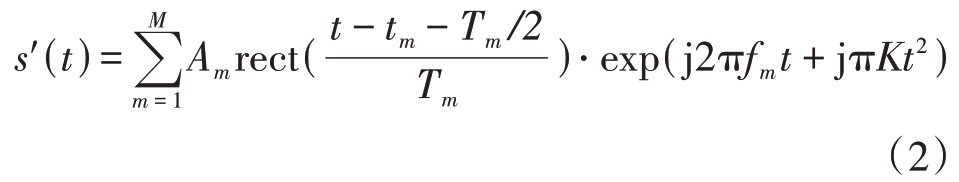
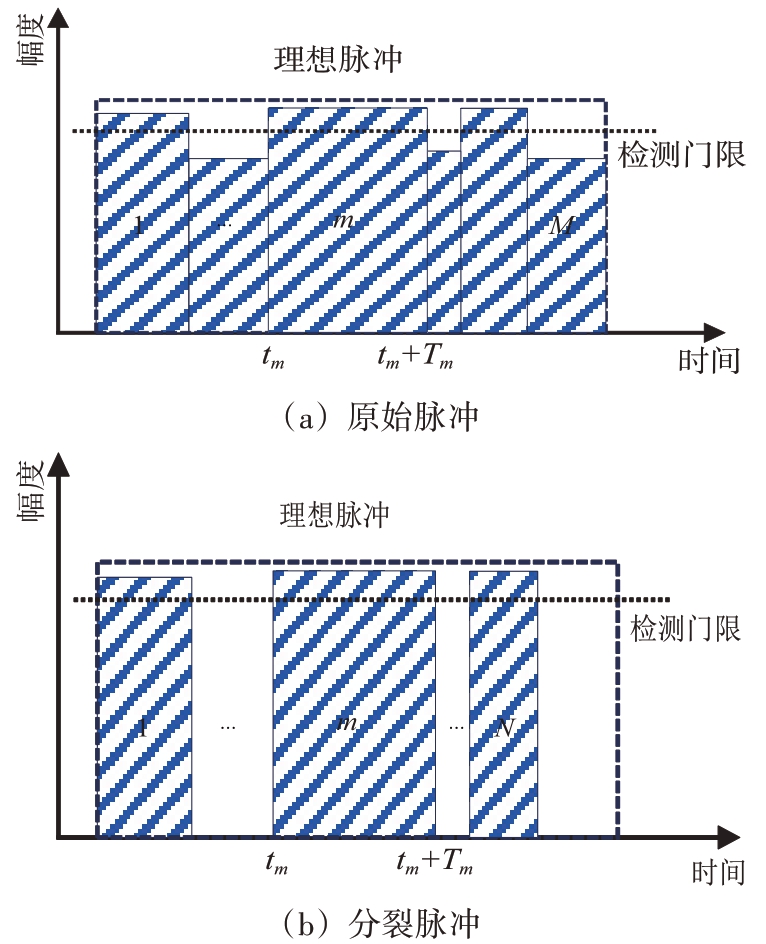
图1 脉冲分裂示意图
式中,Am、tm、Tm 和fm 分别表示第m(1 ≤m ≤M)个窄脉冲的PA、TOA、PW 和RF。其中,窄脉冲的PW和RF满足式(3)和式(4)。
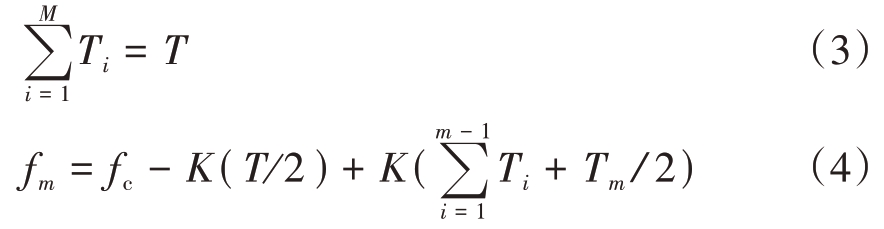
对于这些窄脉冲,幅度超过接收机灵敏度的能够进入接收机并生成PDW,未超过灵敏度的则视为丢失,这种情况下,一个原始的完整LFM 信号脉冲分裂为多个窄脉冲,每个窄脉冲被描述为独立的PDW,并被送入后端进行数据处理和信号参数估计。分裂后的脉冲如图1(b)所示,其表达式如式(5)所示。
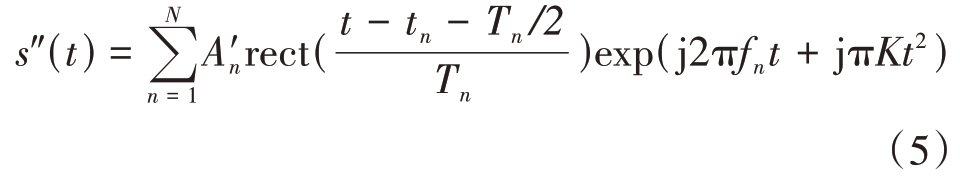
式中,N 为脉冲分裂后实际输出的脉冲数量(N ≤M)。由于窄脉冲频率与其在原始脉冲中的位置有关,故第n个分裂脉冲的中心频率可以表示为
式中,ts为未分裂原始脉冲的到达时间。
从式(2)和式(5)可以看出,分裂脉冲具有以下特征:
1) 分裂脉冲的数量N、TOA、PW都是随机的。
2) 分裂脉冲的PRI 抖动较大,同一个脉冲分裂后的各窄脉冲TOA 间隔较小,不同脉冲的窄脉冲之间TOA 间隔较大。具体关系如式(7)和式(8)所示。
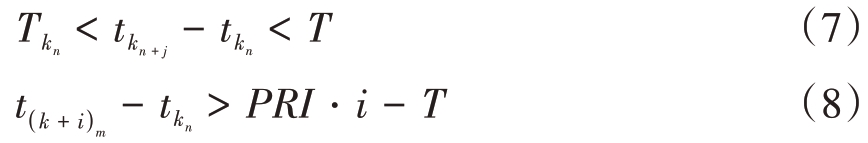
式中,Tkn 和tkn 分别表示第k 个原始脉冲的第n 个分裂脉冲的PW 和TOA,PRI 为原始信号的脉冲重复周期。对于绝大多数的雷达信号而言,占空比一般小于50%[20],因此tkn + j - tkn < t( )k + i m - tkn 在绝大多数情况下均成立。
3) 分裂脉冲具有一定的时序性,且同一原始脉冲的分裂脉冲参数之间存在如式(9)和式(10)所示的关系。
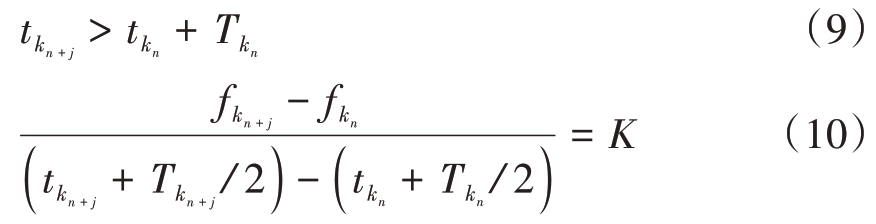
在实际的雷达对抗场景中,单载频脉冲信号、步进频脉冲信号、随机跳频脉冲信号等都存在脉冲分裂的现象,以上特征具有普适性。
2 基于BLSTM-SFMS的两阶段LFM信号提取算法
从交错脉冲流中提取目标LFM 信号,传统的分选方法一般分别利用DOA和TOA信息进行预分选和二次分选,本质上是基于PRI的周期性对脉冲进行关联,适用于PRI 固定或抖动较小的雷达信号。根据第1节的分析,各分裂脉冲的TOA具有随机性导致PRI抖动较大,甚至不具有明显的特征规律,如图2所示,传统分选算法难以处理这种情况。但分裂后的脉冲流中各窄脉冲之间具有较强的时序性,且隐含原始信号的调频斜率等参数信息。
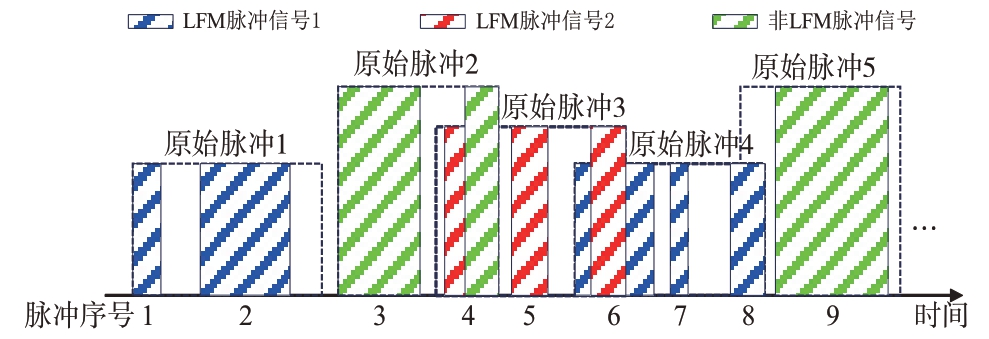
图2 分裂脉冲流示意图
近年来飞速发展的神经网络为挖掘数据间的隐藏关系提供了丰富的工具,基于此,本文提出了一种LFM 信号的两阶段提取方法。首先利用双向长短时记忆网络(Bidirectional Long Short-Term Memory, BLSTM)对原始脉冲流进行分类,得到所有LFM 信号脉冲组成的序列;然后利用序列脉冲间的调频斜率信息,使用序列调频斜率直方图(Sequential Frequency Modulation Slope Histogram,SFMS)提取不同的LFM信号。
2.1 基于BLSTM 的LFM信号脉冲分类
虽然分裂后的LFM 脉冲周期性被打乱,但是各分裂脉冲之间频率的变化率、先后时序、脉宽等特征具有强相关性,这与其他非LFM 信号脉冲的特征具有明显区别。深度神经网络能够学习和挖掘数据中的隐藏特征,且具有强大的分类能力,可以用来实现LFM 信号的提取。针对本文的研究对象——分裂脉冲序列,同一原始信号的分裂脉冲之间具有明显的时序性,因此本节主要研究具有序列数据处理能力的深度神经网络。
在分裂的脉冲流中提取LFM 信号可视为二分类的序列标注,这与自然语言处理领域中词性标注问题类似,都需要综合较长的上下文信息进行准确分类,BLSTM 在处理该类序列标注任务中已经取得了较好的成果,故本文选用BLSTM 来挖掘分裂脉冲流中隐藏的LFM 信号调制特征,实现LFM信号与其他非LFM信号的分类。
BLSTM 是在LSTM 的基础上增加了一条反向传播路径[21],其基本结构如图3所示,网络包括输入层、隐藏层、全连接层和输出层,其中隐藏层包括一个前向层和一个后向层。其核心的LSTM单元不仅包含网络当前时刻的输入,还包含前一时刻的输出,并且引入了遗忘门、输入门和输出门实现对历史信息的选择性传递,使得当前输入可关联序列中较远的数据[22]。由于LFM 脉冲的特征模式对方向性不敏感,例如正调频和负调频都属于线性调制模式,所以双向的LSTM 可以进一步增强对LFM 信号特征模式的挖掘,从而实现准确的LFM脉冲提取。
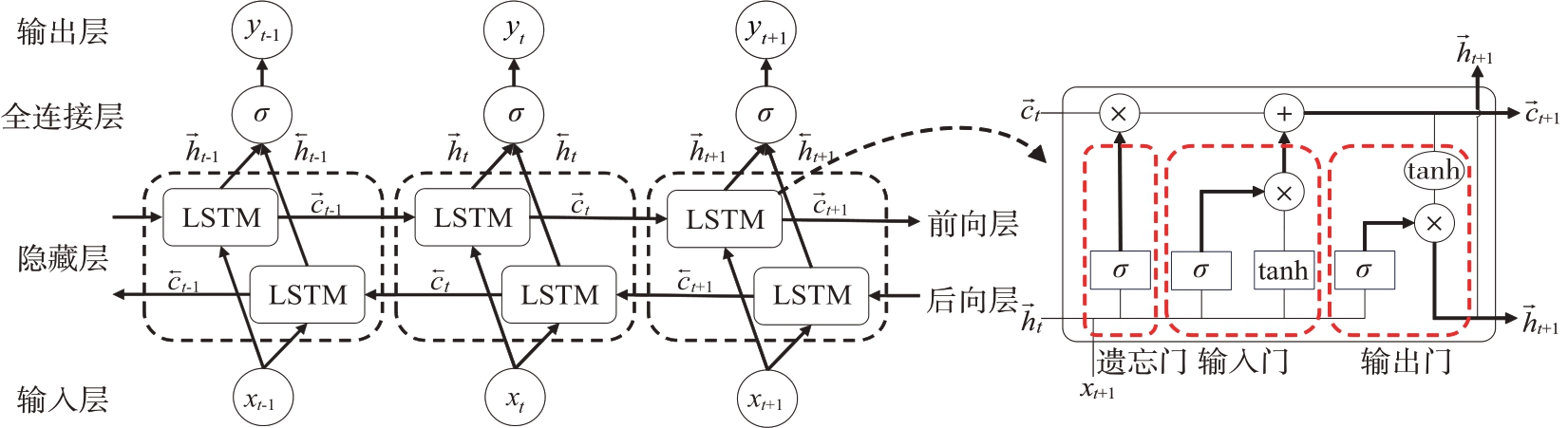
图3 BLSTM基本结构图
本文的工作主要聚焦于信号侦测后的数据处理,在信号侦测后形成的PDW 5 个参数中,PA 受环境或设备的影响较大,对LFM 信号的特征描述能力有限,DOA 通常由不同的信号处理支路测得,属于预处理手段,所以本文将来自同一方向脉冲流中的每一个脉冲描述为由TOA、PW 和RF 组成的三元组。在运用BLSTM 时,网络的输入为脉冲流中所有脉冲的参数信息,即[ TOA, PW, RF ]序列,输出为整个脉冲流的类别标签序列,即每个脉冲是否为LFM信号的类别信息。
对应图3 所示网络,在每个时间步t 输入进网络的xt是一个脉冲3×1维的参数向量[ TOA, PW, RF ],经过前向和后向LSTM 层提取特征后可得到表示脉冲类别信息的d 维隐藏状态向量![]() 和
和![]() ,拼接得到整个隐藏层的输出后通过全连接层映射到每个脉冲的类别信息,最后送至输出层输出yt,即当前时间步输入脉冲的类别标签,单元状态向量ct用来维持序列长期的依赖关系。
,拼接得到整个隐藏层的输出后通过全连接层映射到每个脉冲的类别信息,最后送至输出层输出yt,即当前时间步输入脉冲的类别标签,单元状态向量ct用来维持序列长期的依赖关系。
2.2 基于SFMS的LFM信号脉冲提取
2.1 节利用BLSTM 可对LFM 信号脉冲与其他非LFM 信号脉冲进行区分,主要利用了两者的调制模式差异,在交错的分裂脉冲流中存在多组LFM 脉冲子流,如图2所示,为准确估计不同LFM信号的参数,还需要进一步提取每个LFM 信号的脉冲子流,即挖掘不同LFM信号的差异信息。
对于网络分类提取到的所有LFM 信号组成的脉冲序列,设其中第i和第j个脉冲的[ TOA,PW,RF]参数分别为[ ti,Ti, fi ]和[ tj,Tj, fj](tj > t)i,两脉冲间的调频斜率为
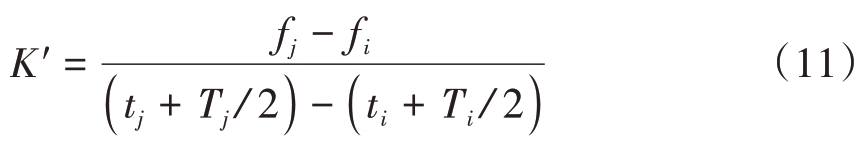
由第1节对分裂脉冲特征的分析可知,同一脉冲分裂出的窄脉冲参数之间隐含原始脉冲的调频斜率信息,且不同辐射源信号的调频斜率不同。因此K′值不同可反映出脉冲来自不同的雷达辐射源,由于同一部雷达所辐射信号的脉冲之间具有相对一致的调频斜率,所以真实的LFM 信号调频斜率将会有大量窄脉冲对对应,据此可实现同一部雷达辐射源的各分裂脉冲关联。通过式(11)计算多组脉冲间的K′值,可统计出不同K′值对应的脉冲个数,即得到调频斜率直方图。
式(11)中,根据i和j的差值| i - j |= C不同,可统计出不同阶数的调频斜率直方图,C = 1 时称为1阶直方图,C = 2时称为2阶直方图等。随着直方图阶数C 增加,计算K′值两个脉冲的间隔增大,关联脉冲的距离变长。基于以上思想,本文提出了SFMS算法,算法流程图如图4所示。
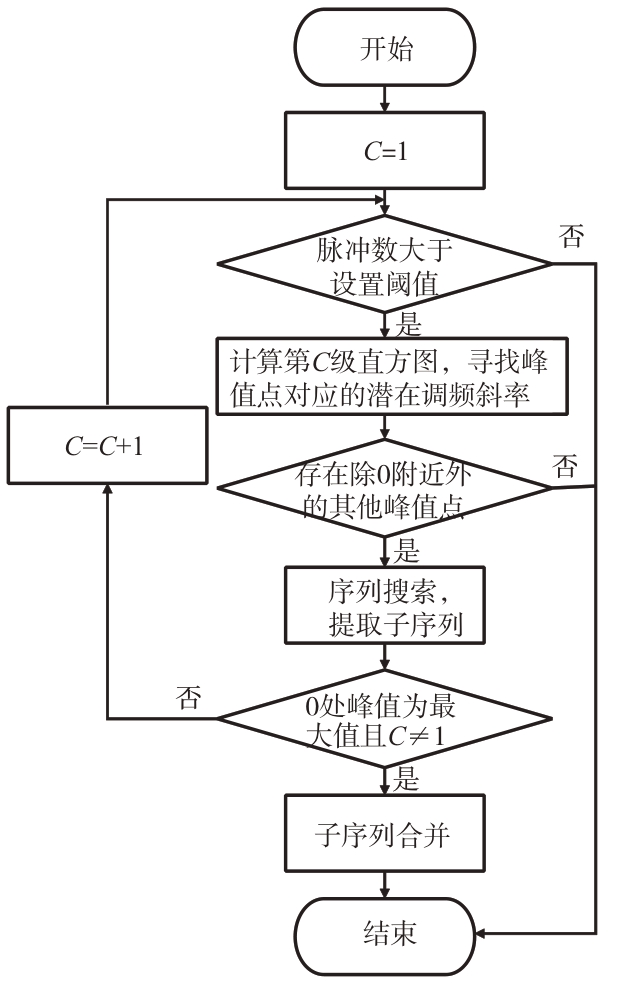
图4 SFMS算法流程图
SFMS算法的步骤可归纳为以下4个步骤。
步骤1:将包含分裂后脉冲的序列按TOA 由小到大排序,根据式(11)计算相邻两个脉冲的调频斜率K′,统计形成1阶直方图;
步骤2:根据直方图中0 值附近以外的峰值对脉冲序列进行检索,每个峰值提取一个子序列,若无峰值,则跳转至步骤4;
步骤3:若直方图中0 值附近无最大峰值或直方图阶数为1,则计算下一阶直方图并返回至步骤2,否则进行下一步;
步骤4:若直方图为1 阶,则使用传统SDIF 进行分选,若直方图阶数大于1,则将相近调频斜率值对应的子序列进行合并,得到最终的脉冲提取结果。
SFMS 算法的实质是基于调频斜率存在的稳定模式,在SDIF 算法的基础上引入脉冲的RF 和PW 信息,在包含参数随机、PRI不固定的分裂脉冲序列中寻找潜在的调频斜率值,并据此对序列进行检索,得到不同调频斜率的LFM 脉冲子序列,完成对LFM信号的提取。
3 分裂脉冲的合并与参数估计
经过第2节LFM信号两阶段提取算法处理,可从截获到的原始脉冲流中分别得到调频斜率不同的LFM 信号脉冲子序列。为准确估计不同LFM 信号的参数,需对提取到的子序列进行分裂脉冲合并并估计相应参数,具体步骤如下。
步骤1:对脉冲子序列求到达时间差(Difference of Time of Arrival, DTOA),使用K-means 聚类算法将DTOA 序列分为两类,以值较大的类别中对应的分裂脉冲为分界将脉冲序列划分为若干组,每组对应一个原始脉冲。若组内只有一个脉冲则剔除该组,得到Z个组。
步骤2:根据组内脉冲估计原始脉冲的调频斜率、PW、RF 和TOA。在每组内取第一个和最后一个 分 裂脉 冲,[ TOA,PW,RF ]分 别 为[ tz,1,Tz,1, fz,1 ]和[ tz,n,Tz,n, fz,n ],z 为组号。计算脉冲间调频斜率后求平均得到原始信号调频斜率的估计值K̂,具体计算方式如式(12)所示。
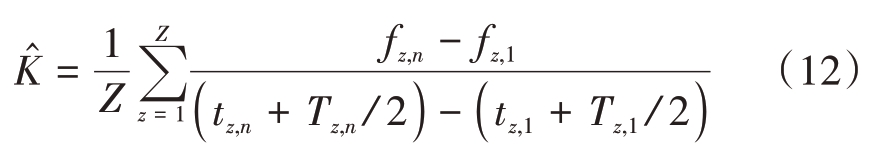
在每组内分别估计第一个分裂脉冲的前沿频率和最后一个分裂脉冲的后沿频率,若调频斜率为正,则取所有组中前沿频率的最小值和后沿频率的最大值作为原始脉冲的前、后沿频率![]() 和
和![]() 具体计算方式如式(13)和式(14)所示。
具体计算方式如式(13)和式(14)所示。
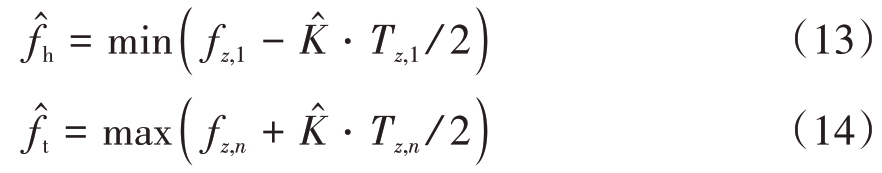
则每组对应原始脉冲的PW、RF 和TOA 的估计值可分别由式(15)、(16)和(17)得到。
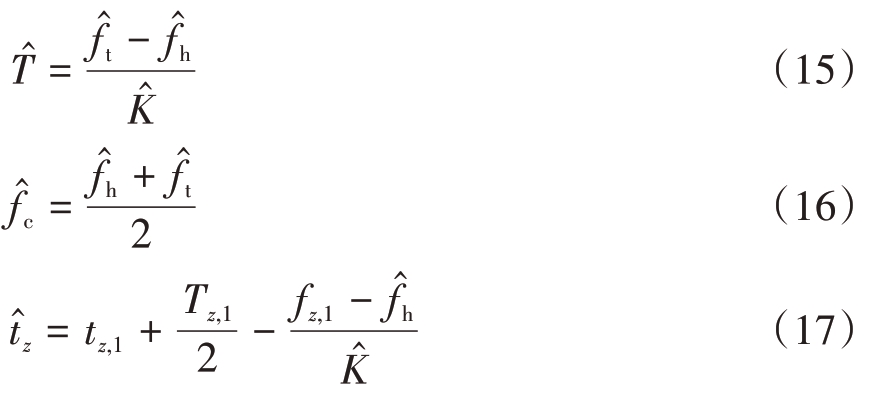
步骤3:根据合并后每组脉冲的TOA 计算DTOA,剔除异常值(一般约为正常值的整数倍,视为由脉冲丢失或剔除引起)后对所有元素求平均,作为原始脉冲的PRI估计值。
4 仿真实验与分析
4.1 实验设置
4.1.1 实验数据
实验模拟复杂的电磁环境,生成多辐射源脉冲交错、交叠、分裂的脉冲流。共设置了4 种辐射源信号,分别为LFM 脉冲信号、单载频脉冲信号、步进频脉冲信号和随机跳频脉冲信号,具体设置如下:
1) 每个辐射源信号起始时间随机,其他参数取值范围如表1所示。其中,LFM 信号参数模拟国际上典型雷达系统,步进频脉冲信号和随机跳频脉冲信号的跳频间隔与子脉冲带宽相等,都为50 MHz,跳频数都为8。
表1 信号参数设置
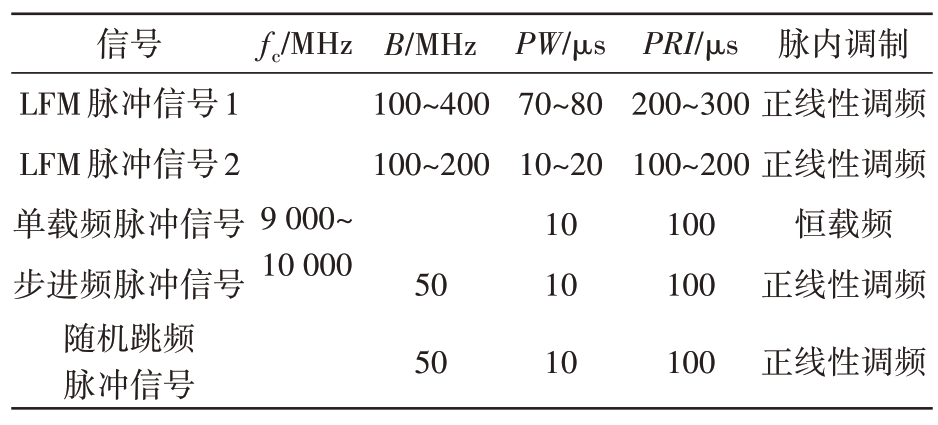
信号LFM脉冲信号1 LFM脉冲信号2单载频脉冲信号步进频脉冲信号随机跳频脉冲信号fc/MHz 9 000~10 000 B/MHz 100~400 100~200 50 50 PW/μs 70~80 10~20 10 10 10 PRI/μs 200~300 100~200 100 100 100脉内调制正线性调频正线性调频恒载频正线性调频正线性调频
2) 模拟实际脉冲分裂情况,每个原始脉冲分裂后的窄脉冲个数在4~7之间随机取值,分裂后的窄脉冲以0.5的概率超过接收机检测门限。
3) 交叠脉冲的参数测量以数字信道化接收机的测量方法为依据[23]。当两个时域交叠的脉冲信号进入接收机,若两脉冲的频率之差大于接收机信道宽度即频率分辨率,则两脉冲会分别进入两个信道,此时可以正确测得两个脉冲的参数信息。反之,这两个脉冲会进入同一信道,被当作一个脉冲进行处理,此时可能会产生较大的参数测量误差。
4) 所有脉冲的TOA、PW 和RF 测量误差设置为服从标准差为0.1的高斯分布。
实验中所用BLSTM 的主要参数设置如表2所示,其中输入层维度和输出层维度与网络的输入与输出数据形式相对应,隐藏层维度和层数是经过多次实验选择的最优结果,序列长度表示网络在训练和预测中能看到的上下文数据的范围,设置为30是综合考虑分裂脉冲序列长度和模型性能等因素的结果。网络训练和测试所用数据集的样本总数及5 个辐射源脉冲数量的占比如表3所示。其中,训练集和验证集中非LFM 脉冲与LFM 脉冲数量之比均为1∶1,4 个测试集分别用来测试非LFM脉冲与LFM脉冲数量之比为1∶1,2∶1,3∶1,4∶1条件下网络的性能。
表2 网络主要参数设置
输入层维度3隐藏层维度256隐藏层层数2输出层维度1序列长度30
表3 数据集样本设置
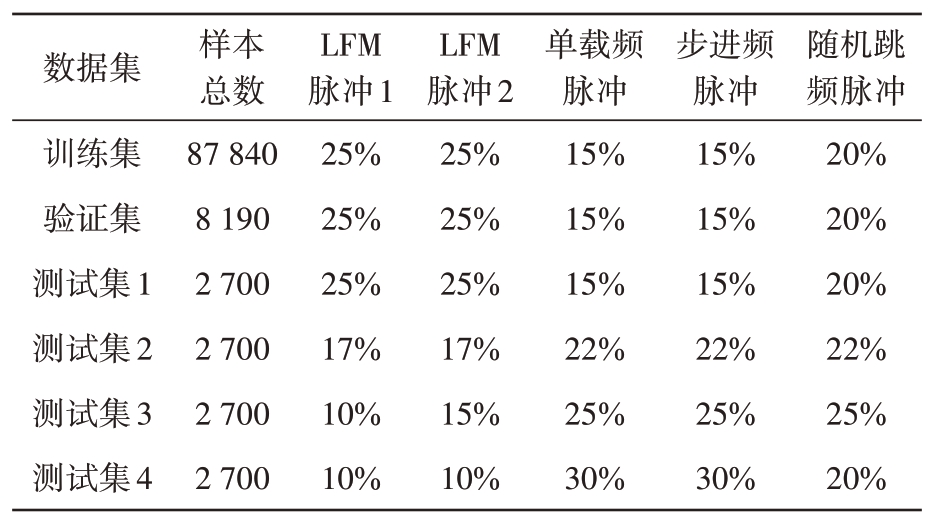
数据集训练集验证集测试集1测试集2测试集3测试集4样本总数87 840 8 190 2 700 2 700 2 700 2 700 LFM脉冲1 25%25%25%17%10%10%LFM脉冲2 25%25%25%17%15%10%单载频脉冲15%15%15%22%25%30%步进频脉冲15%15%15%22%25%30%随机跳频脉冲20%20%20%22%25%20%
4.1.2 对比算法
为了验证BLSTM 在脉冲分类任务中的性能,实验选用传统的辐射源信号分选方法SDIF算法和基于机器学习的RNN 分类方法作为对比算法对相同的数据集进行处理。
SDIF 算法基于PRI 的周期性,通过统计脉冲流中脉冲的到达时间差来寻找潜在的PRI 值并对脉冲序列进行检索和提取,实现雷达脉冲流去交错。RNN 原理与LSTM 类似,其循环连接的结构特点使网络在某时刻的输出可以作为输入再次输入到网络中,能够挖掘序列数据中的时序信息,对脉冲类别进行预测。
4.2 基于BLSTM 的LFM信号脉冲分类性能
本文算法和对比算法在表3所示测试集上的分类结果如表4所示。
表4 不同算法的分类结果
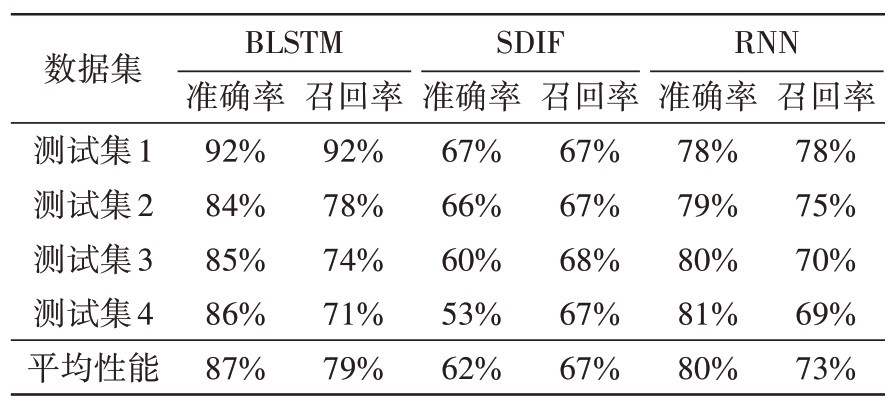
数据集测试集1测试集2测试集3测试集4平均性能BLSTM准确率92%84%85%86%87%召回率92%78%74%71%79%SDIF准确率67%66%60%53%62%召回率67%67%68%67%67%RNN准确率78%79%80%81%80%召回率78%75%70%69%73%
从表4可以看出,BLSTM整体上相比于其他两种算法表现优异,在每个指标上都高于其他两种算法,这是由于BLSTM 能够利用脉冲流的双向信息,并且“门控机制”也使其能够维持序列数据中更长的依赖关系。随着测试集中LFM 脉冲比例降低,3 种算法的准确率和召回率都呈现下降趋势,这是因为序列中LFM 脉冲减少导致脉冲流中需要关联的脉冲间距变长,上下文关联难度变大,算法性能普遍下降。虽然BLSTM 与其他两种算法的性能差距随着LFM 脉冲比例降低而减小,尤其是在测试集1 上BLSTM 比RNN 在召回率指标上高出14%,但是在测试集4上只高出2%,但BLSTM 对长序列更强的处理能力使其在两类样本数量极不平衡的条件下性能仍优于其他两种算法,而RNN 由于梯度在时间步中连续累乘的计算方式导致其在处理长序列数据时存在梯度消失(或爆炸)问题。
为了更加直观对比3 种算法的性能,图5 给出了在测试集1上的分类结果。

图5 测试集1上不同方法分类结果
从图5可以看出,3 种算法对LFM 信号和非LFM 信号都具有一定的区分能力。但对比图5(a)和图5(b)可以发现,BLSTM 少量的分类错误主要集中在两个LFM 脉冲信号和随机跳频脉冲信号三者时频交叠的区域,而从图5(c)和图5(d)可以看出,其他两种对比算法在两个LFM 脉冲信号交叠的区域就已经产生了较多的分类错误。主要原因是BLSTM 对脉冲流两个方向时序信息的选择性记忆能够帮助其更好地关联长序列数据。
4.3 基于SFMS的LFM信号脉冲提取与参数估计性能
测试集1 数据经过两阶段提取算法处理得到如图6所示的结果,其中图6(a)为BLSTM 网络分类得到的LFM 信号脉冲序列,利用SFMS算法对其进行处理,得到如图7所示的2 个潜在的调频斜率值,分别在4.5和9附近,据此对序列进行提取可得到对应的2 个LFM 信号脉冲子流,结果如图6(b)所示。经统计,84%的脉冲被分别提取两个LFM脉冲子序列中,且提取的准确率为99%,如表5所示。
表5 SMFS算法性能
提取率84%LFM脉冲1准确率99%LFM脉冲2准确率99%
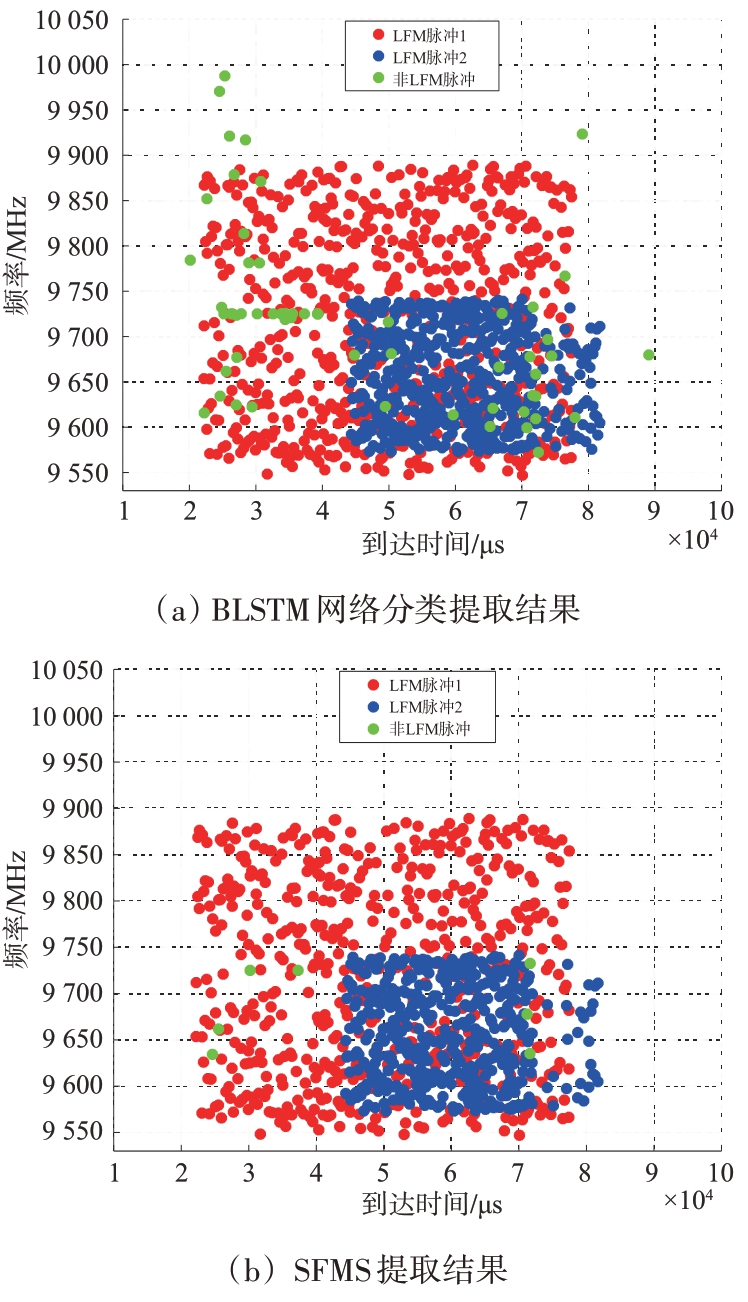
图6 SFMS算法提取结果
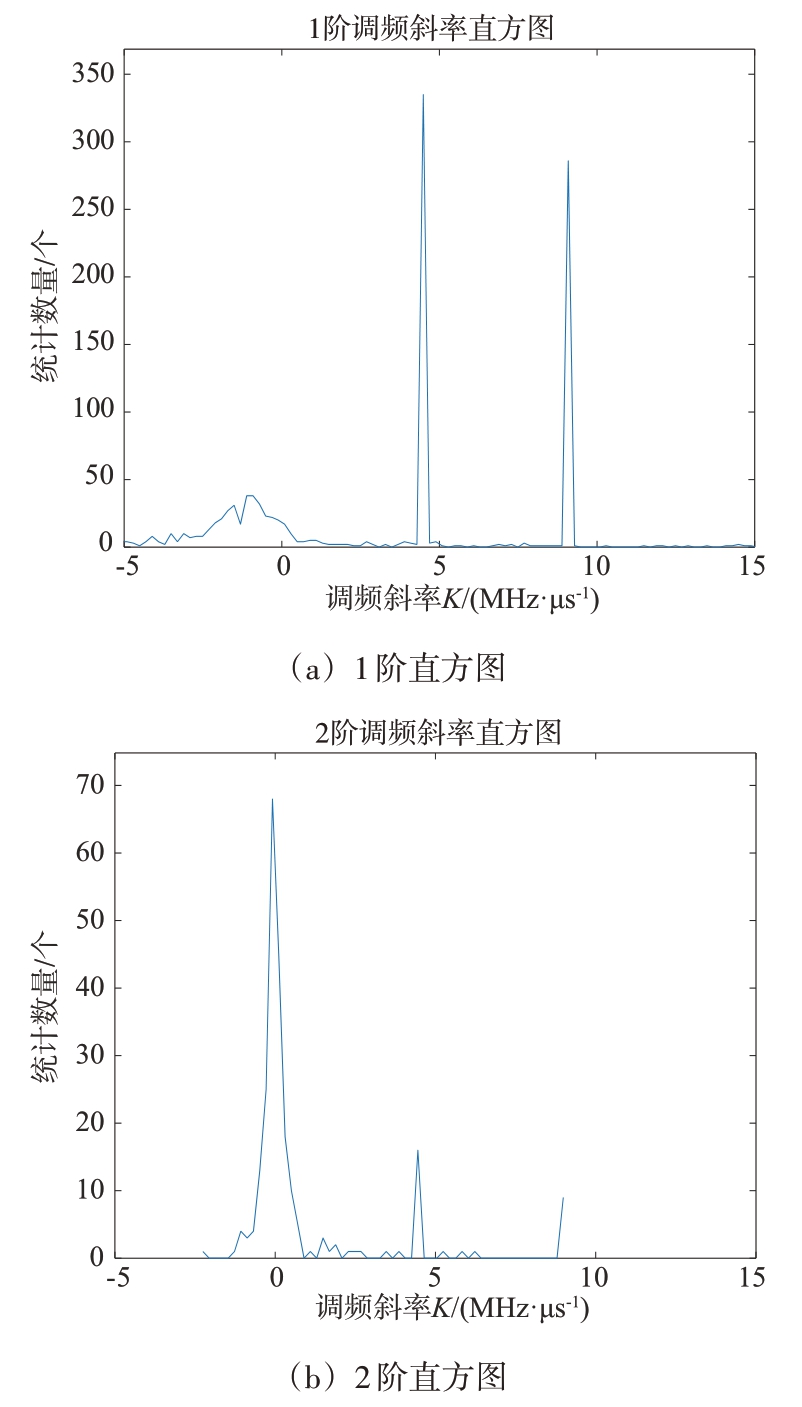
图7 调频斜率确定过程
根据提取到的两个LFM 脉冲子序列对测试集1 中2 个原始LFM 信号进行参数估计,结果如表6所示。可以看出,信号参数的估计结果整体误差较小,但带宽和脉冲宽度的估计误差相比于其他3 个参数相对偏大,主要是由于这两个参数在估计时采用了取最值的思想,导致估计结果保留了实验中人为添加的测量误差。整体来看,估计结果非常接近真实值,验证了本文方法的有效性。
表6 参数估计结果
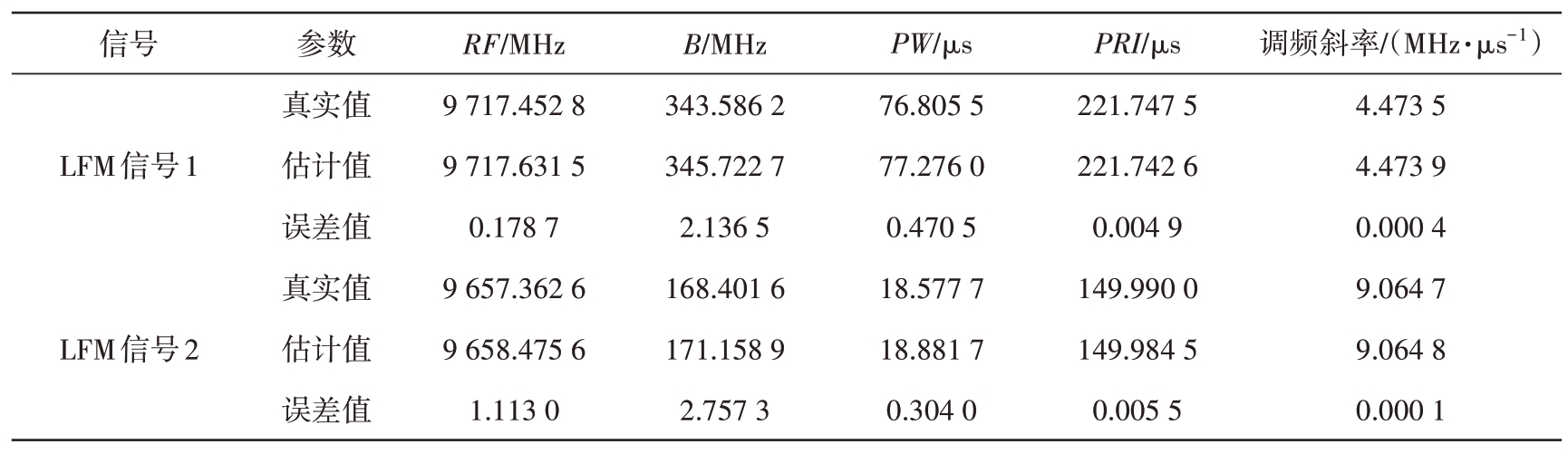
信号LFM信号1 LFM信号2参数真实值估计值误差值真实值估计值误差值RF/MHz 9 717.452 8 9 717.631 5 0.178 7 9 657.362 6 9 658.475 6 1.113 0 B/MHz 343.586 2 345.722 7 2.136 5 168.401 6 171.158 9 2.757 3 PW/μs 76.805 5 77.276 0 0.470 5 18.577 7 18.881 7 0.304 0 PRI/μs 221.747 5 221.742 6 0.004 9 149.990 0 149.984 5 0.005 5调频斜率/(MHz·μs-1)4.473 5 4.473 9 0.000 4 9.064 7 9.064 8 0.000 1
5 结束语
本文针对多辐射源脉冲交错、分裂条件下LFM 信号参数难以估计的问题,分析了LFM 信号脉冲分裂的原因和特点,并根据分裂脉冲的特点提出了一种LFM 信号两阶段提取与参数估计的方法。首先利用BLSTM 对原始脉冲流中所有的LFM脉冲进行提取,其次通过SFMS 算法将不同调频斜率的LFM 信号脉冲分别提取到脉冲子序列中,最后对每个子序列对应的原始LFM 信号进行参数估计。仿真实验结果表明,本文所提方法能够在多辐射源脉冲交错、交叠、分裂的条件下有效提取出不同LFM 脉冲信号,并得到较为准确的参数估计结果,为后续电子战行动提供良好的信息支撑。由于交叠脉冲的参数测量误差对信号提取和参数估计的影响较大,因此对交叠脉冲的影响评估与处理方法将是后续研究的主要方向。
[1] 解丰年.电子对抗侦察的智能化发展刍议[C]//第十二届中国指挥控制大会论文集(上册),北京:中国指挥与控制学会,2024.
[2] 黄知涛,王翔,赵雨睿.认知电子战综述[J].国防科技大学学报,2023,45(5):1-11.
[3] 王天乐.国内复杂电磁环境研究与展望[J].网络安全技术与应用,2021(7):170-172.
[4] 梁兴茹.雷达复杂电磁环境建模与仿真[D].西安:西安电子科技大学,2019.
[5] 隋金坪,刘振,刘丽,等.雷达辐射源信号分选研究进展[J].雷达学报,2022,11(3):418-433.
[6] 刘松涛,赵帅,汪慧阳.雷达辐射源识别技术新进展[J].中国电子科学研究院学报,2022,17(6):523-533.
[7] 闵博.基于小波变换的雷达脉内调制特征分选识别[D].成都:电子科技大学,2020.
[8] 普运伟,侯文太,郭媛蒲,等.基于模糊函数三维特征的雷达辐射源信号分选方法[J].控制与决策,2019,34(10):2178-2184.
[9] MILOJEVIC D J, POPOVIC B M. Improved Algorithm for the Deinterleaving of Radar Pulses[J]. IEE Proceedings FRadar and Signal Processing, 1992(1):98-104.
[10] 关欣,朱杭平.基于序列时延相关性的PRI 变换改进算法[J].雷达科学与技术,2018,16(1):49-54.
[11] 李斌,李杨,彭平.基于PRI 变换快速雷达信号分选方法[J].电子信息对抗技术,2023,38(2):42-50.
[12] 贾金伟,韩壮志,刘利民,等.基于SDIF 门限失效的雷达射频隐身信号设计原理[J].系统工程与电子技术,2023,45(6):1693-1701.
[13] 刘俞辰.复杂环境下雷达信号分选算法研究[D].哈尔滨:哈尔滨工程大学,2022.
[14] 吕松玲.脉冲雷达信号分选识别算法研究[D].成都:电子科技大学,2016.
[15] LIU Zhangmeng, YU P S. Classification, Denoising, and Deinterleaving of Pulse Streams with Recurrent Neural Networks[J]. IEEE Trans on Aerospace & Electronic Systems, 2019, 55(4):1624-1639.
[16] 王超,孙丽婷,王翔,等.基于脉内线性调频的雷达脉冲分裂信号分选与参数估计[J].信号处理,2023,39(7):1222-1232.
[17] 李雪琼.基于机器学习的雷达辐射源分选与识别技术研究[D].长沙:国防科技大学,2020.
[18] 乔平娟,谢钧,李林,等.辐射源个体识别研究综述[J].信息技术与信息化,2023(12):156-164.
[19] 王星,王俊迪,金政芝,等.机载雷达告警接收机发展现状及趋势[J].雷达学报,2023,12(2):376-388.
[20] STIMSON G W.机载雷达导论[M].2 版.吴汉平,等译.北京:电子工业出版社,2005.
[21] GRAVES A, SCHMIDHUBER J. Framewise Phoneme Classification with Bidirectional LSTM and Other Neural Network Architectures[J]. Neural Networks, 2005, 18(5): 602-610.
[22] HOCHREITER S, SCHMIDHUBER J. Long Short-Term Memory[J]. Neural Computation, 1997, 9(8):1735-1780.
[23] 陈涛,郭立民,潘大鹏,等.被动雷达宽带数字接收机技术[M].北京:电子工业出版社,2021.