0 引 言
随着电子干扰和无线电技术的快速发展,雷达的工作环境日益复杂。一方面,间歇采样转发干扰(Interrupted Sampling Repeater Jamming, ISRJ)在雷达接收端中快速形成多个高保真的虚假目标,导致雷达难以分辨真实目标,从而引起检测或跟踪任务失败[1-2]。另一方面,频谱拥塞问题(Spectrum Congestion Problem, SCP)愈加严重。雷达和各种电子设备被迫在有限的频谱分配中共存[3-4]。工作频段的重叠引发相互干扰,严重影响雷达的检测性能和其他设备的正常工作[5-6]。因此,开发有效的抗干扰策略,以同时应对ISRJ 和SCP带来的不利影响,显得尤为重要。
目前,对抗ISRJ 的主要方法之一是干扰参数估计和抑制[7-13],该方法通常包括两个步骤:首先,通过时频分析[7-10]、反卷积处理[11]或其他优化方法[12-13]来估计干扰参数;然后,根据所估计的参数构建特定的信号处理方法来抑制干扰。该方法充分利用了ISRJ 干扰的时频不连续特性,但对抗干扰的方式较为被动,且优化维度较低。对抗ISRJ的第二种方法是波形设计[14-16]。通过波形设计,可结合雷达对干扰特性的感知,将波形运用于特定的干扰场景中,甚至赋予波形有利的低峰值旁瓣电平或频谱凹陷特性。这不仅提供了一种主动对抗干扰的方案,而且增大了雷达抗干扰的自由度。然而,在匹配滤波条件下,ISRJ 的零阶假目标,即雷达脉冲压缩信号处理后在等效零多普勒频移处输出的干扰峰值,难以消除,因此,非匹配滤波器与发射波形联合优化的方法引起了学者的广泛关注[17-25]。通过引入非匹配滤波器的优化,不仅可以降低零阶假目标的影响,而且增加了雷达波形与干扰波形经滤波后的差异。
鉴于第三种对抗方案的优越性,本文专注于抗ISRJ 的发射波形和非匹配滤波器的联合设计。该思路最早由文献[17]提出,文中通过建立加权优化模型来抑制不利的互相关能量电平,旨在同时提高雷达对抗ISRJ 和弱目标检测的能力,并采用交替方向乘子(Alternating Direction Multiplier Method, ADMM)算法和迭代算法对所建立的二次非凸问题进行求解。文献[18]基于波形恒模约束推导了迭代优化发射波形和滤波器的闭式解。然而,文献[17]和文献[18]均未考虑滤波器的能量约束,这可能会导致较大的信噪比输出,这不利于目标检测。文献[19]指出,ISRJ 基于波形的高多普勒容限和匹配滤波特性产生多个伪目标,并提出设计低多普勒容限的相位编码波形和相应的失配滤波器来对抗ISRJ,分别为波形和滤波器引入恒模约束和能量约束,并基于主分量最小化(Majorization Minimization, MM)算法来解决相应的非凸问题。文献[20]基于迭代算法优化了具有信噪比损失约束的发射波形和接收滤波器联合设计模型。文献[21]建立了同时全极化雷达体制下发射波形与接收滤波器的联合优化模型,通过交替迭代方法对模型进行求解,利用数字仿真和半实物硬件系统说明了所提方法的有效性。针对干扰先验信息不准确的情况,文献[22]设计了鲁棒的发射波形和接收滤波器,采用交替方向惩罚(Alternating Direction Plenty Method, ADPM)算法求解问题,同时推导了所用算法的收敛性。文献[23]考虑了波形设计序列的多普勒容限,提出基于MM 框架的交替迭代优化算法解决所建立的非凸优化问题,显著提升了雷达在干扰场景下对运动目标的检测能力。文献[24]针对全极化宽带雷达条件下现有抗ISRJ 问题表征中未考虑目标特性对信号调制作用这一短板,将目标特性调制加入信干比的优化中,进一步提高了雷达抗ISRJ 的能力。为了避免脉冲压缩输出后的高旁瓣电平引起检测虚警,文献[25]建立了极小-极大优化框架来抑制高旁瓣电平,并通过扩展滤波器的长度来提高优化自由度,所采用的算法基于MM 框架,首先利用lp范数对最大值函数进行平滑,然后通过两次求解上界函数,将问题转化为具有闭式解形式的优化问题,最终求解出具有较低且平整脉冲压缩旁瓣的波形和滤波器。
尽管上述文献在发射波形和失配滤波器联合设计的框架下实现了良好的抗干扰性能,但仍有需要改进的空间:一方面,虽然许多工作通过引入电平等式约束或最小化与期望电平大小差值的方式来避免非匹配滤波器带来的脉冲压缩能量损失以及降低干扰信号与非匹配滤波器互相关后在零时延处出现的峰值,然而,严格的数值等式约束会使问题的解空间变得有限,这可能导致问题难以收敛或目标函数性能不佳。此外,最小化互相关主瓣电平和期望电平之间的大小会使得问题需要同时优化的目标函数过多,需要通过引入多个权重变量来实现多目标函数之间的平衡,难以精确控制优化效果。另一方面,上述工作没有考虑SCP问题。如前所述,SCP问题不容忽视。已有许多公开文献基于波形设计重点研究了SCP 问题[26-29],主要的思路是基于对电磁频谱占用信息的获取,将所占用频段的能量控制在一定水平之下,形成特定的频谱凹陷,从而实现设备间的共存。然而,这些也仅仅关注了设备间的互扰问题,并没有考虑ISRJ 所带来的威胁。据目前所知,尚未有公开文献同时研究ISRJ 和SCP 问题。而ISRJ 和SCP 已然成为脉冲压缩雷达在电磁空间中生存和发展无法避免的问题,亟需引起重视。
基于以上分析,本文对频谱拥塞环境下雷达抗间歇采样转发干扰的发射波形和非匹配滤波器联合设计问题进行了研究。目标函数旨在同时抑制信号脉冲压缩积分旁瓣和抑制干扰信号滤波输出积分能量,并引入帕累托因子来平衡两者之间的重要性。在约束条件中,为发射波形脉冲压缩主瓣能量设置能量下界,为干扰信号非匹配滤波输出主瓣能量设置能量上界,从而将雷达的主瓣探测能力以及高威胁的干扰零时延输出电平约束在可控范围内。此外,频谱兼容约束将指定频段能量控制在了指定能量下,能够避免频段间的互扰。信号的能量约束和峰值电平约束考虑了波形能量有限且信号幅度不能过高的实际需求。滤波器能量约束则避免了噪声通过滤波器后产生较高的噪声能量。为处理所建立的非凸多约束问题,基于交替求解框架,使用半正定规划算法和MM 算法对问题进行求解。最后,仿真实验说明了所建立模型和所使用的算法的有效性。
1 模型建立
1.1 问题背景
考虑图1所示的工作场景,单站脉冲压缩雷达系统向空间发射雷达信号,并同时接收来自目标、干扰机以及与雷达在重叠频带内工作的设备的信号。
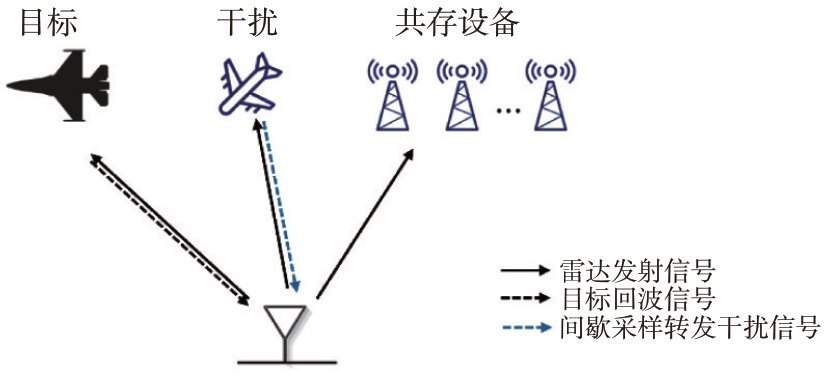
图1 雷达工作场景
设一个脉冲内雷达发射信号为x=[x1, x2,…, xN]T ∈ℂN,则雷达在接收端所接收的信号为
式中,α1 为回波信号的复幅值,α2 为干扰信号的幅值,n为高斯白噪声。
该脉冲雷达接收到信号y后,将通过非匹配滤波器w ∈ℂN 进行信号检测。假设需要共存的频带以及敌方干扰机间歇采样的采样时间和采样间隔先验已知,本文需要优化雷达发射波形x和非匹配滤波器w,以降低雷达在与其他设备共存的频带上所发射的能量,并尽可能消除间歇采样转发干扰所带来的影响,提高雷达系统的探测能力和生存能力。
在接下来的小节中,将根据间歇采样转发干扰的信号模型建立本文的数学模型。
1.2 间歇采样转发干扰信号模型
间歇采样转发干扰通过对雷达信号间歇的采样和转发,能够在雷达接收端形成高保真假目标,对雷达的正常探测造成严重威胁。按照转发方式的不同,ISRJ 主要包含3 种类型:直接转发干扰(Direct Repeater Interference, DRI)、重复转发干扰(Repetitive Repeater Interference, RRI)和循环转发干 扰(Cyclic Repeater Interference, CRI)[22]。ISRJ的采样和3 种转发方式如图2所示,转发信号通常会延迟采样信号一个采样脉宽[22]。
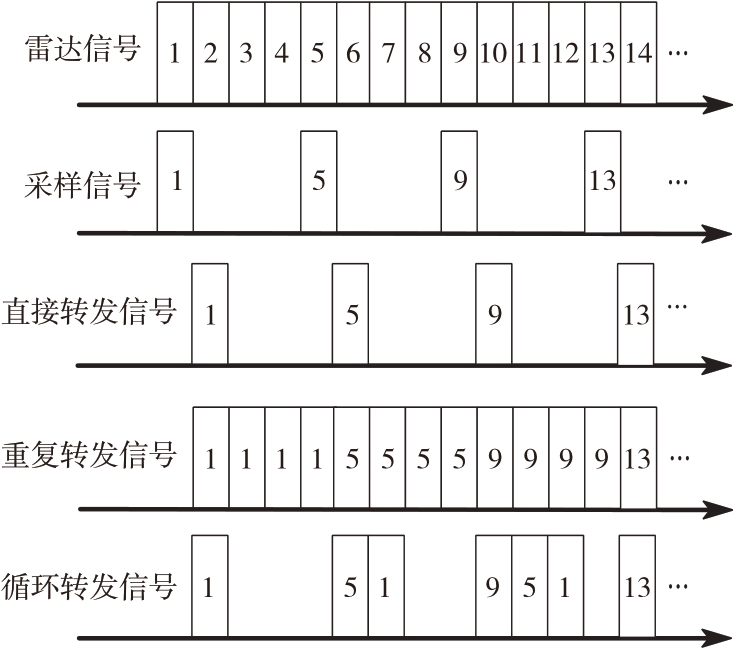
图2 间歇采样转发干扰的工作流程
假设采样信号为p(t),其脉宽为τ,工作周期为Ts,干扰机截获的雷达信号为x(t),脉宽为T,则采样信号矩形脉冲串的个数![]() p(t)可表示为
p(t)可表示为
采样后的信号可以表示为
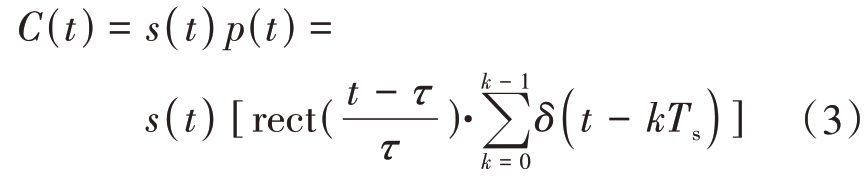
直接转发干扰直接转发采样后的信号,其信号表示形式为
对于重复转发干扰,在重复转发阶段,采样后的信号会被重复填充至相邻的空白时隙中,转发次数![]() 这一过程生成的干扰信号为
这一过程生成的干扰信号为
对于间歇采样循环转发干扰,其将前几个采样周期的信号按次序依次进行时延后转发。其原理等效于将采样得到的干扰信号分别增加时延n(τ + Ts)+ τ,n = 0,1,…,R - 1,R = min{Q, K},这一过程生成干扰信号为
假设干扰机截获的雷达信号序列为x =[x1, x2,…, xN]T ∈ℂN,N 为单脉冲采样长度,令采样转发的干扰矩阵为J ∈RN × N,则干扰信号可表示为
在不考虑转发时延的条件下,假设干扰机的采样频率为fs。则单个采样点对应的时间为ts =1/fs,单个采样脉冲的采样点数![]() 单个采样周期的采样点数
单个采样周期的采样点数![]() 直接转发干扰对应的干扰矩阵为
直接转发干扰对应的干扰矩阵为
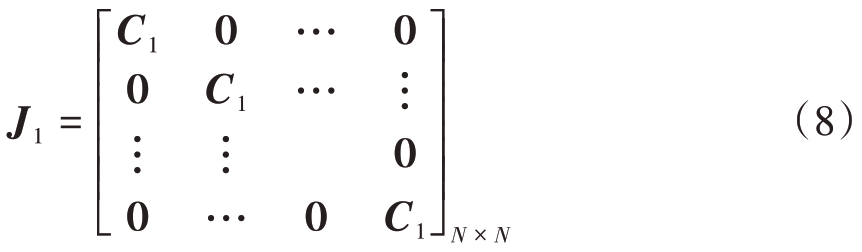
式中,

IN1 表示大小为N1 × N1,除对角线元素为1,其他元素均为0的矩阵。
重复转发干扰的干扰矩阵J2 的定义与J1 类似,但是矩阵C1的定义不同:
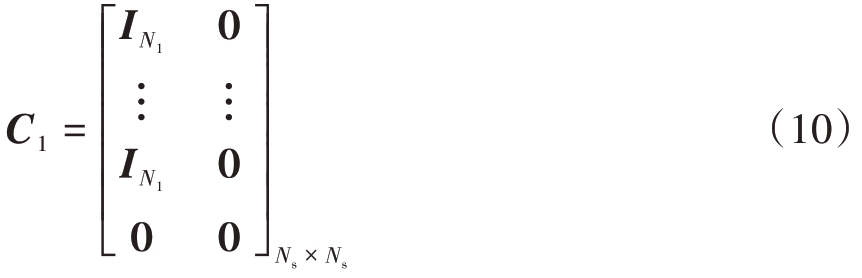
循环转发干扰的干扰矩阵![]() N × N,其中
N × N,其中
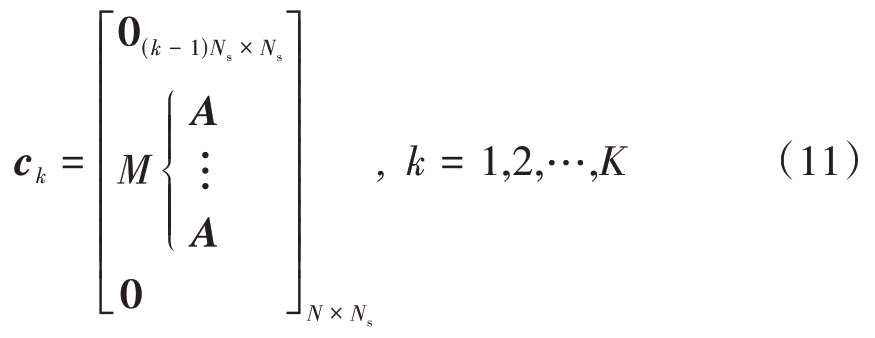
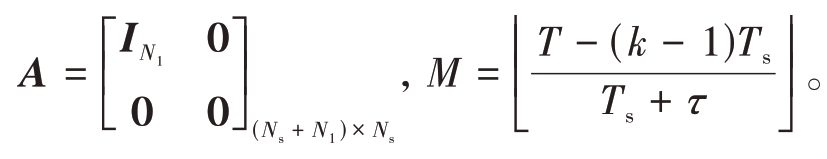
1.3 模型建立
非匹配滤波输出是非匹配滤波器与雷达发射信号的互相关。在延时k 处,发射波形x 与非匹配滤波器w的互相关输出为
其中Dk表示移位矩阵:
发射波形滤波输出的积分旁瓣电平(Integrated Sidelobe Level, ISL)为
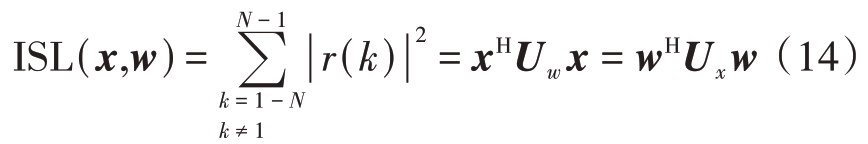
式中,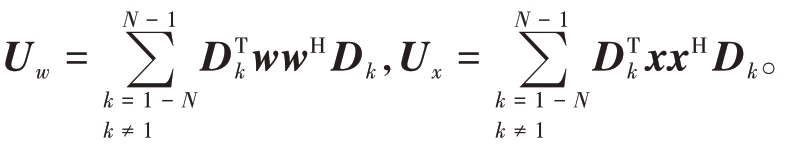
干扰波形滤波输出的加权总电平(Weighted Integrated Level,WIL)为
式中![]()
降低发射波形滤波输出的ISL(x,w)有利于雷达对弱目标的检测,避免脉压旁瓣过高遮挡弱目标;降低干扰波形滤波输出的WIL(x,w),有利于提高非匹配滤波器与干扰信号的正交性,降低间歇采样干扰带来的影响。为了保证雷达良好的探测性能,应同时降低ISL(x,w)和WIL(xj,w)。为便于同时优化,此处引入加权因子μ1和μ2来平衡两者之间的重要性, μ1 + μ2 = 1。因此,本文建立的目标函数为
需要注意的是,采用非匹配滤波器会导致信噪比的损失,因此在设计时必须对主瓣电平能量进行约束,避免主瓣损失过大:
其中δ ∈(0,1)决定了所优化的雷达波形脉冲压缩后主瓣电平的下界,是用户自定义的数值。
同时,间歇采样干扰信号经过非匹配滤波后在零时延位置易出现峰值,因此也需对干扰信号滤波后的主瓣电平进行能量约束。
其中ξ ∈(0,1)决定了干扰波形经非匹配滤波器后主瓣电平的上界,是用户自定义的数值。
考虑到雷达系统的功率一定,且发射波形峰值功率过高会造成信号经过非线性放大器后产生失真,因此还需要对波形施加能量约束和峰值功率约束。
其中,式(19)表示能量约束,式(20)表示峰值功率约束,σ 表示波形峰值模量的上界,Ei 矩阵除对角线上第i个元素为1外,其他元素均为0。
进一步,较高的滤波器能量也会影响信噪比输出,因此,也需要对滤波器施加能量约束。
假设雷达工作在归一化频段Ω ∈[0,1),共含K个频段需要与其他设备共享。第k 个频段为Ωk =![]()
![]() 和分别表示第k 个频段的下界和上界。根据文献[29],雷达在第k个频段上发射的能量为
和分别表示第k 个频段的下界和上界。根据文献[29],雷达在第k个频段上发射的能量为
其中,
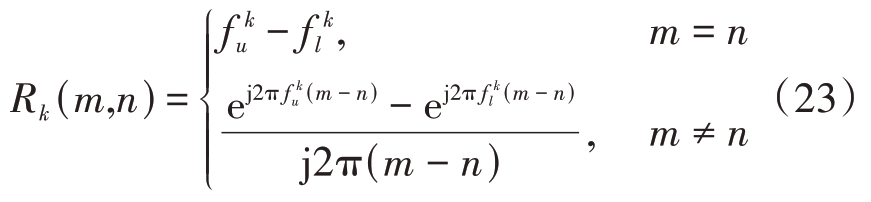
为避免与其他的工作设备产生互扰,雷达需要管理其在共享频段上产生的能量,为此,建立如下频谱兼容约束:
式中:η表示所允许的最大干扰能量![]()
![]() 表示第k 个频带对应的权重。通过选择适当的权重系数,可对不同的频带赋予不同的重要性。
表示第k 个频带对应的权重。通过选择适当的权重系数,可对不同的频带赋予不同的重要性。
综合上述分析,本文所构建的数学模型如下:
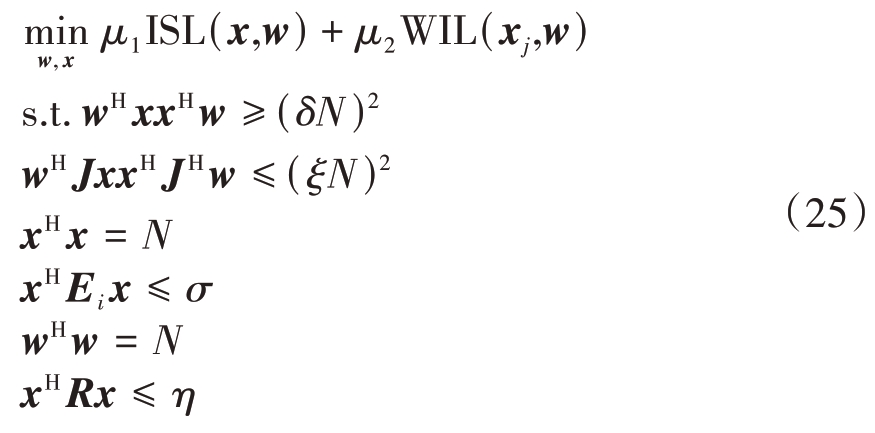
2 算法求解
由于非凸模量约束、能量约束和主瓣电平约束的存在,式(25)是非凸的,难以直接求解,为此,我们基于交替优化(Alternating Optimization, AO)框架,交替优化非匹配滤波器和发射波形。具体求解步骤如下。
2.1 固定x,优化w
去除无关变量后,仅与w 有关的优化问题如下:
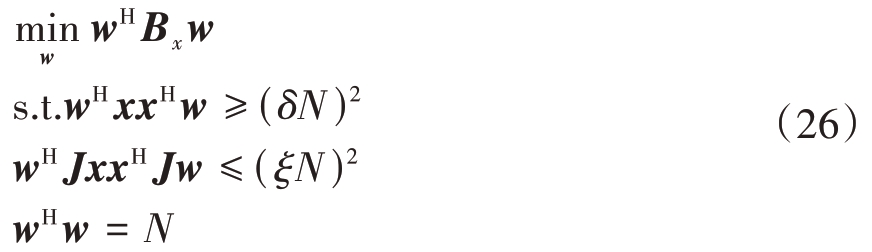
式中,Bx = μ1Ux + μ2Uxj。令![]()
![]() ,原问题被等价转化为
,原问题被等价转化为
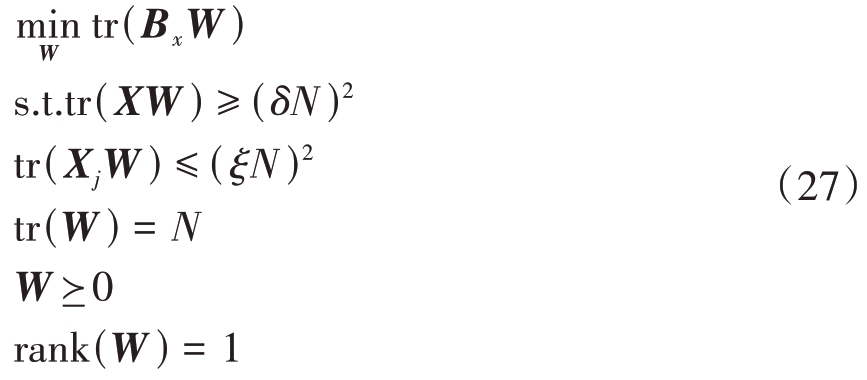
去除秩一约束后,转化为SDP问题:
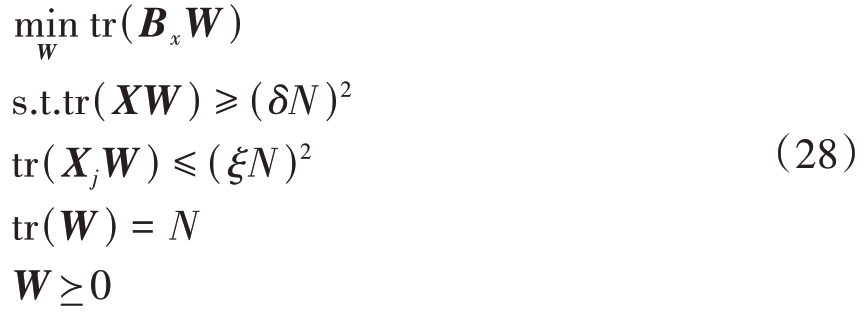
式(28)可通过内点法进行求解。鉴于其忽略了滤波器协方差矩阵的秩约束,在获得优化的滤波器协方差矩阵W*后,需要从W*从提取滤波器w*。若rank(W*)= 1,直接通过W* = w*(w*)H对W*进行秩一分解,得到最优接收滤波器w*。若rank(W*)> 1,采用文献[30]中的主分量最小化(Majorize-Minimization, MM)算法获取最优滤波器。简单来说,该方法在式(28)的基础上向目标函数添加一个rank 函数的惩罚项,通过最小化目标函数来迫使所得的解秩为1。
2.2 固定w,优化w
去除无关变量后,仅与发射波形有关的数学模型为
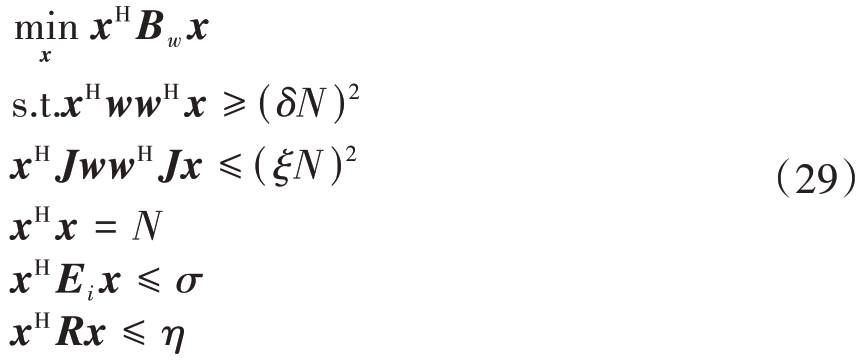
式中,Bw = μ1Uw + μ2Uwj。
式(29)的类型与式(26)一致,可通过同样的SDP算法求解波形协方差矩阵后,再采取同样提取秩一解的方法提取优化波形,此处不再赘述。
2.3 算法总结
通过2.1 节和2.2 节交替更新非匹配滤波器和发射波形。假设第t + 1次更新发射波形后输出的目标函数值为 f(x,w)t + 1,算法在满足![]() 或达到最大迭代次数T时停止更新。
或达到最大迭代次数T时停止更新。
3 仿真实验
本节通过仿真实验来证明所建立模型及所使用算法的有效性。实验基于主频为3.2 GHz 的CPU 和RAM 为16 GB 的硬件环境,并依托MATLAB R2021b 的软件平台进行仿真。主要从3 个方面出发验证实验性能。3.1 节为ISRJ 的干扰性能,3.2节为算法的收敛性分析,3.3节为算法的有效性和性能分析。
3.1 ISRJ干扰性能分析
本小节通过仿真间歇采样转发干扰来研究其干扰性能。假设存在一个脉冲持续时间为256 μs、带宽为10 MHz的线性调频(Linear Frequency Modulation, LFM)信号。该信号被干扰机以65 μs 的采样重复周期和15 μs 的采样持续时间采样并转发。干扰信号滞后原信号1个采样持续时间。图3(a)绘制了LFM信号和3个ISRJ干扰信号的波形,图3(b)展示了这些信号与匹配滤波器的互相关电平。从图3可以看出,DRI、RRI 和CRI 信号分别产生了1次、4次和3次转发过程,从而产生了相应数量的假目标组,当干扰信号的功率较大时,ISRJ 信号会导致所接收的真实目标回波信号与脉冲压缩后的干扰信号混合在一起时,脉冲压缩雷达难以区分真假目标,对雷达的正常工作产生严重威胁。
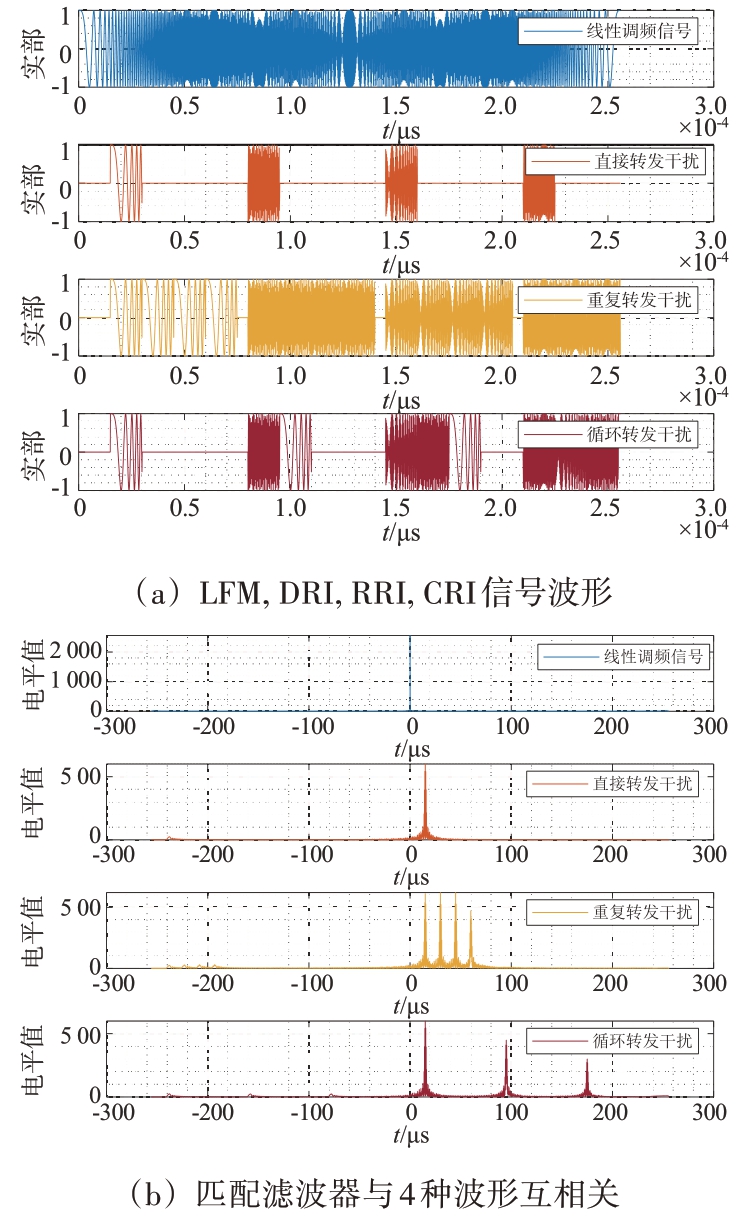
图3 干扰信号的波形以及干扰效果
3.2 算法的收敛性分析
假设所设计的相位编码波形的带宽和脉宽分别为B = 10 MHz 和T = 25.6 μs,则波形长度为N =B ⋅T = 256。干扰机的采样重复周期Ts = 6.5 μs,采样持续时间τ = 1.5 μs。雷达需要与其他设备共享的一个频段为Ω1 =[ fl, fu ],其中fl = 0.565, fu =0.625。设置μ1 = μ2 = 0.5,σ = 1.3,δ = 0.9,ξ = 0.01,ε = 10-3,η = 0.066 2。发射波形和接收滤波器均是随机生成的。图4 为在同一组初始波形和滤波器下,不同干扰场景中目标函数值随迭代次数的变化曲线。由于转发次数RRI > CRI > DRI,各干扰所对应的初始目标函数值大小fRRI(x,w) >fCRI(x,w) > fDRI(x,w),但是随着迭代过程的运行,目标函数相对大小与初始值产生差异,从整体趋势来看,3 个干扰所对应的目标函数值均单调递减,体现了所用算法的良好收敛性。
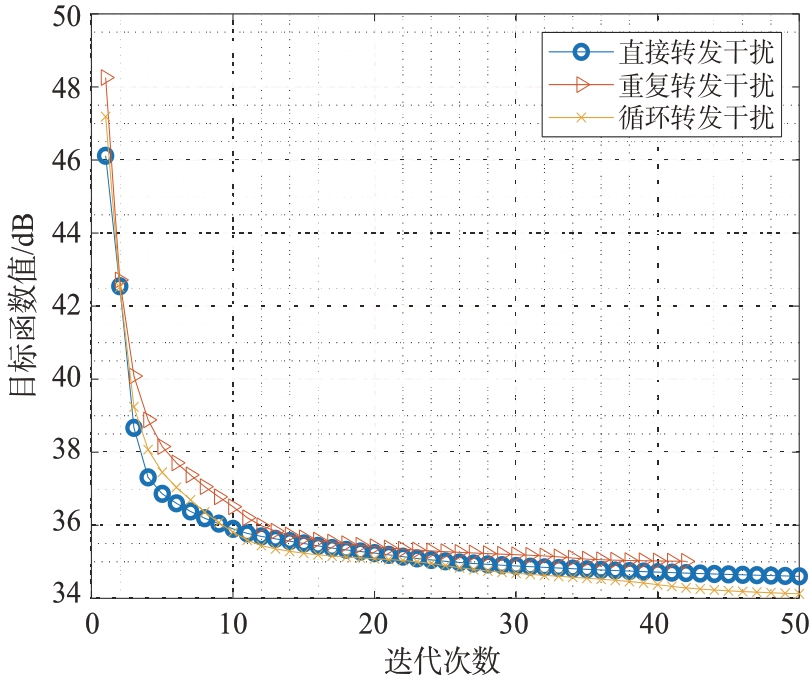
图4 目标函数值随迭代次数的变化
3.3 算法的有效性和性能分析
设置干信比为15 dB,信噪比为0 dB。图5(a)为随机初始化信号的频谱图,从图中可以看出,初始信号的频谱能量在各频点分布相对均匀,没有明显的零陷;图5(b)为信号遭受不同干扰后,雷达所接收信号经过匹配滤波器后的脉压结果,显然,受干扰的雷达信号在脉冲压缩后将难以通过检测门限判断真实目标。
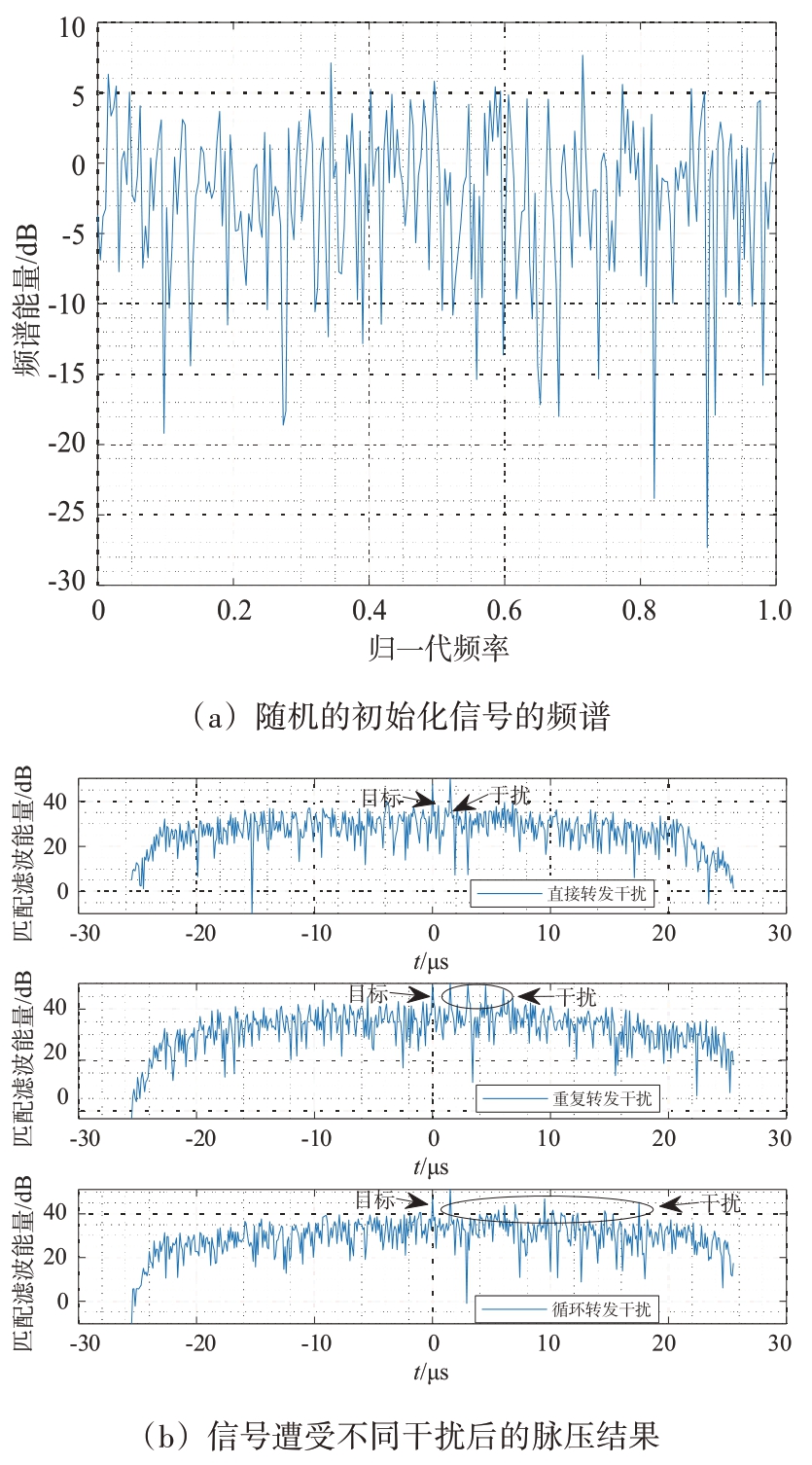
图5 初始化信号的频谱以及信号遭受不同干扰后的脉压结果
图6 展示了不同干扰条件下优化得到的3 种波形频谱图、模值图,以及接收信号(含发射信号、干扰信号以及噪声信号)及与其对应非匹配滤波器的脉压图。图6(a)~(c)是针对直接转发干扰的优化结果,图6(d)~(f)是针对重复转发干扰的优化结果,图6(g)~(i)是针对循环转发干扰的优化结果。从图6中可以得出如下结论:1)优化信号的频谱在特定频段形成了较深的零陷,有利于雷达与其他电子设备在该频段共存;2)优化信号的模值均没有超过峰值门限,避免了信号经过非线性放大器产生削顶失真;3)优化的信号被干扰后,所接收的信号与其对应的非匹配滤波器的脉压结果仅在目标处产生峰值,有效抑制了干扰。上述结论充分体现了所用算法的有效性。
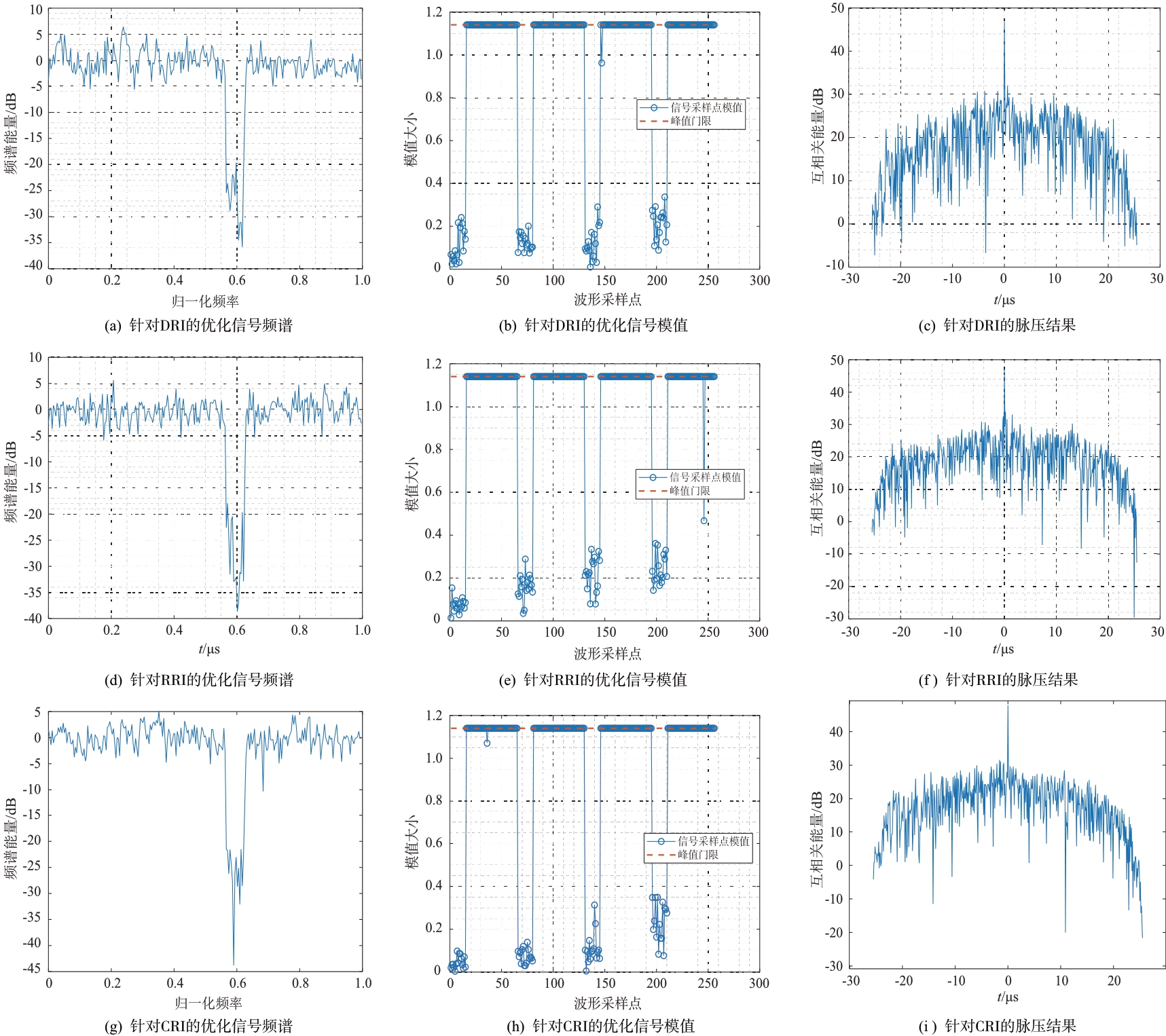
图6 不同信号的频谱图、模值图以及脉压结果图
以DRI 为例,图7 探究了不同权重因子μ1 下,算法输出的ISL(x,w)和WIL(xj,w)的数值变化。从图7可以看出,ISL(x,w)随着μ1的增大呈现单调递减的趋势,而WIL(xj,w)随着μ1的增大单调递增。这是因为μ1 在目标函数中起着平衡ISL(x,w)与WIL(xj,w)重要性的作用,μ1越大,ISL(x,w)的重要程度越大,对应的数值将会减少,反之,WIL(xj,w)对应的数值将会增大。
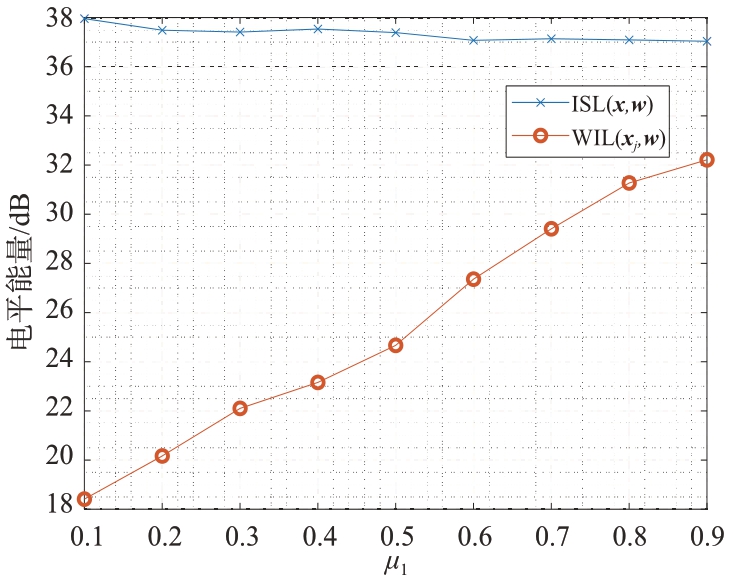
图7 ISL(x,w)和WIL(xj,w)随μ1值的变化
4 结束语
本文探究了频谱拥塞条件下抗间歇采样转发干扰的雷达发射波形和非匹配滤波器设计方法。从同时最小化发射波形与滤波器的互相关旁瓣电平以及干扰波形与滤波器的互相关总电平入手建立目标函数,同时对主瓣电平能量进行约束,以提高雷达的探测能力和生存能力。针对所建立的非凸模型,运用SDP 结合MM 算法进行了有效求解。仿真实验说明了模型和算法的有效性。本文所采用的算法可推广至对各类复杂的多目标二标函数及二次约束问题的求解。所建立的数学模型不局限于所提出的三类ISRJ 干扰,可针对多种与信号相干但不完全一致的干扰,原因在于:非匹配滤波器的引入增强了信号处理过程中发射信号与干扰信号之间的差异性,能够降低相干信号匹配滤波后带来的高增益影响,有利于干扰抑制。然而,本文的模型对先验信息要求较高,下一步可探究先验信息不准确条件下的发射波形和接收滤波器设计问题。
[1] 王雪松,刘建成,张文明,等.间歇采样转发干扰的数学原理[J].中国科学:E辑,2006,36(8):891-901.
[2] FENG Dejun, XU Letao, PAN Xiaoyi, et al. Jamming Wideband Radar Using Interrupted - Sampling Repeater[J].IEEE Trans on Aerospace and Electronic Systems,2017,53(3):1341-1354.
[3] FENG Dejun, TAO Huamin, YANG Yong, et al. Jamming De-Chirping Radar Using Interrupted Sampling Repeater[J].Science China (Information Sciences),2011,54(10): 2138-2146.
[4] GRECO M S, GINI F, STINCO P, et al. Cognitive Radars:on the Road to Reality: Progress Thus Far and Possibilities for the Future[J].IEEE Signal Processing Magazine,2018,35(4):112-125.
[5] HUANG Chao, HUANG Zhongrui, ZHOU Qingsong, et al.Unimodular Waveform Design for Integrated Radar Communication and Jamming[J].Digital Signal Processing: A Review Journal, 2023, 143:104236.
[6] QIAN Junhui, LIU Ziyu, LU Yuanyuan, et al.Radar and Communication Spectral Coexistence on Moving Platform with Interference Suppression[J].Remote Sensing, 2022,14(19):5018.
[7] LIU Zhen, PENG Bo, SHEN Rui, et al. ECCM Scheme Against Interrupted Sampling Repeater Jammer Based on Parameter-Adjusted Waveform Design[J].SENSORS,2018,18(4):1141.
[8] GONG Shixian, WEI Xizhang, LI Xiang. ECCM Scheme Against Interrupted Sampling Repeater Jammer Based on Time-Frequency Analysis(Article)[J].Journal of Systems Engineering and Electronics, 2014, 25(6):996-1003.
[9] CHEN Jian, WU Wenzhen, XU Shiyou, et al.Band Pass Filter Design Against Interrupted-Sampling Repeater Jamming Based on Time-Frequency Analysis[J].IET Radar,Sonar and Navigation, 2019, 13(10):1646-1654.
[10] FAN Beichen, DU Xiaoyong, HU Weidong. False Targets Suppression of Integral Power Frequency Modulated Waveform for Countering Interrupted Sampling Repeater Jamming[J].IEEE Geoscience and Remote Sensing Letters,2023, 20:1.
[11] ZHOU Chao, LIU Quanhua, CHEN Xinliang. Parameter Estimation and Suppression for DRFM-Based Interrupted Sampling Repeater Jammer[J].IET Radar Sonar and Navigation, 2018, 12(1):56-63.
[12] 刘孟斐,陈吉源,潘小义,等.基于信息熵的分段脉压间歇采样干扰抑制[J].雷达科学与技术,2023,21(3):264-272.
[13] WANG Chaoyu, HU Wanwan, ZHE Geng, et al. Parameter Estimation for Interrupted Sampling Repeater Jamming Based on ADMM[J].Sensors, 2021, 21(24):8277.
[14] CAO Fei, CHEN Zihan, FENG Xiaowei, et al. Optimal Design of Anti-Interrupted Sampling Repeater Jamming Waveform for Missile-Borne Radar Based on an Improved Genetic Algorithm[J]. IET Signal Processing,2021, 15(9):622-632.
[15] 周畅,汤子跃,余方利,等.基于脉内正交的抗间歇采样转发干扰方法[J].系统工程与电子技术,2017,39(2):269-276.
[16] ZHANG Jianzhong, MU Heqiang, WEN Shuliang, et al.Anti-Intermittent Sampling Jamming Method Based on Intra-Pulse LFM-Costas Frequency Stepping[J]. Systems Engineering and Electronics, 2019, 41(10):2170-2177.
[17] LI Dexin, LIU Tao, SU Yi, et al. Joint Design of Transmit Waveform and Mismatch Filter in the Presence of Interrupted Sampling Repeater Jamming[J].IEEE Signal Processing Letters, 2020, 27:1610-1614.
[18] 周凯,李德鑫,毅何,等.基于雷达发射波形和非匹配滤波联合设计的间歇采样转发干扰抑制方法[J].电子与信息学报,2021,43(7):1939-1946.
[19] LI Dexin, QUAN Sinong, LIU Tao, et al.SAR Waveform and Mismatched Filter Design for Countering Interrupted-Sampling Repeater Jamming[J].IEEE Trans on Geosciences and Remote Sensing, 2022, 60:1-14.
[20] WANG Fulai, LI Nanjun, PANG Chen, et al. Complementary Sequences and Receiving Filters Design for Suppressing Interrupted Sampling Repeater Jamming[J]. IEEE Geoscience and Remote Sensing Letters,2022,19:1-5.
[21] 王福来,庞晨,黄大通,等.一种同时全极化雷达发射波形和接收滤波器联合设计的抗间歇采样转发干扰方法[J].中国科学(信息科学),2022,52(7):1333-1348.
[22] GE Mengmeng, YU Xianxiang, YAN Zhengxin, et al.Joint Cognitive Optimization of Transmit Waveform and Receive Filter Against Deceptive Interference[J].Signal Processing, 2021, 185:108084.
[23] 王福来,庞晨,殷加鹏,等.一种多普勒容忍的抗间歇采样转发干扰恒模互补波形和接收滤波器联合设计方法[J].雷达学报,2022,11(2):278-288.
[24] 王伟,李梦良,王福来,等.一种抗间歇采样转发干扰的全极化雷达发射波形优化方法[J].电子与信息学报,2023,45(11):3877-3886.
[25] GAO Yuhang, FAN Huayu, REN Lixiang, et al. Joint Design of Waveform and Mismatched Filter for Interrupted Sampling Repeater Jamming Suppression[J]. IEEE Trans on Aerospace and Electronic Systems, 2023, 59(6):1-16.
[26] CHEN Qinxian, SHI Shasha, LI Xiaobo, et al. Radar Spectrum Coexistence Waveform Design with Multiple Waveform Constraints[C]//2023 8th International Conference on Computer and Communication Systems, Guangzhou, China:IEEE, 2023:1-8.
[27] LIANG Junli, SO H C, LEUNG C S, et al. Waveform Design with Unit Modulus and Spectral Shape Constraints via Lagrange Programming Neural Network[J]. IEEE Journal of Selected Topics in Signal Processing, 2015, 9(8):1377-1386.
[28] LI Da, TANG Bo, XUE Lei. Multi-Spectrally Constrained Low -PAPR Waveform Optimization for MIMO Radar Space-Time Adaptive Processing[J].IEEE Trans on Aerospace and Electronic Systems, 2023, 59(5):1-15.
[29] AUBRY A, DE MAIO A, PIEZZO M, et al. Radar Waveform Design in a Spectrally Crowded Environment via Nonconvex Quadratic Optimization[J]. IEEE Trans on Aerospace and Electronic Systems, 2014, 50 (2):1138-1152.
[30] LIU Tian, SUN Bo, TSANG D H K. Rank-One Solutions for SDP Relaxation of QCQPs in Power Systems[J].IEEE Trans on Smart Grid, 2019, 10(1):5-15.