0 引 言
相控阵雷达具备多目标探测、多功能、波束捷变、抗干扰能力强、自适应能力强以及高可靠性等特点,在国内外军民领域得到广泛的应用。在武器系统跟踪雷达领域,由于相控阵雷达的多波束以及波束捷变等特点,与常规机械扫描跟踪雷达相比,可对目标实现快速捕获以及多目标跟踪,极大提升武器系统的作战效能。但是相控阵雷达也具有先天缺陷,例如相控阵雷达存在最小波速跃度[1],在对目标跟踪时,其波束在三维空间内是离散扫描的,难以像机械扫描雷达那样连续扫描,会对目标跟踪带来一定的影响;另外,相控阵雷达当跟踪波束远离方位、俯仰法线时,会出现和差波束展宽、扭曲等现象,在进行单脉冲和差波束测角时[2-3],严重影响了相控阵雷达测角精度。本文主要针对其中的和差波束展宽、扭曲带来的测角精度影响进行了研究。
为了解决相控阵雷达远离方位、俯仰法线的和差波束展宽、扭曲带来的测角精度问题,本文分析对比了阵面坐标系和正弦空间坐标系内相控阵雷达波束,利用扫描波束在正弦空间坐标系内不会出现展宽、扭曲的特点[4-5],提出了一种基于正弦空间的相控阵雷达单脉冲和差测角方法,并进行了仿真验证。
1 相控阵空间坐标定义
在讨论相控阵雷达单脉冲和差测角时,需计算和差波束空间方向图以及差/和比形成鉴角曲线,为此首先明确几种坐标系。在直角坐标系中,以阵面所在平面为XY 面,阵面法线指向为Z 轴方向,空间任一点R 在该三维坐标系中坐标为( x,y, z ),如图1所示。另外,还有阵面坐标系、天线坐标系、正弦空间坐标系、雷达坐标系以及天线圆锥角坐标系等[6],本文讨论的问题主要涉及到前三种坐标系。
图1 阵面在三维空间示意图
1.1 阵面坐标系
以图1阵面为例,阵面坐标系如图2所示,空间中任一点R与阵面中心O 点的连线与XZ面的投影PXZ间的夹角记为θEL,Z轴正方向与R点在XZ面投影线夹角为θAZ。阵面坐标系比天线坐标系和正弦空间坐标系更为直观,一般在雷达战技指标中出现的阵面方位、俯仰扫描范围、阵面波束指向、方位俯仰误差等指的是阵面坐标系中的方位θAZ和俯仰θEL。
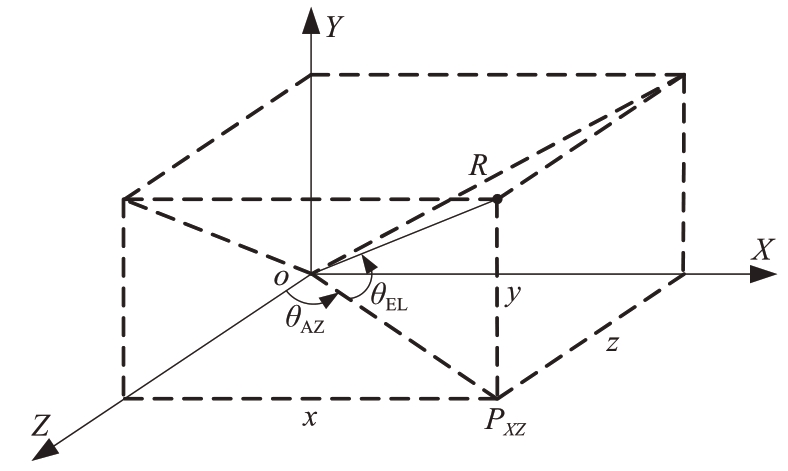
图2 阵面坐标系
1.2 天线坐标系
以图1阵面为例,天线坐标系如图3所示,对于空间中任一点R,Z 轴正方向到点R 的夹角为θ,X 轴正方向到点R 在XY 面投影PXY 的夹角为ϕ,这种坐标实际上就是直观的球面坐标系,在描述阵面方向图表达式时经常用到。
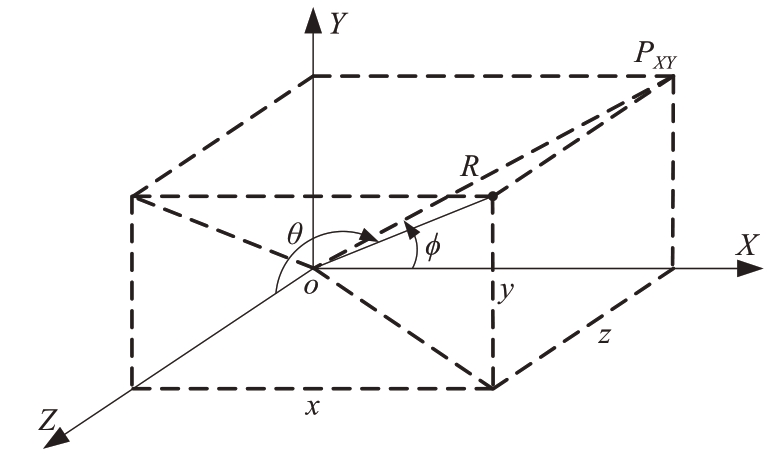
图3 天线坐标系
1.3 正弦空间坐标系
正弦空间就是三维空间到二维平面的半球映射,以图1阵面为例,如图4所示,U、V 是θ、ϕ 在XY平面上的投影,正弦空间坐标系与阵面坐标系和天线坐标系的关系如表1所示。
表1 角度坐标到正弦空间的变换关系

正弦空间uv天线坐标系(θ, ϕ)sin θ cos ϕ sin θ sin ϕ阵面坐标系(θAZ, θEL)sin θAZ cos θEL sin θEL
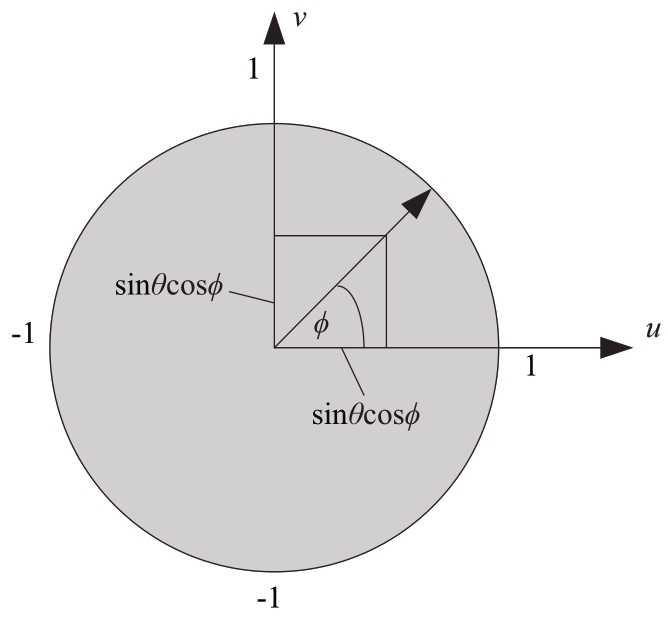
图4 正弦空间UV平面
2 和差波束展宽扭曲分析
2.1 波束方位对称性分析
假设二维阵面X、Y 方向阵元间距分别为dx 和dy,X、Y方向阵元数分别为M和N,阵面中心位于坐标原点处,则每一个阵元在XY平面内坐标为(xm, yn)。
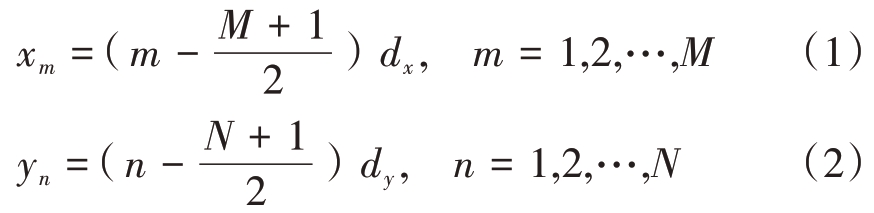
在阵面坐标系中,波束指向(θ AZ0, θEL0 )的二维阵面波束方向图表达式为
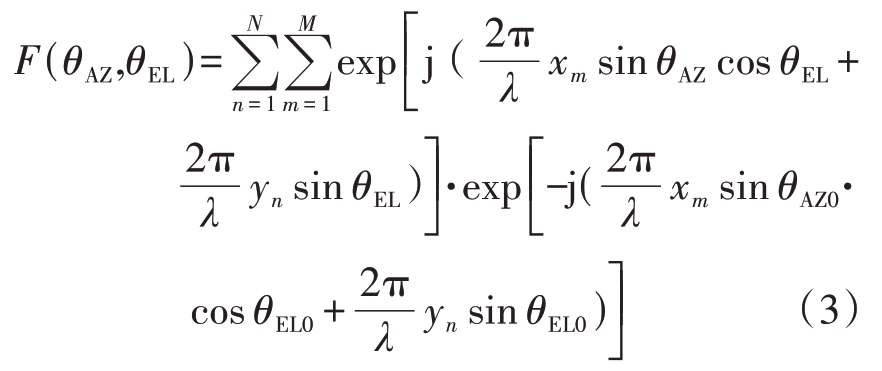
波束指向(θAZ0,θEL0)时,偏离波束中心(ΔθAZ,0),![]() 为方位3 dB 波宽,二维阵面波束方向图值为
为方位3 dB 波宽,二维阵面波束方向图值为
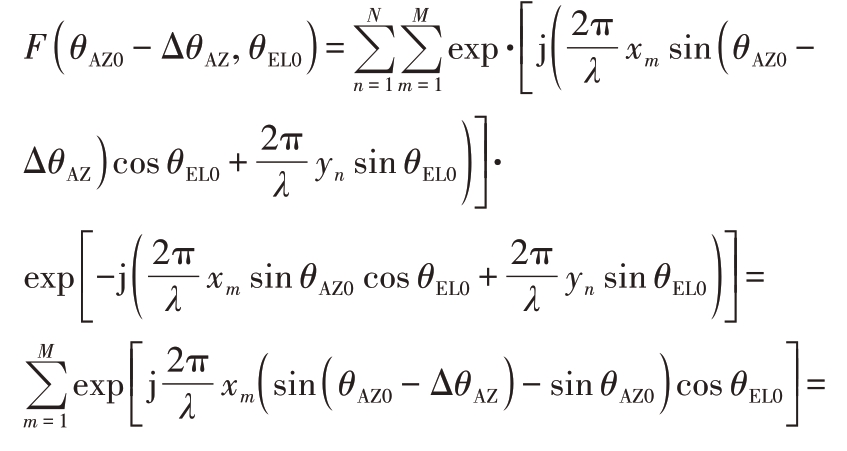
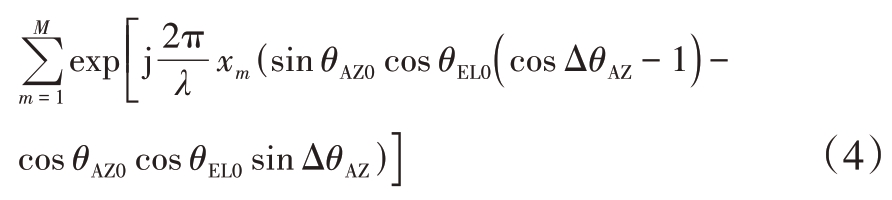
同理,波束指向(θ AZ0,θEL0 )时,偏离波束中心(- ΔθAZ,0 ),二维阵面波束方向图值为
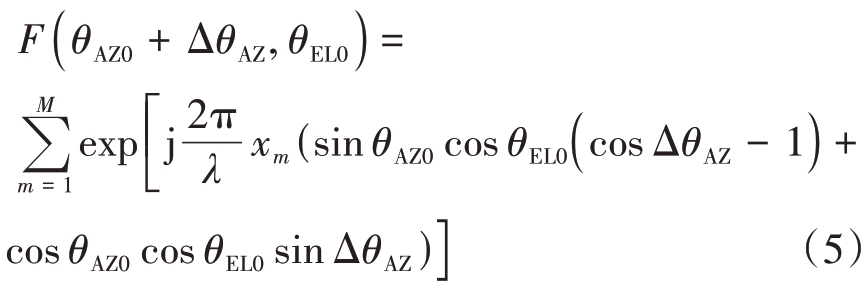
由式(4)和式(5)可知,偏离波束中心(Δ θAZ,0)和(- ΔθAZ,0 )方向图幅值分别为| F(θ AZ0 - ΔθAZ,θEL0)|与|F(θ AZ0 + ΔθAZ,θEL0 )|,且幅值不对称,波束方位对称性影响因子:
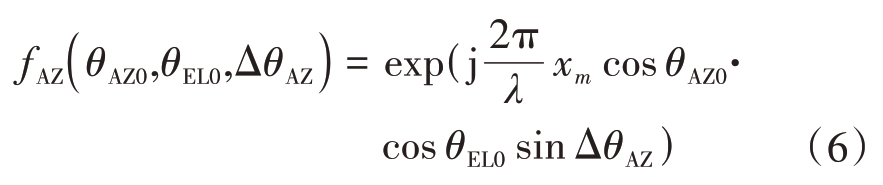
由式(6)可知,当偏离波束中心ΔθAZ时,存在影响因子fAZ(θ AZ0,θEL0,ΔθAZ )不为1,造成| F(θAZ0-ΔθAZ,θEL0)|与|F(θ AZ0+ΔθAZ,θEL0 )|不相等,波束方位不对称。
2.2 波束俯仰对称性分析
波 束 指 向(θ AZ0,θEL0 )时,偏 离 波 束 中 心![]() 为俯仰3 dB 波宽,二维阵面波束方向图值为
为俯仰3 dB 波宽,二维阵面波束方向图值为
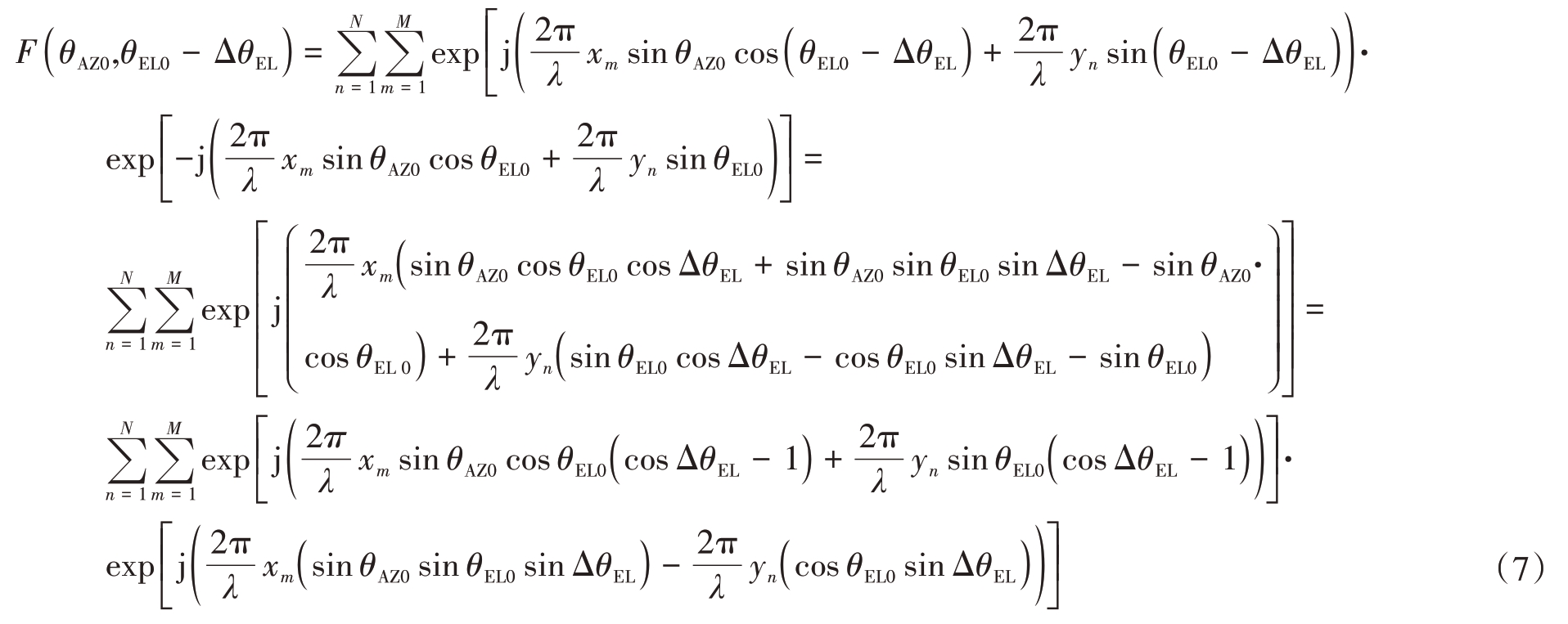
同理,波束指向(θ AZ0,θEL0 )时,偏离波束中心(0 ,-ΔθEL ),二维阵面波束方向图值为
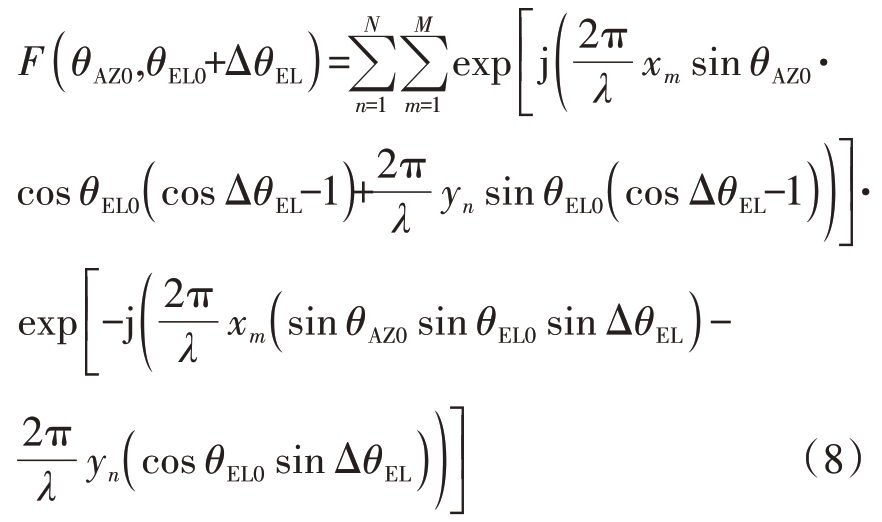
由式(7)和式(8)可知,偏离波束中心(0 ,ΔθEL)和(0 ,-ΔθEL )方向图幅值分别为 |F(θ AZ0,θEL0-ΔθEL)|与|F(θ AZ0,θEL0 + ΔθEL )|,波 束 俯 仰 对 称 性 影 响因子:
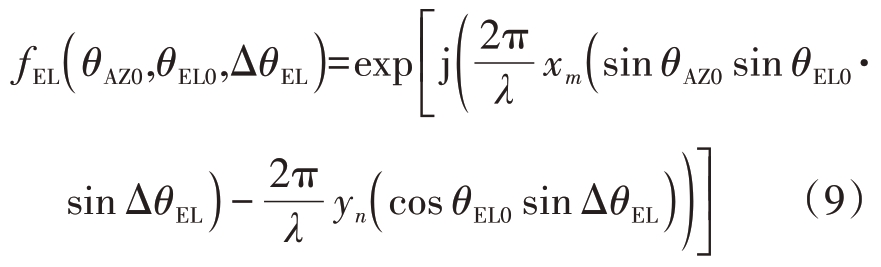
由式(9)可知,扫描波束俯仰对称性不仅与ΔθEL 有关,还与阵面X 方向、Y 方向阵元数和尺寸有关,当阵面X 方向、Y 方向阵元数和尺寸相近时,xm ≈yn,式(9)可以简化为
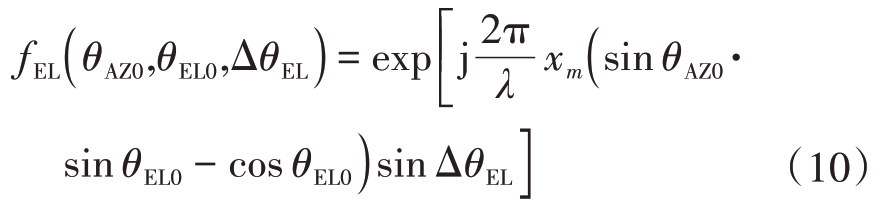
由式(9)和式(10)可知,当偏离波束中心ΔθEL时,存在影响因子fEL(θ AZ0,θEL0,ΔθEL ),且不为1,造成|F(θ AZ0 - ΔθAZ,θEL0 )|与 |F(θ AZ0 + ΔθAZ,θEL0 )|不 相等,波束俯仰不对称。
2.3 和差波束展宽扭曲仿真分析
根据以上分析,二维相控阵雷达,当波束扫描时,波束存在方位、俯仰不对称,造成波束扭曲,以下对大扫描角情况下,和、差波束进行仿真分析验证,如图5所示。

图5 阵面坐标系中波束指向(40°,40°)方向图
方位差方向图仿真如图6 和图7 所示,方位差波束在俯仰方向上会出现一条零深线,理想情况下在阵面坐标系中,希望方位差波束零深线和俯仰差波束零深线在波束中心处正交垂直,如图6所示。但是当扫描波束方位、俯仰远离法线时,方位差波束零深线出现倾斜,不与方位向垂直,波束出现不对称、扭曲现象,如图7所示,并且扫描角越大,方位零深线倾斜越严重,波束扭曲越严重。
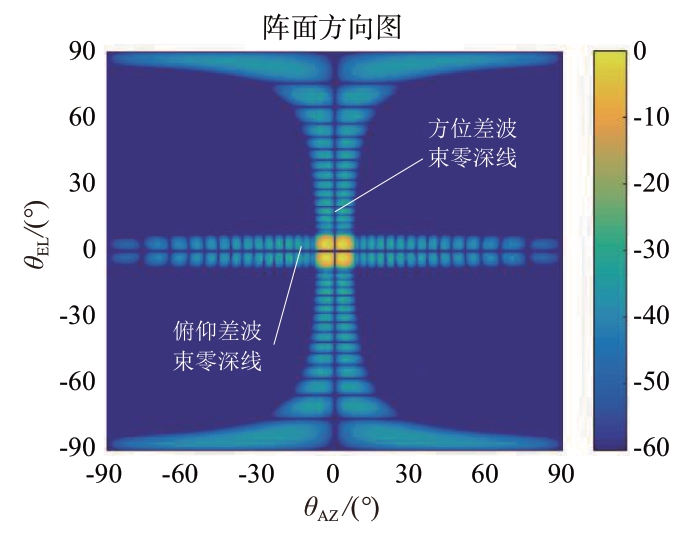
图6 阵面坐标系中方位俯仰零深线
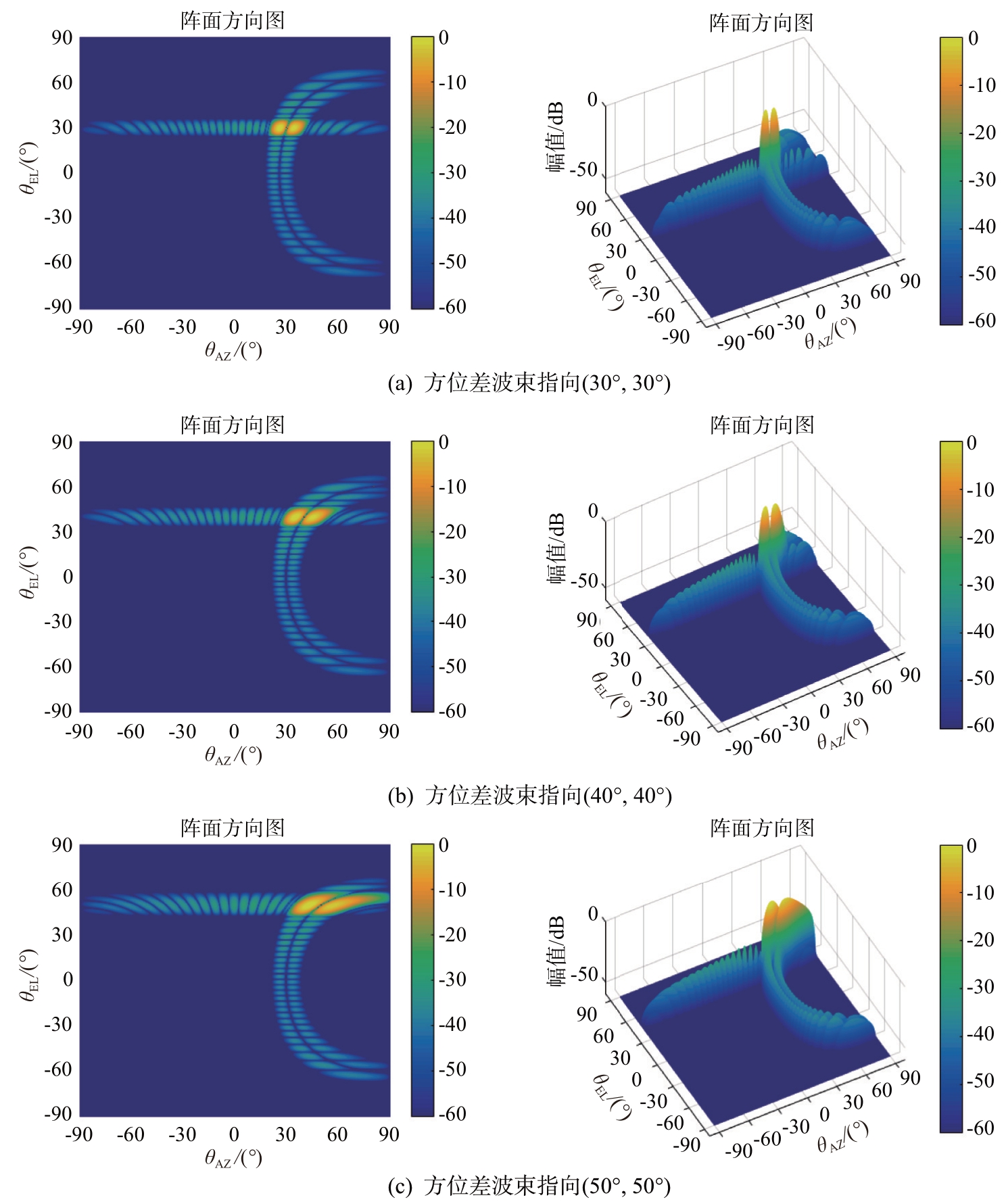
图7 阵面坐标系中非法线方位差波束方向图
3 相控阵和差测角改进
在阵面坐标系中,和差测角是通过差/和比值![]() 除以鉴角曲线斜率得到目标偏离波束中心(θ AZ0,θEL0 )的角度误差(Δ θAZ,ΔθEL )。
除以鉴角曲线斜率得到目标偏离波束中心(θ AZ0,θEL0 )的角度误差(Δ θAZ,ΔθEL )。

式中,kAZ,kEL分别为阵面坐标系内波束中心处的方位、俯仰鉴角曲线斜率,ΔAZ,ΔEL,∑分别为目标方位差、俯仰差以及和路幅值。
根据以上分析,当远离方位、俯仰法线的方位差波束出现扭曲,由于此时方位差波束零深线在阵面坐标系中已经不与方位向垂直,导致方位差波束中非波束中心处的方位零深,在方位向已发生严重偏移,如果继续采用扭曲后波束中心的鉴角曲线斜率进行测角,则对目标跟踪方位测角精度造成严重影响。
但是在正弦空间坐标系中不会出现该现象,如图8 和图9 所示,因此,可以考虑在正弦空间坐标系中进行和差测角,通过差/和比值除以正弦空间坐标系中鉴角曲线斜率,得到目标在正弦空间中的误差,结合波束指向在正弦空间的指向位置,得到目标在正弦空间的位置,然后通过表 1坐标转换得到目标在阵面坐标系中的位置以及相对波束中心的偏差。
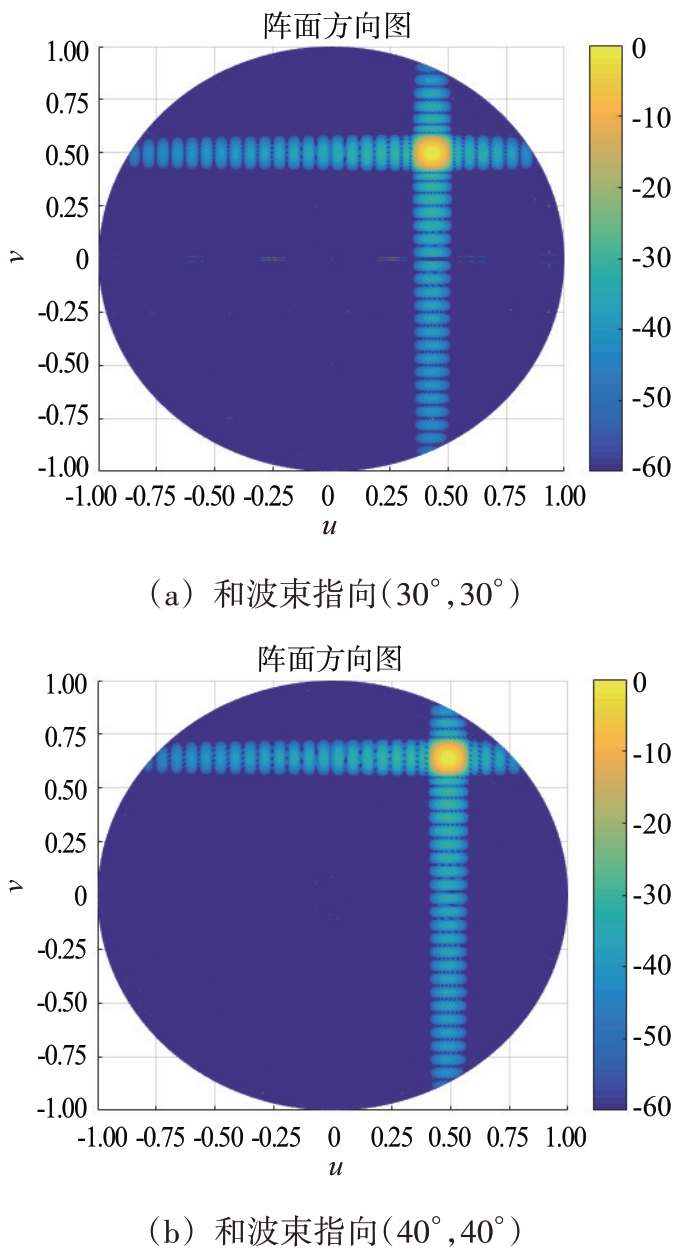
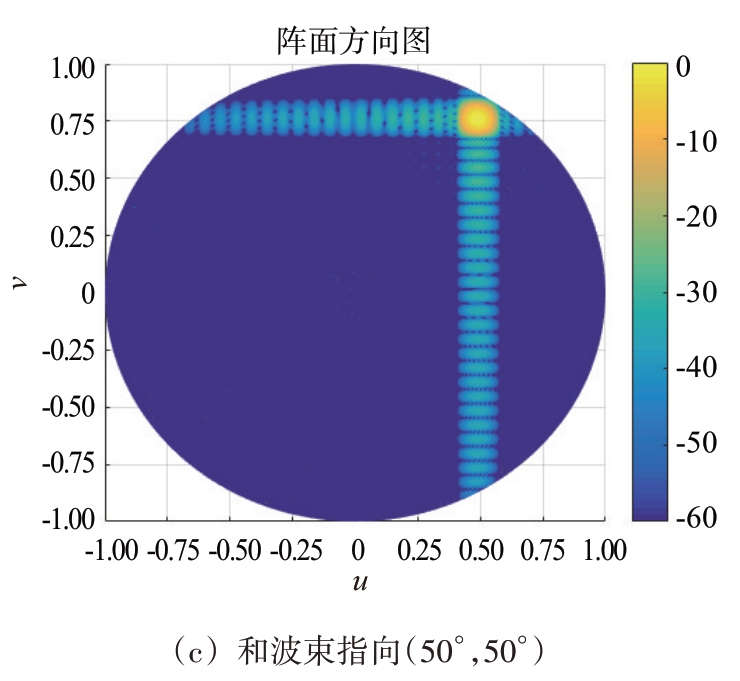
图8 正弦空间坐标系中非法线和波束方向图
图9 正弦空间坐标系中非法线方位差波束方向图
正弦空间中和差测角步骤如下:
1) 测得正弦空间中偏离波束中心误差值Δu和Δv。

式中,ku,kv 分别为正弦空间中u 方向和v 方向鉴角曲线斜率。
2) 求得目标在正弦空间中坐标。
阵面坐标系中波束中心指向(θ AZ0,θEL0 ),在正弦空间中波束中心为( u0,v0 )。
则目标在正弦空间中坐标为(u 0 + Δu,v0 + Δv )。
3) 通过坐标转换得到阵面坐标系中目标偏差。
根据表1关系将在正弦空间坐标系内测得的位置转换成阵面坐标系目标误差。
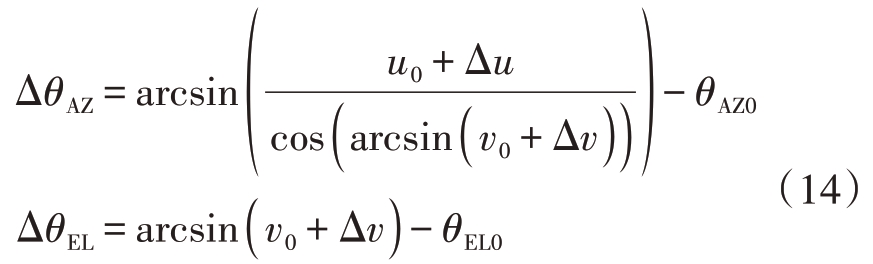
4 仿真验证
仿真采用均匀阵面矩形布阵,阵元间距为半波长,阵元数为32×32,采用直接加权(Taylor 加权和Bayliss 加权)法形成和差波束[7-8]。图10至图12为不同扫描角下,阵面坐标和正弦空间坐标下鉴角曲线。表2统计了不同波束指向时,阵面坐标系和正弦空间坐标系内方位、俯仰鉴角曲线斜率,从表中可以看出,正弦空间坐标系内鉴角曲线斜率远远大于阵面坐标系内的,具有更好的测角精度。
表2 不同波束指向鉴角曲线斜率
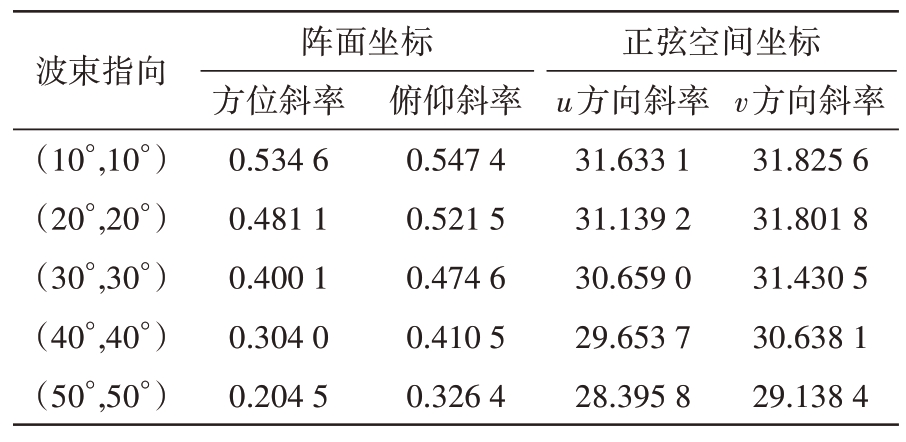
波束指向(10°,10°)(20°,20°)(30°,30°)(40°,40°)(50°,50°)阵面坐标方位斜率0.534 6 0.481 1 0.400 1 0.304 0 0.204 5俯仰斜率0.547 4 0.521 5 0.474 6 0.410 5 0.326 4正弦空间坐标u方向斜率31.633 1 31.139 2 30.659 0 29.653 7 28.395 8 v方向斜率31.825 6 31.801 8 31.430 5 30.638 1 29.138 4
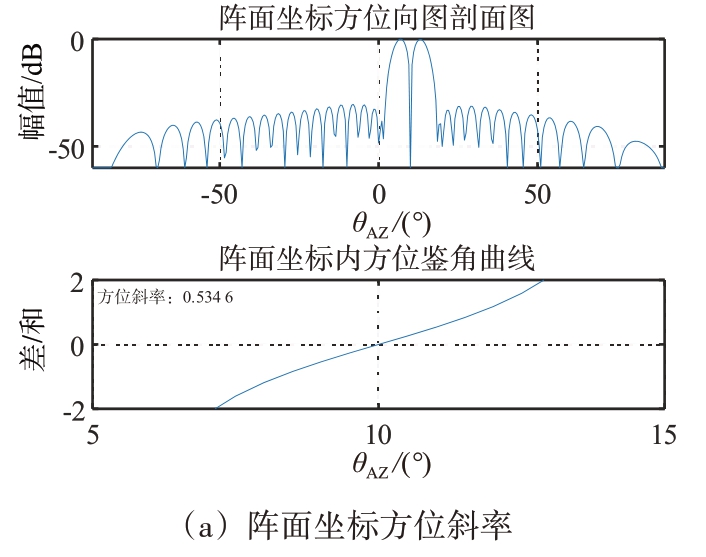
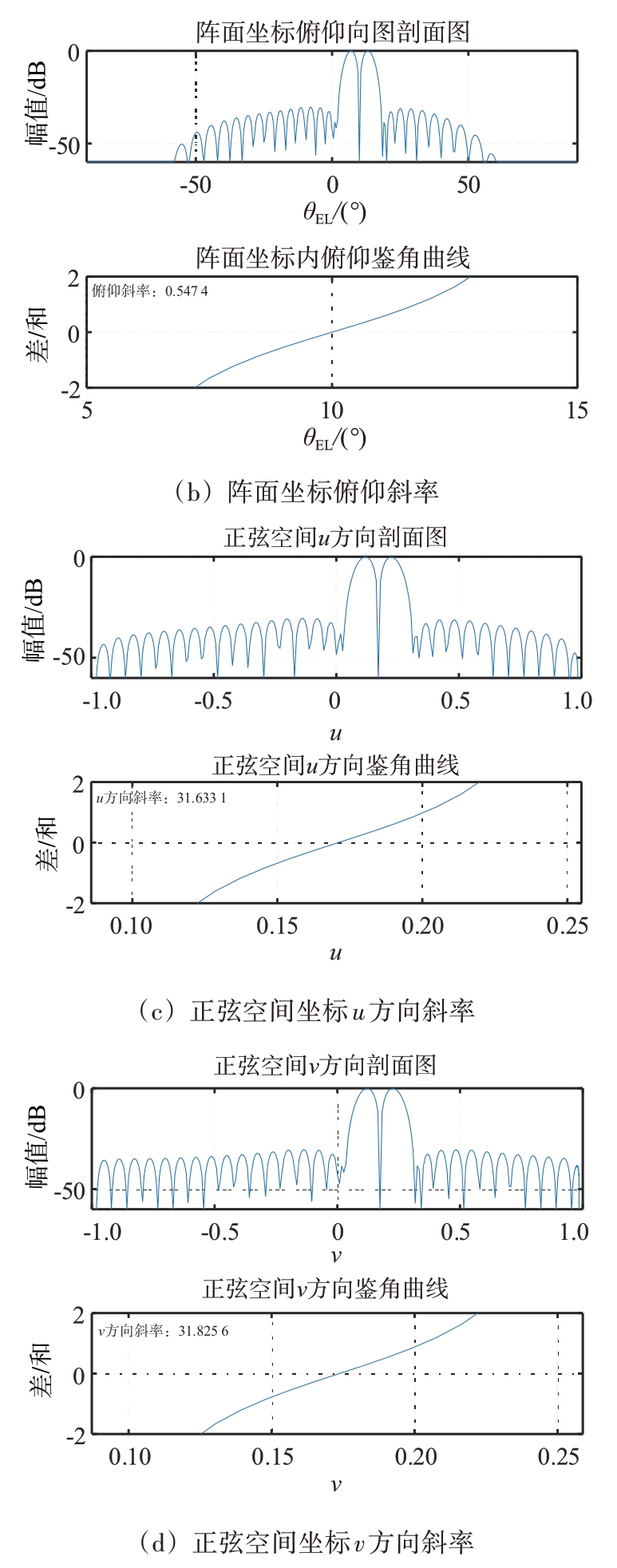
图10 波束指向(10°,10°)鉴角曲线斜率
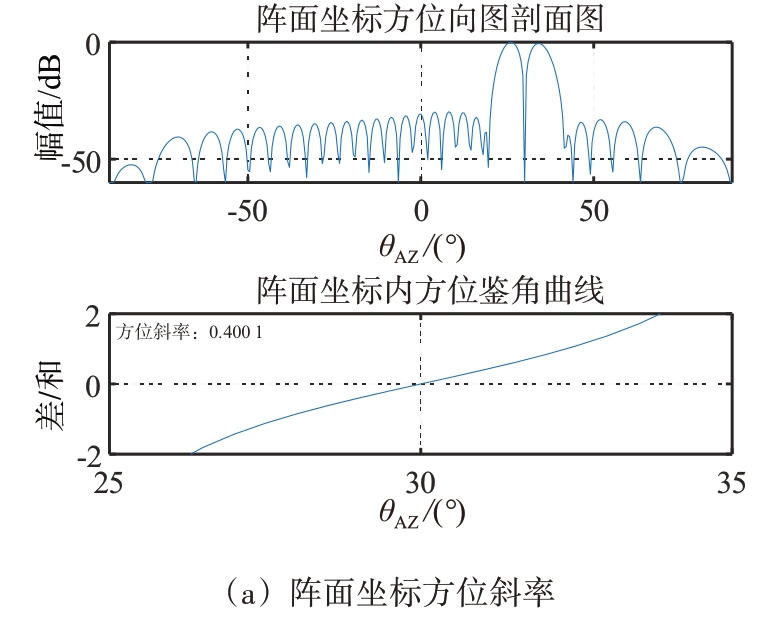
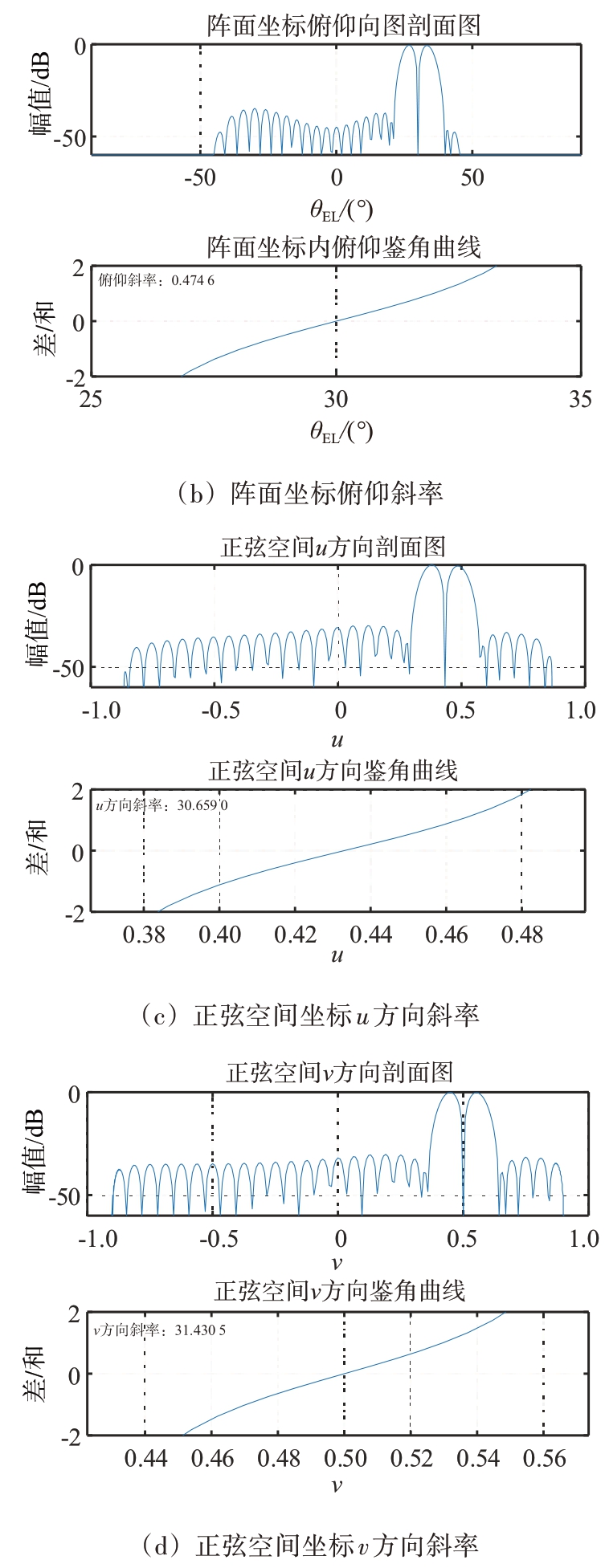
图11 波束指向(30°,30°)鉴角曲线斜率
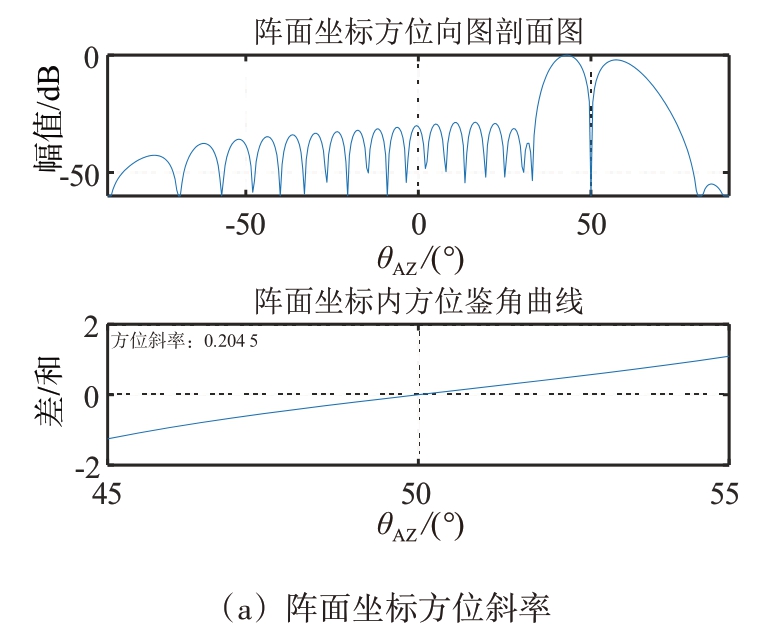
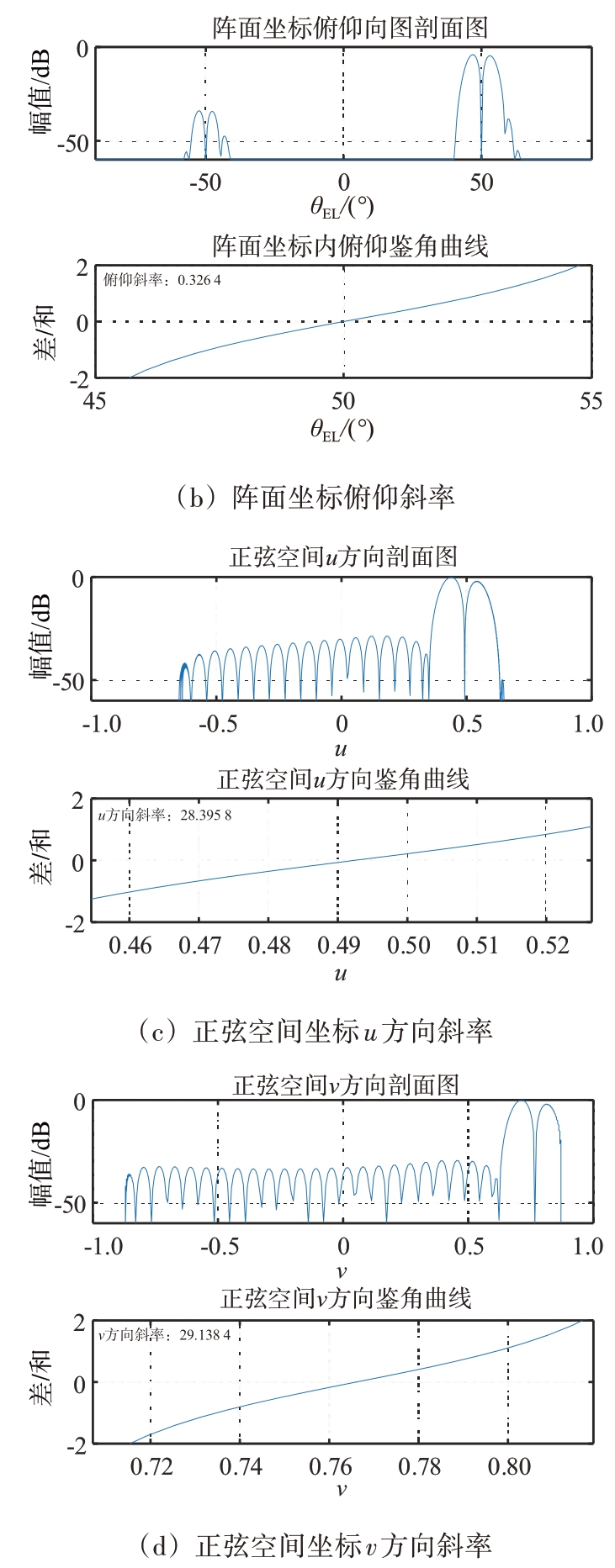
图12 波束指向(50°,50°)鉴角曲线斜率
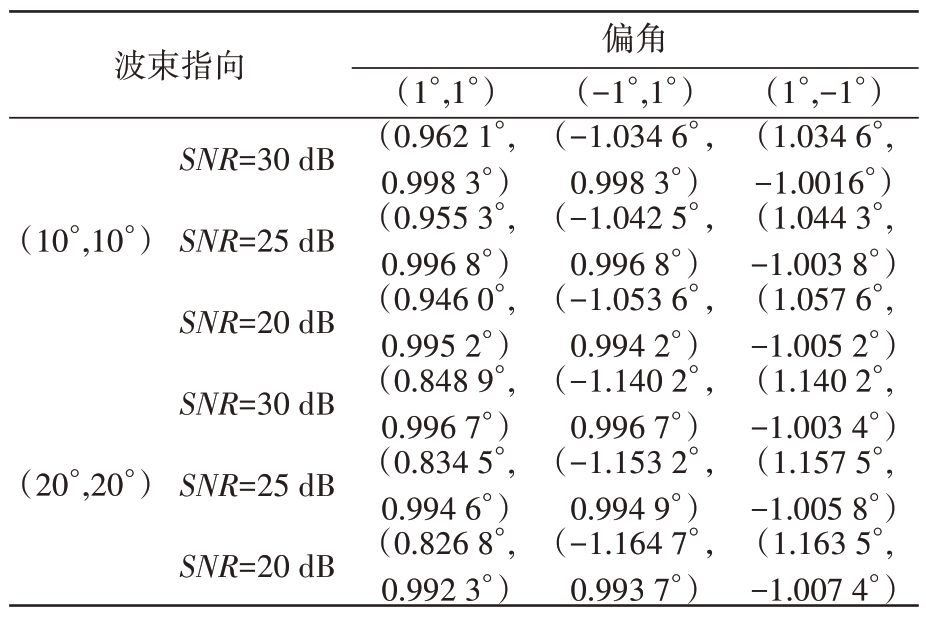
目标相对波束中心不同偏角、不同信噪比的条件下,分别在阵面坐标系和正弦空间坐标系内进行测角,得到目标偏差如表3、表4所示。
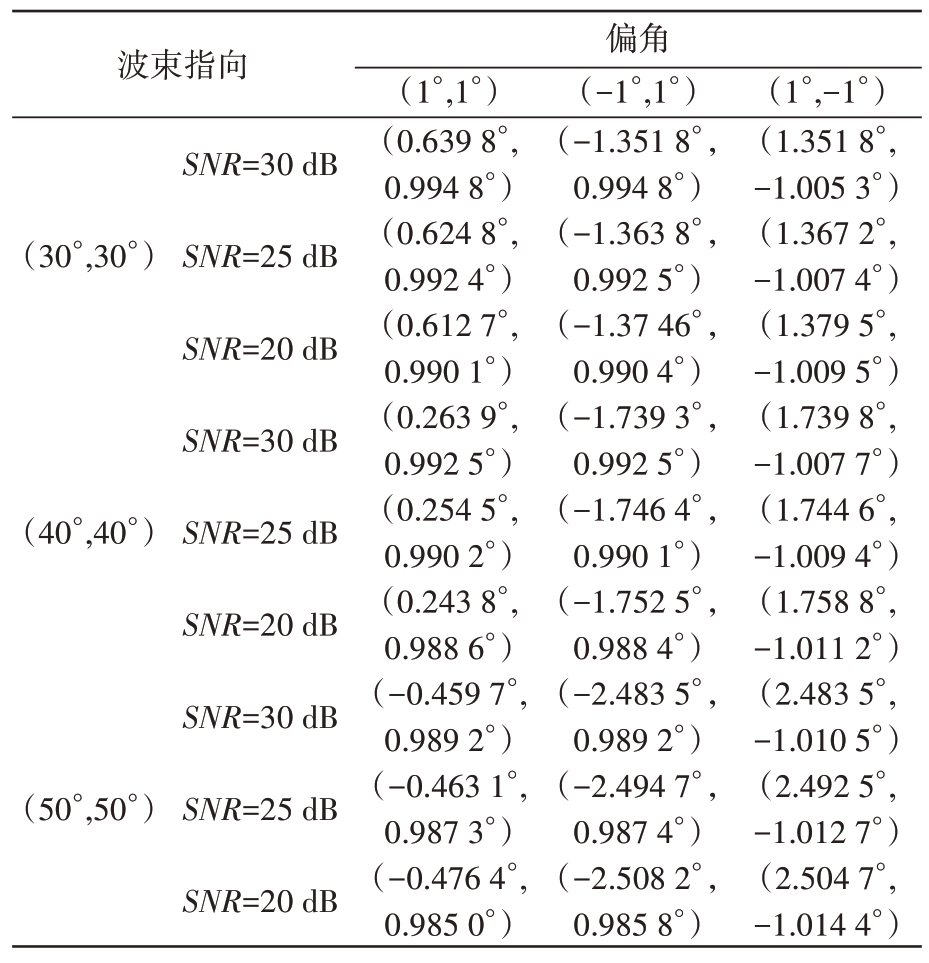
表3 波束指向不同、目标偏角不同阵面坐标系内和差测角结果
(10°,10°)(20°,20°)SNR=30 dB SNR=25 dB SNR=20 dB SNR=30 dB SNR=25 dB SNR=20 dB(0.962 1°,0.998 3°)(0.955 3°,0.996 8°)(0.946 0°,0.995 2°)(0.848 9°,0.996 7°)(0.834 5°,0.994 6°)(0.826 8°,0.992 3°)(-1.034 6°,0.998 3°)(-1.042 5°,0.996 8°)(-1.053 6°,0.994 2°)(-1.140 2°,0.996 7°)(-1.153 2°,0.994 9°)(-1.164 7°,0.993 7°)(1.034 6°,-1.0016°)(1.044 3°,-1.003 8°)(1.057 6°,-1.005 2°)(1.140 2°,-1.003 4°)(1.157 5°,-1.005 8°)(1.163 5°,-1.007 4°)波束指向 偏角(1°,1°) (-1°,1°) (1°,-1°)
续表
(30°,30°)(40°,40°)(50°,50°)SNR=30 dB SNR=25 dB SNR=20 dB SNR=30 dB SNR=25 dB SNR=20 dB SNR=30 dB SNR=25 dB SNR=20 dB(0.639 8°,0.994 8°)(0.624 8°,0.992 4°)(0.612 7°,0.990 1°)(0.263 9°,0.992 5°)(0.254 5°,0.990 2°)(0.243 8°,0.988 6°)(-0.459 7°,0.989 2°)(-0.463 1°,0.987 3°)(-0.476 4°,0.985 0°)(-1.351 8°,0.994 8°)(-1.363 8°,0.992 5°)(-1.37 46°,0.990 4°)(-1.739 3°,0.992 5°)(-1.746 4°,0.990 1°)(-1.752 5°,0.988 4°)(-2.483 5°,0.989 2°)(-2.494 7°,0.987 4°)(-2.508 2°,0.985 8°)(1.351 8°,-1.005 3°)(1.367 2°,-1.007 4°)(1.379 5°,-1.009 5°)(1.739 8°,-1.007 7°)(1.744 6°,-1.009 4°)(1.758 8°,-1.011 2°)(2.483 5°,-1.010 5°)(2.492 5°,-1.012 7°)(2.504 7°,-1.014 4°)波束指向 偏角(1°,1°) (-1°,1°) (1°,-1°)
表4 波束指向不同、目标偏角不同正弦空间坐标系内和差测角结果

波束指向(10°,10°)(20°,20°)(30°,30°)(40°,40°)(50°,50°)SNR=30 dB SNR=25 dB SNR=20 dB SNR=30 dB SNR=25 dB SNR=20 dB SNR=30 dB SNR=25 dB SNR=20 dB SNR=30 dB SNR=25 dB SNR=20 dB SNR=30 dB SNR=25 dB SNR=20 dB偏角(1°,1°)(0.999 8°,0.999 5°)(0.984 5°,0.997 9°)(0.976 8°,0.995 2°)(0.995 1°,0.995 8°)(0.974 6°,0.993 4°)(0.983 8°,0.991 2°)(0.985 5°,0.997 5°)(0.974 5°,0.995 9°)(0.968 3°,0.993 5°)(0.998 9°,1.003 1°)(0.986 8°,1.001 1°)(0.978 8°,0.999 5°)(0.997 4°,0.995 8°)(0.986 5°,0.993 4°)(0.976 6°,0.991 6°)(-1°,1°)(-1.003 6°,0.999 5°)(-1.015 3°,0.997 8°)(-1.027 8°,0.995 4°)(-1.009 9°,0.995 8°)(-1.018 5°,0.993 7°)(-1.027 5°,0.991 6°)(-1.013 3°,0.997 5°)(-1.024 5°,0.995 1°)(-1.037 2°,0.993 5°)(-1.032 4°,1.003 1°)(-1.047 5°,1.001 6°)(-1.055 5°,0.999 4°)(-1.068 9°,0.995 8°)(-1.074 5°,0.993 4°)(-1.088 6°,0.991 3°)(1°,-1°)(1.002 3°,-1.002 0°)(1.014 5°,-1.000 1°)(1.023 5°,-0.998 6°)(1.009 6°,-1.004 1°)(1.012 5°,-1.006 7°)(1.024 4°,-1.008 3°)(1.010 3°,-1.000 6°)(1.024 6°,-1.002 4°)(1.038 2°,-1.004 3°)(1.032 8°,-1.001 5°)(1.044 3°,-1.001 1°)(1.056 6°,-1.005 0°)(1.060 8°,-1.000 8°)(1.073 8°,-1.002 6°)(1.086 4°,-1.004 5°)
表 3为不同波束指向,目标相对波束中心不同偏角、不同信噪比时,在阵面坐标系内进行和差测角,测得目标相对于波束中心偏差值;表 4 为不同波束指向,目标相对波束中心不同偏角、不同信噪比时,采用改进后的相控阵雷达单脉冲和差测角方法,在正弦空间坐标系内进行和差测角,随后根据坐标转换关系,得到目标在阵面坐标内相对于波束中心偏差值。
从表3可以看出,方位误差随波束扫描角增大而急剧增大;波束扫描角增大时,俯仰误差变化相对较平稳,但仍会随波束扫描角增大而缓慢增大。从表4可以看出,波束扫描角增大时,方位俯仰误差均相对较平稳,未随波束扫描角增大而急剧变化。
比较表3和表4可以发现,改进后的相控阵雷达单脉冲和差测角方法对方位向测角精度有明显提高,俯仰测角精度也有一定提高;并且方位俯仰测角精度在波束扫描范围内总体相对平稳,不受扫描角变化而急剧变化。因此,验证了改进后的相控阵雷达单脉冲和差测角方法对提高相控阵雷达测角精度具有良好效果。
另外,由于相控阵雷达波束在正弦空间坐标系内不随扫描角变化的特点,根据表 2 可以看出,正弦空间内的鉴角曲线斜率随波束扫描变化很小。因此,在工程实现中,采用本文的正弦空间和差测角方法时,同一频点无需随扫描角不同而装订多条鉴角曲线,极大地缩减相控阵雷达阵面调试和参数装订工作量,具有很好的工程实用价值。
5 结束语
本文分析了相控阵雷达远离方位、俯仰法线波束对目标跟踪时,在阵面坐标系内和差波束出现展宽、不对称、扭曲等现象,并且该现象会严重影响测角精度,经过详细分析比较发现,在正弦空间坐标系内不会出现该现象,因此,创新性提出了将在阵面坐标系内进行的和差测角改为在正弦空间坐标内完成和差测角,然后根据坐标转换关系,得到阵面坐标系内的测角偏差,与原方法相比,不仅消除方位差波束扭曲带来的影响,而且还提高相控阵雷达单脉冲和差测角精度,具有重要的工程实用价值。
[1] 张光义.相控阵雷达原理[M].北京:国防工业出版社,2006.
[2] 杨顺平,母王强,曾浩.多波束相控阵天线角度测量方法[J].电讯技术,2023,63(4):481-489.
[3] 杜丹,王文政,扈景召.全空域球面相控阵测控系统角跟踪方法概论[J].电讯技术,2021,61(7):800-806.
[4] 催向阳,付学斌,朱永杰,等.两维相控阵UV 域测角分析及应用[J].火控雷达技术,2021,50(4):44-48.
[5] 张孟达,余颖菲.一种改进的U-V 空间测角方法[J].雷达科学与技术,2023,21(4):400-404.
[6] 赵海东,付林,贾然.一种舰船摇摆下基于正弦空间的多波束覆盖范围计算方法[J].雷达与对抗,2023,43(3):40-42.
[7] 员琳红.和差多波束跟踪算法及工程实现[D].西安:西安电子科技大学,2012.
[8] ALVAREZ FOGUERIRAS M, RODRIGUEZ GONZALEZ J A, ARES PENA E. Synthesising Taylor and Bayliss Linear Distributions with Common Aperture Tail [J]. Electronics Letters,2009,45(1):18-19.