0 引 言
机动目标跟踪是雷达数据处理领域中的一项重要且复杂的问题,该问题因其高度的技术性和挑战性而备受相关学者的广泛关注。学者们通过大量的研究和实践,致力于寻找更为高效、准确的机动目标跟踪方法,以应对日益复杂多变的雷达应用场景［1-2］。传统的机动目标跟踪技术分为两类:一类是机动检测跟踪算法,通过调整滤波器参数或结构以应对目标机动性的变化［3-5］；另一类是自适应跟踪算法,不需要进行机动检测,在对目标进行滤波的同时自适应地对滤波增益进行修正［6-9］。经典的自适应跟踪算法,如Singer、“当前”统计（Current Statistical, CS）、Jerk模型等［10-13］,定义加速度扰动是有色噪声,给出了目标运动状态向量迭代更新的离散形式。考虑到在目标跟踪过程中,无法实时在线判断目标在做何种运动,因此在上述经典运动模型的基础上,发展出了多模型（Multiple Model, MM）跟踪方法［14］,并进一步演化为性能更加优异的交互式多模型（Interacting Multiple Model, IMM）技术［15-18］,该技术能够自适应地为目标跟踪匹配提供更加优化的运动模型。
上述研究大都集中在单维运动模型,即三维空间坐标每一维向量的位置分量,仅与同维的速度、加速度或加加速度分量有关,且研究的重点是将加速度或加速度扰动定义为某一类随机噪声,推导获得运动状态向量的线性递推方程或称之为过程方程,进而实现跟踪滤波。这类运动模型可以看作是空间解耦的,或称之为无耦合关系模型。相比耦合运动模型,无耦合模型构造相对简单,难以适应转弯类机动目标运动。协同转弯（Coordinated Turn, CT）模型［19］是最早考虑坐标耦合问题的模型,在解决二维平面转弯问题时,有较好的技术性能表现,但在三维机动目标跟踪中,仅适用于水平机动情形,如盘旋机动。对于作战飞机逃逸等情况下做出的高机动动作,跟踪性能不佳。
针对三维高机动目标跟踪,文献［20］进行了较为深入的研究,给出了常速率协同转弯模型（CSCT）,但该模型对三维高机动目标跟踪的效果改进有限。文献［21］在此基础上结合交互式多模型进行了改进,将三维解耦的（无耦合的）CS模型、CV 模型和CSCT 模型组合在一起,构成三维高机动目标交互式跟踪的模型集（CSCT-IMM）,取得了更好的跟踪性能。
三维耦合运动模型需要确定3个坐标轴（X轴-Y 轴-Z 轴）的位置、速度和加速度分量之间的耦合关系,相比单维运动和二维耦合运动,模型构造难度大幅增加,目前还没有性能优异的模型或模型集提出。无论是CSCT模型,还是CSCT-IMM 模型,虽然有一定改进,但从机理上并没有给出三维状态向量之间耦合关系的准确描述,但这恰恰是有效解决三维高机动目标跟踪问题的关键所在。
基于上述分析,本文提出了一种用二维耦合CT 模型重构三维高机动运动模型的技术思路,即利用3 个不同平面（X-Y 平面,Y-Z 平面,X-Z 平面）盘旋机动模型,来替代三维高机动运动模型,同时增加不同过程噪声系数的CV 模型集来覆盖解耦运动情况。将这些模型汇聚到一个集合中,利用交互式多模型架构来自适应优化选择,以满足对三维高机动目标跟踪的技术要求。该方法虽然没有完全实现三维向量之间耦合关系的精确描述,但相比一维解耦模型具有一定的改进和提升。
1 无耦合的三维空间机动模型
1.1 三维匀速、匀加速模型
匀速（CV）模型是一种基础且简单的运动状态描述,它假设目标以恒定的速度移动,其运动状态的微小变化或机动性被建模为零均值、高斯白噪声的随机扰动,并通过过程噪声协方差矩阵量化这种扰动的大小。此模型作为众多复杂运动模型的基础,体现了简洁而有效的运动状态预测机制。
经典一维CV模型的目标状态方程为
式中,vk 为过程噪声向量,且对应的状态转移矩阵和过程噪声分布矩阵分别为
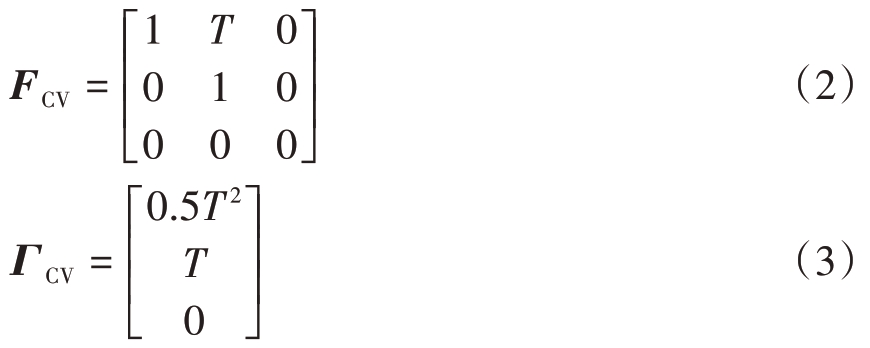
匀加速（Constant Acceleration, CA）模型是对匀速模型的一种扩展,它引入了加速度项来描述目标的运动状态。通过这一改进,CA 模型能够更全面地反映目标的运动状态,并提供更为精确的目标位置预测,这使得CA 模型能够很好地适用于跟踪匀加速运动的目标。然而,在实际应用中,目标往往不会长时间保持匀速或匀加速这种理想化的运动状态。由于外部干扰、控制指令变化或目标自身的机动性,目标的运动状态可能会发生变化,导致所建立的目标模型参数具有不确定性。因此,虽然匀速和匀加速模型具有简单方便、计算量小的优点,但由于它们无法准确描述目标在机动情况下的运动,其应用范围受到了很大的限制。在需要高精度跟踪或目标机动性较强的场景中,通常需要采用更为复杂和灵活的模型来描述目标的运动状态。
经典的一维CA 模型对应的状态转移矩阵和过程噪声分布矩阵分别为
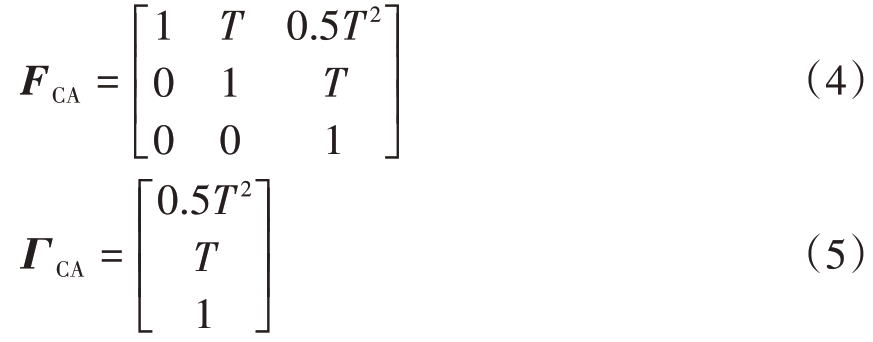
匀速模型和匀加速模型没有考虑坐标之间的耦合关系,将经典的CV 和CA 模型扩展到三维空间,实现三维目标跟踪模型的重构,可以得到CV模型对应的三维状态转移矩阵和过程噪声分布矩阵分别为
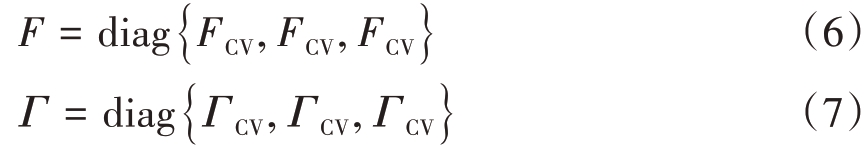
式中,diag 用于构造一个对角矩阵,不在对角线上元素全为0。CA 模型对应的三维状态转移矩阵和过程噪声分布矩阵分别为
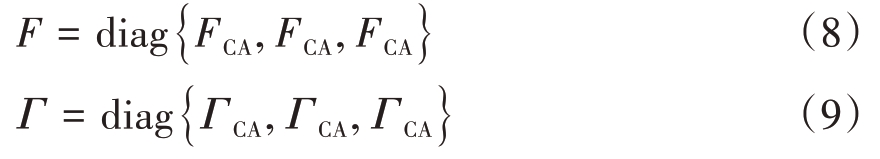
1.2 三维Singer模型
在Singer模型中,目标加速度的变化遵循一种特定的模式,即指数衰减的自相关性。这种模型认为,目标在机动过程中,其加速度不会保持恒定,而是会随着时间的推移而逐渐减小,直至趋于稳定或再次发生显著变化。这种建模方法不仅有助于我们理解目标的机动行为,也为设计高效的机动目标跟踪算法提供了重要的理论基础。目标加速度相关函数r(τ)表示为
式中
为目标加速度的方差；α 为机动频率,即机动时间常数的倒数,α =1
τ。α的确切值只有通过实时测量才能确定。一般经验取值为:慢速转弯机动α =1
60,逃避机动α =1
20,大气扰动α = 1。
利用加速度相关函数r(τ),加速度a(t)可以通Wiener-Kolmogorov 白化过程表示为输入为白噪声的一阶时间相关模型,即
式中:ȧ(t)为加速度a(t)的导数；ω(t)为均值为0、方差为
的高斯白噪声。
其离散状态方程为Xk + 1 = FSingerXk + Vk,其中
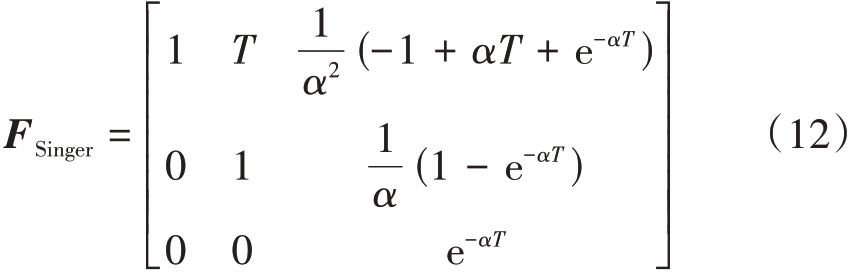
将经典的Singer 一维模型重构成三维机动目标跟踪模型,可以得到其对应的三维状态转移矩阵
1.3 三维“当前”统计模型
“当前”统计模型可以描述为非零均值的时间相关模型,适用于描述机动目标的动态行为。该模型假设机动加速度在当前时刻的分布服从修正的瑞利分布,并且这一分布的均值对应于当前时刻的加速度预测值。此外,该模型还考虑到随机加速度在时间轴上的一阶时间相关性,即加速度的变化不仅与当前时刻有关,还受到前一时刻加速度的影响。这种设计使得当前统计模型能够更准确地反映机动目标的动态行为,为目标跟踪和控制系统提供了更为精确的模型基础。
式中
为机动加速度“当前”均值,在每一采样周期内为常数。若将a1(t) = aˉ(t) + a(t)代入上面两式,可得
其相应的离散形式为
式中:
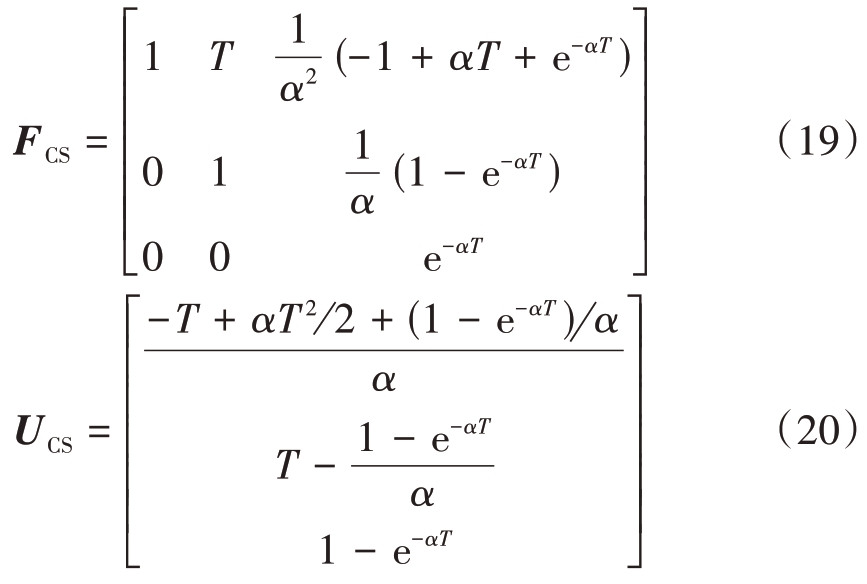
拓展到三维机动目标跟踪形式
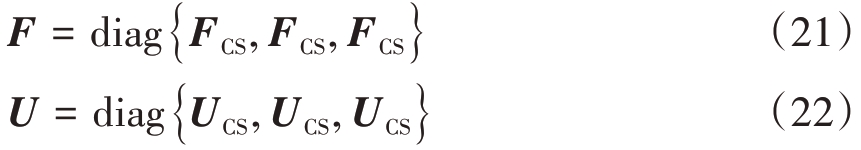
1.4 三维Jerk模型
20 世纪末,Kishore 等人深入分析了目标运动模型,并指出当时普遍使用的模型在描述目标真实运动状态时存在局限性,其根本原因在于对目标状态向量导数的阶数选取不足。为了更精确地捕捉目标的机动性,他们创新性地引入了运动目标加速度的变化率作为新的状态变量,进而提出了Jerk 模型。该模型利用一个四维状态向量,涵盖了位置、速度、加速度以及加速度变化率,全面刻画了目标的运动状态。对于加速度变化率j(t),Kishore 等人借鉴了Singer 模型中对加速度处理的成功经验,以类似的方式进行了合理的假设和建模,从而使得Jerk 模型能够更有效地模拟和预测目标的实际运动行为。
设j(t) = x…(t),则有
其对应的离散时间动态方程为
式中:
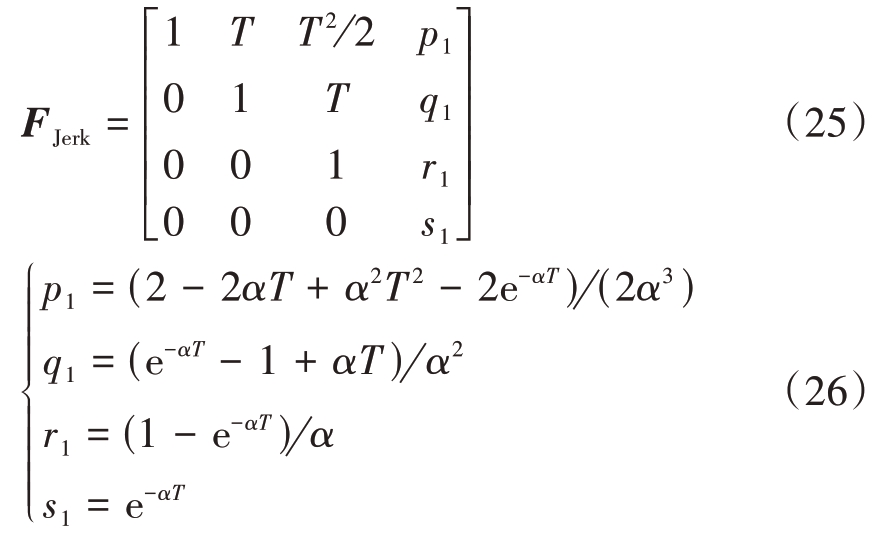
则拓展到三维机动目标跟踪,其三维状态转移矩阵为
2 常速率协同转弯模型（CSCT）
匀速和匀加速等传统的解耦模型,在构建状态转移矩阵时,并未将坐标间的耦合效应纳入考量。即便在物体发生转向的情况下,这些模型也仅仅是将各个坐标维度的动态视为相互独立的变量进行处理。然而,协同转弯模型剖析了二维坐标在物体运动过程中的内在关联性,考虑了转弯过程中各坐标轴之间的相互影响和耦合关系从而更准确地描绘了物体的实际运动轨迹。
文献［20］提出了一种三维空间下的常速率协同转弯模型,由基本运动学关系可知,常速率（即加速度为0）运动对应于a·v = 0（即a ⊥v）,并且可以等效地用a = Ω × v表示。
假设目标在某一非特定的平面内,以恒定的速率进行圆周运动,其中速度的大小保持不变,并且与加速度方向保持垂直。
对于在任意平面内的机动目标,其加速度为
式中,Ω为角速度向量,v为速度向量。对式（28）求导可得
由于假设目标的运动轨迹是在同一个平面内,则Ω垂直于a与v决定的平面,即Ω ⊥v,因此有
式中,ω定义为
若加速度受到白噪声干扰,即
w 为白噪声,当状态向量x =(x,ẋ,ẍ,y,ẏ,ÿ,z,ż,z̈)T时,对应于三维连续匀速转弯模型为
式中:
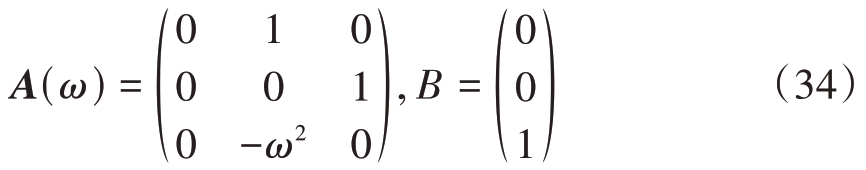
对应的离散形式为
式中:
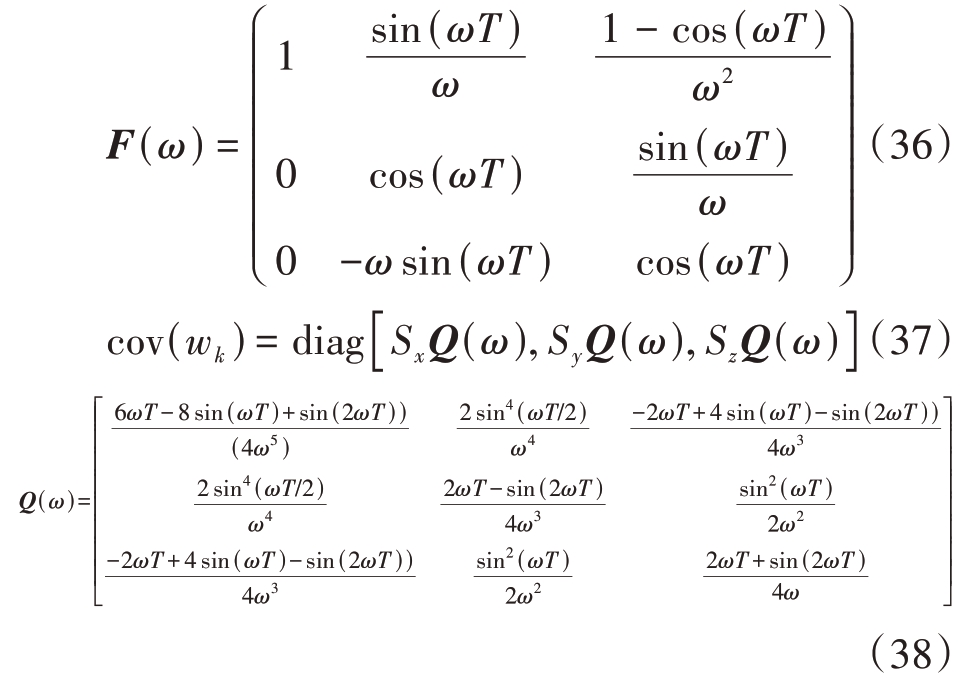
式中:T为采样周期；w(k)为白噪声,w(k)具有功率谱密度矩阵diag[ Sx, Sy, Sz ]。
3 交互式常速率转弯模型（CSCT-IMM）
文献［21］在CSCT 模型基础上,提出了一种基于CV模型、CS模型、带约束的CSCT模型的交互式多模型算法（CSCT-IMM）,并对包括CV 模型、CA模型、Singer 模型、CS 模型、CSCT 模型在内的不同模型组合的IMM 方法进行了Monte-Carlo 仿真,结果表明,其算法对三维高速机动目标跟踪是有效的。CSCT-IMM模型对应的流程框架图如图1所示。
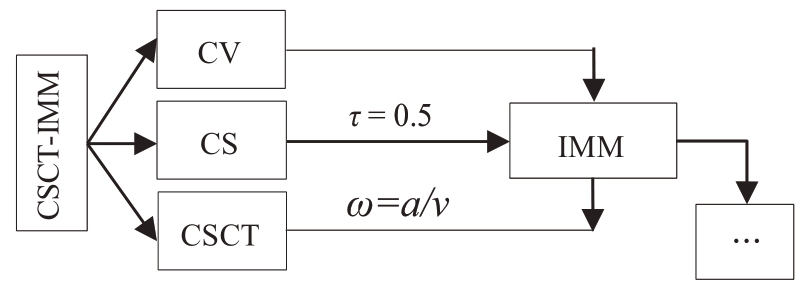
图1 新模型集框架图
根据式（35）看出,CSCT 模型以及在其基础上提出的CSCT-IMM 模型本质上还是解耦的,并没有实现真正意义上的耦合跟踪。并且在实际的机动目标跟踪中,在跟踪精确度较低的条件下,CSCTIMM 模型对ω 的估计精度不高,难以满足实际工程要求。为此本文提出了一种用二维耦合模型、CT模型集重构三维耦合模型的基础思路。同时为了满足解耦运动跟踪需要,增加了具有不同过程噪声系数的CV模型集。
4 基于二维CT模型重构技术的交互式多模型（CVCT-IMM）
4.1 不同转弯率的CT模型集
将CT 模型按照以下3 种方式拓展到三维机动目标跟踪:1）X-Y 平面CT 模型,Z 坐标轴CV 模型；2）Y-Z 平面CT 模型,X 坐标轴CV 模型；3）X-Z 平面CT 模型,Y 坐标轴CV 模型。对应的状态转移矩阵分别为如下公式所示。
X-Y 平面CT 模型,Z 坐标轴CV 模型 的 状态转移矩阵为
式中:
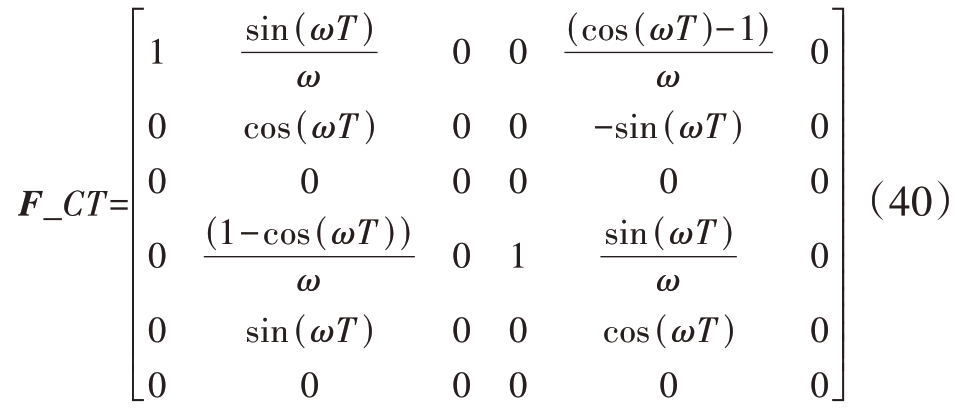
F_CV同一维CV模型的状态转移矩阵。
同理,Y-Z平面CT模型,X坐标轴CV模型的状态转移矩阵为
X-Z 平 面CT 模型,Y 坐标轴CV 模型 的 状态转移矩阵为
三类模型的过程噪声分布矩阵为
传统的CT 模型具有固定的转弯率ω,但对于三维空间中的高机动目标来说,固定的转弯率不能满足其对于不同跟踪精度和跟踪延时的要求。如图2所示,这是某三维机动目标运动轨迹的转弯率变换曲线,固定的转弯率不能满足高精度、小延时的变化。
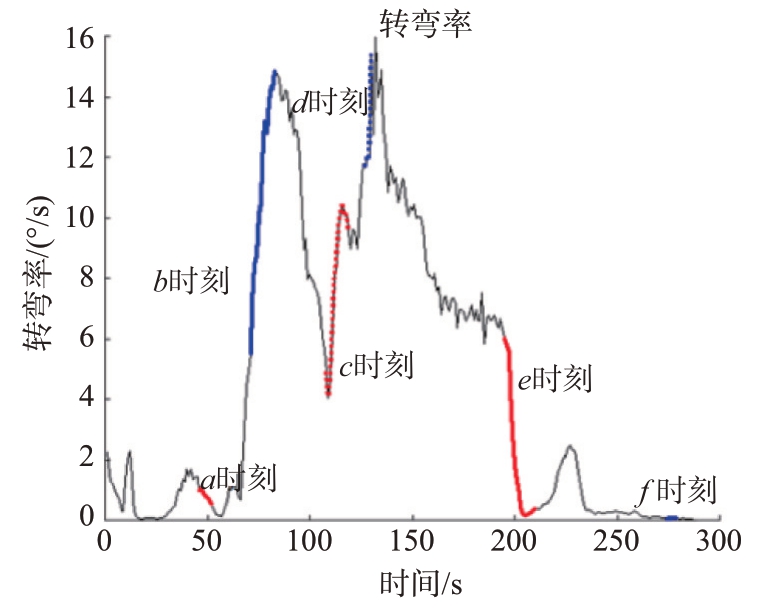
图2 某三维机动目标运动轨迹的转弯率变换曲线
为此可以通过设定几个典型值来对未知的转弯率进行替代,通常选取±1°/s,±5°/s,±10°/s,±20°/s,其中正号代表逆时针旋转,负号代表顺时针旋转。如此一来,给3 种不同的CT 模型赋予8 种不同的转弯率,一共有24种不同的CT 模型组合进行交互式多模型算法,通过交互式竞争来适配不同的转弯率。
4.2 不同过程噪声系数的CV模型集
用传统的具有固定过程噪声的CV 算法跟踪三维直线运动过程中,会出现误差和扰动。为了改善这一情况,借鉴可调白噪声机动目标跟踪的思想［22］,在传统CV 模型的基础上,在过程噪声协方差前面添加一个可调节的系数K,以此来控制过程噪声的大小。
当过程噪声较大时,表示加速度的扰动比较大,当过程噪声较小时,表示运动比较平稳。每一个过程噪声系数对应一个CV 模型,通过交互式多模型框架,比较各模型似然函数的大小来进行不同过程噪声系数之间的竞争,来择优控制。
对于标准的CV 模型,根据式（7）可以得到过程噪声协方差QCV = Γq(k)Γ′,其中q(k) =diag(
,σx, σy, σz 分别是x、y、z 方向的加速度过程扰动噪声。
为了适应不同的扰动程度,对于过程噪声系数可调节的CV 模型,其过程噪声矩阵为Q = KQCV。根据经验,K可以取值为1,5,10。
4.3 模型集框架图
综上所述,这一新的交互式多模型算法主要由CV 模型和CT模型两类构成,简称为CVCT-IMM模型,如图3所示。CT模型集包括3个方向的完全机动,ω =±1°/s,±5°/s,±10°/s,±20°/s,每个方向共有8 个转弯率。CV 模型集共有3 个调节系数,即3 个模型（K=1,5,10）。那么这一新的交互式多模型算法共计27 个模型。跟踪过程中,通过交互式多模型优化框架进行调节。
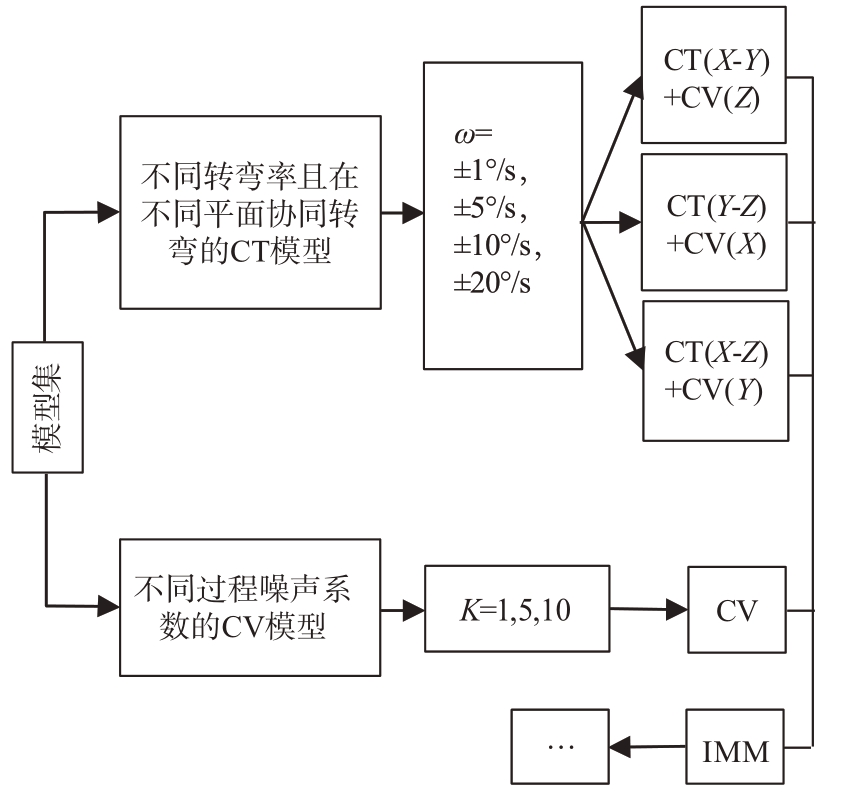
图3 新模型集框架图
5 仿真验证
5.1 仿真轨迹生成
为验证三维机动目标跟踪算法性能,构造如下目标仿真运动轨迹:1）目标从A点（1 741 m,1 283 m,-567 m）出发,0～70 s期间做匀加速直线运动直到B点,加速度为（13 m/s2,-11 m/s2,14 m/s2）；2）70～350 s期间在B点到C点处做逆时针协同转弯运动,转弯率ω = 20°/s；3）350～600 s 期间在C 点到D 点处仍做匀加速直线运动,加速度为（13 m/s2,-11 m/s2,14 m/s2）；4）600～900 s 期间在D 点到E 点处做逆时针协同转弯运动,转弯率ω = 10°/s；5）900～1 000 s期间在E 点到F 点处做匀速直线运动。由此生成了一个如图4所示的目标运动轨迹。
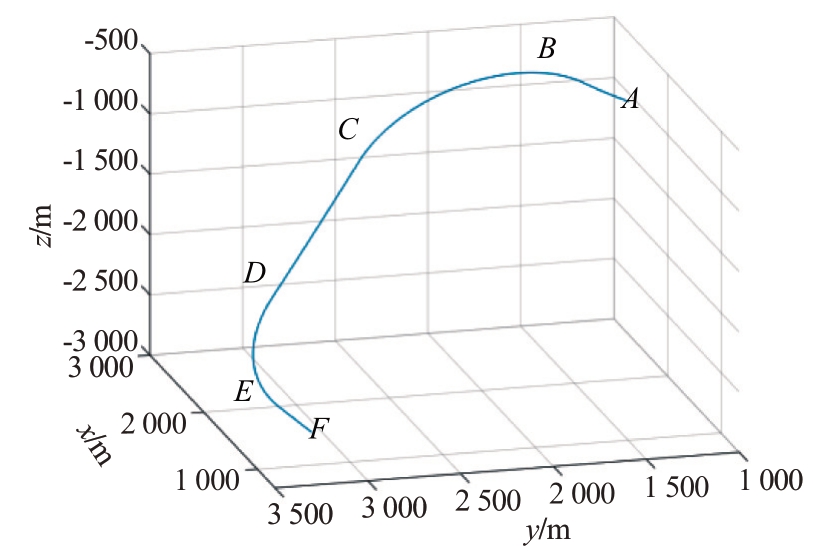
图4 目标飞行轨迹
需要特别说明的是,三维的转弯运动不是盘旋机动,即转弯时法向加速度方向不会与3个平面（X-Y 平面,Y-Z 平面和X-Z 平面）中的任意一个平面存在平行关系。
5.2 无耦合模型与常速率协同转弯模型（CSCT）对比
为了验证无耦合模型和CSCT 模型的性能,将传统的无耦合模型——CV、CA 模型与CSCT 模型进行对比跟踪实验,使二者均跟踪图4所示的目标飞行轨迹,均方根误差（Root Mean Square Error,RMSE）跟踪对比结果如图5所示。
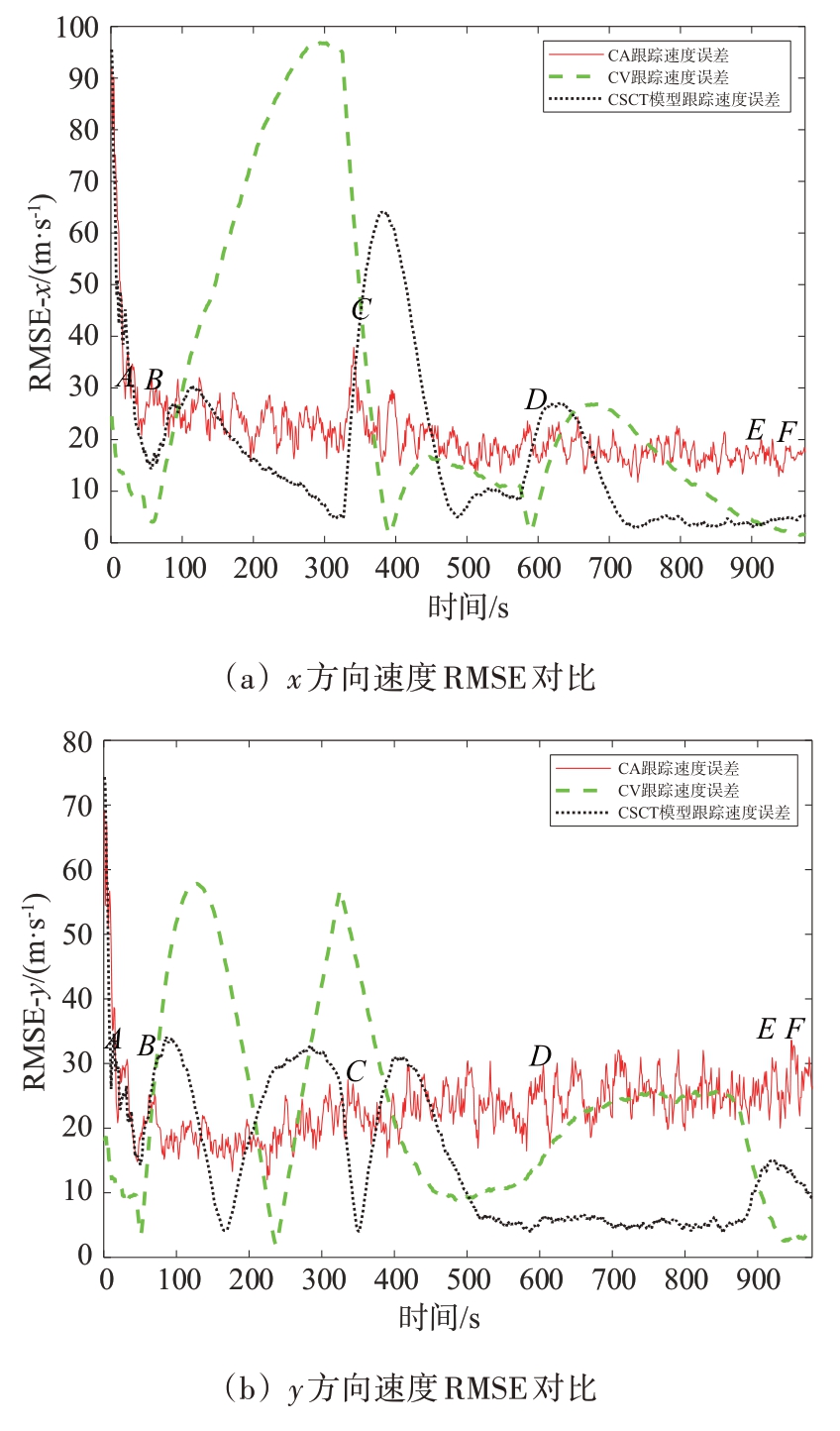
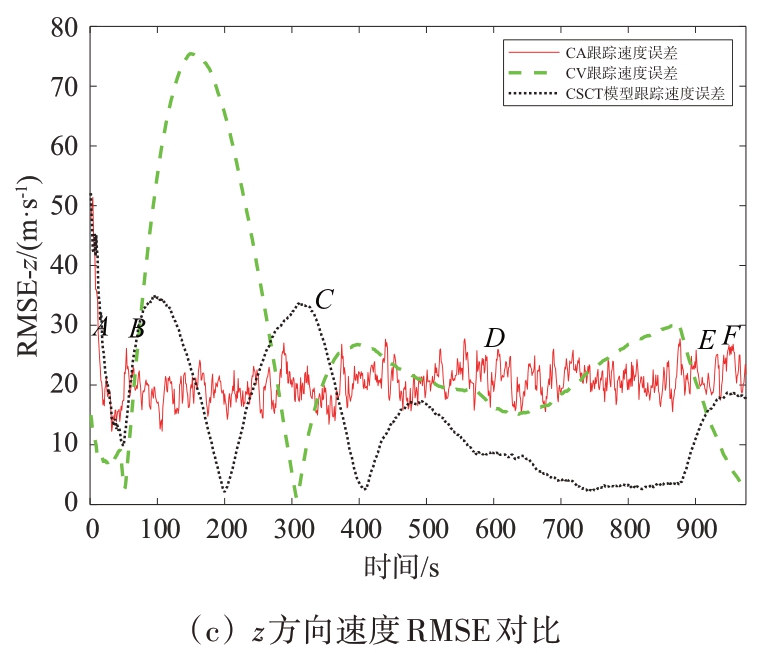
图5 传统CA、CV模型与CSCT模型RMSE跟踪误差对比
通过图5 可以看出,在匀加速运动AB 段和匀速运动EF段,CV模型跟踪效果最好,CSCT模型次之,CA 模型跟踪效果最差。在匀加速运动CD 段,CV 模型和CA 模型的总体跟踪效果要优于CSCT模型,且三者的误差波动都较大。而在协同转弯BC段,CSCT模型的总体跟踪效果要优于CA模型,且明显优于CV 模型。在协同转弯DE 段,CSCT 模型的跟踪精度提高,其跟踪效果明显优于CV 和CA模型。
由此可以看出在目标机动运动部分,CSCT 模型跟踪效果明显优于其他两种传统模型,但在直线运动部分,其跟踪效果不佳。从总体来看,CSCT模型跟踪后的速度及其误差波动仍然很明显,该模型有待改进。
5.3 常速率协同转弯模型（CSCT）与交互式常速率转弯模型（CSCT-IMM）对比
将常速率协同转弯模型（CSCT）与交互式常速率转弯模型（CSCT-IMM）进行对比实验。使二者均跟踪图4 所示的三维空间机动目标,得到的RMSE跟踪误差对比结果如图6所示。
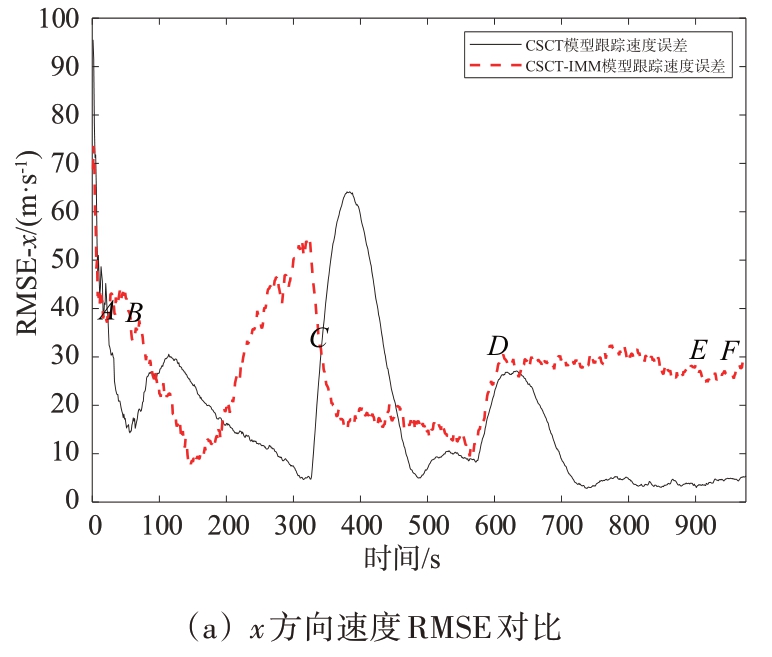
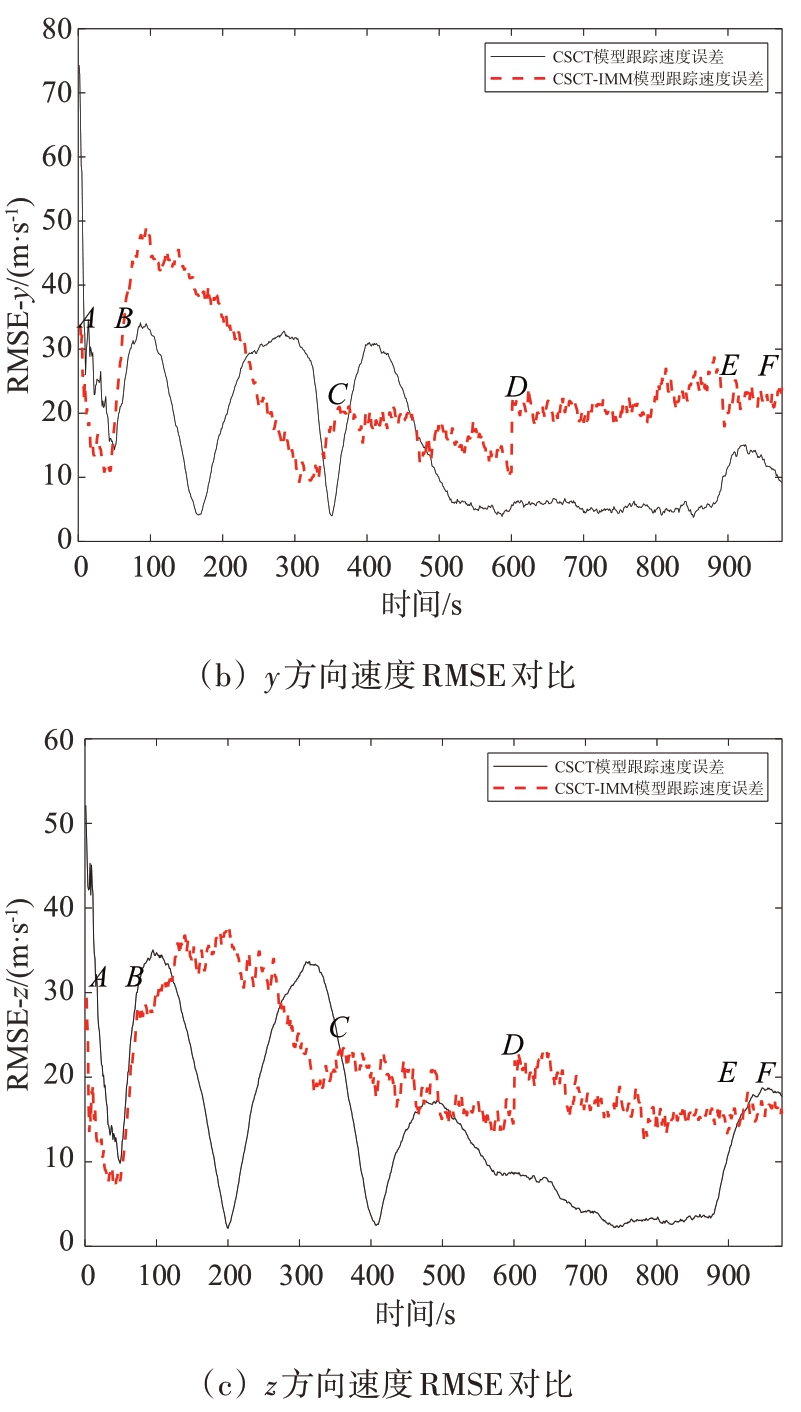
图6 CSCT模型与CSCT-IMM模型RMSE跟踪误差对比
从图6可以看出,在匀加速直线运动AB 段、CD 段和匀速直线运动EF 段,CSCT 模型和CSCTIMM 模型的跟踪效果均不稳定,二者各有所长,有时CSCT-IMM 模型表现更好,有时CSCT 模型更为出色。在协同转弯BC 段,二者跟踪结果波动很大,时好时坏。而在协同转弯DE 段,CSCT 模型的跟踪效果优于CSCT-IMM 模型。总体来看,CSCT模型和CSCT-IMM 模型的跟踪效果均不稳定,这两种模型跟踪后的速度误差和延时有一定的改善和提高,仍需改进。
5.4 交互式常速率转弯模型（CSCT-IMM）、自适应单模型跟踪算法与基于二维CT模型重构技术的交互式多模型（CVCT-IMM）对比
使CSCT-IMM 模型与本文提出的CVCT-IMM模型同时跟踪图4所示的三维目标飞行轨迹,比较二者的跟踪效果。
在本文提出的CVCT-IMM 模型中,CV 模型集的不同过程噪声系数K的取值为1,5和10。3种CT模型集中,使ω的取值可以从±1°/s,±5°/s,±10°/s,±20°/s 这8 组数据中进行选择。将多种模型进行组合,并通过Monte-Carlo 仿真比较得到最终的结果。本文算法与CSCT-IMM 模型算法的RMSE 跟踪误差对比结果如图7所示。
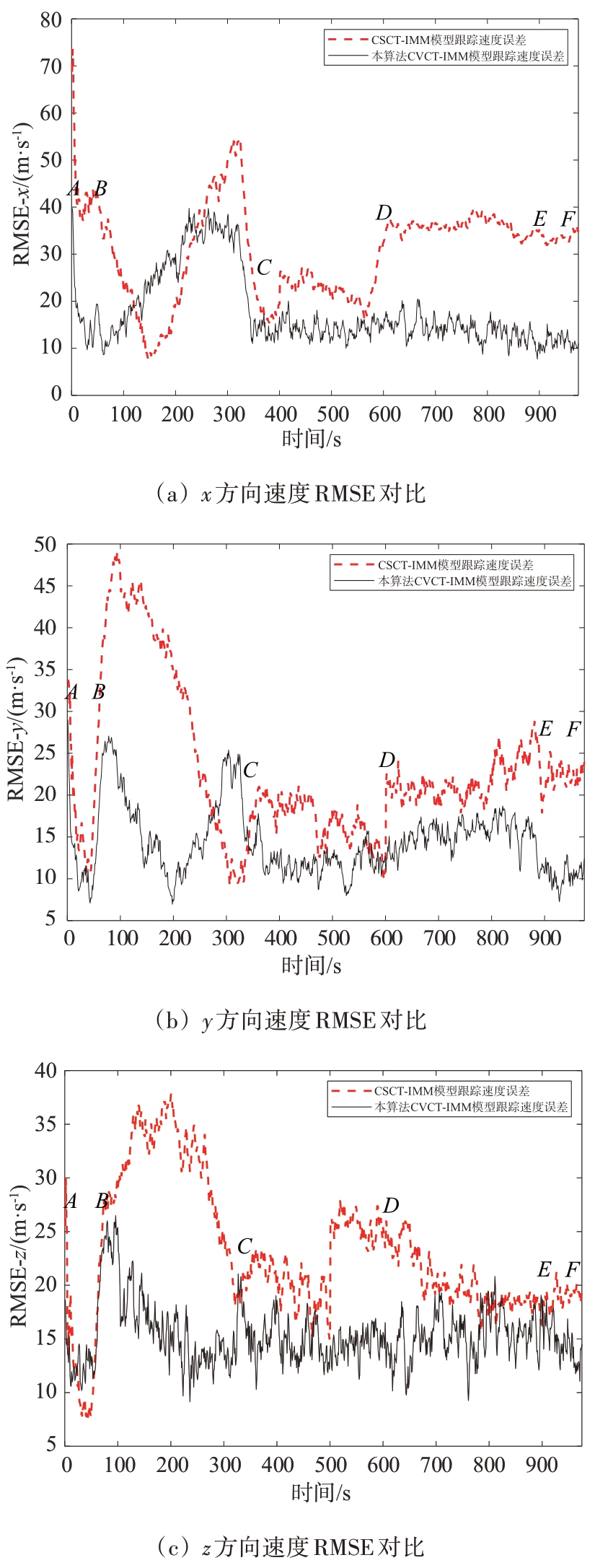
图7 CSCT-IMM模型与CVCT-IMM模型RMSE跟踪误差对比
从图7中本文算法与CSCT-IMM 模型算法的跟踪结果对比可以看出,在匀加速直线运动AB、CD 段和匀速直线运动EF 段,本文提出的CVCTIMM 模型跟踪更加精确,总体误差更小。在协同转弯BC 段,x 方向上本文提出的CVCT-IMM 模型在两端的跟踪效果较好,y 方向上CVCT-IMM 模型在前半部分跟踪精度较高,z 方向上CVCT-IMM 模型的跟踪误差明显更小。在协同转弯DE 段,CVCT-IMM 模型的跟踪效果明显优于CSCT-IMM模型,在目标机动运动跟踪方面有较好的效果。综合而言,本文提出的CVCT-IMM 模型算法的跟踪精度更高,跟踪效果更优。
为进一步验证本文提出的CVCT-IMM 模型算法的跟踪效果,使3种自适应单模型跟踪算法——CS 模型算法、Jerk 模型算法和Singer 模型算法,与CVCT-IMM 模型同时跟踪图4 所示的三维目标飞行轨迹,比较四者之间的跟踪效果,得到的RMSE跟踪误差对比结果如图8所示。
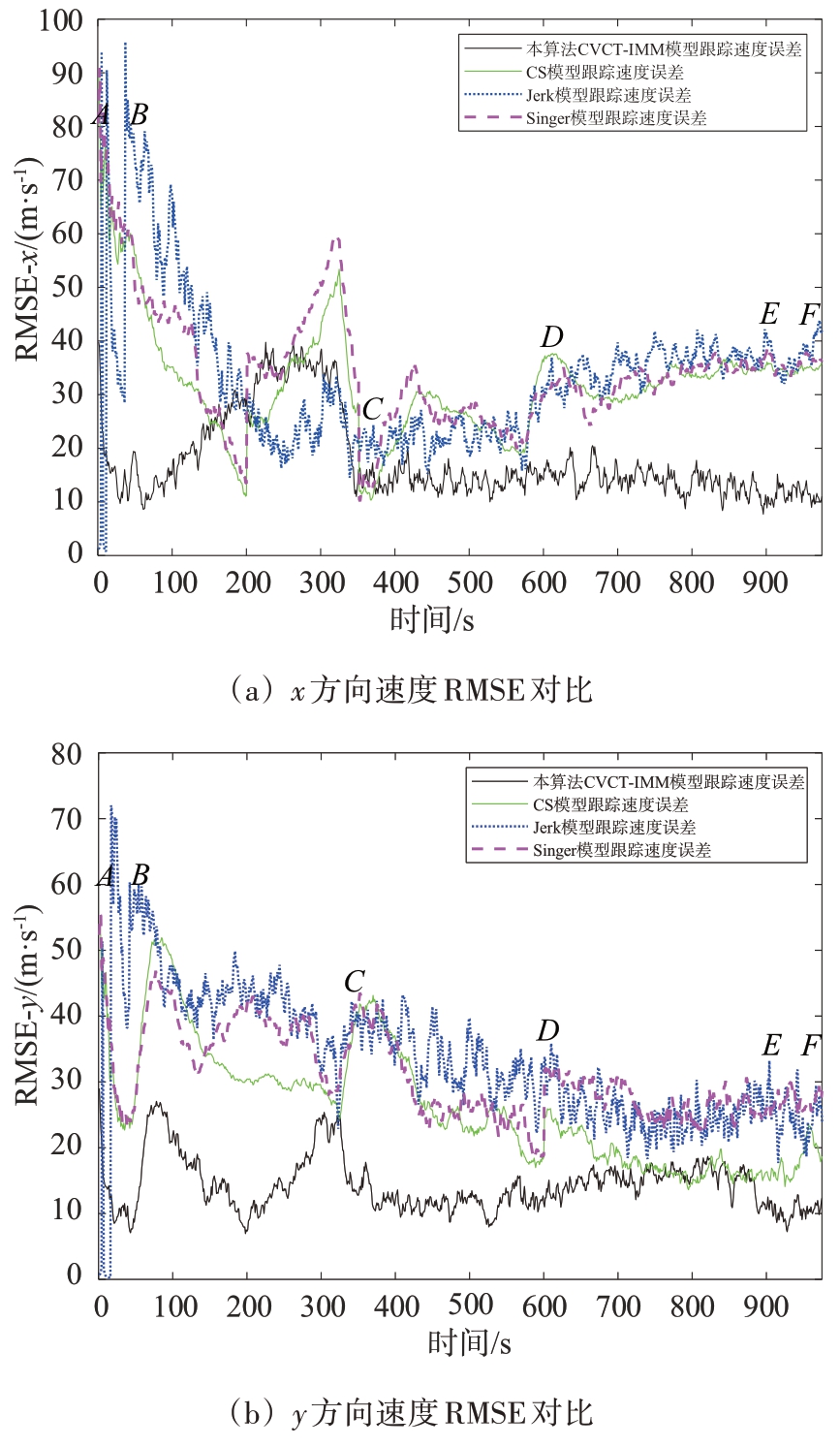
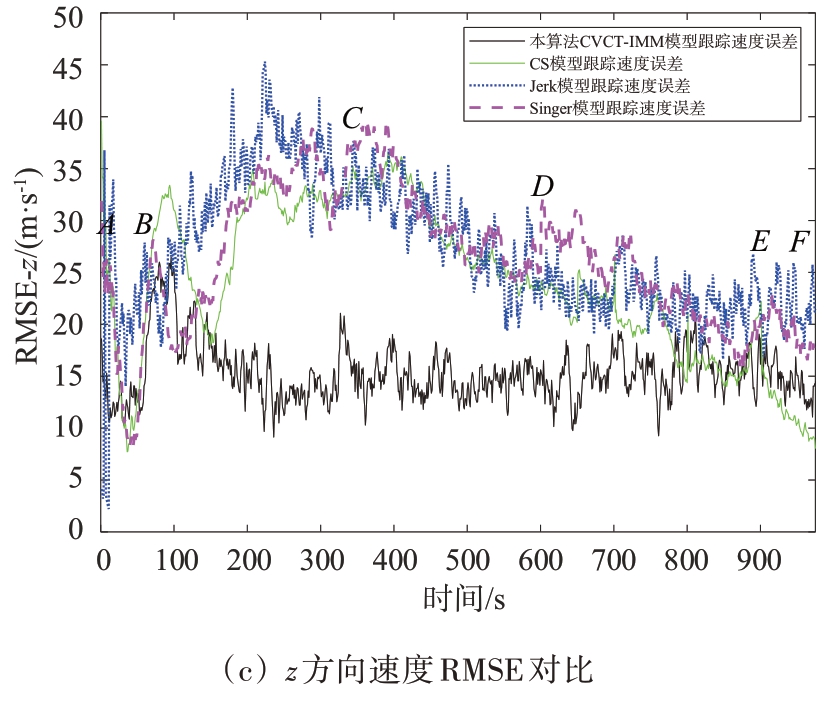
图8 自适应单模型跟踪算法与CVCT-IMM模型RMSE跟踪误差对比
从图8的结果对比中可以看出,在匀加速直线运动AB、CD 段和匀速直线运动EF 段,除z 方向上CS 模型算法在匀速直线运动的跟踪误差较小,在其余方向和直线运动上,CVCT-IMM 模型的跟踪精度明显高于3 种自适应单模型跟踪算法。在协同转弯BC 段,x 方向上CVCT-IMM 模型在两端的跟踪效果较好,3 种自适应单模型跟踪算法在中部的跟踪效果较好,其余方向上CVCT-IMM 模型的跟踪误差明显较小。在协同转弯DE 段,CVCT-IMM模型的跟踪效果明显优于3 种自适应单模型跟踪算法。
总体来看,对于三维机动目标跟踪,本文提出的CVCT-IMM 模型跟踪更加精确,总体误差更小。因此,本文提出的CVCT-IMM 模型具有更高的跟踪精度和更好的跟踪效果,对于三维大机动目标跟踪有重要的意义。
为进一步分析模型竞争对跟踪性能和跟踪结果的影响,现构造一个运动模型个数较少的仿真环境。
假定目标在X-Y平面运动,运动目标在0～100 s做匀速直线运动,100～350 s 做转弯率ω = 20°/s 的逆时针协同转弯运动,350～600 s做匀速直线运动,600～900 s 做转弯率ω = 10°/s 的逆时针协同转弯运动,900～1 000 s 做匀速直线运动。生成的目标运动轨迹如图9所示。
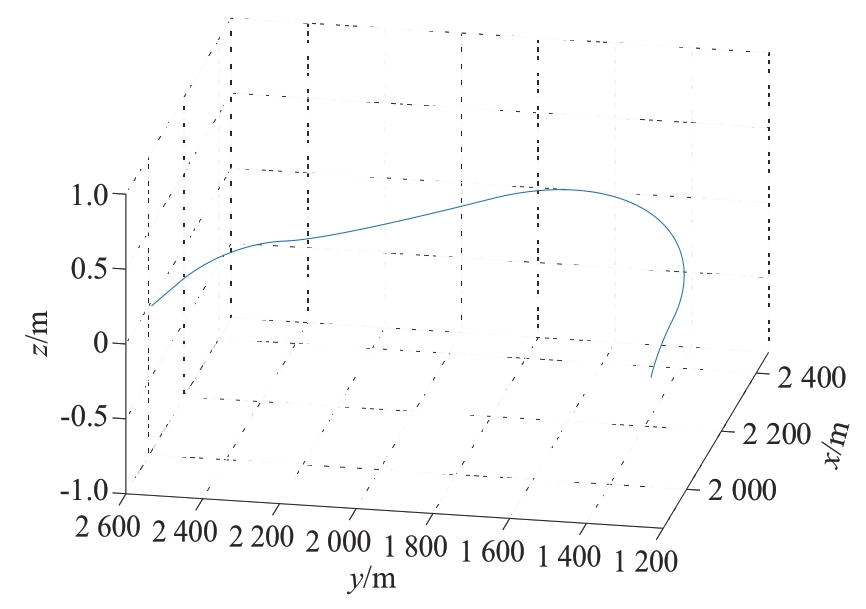
图9 目标运动轨迹
采用两种不同的模型集对图9 所示的目标运动轨迹进行交互式跟踪。一是本文提出的由27个运动模型组成的CVCT-IMM 模型算法；二是由图9仿真轨迹使用的运动模型组成的IMM 算法,简称V5-IMM 算法,其模型集包括K=1 的CV 模型、K=5的CV模型、K=10的CV模型、转弯率为10°
s的X-Y平面CT 模型、转弯率为20°
s 的X-Y 平面CT 模型,V5-IMM 算法共由5 个运动模型组成。V5-IMM 算法模型数较少,模型竞争对其跟踪精度的影响较小。两种模型算法对比跟踪得到的RMSE 跟踪误差对比结果如图10所示。
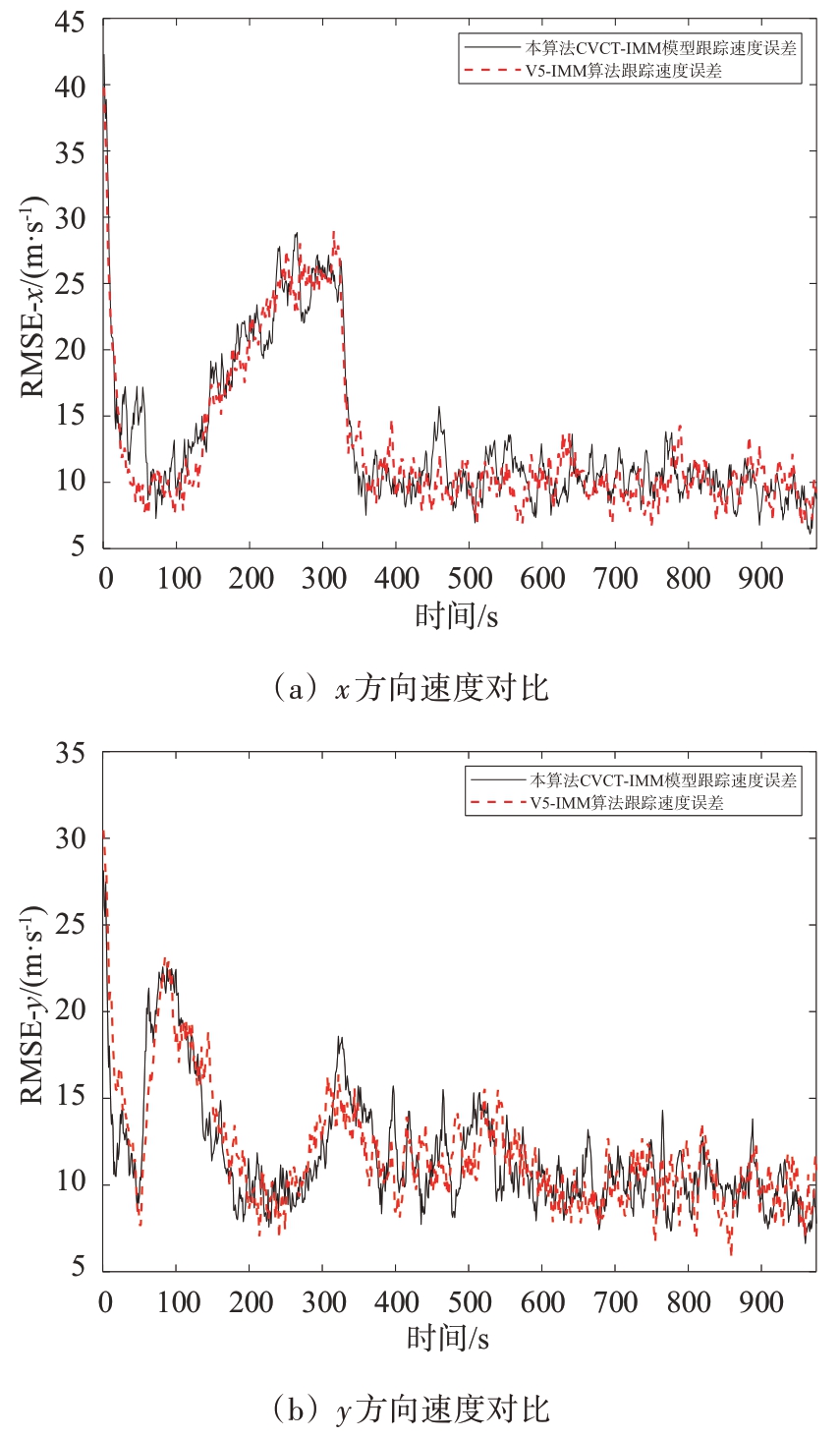
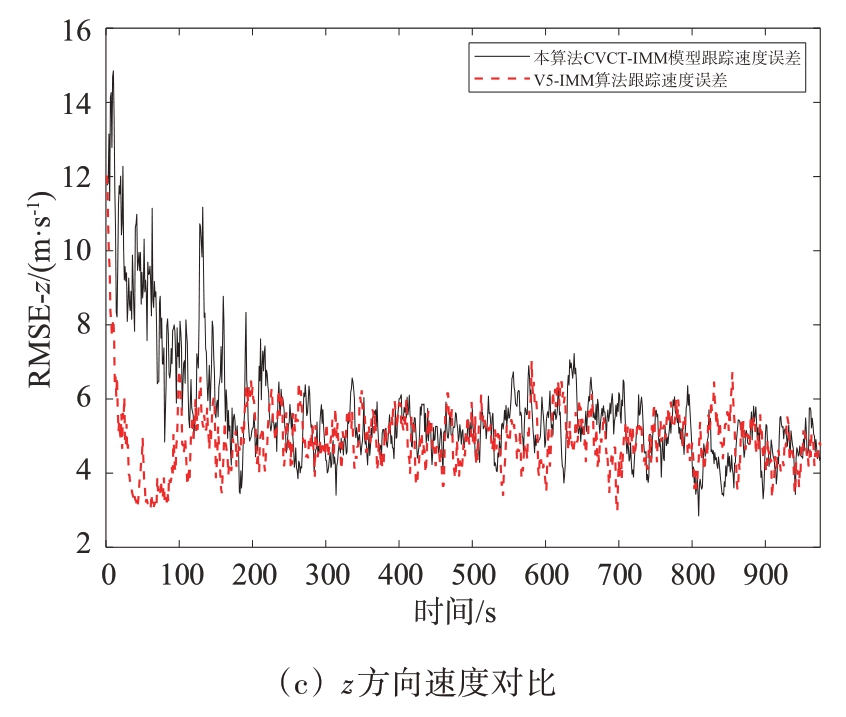
图10 CVCT-IMM模型与转弯率设定在真实值的模型跟踪结果对比
由图10的仿真结果可以看出,V5-IMM 算法的跟踪结果略优于CVCT-IMM 模型算法,说明模型数量增多后,多模型竞争会对跟踪性能产生影响,但从仿真性能对比来看,模型竞争对于最终跟踪结果的准确性作用效果并不显著,影响程度并不明显。
5.5 利用飞行模拟数据测试
为了进一步验证算法的实际效应,采集如图11所示的一段高机动飞行模拟数据,其飞行轨迹由较为逼真的飞行动力学模型生成。将仿真雷达的位置设置在轨迹附近的一固定点,按照三坐标雷达探测的几何关系计算生成无偏差的准确量测。在此基础上,附加随机量测误差,得到雷达的仿真量测。
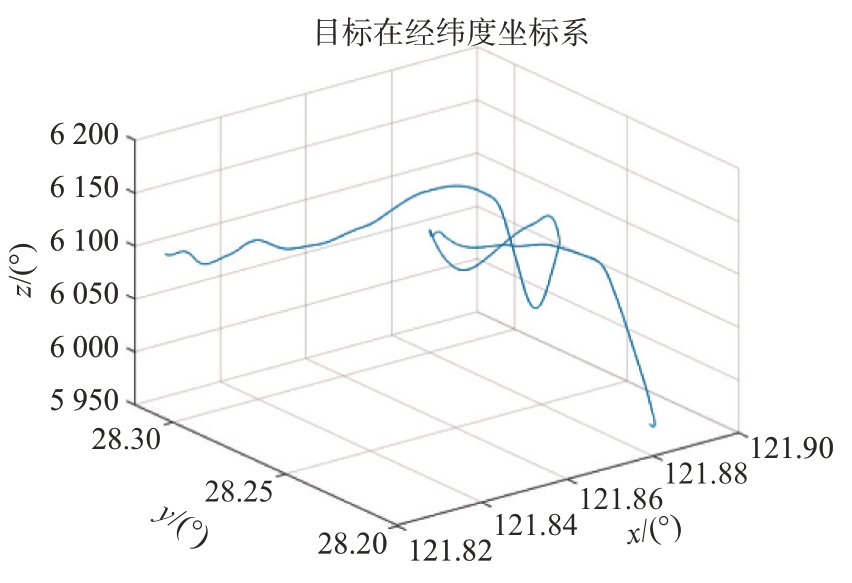
图11 三维高机动目标轨迹
将本文提出的CVCT-IMM 模型与文献［21］提出的CSCT-IMM 模型算法和3 种自适应单模型跟踪算法进行对比跟踪实验,其RMSE跟踪误差对比结果如图12所示。
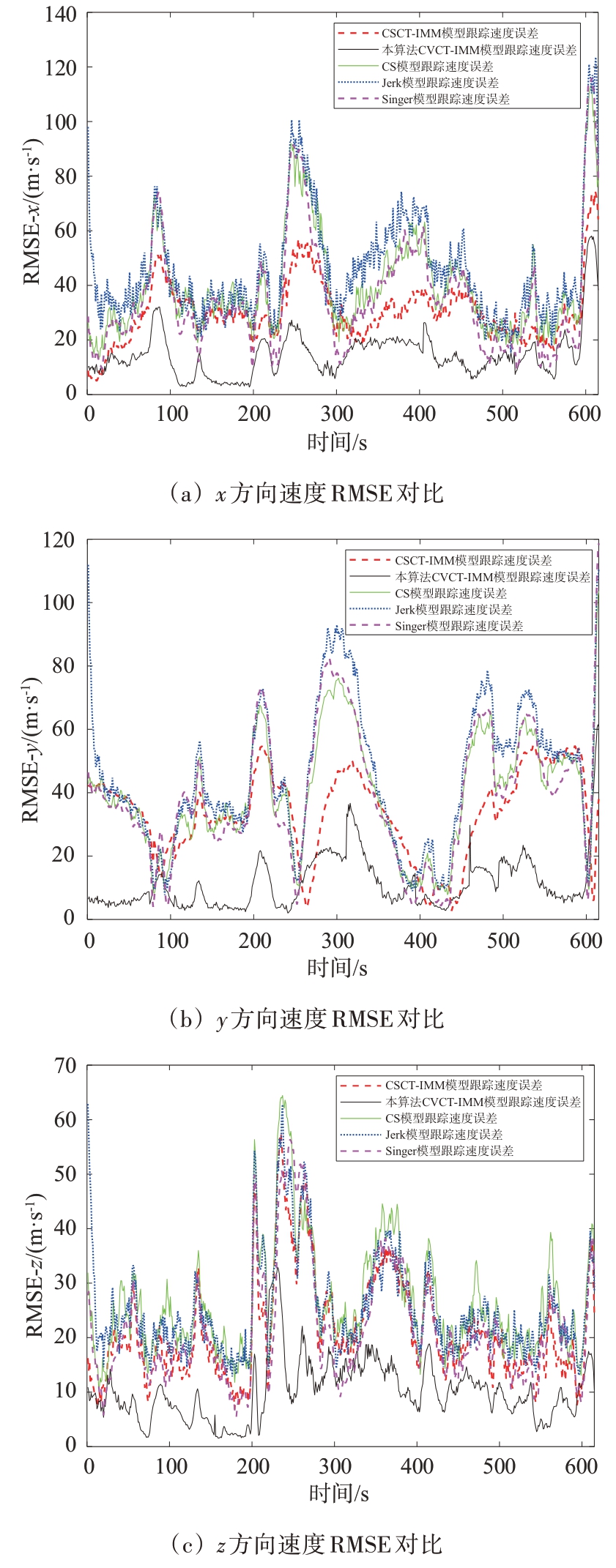
图12 CSCT-IMM模型、自适应单模型跟踪算法与CVCT-IMM模型RMSE跟踪误差对比
由图12可以看出,在跟踪三维空间大机动目标方面,本文模型算法相比于文献［21］中提出的CSCT-IMM 模型算法和3 种自适应单模型跟踪算法,延时更低,跟踪精度更高,处理大机动情况下的目标跟踪能力更强,具有更好的跟踪效果。由图12可以得到,本文跟踪算法的平均跟踪误差更小,可以更有效地跟踪三维强机动目标。因此仿真表明,本文提出的CVCT-IMM 模型算法提高了三维大机动目标的跟踪精度,也减小了跟踪延时,具有很好的跟踪效果和现实意义。
6 结束语
本文提出了一种利用交互式多模型架构、应用3 个平面内的二维耦合运动模型集（CT 模型）来重构三维高机动运动模型的算法。同时,为了更好地适应解耦运动,增加了具有不同过程噪声系数的CV模型集。通过与经典的CSCT-IMM 模型对比仿真分析表明,本算法提高了三维大机动目标的跟踪精度,具有较高的工程使用价值。但该算法仍然没有从本质上实现构建准确的三维高机动运动模型,后续需要进一步深入研究来解决这一技术难题,进一步提升高机动目标跟踪性能。
［1］ 施端阳,林强,胡冰,等.深度学习在雷达目标检测中的应用综述［J］.雷达科学与技术,2022,20（6）:589-605.
［2］ 朱洪峰,熊伟,崔亚奇,等.新的自适应转弯模型的IMM算法研究［J］.计算机工程与应用,2019,55（17）:252-258.
［3］ 张娜,王锐,蔡炯.基于机动检测的参数自适应跟踪算法［J］.信号处理,2022,38（2）:367-374.
［4］ 芮国胜,管旭军.一种机动目标无源定位的新方法［J］.宇航学报,2005（S1）:121-125.
［5］ 陈壮壮,宋骊平.机动目标跟踪的交互多模型泊松多伯努利混合滤波［J］.系统工程与电子技术,2024,46（3）:786-794.
［6］ 兰天,王小虎,张志健.飞行器目标跟踪中的改进自适应滤波算法［J］.航天控制,2022,40（4）:26-32.
［7］ 程婷,何子述,李亚星.一种具有自适应关联门的杂波中机动目标跟踪算法［J］.电子与信息学报,2012,34（4）:865-870.
［8］ 曾浩,母王强,杨顺平.高机动目标跟踪ATPM-IMM 算法［J］.通信学报,2022,43（7）:93-101.
［9］ 陈维义,何凡,刘国强,等.一种自适应变结构交互式多模型算法［J］.火力与指挥控制,2023,48（12）:177-183.
［10］ 李盈萱,王中训,董云龙.两种新的机动目标仿真模型［J］.系统仿真学报,2023,35（7）:1581-1589.
［11］ 鲁其兴,汤新民,周杨.基于双变量自适应“当前”统计模型的场面4D 轨迹跟踪预测［J］.系统工程与电子技术,2024,46（2）:675-683.
［12］ 宁静,陈俊,吴麒.一种基于期望模型的自适应Singer模型滤波算法［J］.电讯技术,2022,62（10）:1464-1469.
［13］ 韩清华,龙伟军,杨振,等.机动目标跟踪时组网机会阵雷达功率分配算法［J］.雷达科学与技术,2023,21（1）:16-23.
［14］ CUI Tao, JING Zhongliang, DONG Peng, et al. Adaptive Distributed Multiple-Model Filter with Uncertainty of Process Model［J］. Signal Processing, 2023, 212:109148.
［15］ 许红,谢文冲,袁华东,等.基于自适应的增广状态-交互式多模型的机动目标跟踪算法［J］.电子与信息学报,2020,42（11）:2749-2755.
［16］ 李俊杰,任博华,王海钢,等.一种结合交互式多模型和自适应UKF 的UWB/INS 紧组合导航算法［J］.电子设计工程,2023,31（8）:32-36.
［17］ 叶瑾,许枫,杨娟,等.一种基于多传感器的复合量测IMM-EKF 数据融合算法［J］.电子学报,2020,48（12）:2326-2330.
［18］ 孔德明,杨丹,王书涛.交互式多模型集自适应协同滤波目标跟踪算法研究［J］.计量学报,2021,42（5）:638-644.
［19］ 张彪,孙超军,徐嘉辉,等.自适应CT 模型的强跟踪CKF算法［J］.舰船电子工程,2024,44（2）:104-108.
［20］ LI X R,JILKOV V P. Survey of Maneuvering Target Tracking. Part I: Dynamic Models［J］.IEEE Trans on Aerospace and Electronic Systems,2003,39（4）:1333-1364.
［21］ 彭冬亮,郭云飞,薛安克.三维高速机动目标跟踪交互式多模型算法［J］.控制理论与应用,2008（5）:831-836.
［22］ 何友,修建娟,刘瑜,等.雷达数据处理及应用［M］.北京:电子工业出版社,2022.