0 引 言
无人机,全称无人驾驶飞行器（Unmanned Aerial Vehicle,UAV）,是指通过无线遥控或自主程序控制,能够执行各种任务的飞行器。无人机的历史可以追溯到20世纪初,由于其自主飞行、遥控操作、载荷多样、隐蔽性强等技术特点,因此最初被用于军事目的,如侦察和靶机［1］。随着人工智能、5G 通信等技术的发展,其自主性和智能化水平也将不断提高。无人机在民用领域也得到广泛应用。无人机作为新时代科技发展的产物,正日益成为推动经济发展、提升社会生产力和维护国家安全的重要力量,因此成为当前研究的热点。但是无人机的滥用也存在许多潜在的问题。比如,无人机的黑飞现象对公共安全、隐私保护、航空安全等方面构成了严重威胁［2-4］。
旋翼无人机因其灵活、易操作的特点,已经成为最受欢迎的无人机类型之一。旋翼无人机通过改变多个电机的转速来控制飞行,具有平动（快速机动、缓慢移动）、悬停等运动姿态。因此,对于旋翼无人机的有效检测和运动参数估计具有重要的意义。目前国内外研究大多集中于对已知目标为无人机时的旋翼特征提取和参数估计,从而缺少对缓慢移动尤其是悬停状态的无人机进行有效的检测手段［5-7］。对于无人机的平动检测可以采用传统的雷达相参积累方法,比如动目标检测（Moving Target Detection,MTD）和动目标指示（Moving Target Indicator,MTI）等［8-10］。但这些传统的积累检测方法仅适用于常规的平动,当无人机悬停时,尽管旋翼在旋转,但旋翼的长度往往小于一个距离分辨单元,因此无法观察到旋翼的运动情况,使得旋翼无人机被视为静止背景,从而使无人机目标无法得到有效的检测。
面对这些问题一些学者通过利用双通道合成孔径雷达（Synthetic Aperture Radar,SAR）的相位中心偏置天线技术（Displaced Phase Center Antenna,DPCA）来对微动目标进行检测［11-12］,文献［13］提出了一种基于频域拉伸处理和Chirp-z变换的相干积分方法检测无人机。文献［14］对无人机等低慢小目标运动时的多普勒和微多普勒信息联合利用,对其进行检测。这些方法对于运动中的无人机有良好的检测性能,但面对悬停无人机时稍显不足。文献［15］提出了一种改进的 Kalmus 滤波算法可以对悬停无人机进行有效检测。但该方法只对一个旋翼进行研究,而其他旋翼回波对检测的影响考虑不足。
本文以旋翼无人机为研究对象,提出一种基于转速补偿的悬停无人机时频域积累检测的算法用以检测悬停的无人机。首先建立旋翼无人机的回波模型,并通过经验模态分解（Empirical Mode Decomposition,EMD）和快速傅里叶变换（Fast Fourier Transform,FFT）相结合的方法估计旋翼转速。随后,利用估计的旋翼无人机旋翼转速,得到转速信息构造补偿函数,将补偿后的旋翼回波信号在时频域进行相参积累,以达到对悬停无人机的检测。该算法能够有效得到悬停无人机的多普勒特征,实现悬停无人机的检测和运动参数估计。
1 旋翼无人机回波信号建模
学者Chen教授建立了旋翼的微多普勒数学模型［16-17］,本文在此基础上构建了旋翼无人机旋翼回波模型,旋翼无人机和雷达的几何关系如图1所示。
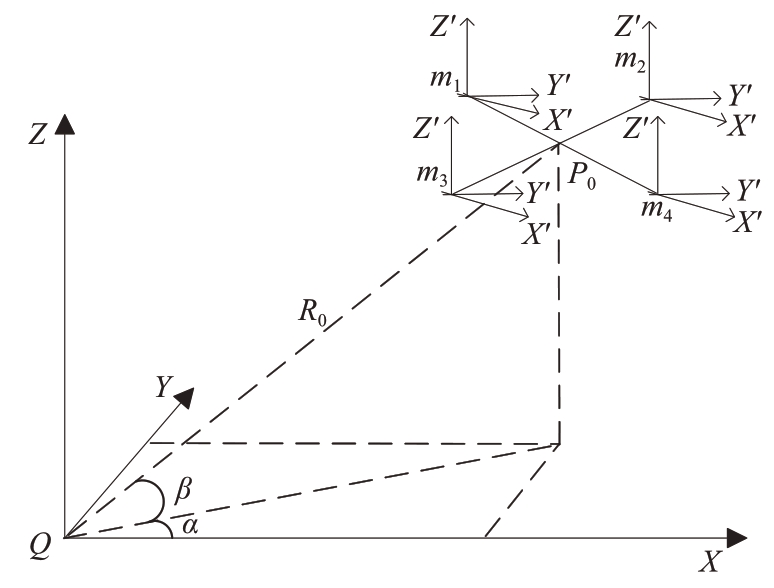
图1 旋翼无人机与雷达的几何关系
雷达为脉冲多普勒雷达,发射线性调频信号（Linear Frequency Modulated,LFM）。雷达位于原点Q（0,0,0）处,雷达坐标系中P0点为目标中心,参考坐标系（X′, Y′, Z′）和雷达坐标系平行。雷达视线方向上目标P0点与雷达距离为R0,则P0点在雷达坐标系中的坐标为(R 0 cos β cos α,R0 cos β sin α,R0 sin β) ,α 为方位角,β 为俯仰角。在此模型中假定无人机具有M 个旋翼,每个旋翼具有N 个叶片。多旋翼无人机回波模型可以表示为每个单旋翼回波的线性叠加:
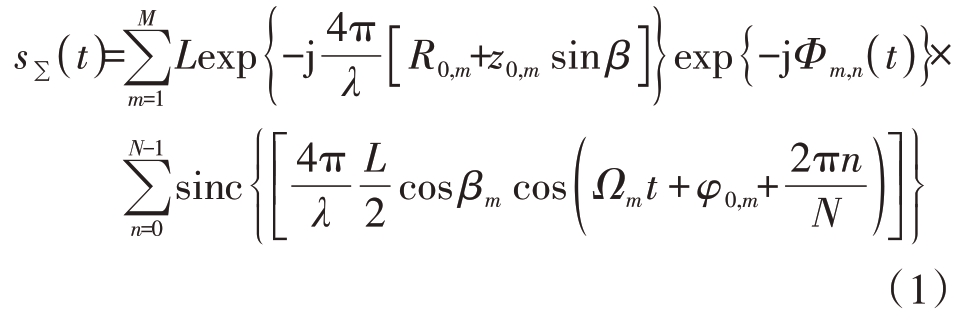
式中,相位函数
为
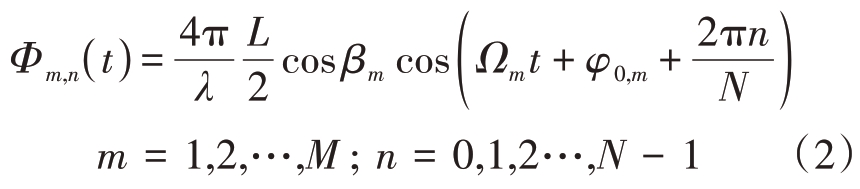
其中,L为无人机旋翼长度,R0,m 为某时刻第m 个旋翼到雷达的距离,z0,m为第m个旋翼的高度,βm为雷达与第m 个旋翼之间的俯仰角,Ωm 为第m 个旋翼的旋转角频率,φ0,m 为第m 个旋翼的某一叶片的初始旋转角,λ为波长。
一般地,对信号的相位函数求时间导数可以得到信号的瞬时频率。因此,对式（2）求时间导数可以得到第m 个旋翼第n 个叶片的瞬时多普勒频率fm,n:
对于一个悬停的旋翼无人机,旋翼到雷达的距离R0,m、高度z0,m与俯仰角βm基本相等:
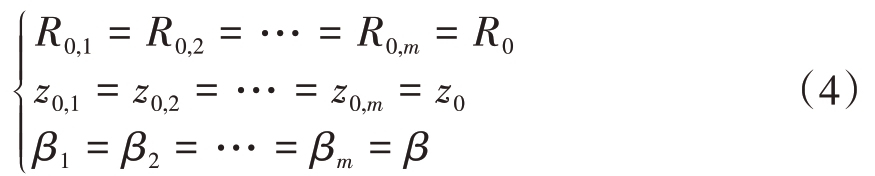
因此,回波信号可以表示为
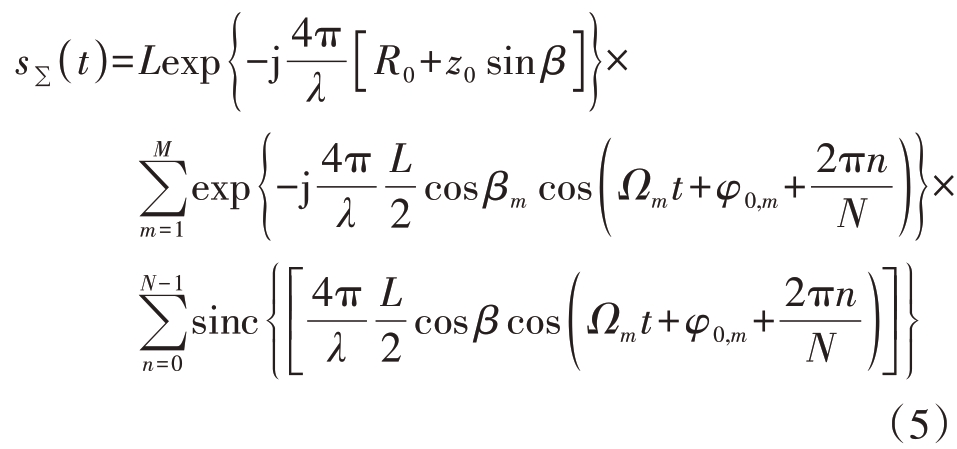
为简化后续计算,令
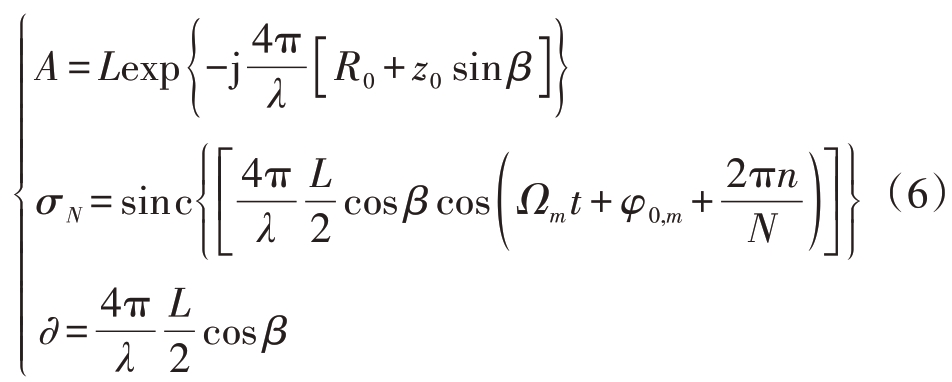
对于一个悬停的无人机,A、∂为常数,σN 对信号的时频分布无影响,也可以看作为一个常数。旋翼回波表达式可以简化为
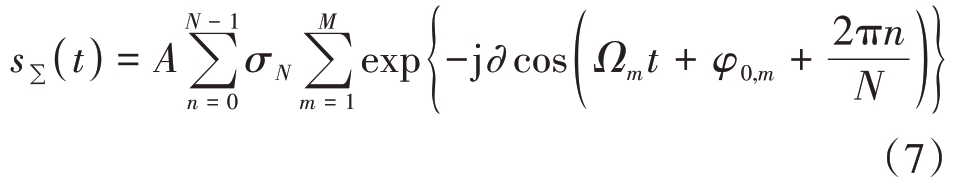
2 基于转速补偿的悬停无人机时频域积累检测算法
2.1 旋翼无人机转速估计
由于旋翼的周期性旋转,所产生的雷达回波是一种相位呈周期变化的正弦调频信号（Sinusoidal Frequency-Modulated,SFM）,这是一种非平稳信号。为提取回波信号中多个旋翼的转速信息,传统的时频分析方法如短时傅里叶变换（Short-Time Fourier Transform, STFT）。STFT 进行转速特征提取非常依赖窗长的选取,若选取的窗大,则时间分辨率下降,从而导致周期的估计出现较大误差；若选取的窗较小,则频率分辨率下降,从而无法得到有效的微多普勒频率信息。如果旋翼转速很大并且多个回波的叠加导致STFT 后得到的时频图也会变得非常密集从而很难提取旋翼的有效信息。为准确地提取旋翼的转速信息,本文EMD和FFT相结合的方法估计旋翼转速。
EMD 是由学者黄锷（Huang N E）于1998 年提出的一种新型的信号分析方法。因为一个信号由高频、中频和低频等许多频率信号组成,频谱分解是将信号分解成不同频率的成分。而频率的实质的信号波形的振荡剧烈程度,振荡通过信号的极值点信息来反映。所以EMD的思想是利用信号极值点信息,将信号分解为若干本征模态函数（Intrinsic Mode Function,IMF）［18-20］。
本征模态函数需要满足以下2个条件:
1） 极值点与零点的数目相差不超过1；
2） 上下包络函数的均值为0。
所以EMD的分解公式可以表示为
式中,u( t )为原始信号,Imfn(t)为分解的本征模态函数,rn( t )为分解后剩余的单调残差。这个方法的关键是寻找IMF。其方法为:
1） 找到原始信号u( t )全部的极值点,通过三次样条插值得到信号的上包络emax( t )和下包络emin( t)；
2） 求出上包络和下包络的平均值
3） 再将原始信号u( t )减去均值包络平均值得到中间信号h( t ):
4） 判断中间信号h( t )是否满足IMF 的两个条件,若满足,该信号就是IMF 分量,若不是,就以该信号为基础重复步骤1）到步骤4）,直至找到全部IMF分量；
5） 将原始信号减去全部的IMF 分量得到单调残差rn( t )。
多个旋翼的回波信号虽然会有叠加而改变回波信号的幅度大小,但每个信号中所携带的转速信息是固定的。EMD 方法应用到多旋翼的研究,将旋翼回波信号进行EMD 分解为若干个IMF 分量,这些IMF 分量中也会携带旋翼的转速信息,且这些IMF 分量相比于原始信号更为简洁。对这些IMF 分量分别作FFT,可以估算旋翼的转速Ωm 和旋翼频谱带宽2fd(max)。
2.2 转速补偿函数
在雷达系统中,回波信号处理的一个必要操作是对接收到的所有信号能量进行积累来提高信杂噪比（Signal-to-Clutter-plus-Noise Ratio,SCNR）,相干（相参）在雷达技术中主要指雷达信号之间的相位关系。对于一个悬停的无人机,其主体是静止的,没有速度变化,从而雷达回波不会产生多普勒效应,进而导致雷达几乎很难通过对无人机主体的回波进行积累而检测目标。但是无人机悬停时它的旋翼是一直在运动的,不过由于旋翼的运动幅度非常小,旋翼产生的回波在二维时域平面基本分布在一个距离单元内,无法与常规目标区分开。而且旋翼的周期性旋转,导致回波信号的相位不是相参的,因此采用常规的MTD 方法无法检测出悬停的无人机目标。未解决这一问题,本文提出将旋翼回波信号放在时频域内进行积累检测的方法。无人机的旋翼回波虽然在二维时域内没有很好的分辨率,但其经过STFT 后能更好观察到旋翼回波的微多普勒频率。由式（2）、式（3）可知,旋翼的回波信号是非平稳信号,其微多普勒频率在时频域内呈正弦周期性变化而分布在不同的多普勒单元中,这不利于旋翼回波信号在时频域的积累检测。
如果尝试构建一个补偿函数
φc)],将分布在不同多普勒单元内的频率补偿到同一个多普勒频率单元内,此时就有利于旋翼回波信号在时频域内的积累。 补偿函数
exp[j∂c cos(ω ct + φc )]的构造需要已知∂c、ωc、φc 3个参数,分别为振幅、转速和初始旋转角。
又由旋翼的回波式（6）可知,振幅∂为
旋翼最大多普勒频率fd(max)为
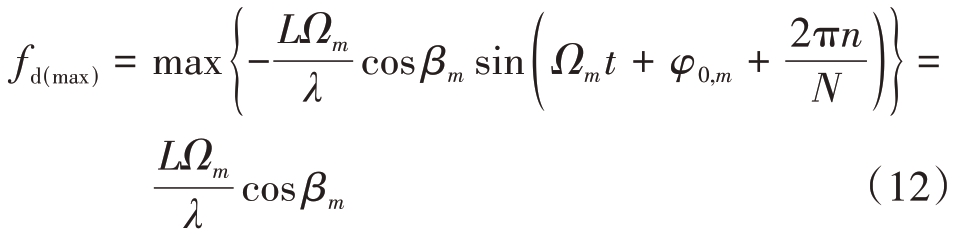
所以,∂c 的值为,即转速Ωm 和俯仰角βm 相等时的构造值与实际值相等:
由2.1 节得到旋翼转速和旋翼频谱带宽,此时只需调整初项就可以构造补偿函数
。补偿函数对4个旋翼的回波同时进行补偿,对其中某个旋翼回波sm( t )的补偿情况有以下3种情况:
情况1,当转速和初项完全补偿,ωc = Ωm、φc =φm:
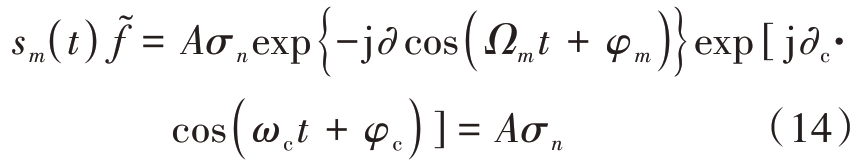
回波信号补偿前如图2（a）所示。经过补偿函数补偿后,此时,回波信号sm( t )相位被完全补偿,在时频域呈一条直线。如图2（b）所示,补偿函数的转速和初项都与仿真的回波信号数据完全相同。
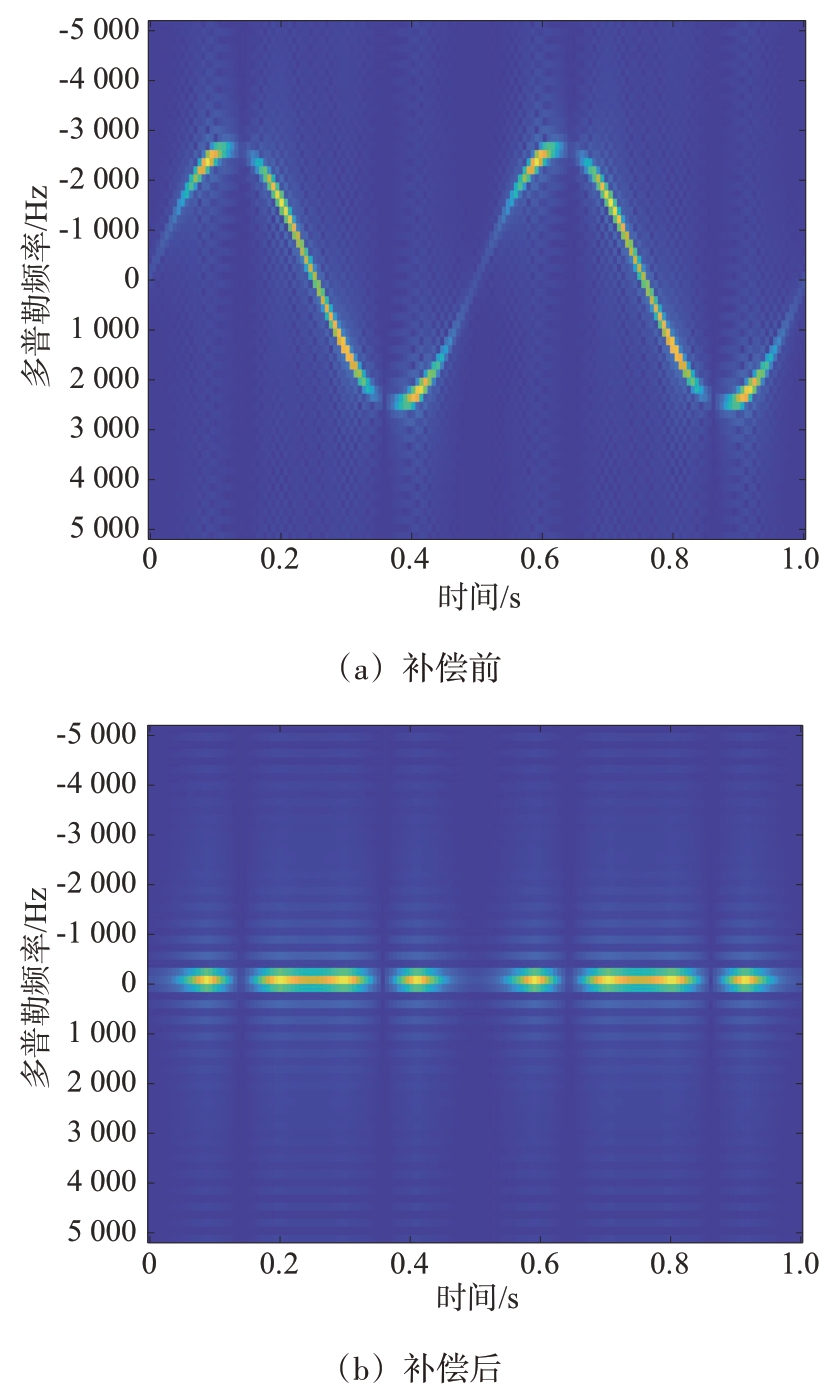
图2 转速与初项完全补偿后的旋翼回波时频分布图
情况2,转速补偿,但初项未完全补偿,
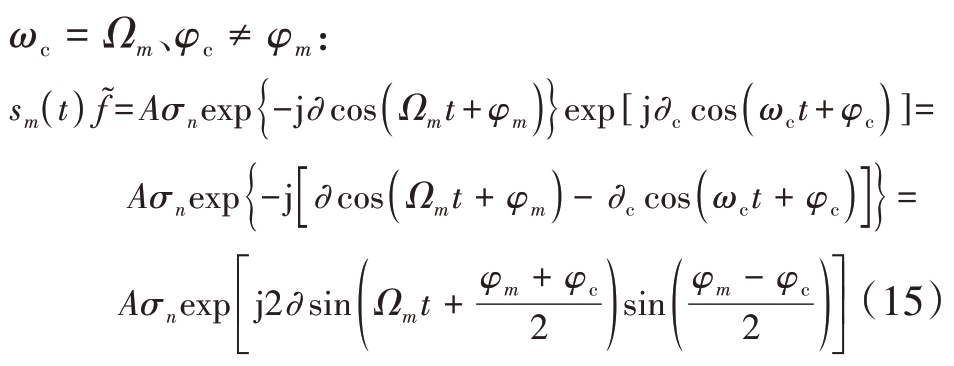
回波信号补偿前如图3（a）所示。经过补偿函数补偿后,此时,原始回波信号sm( t )与补偿后的信号在时频图上出现(φm+φc)/2的相位和sin[ (φm-φc)/2]的幅度变化,幅度sin[ (φm - φc)/2 ]为一个常数。如图3（b）所示,补偿函数的转速与仿真的回波信号数据相同,初项相差
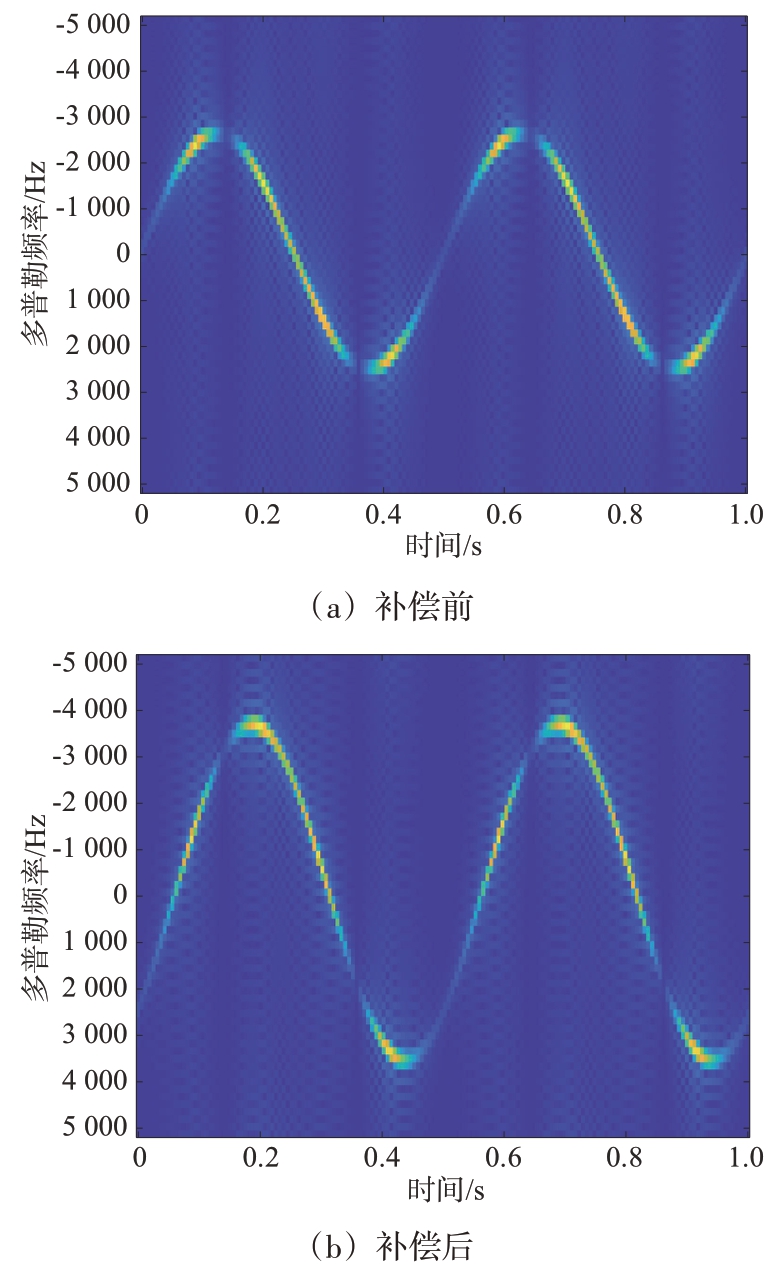
图3 转速补偿但初项未完全补偿的旋翼回波时频分布图
情况3,当转速和初项都未完全补偿,ωc ≠Ωm、φc ≠φm:
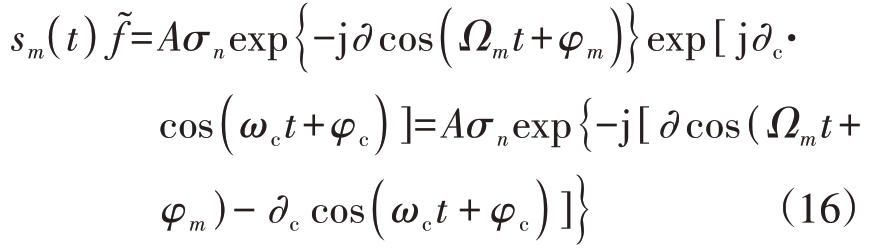
回波信号补偿前如图4（a）所示。经过补偿函数补偿后,此时,原始回波信号sm( t )与补偿函数
相位的振幅、转速、初项都不相同,无法得到有效的补偿。如图4（b）所示,转速与仿真的回波信号数据相差0.5倍,初项相差
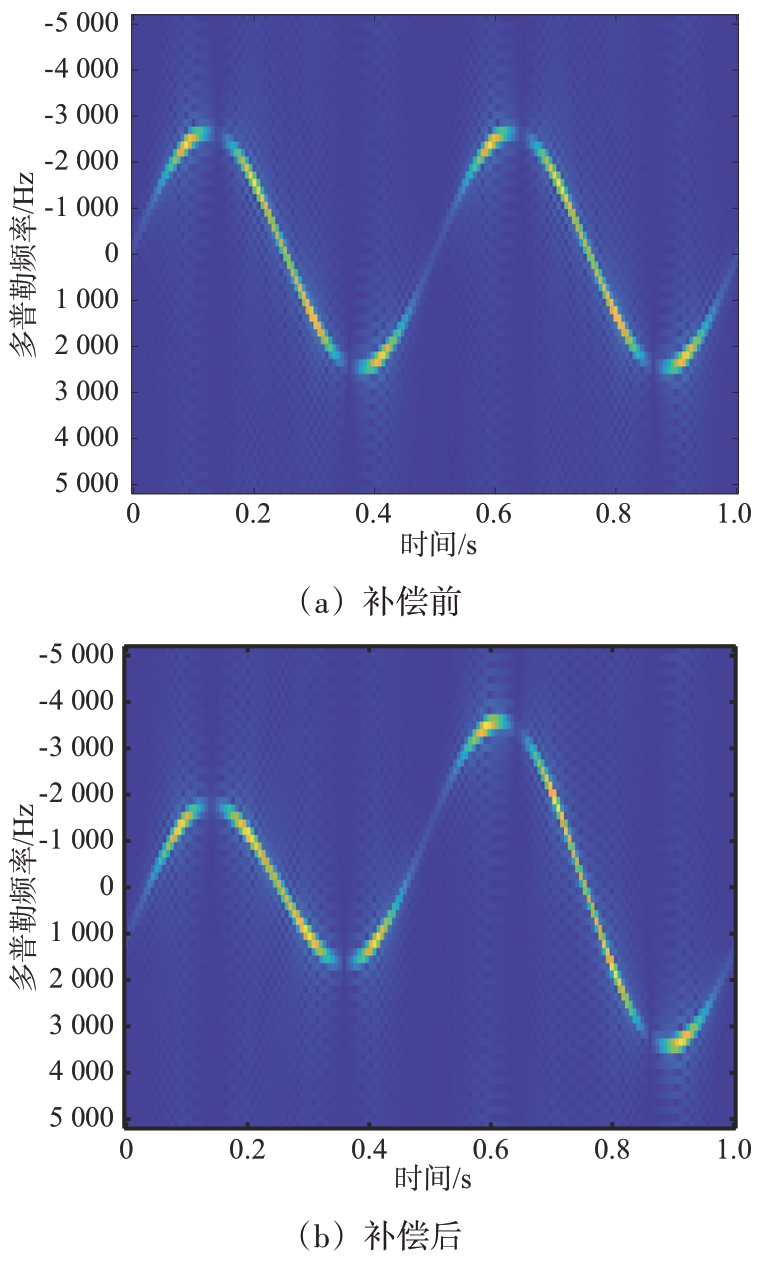
图4 转速和初项都未完全补偿的旋翼回波时频分布图
2.3 时频域积累检测
由2.2 节可知,旋翼回波经过不同情况的补偿后在时频域的分布形式不同。当旋翼回波信号完全补偿后,在时频域内的分布为一个多普勒单元内的直线,此时信号的相位是相参的,通过FFT 可以对信号能量进行有效积累。当旋翼回波信号未完全补偿时,在时频内的分布不在一个多普勒单元内,同一多普勒单元内的信号相位是非相参的,FFT无法对信号能量进行有效积累。
当无人机悬停时,每个旋翼之间转速基本相等,但仍会有些许误差,不同旋翼的回波信号叠加在一起被雷达接收机接收,通过EMD-FFT 算法估计每个旋翼的转速,再根据每个旋翼的转速分别构造对应转速旋翼的补偿函数,之后将补偿后的数据经过STFT 后再相加,最后通过FFT 对信号能量进行积累。流程图如图5所示。
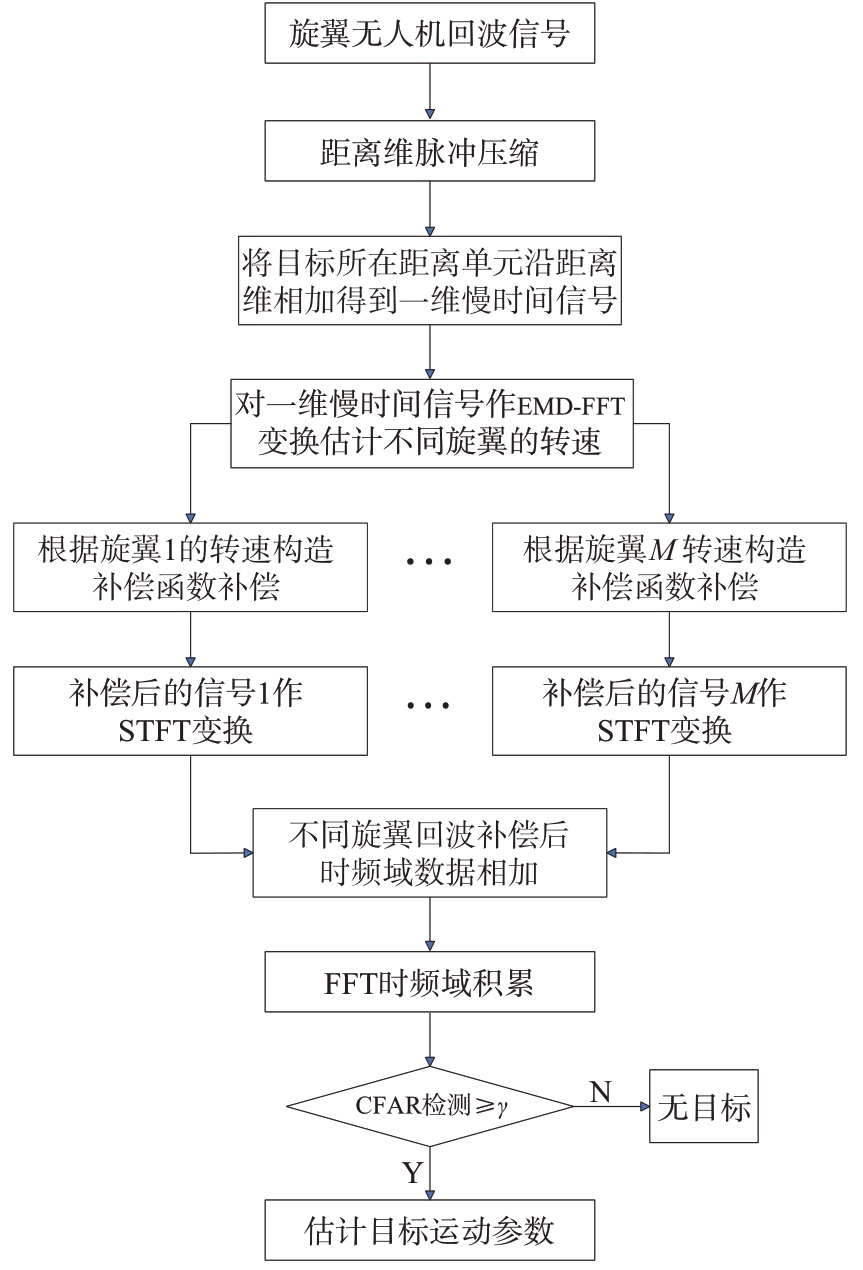
图5 转速补偿积累检测流程图
3 仿真实验
为验证提出的算法,采用了MATLAB 2023 进行实验仿真与分析。对四旋翼无人机进行仿真实验。仿真实验参数设置为:雷达发射线性调频信号,载频为5 GHz,带宽为1 MHz,脉冲重复频率为10 240 Hz,脉宽为2 μs；旋翼个数为4,其中每个旋翼的叶片数为2,旋翼长度为0.06 m,检测时间为1 s。无人机旋翼叶片转速一般为2 000～10 000 r/min,即33～166 r/s。无人机悬停时转速大概在80 r/s 左右。因此无人机旋翼的转速设置为80 r/s。单个旋翼叶片得到STFT时频图如图6所示。
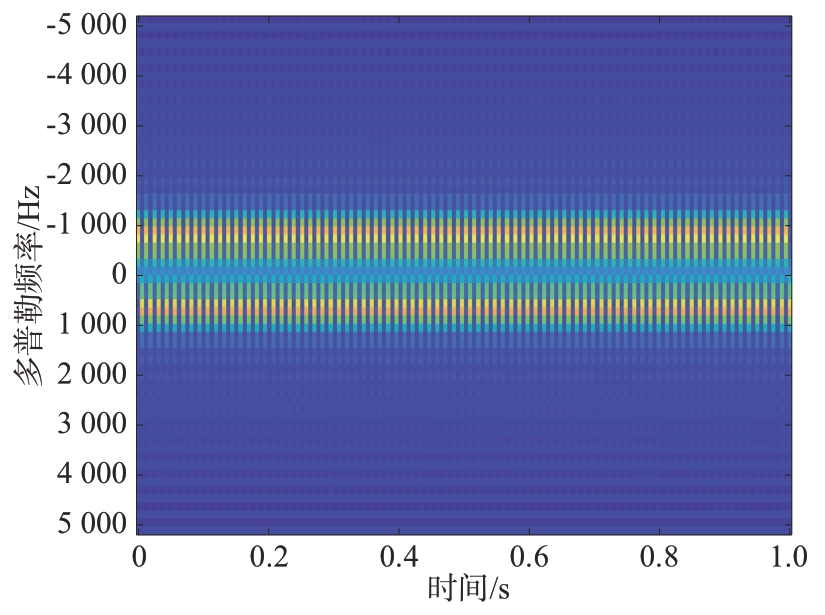
图6 单个旋翼叶片旋翼的时频分布图
3.1 转速估计仿真实验
由图6可以发现当旋翼转速较大时,旋翼的瞬时微多普勒频率分布非常密集,对于旋翼转速的估计存在一定困难。因此,本文提出EMD-FFT 方法估计旋翼转速。当旋翼转速为80 r/s 时的微多普勒信号模型进行EMD 得到前3 个IMF 分量,仿真结果如图7所示。
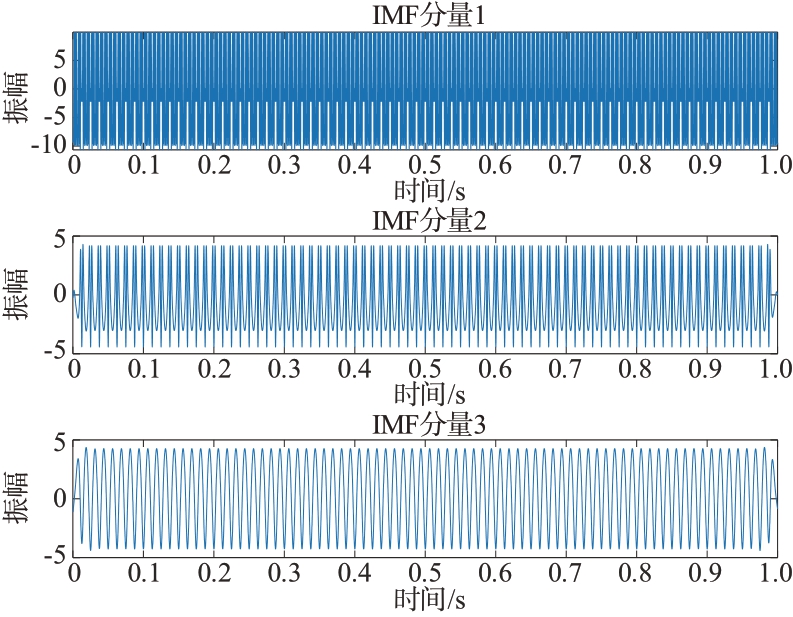
图7 转速为80 r/s时EMD分解
通过EMD 分解的IMF 包含旋翼的转速信息,IMF1、IMF2 和IMF3 经过FFT 后得到IMF-FFT 频谱图如图8所示。原始信号每经过一次EMD 分解得到的IMF 分量经过FFT 后得到的频谱图中谱峰都包含旋翼的转速信息。如IMF1-FFT 中,第1 个频谱对应频率为80×1=80 Hz,第2个频谱对应频率为80×2=160 Hz,第4个频谱对应频率为80×4=320 Hz,第10个频谱对应频率为80×10=800 Hz,以此类推,根据频谱对应频率大小可以估计旋翼转速。设置的转速80 r/s为它们的一个最大公因数。
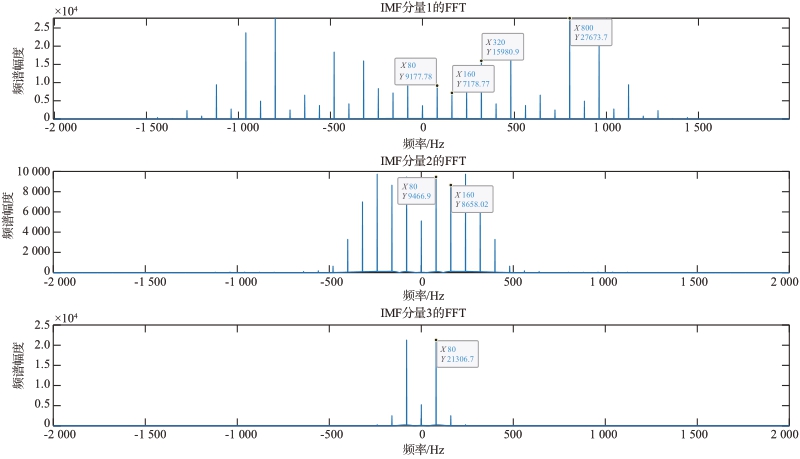
图8 转速为80 r/s时EMD-FFT
当无人机处于悬停状态时各个旋翼之间的转速由于电机、环境等因素影响,会导致每个旋翼转速不可能处于完全相同的理想状态。各个旋翼之间转速不同才是常态。若4 个旋翼转速分别为79.5、80、80.5 和81 r/s 时,其EMD 分解如图9所示,EMD分解后的FFT结果如图10所示。
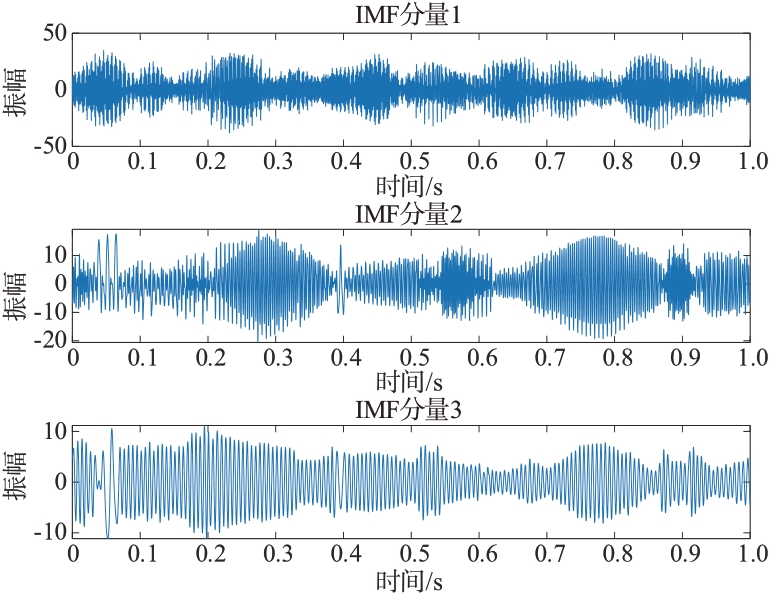
图9 转速不同时EMD分解
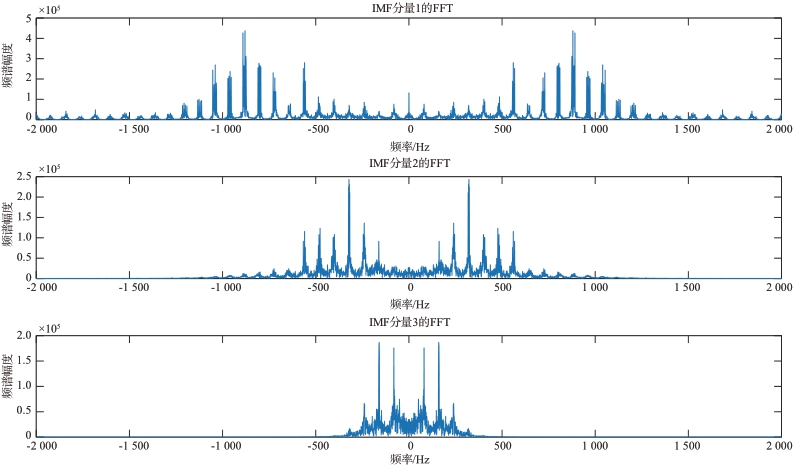
图10 转速不同时EMD-FFT
分析IMF1-FFT 中的数据如图11所示,4 个旋翼转速接近时,会形成一个多普勒频率聚集区分布在频域中,每个多普勒频率聚集区中的谱峰与实际转速都相差一个固定常数,即实际转速为谱峰的一个公因数。例如第11个集合束,79.5×11=874.5≈875 Hz、 80×11=880 Hz、 80.5×11=885.5≈886 Hz、 81×11=891 Hz；第13 个 集 合 束,79.5×13=1 033.5≈1034 Hz、 80×13=1 040 Hz、 80.5×13=1 046.5≈1 046 Hz、 81×13=1 053 Hz。
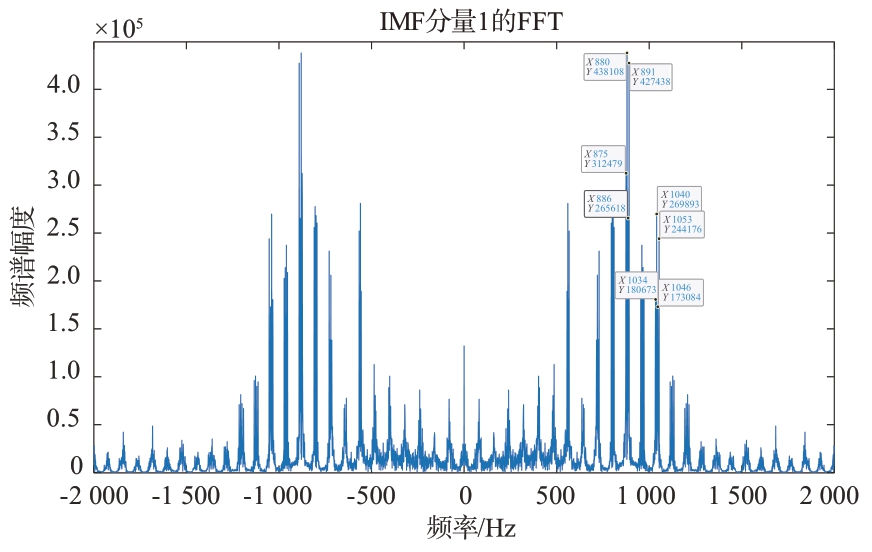
图11 IMF分量1的FFT
通过上述仿真实验分析,EMD-FFT 可以有效地估计旋翼转速,并且旋翼旋转接近时仍有良好的分辨率。
3.2 转速补偿仿真实验
根据EMD-FFT算法估计出旋翼转速之后就可以构造对应转速旋翼的补偿函数。又由2.2 节可知,对于转速对应的补偿函数可以将旋翼的频谱补偿到一个多普勒单元内,当转速不对应时则不能补偿到一个多普勒单元内。
当无人机的4 个旋翼回波信号叠加后的时频图如图12所示。
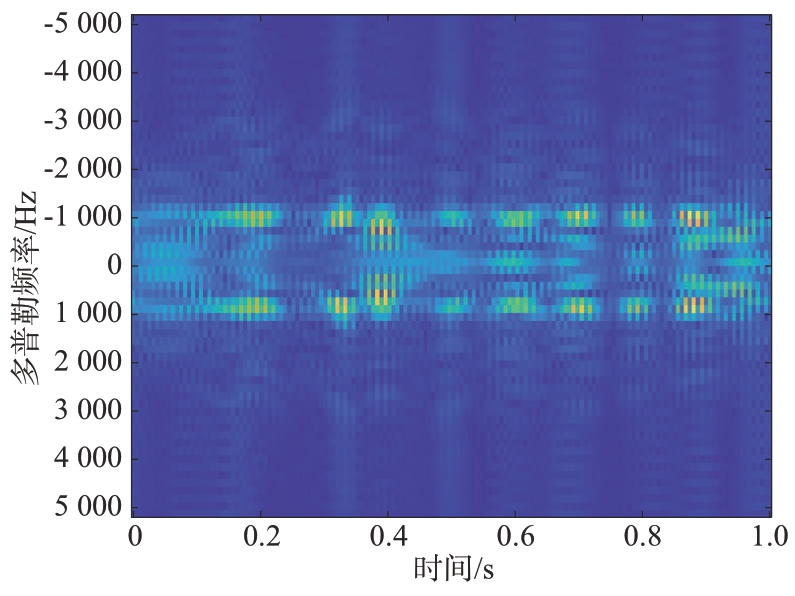
图12 4个旋翼回波信号叠加后的时频分布图
各个旋翼回波对应补偿后的结果如图13所示,不同转速与对应的补偿函数补偿后频谱能量集中在0 Hz多普勒频率。
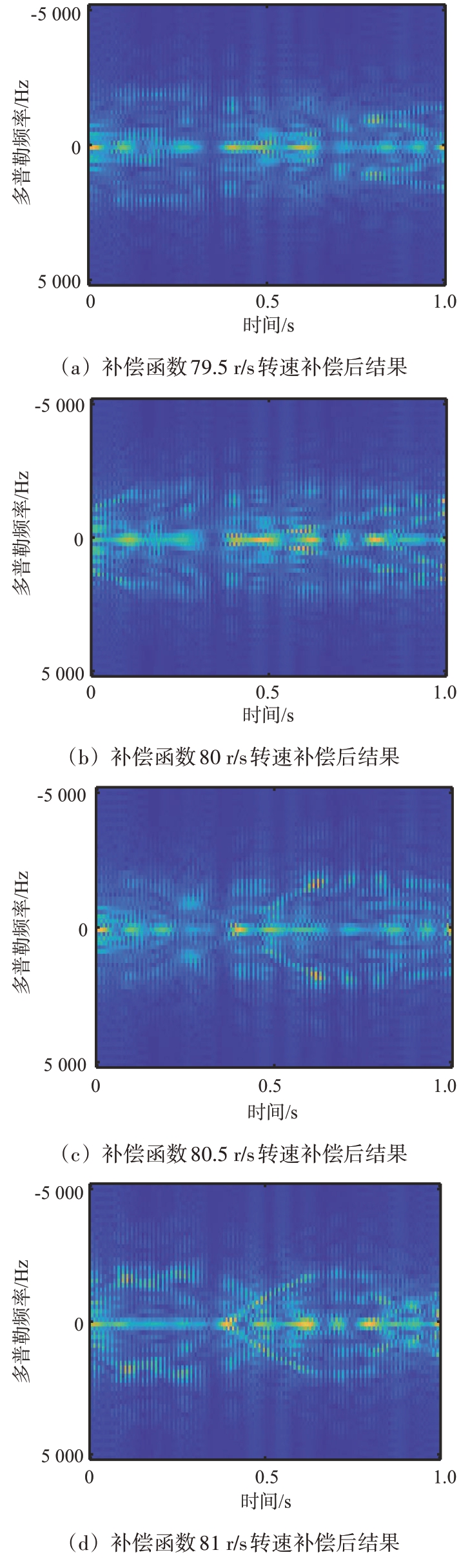
图13 不同转速对应补偿后的时频分布图
3.3 时频域积累仿真实验
将分别补偿后的结果相加,结果如图14所示,不同转速与对应的补偿函数补偿后频谱能量集中在0 Hz 多普勒频率。再将相加后的结果通过FFT进行积累,从图15可以看出,通过此算法积累后的结果形成了一个明显的尖峰,验证了该算法对悬停无人机检测的可行性。对比不同方法的检测概率如图16所示,因为旋翼的回波信号非常弱,在二维时域用常规的MTD 方法进行积累检测受噪声影响非常大,几乎不能检测出悬停的无人机目标；在时频域进行积累可以改善检测性能,并且在经过旋翼转速补偿后检测性能更好,提高了8个信噪比以上。
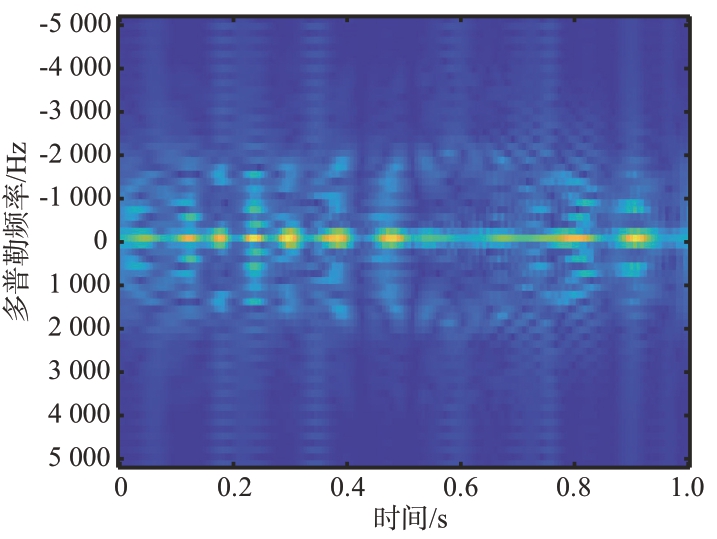
图14 补偿结果叠加后的时频分布图
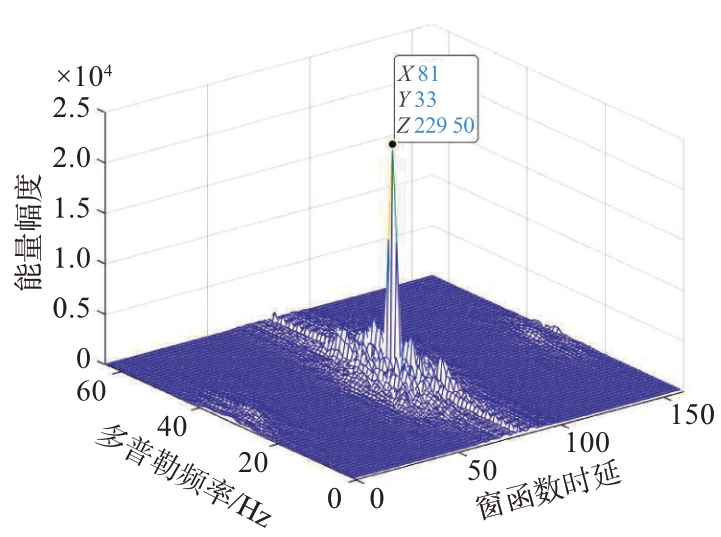
图15 时频域相参积累结果
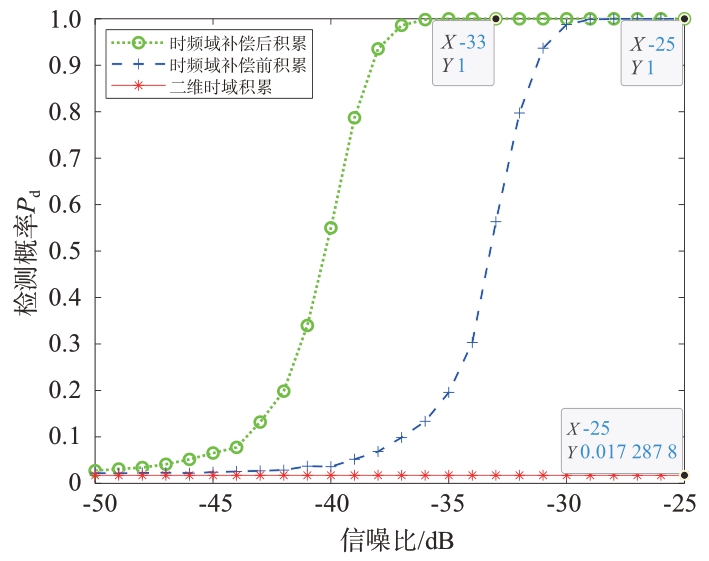
图16 检测概率曲线
3.4 算法的硬件资源需求
表1给出了该算法的构成和相应的计算复杂度,便于为检测算法的硬件资源需求提供参考,以指导工程实现。EMD-FFT 算法的主要操作是计算函数上下包络平均值与原始函数之间的差和FFT计算,因此该部分算法的计算量为O[ 3 × Mt +(M t log2Mt )]；转速补偿算法的主要操作是将构造的补偿函数与原始回波信号进行复数乘法运算,因此该部分算法的计算量为
；补偿信号STFT 算法的主要操作是将补偿信号进行加窗处理,再将加窗处理后的信号作FFT,FFT 的计算次数与窗长有关,STFT 的重复次数与旋翼个数有关,因此该部分算法的计算量为O[ M(Mt/Wd)2 log2(Mt/Wd) ]；信号补偿后积累算法的主要操作是将补偿后的各个信号相加再进行FFT 计算,需要注意的是,FFT 计算是在时频域进行,所以FFT 的计算次数与窗长有关,因此该部分算法的计算量为O[ MMt +(Mt/Wd)Wd log2Wd ]。其中Mt为算法样本数,M为旋翼个数,Wd为短时傅里叶变换的窗长。
表1 算法构成和相应的计算复杂度
算法构成EMD-FFT转速补偿补偿信号STFT信号补偿后积累计算复杂度O[ ]3 × Mt +（Mt log2Mt）O[ ]M2t O[ ]M(Mt/Wd)2 log2(Mt/Wd)O[ ]MMt +(Mt/Wd)Wd log2Wd
4 结束语
对于一个悬停的无人机常规的方法无法对其进行有效检测,本文通过EMD-FFT 算法估计无人机旋翼各个旋翼的转速,再根据转速信息构造各个旋翼对应的构造函数并对其进行补偿,最后将补偿后的结果叠加再在时频域内进行相参积累。并通过实验仿真验证了该方法的可行性。
因为采样率大于两倍旋翼回波最大多普勒频率时,时频域就不会出现频谱混叠现象,此时在时频域进行积累,都可以得到有效结果。无人机旋翼叶片转速一般为2 000～10 000 r/min,即33～166 r/s,旋翼长度一般不超过20 cm,常用的雷达的工作频率范围为3 MHz～300 GHz,其波长为1 mm～100 m之间。因此,旋翼回波的多普勒频率不超过66.4 kHz,即雷达的最小采样频率为132.8 kHz。在大多数情况下,例如对于一个X 波段雷达,230 m/s的叶尖速度可以产生15 kHz 的多普勒频移,雷达所需的采样频率为30 kHz。理论上这个方法只要雷达的采样频率足够高,就适用于任何转速的旋翼无人机的检测和运动参数估计。
［1］ 龚静,冯笛恩,夏林.微型无人机发展现状及未来趋势［J］.飞行力学,2023,41（5）:12-22.
［2］ 智祥.民用无人机领域风险及飞行安全法律规制探析［J］.法制博览,2024（8）:139-141.
［3］ VINAY C, PAVAN K, AAYUSH A, et al. A Comprehensive Review of Unmanned Aerial Vehicle Attacks and Neutralization Techniques［J］. Ad Hoc Networks, 2021,111:102324.
［4］ 邴政,周良将,董书航,等.一种基于微多普勒和机器学习的无人机目标分类识别技术［J/OL］.雷达科学与技术,2024,22（5）:549-556［2024-09-10］.http://kns.cnki.net/kcms/detail/34.1264.tn.20240623.1119.002.html.
［5］ 王磊,苏倩,韦高,等.基于同步提取变换和脊线检测的空间锥体目标微多普勒特征提取方法［J/OL］.系统工程与电子技术,2024（1）: 1-8［2024-09-10］.http://kns.cnki.net/kcms/detail/11.2422.TN.20240108.1709.004.html.
［6］ 马娇,董勇伟,李原,等.多旋翼无人机微多普勒特性分析与特征提取［J］.中国科学院大学学报,2019,36（2）:235-243.
［7］ YANG Jiachen, ZHANG Zhuo, MAO Wei, et al. Identification and Micro-Motion Parameter Estimation of Non-Cooperative UAV Targets［J］. Physical Communication, 2021,46:101314.
［8］ ENDER J, KLEMM R. Airborne MTI via Digital Filtering［J］. IEE Proceedings F （Radar and Signal Processing）,1989（1）:22-28.
［9］ 贺坤,罗丰,王炜,等.MTD 雷达中滤波器组的设计和实现［J］.火控雷达技术,2006,35（3）:57-59.
［10］ 方鑫.小型无人机目标雷达探测关键技术研究［D］.成都:电子科技大学,2019.
［11］ 周阳.双通道SAR微动目标检测与参数估计关键技术研究［D］.长沙:国防科技大学,2020.
［12］ 陈颍滨.双通道SAR 振动目标检测与成像方法研究［D］.长沙:国防科技大学,2011.
［13］ ZUO Luo, WANG Jun, WANG Jipeng, et al. UAV Detection via Long-Time Coherent Integration for Passive Bistatic Radar［J］. Digital Signal Processing, 2021, 112:102997.
［14］ 范世琦,涂刚毅,申鑫.基于改进Kalmus 滤波的悬停无人机检测技术［J］.电子测量技术,2023,46（16）:32-37.
［15］ 宋志勇,许云涛.基于多普勒与微多普勒联合利用的弱小目标检测与估计方法［J］.电子与信息学报,2023,45（11）:4083-4091.
［16］ CHEN V C,LI F,HO S S,et al. Micro-Doppler Effect in Radar: Phenomenon,Model and Simulation Study［J］.IEEE Trans on Aerospace and Electronic Systems,2006,42（1）:2-21.
［17］ 维克托C·陈.雷达微多普勒信号特征的原理与应用（英文）［J］.雷达科学与技术,2012,10（3）:231-240.
［18］ HUANG N E, SHEN Zheng, LONG S R, et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis［J］. Proceedings of the Royal Society A, 1998, 454:903-995.
［19］ 王婷.EMD算法研究及其在信号去噪中的应用［D］.哈尔滨:哈尔滨工程大学,2010.
［20］ CHUI C K, HE Wenjie. Spline Manipulations for Empirical Mode Decomposition （EMD） on Bounded Intervals and Beyond［J］. Applied and Computational Harmonic Analysis,2024, 69:101621.